Voltage-sensor movements describe slow inactivation of voltage-gated sodium channels II: A periodic paralysis mutation in Na_V1.4 (L689I)

Abstract

In skeletal muscle, slow inactivation (SI) of Na_V1.4 voltage-gated sodium channels prevents spontaneous depolarization and fatigue. Inherited mutations in Na_V1.4 that impair SI disrupt activity-induced regulation of channel availability and predispose patients to hyperkalemic periodic paralysis. In our companion paper in this issue (Silva and Goldstein. 2013. J. Gen. Physiol. http://dx.doi.org/10.1085/jgp.201210909), the four voltage sensors in Na_V1.4 responsible for activation of channels over microseconds are shown to slowly immobilize over 1–160 s as SI develops and to regain mobility on recovery from SI. Individual sensor movements assessed via attached fluorescent probes are nonidentical in their voltage dependence, time course, and magnitude: DI and DII track SI onset, and DIII appears to reflect SI recovery. A causal link was inferred by tetrodotoxin (TTX) suppression of both SI onset and immobilization of DI and DII sensors. Here, the association of slow sensor immobilization and SI is verified by study of Na_V1.4 channels with a hyperkalemic periodic paralysis mutation; L689I produces complex changes in SI, and these are found to manifest directly in altered sensor movements. L689I removes a component of SI with an intermediate time constant (∼10 s); the mutation also impedes immobilization of the DI and DII sensors over the same time domain in support of direct mechanistic linkage. A model that recapitulates SI attributes responsibility for intermediate SI to DI and DII (10 s) and a slow component to DIII (100 s), which accounts for residual SI, not impeded by L689I or TTX.

INTRODUCTION

Slow inactivation (SI) of voltage-gated sodium (Na_V) channels in response to repetitive or prolonged depolarization has a significant role in normal physiology and pathophysiology through the regulation of channel availability in the nervous system (Toib et al., 1998), heart (Shaw and Rudy, 1997), and skeletal muscle (Bendahhou et al., 2002). Thus, inherited mutations that impair SI are known to predispose to hyperkalemic periodic paralysis: muscle weakness in response to elevated serum potassium that causes myocyte membrane potential depolarization and Na_V1.4 channel inactivation (Cummins et al., 1993; Hayward et al., 1997; Bendahhou et al., 2002; Webb and Cannon, 2008). Here, we study L689I in Na_V1.4, a hyperkalemic periodic paralysis–associated point mutation in the DII S4–S5 linker (Fig. 1 A) that has complex effects on SI (Bendahhou et al., 2002), to elucidate the mechanistic basis for SI.

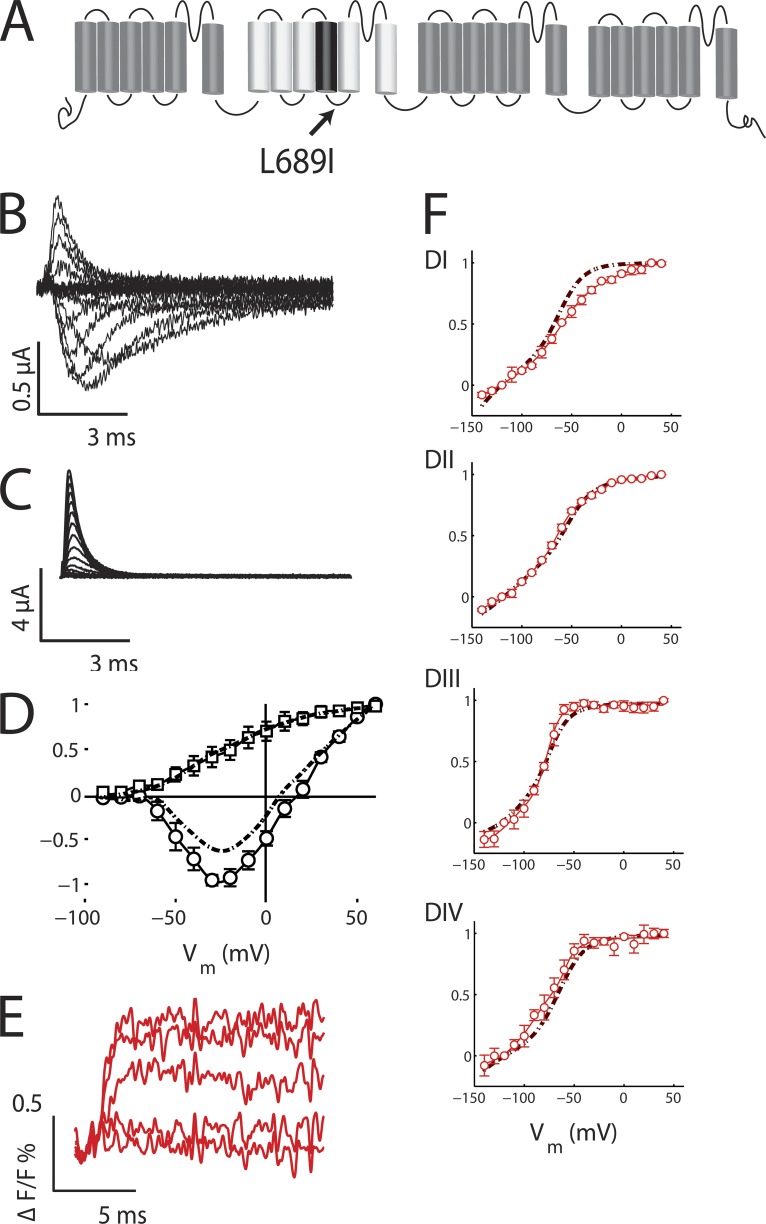
Figure 1.

The L689I mutation does not significantly affect fast gating transitions. Ionic and gating currents of Na_V1.4 channels bearing the L689I mutation are studied as described in our companion paper (Silva and Goldstein, 2013). Changes in the fluorescence magnitude (ΔF/F) of tetramethylrhodamine maleimide conjugated to each domain (via DI-S216C, DII-S660C, DIII-L115C, or DIV-S1436C) are recorded during fast voltage-dependent gating transitions to follow induction of SI and recovery. The mean ± SEM for groups of three to six cells is reported. (A) Drawing of the Na_V1.4 channel subunit indicating the location of the L689I change on the DII S4–S5 linker. (B) Sodium currents. Activation and fast inactivation of ionic current are apparent with steps from a holding voltage of −100 mV to test potentials of −90 to +60 mV for 60 ms (10 ms shown) in 10-mV steps with a 10-s interpulse interval. For all recordings of ionic currents, gating currents were subtracted. (C) Gating current recorded as in A, with 2 µM TTX to block ionic current. (D) Current–voltage (circles) and charge–voltage (squares) relationships. Dotted-dashed lines correspond to previously reported data with WT (Silva and Goldstein, 2013). Protocol as in B and C. Conductance was calculated by normalizing the current to the driving force (E_rev = 7.9 mV) and was fit with a Boltzmann of the form $1/(1+e^{\frac{zF}{RT}(V-V_{mid})})$ (V_mid = −19.1 mV and z = 2.4). For the charge–voltage relationship, the fit gave V_mid = −23.3 mV and z = 1.0. (E) Fluorescence. VCF assessment of ΔF/F for DI-S216C L689I channels using steps from a holding potential of −120 to test potentials of −140 to 40 mV in 10-mV steps. Shown are traces from −140 to 20 mV in 40-mV steps. (F) L689I channel F-V relationship for each domain by protocol and data analysis as in D. The fits gave the following: DI: V_mid = −65.1 mV and z = 0.95; DII: V_mid = −70.2 mV and z = 1.1; DIII: V_mid = −83.1 mV and z = 2.3; DIV: V_mid = −79.1 mV and z = 1.5. Dotted-dashed lines correspond to data reported previously with WT (Silva and Goldstein, 2013).

In our companion paper in this issue (Silva and Goldstein), we use voltage-clamp fluorimetry (VCF) to study slow immobilization of the four S4 voltage-sensing segments in Wild-type Na_V1.4 channels (WT) over 1–160 s and show that the four sensors track SI development and recovery in nonidentical fashion. The onset of SI was well reflected by the time course and voltage dependence of immobilization of the voltage sensors in DI and DII, and evidence for direct coupling was provided by tetrodotoxin (TTX) suppression of both SI development and slow immobilization of DI and DII. The kinetics of immobilization and restored mobility of the voltage sensor in DIII implicated it in SI onset and recovery as well. Here, a point mutation is found to perturb sensor movements in a manner that correlates directly with the complicated changes it produces in SI. The findings verify the roles of DI and DII in SI development and support the function of DIII in SI onset and recovery. A model that recapitulates the voltage dependence and kinetics of SI based on movements of the voltage sensors in DI, DII, and DIII in WT and L689I Na_V1.4 channels demonstrates potential sensor roles in the mediation of SI onset and recovery.

MATERIALS AND METHODS

Our companion paper describes cut-open oocyte recording, fluorescence measurements, and modeling methods in detail (Silva and Goldstein, 2013). The L689I mutation was introduced into WT channels and into the four mutant channels used for VCF (DI-S216C, DII-S660C, DIII-L115C, and DIV-S1436C) using standard overlap extension PCR site-directed mutagenesis (Green et al., 2012).

RESULTS

L689I channels: Fast activation gating attributes are maintained

The kinetics and voltage dependence of activation and fast inactivation of L689I channels have been reported to show relatively minor differences when compared with WT channels when studied in human embryonic kidney (HEK) cells (Bendahhou et al., 2002). Our observations are similar, although we express the channels in Xenopus laevis oocytes for these experiments, and oocytes modify the operation of mammalian Na_V channels (Baroudi et al., 2000). For L689I channels, we find that the time constant of fast inactivation is moderately slowed (0.68 ± 0.08 vs. 0.47 ± 0.02 ms for WT), whereas Bendahhou et al. (2002) observe no change. In oocytes, L689I channels show an increase in late current of 10.3 ± 1.5%, whereas WT show 4.5 ± 1.1% (Fig. 1 B), and this change is larger than in HEK cells. The G-V relationship for L689I is similar to WT, showing a 10-mV shift to depolarized potentials (V_mid = −19.1 vs. −29.1 mV for WT), whereas HEK cells showed a small shift with the opposite polarity. Here, we additionally assess gating charge, as determined from the integral of the gating current (Fig. 1 C), and find that it is quite similar for L689I and WT channels (V_mid = −23.1 vs. −27.5 mV for WT) (Fig. 1 D).

As expected, based on only small change in fast gating with the L689I mutation, the four channels carrying L689I and a second point mutation to allow fluorophore attachment on cysteine substituted into one of the voltage-sensor domains (DI-S216C, DII-S660C, DIII-L115C, or DIV-S1436C) all expressed well and produced robust VCF signals, as seen previously with WT channels (Fig. 1 E). The fluorescence–voltage (F-V) relationships of the four L689I channels were almost identical to those with a WT background, except for DI-S216C, which showed a slightly greater fraction of activated channels at potentials above −50 mV when present with L689I (Fig. 1 F).

L689I: SI onset and recovery, ionic and gating currents

As before (Silva and Goldstein, 2013), the development of SI is induced using a triple-pulse protocol repeated 320 times to study 1–160 s (Fig. 2 A). Each cycle includes a 5-ms step to +45 mV to measure peak current (phase a), an SI induction phase of 500 ms at various voltages (phase b), and a third phase (c) at the holding voltage of −100 mV lasting 30 ms, a duration sufficient to allow recovery from fast inactivation, but not SI, before the next pulse. Unlike WT, applying test pulses to probe SI induced significant SI, even when the 500-ms interpulse was at −100 ms (Fig. 2 A, −100-mV trace). Similar to another periodic paralysis mutation in the DII S4–S5 linker (Melamed-Frank and Marom, 1999), L689I channels show global disruption of the relationship between prior activity and availability (Fig. 2 A), slowing the onset of SI, speeding its recovery from SI of short duration, and slowing recovery after an extended pulse.

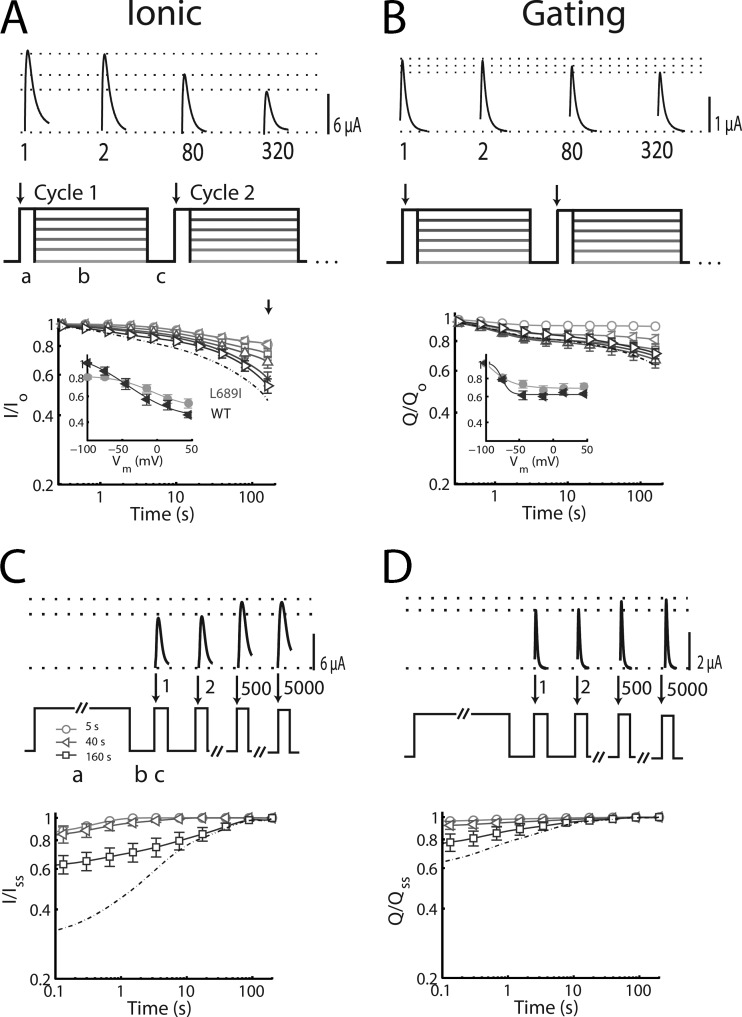
Figure 2.

SI onset and recovery for L689I channels: Ionic and gating currents. SI induction and recovery of ionic and gating currents measured as described in our companion paper (Silva and Goldstein, 2013). Groups of four to seven cells reported as mean ± SEM. (A) SI is probed by 320 repetitions of a triple-pulse protocol from a holding potential of −100 mV: a 5-ms test pulse to +45 mV was used to measure peak current (phase a); SI was induced by a 500-ms pulse at −100, −75, −45, −15, 15, or 45 mV (phase b); and a 30-ms pulse at −100 mV used (phase c) to allow for recovery from fast inactivation before the next test pulse. Above the protocol, sample traces are shown for cycles 1, 2, 80, and 320 and demonstrate progressive decrease in peak current with SI at +45 mV. Dotted-dashed lines correspond to data reported previously with WT (Silva and Goldstein, 2013). Parameters for L689I SI onset are reported in Table 1. Insets compare L689I ionic current (circles) at 160 s to WT (triangles). (B) Loss of gating current with SI induced as in A. (Top) Sample traces from cycles 1, 2, 80, and 320 show progressive reduction in peak gating current with SI at +45 mV. (Bottom) Plot of the gating charge (Q, the integral of the gating current) with time at different potentials. Insets compare L689I gating current at 160 s to WT. (C) Sodium current. (Top) Recovery from SI is probed after induction pulses to +45 mV for 5, 40, or 160 s (phase a) during 5,000 cycles of 20 ms at −100 mV (phase b), followed by 4 ms at +45 mV when peak current is recorded (phase c). Sample traces from cycles 1, 2, 500, and 5,000 show the recovery of peak current. (Bottom) Voltage and cycle dependence of recovery from SI on log–log plots of peak current. Parameters for recovery from SI are shown in Table 2. Dotted-dashed lines correspond to data reported previously with WT (Silva and Goldstein, 2013). (D) Gating current. Recovery from SI is probed as in A, with 2 µM TTX.

As for WT channels (Silva and Goldstein, 2013), the kinetics of SI onset for L689I channels are well-described by three exponentials: setting the seed values to the WT parameters, τ_Fast = 1.3 ± 0.1 s, τ_Intermediate = 12.2 ± 1.4 s, and τ_Slow = 202 ± 25 s, with amplitudes of 0.10 ± 0.02, 0.06 ± 0.02, and 0.55 ± 0.05, respectively, and a constant remainder of 0.29 ± 0.06, which is quite similar to the time constants that were used to fit WT (τ_Fast = 1.8 ± 0.2 s, τ_Intermediate = 13.1 ± 1.1 s, and τ_Slow = 195 ± 33 s). As with WT, τ_Slow reflects SI over time scales beyond those well studied with 320 cycles and must be considered to be suggestive. To compare with WT, we fixed the time constants to be identical, allowing only the magnitudes to vary. Only the intermediate component (∼10-s time domain) of SI is significantly different in L689I channels (0.06 ± 0.02 vs. 0.11 ± 0.01 for WT; Table 1).

Table 1.

Fractional magnitudes of time constants for L689I ionic current, gating current, and fluorescence during the onset of SI

Channel variant (measured parameter)	AF	AI	AS	C	n
L689I (I)	0.10 ± 0.01	0.06 ± 0.02a	0.54 ± 0.04	0.30 ± 0.05	7
L689I (Q) (2 µM TTX)	0.11 ± 0.04	0.05 ± 0.02	0.20 ± 0.05	0.63 ± 0.04	5
L689I DI (F)	0.15 ± 0.02a	0.12 ± 0.05	0.29 ± 0.06	0.45 ± 0.03a	7
L689I DII (F)	0.12 ± 0.05	0.06 ± 0.03a	0.21 ± 0.03	0.61 ± 0.05a	4
L689I DIII (F)	0.26 ± 0.07	0.15 ± 0.06	0.31 ± 0.04	0.28 ± 0.09	8
L689I DIV (F)	0.28 ± 0.08	0.04 ± 0.02	0.26 ± 0.13	0.42 ± 0.12	6

First, SI of ionic current at +45 mV was fit using three exponentials with time constants for fast, intermediate, and slow components: τ_F = 1.8 ± 0.2 s, τ_I = 13.1 ± 1.1 s, and τ_S = 195 ± 33 s. Because the three time constants span the time domains of our protocol, they can be held constant and used to describe data from ionic, gating, and fluorescence measurements by varying the fractional magnitude of each component. The table shows the fractional magnitude of each component for all studies in this paper. n, the number of cells studied; I, current assessed after subtraction of Q; F indicates a fit to fluorescence; DI, DII, DIII, and DIV indicate L689I channels that also carry the single site changes DI-S216C, DII-S660C, DIII-L115C, and DIV-S1436C, respectively.

^aParameter is significantly different from WT.

Inhibition of SI over the 10-s time domain by the L689I mutation was similar to application of the pore blocker TTX on WT channels, which at 200 nM also reduced the same intermediate component by 45% (Silva and Goldstein, 2013), suggesting that the two means of perturbing channel operation acted via common sites or overlapping processes. Indeed, gating charge is measured in the presence of TTX and, as would be expected if TTX and L689I shared a common mechanism, gating charge immobilization was not significantly different for L689I and WT channels (Fig. 2 B and Table 1).

To study recovery, SI is induced by pulses to +45 mV that last 5, 40, or 160 s, followed by two steps repeated 5,000 times to study the kinetics of recovery: the first step allows recovery for 20 ms at the holding voltage of −100 mV, and the second step measures peak current at +45 mV (Silva and Goldstein, 2013). With L689I channels, SI recovery is faster than normal after brief periods of induction and slower than WT after prolonged stimulation (Fig. 2, C and D, and Table 2). Thus, L689I channels recover identically after induction pulses of 5- and 40-s induction pulses (Fig. 2 C), whereas WT channels display a progressively lower starting point (Fig. 6 A in our companion paper, Silva and Goldstein, 2013); indeed, the amplitude of τ_Slow after a 40-s pulse is not even required to fit L689I channel recovery, and instead, 70% of recovery can be fit with τ_Fast (Table 2) versus 35% for WT SI recovery (Silva and Goldstein, 2013). This finding is consistent with the onset of SI in L689I channels, which takes place most prominently in the 5- and 100-s time domains, but not in the 40-s domain, so that the fraction of inactivated channels at 40 s is not significantly different than the fraction at 5 s (Fig. 2 A and Table 1). Similarity in the recovery kinetics of the 5- and 40-s pulses is also observed in the gating charge (Fig. 2 D), suggesting that this effect will also be manifest in the fluorescence recordings that report on voltage-sensor immobilization.

Table 2.

Recovery fractional magnitudes of recovery from SI

Channel variant (measured parameter)	Pulse	AF	AI	AS	C	n
	s
L689I (I)	5	0.21 ± 0.06 (1.00)	0.00 ± 0.00 (0.00)	0.00 ± 0.00 (0.00)	0.79 ± 0.06	3
L689I (I)	40	0.16 ± 0.06 (0.70)a	0.07 ± 0.04 (0.30)	0.00 ± 0.00 (0.00)a	0.77 ± 0.09	3
L689I (I)	160	0.07 ± 0.01 (0.21)	0.13 ± 0.05 (0.35)	0.16 ± 0.09 (0.45)	0.64 ± 0.08	3
L689I (Q)	5	0.02 ± 0.01 (0.52)	0.01 ± 0.00 (0.24)	0.01 ± 0.01 (0.24)	0.96 ± 0.01	4
L689I (Q)	40	0.03 ± 0.01 (0.34)	0.03 ± 0.03 (0.35)	0.03 ± 0.02 (0.32)	0.92 ± 0.04	4
L689I (Q)	160	0.11 ± 0.08 (0.43)	0.09 ± 0.06 (0.37)	0.05 ± 0.02 (0.20)	0.76 ± 0.08	4
L689I DI (F)	5	0.15 ± 0.03 (0.84)	0.01 ± 0.01 (0.05)	0.02 ± 0.02 (0.11)	0.81 ± 0.02	3
L689I DI (F)	40	0.18 ± 0.01 (0.80)	0.00 ± 0.00 (0.00)a	0.05 ± 0.03 (0.20)a	0.78 ± 0.03	3
L689I DI (F)	160	0.11 ± 0.29 (0.35)	0.08 ± 0.03 (0.27)	0.12 ± 0.06 (0.38)	0.69 ± 0.05	3
L689I DII (F)	5	0.09 ± 0.01 (0.89)	0.01 ± 0.01 (0.11)	0.00 ± 0.00 (0.00)	0.90 ± 0.02	3
L689I DII (F)	40	0.15 ± 0.07 (0.63)	0.04 ± 0.02 (0.19)	0.04 ± 0.02 (0.18)	0.77 ± 0.03	3
L689I DII (F)	160	0.21 ± 0.09 (0.70)	0.00 ± 0.00 (0.00)	0.09 ± 0.05 (0.31)	0.69 ± 0.05	3
L689I DIII (F)	5	0.38 ± 0.10 (0.82)	0.02 ± 0.02 (0.04)	0.06 ± 0.04 (0.14)	0.54 ± 0.09	4
L689I DIII (F)	40	0.30 ± 0.14 (0.49)	0.13 ± 0.10 (0.21)	0.19 ± 0.05 (0.30)	0.38 ± 0.15	4
L689I DIII (F)	160	0.04 ± 0.04 (0.06)	0.31 ± 0.11 (0.42)	0.39 ± 0.10 (0.53)	0.26 ± 0.06	4
L689I DIV (F)	5	0.12 ± 0.06 (0.57)	0.01 ± 0.01 (0.04)	0.08 ± 0.05 (0.39)	0.79 ± 0.06	5
L689I DIV (F)	40	0.25 ± 0.07 (0.75)a	0.07 ± 0.04 (0.22)a	0.01 ± 0.01 (0.03)	0.67 ± 0.12	5
L689I DIV (F)	160	0.13 ± 0.05 (0.38)	0.04 ± 0.02 (0.12)	0.16 ± 0.08 (0.39)	0.68 ± 0.07	5

Similar to SI onset, recovery from SI can be fit with three time constants: τ_F = 0.6 ± 0.3 s, τ_I = 4.5 ± 1.1 s, and τ_S = 43.1 ± 4.8 s, which were found by fitting the recovery of the WT ionic current after a 160-s depolarizing pulse to +45. The fractional magnitudes below are for pulses to +45 mV lasting 5, 40, and 160 s. I, the ionic current recovery in Fig. 3 A; Q, the gating current recovery in Fig. 3 B; DI, DII, DIII, and DIV, the fluorescence recoveries in Fig. 3 C. Similarly, the L689I magnitudes are for experimental data shown in Fig. 4. The fraction of inactivation corresponding to a given time constant is in parentheses. Channel variant abbreviations as in Table 1.

^aSignificantly different from the WT parameter (P < 0.05).

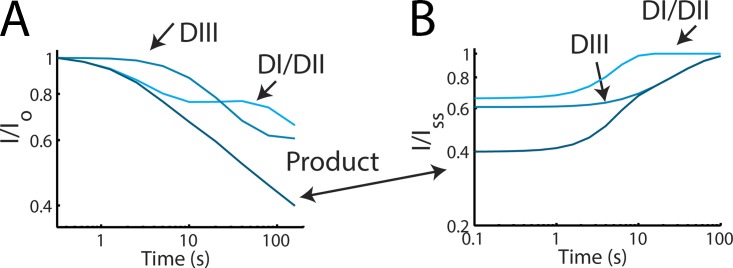
Figure 6.

Proposed participation of DI/DII and DIII components in SI. (A) Simulation of L689I/TTX-sensitive component of DI/DII and the slow components of DIII during SI onset at +45 mV (arrows). Dark trace (Product) is the combination of both components at +45 (also plotted in Fig. 5 F). (B) Simulation of L689I/TTX-sensitive component of DI/DII and the slow components of DIII during SI recovery after a 160-s pulse to +45 mV. Dark trace (Product) is the combination of both components after a 160-s pulse (also plotted in Fig. 5 H).

L689I channels: Voltage-sensor movements with SI onset and recovery

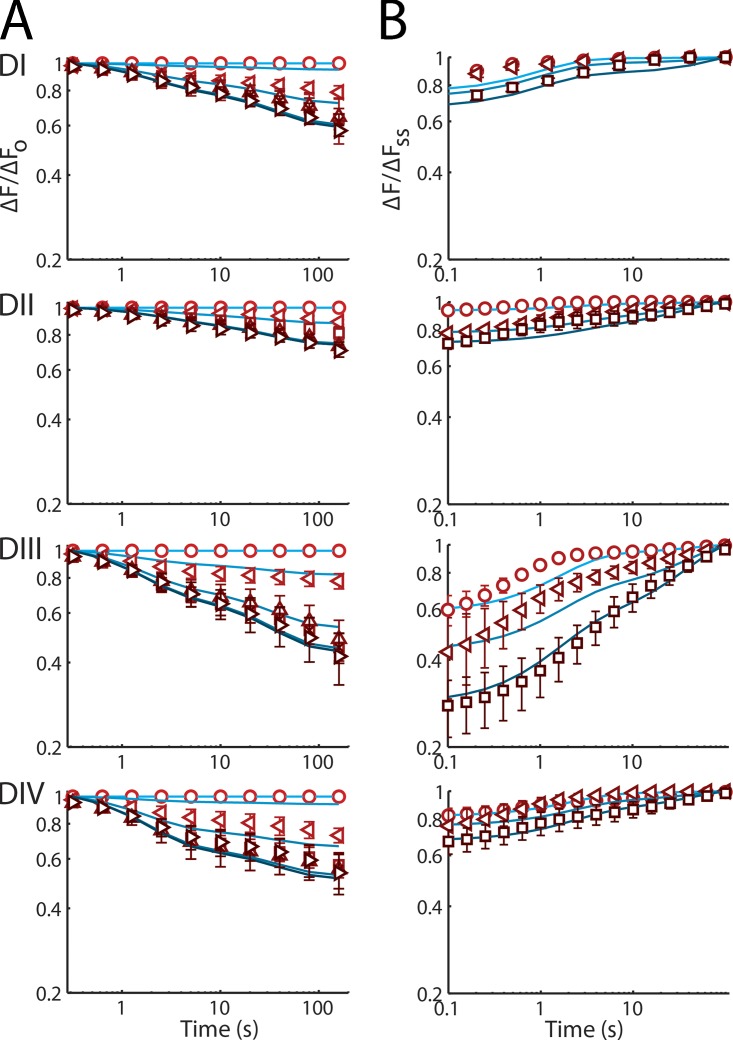
As shown above, the L689I mutation has little impact on fast channel kinetics while significantly disrupting the intermediate component of the onset of SI. These observations are reflected in L689I channel voltage-sensor movements; thus, fast fluorescent recordings are like WT (Fig. 1 F), whereas immobilization of the DI and DII sensors is impeded compared with WT. Over the course of 320 pulses to +45 mV to induce SI, immobilization of DI and DII in L689I channels is reduced by 20 and 50%, respectively, compared with WT, whereas immobilization of the DIII and DIV voltage sensors is not significantly affected (Fig. 3, A and B, and Table 1). Given the similar effects of TTX and L689I on SI as reflected in gating and ionic currents, these TTX-like voltage-sensor responses to the mutation were not unexpected.

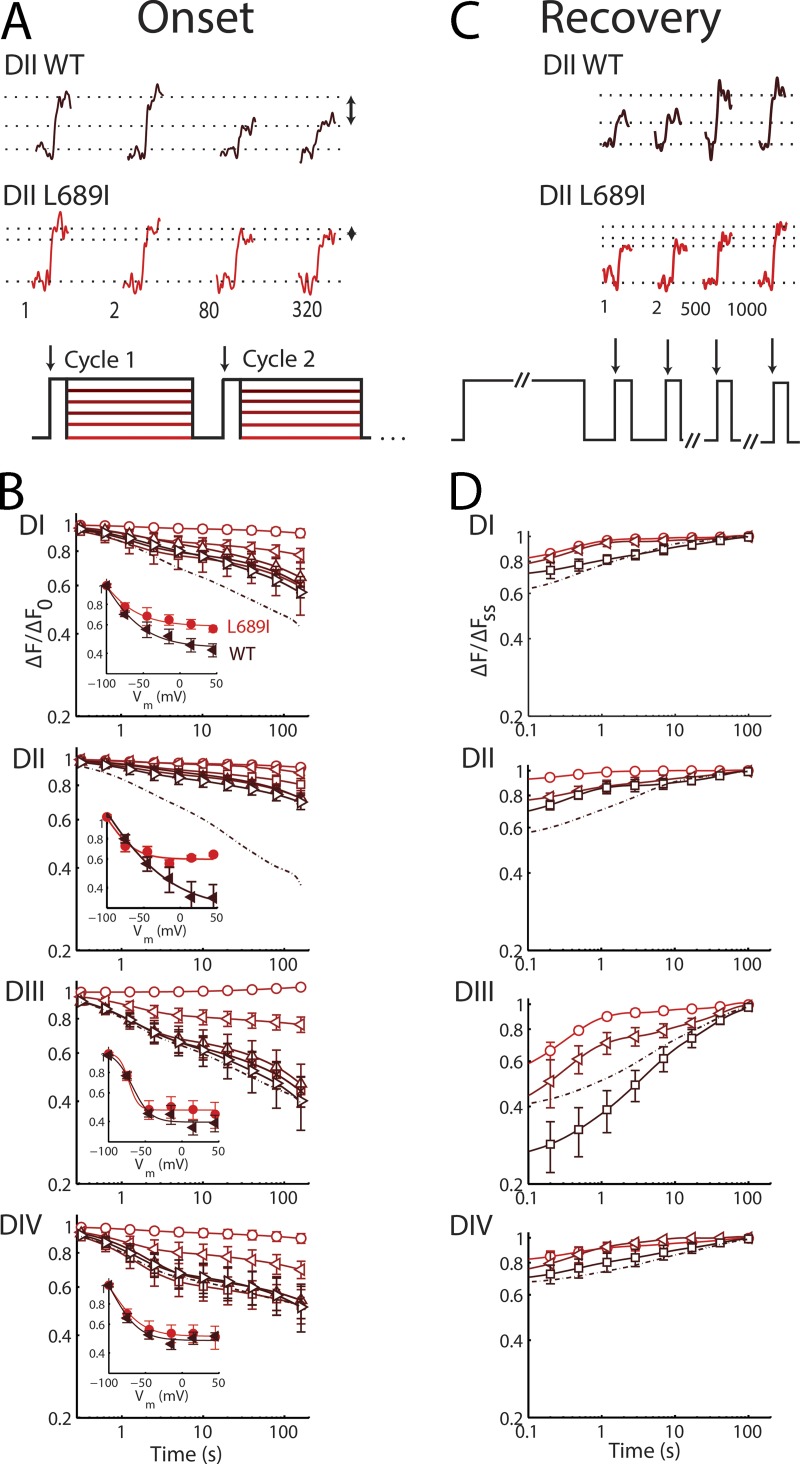
Figure 3.

L689I alters sensor mobility. Slow voltage-dependent changes in L689I channel fluorescence magnitude (ΔF/F₀) during SI induction and recovery studied with tetramethylrhodamine maleimide linked via DI-S216C, DII-S660C, DIII-L115C, or DIV-S1436C. Groups of three to eight cells are reported as mean ± SEM. (A) Fluorescence. (Top) Application of the triple-pulse protocol reveals reduction in the ΔF/F0 with increasing cycle number; 4 ms before and 4 ms after the test step to +45 mV (phase a) is shown. (B) Time-dependent change in the magnitude of ΔF/F0 for the four channels using the triple-pulse protocol shown in Fig. 2 A. Parameters are shown in Table 1. Voltage and cycle dependence of recovery from SI of ΔF/F0 for the four channels are presented on log–log plots. Dotted-dashed lines correspond to data reported previously with WT (Silva and Goldstein, 2013). Insets compare L689I (triangle) to WT (circle). For DI, the mutant reaches 0.55 ± 0.03 immobile versus 0.70 ± 0.04 for WT; for DII mutant, the mutant is 0.39 ± 0.05 immobile versus 0.77 ± 0.06 for WT channels. (C) Changes in ΔF/F0 with DI-S216C by the protocol shown in Fig. 2 C with a duration of 40 ms in phase b. (D) Voltage and cycle dependence of recovery from SI of ΔF/F0 for the four channels on log–log plots. Parameters are shown in Table 2.

Analysis of the kinetic components of SI onset for L689I channels shows a significant reduction in the amplitude of the intermediate time domain (A_I) for immobilization of the DII sensor (Table 1). This is yet another impact of the L689I mutation on SI that is like that seen with TTX application. In contrast, when compared with WT, DI shows a significantly reduced amplitude of the fast component, A_F. The difference between the DI and DII inhibition by L689I suggests one of two possibilities: either DI movement precedes DII, or the time constant of the conformational change that was affected by L689I resides in between τ_F and τ_I. In the latter case, DI immobilization would be similarly well described by assigning magnitude to either A_F or A_I, and the difference is an artifact of the fitting.

A model of SI

The experiments reported here and in our companion study of WT channels show Na_V1.4 voltage-sensor motions to be correlated to SI. To describe the onset of voltage-sensor immobilization for the WT channel (Silva and Goldstein, 2013), we parameterized discrete-state Markov models to fit experimental fluorescence recordings. Here we repeat this modeling approach for L689I channels. Like WT, L689I sensor kinetics are well fit with a five-state model: a closed state, followed sequentially by an active state and three inactive states: C↔A↔I1↔I2↔I3 (Fig. 4). As before, the C↔A transition is assumed to be in equilibrium and its voltage dependence to be described by a Boltzmann fit to the F-V curve (Table 3).

Figure 4.

Models of L689I mutant voltage-sensor slow immobilization. Experimental data from this paper are shown with symbols, and solid lines represent models. The effect of the protocol was removed for model fitting by subtracting the change with pulses to −100 mV, which accounts for any effects on the measurement caused by the short pulses to +45 mV. For model fitting, experimentally determined recovery is scaled so that it begins where onset terminated. Ionic current recovery is simulated using the same parameters and models used to simulate ionic onset. (A) Model of WT channel voltage-sensor slow immobilization for all four domains. (B) Recovery of WT channels.

Table 3.

Boltzmann fits to F-V curves

Channel variant	A1	B1	C1	A2	B2	C2	D
L689I DI	0.53	0.01677	15.01	2.81	0.1601	137.7	−2.04
L689I DII	0.16	0.00003	6.07	1.04	0.0707	28.4	−0.19
L689I DIII	0.74	0.00001	6.58	0.41	0.0002	12.9	−0.19
L689I DIV	0.21	0.000001	4.23	0.87	0.0075	18.0	−0.11

For F-V curves, two Boltzmann functions fit the curve well: ${\displaystyle {\sum }_{i=1}^2\frac{A_i}{1+B_i{e}^{-V_m/C_i}}+D.}$ In each case, only one Boltzmann described voltage dependence above −100 mV. To derive the steady-state activated probability for modeling purposes, A was set to 1 and D to 0. The values predicted by this normalized function were used to calculate the steady-state occupancy. Channel variant abbreviations as in Table 1.

In contrast to the WT channel that required voltage-dependent rates to describe DI and DII sensor inactivation, none of the L689I channel domains required voltage-dependent rate constants of inactivation to describe the sensors (parameters in Table 4). Thus, voltage dependence was derived solely from the movement between C and A. This requirement suggests that a unique voltage-dependent process is inhibited by the presence of the L689I mutation, consistent with previous reports of intrinsic SI voltage dependence (Ruben et al., 1992).

Table 4.

Model parameters

Channel domain	Transition	Forward rate	Reverse rate
DI L689I	A↔I1	1.11E-04	4.45E-04
	I1↔I2	3.97E-05	2.24E-05
	I2↔I3	3.33E-04	9.48E-01
DII L689I	A↔I1	4.91E-05	3.56E-04
	I1↔I2	4.79E-05	3.03E-05
	I2↔I3	6.19E-09	4.91E-02
DIII L689I	A↔I1	2.18E-04	4.63E-04
	I1↔I2	3.82E-05	2.38E-05
	I2↔I3	2.97E-04	3.55E-03
DIV L689I	A↔I1	2.13E-04	3.99E-04
	I1↔I2	1.83E-05	2.27E-05
	I2↔I3	4.88E-04	9.91E-01

The discrete-state Markov models used in Fig. 8 in our companion paper (Silva and Goldstein, 2013) are parameterized for the forward and reverse rate transitions between states A and I₁, states I₁ and I₂, and states I₂ and I₃ for the L689I mutation in each of the voltage-sensor domains.

With these descriptions of voltage-sensor immobilization, we attempted to recapitulate the observed changes in ionic current with SI by combining components of the L689I and WT models. Consistent with the experimental results, the most successful model was found to couple the portions of DI and DII immobilization shown to be impeded by the L689I mutation and TTX and the slow components of DIII immobilization and remobilization. To arrive at this conclusion, the following couplings were evaluated.

The first trial model tested the hypothesis that SI kinetics and voltage dependence could be reproduced if all four voltage sensors in the WT model were required to be in an inactivated state (I₁, I₂, or I₃) to cause ionic current SI. One minus the probability that all four sensors are in any inactive state represents the linkage to ionic current mathematically. The probability that a single sensor is inactive is 1 − A_i(t), where A_i(t) is the probability of a voltage sensor being in the activated state A, and i is the domain (I, II, III, or IV) in which the voltage sensor resides. t is time. Assuming the voltage-sensor movements are independent, the probability that all four sensors in a single channel are inactive is the product of the inactive probabilities:

$${\displaystyle {\prod }_{i=DI}^{DIV}(1-A_i(t\left)\right).}$$

Therefore, the ionic current is represented by the remaining fraction, where all four sensors are not inactive:

$$I\left(t\right)=1-{\displaystyle {\prod }_{i=DI}^{DIV}(1-A_i(t\left)\right).}$$

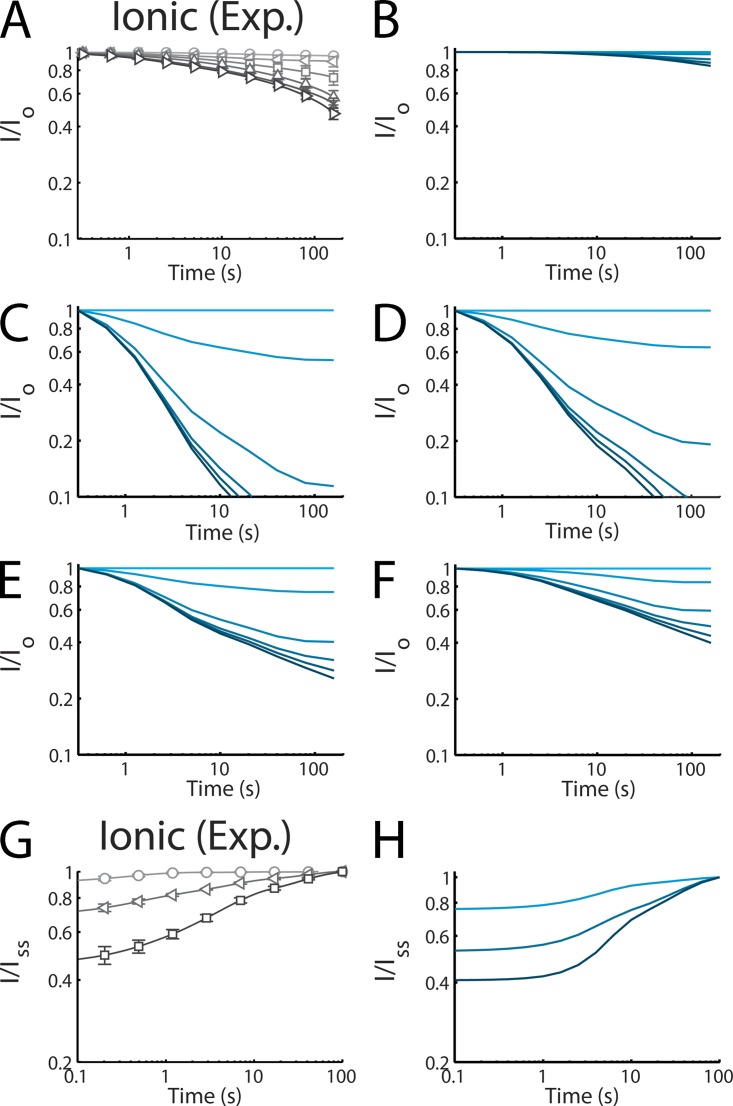
I is ionic current. This model yields a much smaller fraction of channels in the SI state than is observed experimentally (Fig. 5 B). This outcome is not unexpected because the probability of all four sensors being in an inactivated state is quite low.

Figure 5.

Reconstruction of SI based on voltage-sensor models. Models of the voltage sensors from our companion paper (Fig. 8 in Silva and Goldstein, 2013) and Fig. 4 are linked in various ways in an effort to recapitulate SI kinetics. (A) WT ionic SI from our companion paper (Fig. 2 in Silva and Goldstein, 2013). Axes adjusted for comparison to other panels. (B) Simulated ionic SI requiring all four sensors makes a slow transition. (C) Simulated ionic SI requiring any one voltage sensor makes a slow transition. (D) Simulated ionic SI requiring DI, DII, or DIII, but not DIV. (E) Simulated ionic SI requiring the L689I/TTX-sensitive component of DI and DII coupled with the sensor transition of DIII. (F) Simulated ionic SI requiring the L689I/TTX-sensitive component of DI and DII with the slow I₁→I₂ and I₂→I₃ movements of DIII. (G) Experiment from our companion paper (Fig. 6 in Silva and Goldstein, 2013) showing ionic current recovery from SI for comparison to the model. (H) Simulated recovery from SI using the same mathematical model applied to simulate SI onset in F.

In trial model 2, we allowed any of the four voltage sensors to cause SI on its own. Here, if any voltage sensor moves into any inactivated state, the channel is assumed to be in the SI state. In this case, the ionic current is represented by the probability that all four sensors in a single channel are in the active A state (that is, none of the voltage sensors have entered an inactive state):

$$I\left(t\right)={\displaystyle {\prod }_{i=DI}^{DIV}{A}_i\left(t\right).}$$

In contrast to the first trial, this produces a much greater fraction of channels in the SI state compared with observation (Fig. 5 C).

To limit the extent of SI, a contribution from the DIV sensor was disallowed in trial model 3. The rationale to exclude DIV was that changes in slow immobilization of this voltage-sensor domain with the L689I mutation or addition of TTX to WT channels (Silva and Goldstein, 2013) were small compared with those observed in DI and DII. A model that disallows a DIV contribution is shown in Fig. 5 D and is represented by:

$$I\left(t\right)={\displaystyle {\prod }_{i=DI}^{DIII}{A}_i\left(t\right).}$$

Even without a DIV contribution, too many channels enter the SI state (Fig. 5 D).

Because adjacent voltage-sensor domains in Na_V channels exhibit a strong degree of coupling (Chanda et al., 2004), it would not be surprising if DI and DII sensor movements were linked and that perturbation of SI transitions were observed in both sensors. This situation would imply that the immobilization seen in either sensor would be sufficient to recapitulate the DI/DII component of SI, whereas both would overrepresent the conformational change. Trial model 4 reflects a strongly coupled DI and DII sensor transition that is linked to SI. The VCF recordings with L689I channels (Table 1) and WT channels with TTX (see Table 2 in our companion paper, Silva and Goldstein, 2013) show an altered ∼10-s component in the immobilization of DI and DII, and a reduction in SI in the same time frame. This component was most strongly inhibited in the L689I DII voltage sensor. To isolate it, the inactivated L689I DII channels, 1 − A_DII,L689I, are added back to the fraction of channels in the WT DII active state (A_DII) to find the DI/DII component that is sensitive to L689I and TTX (A_DI,DII):

$$A_{DI,DII}\left(t\right)=A_{DII}\left(t\right)+(1-A_{DII,L689I}(t\left)\right).$$

Fig. 5 E shows SI described by the combined immobilization of DI/DII, A_DI,DII, and DIII, A_DIII:

$$I\left(t\right)=A_{DI,DII}\left(t\right)\cdot A_{DIII}\left(t\right).$$

This model is much closer to the observed SI, although it still places too many channels in the SI state compared with observation.

In the final model 5, we isolate the slow movements of DIII with the aim of improving how accurately the model reproduces SI. As seen in the DIII L689I fluorescence recordings, the DIII sensor has a pronounced fast component of recovery (Fig. 3 and Table 2). However, ionic current recovery is delayed and is not observed in this early time domain (Fig. 2 and Table 2). So, although the slow components of the DIII immobilization are well correlated to SI, the fast component is not. Therefore, the slow components of DIII movement are isolated and coupled to the DI/DII component. The slow components of DIII are described by the probability that the voltage sensor has not undergone slow transitions:

$$A_{DIII,slow}\left(t\right)=1-I_{2,DIII}\left(t\right)-I_{3,DIII}\left(t\right).$$

Fig. 5 F shows A_DI,DII coupled with the slow component of DIII:

$$I\left(t\right)=A_{DI,DII}\left(t\right)\cdot A_{DIII,slow}\left(t\right).$$

This model reproduces the onset of ionic SI quite well. Fig. 5 G shows that model 5 also reproduces recovery of the ionic current (Fig. 5 H). To illustrate the role of each component, DI, DII, and DIII, we plot the two components for a 160-s pulse at +45 mV and their recovery (Fig. 6). As is shown in Fig. 6 A, DI and DII inactivation track the early phases of SI onset, whereas DIII is reflected at longer times (Fig. 6 B).

DISCUSSION

Voltage-sensor immobilization and a working hypothesis for SI

DI and DII immobilization is physically linked to SI.

A prominent consequence of the L689I mutation is to impair a component of the onset of SI in the ∼10-s time frame. Correspondingly, a significant reduction of immobilization of DI and DII is observed using VCF. These findings are consistent with our finding that TTX significantly reduces both DI and DII immobilization and SI in the same time range. Collectively, these results provide evidence of a physical coupling of SI and voltage-sensor immobilization in DI and DII that is perturbed by TTX in the external pore or L689I mutation on the intracellular S4–S5 loop of the DII channel domain.

DIII appears to play an important role in SI.

A prominent slow component of SI remains after introducing L689I mutation or TTX application to WT channels. These manipulations suppress most of DI and DII immobilization, and this suggests that DIII and/or DIV also participate in SI. A role for DIII in the slower phases of SI is suggested by examination of the kinetics of DIII recovery. In the WT channel (Silva and Goldstein, 2013), DIII recovery shifts such that more channels recover with a slower time constant after a 160-s pulse compared with a 40-s pulse (Table 3 in our companion paper, Silva and Goldstein, 2013). This shift in sensor recovery correlates with a similar shift observed between 40- and 160-s pulses in SI recovery and is maintained with the L689I mutation (Table 2). Further, supporting a role for DIII, modeling revealed that a combination of both DI/DII and DIII components best recapitulated voltage and kinetic characteristics of SI (Figs. 5 and 6).

DIV has an inferred role.

Recent work shows that the voltage dependence of gating pore current in a mutant DIV sensor is affected by TTX (Capes et al., 2012). In contrast, we did not observe changes in DIV mobility with TTX application or the L689I mutation. Because our protocol was able to resolve SI in a time domain of seconds to minutes, it is possible that the TTX affects DIV during the first pulse of our protocol and may have a role in an earlier phase of SI. Indeed, previous results showing DIV participation in SI identified its participation over hundreds of milliseconds (Mitrovic et al., 2000). Additional support for a role for DIV in rapid SI are the kinetics of DIV immobilization, which show it to have highest fraction of immobilized sensors after several seconds of the four domains; thus, 55% of DIV sensors immobilized with the fast time constant compared with 36, 30, and 39% for DI, DII, and DIII, respectively (Silva and Goldstein, 2013).

A working hypothesis.

SI spans many time ranges, and a working hypothesis for the structural basis for the process posits a role for the voltage sensors in each protein domain as critical to different time domains. The observations, model, and previous results discussed above support the proposition that the DIV sensor has a prominent role in SI at times <1 s, DI and DII have their major impact in the ∼10-s time domain, and DIII trails, with a primary role in SI that proceeds over hundreds of seconds. Once DIII-mediated SI takes place, it appears to have the slowest remobilization and therefore a dominant role in recovery from SI.

Complex sensor kinetics

We have focused on changes in sensor mobility and kinetics that are the most prominent over seconds to minutes and most significantly perturbed by the L689I mutation and TTX application. Close examination of the VCF records reveals complex behavior in all four sensors that challenges simple, direct assignment of SI components to individual channel locales.

Coupling between voltage sensors (Chanda et al., 2004) certainly contributes to observed complexity. Consequently, it would not be surprising if impairing the movement of one sensor, for example, inhibiting the DII motion, would be evident in the inactivation DI, DIII, and DIV. Immobilization of DIV may also be affected, particularly by the adjacent DI sensor, which was reported to be tightly coupled to DI by others using VCF to study WT Na_V1.4 channels (Chanda et al., 2004). Also, the movements of DIII and DIV are both closely linked to the fast inactivation process (Cha et al., 1999). Collectively, these results suggest that movements of DIV associated with SI (Kontis and Goldin, 1997) may be secondary to its placement between and cooperatively with DI and DIII. Our interpretations are based on the assumptions that sensors primarily involved in the phenotype show the most dramatic changes.

Additional complexity in the fluorescence signal is caused by participation of the environment around the voltage sensor in altering the signal magnitude. Thus, conformational changes that are not necessarily associated with sensor movement contribute to our recordings. An environmental effect was most clearly observed in the fluorescence recordings in the presence of TTX, which demonstrated SI at −75 mV, which is not observed in the gating current; please see Figs. 5 C and 2 B in our companion paper (Silva and Goldstein, 2013). The difference in fluorescence and gating current implies that a protein motion that is not involved with transfer is being reported by the fluorescence. This motion is most likely a change in the environment around S4 rather than the movement of the sensor itself.

Clearly, description of SI kinetics is not straightforward. Although traces can be fit with a sufficient number of exponential terms, the results are dependent on the seed values used for fitting. In response, we have reduced the number of parameters by holding the time constants fixed. The drawback of this strategy is that some resolution is lost, as seen in the difference between L689I fit freely and when parameters are held equivalent to WT in the results. Nonetheless, by reducing the number of parameters, we reduce variability in fitting results and are better able to compare the effects of the L689I mutation in the 1-, 10-, or 100-s time domains.

Previous results considered

SI has resisted mechanistic inquiry because it extends over many time scales and recovery is stimulation history dependent. Additionally, probing many parts of the channel affects SI, including the S4 voltage sensors (Kontis and Goldin, 1997), the external pore (Vilin et al., 2001; Xiong et al., 2006), the internal pore (McNulty et al., 2006), and the fast inactivation gate (Featherstone et al., 1996). Some of these previous results can now be better understood.

It was observed early on that Na_V channel gating current inactivates on a slow time scale comparable to that of ionic SI (Bezanilla et al., 1982), that channel activation is linked to SI (Ruben et al., 1992), and that neutralizing mutations in the S4 segment on all four domains can cause a significant shift in SI voltage dependence (Kontis and Goldin, 1997). Thus, Ruben et al. (1992) showed that availability is coupled to ON gating charge movement but not OFF gating currents. This correlation can be understood by the sensor roles proposed here: DI, DII, and DIII contribute to both ON current and development of SI, whereas DI and DII recover rapidly, producing large OFF currents uncoupled to the slow recovery of DIII and ionic currents.

Our results also highlight previous work that indicates a role for DII in SI. Chimeric analysis has suggested the DII pore loop is largely responsible for SI that is less complete in the cardiac channel Na_V1.5 compared with the muscle channel Na_V1.4 (Vilin et al., 1999). Further work has shown that homologous substitution of single residue in the outer DII pore is able to confer the impaired Na_V1.5 phenotype to Na_V1.4. Conversely, introducing the homologous Na_V1.4 residue into Na_V1.5 causes the reverse, where more channels enter the SI state (Vilin et al., 2001). Collectively with our results, this finding suggests that the DI/DII immobilization is responsible for the differences in the phenotype of SI in the cardiac and muscle Na_V isoforms.

Physiological relevance

The impact of Na_V channel SI on physiology and disease is considered here with the skeletal muscle channel. In the heart, SI of Na_V1.5 impacts pacemaker function, action potential duration, and conduction velocity (Gintant et al., 1984; Carmeliet, 1987). In neurons, SI of Na_V1.2 determines threshold potential and confers memory of prior activity (Toib et al., 1998). Furthermore, the action of many small molecule drugs depends on their preferential binding to channels in the SI state; this includes anesthetics (Balser et al., 1996), antiarrhythmics (Antzelevitch et al., 2007; Sheets et al., 2010), antiepileptics (Errington et al., 2008), and insecticides (Song et al., 2011).