Abstract
Recently a polymer crowder and two protein crowders were found to have opposite effects on the folding stability of chymotrypsin inhibitor 2 (CI2), suggesting that they interact differently with CI2. Here we propose that all the macromolecular crowders act similarly, with an entropic component favoring the folded state and an enthalpic component favoring the unfolded state. The net effect is destabilizing below a crossover temperature but stabilizing above it. This general trend is indeed observed in recent experiments and hints experimental temperature as a reason for the opposite crowding effects of the polymer and protein crowders.
Keywords: macromolecular crowding, protein folding, crossover temperature
1. Introduction
There is now growing recognition that the crowded conditions found in cellular environments can significantly impact the equilibria of biochemical processes such as protein folding [1]. A number of studies [2–6] reported increases in protein folding stability by polymer crowders such as Ficoll and dextran, although the magnitudes are modest, of the order of 1–2 kBT (kB: Boltzmann constant; T: absolute temperature) around room temperature. Extending these studies, Pielak and co-workers [7–9] investigated the effects of both a polymer crowder, poly(vinylpyrrolidone) (PVP), and two protein crowders, lysozyme and bovine serum albumin (BSA), on the folding stability of a small protein chymotrypsin inhibitor 2 (CI2), a known reversible two-state folder [10]. In line with the other studies, the polymer crowder PVP was found to have a moderate stabilizing effect on CI2, but the two protein crowders were found to be destabilizing, leading to the suggestion that polymers and proteins behave differently as crowding agents. Here we propose that both polymer and protein crowders act similarly on the test protein, with an entropic component that favors the folded state and an enthalpic component that favors the unfolded state. This unifying mechanism explains the apparently opposite effects of the polymer and protein crowders as well as the very recent temperature-dependent crowding effects of Pielak and co-workers [11, 12].
2. Temperature dependence of crowding effects on folding stability: existence of a crossover temperature
The temperature dependence of the unfolding free energy, ΔG, can be derived based on the generally accepted assumption that ΔCp, the change in heat capacity upon unfolding, is temperature-independent. Then the unfolding enthalpy and unfolding entropy depend on temperature as [13]:
| (1) |
| (2) |
where Tref is an arbitrary reference temperature. From these two components, one obtains
| (3a) |
Another standard thermodynamic relation is
| (3b) |
We choose Tref to be the temperature, denoted as Ts where ΔG(T) is maximum. The maximum of any function corresponds to a zero slope, therefore it follows from Eq. (3b) that, at T = Ts, ΔS is zero and hence the value of ΔH, denoted as ΔHs, is the same as the ΔG maximum. Consequently
| (4) |
| (5) |
Now consider the folding equilibrium in a crowded solution. The changes in ΔH, ΔS, and ΔG by crowding will be denoted as δΔH, δΔS, and δΔG, respectively. We first make the simplifying assumption that crowding does not affect ΔCp. This amounts to neglecting the temperature dependence of δΔH. Given that the effects of crowding on folding stability are found to be small in all cases and the “observable” temperature range is usually narrow, this zeroth-order assumption seems justified. Then crowding can only affect the other two parameters, Ts and ΔHs. Let the temperature at which the unfolding free energy in the crowded solution achieves maximum change to Ts + δTs, and the latter maximum be ΔHs +δΔHs. We have
| (6) |
| (7) |
Note that δΔS is only affected by δTs but δΔH can be affected by both δTs and δΔHs.
Based on the preceding observation, we define three kinds of crowding behaviors (Fig. 1). A purely “entropic” crowder is one that results in a nonzero δΔS but a zero δΔH, and is obtained when a change in the maximum-stability temperature is accompanied by a compensating change in the maximum stability such that δΔHs = ΔCpδTs. Assuming δΔS < 0 5 (corresponding to a positive δTs), an entropic crowder results in an increase in the unfolding free energy at every temperature, and the increase grows with increasing T (since the entropic component of ΔG is weighted by T). An “enthalpic” crowder, obtained when only ΔHs, not Ts, is changed, results in a uniform decrease in ΔG (assuming δΔHs < 0) at all temperatures. Finally a “compound” crowder has both δΔH and δΔS nonzero. For δTs > 0 and δΔH <0, the compound crowder results in a ΔG-vs.- T curve that crosses that for the dilute solution. The existence of a crossover temperature, Tx, is a signature of the compound crowding behavior. At the crossover temperature, δΔG = 0, by which we find
| (8) |
When the temperature goes from below Tx to above it, the crowder changes from being a destabilizer to a stabilizer.
Fig. 1.
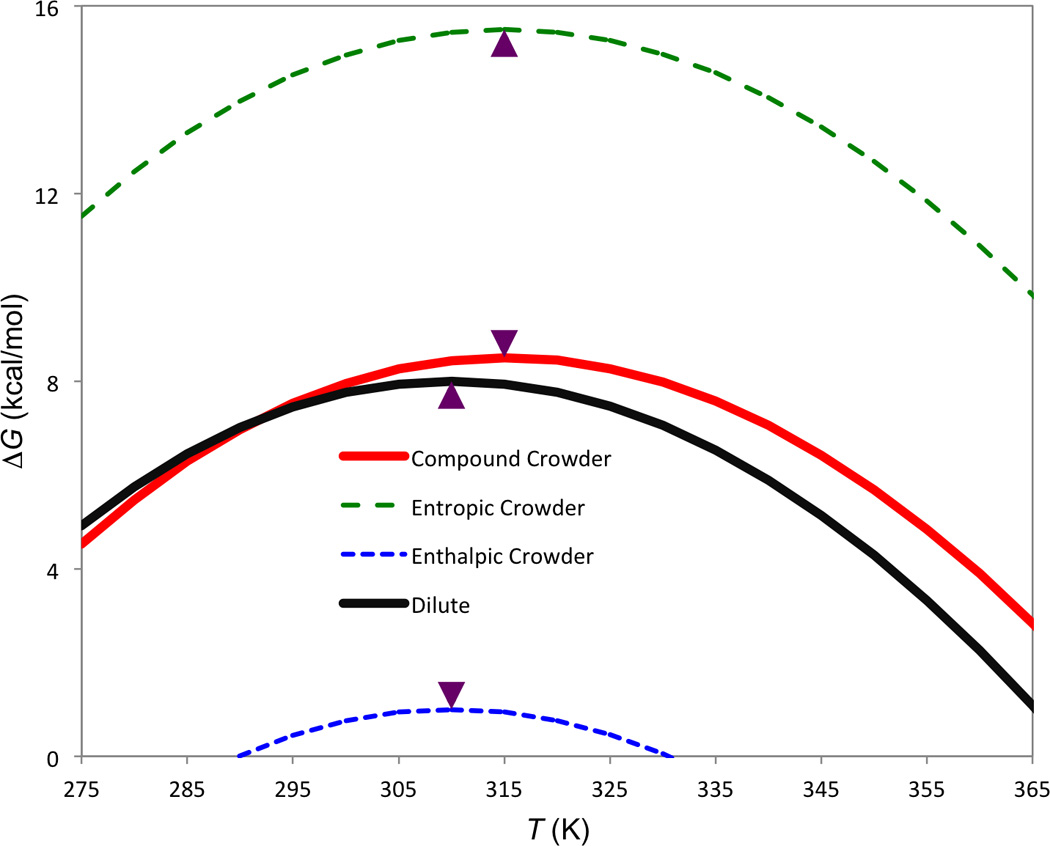
Three kinds of crowding behaviors. The curve for the dilute solution is calculated using typical experimental values (ΔCp = 1.5 kcal/mol/K; Ts = 310 K (indicated by arrow); and maximum stability ΔHs = 8 kcal/mol). The enthalpic, entropic, and compound crowders have δTs = 0, 5, and 5 K; and δΔH = −7, 0, and −7 kcal/mol, respectively.
All intermolecular interactions have hard-core repulsion. This repulsion between the test protein molecule and the surrounding crowder molecules leads to an entropic component favoring the folded state of the test protein (i.e., δΔS < 0), because the folded state is more compact and hence experiences less repulsion by the crowder molecules (Fig. 2A, B). This was predicted initially by theoretical models based on representing test protein and crowders as hard particles [14] and more recently by molecular simulations based on atomistic or coarse-grained representations [15–17]. (The hard-core repulsion could result in compaction of unfolded proteins, as observed in some experiments [18–20].) Potentially macromolecular crowders could behave like an entropic crowder. However, intermolecular interactions do not die out beyond the hard core; the soft part of the interactions is generally attractive. This soft part of interactions (also referred to as chemical interactions [12, 21]) between a test protein molecule and crowder molecules is modeled in recent simulations [22–24]. As the unfolded state is more open and hence the residues are more accessible to crowder molecules, the soft part of interactions will lead to an enthalpic component that favors the unfolded state (i.e., δΔH < 0) (Fig. 2A, B). Therefore all macromolecular crowders are expected to exhibit the compound crowding behavior, with a crossover temperature at which, δΔG, the effect of crowding on the unfolding free energy, changes sign (Fig. 2C). Note that, according to Eq. (8), Tx is increased by increasing the magnitude of δΔH and decreased by increasing δTs. A crossover temperature has also been predicted for the effects of crowding on protein binding stability [25].
Fig. 2.
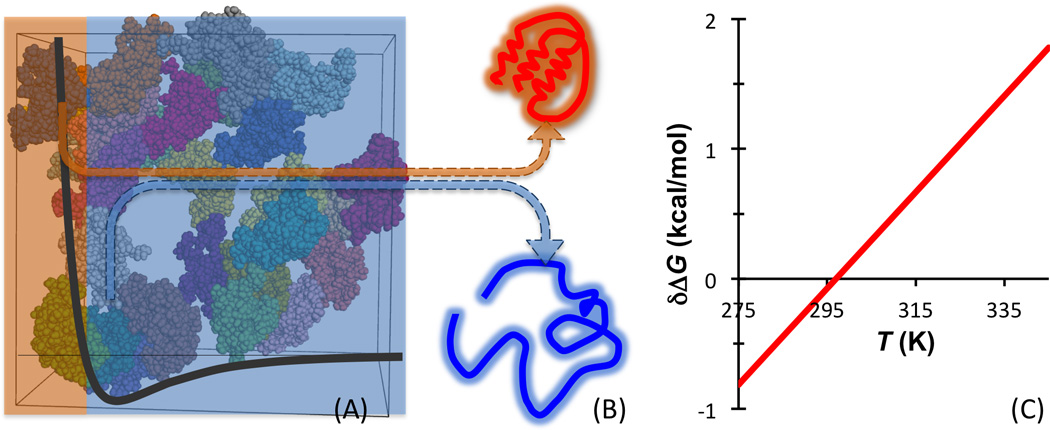
Illustration of the effects of macromolecular crowders on protein folding stability. (A) The interactions between a test protein and surrounding crowder molecules consist of hardcore repulsion and longer-ranged attraction. (B) The hard-core repulsion leads to an entropic component that favors the folded state of the test protein, whereas the longer-ranged attraction leads to an enthalpic component that favors the unfolded state. (C) Because in the folding free energy the entropic component is weighted by the temperature, the net effect of macromolecular crowding has a crossover temperature. The net effect is destabilizing (i.e., δΔG < 0) below the crossover temperature but stabilizing above it. δΔG is calculated using the parameters in Fig. 3 legend for lysozyme as a crowder for the folding of ubiquitin.
3. Experimental evidence for crossover temperature
Recently Pielak and co-workers studied the temperature-dependent crowding effects of two polymers (PVP and Ficoll) and two proteins (lysozyme and BSA), all at 100 g/l, on the folding stability of ubiquitin [12]. Their results for all the four crowders, re-analyzed here (Fig. 3 and Supplementary Fig. S1), conform to the compound crowding behavior, with upshift in the maximum-stability temperature (signifying δΔS <0) and crossing of the ΔG- vs.- T curves for dilute and crowded solutions (signifying δΔH < 0). For each crowder, the net effect is destabilizing below a crossover temperature but stabilizing above it. The crossover temperatures for PVP, Ficoll, lysozyme, and BSA are 48 °C, 28 °C, 24 °C, and 37 °C, respectively.
Fig. 3.
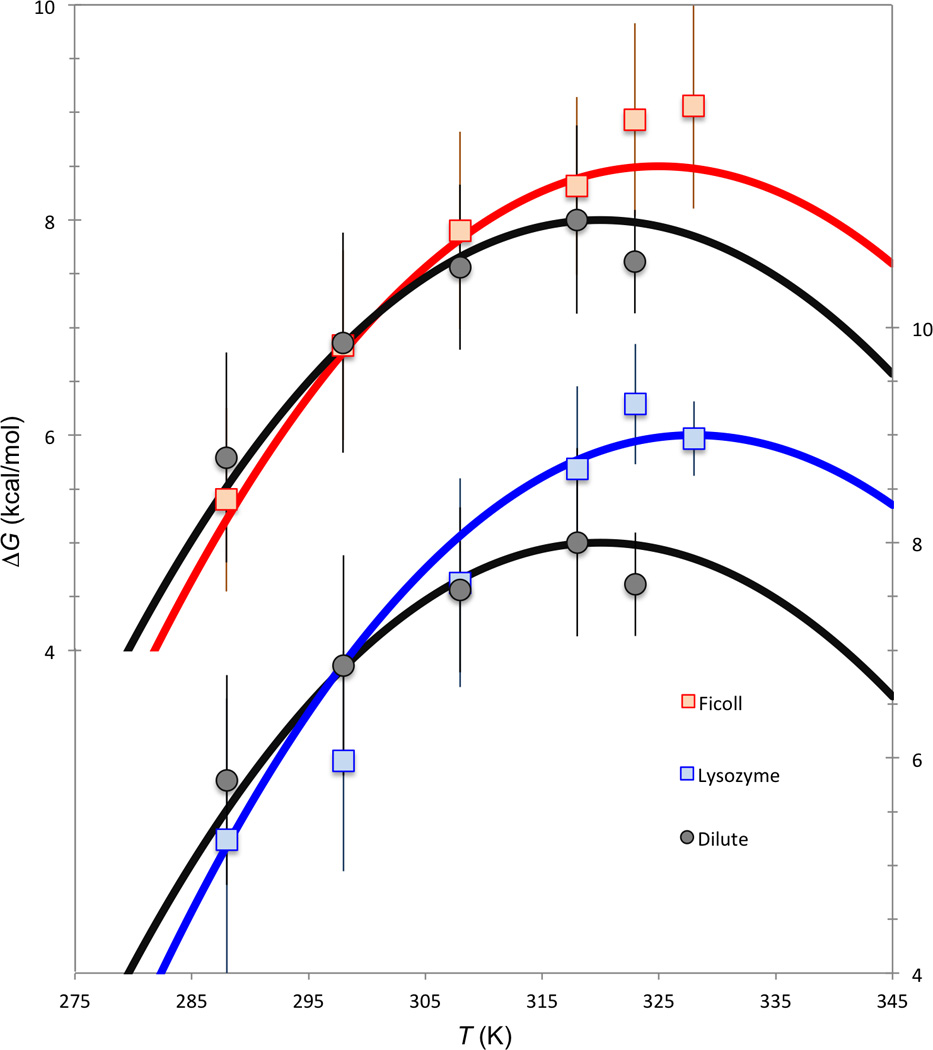
Re-analysis of the Wang et al. [12] data on the folding stability of ubiquitin. ΔCp = 1.5 kcal/mol/K for the dilute solution [12, 28] and for all the crowders; though Wang et al. [12] allowed ΔCp to float in their fitting, this seems uncalled for, given the large uncertainties of the data (see Fig. S1 legend) and the narrow experimental temperature range. Ts = 320 K and ΔHs = 8 kcal/mol for the dilute solution; δTs = 5 and 8 K and δΔH = −7 and −11 kcal/mol, respectively, for Ficoll and lysozyme. Scales on the left are for the upper two curves (Ficoll and dilute) and those on the right are for the lower two curves (lysozyme and dilute); the curve for dilute solution is duplicated to serve as reference for the two crowders.
This brings us to a simple explanation for the opposite effects of the polymer and protein crowders observed by Pielak and co-workers on the CI2 stability [7–9]. We notice that the experiments with the polymer crowder (PVP) were done at a higher temperature, 37 °C, whereas the experiments with the lysozyme and BSA crowders were done at a lower temperature, 20 °C. As any crowder exhibiting the compound crowding behavior would have a stabilizing effect at some higher temperature and a destabilizing effect at some lower temperature, the difference in the experimental temperatures seems to be a significant contributing factor for the opposite crowding effects observed.
This conclusion is reinforced by a re-analysis (Fig. 4) of the limited temperature-dependent data of 100 g/l Ficoll crowding on CI2 published very recently [11]. The data is consistent with a 5 °C upshift in the maximum-stability temperature and a 3.8 kcal/mol decrease in ΔH. These parameter values result in a crossover temperature of 12 °C, below which Ficoll is expected to become destabilizing.
Fig. 4.
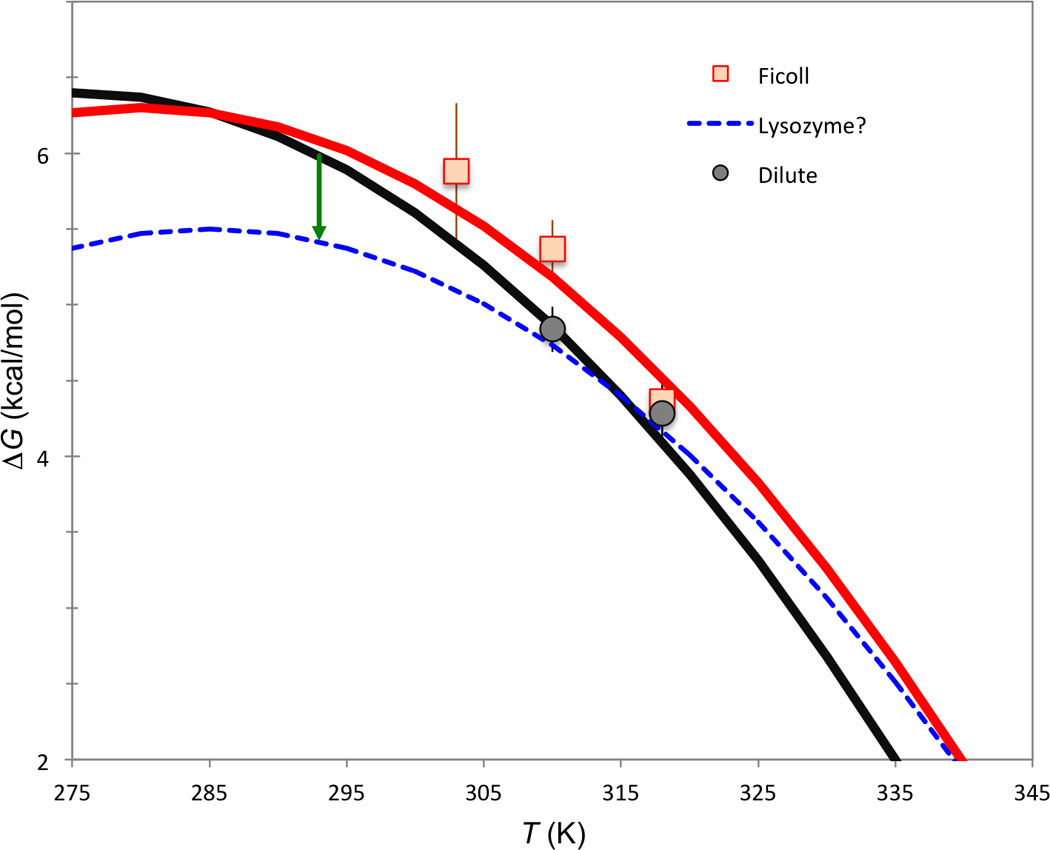
Illustrative analysis of the limited data of Benton et al. [11] on the folding stability of CI2. The curve for the dilute solution has ΔCp = 0.72 kcal/mol/K [10], Ts = 2 °C, and ΔHs = 6.4 kcal/mol (the corresponding melting temperature, 75 °C, and melting enthalpy, 60 kcal/mol, are comparable to experimental data [10]). The Ficoll curve has δTs = 5 °C and δΔH = −3.7 kcal/mol; a hypothetical lysozyme curve, with a 0.6 kcal/mol destabilizing effect at 20 °C (indicated by arrow), has δTs = 10 °C and δΔH = −8.1 kcal/mol.
The destabilization of CI2 by 100 g/l lysozyme at 20 °C was 0.6 kcal/mol [9]. No temperature dependent data are available for this crowder. As illustration, the 0.6 kcal/mol destabilization at 20 °C can be produced by a 10 °C upshift in the maximum-stability temperature and an 8.1 kcal/mol decrease in ΔH. The crossover temperature is then 42 °C, above which lysozyme is expected to become stabilizing. Hopefully these predictions will motivate new experiments.
While the existence of a crossover temperature is predicted to be universal, its exact value for a given test protein depends on the size, shape, and chemical nature of the crowders. It is possible that synthetic polymer crowding agents such as Ficoll and dextran may exert weaker soft attraction than protein crowders toward a test protein. Pielak and co-workers measured the effects of polymer and protein crowders on the translational and rotational diffusion and the NMR relaxation of CI2 [21]. The results are consistent with the protein crowders exerting stronger soft attraction toward CI2. Stronger soft attraction will produce a larger enthalpic component favoring the unfolded state of the test protein, leading to a higher crossover temperature (assuming fixed δTs). On the other hand, for a given test protein, whether synthetic polymers produce a larger or smaller entropic component than protein crowders is uncertain.
The foregoing remarks concern the comparison among different crowders acting on the same test protein. Since the effect of crowding is determined by the interaction between the test protein and the crowder, analogous comments can be made about a given crowder acting on different test proteins. To a crude approximation, the enthalpic component of the crowding effect can be modeled as proportional to the change, ΔA, in protein-crowder contact surface area on going from the folded and to the unfolded state. So a test protein with a larger ΔA will have a larger enthalpic component. One expects that the entropic component of the crowding effect also grows with increasing ΔA. Such enthalpy-entropy compensation makes the dependence of the crossover temperature on ΔA uncertain. Quantitative predictions on the enthalpic and entropic components of the crowding effect are beyond the scope of the present analysis and will require atomistic modeling of the test protein in the folded and unfolded states and its interactions with crowder molecules.
In summary, disparate data for polymer and protein crowders on folding stability can be explained by a unified mechanism, with all macromolecular crowders producing an entropic component that favors the folded state and an enthalpic component that favors the unfolded state. The size, shape, and chemical nature of the crowders determine the relative weights of the two components, but in all cases the net effect is destabilizing below a crossover temperature and stabilizing above it. Stabilization at higher temperatures has now indeed been observed for a protein crowder [26] and in living cells [27]. The conclusion drawn here can be further tested by measuring folding stability of thermophilic proteins under crowding at very high temperatures. It will indeed be interesting to see whether macromolecular crowding contributes more to the protein folding stability in thermophiles than in mesophiles at their respective living temperatures.
Supplementary Material
Highlights.
A unified mechanism is proposed for macromolecular crowding on folding stability
Enthalpy and entropy of crowding favor unfolded and folded states, respectively
At its crossover temperature, a crowder changes from a destabilizer to a stabilizer
Acknowledgement
I thank Gary Pielak and an anonymous reviewer for insightful comments on the manuscript. This work was supported in part by Grant GM88187 from the National Institutes of Health.
Abbreviations
- BSA
bovine serum albumin
- CI2
chymotrypsin inhibitor 2
- PVP
poly(vinylpyrrolidone)
Footnotes
Publisher's Disclaimer: This is a PDF file of an unedited manuscript that has been accepted for publication. As a service to our customers we are providing this early version of the manuscript. The manuscript will undergo copyediting, typesetting, and review of the resulting proof before it is published in its final citable form. Please note that during the production process errors may be discovered which could affect the content, and all legal disclaimers that apply to the journal pertain.
References
- 1.Zhou HX, Rivas G, Minton AP. Macromolecular crowding and confinement: biochemical, biophysical, and potential physiological consequences. Annu Rev Biophys. 2008;37:375–397. doi: 10.1146/annurev.biophys.37.032807.125817. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 2.Qu Y, Bolen DW. Efficacy of macromolecular crowding in forcing proteins to fold. Biophys Chem. 2002;101–102:155–165. doi: 10.1016/s0301-4622(02)00148-5. [DOI] [PubMed] [Google Scholar]
- 3.Spencer DS, Xu K, Logan TM, Zhou H-X. Effects of pH, salt, and macromolecular crowding on the stability of FK506-binding protein: an integrated experimental and theoretical study. J Mol Biol. 2005;351:219–232. doi: 10.1016/j.jmb.2005.05.029. [DOI] [PubMed] [Google Scholar]
- 4.Ai X, Zhou Z, Bai Y, Choy WY. 15N NMR spin relaxation dispersion study of the molecular crowding effects on protein folding under native conditions. J Am Chem Soc. 2006;128:3916–3917. doi: 10.1021/ja057832n. [DOI] [PubMed] [Google Scholar]
- 5.Roberts A, Jackson SE. Destabilised mutants of ubiquitin gain equal stability in crowded solutions. Biophys Chem. 2007;128:140–149. doi: 10.1016/j.bpc.2007.03.011. [DOI] [PubMed] [Google Scholar]
- 6.Batra J, Xu K, Zhou H-X. Nonaddtive effects of mixed crowding on protein stability. Proteins. 2009;77:133–138. doi: 10.1002/prot.22425. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 7.Charlton LM, Barnes CO, Li C, Orans J, Young GB, Pielak GJ. Residue-level interrogation of macromolecular crowding effects on protein stability. J Am Chem Soc. 2008;130:6826–6830. doi: 10.1021/ja8005995. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8.Miklos AC, Li CG, Sharaf NG, Pielak GJ. Volume exclusion and soft interaction effects on protein stability under crowded conditions. Biochemistry. 2010;49:6984–6991. doi: 10.1021/bi100727y. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 9.Miklos AC, Sarkar M, Wang Y, Pielak GJ. Protein crowding tunes protein stability. J Am Chem Soc. 2011;133:7116–7120. doi: 10.1021/ja200067p. [DOI] [PubMed] [Google Scholar]
- 10.Jackson SE, Moracci M, elMasry N, Johnson CM, Fersht AR. Effect of cavity-creating mutations in the hydrophobic core of chymotrypsin inhibitor 2. Biochemistry. 1993;32:11259–11269. doi: 10.1021/bi00093a001. [DOI] [PubMed] [Google Scholar]
- 11.Benton LA, Smith AE, Young GB, Pielak GJ. Unexpected effects of macromolecular crowding on protein stability. Biochemistry. 2012;51:9773–9775. doi: 10.1021/bi300909q. [DOI] [PubMed] [Google Scholar]
- 12.Wang Y, Sarkar M, Smith AE, Krois AS, Pielak GJ. Macromolecular crowding and protein stability. J Am Chem Soc. 2012;134:16614–16618. doi: 10.1021/ja305300m. [DOI] [PubMed] [Google Scholar]
- 13.Becktel WJ, Schellman JA. Protein stability curves. Biopolymers. 1987;26:1859–1877. doi: 10.1002/bip.360261104. [DOI] [PubMed] [Google Scholar]
- 14.Minton AP. Models for excluded volume interaction between an unfolded protein and rigid macromolecular cosolutes: macromolecular crowding and protein stability revisited. Biophys J. 2005;88:971–985. doi: 10.1529/biophysj.104.050351. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 15.Cheung MS, Klimov D, Thirumalai D. Molecular crowding enhances native state stability and refolding rates of globular proteins. Proc Natl Acad Sci U S A. 2005;102:4753–4758. doi: 10.1073/pnas.0409630102. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 16.Qin S, Zhou H-X. Atomistic modeling of macromolecular crowding predicts modest increases in protein folding and binding stability. Biophys J. 2009;97:12–19. doi: 10.1016/j.bpj.2009.03.066. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 17.Mittal J, Best RB. Dependence of protein folding stability and dynamics on the density and composition of macromolecular crowders. Biophys J. 2010;98:315–320. doi: 10.1016/j.bpj.2009.10.009. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 18.Hong J, Gierasch LM. Macromolecular crowding remodels the energy landscape of a protein by favoring a more compact unfolded state. J Am Chem Soc. 2010;132:10445–10452. doi: 10.1021/ja103166y. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 19.Johansen D, Jeffries CMJ, Hammouda B, Trewhella J, Goldenberg DP. Effects of macromolecular crowding on an intrinsically disordered protein characterized by small-angle neutron scattering with contrast matching. Biophys J. 2011;100:1120–1128. doi: 10.1016/j.bpj.2011.01.020. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 20.McNulty BC, Young GB, Pielak GJ. Macromolecular crowding in the Escherichia coli periplasm maintains alpha-synuclein disorder. J Mol Biol. 2006;355:893–897. doi: 10.1016/j.jmb.2005.11.033. [DOI] [PubMed] [Google Scholar]
- 21.Wang Y, Li C, Pielak GJ. Effects of proteins on protein diffusion. J Am Chem Soc. 2010;132:9392–9397. doi: 10.1021/ja102296k. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 22.McGuffee SR, Elcock AH. Diffusion, crowding , protein stability in a dynamic molecular model of the bacterial cytoplasm. PLoS Comput Biol. 2010;6:e1000694. doi: 10.1371/journal.pcbi.1000694. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 23.Mereghetti P, Gabdoulline RR, Wade RC. Brownian dynamics simulation of protein solutions: structural and dynamical properties. Biophys J. 2010;99:3782–3791. doi: 10.1016/j.bpj.2010.10.035. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 24.Feig M, Sugita Y. Variable interactions between protein crowders and biomolecular solutes are important in understanding cellular crowding. J Phys Chem B. 2012;116:599–605. doi: 10.1021/jp209302e. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 25.Jiao M, Li HT, Chen J, Minton AP, Liang Y. Attractive protein-polymer interactions markedly alter the effect of macromolecular crowding on protein association equilibria. Biophys J. 2010;99:914–923. doi: 10.1016/j.bpj.2010.05.013. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 26.Denos S, Dhar A, Gruebele M. Crowding effects on the small, fast-folding protein lambda6-85. Faraday Discuss. 2012;157:451–462. doi: 10.1039/c2fd20009k. discussion 475–500. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 27.Guo MH, Xu YF, Gruebele M. Temperature dependence of protein folding kinetics in living cells. Proc Natl Acad Sci U S A. 2012;109:17863–17867. doi: 10.1073/pnas.1201797109. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 28.Ibarra-Molero B, Loladze VV, Makhatadze GI, Sanchez-Ruiz JM. Thermal versus guanidine-induced unfolding of ubiquitin. An analysis in terms of the contributions from charge-charge interactions to protein stability. Biochemistry. 1999;38:8138–8149. doi: 10.1021/bi9905819. [DOI] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.


