A generalized G-SFED continuum solvation free energy calculation model

Significance

This paper deals with a long-standing problem in biophysics, which is resolved here. The model has a strong physical background and will have a wide range of applications to physical and biological problems. The model proposed in this article, GSFED model, can be used for the solvation free energy calculation of most organic solutes in most organic solvents. Since the computing time depends linearly on the size of the molecule, the model can be applied easily to large molecules, for example proteins. The model can provide reliable salvation free energies of experimentally unavailable solute-solvent pairs.

Abstract

An empirical continuum solvation model, solvation free energy density (SFED), has been developed to calculate solvation free energies of a molecule in the most frequently used solvents. A generalized version of the SFED model, generalized-SFED (G-SFED), is proposed here to calculate molecular solvation free energies in virtually any solvent. G-SFED provides an accurate and fast generalized framework without a complicated description of a solution. In the model, the solvation free energy of a solute is represented as a linear combination of empirical functions of the solute properties representing the effects of solute on various solute–solvent interactions, and the complementary solvent effects on these interactions were reflected in the linear expansion coefficients with a few solvent properties. G-SFED works well for a wide range of sizes and polarities of solute molecules in various solvents as shown by a set of 5,753 solvation free energies of diverse combinations of 103 solvents and 890 solutes. Octanol-water partition coefficients of small organic compounds and peptides were calculated with G-SFED with accuracy within 0.4 log unit for each group. The G-SFED computation time depends linearly on the number of nonhydrogen atoms (n) in a molecule, O(n).

An accurate description of the effect of solvent on solvation is crucial for understanding chemical and biological phenomena. Because many peptide and protein drugs are currently being developed (1, 2), computational efficiency as well as accuracy are very important. Among the different approaches that have been used, continuum solvation models are appealing because of the simplified yet accurate description of the solvent effect (3–8).

Continuum solvent models have been developed based on the early work of Born (9), Bell (10), Kirkwood (11), and Onsanger (12). They focus primarily on the description of the solute either at the quantum mechanical level or as a classical collection of point charges and try to represent the influence of the solvent based on an approximate treatment as a dielectric continuum medium. The charge distribution of the solute induces electric polarization of the surrounding solvent, and the electric field generated by the polarized solvent, the reaction field, in turn perturbs the solute, leading to a modification of the charge distribution of the solute. This electrostatic problem of the mutual polarization between solute and solvent can be recast by using boundary conditions at the cavity surface, leading to significant simplifications in the associated equations.

In the classical approaches, most work is concerned with describing the electrostatic contribution to the solvation in terms of the Poisson–Boltzmann equation (PBE) (13). Several different computational techniques for solving the PBE have been developed, for example, finite difference methods in which the dielectric property of the solvent is described in terms of a 3D grid around the solute (14–17) and boundary element methods in which the reaction potential is described by an apparent charge spread on the cavity surface (18–22).

In the quantum mechanical approaches, the mutual polarization is taken into account by the self-consistent reaction field (SCRF) method (23). A polarizable continuum model (PCM), proposed by Tomasi and colleagues (24), casts the quantum mechanical SCRF equations into a boundary element problem with apparent surface charges spread on the cavity surface. Three types of PCMs have been used frequently: the original method, dielectric PCM (24); integral equation formalism PCM (25–27); and an alternative model in which the surrounding medium is modeled as a conductor instead of as a dielectric (28, 29).

Moreover, some models complement the description of the solute–solvent interactions by adding the missing nonelectrostatic terms. Hydrogen bonds are described adequately by density-functional theory exchange-correlation functionals as well as by post-Hartree-Fock (HF) methods (30–32). In the classical approach, the free energy of hydrogen-bond formation can be calculated with a product of parameters characteristic of acidity and basicity of molecules (33, 34). Solvent-accessible surface (SAS) area models are popular choices for nonpolar solute–solvent interactions, such as dispersion, repulsion, and cavitation (35–39).

The continuum models generally are parameterized for a specific solvent to reproduce the interactions of the solvent with a variety of solutes. An important advance in continuum approaches is the development of generalized (or universal) solvation models applicable to any solvent. The conductor-like screening model for realistic solvation (COSMO-RS) (40) extension of COSMO (41) derives the polarization charges of the continuum, caused by the charge distribution of the solute, from a scaled-conductor approximation. SMx models (SM5A, SM5.42R, SM8, and others) implement the parameterization of atomic surface tension not only in terms of the properties of the atoms of the solute but also in terms of the solvent properties (42–44). COSMO-RS and SMx can be applied only to molecules of limited size that can be treated by quantum or semiempirical quantum chemistry.

Previously, we demonstrated that the solvation free energy density (SFED) model is an efficient one for the description of molecular properties in solution with a linear combination of empirical functions of the solute properties (45–50). However, the parameterization of the linear expansion coefficients, optimized for each solvent, limits the application of the model to solvents for which the coefficients were determined. Here we present the generalized SFED (G-SFED) model to calculate the solvation free energies of a molecule including biological molecules in any environment. The effects of the solute on various solute–solvent interactions are represented by the basis functions developed earlier (46–50), and the complementary solvent effects on these interactions are reflected in the coefficients with a few solvent properties.

Theory

The solvation free energy of a solute s in a solvent m, ΔG_solv, was described by two steps: (i) forming a solute-shaped cavity in the polarizable solvent and calculating the cavitation free energy, ΔG_cav, and (ii) transferring the charge distribution of the solute from the gas phase to the cavity and calculating the interaction, ΔG_inter, between the polarizable solvent and the polarizable solute. Because the continuum models used the potential of mean force produced by the solute to calculate ΔG_inter, the contribution to the hydrogen bond, especially from proton tunneling, always is underestimated. Therefore, the contribution of hydrogen bonds to solvation, ΔG_HB, is calculated independently of other possible solute–solvent interactions:

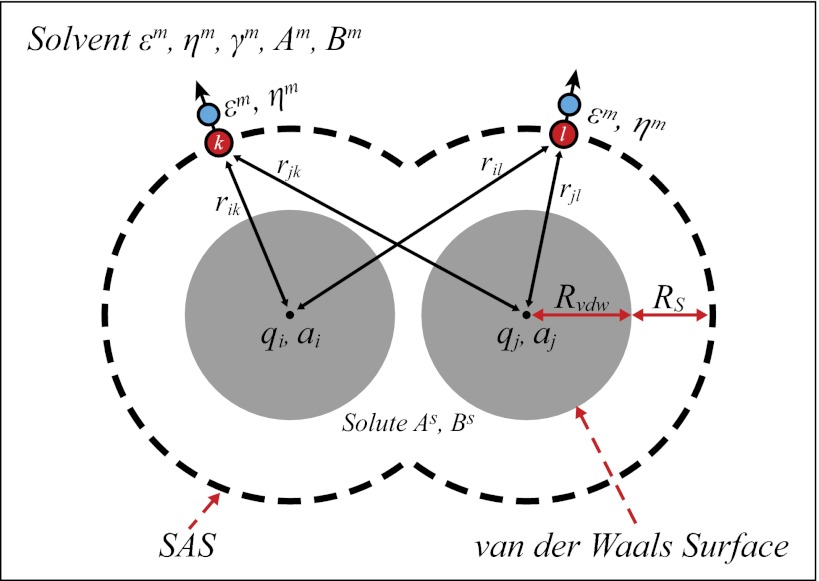
To calculate ΔG_inter, (i) the solute molecule is represented by polarizable atoms with point charges at the center of the atoms in the solute, and (ii) the solvent is represented by an SAS, and each surface unit, represented by a dot in Fig. 1, has an average dipole and an average induced dipole described by macroscopic solvent properties.

Fig. 1.

The solute and solvent of a solution are described as an assemblage of interacting compartments. r_ik is the distance between the ith atom and the kth surface fragment on the SAS of the solute, and γ^m is the macroscopic surface tension of the solvent. A dielectric constant, ε^m, and a refractive index, η^m, of the solvent are placed at the grid points on the SAS. Hydrogen-bond acidity and basicity of the solvent, A^m and B^m, and of the solute, A^s and B^s, represent the contribution of a hydrogen bond.

The electric field produced by the solute aligns the dipoles and induced dipoles on the surface, and the aligned dipoles and induced dipoles of the solvent perturb the electron distribution of each atom of the solute. This perturbed electron distribution in the solute, described by the change of net atomic charge of each atom, which is proportional to the effective atomic polarizability, interacts with the aligned dipoles and the induced dipoles on the surface.

To describe ΔG_inter, which originates from the phenomena described above, previous work (45–50) was carried out to find a proper functional form for ΔG_inter. Several functional forms and several ways to combine the basis functions have been tested to calculate solvation free energies of diverse solutes in diverse solvents. Among the tested functions, ΔG_inter calculated with the following basis functions optimally reproduced the experimental solvation free energies of all pairs of solutes and solvents examined (SI Text):

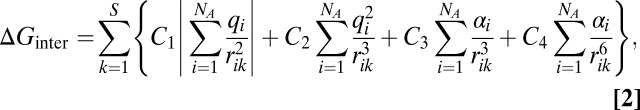where S and N_A are the number of surface fragments on the cavity surface and atoms of the solute, respectively. r_ik is the distance between the ith atom and the kth surface fragment. The net atomic charge q_i and the effective atomic polarizability α_i of the ith atom of the solute were calculated by using the modified partial equalization of orbital electronegativity and the charge dependent effective atomic polarizability methods, respectively (51–55). The cavity surface of a solute is defined by the union of the SAS of atoms in the solute (Fig. 1). The radius of the SAS sphere of each atom is defined as the sum of its van der Waals radius, R_vdw, and the effective solvent shell thickness, R_S (46).

The C_js of Eq. 2 represent the degree of the interaction of the solvent with the field produced by the electron distribution of the solute. Because the first and second terms in Eq. 2 originate from the dipole interaction, and the third and fourth terms originate from polarization, the C_js are described as follows,

where 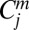represents the jth coefficient of a solvent m, and ε^m and η^m are the dielectric constant and refractive index of the solvent (56, 57), respectively. The macroscopic properties, ε^m and η^m, of the solvent originate from the average dipole moment and average induced dipole of the solvent, respectively.

Because ΔG_cav is the free energy cost to form the cavity in a solvent, it depends linearly on the cavity surface area, S_cav (58):

where γ^m is the macroscopic surface tension of a solvent m in energy per unit area (56, 57).

ΔG_HB is given by the product of hydrogen-bond acidity, A, and basicity, B, of the hydrogen-bonded molecules. In the model, ΔG_HB was divided into two terms based on the role of the solvent molecule on the hydrogen bond, with acceptor and donor represented by subscript “a” and “d,” respectively:

A and B were taken from Abraham's work (59–61).

The solvation free energy calculated with the G-SFED model is

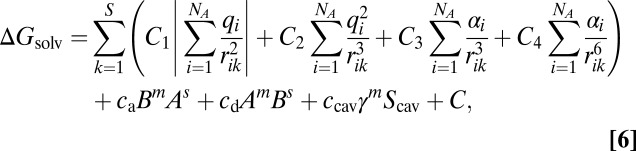where C is a constant to correct for the error in this linear equation. The coefficients c_1,0, c_1,1, c_2,0, c_2,1, c_3,0, c_3,1, c_4,0, c_4,1, c_a, c_d, c_cav, and C can be applied universally for any solvents. The G-SFED model introduces only these 12 parameters to calculate the solvation free energy of any solute–solvent combination.

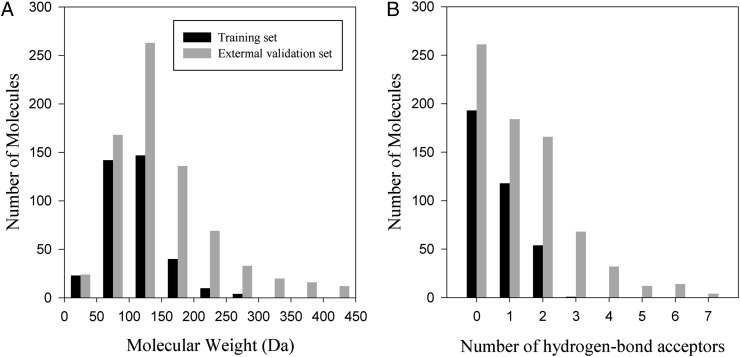
The parameterization and validation of the model were performed with 5,753 experimental solvation free energies of 890 solutes in 103 physically diverse solvents (Table S1 and Fig. S1). Because G-SFED employs parameters that were determined using rigid gas-phase solute structures, parameterization was performed by using a training set composed mainly of non- or unipolar small molecules to minimize the error originating from structural changes upon dissolution. The predictability of the model was validated by using an external validation set containing diverse small nonpolar molecules and large multipolar molecules including drug and natural compounds. Comparison between the training and external validation sets is shown in Fig. 2.

Fig. 2.

Comparison of the training and external validation sets based on molecular weight (A) and number of hydrogen-bond acceptors (B). The training set consists mainly of small non- or uni-polar molecules, and the external validation set includes a large number of multipolar large molecules. The rightmost bars represent the number of molecules that are larger than 400 Da (A) and have more than seven hydrogen-bond acceptors (B), respectively.

The training set consists of 2,173 solvation free energies of 366 neutral molecules in 91 solvents (49). This set encompassed a broad range of common functional groups present in biological and drugable small molecules that possess H, C, N, O, F, S, Cl, Br, and I atoms. The data set for validation of the model is taken from our previous work (50). After exclusion of data in common with the training set, the external validation set consisted of 3,580 unique solvation free energies of 741 neutral molecules in 36 polar solvents. Of these, 524 solutes and 12 solvents were used only to validate the model. The geometries of the solutes were obtained by energy minimization in the gas-phase, using HF/MIDIx in Gaussian (62) software.

The parameters for calculating q_i and α_i of the solute and those describing the cavity surface were taken from our previous work (46–55), and only 12 empirical parameters were determined by minimizing the difference between calculated (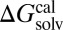) and experimental (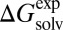) solvation free energies. The optimized 12 empirical parameters and the contribution of each basis function to ΔG_solv are given in Table 1 and Table S2.

Table 1.

Optimized universal solvent G-SFED parameters for Eqs. 3–6

Parameter	Value	Parameter	Value	Parameter	Value
c1,0	−1.76E-03	c3,0	−2.16E-01	ca	−7.53
c1,1	−1.37E-01	c3,1	2.64E-01	cd	−4.35
c2,0	−2.89E-03	c4,0	6.72	ccav	7.12E-05
c2,1	−1.84E-01	c4,1	−8.99	C	−2.66E-01

The parameters have units that enable the product of the basis function and the coefficient to be expressed in kcal/mol.

The following sections discuss the training and validation results of the G-SFED model, followed by application to calculate partition coefficients of organic molecules and peptides.

Results and Discussion

Calculation of ΔG_solv of the Training Set of Non- or Uni-Polar Small Molecules.

The performance of the G-SFED model with the training set is compared with that of the SM5.42R model, one of the most accurate generalized continuum solvation models (63). The SM5.42R calculations were carried out with AMSOL (64) at the AM1 level of theory. Table S3 gives an error summary for each solvent. The results indicate that both the G-SFED and SM5.42R models reproduce the solvation free energies very well for small molecules in diverse solvents. The mean absolute errors (MAEs) of G-SFED and SM5.42R are 0.52 kcal/mol and 0.43 kcal/mol, respectively, over the entire training set. It should be noted that the training set is almost the same as that of SM5.42R (43), and SM5.42R adapted two parameterizations for atomic surface tensions, one for water and another for all organic solvents, whereas G-SFED adapted a single parameterization for all solvents.

Predictability for the External Validation Set Including Diverse Large Multipolar Molecules.

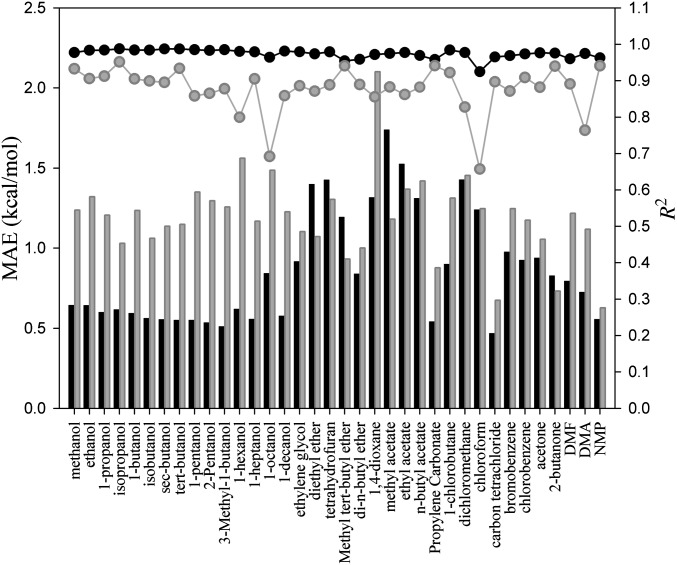
Fig. 3 compares the performance [MAE and coefficient of determinant (R²)] of G-SFED and SM5.42R applied to the external validation set including diverse large multipolar molecules described above (Fig. 2). The MAEs of G-SFED and SM5.42R for the external validation set increased by 63% and 177%, respectively, in comparison with those of the training set, to 0.85 kcal/mol and 1.19 kcal/mol. Although the MAEs increased, G-SFED gives very high correlation between 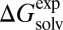and 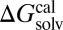in all solvents over the whole MAE range; the lowest R² was 0.92 in chloroform, and R² of other solvents was higher than 0.96. Also, the absolute error of each solute in a solvent increased in proportion to the magnitude of the solvation free energy of the solutes; the slopes from 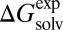vs. 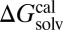were greater than but close to 1 in aliphatic alcohol and haloaromatic solvents and smaller than 1 in other solvents (Table S4). This proportional systematic error may have two main causes. The first one is omission of microscopic solvent effects around the solute molecules, because the solvent effects were reflected through minimal macroscopic solvent properties in Eqs. 3–5. The second is incomplete generalized functional forms for the hydrogen bond in Eq. 3; Abraham’s parameters, adapted to represent the hydrogen-bond acidity and basicity of solute and solvent molecules, were developed only for solute molecules, and c_a and c_d in Eq. 5 are variables of solvent properties (65, 66).

Fig. 3.

Performance, MAE and R², of G-SFED (filled black symbols) and SM5.42R (filled gray symbols) for the external validation set. MAE (left y-axis, bars) and R² (right y-axis, circles) are plotted for each solvent. The MAE and R² values are given in Table S4.

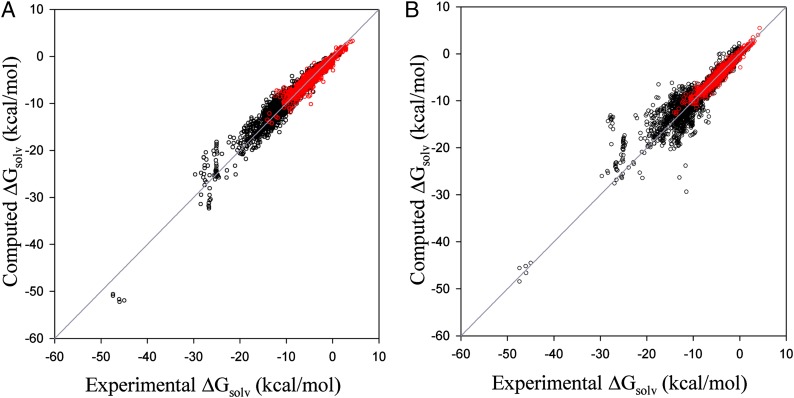
Fig. 4 compares the training and external validation results for G-SFED and SM5.42R with experiments. The MAEs and R²s for all data sets are 0.73 kcal/cal and 0.95, respectively, for G-SFED and 0.90 kcal/mol and 0.89, respectively, for SM.42R. Overall, G-SFED shows consistent accuracy for both small nonpolar and large multipolar molecules.

Fig. 4.

Scatter plots of ΔG_solv calculated with G-SFED (A) and SM5.42 (B) against experimental 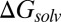. Red and black dots represent the solvation free energies in the training and external validation sets, respectively. The MAEs and R²s were 0.73 kcal/cal and 0.95, respectively, for G-SFED, and 0.90 kcal/mol and 0.89, respectively, for SM.42R.

Calculation of ΔG_solv with Empirical Hydrogen-Bond Acidity and Basicity.

G-SFED, with Abraham’s hydrogen-bond parameters, produces results in good agreement with the experimental solvation free energies. However, because there are a limited number of Abraham’s parameters, the model cannot be applied to molecules for which these parameters are unavailable (for example, peptides and many drugs). For the complete generalization of the model, empirical hydrogen-bond acidity and basicity of solute and solvent molecules (50) were used without additional parameterization instead of with Abraham’s parameters. The results were comparable to those for G-SFED with Abraham’s parameters; compared with those based on Abraham’s parameters, the MAEs increased by only 4% and 8%, to 0.54 kcal/mol and 0.91 kcal/mol, for the training and external validation sets, respectively. The errors increased mainly because of the inaccuracy of empirical hydrogen-bond parameters for the solvent molecules (a 0.1 unit error of solvent hydrogen-bond acidity corresponds to an MAE of 0.1 kcal/mol in methanol solvent).

Calculation of Partition Coefficients of Organic Compounds and Peptides.

G-SFED was applied to predict the octanol-water partition coefficient (log P) of 601 organic compounds (61) and 193 nonzwitterionic peptides (67). Peptide data consist of 185 terminally blocked and eight cyclic neutral peptides of 1–11 amino acids in length. The geometries of the organic molecules and peptides were obtained by energy minimization in the gas-phase, using HF/MIDIx and the consistent force field (CFF, Discovery Studio; Accelrys), respectively. The log P values were calculated directly from the difference between solvation free energies in water (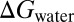) and 1-octanol ():

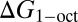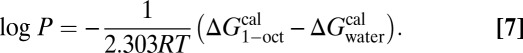Here R is the universal gas constant, and T is the system temperature.

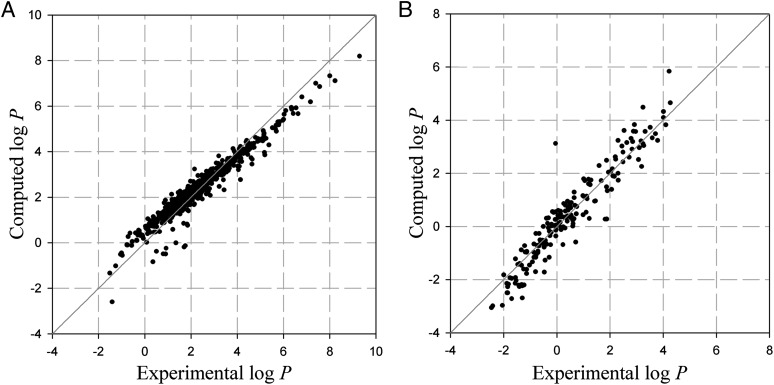
In Fig. 5, calculated partition coefficients of the organic compounds and the peptides are plotted against experimental partition coefficients. The MAE and R² of the organic compounds were 0.33 log units and 0.94, respectively. The model predicts the values well for most of the 601 organic compounds; however, 20 molecules, including sulfonamides and multihalogenated compounds, were predicted with absolute error lager than 1.0 log units because of inaccuracy of q_i for these molecules (54, 55).

Fig. 5.

The calculated octanol-water partition coefficients from G-SFED vs. experimental values for 601 organic molecules (A) and 193 neutral peptides (B). The MAEs and R²s were 0.33 log units and 0.94, respectively, for A, and 0.41 log units and 0.91, respectively, for B. If the single largest outlier [(Me)Arg-Lys-Pro-Trp-tLeu-LeuOEt] in B is removed, the MAE and R² are 0.40 log unit and 0.92, respectively.

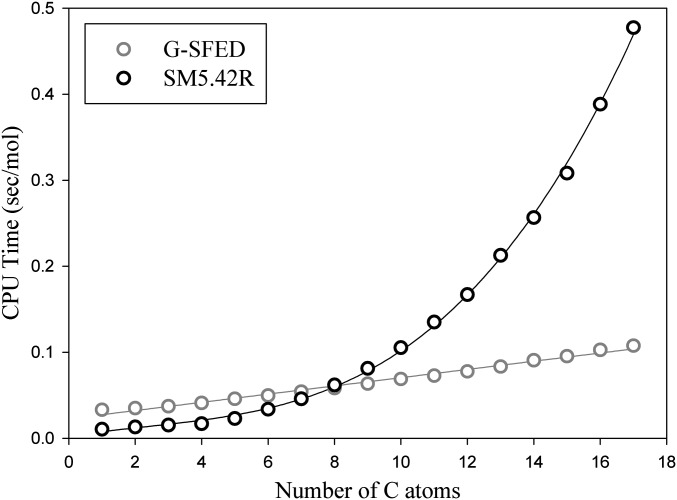
Partition coefficients of peptides were computed with empirical hydrogen-bond acidity and basicity parameters. Prediction accuracy for all peptides was excellent even for large cyclic peptides (RA-V, RA-VII, RA-V_acetate, melanotan, sandostatin, and cyclosporin) within one log unit where other methods are inaccurate (Table S5). The MAE and R² for 193 peptides were 0.41 log units and 0.91, respectively. Of 193 peptides, 133 were predicted within 0.5 log unit, and only 10 peptides were predicted over one log unit. The error originates mainly from structural changes upon dissolution and a proportional systematic error of the model described above. The application of the G-SFED model to macromolecules, especially to proteins, is one of the most important goals of our search. With the computational efficiency shown in Fig. 6, such computational accuracy for large molecules indicates that G-SFED can be applied to macromolecules.

Fig. 6.

Computation time vs. alkane chain length. G-SFED and SM5.42R are written in C++ and FORTRAN 77, respectively. Because the G-SFED model is based on simple empirical functions, the runtime of the model is linearly proportional to the number of nonhydrogen atoms of a molecule.

Conclusions

We have described a generalized empirical continuum solvation model, G-SFED, for calculation of the solvation free energies of any solute and solvent pairs. G-SFED aims to provide a practical uniform framework based on a proper description of the effects of solute and solvent on solvation. In the model, effects of the solute on various solute–solvent interactions were represented by empirical functions of the solute properties, and the complementary effects of the solvent on these interactions were reflected with a few macroscopic solvent properties. G-SFED provides accurate prediction results for both small nonpolar and large multipolar molecules in diverse solvents. Based on the computational efficiency and accuracy for large molecules, as shown by calculation of peptide octanol-water partition coefficients, G-SFED can be applied to very large systems, and even to proteins.