Skip to main content
PMC home page
NIHPA Author Manuscripts logoLink to NIHPA Author Manuscripts
. Author manuscript; available in PMC: 2013 Nov 15.
Published in final edited form as: J Biomech. 2012 Sep 17;45(16):2829–2834. doi: 10.1016/j.jbiomech.2012.08.034

Orientation dependence of progressive post-yield behavior of human cortical bone in compression

Xuanliang N Dong a, Rae L Acuna b, Qing Luo c, Xiaodu Wang b,*
PMCID: PMC3582028  NIHMSID: NIHMS405639  PMID: 22995144

Abstract

Identifying the underlying mechanisms of energy dissipation during post-yield deformation of bone is critical in understanding bone fragility fractures. However, the orientation-dependence of post-yield properties of bone is still poorly understood. Thus, the objective of this study was to determine the effect of loading direction on the evolution of post-yield behavior of bone using a progressive loading protocol. To do so, cylindrical compressive bone samples were prepared each in the longitudinal, circumferential and radial directions, from the mid-shaft of cadaveric femurs procured from eight middle-aged male donors (51.5 ± 3.3 years old). These specimens were tested in compression in a progressive loading scheme. The results exhibited that the elastic modulus, yield stress, and energy dissipation were significantly greater in the longitudinal direction than in the transverse (circumferential and radial) directions. However, no significant differences were observed in the yield strain as well as in the successive plastic strain with respect to the increasing applied strain among the three orientations. These results suggest that the initiation and progression of plastic strain are independent of loading orientations, thus implying that the underlying mechanism of plastic behavior of bone in compression is similar in all the orientations.

Keywords: Cortical bone, Post-yield, Anisotropy, Microdamage, Plastic strain, Viscous response

1. Introduction

Age-related degradation in toughness makes bone more susceptible to fracture (Burstein et al., 1976). Such a decrease in toughness is mainly due to the reduction in the capacity for the tissue to dissipate energy during the post-yield deformation (McCalden et al., 1993; Zioupos and Currey, 1998; Wang et al., 2002). Thus, understanding the post-yield behavior of bone is the key to establish the criteria of bone quality. However, what actually happens during the post-yield deformation of bone at micro/ultrastructural levels is still poorly understood. As an effort to address the issue, we have studied the post-yield behavior of human cortical bone loaded under three distinct modes: tension (Wang and Nyman, 2007), compression (Leng et al., 2009), and shear (Dong et al., 2011) using a novel progressive loading scheme. These studies have shown that the post-yield behavior of bone is associated with an exponential decay of elastic modulus (micro-damage accumulation), linear plastic deformation, and an acute saturation of viscous behavior of the tissue (Nyman et al., 2009).

Bone is known as an anisotropic material (Dempster and Liddicoat, 1952; Bargren et al., 1974; Bonfield and Grynpas, 1977; Katz, 1980; Katz and Meunier, 1987; Ashman et al., 1989). The elastic properties of human cortical bone have been shown to be transversely isotropic based on the results obtained from different techniques, such as mechanical testing (Reilly et al., 1974; Reilly and Burstein, 1975; Burstein et al., 1976; Evans, 1976; Dong and Guo, 2004) and ultrasound measurements (Yoon and Katz, 1976; Katz et al., 1984; Hoffmeister et al., 2000). Although there are numerous studies on the anisotropy of post-yield properties of trabecular bone (Turner, 1989; Kopperdahl and Keaveny, 1998; Morgan and Keaveny, 2001; Shi et al., 2010), only a few studies have reported the orientation-dependence of cortical bone in its post-yield strengths and viscoelastic properties (Cezayirlioglu et al., 1985; Iyo et al., 2004; Yeni et al., 2007; Abdel-Wahab et al., 2011; Novitskaya et al., 2011).

In the present study, our goal was to determine the orientation-dependence of the post-yield behavior of human cortical bone in terms of modulus loss, plasticity, and viscous response using the novel progressive loading protocol developed in the previous studies (Leng et al., 2009; Nyman et al., 2009). Investigating the progressive post-yield behavior of human cortical bone at different directions can facilitate the understanding of bone fragility in the elderly and provide valid information for the optimal design of orthopedic implants.

2. Materials and methods

2.1. Specimen preparation

Human cadaveric femurs were obtained from eight (N=8) middle-aged male donors (51.5±3.3 years old) through the National Disease Research Interchange (NDRI, Philadelphia, PA) in order to avoid confounding effects of age and sex. From each of these femurs, three cylindrical specimens with a diameter of 3 mm and a height of 5 mm were prepared from the anterior quadrant of the femoral middle shafts in the longitudinal, circumferential, and radial directions (Fig. 1a). To prepare the specimens, a cross section of bone slabs (stored at −20 °C) was first thawed and cut on a diamond saw (Buehler Isomet 2000 Precision Saw, Buehler, Lake Bluff, IL) from the diaphysis of the femur under a constant stream of water. Then, a diamond tip coring tool (Starlite Industries, Rosemont, PA) was used to dissect out the cylindrical specimens, which were submerged in a custom-made water chamber on a tabletop drill press. The bone sample was cored with the spindle speed set to approximately 2500 rpm. The cores were then secured in a custom-made lapping fixture that was 5 mm thick with two parallel faces (Fig. 1b). The two ends of the cores that stood out the fixture’s faces were lapped off with 150 grit sand papers to ensure that the height of the specimens was 5 mm and the both ends were parallel. Finally, the cylindrical samples were stored in the phosphate buffered saline (PBS) and kept frozen at −20 °C until testing.

Fig. 1.

Fig. 1

Open in a new tab

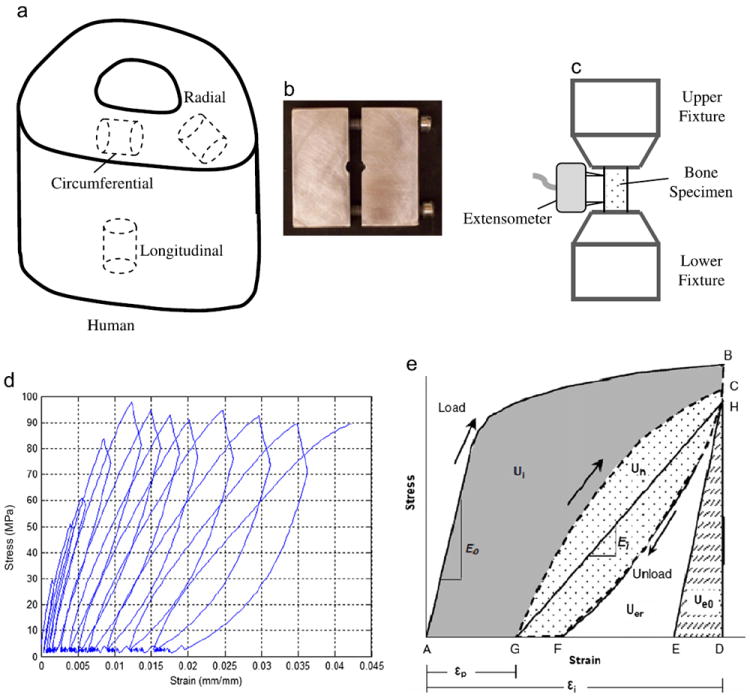
Specimen preparation and progressive loading protocol for human cortical bone under compression. (a) orientation of bone samples; (b) a custom-made fixture with a thickness of 5 mm for preparing bone specimens with parallel ends; (c) an extensometer of 3 mm gage length attaching to bone specimens; (d) a typical curve of stress vs. strain in the progressive loading with an incremental displacement; (e) a diagram showing how to calculate mechanical properties using the progressive stress–strain curve.

2.2. Mechanical testing

An established progressive loading protocol was used to measure the compressive post-yield properties of bone in this study (Leng et al., 2009). Briefly, the cylindrical bone specimen was tested cyclically in an incremental compressive load at room temperature using a load-dwell–unload-dwell–reload scheme on an MTS mechanical testing system (Insight 5000, MTS, Eden Prairie, MN). An extensometer of 3 mm gage was attached to the specimen (Fig. 1c). Based on a physiologically relevant strain rate of 0.001/s (Courtney et al., 1996), the loading rate was set as 0.005 mm/s in displacement control for both loading and unloading processes. Prior to the test, the bone specimen was preloaded to 20 N to ensure a proper engagement between the specimen and the loading fixture. A typical loading curve was shown in Fig. 1d. The sequence of each cycle was as follows: loading (A to B), stress relaxation dwell (B to H), unloading to the preload value (H to F), creep dwell (F to G), and reloading (G through C) to the next designated displacement as depicted in Fig. 1e. After 11 cycles, the samples were loaded to the extensometer limit (0.24 mm). The dwell time was 120 s for both stress relaxation and creep dwelling in order to allow the stress relaxation or creep to reach the quasi-equilibrium state so that viscoelastic response of bone at each applied strain level could be determined. The selection of dwell time was based on a pilot study to ensure that the change in stress in a unit time is reduced to less than 3% of the total stress relaxation per second.

2.3. Calculation of mechanical testing

Mechanical properties of bone specimens were quantified at each progressive strain level (Fig. 1e). All calculations were performed using a custom MATLAB program. The initial elastic modulus (E0) was calculated as the slope of the linear portion of the loading curve in the first cycle. The elastic modulus (Ei) at each cycle was calculated as the slope of a line between the points at the end of stress relaxation dwelling (H) and creep dwelling (G), representing the nominal elastic modulus from two quasi-equilibrium states of bone at different stress levels. It is noted that such definition of elastic modulus is different from the standard use in viscoelasticity literature. The nominal elastic strain energy (Ue0) was partitioned as the area under the triangle DEH shown in Fig. 1d with a slope of E0. The irreversible energy (Ui), hysteresis energy (Uh), and released elastic strain energy (Uer) were calculated as numeric integrals. Ui is the shaded area under the curve ABCG. Hysteresis energy (Uh) is the dotted area under the curve CGFH. Uer is estimated as the difference between the area under the curve HFD and Ue0, which represents the cumulative surface energy dissipation due to formation of new microdamage. Once these values were calculated, the plastic strain energy dissipation (Up) at the incremental strain for each cycle was estimated as the difference between the total irreversible energy dissipation (Ui) and the surface energy dissipation (Uer) manifested by the modulus loss.

The evolution of viscoelastic properties was calculated in the stress relaxation dwells. The stress vs. time data were extracted from each cycle and a built-in MATLAB function for nonlinear regression was applied to fit the data with the following equation:

σ=Δσ0e−t/τ+A (1)

where Δσ0 represents the magnitude of total stress relaxation and τ represents the relaxation time constant, and A is an asymptotic term representing the quasi-equilibrium stress after relaxation.

The yield strain (εy) was determined from the equation of a linear regression fit to the linear portion of the graph of instantaneous strain (εi) and plastic strain (εp). The yield stress (σy) was determined as the stress at εy based on the curve of the maximum stress and the instantaneous strain. The instantaneous strain (εi) at each cycle was defined as the strain at point B (Fig. 1e). The plastic strain (εp) was defined as the residual strain at point G (Fig. 1e). The following equation was obtained from the linear regression to express the relation of εp with εi (Leng et al., 2009):

εp=aεi−b (2)

An exponential decay of elastic modulus (Ei) was observed with respect to instantaneous strain (εi) during the progressive loading. Its relationship was expressed in the following equation by curve fitting:

Ei=E0e−mτi (3)

here, m could be used to estimate the sensitivity of bone to damage accumulation.

2.4. Statistical analysis

The dependency of compressive post-yield properties on orientations was evaluated by one-way analysis of variance (ANOVA) with Tukey’s post hoc tests. In addition, the comparison of slopes of plastic strain vs. instantaneous strain for all three orientations was carried out using analysis of covariance (ANCOVA). All statistical analyses were performed using SPSS. The statistical significance was considered only when the p-value is less than 0.05.

3. Results

Elastic moduli and strengths of human cortical bone were dependent on the loading orientations. The initial elastic modulus (E0), yield stress (σy), and ultimate strength (σu) were significantly (p < 0.001) different among the three orientations (Table 1), showing much higher values in the longitudinal direction than in the transverse directions. However, these properties were not significantly different in the transverse (circumferential and radial) directions (p > 0.05).

Table 1.

Descriptive statistics for compressive properties of human cortical bone at various orientations under progressive loading.

E0 (GPa) σy (MPa) σu (MPa) εy (%)
Longitudinal 19.1±6.35 111±18.6 124±15.0 0.91±0.09
Circumferential 5.65±1.61 41.8±19.4 65.2±13.8 0.83±0.42
Radial 6.49±3.22 44.1±21.1 63.1±20.7 0.84±0.23
ANOVA p < 0.0001 p < 0.0001 p < 0.0001 p=0.83
Open in a new tab

The degradation of the elastic modulus (Ei) versus applied strain (εi) exhibited an exponential decay (Fig. 2). At the same applied strain level, Ei was consistently higher in the longitudinal direction than in the circumferential and radial directions. In addition, the exponent m was significantly higher (m=64.2) in the longitudinal direction than in the circumferential (m=46.4) and radial (m=37.5) directions (p < 0.001), suggesting that the modulus degradation in the longitudinal direction was relatively faster than in the two transverse directions. Nonetheless, the exponential trends of modulus degradation were similar in all three orientations.

Fig. 2.

Fig. 2

Open in a new tab

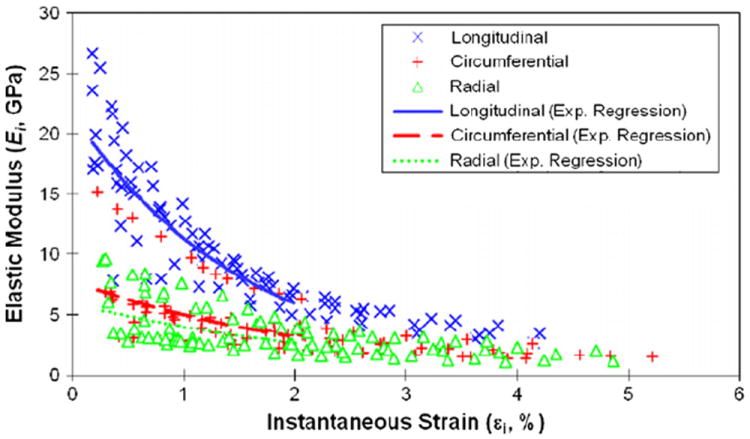
Relationship between instantaneous modulus (Ei) and instantaneous strain (εi) of cortical bone at longitudinal, circumferential and radial directions. Exponential regression was fitted for experimental data with instantaneous strain less than 2% from three orientations: longitudinal direction (Ei = 22.1e−62.4si, R2 = 0.83), circumferential direction (Ei = 8.79e−46.3si, R2 = 0.45), and radial direction (Ei = 6.44e−37.5si, R2 = 0.42).

However, the yield strain (εy) was not significantly (p = 0.89) different among the longitudinal, circumferential and radial directions, suggesting that it is independent of orientations (Table 1). The yield strain data exhibited a greater scattering (larger standard deviation) in the transverse directions than in the longitudinal direction. This is most likely due to a greater variation in microstructure (e.g. the number and orientation of Haversian/Volkmann’s canals) of bone specimens in the transverse directions. In addition, linear relationships were found between the plastic strain (εp) and applied strain (εi) for all three directions (Fig. 3). Analysis of covariance indicated that no significant differences (p > 0.05) were observed among the slopes of the linear regression curves among all of the orientations.

Fig. 3.

Fig. 3

Open in a new tab

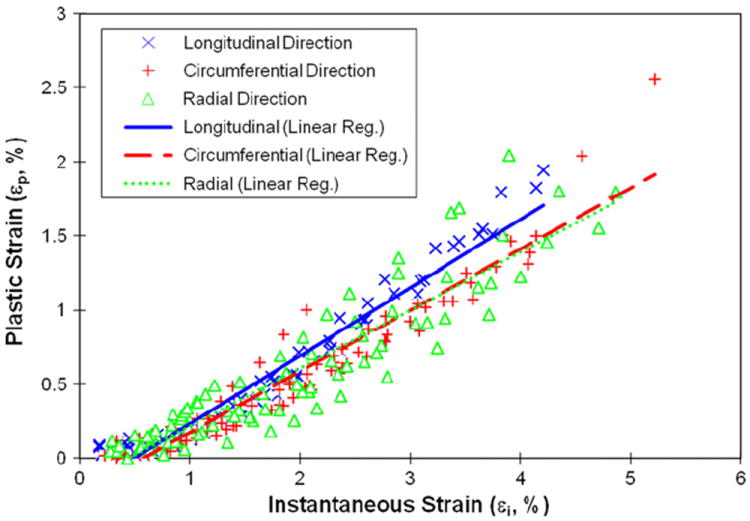
Relationships between plastic strain and instantaneous strain of human cortical bone at three different orientations. Linear regression was fitted for experimental data: longitudinal direction (εp=0.459εi−0.00227, R2=0.95), circumferential direction (εp=0.412εi−0.00239, R2=0.93), and radial direction (εp=0.391εi−0.00175, R2=0.84).

Viscous responses of human cortical bone were represented by the magnitude of stress relaxation (Δσ0), the relaxation time constant (τ), and the asymptotic term of stress relaxation (A). Δσ0 had a sharp increase in the elastic region and reached a plateau in the plastic region (Fig. 4). At all strain levels, Δσ0 was significantly higher (p < 0.04) in the longitudinal direction than in the circumferential and radial directions (Fig. 4). On the other hand, the relaxation time constant scattered largely with the applied strain at initial strain levels (< 1%), and then became converged and consistent for all loading directions afterwards (Fig. 5). The asymptotic term of stress relaxation (A) followed a similar trend (Fig. 6) as the magnitude of stress relaxation (Δσ0).

Fig. 4.

Fig. 4

Open in a new tab

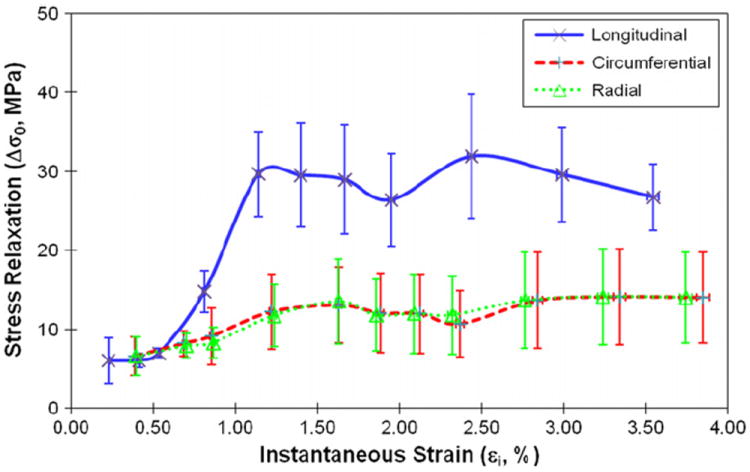
The magnitude of stress relaxation (Δσ0) as the function of instantaneous strain when bone is loaded in longitudinal, circumferential and radial directions.

Fig. 5.

Fig. 5

Open in a new tab

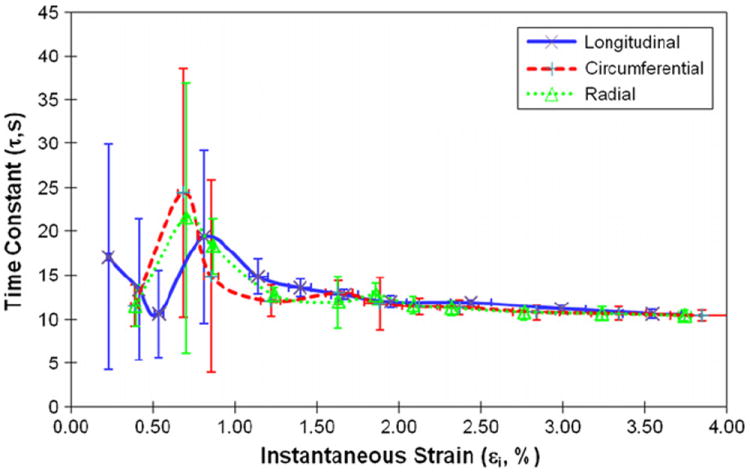
Relationships between the viscoelastic time constant (τ) and instantaneous strain of human cortical bone for longitudinal, circumferential and radial directions.

Fig. 6.

Fig. 6

Open in a new tab

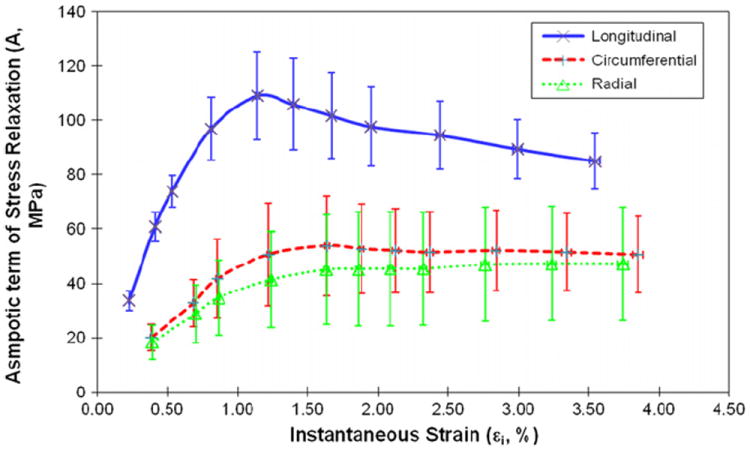
Relationships between the asymptotic term of stress relaxation (A) and instantaneous strain of human cortical bone for longitudinal, circumferential and radial directions.

The energy dissipation in bone demonstrated marked differences (p < 0.04) among three orientations. Plastic strain energy had a linear relationship with instantaneous strain of bone after yielding. The slope of the linear curve between plastic strain energy and applied strain was greater (p < 0.001) in the longitudinal direction than in the circumferential and radial directions (Fig. 7). The released elastic strain energy followed a similar trend, demonstrating no marked differences (p > 0.40) between the transverse directions, but significant differences (p < 0.003) between the longitudinal and transverse directions (Fig. 8). Aside from showing a difference (p < 0.01) in the longitudinal direction compared to the transverse directions, the hysteresis energy showed a linear increase in the elastic region and a more gradual increase after yielding (Fig. 9).

Fig. 7.

Fig. 7

Open in a new tab

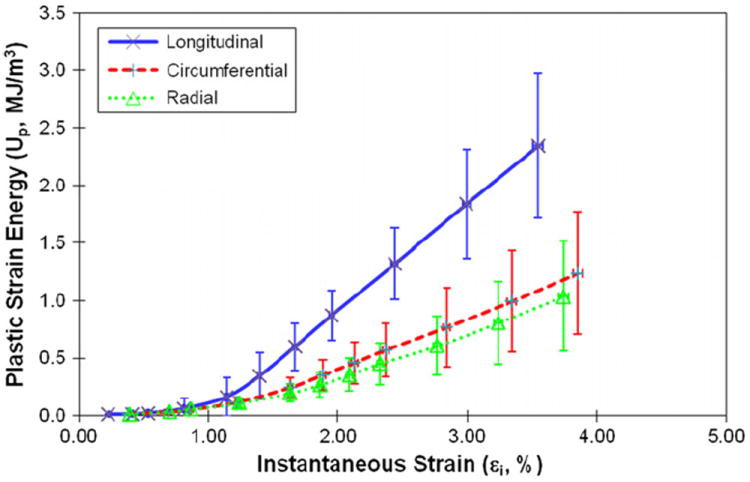
Plastic strain energy as the function of instantaneous strain when bone is loaded in the longitudinal, circumferential, and radial directions.

Fig. 8.

Fig. 8

Open in a new tab

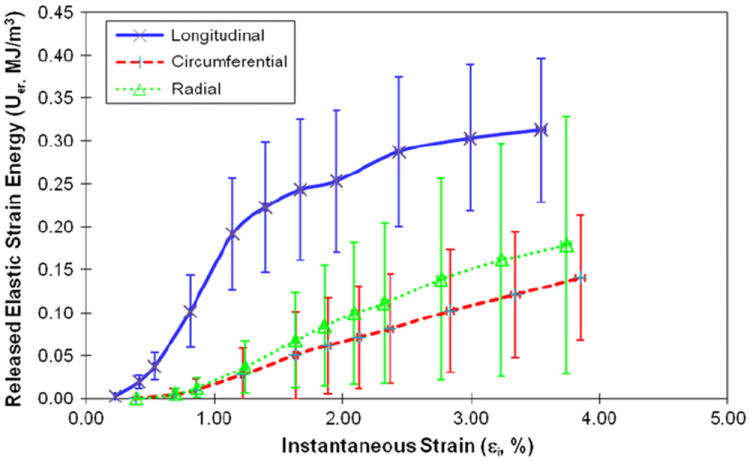
Relationships between the released elastic strain energy and instantaneous strain in the three orientations.

Fig. 9.

Fig. 9

Open in a new tab

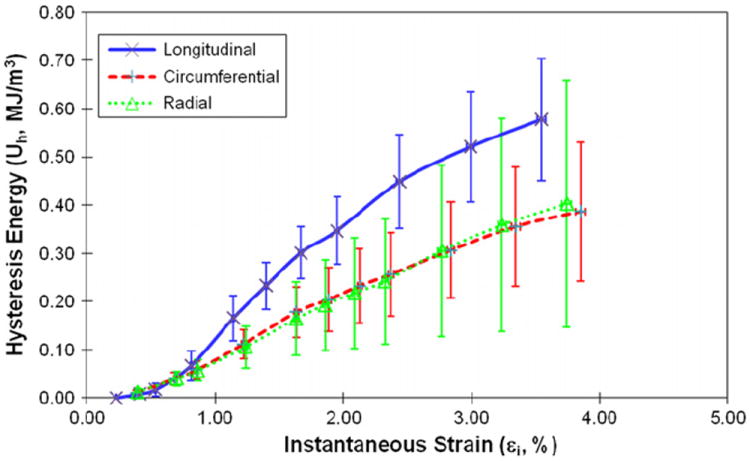
Hysteresis energy as the function of instantaneous strain when bone is loaded in the longitudinal, circumferential and radial directions.

4. Discussion

The results of this study indicate that the elastic modulus, yield stress, ultimate strength, and stress relaxation of human cortical bone in compression are significantly greater in the longitudinal direction, but similar in the transverse (i.e. circumferential and radial) directions as reported in the literature. Such a transverse anisotropy is also found in the magnitude of energy dissipation in microdamage accumulation (Uer), plastic strain (Up), and hysteresis (Uh). These results again verify the assertion supported by the previous studies. However, the intriguing finding of this study is that the yield strain (εy), and progressive plastic deformation with respect to the applied strain (εp) of human cortical bone in compression appear to be independent of loading orientations. The above results implicate that although elastic moduli and strengths of cortical bone are transversely isotropic, the underlying mechanism of the post-yield deformation in human cortical bone may be independent of orientations.

However, there exist several limitations in this study. First, only middle-aged male bone samples were tested in this study. Thus, the results may not be fully representative of other age and gender groups. Next, the experimental condition (e.g. loading rate, incremental strain intervals, etc.) may also affect the experimental results. For example, some drift was observed in the axial strain during stress relaxation dwell (Fig. 1d) since the dwell was implemented under displacement control, rather than strain control. Specifically, the relative changes of strain shift from the point H to the point B [(εH−εB)/εB] were 4.02 ± 1.64% for longitudinal specimens at the last loading cycle. Nonetheless, for relative comparisons the observations of this study could be still deemed valid. Finally, the ultimate strength estimated in this study is not equivalent to that obtained in monotonic tests and is always smaller due to the cyclically induced damage to bone in the previous loading cycles.

The results of this study indicate that more energy is dissipated when bone is loaded in the longitudinal direction rather than the transverse directions for all three mechanisms (i.e. Uer, Up, and Uh). As to the released elastic strain energy dissipation (Uer), it is most likely dissipated through the microdamage accumulation in bone. A greater Uer would mean that more microdamage is created during the deformation of bone. This conjecture is actually supported by the observation that modulus degradation in the longitudinal direction is relatively faster than the transverse directions (Fig. 2).

The anisotropic nature of hysteresis energy dissipation (Uh) found in this study was also reported in a recent study, showing that hysteresis energy was noticeably larger for longitudinal specimens than for transverse ones when cortical bone specimens are tested under tensile cycling loading (Abdel-Wahab et al., 2011). As speculated in a previous study (Iyo et al., 2004), the anisotropy of hysteresis energy dissipation is most likely due to the anisotropic structure of bone at the mineral-collagen fiber level, which serves as the major contributor to the hysteresis energy dissipation.

The higher plastic energy (Up) dissipated in the bone specimens loaded in the longitudinal direction could be explained by the spatial distribution of mineral crystals and collagen fibrils, which are preferentially orientated in the longitudinal direction of bone. Considering the fact that the cross-hatch microdamage is dominant in compression (Ebacher et al., 2007), the shear-induced sliding may be the most likely form of plastic deformation in bone loaded in compression. Thus, it is presumable that the shear-induced sliding requires more force to proceed when loaded in the longitudinal direction, thereby leading to more energy dissipation.

The most important finding of this study is that the yield strain of human cortical bone in compression exhibited little differences among the loading orientations (Table 1). In fact, the previous studies have shown the nature of invariance in the yield strain of bone. For instance, such invariance is observed in the yield strain of specimens from both child and adult cortical bones in compression (Ohman et al., 2011). In addition, Currey et al. have shown that the yield strain of bone is much less variable than the yield stress and elastic modulus among the bone specimens from 22 different species (Currey, 2004). Moreover, the invariance of yield strain is also observed in trabecular bone (Bayraktar and Keaveny, 2004). All of the above results, including those of this study, may suggest that the underlying mechanism of plastic deformation is not dependent on the orientation of human cortical bone. Another piece of evidence from this study that supports the assertion is the consistent change (slope) of the plastic strain with respect to the applied strain in all three (longitudinal, circumferential, and radial) directions (Fig. 3). The similar behavior is also reported in a previous study (Burstein et al., 1975) showing that the plastic slope was consistent irrespective of the degree of decalcification of bone specimens that were partially decalcified in the hydrochloride acid (HCl) solution with varying concentrations, thus suggesting that the plastic deformation of bone is independent of the amount of mineral crystals.

Another interesting finding of this study is that although the magnitude of stress relaxation is orientation-dependent whereas the relaxation time constant is not (Fig. 5). The orientation-independence of relaxation time constant is in good agreement with what is reported in the literature (Iyo et al., 2004; Yeni et al., 2004; Abdel-Wahab et al., 2011). The previous study has shown that the viscous behavior of bovine cortical bone involves two (fast and slow) discrete time-dependent processes (Iyo et al., 2004). Among them, the fast relaxation portion represents the viscoelastic response of bone and is independent of orientations (Iyo et al., 2004). This is also supported by the Dynamical Mechanical Analysis (DMA) tests on sheep cortical bone, showing that the viscoelastic parameters (loss tangent and storage modulus) are independent of orientations (Yeni et al., 2004). On the other hand, the magnitude of stress relaxation (Δσ0) actually corresponds to the contribution of the viscous component in bone to the loading bearing. Thus, the observation that Δσ0 was much greater in the longitudinal direction than in the transverse directions suggests that the viscous component in bone is more involved in the loading bearing when bone is loaded in the longitudinal direction. It is noteworthy to mention that whether some behaviors are anisotropy or not may depend on their definition. For example, expressing the magnitude of stress relaxation as a fraction of peak stress at the dwell may change the observed anisotropy.

In summary, elastic moduli and strengths of human cortical bone in compression are transversely isotropic. However, the underlying mechanism of post-yield deformation of human cortical bone may be independent of its orientations. Such information could help building the anisotropic constitutive models of human cortical bone, which are essential in the finite element modeling of bone as well as in the prediction of bone fragility in the elderly.

Acknowledgments

This study was financially supported by an NIH/NIAMS Grant (1R01AR055955) and an NSF/CREST Grant (HRD-0932339).

Footnotes

Conflict of interest statement

Each author in this manuscript does not have and will not receive benefits in any form from a commercial party related directly or indirectly to the content in this manuscript.

The authors declare that they have no competing financial interests.

References

  1. Abdel-Wahab AA, Alam K, Silberschmidt VV. Analysis of anisotropic viscoelastoplastic properties of cortical bone tissues. Journal of the Mechanical Behavior of Biomedical Materials. 2011;4:807–820. doi: 10.1016/j.jmbbm.2010.10.001. [DOI] [PubMed] [Google Scholar]
  2. Ashman RB, Rho JY, Turner CH. Anatomical variation of orthotropic elastic moduli of the proximal human tibia. Journal of Biomechanics. 1989;22:895–900. doi: 10.1016/0021-9290(89)90073-0. [DOI] [PubMed] [Google Scholar]
  3. Bargren JH, Andrew C, Bassett L, Gjelsvik A. Mechanical properties of hydrated cortical bone. Journal of Biomechanics. 1974;7:239–245. doi: 10.1016/0021-9290(74)90014-1. [DOI] [PubMed] [Google Scholar]
  4. Bayraktar HH, Keaveny TM. Mechanisms of uniformity of yield strains for trabecular bone. Journal of Biomechanics. 2004;37:1671–1678. doi: 10.1016/j.jbiomech.2004.02.045. [DOI] [PubMed] [Google Scholar]
  5. Bonfield W, Grynpas MD. Anisotropy of the Young’s modulus of bone. Nature. 1977;270:453–454. doi: 10.1038/270453a0. [DOI] [PubMed] [Google Scholar]
  6. Burstein AH, Reilly DT, Martens M. Aging of bone tissue: mechanical properties. Journal of Bone & Joint Surgery—American. 1976;58:82–86. [PubMed] [Google Scholar]
  7. Burstein AH, Zika JM, Heiple KG, Klein L. Contribution of collagen and mineral to the elastic–plastic properties of bone. The Journal of Bone and Joint Surgery—American. 1975;57:956–961. [PubMed] [Google Scholar]
  8. Cezayirlioglu H, Bahniuk E, Davy DT, Heiple KG. Anisotropic yield behavior of bone under combined axial force and torque. Journal of Biomechanics. 1985;18:61–69. doi: 10.1016/0021-9290(85)90045-4. [DOI] [PubMed] [Google Scholar]
  9. Courtney AC, Hayes WC, Gibson LJ. Age-related differences in post-yield damage in human cortical bone. Experiment and model Journal of Biomechanics. 1996;29:1463–1471. doi: 10.1016/0021-9290(96)84542-8. [DOI] [PubMed] [Google Scholar]
  10. Currey JD. Tensile yield in compact bone is determined by strain, post-yield behaviour by mineral content. Journal of Biomechanics. 2004;37:549–556. doi: 10.1016/j.jbiomech.2003.08.008. [DOI] [PubMed] [Google Scholar]
  11. Dempster WT, Liddicoat RT. Compact bone as a non-isotropic material. The American Journal of Anatomy. 1952;91:331–362. doi: 10.1002/aja.1000910302. [DOI] [PubMed] [Google Scholar]
  12. Dong XN, Guo XE. The dependence of transversely isotropic elasticity of human femoral cortical bone on porosity. Journal of Biomechanics. 2004;37:1281–1287. doi: 10.1016/j.jbiomech.2003.12.011. [DOI] [PubMed] [Google Scholar]
  13. Dong XN, Luo Q, Giri B, Wang X. Progressive post-yield behavior of human cortical bone in shear. Proceedings of the ASME Summer Bioengineering Conference; Famington, Pennsylvania. 2011. [Google Scholar]
  14. Ebacher V, Tang C, McKay H, Oxland TR, Guy P, Wang R. Strain redistribution and cracking behavior of human bone during bending. Bone. 2007;40:1265–1275. doi: 10.1016/j.bone.2006.12.065. [DOI] [PubMed] [Google Scholar]
  15. Evans FG. Mechanical properties and histology of cortical bone from younger and older men. Anatomical Record. 1976;185:1–11. doi: 10.1002/ar.1091850102. [DOI] [PubMed] [Google Scholar]
  16. Hoffmeister BK, Smith SR, Handley SM, Rho JY. Anisotropy of Young’s modulus of human tibial cortical bone. Medical & Biological Engineering & Computing. 2000;38:333–338. doi: 10.1007/BF02347055. [DOI] [PubMed] [Google Scholar]
  17. Iyo T, Maki Y, Sasaki N, Nakata M. Anisotropic viscoelastic properties of cortical bone. Journal of Biomechanics. 2004;37:1433–1437. doi: 10.1016/j.jbiomech.2003.12.023. [DOI] [PubMed] [Google Scholar]
  18. Katz JL. Anisotropy of Young’s modulus of bone. Nature. 1980;283:106–107. doi: 10.1038/283106a0. [DOI] [PubMed] [Google Scholar]
  19. Katz JL, Meunier A. The elastic anisotropy of bone. Journal of Biomechanics. 1987;20:1063–1070. doi: 10.1016/0021-9290(87)90024-8. [DOI] [PubMed] [Google Scholar]
  20. Katz JL, Yoon HS, Lipson S, Maharidge R, Meunier A, Christel P. The effects of remodeling on the elastic properties of bone. Calcified Tissue International. 1984;36(1):S31–S36. doi: 10.1007/BF02406131. [DOI] [PubMed] [Google Scholar]
  21. Kopperdahl DL, Keaveny TM. Yield strain behavior of trabecular bone. Journal of Biomechanics. 1998;31:601–608. doi: 10.1016/s0021-9290(98)00057-8. [DOI] [PubMed] [Google Scholar]
  22. Leng H, Dong XN, Wang X. Progressive post-yield behavior of human cortical bone in compression for middle-aged and elderly groups. Journal of Biomechanics. 2009;42:491–497. doi: 10.1016/j.jbiomech.2008.11.016. [DOI] [PMC free article] [PubMed] [Google Scholar]
  23. McCalden RW, McGeough JA, Barker MB, Court-Brown CM. Age-related changes in the tensile properties of cortical bone. The relative importance of changes in porosity, mineralization, and microstructure. Journal of Bone & Joint Surgery—American. 1993;75:1193–1205. doi: 10.2106/00004623-199308000-00009. [DOI] [PubMed] [Google Scholar]
  24. Morgan EF, Keaveny TM. Dependence of yield strain of human trabecular bone on anatomic site. Journal of Biomechanics. 2001;34:569–577. doi: 10.1016/s0021-9290(01)00011-2. [DOI] [PubMed] [Google Scholar]
  25. Novitskaya E, Chen PY, Lee S, Castro-Cesena A, Hirata G, Lubarda VA, McKittrick J. Anisotropy in the compressive mechanical properties of bovine cortical bone and the mineral and protein constituents. Acta Biomaterialia. 2011;7:3170–3177. doi: 10.1016/j.actbio.2011.04.025. [DOI] [PubMed] [Google Scholar]
  26. Nyman JS, Leng H, Dong XN, Wang X. Differences in the mechanical behavior of cortical bone between compression and tension when subjected to progressive loading. Journal of the Mechanical Behavior of Biomedical Materials. 2009;2:613–619. doi: 10.1016/j.jmbbm.2008.11.008. [DOI] [PMC free article] [PubMed] [Google Scholar]
  27. Ohman C, Baleani M, Pani C, Taddei F, Alberghini M, Viceconti M, Manfrini M. Compressive behaviour of child and adult cortical bone. Bone. 2011;49:769–776. doi: 10.1016/j.bone.2011.06.035. [DOI] [PubMed] [Google Scholar]
  28. Reilly DT, Burstein AH. The elastic and ultimate properties of compact bone tissue. Journal of Biomechanics. 1975;8:393–405. doi: 10.1016/0021-9290(75)90075-5. [DOI] [PubMed] [Google Scholar]
  29. Reilly DT, Burstein AH, Frankel VH. The elastic modulus for bone. Journal of Biomechanics. 1974;7:271–275. doi: 10.1016/0021-9290(74)90018-9. [DOI] [PubMed] [Google Scholar]
  30. Shi X, Liu XS, Wang X, Guo XE, Niebur GL. Type and orientation of yielded trabeculae during overloading of trabecular bone along orthogonal directions. Journal of Biomechanics. 2010;43:2460–2466. doi: 10.1016/j.jbiomech.2010.05.032. [DOI] [PMC free article] [PubMed] [Google Scholar]
  31. Turner CH. Yield behavior of bovine cancellous bone. Journal of Biomechanical Engineering. 1989;111:256–260. doi: 10.1115/1.3168375. [DOI] [PubMed] [Google Scholar]
  32. Wang X, Nyman JS. A novel approach to assess post-yield energy dissipation of bone in tension. Journal of Biomechanics. 2007;40:674–677. doi: 10.1016/j.jbiomech.2006.02.002. [DOI] [PMC free article] [PubMed] [Google Scholar]
  33. Wang X, Shen X, Li X, Agrawal CM. Age-related changes in the collagen network and toughness of bone. Bone. 2002;31:1–7. doi: 10.1016/s8756-3282(01)00697-4. [DOI] [PubMed] [Google Scholar]
  34. Yeni YN, Christopherson GT, Turner AS, Les CM, Fyhrie DP. Apparent viscoelastic anisotropy as measured from nondestructive oscillatory tests can reflect the presence of a flaw in cortical bone. Journal of Biomedical Materials Research Part A. 2004;69:124–130. doi: 10.1002/jbm.a.20128. [DOI] [PubMed] [Google Scholar]
  35. Yeni YN, Shaffer RR, Baker KC, Dong XN, Grimm MJ, Les CM, Fyhrie DP. The effect of yield damage on the viscoelastic properties of cortical bone tissue as measured by dynamic mechanical analysis. Journal of Biomedical Materials Research Part A. 2007;82:530–537. doi: 10.1002/jbm.a.31169. [DOI] [PubMed] [Google Scholar]
  36. Yoon HS, Katz JL. Ultrasonic wave propagation in human cortical bone—II. Measurements of elastic properties and microhardness. Journal of Biomechanics. 1976;9:459–464. doi: 10.1016/0021-9290(76)90089-0. [DOI] [PubMed] [Google Scholar]
  37. Zioupos P, Currey JD. Changes in the stiffness, strength, and toughness of human cortical bone with age. Bone. 1998;22:57–66. doi: 10.1016/s8756-3282(97)00228-7. [DOI] [PubMed] [Google Scholar]

RESOURCES