Abstract
Few investigations of health event clustering have evaluated residential mobility, though causative exposures for chronic diseases such as cancer often occur long before diagnosis. Recently developed Q-statistics incorporate human mobility into disease cluster investigations by quantifying space- and time-dependent nearest neighbor relationships. Using residential histories from two cancer case-control studies, we created simulated clusters to examine Q-statistic performance. Results suggest the intersection of cases with significant clustering over their life course, Qi, with cases who are constituents of significant local clusters at given times, Qit, yielded the best performance, which improved with increasing cluster size. Upon comparison, a larger proportion of true positives were detected with Kulldorf’s spatial scan method if the time of clustering was provided. We recommend using Q-statistics to identify when and where clustering may have occurred, followed by the scan method to localize the candidate clusters. Future work should investigate the generalizability of these findings.
Keywords: Geographic information systems, Residential mobility, Space–time clustering
1. Background
Disease cluster investigations often result in null findings (Schulte et al., 1987), prompting some to argue there is little value in studying clusters of health events (Rothman, 1990). This perception can be attributed to several factors: (1) historically, cluster investigations were limited to pre-identified subjectively defined disease clusters, as opposed to systematic examination of representative incidence data; (2) residential histories and thus disease latency were ignored; and (3) cases are typically aggregated into arbitrary geographic units, making results ecologic in nature, and subject to the modifiable area unit problem (Meliker et al., 2009; Rothman, 1990). In recent years, epidemiologists have collected detailed address information as part of a residential history for the purpose of geocoding and mapping residences, thereby permitting systematic examination of disease patterns over the life-course. Accurate and complete historical residence locations can be used to overcome the three main limitations described above.
Statistical approaches for investigating space–time patterns are being developed to aid in the analysis of geocoded residential history data in epidemiologic studies. While dozens of approaches are available for quantifying patterns on disease maps (e.g. Besag and Newell, 1991; Cuzick and Edwards, 1990; Kulldorff and Nagarwalla, 1995; Kulldorff et al., 2006; Tango and Takahashi, 2005; Turnbull et al., 1990; Waller and Turnbull, 1993; Waller et al., 1995), most of these tests were developed for spatially static datasets and do not account for mobile populations. Recently, several methods have been developed for investigating space–time patterns in mobility data (Jacquez et al., 2005; Sabel et al., 2009; Webster et al., 2006). Our group has been involved in development of Q-statistics for evaluating space–time clustering in residential histories of case-control data (Jacquez et al., 2005, 2006). The Q-statistics utilize nearest neighbor calculations to evaluate local and global clustering at any moment in the life-course of the residential histories of cases relative to the residential histories of controls.
Given the exploratory nature of space–time clustering investigations, these Q-statistics can be re-calculated whenever a participant changes residence and thus can result in hundreds or thousands of local test statistics depending on the mobility of the population. As a result of these multiple tests, interpreting statistical significance can be a challenge. Bonferonni-type corrections are known to be overly conservative (Hochberg, 1988), with alternatives making use of simulation studies of receiver operating curves and false discovery rate (FDR) adjustments (Kleinman and Abrams, 2006; Narum, 2006; Read et al., 2007; Caldas de Castro and Singer, 2005; Catelan and Biggeri, 2010). Approaches accounting for multiple testing that combine information from two of the Q-statistics, Qi and Qit are presented. These new approaches combine Qit and Qi to identify whether individuals with significant clustering over their life course co-occur in space and time.
The number of nearest neighbors (k) used to calculate a Q-statistic is a user-defined parameter. The selection of k is important, as a k too large can result in over-smoothing and a failure to detect smaller clusters, while a k too small may result in an inability to differentiate true and false positives (Cuzick and Edwards, 1990). Certain cluster and population characteristics influence the most appropriate k and performance of the Q-statistics; these include cluster density (number of cases relative to number of controls in the cluster region), size of the overall population, size of the cluster, and mobility of the population. Though we could not exhaustively evaluate each characteristic here because this would require hundreds of thousands of simulations, we did explore a range of different populations and geographies using different cluster sizes within multiple regions. In this report we create a series of clusters across a range of these cluster and population characteristics to examine performance of Q-statistics and sensitivity of results to choice of k nearest neighbors. Simulations are run using residential history data from two large case-control studies in the United States (US) and Denmark. Our objective is to use these simulations to (1) guide development of protocols for using and interpreting Q-statistics such that researchers can differentiate true local space– time clusters from false positives, and (2) to provide guidance on specification of the appropriate number of k nearest neighbors to use in an analysis.
2. Methods
2.1. Background on Q-statistics
Jacquez et al. (2005) develop global and local tests for case-control clustering of residential histories. Readers unfamiliar with Q-statistics may wish to refer to the original work; these are described briefly here. Q-statistics rely on a matrix representation that describes how spatial nearest neighbor relationships change through time. A person’s residential history is represented as a space–time thread using a step function (Fig. 1).
Fig 1.
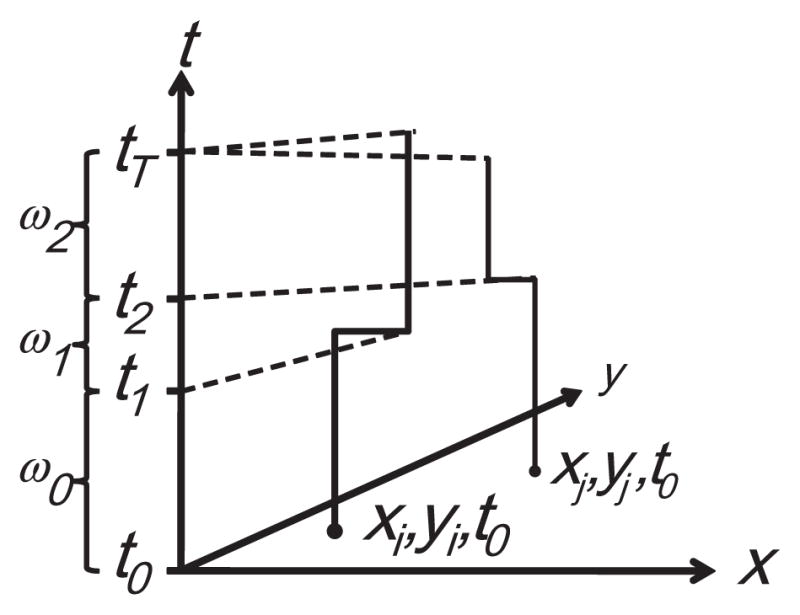
Residential histories as space–time step functions. The axes x and y define a geographic domain (e.g. longitude and latitude decimal degrees), the t axis represents time (e.g. date). The study extends from time t0 to time tT. The residential histories for persons i and j are shown as step functions through space–time. For example, person i begins the study residing at location xi, yi, t0. They remain at that geographic coordinate until the instant before time t1, when they move to xi, yi, t1. The duration of time they reside at this first place of residence is ω0.
To identify the location and timing of significant clustering, the following spatially and temporally local case-control cluster statistic is used:
| (1) |
This quantity is the count, at time t, of the number of k nearest neighbors of case i that are cases, and not controls. Individuals i and j have case-control identifiers, ci and cj defined to be 1 if and only if a participant i is a case, and 0 otherwise. N is the total number of participants (cases and controls) in a study. The term is a binary spatial proximity metric that is 1 when participant j is a k nearest neighbor at time t of participant i; otherwise it is 0. Since a given individual i may have k unique nearest neighbors, the statistic is in the range 0–k. When i is a control, . When i is a case, low values indicate cluster avoidance (e.g. a case surrounded by controls), and large values indicate a cluster of cases. When , at time t all of the k nearest neighbors of case i are cases. The user must specify the value for k before a statistic is calculated; guidelines on the specification of k is a topic of this research.
We also wish to calculate a subject-specific statistic that integrates through time (Eq. (2)).
When integration is accomplished over a subject’s residential history we think of this as a “life-course” statistic that assesses a tendency to have other cases, rather than controls nearby over the life-course
| (2) |
A time-specific statistic that provides an overall measure of case clustering when all of the participants are considered together is given in Eq. (3). It is the sum, over all cases, of the subject-specific and time-specific measure of case clustering in Eq. (1)
| (3) |
Analogous to Cuzick and Edwards test (Cuzick and Edwards, 1990), evaluates global clustering of cases at time t, such that the amount of case-clustering observed when all of the participants are considered together is evaluated. For convenience the summation is over the n1 cases. We call this a “global” test since it is comprised as the sum of the local statistic from Eq. (1)
| (4) |
Eq. (4) provides a global test that sums over the complete set of life course statistics from Eq. (2). It is used to evaluate whether there is significant life-course clustering of cases when all of the participants are considered together.
The unit of time used for the input of the data and subsequent interpretation of the results is user-defined (e.g. day, month, year,) and the local Q-statistics are thus capable of detecting periodicities (e.g. seasonal effects) such as might occur when influenza outbreaks occur during Fall and Winter months. However, the temporal resolution of the time-unit must be fine enough to not average over the periodicity of interest. One cannot, for example, pick up seasonal effects using an annual time resolution. For the analyses presented here, we input data with temporal resolution in years.
To summarize, Eq. (1) ( ) is used to identify when and where an individual is a center of a local cluster. Eq. (2) ( ) identifies which individuals tend to be centers of clusters over their life-course, but not when those clusters occur. Eq. (3) ( ) identifies which time periods display significant global clustering. Finally, Eq. (4) (global Q(k)) identifies whether global clustering tends to occur over the entire residential histories, but not when or where the clustering occurs. For brevity, the remainder of this paper dispenses with the superscript (k), but it is understood the value of the statistic depends on the specification of k. We then write Qit for the local statistic; Qi for the subject-specific life-course statistic, and Qt, the time-specific large-scale spatial cluster statistic.
2.2. Inferential framework
It is now well recognized that an understanding of the evolution, persistence and change in space–time disease patterns is essential in order to make inferences regarding possible underlying disease processes (Gallagher et al., 2010; Lahra and Kooistra, 2010; Myers, 2010; Ostro et al., 2010; Tunstall et al., 2010). With this in mind one may speculate on the kinds of disease models and processes that might give rise to different types of space–time disease patterns.
Sohowmight one use the Q-statistics to gain insights into specific etiologic hypotheses? Notice the subscript i is a case identifier, so Qit and Qi make statements regarding clustering about individual cases. How might these be used to generate inferences regarding space–time cluster processes?
Suppose we have n participants in a study, n1 of which are cases and n0 of which are controls. The beginning of the study period is t = 0, the end is t = T. Consider the sets defined as follows:
| (5) |
| (6) |
| (7) |
Here Q̃it is the set of all Qit that are statistically significant at the type I error level α, Q̃i is the set of all Qi that are statistically significant at α, and Q̃t is the set of all Qt that are statistically significant at α.
Recall that Qt and Qi are global statistics that assess case-clustering at specific times (e.g. Qt) and over the life course of specific cases (e.g. Qi) such that
| (8) |
and
| (9) |
(Eq. (9) is a simplified version of Eq. (3)). Hence the global statistics are the sums of the local statistics Qit. Thus there is a mapping of sets of the local statistics Qit to sets of significant statistics Q̃t and Q̃i. This mapping is comprised of those Qit that contribute to the significant Q̃i (through Eq. (6)) and those Qit that contribute to the significant Q̃t (through Eq. (7)). With this understood we now consider the following operations:
| (10) |
| (11) |
| (12) |
| (13) |
Notice the result of these operations will be sets of the local statistics Qit that contribute to the sets of significant global statistics that are the operands of Eqs. (10)–(13). These operations are represented in Fig. 2.
Fig 2.
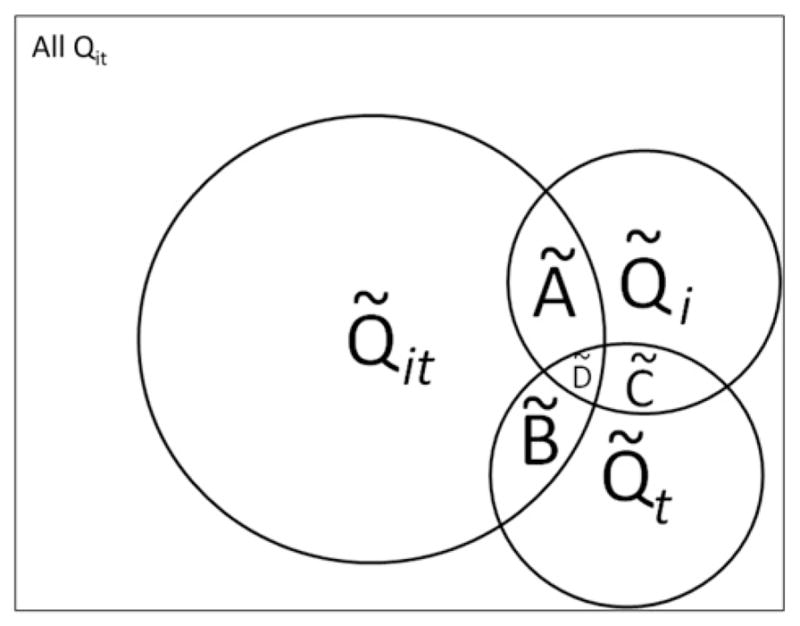
Venn diagram illustrating types of space–time clusters that can be identified using Q-statistics. The rectangle represents all Qit statistics in a study, significant or not. Each circle represents cluster sets that are found statistically significant (e.g. excess of cases about case i at time t, Q̃it ); over a cases life course (e.g. excess of cases about the residential history of case i, Q̃i); and globally at a given time t when all cases are considered together (e.g. large-scale spatial clusters at time t, Q̃t ). These cluster sets and their intersections (Ã; B̃; C̃; D̃) can yield insights into and generate hypotheses regarding disease etiologies. When the underlying Q-statistics have been adjusted for the risk factors and covariates found significant in the parent case-control study, these cluster types identify where, when and to whom to allocate unexplained (e.g. excess) risk (Table 1).
2.3. Assessing overall significance of cluster sets
Examples of etiologic patterns that may be detectable using the various described Q-statistics and their intersections are provided in Table 1. For instance, wide-spread clustering in the population at a specific time point (set B̃) could be suggestive of a Chernobyl-type incident where there is massive exposure at a single time point.
Table 1.
Description of cluster sets, summary space–time pattern descriptions, and example disease etiologies that may give rise to those patterns.
| Cluster set | Description | Pattern | Example etiology |
|---|---|---|---|
| Q̃it | Local case-time clustering | Cases (i) that at times t have a significant number of nearest neighbors that are cases | Infectious: contagious process such that infection spreads from a case to its susceptible neighbors. Vector-borne disease process such that individuals in specific areas have increased risk of infection Chronic (e.g. cancer): increased cancer risk for individuals residing in local areas over a defined time period Duration of elevated risk must be sufficiently long relative to the duration of time individuals live in the affected areas (e.g. exposure time must be sufficient to induce disease response) |
| Q̃i | Clustering over the life course | Cases (i) who, over the study period, have a significant number of nearest neighbors that are cases | Infectious: the “typhoid Mary” or “super-spreader” process, whereby case (i) (the super-spreader) is infectious over the study period and transmits infections to nearest neighbors. Vector-borne disease process where case i has behaviors that enhance the vector life-cycle (e.g. provides water receptacles such as empty cans and tires for container-breeding mosquitoes) Chronic (e.g. cancer): a process whereby neighbors of case i have increased cancer risk and such risk is elevated over the life course of case i. An example would be behaviors that increase cancer risk for others nearby such as second hand smoke. May also arise when groups with elevated risk tend to move or remain together over their life course (e.g. familial groups with common genetic and/or behavioral risk factors) |
| Q̃t | Temporal case clustering | Large-scale spatial clustering of cases at time t. Clustering of cases relative to controls is significant at time t when all cases and controls are considered | Infectious: infection outbreak such that the infection impacts a large portion of the study population; endemic phase of infection with multiple local outbreaks Chronic (e.g. cancer): chronic disease with an underlying infectious etiology (e.g. viral hypothesis of cancer) that impacts a large portion of the study participants; disease risk mediated by environmental exposures that vary across the study area such that risk is elevated for a large number of study participants. Duration of elevated risk must be sufficiently long relative to the duration of time individuals live in the affected areas (e.g. exposure time must be sufficient to induce disease response) |
| Ã | Q̃it ∩ Q̃i | Locations and times when cases with significant clustering over their life course are members of a geographically localized cluster. Includes both ephemeral and persistent clusters. |
Infectious: local geographic foci of periodic infections with long infectious periods from which some of the infected and infectious cases move away. Mobile infectious individuals infect others over their life course, leading to an elevated Qi statistic; infectious individuals who continue to reside in the area after an infectious period lead to a significant Qi statistic Chronic (e.g. cancer): local areas of persistent elevated risk that are sustained for a sufficient period of time that (1) disease risk is increased for individuals residing in the local area and (2) the duration of residence of cases in the area is of sufficient length to result in a significant Qi statistic |
| B̃ | Q̃it ∩ Q̃t | Local clusters of cases that occur over a large portion of the study area at time t | Infectious: large-scale outbreak at specific times, t, that may be comprised of local pockets of infection. For vector-borne diseases this can arise when large portions of the study area have suitable vector habitat during some parts of the study period Chronic (e.g. cancer): large scale exposures that occur at a specific time(s) t. An example would be leukemia in response to the Chernobyl and Hiroshima incidents |
| C̃ | Q̃t ∩ Q̃i | Cases that have clustering over their life course and are part of large-scale spatial clusters at times t Includes cases whose Qit are not statistically significant, and some whose Qit are statistically significant |
Infectious: large-scale outbreak at times t with at least some of the resulting cases that (i) move together over their life course; and/or (ii) remain infectious over their life course and continue to infect their neighbors. For a vector-borne disease this may arise when there is an initial large scale outbreak with some of the resulting cases continuing to be disease reservoirs (e.g. pathogen sources) whose infection can then be transmitted to others in the same family or tribal group Chronic (e.g. cancer): large scale exposures that occur at a specific time(s) t with some of the resulting cases that (i) move together through life course or (ii) continue to reside in the affected area over most of the study period |
| D̃ | Q̃it ∩ Q̃i ∩ Q̃t | Cases that have clustering over their life course, are part of large scale clusters at time t and whose local clusters Qit are all statistically significant. | Etiology is similar to set C̃, but is restricted to include only those individuals that are centers of significant local clustering of cases at times t. For infection, this may be indicative of index cases; for chronic diseases this may indicate individuals who are within local pockets of the largest exposure |
The cluster sets defined by Eqs. (5)–(13) are constructed using the local space time statistic Qit, the life course statistic Qi and the spatial clustering statistic Qt. The significance at a given α level yields membership in the sets illustrated in Fig. 2. Notice that the number of local statistics can be large, and the use of the nominal type I error α will yield false positives. It thus is necessary to derive approaches for evaluating the significance of the cluster types in Fig. 2 that are not subject to erroneous inference attributable to multiple testing.
Each cluster set defined in Table 1 is comprised of significant local statistics. For example recall from Eq. (5) that Q̃it = {Qit |P(Qit ≤ α); 1 ≤ i ≤ n1; 0 ≤ t ≤ T}. The number of elements in this set, |Q̃it |, in a setting where true clustering exists, is comprised of both true positives and false positives (call this ). Hence if we can evaluate the probability of under the null hypothesis of random labeling of the residential histories as cases or controls, and conditioned on the observed number of cases and controls, we will be able to evaluate significance of the size of the cluster sets in Fig. 2 with a single test. Put another way, we wish to evaluate the probability of observing the number of elements in the set Q̃it, an approach that avoids issues of multiple testing that occurs with the many possible local tests. Table 2 enumerates the test statistics we wish to evaluate, the cluster sets they correspond to, and the probabilities we wish to evaluate.
Table 2.
Statistics to evaluate the overall significance of the size of the cluster sets.
| Cluster type | Cluster description | Test statistic | Probability of test statistic | ||
|---|---|---|---|---|---|
| Q̃it | Local case-time |
|
|
||
| Q̃i | Life course |
|
|
||
| Q̃t | Temporal case clustering |
|
|
||
| Ã | Q̃it ∩ Q̃i | |
|
|
||
| B̃ | Q̃it ∩ Q̃t | |
|
|
||
| C̃ | Q̃t ∩ Q̃i |
|
|
||
| D̃ | Q̃it ∩ Q̃i ∩ Q̃t |
|
|
The predicted probabilities of the first three test statistics in Table 2 should follow a binomial probability. The general form of this probability is:
| (14) |
| (15) |
Here P(|Q̃|H0) is the probability of the cluster set denoted |Q̃| under the null hypothesis; these correspond to the entries in the column “probability of test statistic” in Table 2. |Q̃| is the cluster set being considered; these are the entries in the column “test statistic” in Table 2 and are the count of the number of significant clusters of that type. For example, recall that is the count of the number of participants that have significant clustering of cases about them over their life course. Here n(Q) is the total number of occurrences of the statistic under consideration, whether significant or not. For example, n(Qi) = n1, where n1 is the number of cases in the study. Table 3 enumerates n(Q) for the different cluster types. Finally, α is the desired type 1 error of the test, often set to α = 0.05.
Table 3.
Number of possible test statistics including those significant and not significant for each cluster set. Here n1t is the number of cases extant in the study area at time t.
As mentioned in the introduction, this research used simulated data to investigate the performance of the described Q-statistics. The characteristics of each simulated population are given in Table 4, and the background for this approach is explained in detail in Section 2.5. When we simulate data so there is no space–time case clustering, |Q̃it |H0| is the number of false positives observed under the null hypothesis. Notice the total number of possible tests as per Table 4 is , since the number of cases recorded in the data set will vary from one time to another, and since a local test is calculated for each case at each time point considered. The empirical type I error may then be estimated as
Table 4.
Characteristics of the simulated cluster regions.
| Number of cases | Cluster sizea (%) | Cluster densityb (%) | Case mobilityc (%) | |
|---|---|---|---|---|
| US Case-Control Dataset, Clusters Created in 1960 | ||||
| 1000 Residential histories | ||||
| Iowa | 5 | 1.0 | 100 | 99 |
| 12 | 2.4 | 100 | 90 | |
| 18 | 3.6 | 95 | 83 | |
| 27 | 5.4 | 90 | 84 | |
| Californiad | 43 | 8.6 | 63 | 47 |
| 2378 Residential histories | ||||
| Iowa | 6 | 0.5 | 75 | 87 |
| 14 | 1.2 | 70 | 80 | |
| 23 | 1.9 | 66 | 84 | |
| 33 | 2.8 | 69 | 78 | |
| Danish Case-Control Dataset, Clusters Created in 1971 | ||||
| 6594 Residential histories | ||||
| 11 | 0.3 | 89 | 50 | |
| 41 | 1.2 | 84 | 74 | |
| 90 | 2.7 | 82 | 70 | |
| 127 | 3.9 | 81 | 80 | |
Cluster size: percent of cases in cluster out of total number of cases in study.
Cluster density: percent of cases in cluster region out of total number of cases and controls in cluster region from 1960 to 1975 in US dataset, 1971 to 1980 in Danish dataset.
Case mobility: percent of person-years of cases in cluster region out of maximum possible person-years from 1960 to 1975 in US dataset, 1971 to 1980 in Danish dataset.
California cluster included all cases in the region in 1960, plus more residentially stable cases in the region from 1960 to 1975, as described in Section 2.
| (16) |
This can be calculated for Q̃i and Q̃t as
| (17) |
| (18) |
In practice we thus can calculate the empirical type I error rate for a specific data set with a given conformation of residential histories, number of cases and number of controls. We also can calculate the observed distribution of p-values ≤ ∝ that are observed for a given set (say ) under the null hypothesis and using a specific type I error (∝) and number of simulation runs. Notice this distribution is bounded on the right side by ∝, and on the left side by 1/nruns + 1, where nruns is the number of simulation runs conducted.
2.4. Adjusting for multiple testing
It is clear from Table 3 that the number of possible tests can become quite large, especially for the local test Qit when there are many cases and individuals are moving fairly often. One advantage of defining the cluster sets illustrated in Fig. 2 is that the underlying tests are based on the number of elements in a set of a given cluster type, for example . Should this statistic prove significant (e.g. ), we then may wish to identify those subsumed within the set that are themselves statistically significant. This is a much smaller number than the maximum number of Qi that can be calculated, yet we still have a multiple testing issue. One simple approach is to rank the p-values for the individual Q-statistics comprising the significant cluster set from smallest to largest, and the most extreme p-value (the smallest) is then the most likely cluster. This is similar in spirit to the scan statistic and other approaches that identify that most likely cluster as the one with largest likelihood. From this ranking we also can winnow out those test statistics that we might expect to be false positives at a given alpha, there are n(Q) (from Table 3) times alpha of these. The remaining elements in the cluster set are those test statistics found significant at the given alpha level, once the number of tests conducted is accounted for.
A second approach to adjusting for multiple testing is to use a traditional multiple test correction to control the family-wide error for each Q-statistic such as a Bonferroni correction or sequential methods like the Simes–Hochberg method (Simes, 1986; Hochberg, 1988; Hommel, 1988), but these approaches tend to be conservative, especially for exploratory tests.
A third approach we have used with some success is to control for the false discovery rate (FDR) (Benjamini and Hochberg, 1995). This approach evaluates the fraction of false positives among all tests declared significant, controlling for family-wide Type one error. Several variants of FDR approaches exist and an approach that allows us to optimally tune the threshold p-value we use for significance to achieve the desired FDR (Storey and Tibshirani, 2003) appears promising. This generates a q-value (no etymological relationship with Q-statistics) for each p-value based on the overall distributions of p-values. The q-value represents the proportion of false positives among significant tests if this particular p-value is used as the significance threshold. Choice of a critical q-value thus is determined by the desired FDR. An additional advantage is that this approach also estimates the total number of true positives (not just detected positives) in the family of tests, a measure of family-wide Type two error.
A fourth approach, and the one evaluated in this research, is disease process and pattern oriented, and for that reason seems most desirable. Here the idea is to identify the type of pattern one wishes to detect based on the disease process being considered, and to then use Table 1 to identify the type of cluster set one is interested in detecting. This requires some knowledge of the disease process being studied sufficient to formulate a prior hypothesis regarding the expected space–time patterns. In our studies, we simulate geographically-defined areas of excess risk that persist for several years. We therefore expect to find both clustering over the life course for cases that remain within the area of increased risk, and subject and time-specific case clustering for cases that migrate rapidly in and out of the area of elevated risk. Because the modeled risk areas are quite small and only a handful of cases are impacted, we do not expect to see time-specific global clustering over all cases. Returning to Table 1 and Fig. 2, this type of pattern corresponds to cluster set Ã, defined as Q̃it ∩ Q̃i. Within such a hypothesis-driven framework, the problem of multiple testing becomes less onerous, as we now can use significance of single cluster sets (e.g. set Ã,) as detailed above to evaluate space–time pattern. One of the diagnostics we will explore in our simulation design is the membership of cluster set Ã.
Specifically, we consider the significance of Qit and Qi together in order to identify when individuals with significant clustering over their life course co-occur in space and time. This hypothesis-driven approach based on space– time cluster processes to our knowledge has not been explored before. Because they represent human locations as a space–time thread (Fig. 1), Q-statistics are sensitive to clustering over the life course (using Qi which identifies individuals who have an excess of cases about them over their entire residential history) as well as clustering of cases at specific instances in time (using Qit which identifies local spatial clustering of cases at specific time points, t). The intersection of those (1) cases with significant clustering over their life course, with (2) cases who are constituents of significant local clusters at given times, t, may allow us to identify cases that are consistently in areas of higher rates and when, if only for a short time, they are detectable as clusters. Since we can use a single statistical test to evaluate the size of cluster set Ã, this approach could reduce the problem of multiple testing, although one still may wish to identify those individuals in cluster set à that are the most unlikely under the null hypothesis and have the smallest p-values.
Statistical significance of the individual subject and time specific Q -statistics is determined by randomizing the case-control identifiers over the residential histories under the null hypothesis of no association between places of residence and case-control status. Derivation of the theoretical distributions of the individual Q-statistics has yet to be accomplished, and therefore Monte Carlo simulations are used to generate distributions for hypothesis testing. These randomizations are conditioned on the number of cases and controls, the residential histories, and, for the local statistics, hold the case-identifier for the case being considered constant. Only case-control status is randomized, maintaining the integrity of the individual residential histories, which are then used to calculate the Q-statistics. The randomization procedure is repeated over many iterations to build up the distributions of the Q-statistics under the null hypothesis. When information on covariates and other risk factors is available, the null hypothesis can account for them by employing the adjusted probabilities of being a case as calculated from logistic regression (Jacquez et al., 2006), but this is not used in these simulations. Note that the range of possible p-values is determined by the number of randomizations of the null hypothesis applied. Given the computational power and time required for these analyses, 999 randomizations was the maximum reasonable number of iterations, generating a minimum p-value of 0.001. (At 999 randomizations each test of the Denmark dataset required approximately 12 h). Given that we investigated more than 50 individual simulation experiments (combinations of data sets, simulated clusters, and parameter values) for Qi, we required our most stringent possible threshold, a Qi p-value of 0.001 to be considered significant. We only investigated Qit among those individuals whose Qi is significant at the p = 0.001 level. We considered several possible p-values (0.05, 0.01, 0.001) for Qit; p = 0.05 showed the best performance with a high ratio of true positives to false positives. We combined Qi results with those from Qit analyses to identify membership in cluster set Ã, and to define the location and timing of significant clustering; a detailed examination of results is presented using simulated clusters. We also compare this combined Qi, Qit approach with SatScan (v.9.0.1) analyses.
2.5. Residential histories
Residential histories from two case-control studies were used to carry out simulations for different types of populations. Information about these populations is provided so the reader is familiar with population demographics; true case-control identifiers were not used in these simulations.
2.5.1. Case-control mobility data in the United States
Residential histories from a multi-center population-based case-control study of non-Hodgkin lymphoma (NHL) in the United States (US) were used in the simulations. This study comprised four areas of the US served by the National Cancer Institute (NCI) Surveillance, Epidemiology, and End Results (SEER) registries: the Detroit metropolitan area (Macomb, Oakland, and Wayne Counties), King and Snohomish counties in northwestern Washington State, the state of Iowa, and Los Angeles (LA) County (Chatterjee et al., 2004). Incident cases and controls, age 20–74, were recruited during the period from July 1, 1998 to June 30, 2000, producing 2378 participants. Participants were approximately evenly drawn from the four areas. For the purpose of these simulations, we created a base dataset of 1189 individuals randomly assigned to be cases, and 1189 controls.
Participants provided written residential histories of each home they lived-in for at least six consecutive months, which were reviewed during an in-person interview. Participants lived in eight or nine residences, on average over their lifetime, and most lived in single-family homes at time of diagnosis or selection. There were 21,442 different homes reported for the 2378 participants, accounting for 99.6% of total person-years. The duration of residence and exact street address were requested. If exact street address was not known, participants were asked to provide their best attempt at a complete address. Addresses were geocoded using Geographic Data Technology’s MatchMaker SDK Professional Version 4.3. The latitude and longitude returned is based on the coordinate projection NAD 83 and is set to an offset of 25′ from the centerline of the street segment. Of the residences within the study states, 74% were automatically geocoded or interactively geocoded with minor operator assistance. The addresses not matched at the street-level were geocoded to zip code centroid yielding cases and controls at the same location (8%); otherwise, the address was not matched (12%). Geocoding efficiency decreased in areas outside of the study states due to more frequent missing street information for older addresses. All geocoded locations were used in the simulation analyses.
2.5.2. Case-control mobility data in Denmark
Residential histories from a testicular cancer case-control study in Denmark were also used for simulations. The complete dataset contains 1:1 matching of 3297 case-control pairs. Cases represent all males with primary diagnosis of testicular cancer in Denmark from 1991 to 2003, and with complete residential histories dating to 1971. Controls were matched on date of birth, and also had complete residential histories. Residential histories beginning in 1971 were available from the Danish Civil Registration System (CRS) and linked to case-control data. The addresses were linked to a register of all official addresses in Denmark, resulting in geographic coordinates for 98% of the addresses (44,897/45,813). The remaining 2% of the addresses could not be geocoded. In the geocoding procedure of the 44,897 addresses that matched with the register, 90% of the addresses of both cases and controls matched to the exact house (defined within 5 m of the front door of the house). Five percent matched to the street level, and the last 5% were geocoded to municipality centroid (average size of a municipality in Denmark before 2007 was 158 km2).
Density and movement of populations are important considerations when designing statistics specifically to incorporate residential mobility. In most populations, higher density areas (urban) typically experience higher mobility than rural areas. The density and amount of mobility could potentially influence the ability for Q-statistics to detect clusters. Therefore, these characteristics are used to define cluster regions in the simulation studies, as further described in the following section.
2.6. Simulation analyses
Clusters of multiple size and density were created in different geographic regions to evaluate performance of the Q-statistics under a range of scenarios. As established metrics do not yet exist for describing and characterizing space–time clusters, we defined quantitative measures of our own which we think well-describe their primary characteristics (Table 4). These are: number of cases: the number of cases in a cluster, cluster size: the percent of cases in the cluster region out of the total number of cases in the study, cluster density: the percent of cases in the cluster region out of the total number of participants in the cluster region, and case mobility: the percent of person-years of cases in the cluster region out of the maximum possible person-years of cases in the cluster region over a given time period. These metrics were used to help assess the relationship between characteristics of clusters, sensitivity to choice of k nearest neighbors, and performance of Q-statistics. A comprehensive examination of the relative importance of these cluster characteristics would involve creating a series of simulated clusters changing only one characteristic at a time. Given five characteristics of clusters (size, density, mobility, location, number of cases), two-to-three values for each characteristic, and the importance of investigating sensitivity to different datasets and geographies, a comprehensive examination would require hundreds of simulations using repeated analyses to investigate sensitivity to k. Given the impractical magnitude of such an exercise, we created several simulated clusters with a range of characteristics to begin to evaluate performance of the Q-statistics and sensitivity to k.
2.6.1. Simulated clusters in US case-control residential histories
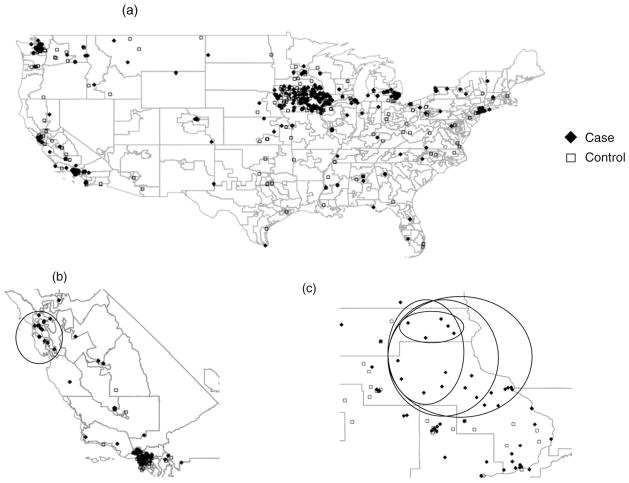
Case-control status was first randomly assigned to each individual’s residential history. No clusters would be expected in this randomized dataset. We then randomly selected 500 cases and 500 controls to create a partial dataset to more efficiently run repeated analyses since very large datasets can be computationally intensive. Four clusters were created in Iowa of increasing size (Fig. 3). The created clusters overlap in order to maintain consistency with regard to other cluster characteristics such as mobility, resulting in a more controlled test than placing the clusters in different locations. We created a cluster by defining an area as being high-risk from 1960 to 1975, such that almost everyone who lived in that area during the time period was designated as a case (Table 4). We began with a cluster region composed of 5 cases and 0 controls, then expanded outward geographically to 12 cases and 0 controls, and then to 18 cases and 1 control, and finally, to 27 cases and 3 controls. These cases, on average spent 13 years in the cluster region, with many cases not moving for decades. Separate analyses were run on each cluster. We note that these clusters are very small compared to many of the simulation studies published to date, but in our estimation they are more realistic in representing highly local elevations in disease risk.
Fig 3.
(a) Randomized case-control status for individuals in the NHL study in 1960; (b) simulated cluster region in California, 1960; (c) four simulated cluster regions in Iowa, 1960. Locations jiggled to preserve anonymity.
A second cluster region was added to the 500 case, 500 control dataset, and was located in Northern California, including San Francisco, among a more mobile population. This mobile population was selected to compare results with those from the residentially stable Iowa clusters. The cluster included all 20 individuals (defined as cases) living in that area in 1960, plus 23 other cases who lived in the area between 1960 and 1975. This resulted in a cluster region comprised of 43 cases living in the area for an average of seven years each between 1960 and 1975, and another 25 controls who spent an average three years in the cluster area. Simulation analyses were first run using just the created California cluster, and then using both the California cluster region and the largest Iowa cluster region (N = 27 cases) to determine whether Q-statistics behave similarly when using more than one cluster region.
The Iowa cluster simulation was expanded to the full dataset (N = 2378 participants) to produce clusters characterized by a range of values for sample size, cluster size, cluster density, and number of cases in a cluster. The randomized case-control dataset was used along with the same Iowa cluster cases described for the partial dataset; the California cluster was not included in these analyses (Table 4). Cases in the cluster regions came from two sources: (a) those defined as Iowa cluster cases in the partial dataset plus (b) those defined as cases by randomization of case-control status in the full dataset. There were 6 cases and 2 controls residing in the smallest geographic cluster area between 1960 and 1975. In progressively larger cluster areas, there were 14 cases and 6 controls; then 23 cases and 12 controls; and finally, 33 cases and 15 controls.
2.6.2. Simulated clusters in Danish case-control residential histories
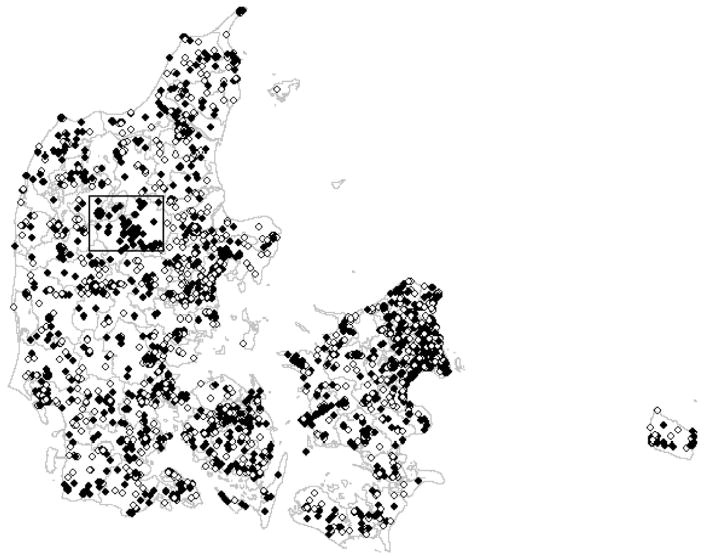
Clusters were also created in the larger Danish dataset of 3297 case-control pairs (6594 residential histories) to further examine impact of sample size, cluster size, cluster density, number of cases in a cluster, and case mobility on Q-statistic performance. Like the US dataset, case-control status was first randomized so that no clusters would be expected. We then selected a relatively low-mobility area in a central region of Denmark and assigned everyone within a square perimeter a case in 1971 (Fig. 4). The region was enlarged three times to create a total of four different clusters to be tested (Table 4). Between 1971 and 1980 the four cluster regions included 11 cases and 1 control, 41 cases and 10 controls, 90 cases and 21controls, and 127 cases and 34 controls, respectively.
Fig 4.
A large simulated cluster is framed in Denmark in 1971. Cases are represented as black diamonds, while controls are white. Locations jiggled to preserve anonymity.
2.6.3. Cluster analyses
In both case-control datasets, the sensitivity of the clustering statistics to k = 5, 10, 15 and 20 nearest neighbors was evaluated on each pre-defined cluster and on the randomized dataset that did not contain any clusters. For each scenario, the global statistic Q, the local statistics Qi and Qit, and the associated p-values were calculated. We also analyzed each of the intersecting sets described in Eqs. (10)–(15) and shown in Table 2, as a means of determining which individual Qit’s were driving the other statistics.
When multiple individuals were declared significant centers of local clusters by Qi and Qit, we needed to assess whether they were part of the same cluster or part of unique clusters. This assessment was based on the number of k-nearest neighbors used in calculating the Q-statistics. For example, if k = 15 and two significant cases would be among each other’s 15 nearest neighbors, then they were defined as part of the same cluster; otherwise they would be labeled as part of separate clusters.
The Q-statistics were calculated in SpaceStat (v.2), and circular spatial scan statistics were calculated using SatScan (v.9.0.1), specifying the Bernoulli model for case-control data with a maximum cluster size equal to 50% of the study population.
3. Results
The global Q statistic (Eq. (4)) and the cluster set statistics (Tables 1 and 2) were consistently significant in detecting clusters of size 18 and 27 in Iowa in the 500 case, 500 control dataset in the US (Supplementary Table 1). These statistics, however, were unable to consistently detect the California cluster whose members had greater mobility compared with Iowa; the Iowa clusters in the 1189 case, 1189 control dataset, where clusters were smaller and less densely populated with cases than the Iowa clusters in 500 case, 500 control dataset; or the clusters in the large 3297 case, 3297 control Danish dataset. This performance of the global Q statistic is not unexpected, as global statistics are known to be insensitive to local elevations in risk in a larger population. As a global statistic, Q is designed to be sensitive to a clustering of residential histories of the cases relative to the controls that affects a large number of participants and is persistent through time (a big signal). It thus may prove to be more useful in studies of infectious diseases with an underlying contagious process. The cluster set statistics, on the other hand, were developed to identify signals for a range of different types of clusters. The cluster set statistics for Qt and for Qit, Qi (Ã, Table 1) were also able to detect the larger clusters in Iowa in the full dataset (Supplementary Table 1); however none of the cluster set statistics were significant in detecting the clusters in Denmark.
We also considered whether the local Qi and Qit statistics together might be able to identify case members of the simulated clusters. Using a critical value of p = 0.05, each of these statistics identified significant case members of the true cluster regardless of cluster size or number of k nearest neighbors; however they also identified cases in many other regions as significant, indicating type 1 error (not shown) and confirming the need to account for multiple testing. Setting the critical value to p = 0.001 for Qi improved performance. All significant Qi cases also were significant p < (0.05) for Qit during the time when the cluster was simulated, indicating Qi and Qit together were able to identify where and when true clusters occurred among strong clusters. Smaller critical values for Qit were investigated (<0.01, 0.001), but these values did not improve differentiation of true positives from false positives. Supplementary Table 1 shows, for each simulation, analyses and results for increasing levels of k using Qi (p = 0.001) and Qit (p < 0.05) together to define a true positive. The numbers of true and false positive individuals (i.e. significant Q-statistics in and outside of the simulated cluster region) are reported, along with the size of the largest false positive cluster. False positives were detected but never more than three in a given cluster region under all simulation scenarios. Therefore, for interpretation in this rule set, a benchmark of a cluster of at least four individuals in the simulated cluster region is considered a “true” cluster. Although intuitive and useful for application to these simulation results, using this type of a strict cutoff should be approached cautiously to other studies in other regions. The strongest clusters, those defined as larger, more dense clusters in low mobility areas, were detected more easily with 11–13 significant case members of a true positive cluster for k = 10 or 15 in the Iowa 27 case cluster region of the 500 case, 500 control dataset, and 5–30 true positive cases for k = 5, 10, 15, or 20 in the 127 case cluster region of the 3297 case, 3297 control Danish dataset. Among smaller clusters, those less densely comprised of cases, or those containing more mobile populations, there was diminished ability to differentiate true positives from false positives (Supplementary Table 1).
Results were somewhat sensitive to choice of k-nearest neighbors used for calculating the Q-statistics within a range of k = 5–20. True positives were detected in the strongest clusters for a range of k-nearest neighbors, although as the choice of k approached the number of cases in the cluster, there was diminished ability to detect the cluster. For example, in the Iowa 27 case cluster region of the 500 case, 500 controls dataset, there were 3, 13, 11, and 6 significant case members of a true positive cluster for k = 5, 10, 15, or 20 nearest neighbors, respectively. In the Denmark dataset there was an increase in the number of true positives as the number of cases increased. Higher k’s (15 and 20) were more successful at locating the larger clusters in this dataset than were the smaller k’s. For example in the cluster containing 90 cases and 21 controls ever living in the cluster region of Denmark between 1971 and 1980, a k of 10 found 2 true positives and 0 false positive. A k of 15 found 10 true positives and 0 false positives.
Last, we compared results using the Q-statistics with those using the spatial scan method implemented in SaTScan (Table 5). Importantly, whereas SaTScan is able to detect clusters at different time periods, it is not able to incorporate residential mobility. SaTScan was run using residential locations in the year of the greatest simulated clustering (1960 for the US datasets, 1971 for the Danish datasets). Given this guidance, there was a good deal of similarity in the results although SaTScan was able to detect clusters with a p-value <0.05 more frequently than the Q-statistics. Both methods were unable to detect cluster sizes smaller than 15.
Table 5.
Summary table of Q-statistic and SaTScan detection of simulated clusters. (Please see Supplementary Table 1 for complete results).
| Cluster region | N cases in cluster | k nearest neighbors | Q-stats detecteda | SaTScan detectedb |
|---|---|---|---|---|
| Iowa (500 cases, 500 controls) | 0 | 5, 10, 15, 20 | N | N |
| 5 | 5, 10, 15, 20 | N | N | |
| 12 | 5, 10, 15, 20 | N | N | |
| 18 | 5, 10 | N | Y | |
| 15 | Y | Y | ||
| 27 | 5 | N | Y | |
| 10, 15, 20 | Y | Y | ||
| California (500 cases, 500 controls) | 43 | 5, 10, 15, 20 | N | Y |
| California + Iowa (500 cases, 500 controls) | 43 CA, 27 IA | 5, 10, 15,20 | Yc | Y |
| Iowa (1189 cases, 1189 controls) | 0 | 5, 10, 15 | N | N |
| 6 | 5, 10, 15 | N | N | |
| 14 | 5, 10, 15 | N | N | |
| 23 | 5, 10 | Y | N | |
| 15, 20 | N | N | ||
| 33 | 5, 10 | N | Y | |
| 15 | Y | Y | ||
| 20 | N | Y | ||
| Denmark (3297 cases, 3297 controls) | 0 | 5, 10, 15, 20 | N | N |
| 11 | 5, 10, 15, 20 | N | N | |
| 41 | 5, 10, 15 | N | Y | |
| 20 | Y | Y | ||
| 90 | 5, 10 | N | Y | |
| 15, 20 | Y | Y | ||
| 127 | 5, 10, 15, | Y | Y | |
| 20 |
At least four individuals in a cluster with Qi < 0.001 and Qit < 0.05.
p-Value < 0.05.
Only the Iowa cluster was detected (not California).
4. Discussion
This report presents the first simulation analyses of the recently developed Q-statistics for examining space–time cancer clustering in case-control residential histories. Overall, simulations indicate global Q and the cluster set statistics are conservative and exhibit type II error, unable to identify the majority of the simulated clusters. This is not surprising for global Q since global tests, by definition, are sensitive to clustering that affects most if not all of the cases in the dataset, a scenario not considered in the simulation design. The cluster set statistics, however, were designed to identify signals for a range of different types of cluster sizes but were unable to detect any of the simulated clusters in Denmark. When considered together, local Qi and Qit showed strong performance across the range of geographic areas, identifying larger, denser true clusters, with few false positives, using a critical value for Qi of p = 0.001 and p ≤ 0.05 for Qit only among those individual cases significant for Qi. In our simulations, a critical value of 0.01, or 0.001 for Qit resulted in the elimination of several true positives. Selection of these joint Qi, Qit statistics is a direct consequence of disease process pattern theory we develop here (Table 1); for localized cancer clusters we would expect to see local significance (Qit) and individual case significance (Qi) when the cluster may persist for some time, or when there is little residential mobility. The spatial scan method detected a larger proportion of the true positives, but only after knowledge of when the clustering occurred was provided as prior information. These results suggest using joint Qi, Qit statistics to identify when and where clustering may have occurred, followed by the scan method to localize the candidate clusters.
The computational time for each analysis when run on a single desktop can be quite high (>12 h for a dataset of 6000 individuals). An analysis of the algorithm suggests a maximum computational time of f(n) = O(n2)log(n); see Supplementary Table 2 and Supplementary Fig. 1 for details on computational time). Therefore conducting a full sweep of Q-statistics at many different k’s, or enough randomizations to calculate small p-values is computationally unreasonable for many investigations. Within a small range of k’s (5–20) and no more than 999 randomizations we found k of 15 is consistently useful as a starting point. k = 5 proved less efficient at differentiating true and false positives, while, for smaller clusters, larger k’s begin to over-smooth the data and reduce the cluster signal. For the cluster simulations in Denmark it was determined that a k of 20 may provide more true positives, though k = 15 also performed well. According to the patterns seen in our results, a cluster of four individuals or larger using k = 15 could safely be called a true positive and is a good starting point for follow-up studies with these datasets.
When deciding if a dataset or scientific question can be appropriately approached with Q-statistics, the two most important considerations are whether the population is sufficiently large and sufficiently mobile. As our results have demonstrated, the larger a population, the more statistical power there will be to detect true clusters and avoid false positives. In some situations (e.g. some of the Iowa/California simulations shown here) small true cluster sizes can be difficult to detect. If the disease under study is, for example, a rapidly moving infectious disease, then it may be reasonable to assume a priori that there will be large true clusters and therefore easier to detect. However, for chronic diseases where the presence of true clusters cannot be assumed, it is especially important to use other methods (such as scan statistics) to confirm findings, once Q-statistics have been used to focus in on potential times when clusters may have occurred.
The strength of Q-statistics is their ability to incorporate human mobility. Therefore, if the population under study is static, other cluster detection methods will perform well and the comparatively high computational requirements of Q-statistics are not warranted. Mobility may be defined on different temporal scales; for instance, movement over the course of a week in an infectious disease study, or movement over the course of years in investigation of a chronic disease. Investigators should examine the average number of location changes per individual, and consider their scientific question to determine whether Q-statistics are the best possible method. Some potential scenarios that may be appropriately approached with Q-statistics are given in Table 1.
There is no established protocol for defining space–time clusters in mobile populations. In the spatial-only realm, it is straightforward to define and calculate cluster size and cluster density. When considering mobility, however, one must consider that cases may spend different durations of time in a cluster region, and this needs to be incorporated into the definition of a cluster. In these simulations, we characterized clusters by their number of cases, size, density, and mobility. In creating many different types of clusters in two large residential history datasets, we arrived at a rule of thumb to help distinguish true clusters from false positives. This rule of thumb, a cluster of 4 or more individuals (Qi, p = 0.001 and Qit p ≤ 0.05) using k = 15, however, was successful only for distinguishing dense, large, low mobility clusters. Even when successfully identifying cluster regions, not all members of a cluster region were identified as significant cases; this is a consequence of lower density clustering around the edges of a simulated cluster region and the stringent p-value used for determining significance. Smaller, less dense clusters were also not captured by this rule of thumb; however at this stage in development of space–time cluster statistics, we feel this is an acceptable compromise since it limits inquiry into false positives, thereby conserving limited resources for more thorough investigations of true clusters.
While many scenarios and simulations were considered, one cannot explore the entire space of possible clusters nor the entire span of possible geographies and populations; therefore generalizability of these results is uncertain. Given differences such as edge effects, population density, mobility patterns, case-control ratio, and cluster shape, size, and density, additional research is needed to determine the broad applicability of our findings. In addition, we have not yet examined sensitivity of Q-statistics to the influence of temporal resolution, e.g. days, weeks, months, seasons, or years, or temporal orientation, e.g. age, calendar year, or years prior to diagnosis (analogous to age-period-cohort modeling in epidemiology) (Meliker and Jacquez, 2007). Other future research avenues include quantifying the relative importance of cluster size, density, and case mobility in determining characteristics of clusters detectable by Q-statistics, and exploring alternatives for multiple testing adjustments in Qit. Characterizing the influence of nonresponse and geocoding incompleteness/inaccuracies on clustering patterns through time is also important in many datasets. Comparing results of Q-statistics with other recently developed cluster detection methods for mobile populations (Sabel et al., 2009; Webster et al., 2006) is an important research direction.
We had hoped the cluster set statistic for joint Qit, Qi (Ã, Table 1) could be used to narrow down which individuals to investigate for significant local Qi, and Qit clusters. However, the cluster set statistics were not sensitive enough to detect several of the simulated clusters, especially those in the large Danish dataset. Future investigations may identify circumstances in which these cluster set statistics are able to assist in cluster detection. These joint Qit, Qi statistics appear to be potentially important diagnostics of space–time cluster processes.
Analysts looking to conduct Q-statistics on their own data can use these results to help guide their analytic strategy. As a first step, we believe that researchers should conduct their own set of simulation analyses similar to these in order to determine the best criteria (p-values, number of k nearest neighbors) for identifying true positive clusters. Ideally, this could be created using the researchers own data, specifically the geography in the study, observed residential histories, and the actual number of cases and controls, along the line of simulation designs used in cluster morphology analysis (Jacquez, 2009). If the user has an a priori hypothesis about cluster size (which is rarely the case), then k can be specified at a value smaller than the anticipated cluster size, and need not be explored. If a simulation experiment is not practicable, based on results presented here we recommend starting with k = 15 as an initial investigation. A cluster of 4 or more individuals (Qi, p = 0.001 and Qit p ≤ 0.05) will point toward a region of potential clustering. Further comparisons can then be made using FDR-adjusted Q-statistics if the dataset is not too large. Additionally, once a cluster is identified during a known time period, spatial-only clustering methods could be adopted for comparison (e.g. SaTScan) (Kulldorff et al., 2006). SaTScan was shown to be highly useful at identifying true clusters after Q-statistics have narrowed the range of possible years and locations.
Q-statistics, a space–time extension of the established Cuzick–Edwards’ test for clustering in static case-control populations, enable scientists to investigate clustering in mobile populations, overcoming many of the limitations of previous cancer clustering analyses (Rothman, 1990). The real test of these statistics, however, is whether or not they will identify space–time clusters which can be linked with potential environmental causes; future analyses by our group for cancers of the testis, breast, and NHL, should help answer this question.
In these simulations, Q-statistics have shown that they are able to perform well for detecting large clusters in a wide variety of situations and that applying Q-statistics with a relatively small range of k’s is sufficient to be able to separate false and true positive significant individuals at centers of clusters. Results of these simulations produced a guide for interpreting clustering results from analyses of these two case-control datasets; however, additional work is needed to investigate whether this guide can be generalized to other case-control study populations.
Supplementary Material
Acknowledgments
This research was funded by the US National Institute of Environmental Health Sciences, R21 ES015501, and the National Cancer Institute R03 CA125827, 5R44CA135818- 03, and 5R44CA112743-03. The perspectives are those of the authors and do not necessarily represent the official position of the funding agency. We thank Patricia Hartge, ScD, principal investigator of the NCI-SEER NHL case-control study for use of the data, and Andy Kaufmann and Robert Rommel of BioMedware for their useful discussions of Q-statistics and for programming support. We also acknowledge the contribution of the staff and scientists at the SEER centers of Iowa, Los Angeles, Detroit, and Seattle for the conduct of the study’s field effort. The NCI-SEER study was supported by the Intramural Research Program of the National Cancer Institute, National Institutes of Health, Public Health Service (Contracts N01-PC-65064, N01-PC-67008, N01-PC-67009, N01-PC-67010, N02- PC-71105).
Appendix A. Supplementary data
Supplementary data associated with this article can be found, in the online version, at http://dx.doi.org/10.1016/j.sste.2012.09.002.
References
- Benjamini Y, Hochberg Y. Controlling the false discovery rate: a practical and powerful approach to multiple testing. J R Stat Soc Series B Stat Methodol. 1995;57:289–300. [Google Scholar]
- Besag J, Newell J. The detection of clusters in rare diseases. J R Stat Soc A. 1991;154:143–55. [Google Scholar]
- Caldas de Castro M, Singer BH. Controlling the false discovery rate: a new application to account for multiple and dependent tests in local statistics of spatial association. Geogr Anal. 2005;38:180–208. [Google Scholar]
- Catelan D, Biggeri A. Multiple testing in disease mapping and descriptive epidemiology. Geospat Health. 2010;4:219–29. doi: 10.4081/gh.2010.202. [DOI] [PubMed] [Google Scholar]
- Chatterjee N, Hartge P, Cerhan JR, Cozen W, Davis S, Ishibe N, Colt J, Goldin L, Severson RK. Risk of non-Hodgkin’s lymphoma and family history of lymphatic, hematologic, and other cancers. Cancer Epidemiol Biomarkers Prev. 2004;13:1415–21. [PubMed] [Google Scholar]
- Cuzick J, Edwards R. Spatial clustering for inhomogeneous populations. J R Stat Soc B. 1990;52:73–104. [Google Scholar]
- Gallagher LG, Webster TF, et al. Using residential history and groundwater modeling to examine drinking water exposure and breast cancer. Environ Health Perspect. 2010;118:749–55. doi: 10.1289/ehp.0901547. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hochberg Y. A sharper Bonferroni procedure for multiple tests of significance. Biometrika. 1988;75:800–2. [Google Scholar]
- Hommel G. A stagewise rejective multiple test procedure based on a modified Bonferroni test. Biometrika. 1988;75:383–6. [Google Scholar]
- Jacquez GM. Cluster morphology analysis. Spat Spatiotemporal Epidemiol. 2009;1:19–29. doi: 10.1016/j.sste.2009.08.002. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Jacquez GM, Kaufmann A, Meliker J, Goovaerts P, AvRuskin G, Nriagu J. Global, local and focused geographic clustering for case-control data with residential histories. Environ Health. 2005;4:4. doi: 10.1186/1476-069X-4-4. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Jacquez GM, Meliker JR, AvRuskin GA, Goovaerts P, Kaufmann A, Wilson M, Nriagu J. Case-control geographic clustering for residential histories accounting for risk factors and covariates. Int J Health Geogr. 2006;5:32. doi: 10.1186/1476-072X-5-32. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kleinman KP, Abrams AM. Assessing surveillance using sensitivity, specificity and timeliness. Stat Methods Med Res. 2006;15:445–64. doi: 10.1177/0962280206071641. [DOI] [PubMed] [Google Scholar]
- Kulldorff M, Nagarwalla N. Spatial disease clusters: detection and inference. Stat Med. 1995;14:799–810. doi: 10.1002/sim.4780140809. [DOI] [PubMed] [Google Scholar]
- Kulldorff M, Huang L, Pickle L, Duczmal L. An elliptic spatial scan statistic. Stat Med. 2006;25:3929–43. doi: 10.1002/sim.2490. [DOI] [PubMed] [Google Scholar]
- Lahra J, Kooistra L. Environmental risk mapping of pollutants: state of the art and communication aspects. Sci Total Environ. 2010;408:3899–907. doi: 10.1016/j.scitotenv.2009.10.045. [DOI] [PubMed] [Google Scholar]
- Meliker JR, Jacquez GM. Space-time clustering of case-control data with residential histories: insights into empirical induction periods, age-specific susceptibility, and calendar year specific effects. Stoch Environ Res Risk Assess. 2007;21:625–34. doi: 10.1007/s00477-007-0140-3. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Meliker JR, Jacquez GM, Goovaerts P, AvRuskin GA, Copeland G. Breast and prostate cancer survival in Michigan: can geographic analyses assist in understanding racial disparities? Cancer. 2009;115:2212–21. doi: 10.1002/cncr.24251. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Myers SM. Connecting the demographic dots: geographic mobility and birth intentions. J Fam Issues. 2010;31:1622–51. [Google Scholar]
- Narum SR. Beyond Bonferroni: less conservative analyses for conservation genetics. Conserv Genet. 2006;7:783–7. [Google Scholar]
- Ostro B, Lipsett M, Reynolds P, Goldberg D, Hertz A, Garcia C, Henderson K, Bernstein L. Long-term exposure to components of fine particulate air pollution and mortality: the California teachers study. Environ Health Perspect. 2010;118:363–9. doi: 10.1289/ehp.0901181. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Read J, et al. A test of association between spatially defined exposure patterns and health outcome risk contours. J Toxicol Environ Health A. 2007;70:2056–63. doi: 10.1080/15287390701601210. [DOI] [PubMed] [Google Scholar]
- Rothman KJ. A sobering start for the cluster busters’ conference. Am J Epidemiol. 1990;132(1 Suppl):S6–S13. doi: 10.1093/oxfordjournals.aje.a115790. [DOI] [PubMed] [Google Scholar]
- Sabel CE, Boyle P, Raab G, Löytönen M, Maasilta P. Modeling individual space–time exposure opportunities: a novel approach to unraveling the genetic or environment disease causation debate. Spat Spatiotemporal Epidemiol. 2009;1:85–94. doi: 10.1016/j.sste.2009.07.002. [DOI] [PubMed] [Google Scholar]
- Schulte PA, Ehrenberg RL, Singal M. Investigation of occupational-cancer clusters – theory and practice. Am J Public Health. 1987;77:52–6. doi: 10.2105/ajph.77.1.52. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Simes RJ. An improved Bonferroni procedure for multiple tests of significance. Biometrika. 1986;73:751–4. [Google Scholar]
- Storey JD, Tibshirani R. Statistical significance for genomewide studies. PNAS. 2003;100:9440–5. doi: 10.1073/pnas.1530509100. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Tango T, Takahashi K. A flexibly shaped spatial scan statistic for detecting clusters. Int J Health Geogr. 2005;4:11. doi: 10.1186/1476-072X-4-11. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Tunstall H, Pickett KE, et al. Residential histories and contemporary mortality geography: using data linkage to develop a data set describing mobility between birth and death. J Epidemiol Community Health. 2010;64:A56–7. [Google Scholar]
- Turnbull BW, Iwano EJ, Burnett WS, Howe HL, Clark LC. Monitoring for clusters of disease: application to leukemia incidence in upstate New York. Am J Epidemiol. 1990;132:136–43. doi: 10.1093/oxfordjournals.aje.a115775. [DOI] [PubMed] [Google Scholar]
- Waller LA, Turnbull BW. The effects of scale on tests for disease clustering. Stat Med. 1993;12:1869–84. doi: 10.1002/sim.4780121913. [DOI] [PubMed] [Google Scholar]
- Waller LA, Turnbull BW, Gustafsson G, Hjalmars U, Andersson B. Detection and assessment of clusters of disease: an application to nuclear power plant facilities and childhood leukemia in Sweden. Stat Med. 1995;14:3–16. doi: 10.1002/sim.4780140103. [DOI] [PubMed] [Google Scholar]
- Webster T, Vieira V, Weinberg J, Aschengrau A. Method for mapping population-based case-control studies using generalized additive models. Int J Health Geogr. 2006;5:26. doi: 10.1186/1476-072X-5-26. [DOI] [PMC free article] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.