Abstract
Learning about the structure of the world requires learning probabilistic relationships: rules in which cues do not predict outcomes with certainty. However, in some cases, the ability to track probabilistic relationships is a handicap, leading adults to perform non-normatively in prediction tasks. For example, in the dilution effect, predictions made from the combination of two cues of different strengths are less accurate than those made from the stronger cue alone. Here we show that dilution is an adult problem; 11-month-old infants combine strong and weak predictors normatively. These results extend and add support for the less is more hypothesis: limited cognitive resources can lead children to represent probabilistic information differently from adults, and this difference in representation can have important downstream consequences for prediction.
Keywords: probability learning, probabilistic prediction, less is more, language acquisition
Succeeding in the world requires making accurate predictions. From patterns of light on the retina, one must predict the structure of the environment. From a set of job applicants, one must predict which will be the best employee. From a set of potential foods, one must predict which will result in a delicious dinner and which will result in an upset stomach. These are difficult problems because they involve probabilistic relationships: no cue predicts the desired outcome with 100% certainty. Probabilistic prediction is a general problem faced by cognitive systems (Brunswik, 1943; Ramscar, Yartlett, Dye, Denny, & Thorpe, 2010).
Humans are remarkably good at this. For instance, Griffiths and Tenenbaum (2006) showed that the average undergraduate can predict movie runtimes, lengths of poems, and reigns of pharaohs with high accuracy from a single piece of information. Even young infants are able to track (Saffran, Aslin, & Newport, 1996) and make predictions (Xu & Garcia, 1998) from probabilistic events in their environments. These processes appear across tasks (e.g. visual perception: Kersten & Yuille, 2003; motor control: Körding & Wolpert, 2006; memory retrieval: Shiffrin & Steyvers, 1997) and are available quite early (e.g. newborns: Bulf, Johnson, & Valenza, 2011; 2-month-olds: Kirkham, Slemmer, & Johnson, 2002, 6-month-olds: Shukla, White, & Aslin, 2011). Their ubiquity has inspired hope for a unified understanding of both mature and developing cognitive systems as probabilistic prediction machines (Chater, Tenenbaum, & Yuille, 2006; Tenenbaum, Kemp, Griffiths, & Goodman, 2011; Clark, in press). Unsurprisingly, the efficiency of these processes generally improves over development (Smith & Yu, 2008; Thiessen, 2010; Xu & Tenenbaum, 2007); however, on some probabilistic prediction tasks, young children actually outperform adults.
In perhaps the simplest such task (Derks & Paclisanu, 1967, see also Gardner, 1957) participants are presented with two lights, and, in a series of trials, must predict which light will activate. If they make the correct prediction, they receive a reward. The stimuli are probabilistic – one light activates on 70% of the trials, and the other light activates on the remaining 30%. The optimal strategy – the one which maximizes rewards – is to always select the more probable light. This is precisely how three and four-year-old children behave. However, it is not how adults behave; adults probability match, selecting each light in proportion to its probability of activation, reducing their total reward (Estes, 1976). This perplexing result has been explained as a type of apophenia: search for local sequential patterns in the light sequences that do not exist (Wolford, Newman, Miller, & Wig, 2004, Yu & Cohen, 2009). Thus, adults’ prowess in tracking probabilities at multiple levels leads to suboptimal performance in this task. This argument is reinforced by two further sources of evidence. First, adults who are more likely to probability match are also more likely to discover local pattern structure if it does exist (Gaissmaier & Schooler, 2008). Second, adults perform more normatively when they have fewer cognitive resources available; maximizing more often under dual-task conditions (Gaissmaier, Schooler, & Rieskamp, 2006, Wolford et al., 2004).
Newport and colleagues (Johnson & Newport, 1989 Newport, 1990, Hudson Kam & Newport, 2005) have proposed that children’s resource constraints in probabilistic prediction are adaptive. Under their less is more hypothesis, children outperform adults in learning languages precisely because their resource constraints limit their ability to entertain complex hypotheses. Elman (1993) formalized this claim, showing that initially resource-constrained neural networks learned grammatical structure better than unconstrained nets. Resource constraints prevented the search for complex patterns, keeping networks from getting stuck in local maxima. In a language-learning task analogous to the light prediction task above, Hudson Kam and Newport (2005) showed that adults probability match their language input, whereas 6-year-olds maximize, always picking the most probable alternative. Further, as before, increasing task demands lead to increased maximizing in adults (Hudson Kam & Newport, 2009). The less is more hypothesis (Newport, 1990) thus suggests that the representation of probabilistic information changes over development. If maximizing is a general property of young children’s probability learning, then they should also outperform adults in other cases in which optimal performance results from maximizing rather than probability matching. This paper tests this prediction in the context of combining information from two probabilistic predictors of different strengths.
Across a range of domains, tasks, and developmental ages, evidence from two strong predictors leads to better learning and prediction than a single strong predictor alone (Shanteau, 1975; Ernst & Banks, 2002; McKenzie, Lee, & Chen, 2002; Yoshida & Smith, 2005; Frank, Slemmer, Marcus, & Johnson, 2009). However, the addition of evidence from a weaker predictor to a stronger predictor can lead to non-normative behavior in adults. For instance, in the “bookbags-and-pokerchips” task, adults are shown two bookbags and told that one contains 70 white chips and 30 red chips, and the other contains the opposite red/white ratio. The experimenter then secretly chooses one of the bags, and randomly draws a white chip. When asked to guess the bag’s identity, participants are 60% certain it is the 70 white/30 red bag. Then, a second sample is drawn – 3 white chips, and 3 red chips – and participants are again asked to guess the bag’s identity. While this second sample is nondiagnostic (i.e., equally likely to have come from either bag), participants decrease their certainty in the white-heavy bag (Shanteau, 1975). This dilution effect is also found in more naturalistic settings (Nisbett, Zuckier & Lemley, 1981) and even when the additional evidence is a weaker positive predictor rather than a nondiagnostic predictor (McKenzie, et al. 2002). But the less is more hypothesis predicts that young learners will combine strong and weak predictors more optimally.
The dilution effect should depend critically on how the strength of each predictor is represented. The addition of a Weak Cue can dilute evidence from a Strong Cue only if the cognitive system represents the strength of each cue in proportion to its probability (probability matching). On the other hand, if the system represents only the most probable outcome (maximizing), then a Weak Cue can only add to a Strong Cue. Because they are both coded as strong cues, their combination should act as an even stronger cue (e.g. Ernst & Banks, 2002; McKenzie, et al., 2002; Frank, et al. 2009). Thus, we predict that where adults average a strong and weak probabilistic predictor, 11-month-old infants should treat their combination additively. In the Experiments to follow, two centrally-presented geometric shapes differed in the probability with which they predicted the appearance of a reinforcing cartoon character stimulus. One shape was a Strong Cue, and the other was a Weak Cue. Then, after learning these shape-outcome relationships, participants were tested on trials in which Both Cues appeared together. We predicted that adults would probability match – predicting more for the Strong Cue than for the Weak Cue – and that Both Cues would be treated as intermediate evidence. Infants, in contrast, would maximize in response to both the Strong and Weak Cues – treating them similarly – and predict even more strongly in response to Both Cues.
Experiment 1
Method
Participants
Twenty-four undergraduate students at Indiana University, and 24 11-month-old infants (mean age 11 mo 15 days; range – 10 mo 15 days to 12 mo 7 days, 13 female) participated in the experiment. Three additional adults and 11 additional infants were excluded because of failure to calibrate, incomplete data, and (infants only) fussiness. Participants received partial course credit (adults) or a small gift (infants) as compensation.
Stimuli
Stimuli fell into two categories – cues and reinforcers. Cues were videos of monochromatic geometric shapes looming and shrinking. Four such shapes were created: a red square, a blue circle, a green triangle, and a yellow diamond. Reinforcers were videos of cartoon characters, each of which displayed a different animated behavior. For instance, one reinforcer consisted of a bouncing purple stuffed animal. Each of the three reinforcer videos was accompanied by a unique sound. Videos for all stimuli were two seconds long.
Design and Procedure
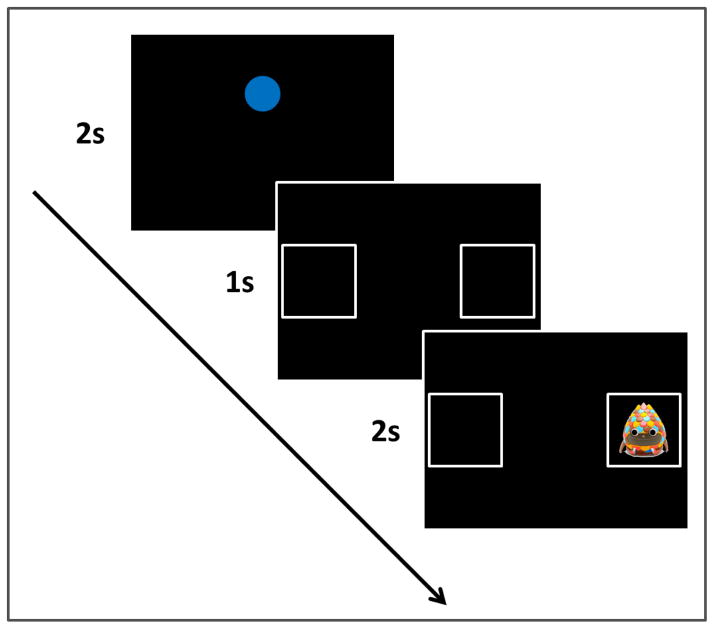
The experiment consisted of a series of trials in which a cue appeared centrally on the screen for 2 seconds and then was followed by two blank boxes that appeared for 1 second on each side of the central location. After this, on some trials a reinforcer would appear in one of the boxes for 2 seconds. On other trials, the boxes would remain blank for 2 seconds. Figure 1 shows a schematic of an example reinforcement trial.
Figure 1.
A schematic of one experimental trial. A cue loomed on the screen for two seconds, was replaced by two empty boxes for one second, and then a reinforcer played in one of the boxes for two seconds.
Each participant saw ten such trials for each of two unique cues. One shape was a Strong Cue – predicting the appearance of a random reinforcer on seven of ten trials. On the other three trials, the boxes remained blank. The other shape was a Weak Cue – predicting the appearance of a random reinforcer on only four of ten trials. After 20 single-cue trials, participants saw five trials on which Both Cues appeared together, and which were never followed by a reinforcer.
All reinforcers appeared on the same side of the screen for a given participant, and reinforcer sides and cue identities were counterbalanced across participants. Single-cue trials appeared in random order until all 10 trials of each cue had been seen. Finally, an attention-getter was shown prior to the onset of each trial and remained on screen until fixated for at least 100ms.
Participants watched the experimental videos on a 17-inch monitor while their eye movements were recorded by a Tobii 1750 eye tracker (see Appendix for details). The eye tracker was calibrated for each participant before the experiment began. To facilitate fair comparison between adult and infant participants, adults were only instructed to watch the screen for the duration of the experiment.
In order to determine how cues affected participants’ predictions about the appearance of reinforcers, we analyzed predictive looking after the offset of the cue, and thus, the dependent measure of interest was latency to saccade to either of the boxes. However, because reinforcers appeared in these boxes after 1 second on reinforcement trials (Figure 1), any saccades initiated after this point were more likely reactive than predictive. Allowing 200 milliseconds for saccade initiation (Engel, Anderson, & Soechting, 1991), only eye movements within 1.2 seconds of cue-offset were analyzed. For a related location-based prediction paradigm, and another comparison of predictive learning in adults and infants, see Richardson and Kirkham (2004).
Results and Discussion
The key empirical question is how participants’ probability of predicting the appearance of the reinforcer in each box varied in Weak, Strong, and Both Cues conditions. To answer this question, one wants to estimate the relative probability of looking to either the Correct or Incorrect box over time as a function of cue. To ensure we measured predictive rather than reactive saccades, we analyzed only eye movements in the first 1.2 seconds after cue-offset (see above). However, not all participants made a saccade on all trials in this window, leading to right-censored data. Since simply excluding these trials would produce a biased estimate of saccade probability, the appropriate statistical analysis is a proportional hazards regression (Cox, 1972). This analysis estimates a hazard function for each condition – the probability of making a saccade at each time-point given that no saccade has yet been made (for other examples of Cox regression in developmental studies, see e.g. Zosuls, Ruble, Tamis-Lemonda, Shrout, Bornstein, & Greulich, 2009; Kidd, Piantadosi, & Aslin, 2012).
Cox regression is a semi-parametric model: it makes no assumptions about the functional form of the hazard function. Instead, a baseline hazard function is estimated empirically from one condition, and other conditions are assumed to have hazard functions proportional to that baseline. Here, the baseline function was estimated from the Strong Cue condition, both because subsequent analysis becomes most straightforward, and because it contains the greatest proportion of valid eye-tracking data. This produces the most robust function estimate. Because participants could make a saccade to one of two locations on each trial (Correct or Incorrect), the regression model was stratified by location (Lunn & McNeil, 1995). That is, cues could have different effects on the hazard rate for different locations. Models were fit separately for adults and infants using the last 5 trials of each single cue (Weak and Strong) condition, and all 5 trials of the Both Cue condition.
These analyses indicate that adults and infants alike were more likely to look predictively to the Correct than the Incorrect location (Adults: β = −2.05, z = −6.72, p < .001; Infants: β = −.779, z = −3.48, p = .001). However, adults and infants treated the cues differently. The adult data are shown in Figure 2a. Compared to the Strong Cue, both the Weak Cue (β = −.388, z = −2.05, p < .05) and Both Cues (β = −.401, z = −2.09, p < .05) elicited less predictive looking to the Correct location. The Weak Cue (β = .77, z = 2.24, p < .05), but not Both Cues (β = .507, z = 1.41, n.s.), produced more prediction to the Incorrect location than the Strong Cue. Thus, the Strong Cue elicited the proportionally highest correct predictions, the Weak Cue the lowest, and Both Cues were intermediate. This is evidence for a dilution effect in the visual domain.
Figure 2.
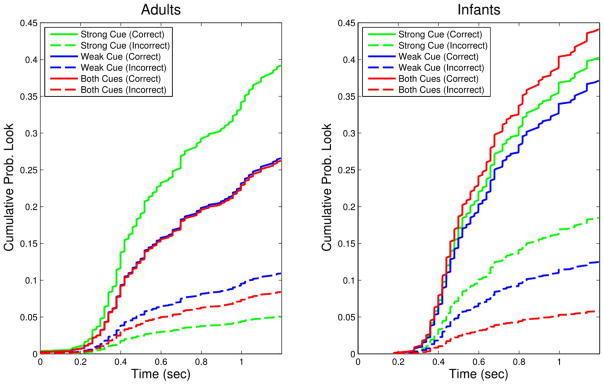
Cumulative hazard functions for each cue/location combination for both groups. Each curve shows the estimated cumulative probability of a predictive look to a location (Correct/Incorrect) in the presence of a particular cue (Strong/Weak/Both) over time. Adults (a) were more likely to make the Correct prediction when seeing the Strong Cue than the Weak Cue or Both Cues. Further, the Weak Cue increased their probability of predicting to the Incorrect location, but Both Cues did not. Thus, Both Cues were treated as intermediate between the Strong and Weak cues, indicating dilution. Infants (b) treated the Strong and Weak cues identically, indicating that, in contrast to adults, they were maximizing. Further, they were less likely to predict to the Incorrect location when cued by Both Cues than the Strong Cue. This is evidence of additive cue combination by way of reduced prediction of incorrect alternatives.
The infant data (Figure 2b) show maximizing in the face of both cues and no dilution effect. Predictive looking to the Correct location was unaffected by cue type (Weak vs. Strong: β = −.082, z = −.421, n.s.; Both vs. Strong: β = .091, z = −.475, n.s.). But, relative to the Strong Cue, Both Cues (β = −1.16, z = −3.19, p < .01) but not the Weak Cue (β = −.391, z = −.1.38, n.s.) reduced prediction to the Incorrect (i.e., non-reinforced) location. Thus, seeing Both Cues significantly decreased infants’ probability of making Incorrect predictions, producing a relatively higher proportion of Correct predictions. Infants maximized when they saw the Weak Cue – treating it just like the Strong Cue – and Both Cues reduced incorrect prediction.
In brief, when exposed to the same multi-modal regularities, infants and adults responded by making different predictions. Adults discriminated strongly between the Correct and Incorrect location for the Strong Cue, weakly between the two locations for the Weak cue, and showed intermediate discrimination when Both Cues were presented together. Infants, in contrast, predicted to the Correct side at the same rate in each condition, but predicted less often to the Incorrect location in the presence of Both Cues.
For both groups, the proposed interpretation of the data draws on looking to both the Correct and Incorrect locations. But why do participants ever look to the Incorrect location at all? One likely explanation is that the observed gaze behavior results not just from participants’ learning in the task, but also from their expectation before coming into the experiment (or prior). On the very first trial, participants could reasonably make a prediction to either box even though they have not seen a single reinforcer. The key idea is that unobserved events should be treated not as impossible, but only as less and less likely the longer they are unencountered. Thus, each reinforcer acts not only as evidence for the Correct location, but also as evidence against the Incorrect location. When Both Cues are seen together, both aspects of the cues are combined. Thus, while 11-month-olds prediction systems may be too noisy to produce faster predictions to the correct locations (as evidenced by their low ceiling-level performance in other tasks), we can see evidence of their more normative combination in the reduction of Incorrect looks.
While this account is consistent with both the adult and infant data, the infant data may have a simpler explanation. A similar pattern of looking would be observed if infants did not learn anything about the cues and the cue-specific predictive probabilities, but simply learned over the course of training that outcomes appeared in the Correct but not Incorrect locations. Because the Both Cues test trials occurred after 20 training trials, we would expect better prediction on these test trials than on the single Cue training trials. Experiment 2 was designed to test this alternative possibility.
Experiment 2
In Experiment 2, infants were exposed to the same training trials as in Experiment 1, but training was followed by two kinds of test trials. On the first, infants were shown two New Cues in the same positions as the cues they had seen in training. If training led to a general preference to look to the Correct location rather than specific cue-reinforcer relationships, predictive looking on these New Cues trials should be similar to that observed on Both Cues trials in the previous experiment. In contrast, if infants learned cue-specific predictive relationship, their looking patterns should be different, perhaps providing information about their starting point (or prior) in the absence of cue-specific information. These New Cues trials were subsequently followed by the original Both Cues trials. These trials were included to test the robustness of infants’ predictive learning from the single Cue trials. If infants again showed improved prediction in the face of Both Cues after the intervening New Cues trials, this would be strong evidence that they learned and combined cue-specific predictive relationships.
In order to limit fussiness and fatigue, infants were shown three New Cues trials and three Both Cues trials, resulting in a total of six as compared to the five test trials of Experiment 1.
Method
Participants
Twenty 11-month-old infants (mean age 11 mo 15 days; range – 11 mo 4 days to 12 mo 3 days, 8 female) participated in the experiment. Ten additional infants were excluded because of failure to calibrate, incomplete data, and/or fussiness. Each infant received a small gift as compensation.
Stimuli
Stimuli for Experiment 2 were identical to those used in Experiment 1.
Design and Procedure
As in Experiment 1, infants were exposed to a series of trials on which a centrally-located cue probabilistically predicted the appearance of a reinforcer in one of the on-screen boxes. Infants were again exposed to twenty training trials – ten on which they saw a Strong Cue and ten on which they saw a Weak Cue. These training trials were identical to those presented in Experiment 1. Subsequently, these training trials were followed by two kinds of test trials.
The first three test trials were New Cues trials on which infants saw two new cues on the screen, one in each of the locations previously occupied by the cues from training. After these trials, infants saw three Both Cues trials identical to those in Experiment 1. For example, if the training trials each showed either a red square or a blue circle, the New Cues trials would show a green triangle and a yellow diamond, and the Both Cues trials would show the red square and blue circle again. As in Experiment 1, reinforcer side and shape/cue type/location mappings were counterbalanced across infants.
Results and Discussion
As in Experiment 1, infants’ predictions were measured only during the first 1.2 seconds after cue-offset, and look latencies to the correct and incorrect locations for each cue type were analyzed using a proportional hazards regression. The Strong cue trials were again used to estimate the baseline hazard function. Because infants received only three test trials of each type, we analyzed the last three training trials for each Cue.
Figure 3 shows infants cumulative hazard functions for each cue type and location. As in Experiment 1, infants were more likely to look predictively to the Correct than the Incorrect location (β = −.842, z = −2.57, p = .01). As in Experiment 1, infants showed evidence of maximizing, with no effect of the Weak cue on looking to either the Correct (β = −.07, z = −.26, n.s.) or the Incorrect location (β = −.26, z = −.63, n.s.). Also, as in Experiment 1, Both Cues did not affect infants looking to the Correct location (β = −.05, z = −.19, n.s.) but significantly decreased their looking to the Incorrect location (β = −1.22, z = −2.15, p < .05). Thus, as in Experiment 1, infants maximized in the face of both Cues, and showed proportionally stronger prediction when cued by Both Cues.
Figure 3.
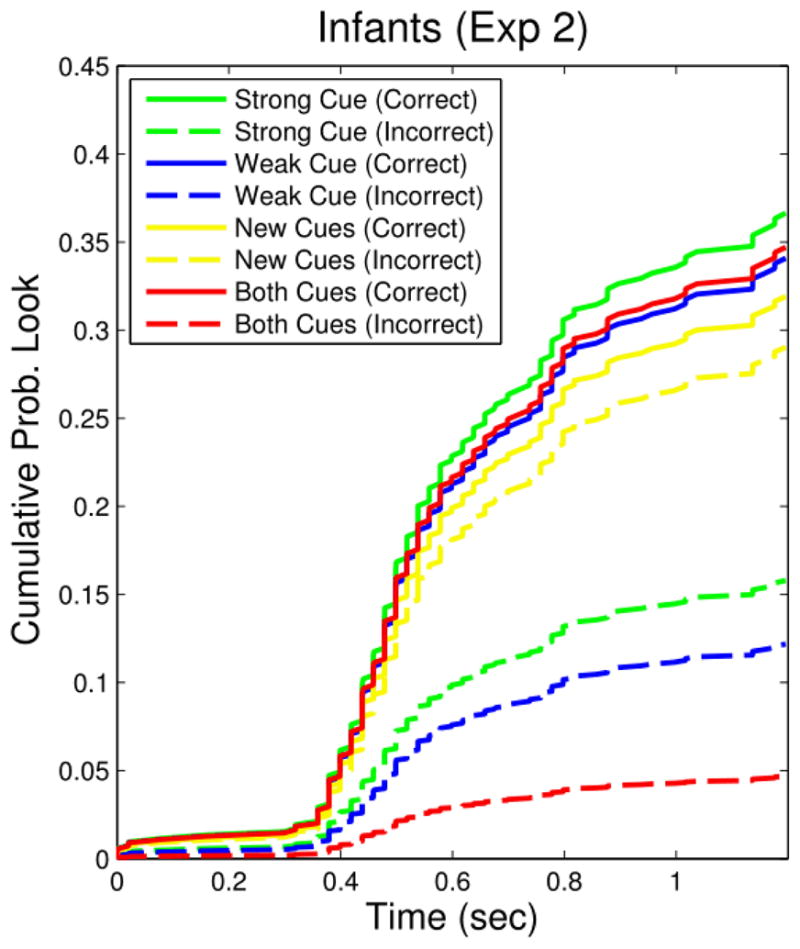
Cumulative hazard functions for each cue/location combination for infants in Experiment 2. Each curve shows the estimated cumulative probability of a predictive look to a location (Correct/Incorrect) in the presence of a particular cue ( Strong/Weak/New/Both) over time. Infants predicted the appearance of a reinforcer to in the Correct location equally under all cue conditions. However, relative to the Strong and Weak Cues they predicted the reinforcer on the Incorrect side less in the presence of Both Cues and more in the presence of the New Cues.
When presented with the New Cues, infants did not alter their looking to the Correct location (β = −.14, z = −.50, n.s.), but were marginally more likely to look the Incorrect location (β = .61, z = 1.78, p = .08). As shown in Figure 3, infants showed no discrimination between the Correct and Incorrect sides in the presence of the New Cues. These results thus rule out the possibility that infants simply learned to look at the Correct location following the offset of any cue. Infants did not show a preference when presented with the New Cues, and therefore likely learned cue-specific predictive probabilities and not a general preference for the Correct side. Further, Experiment 2 shows that the result for the Both Cues trials is quite robust: infants showed improved prediction in the face of Both Cues even after the three non-reinforcing New Cues trials.
General Discussion
Although development is generally accompanied by increased efficiency (Kail, 1991), sometimes this efficiency comes at a cost. For humans, the cost may include reduced ability to learn language (Johnson & Newport, 1989). The less is more hypothesis proposes that young children’s resource constraints are actually critical for their success in learning language. Key evidence for this claim has taken the form of artificial language learning experiments. When exposed to inconsistent input, adults probability match – reproducing this inconsistency in their output. In contrast, children maximize, learning a simple regular pattern. The evidence presented in this paper strengthens and extends this hypothesis in two key ways. First, we show maximizing in young children in a novel domain. In addition to language learning and explicit prediction tasks (Derks & Paclisanu, 1967; Hudson Kam & Newport, 2005), maximizing is elicited even in viewing visually-presented probabilistic prediction. This is strong evidence that the kind of processing critical to the less is more hypothesis is a general property of young learners. Second, evidence that children do not show a dilution effect suggests that the resource constraints which lead to maximizing have important downstream consequences. Just as in language, in which the nature of early learning can fundamentally change what is learned down the line (Elman, 1993), what is learned about probabilistic cues can fundamentally change the way that they are combined.
Following other infant prediction experiments (e.g. Kovács & Mehler, 2009; McMurray & Aslin, 2004), we designed a task to test a perceptual analogue of the dilution effect (Nisbett, Zuckier, & Lemley, 1981). While dilution is traditionally studied in explicit reasoning tasks, comparison between adults and infants necessitated construction of a perceptual paradigm. Nonetheless, our results replicate those found in explicit reasoning tasks, suggesting even more strongly that dilution is a fundamental property of the adult cognitive system, and licensing comparison to our younger participants (see also Knowlton, Mangels, & Squire, 1996 and Gluck, Shohamy, & Myers, 2002 for a similar task with adults). Whereas adult participants encoded the strengths of predictors in proportion to their probability of prediction, and subsequently combined information from them non-normatively, infants maximized in response to both the Strong and Weak Cues and their combination reduced prediction error. Thus, resource constraints may not only prevent children from learning probabilistic relationships that are too complex (in essence, over-fitting the data – Zhu, Rogers, & Gibson, 2009), they also support prediction for multiple cues that have never been experienced together (Téglás, Vul, Girotto, Gonzalez, Tenenbaum, & Bonatti, 2011).
Building on other work suggesting that the statistical learning mechanisms involved in language are domain-general (Kirkham, Slemmer, & Johnson, 2002; Fiser & Aslin, 2002; Saffran, Pollack, Seibel, & Shkolnik, 2007), these results suggest that more normative statistical learning in young infants may characterize other cognitive domains. For example, statistical regularities between scenes and objects play an important role in rapid object recognition (Brockmole, Castelhano, & Henderson, 2006, Oliva & Torralba, 2006); cues that guide common grounding in social interactions are complex, culturally specific, and probabilistic (Bruner, 1975, Butko & Movellan, 2010, Yuki, Maddux, & Masuda, 2007); noisy data about categories and category memberships often lead to rule like over-hypotheses (Colunga & Smith, 2005, Kemp, Perfors, & Tenenbaum, 2007). In all of these domains, as in language, it is interesting to ask whether the developing statistical learner might have an advantage. Could it be that for object recognition, cultural norm induction, and categorization less is also more?
Nonetheless, the adult system does develop from the infant system, and probability matching develops along with it (Derks & Paclisanu, 1967). Why develop a non-normative system? For a speculative potential explanation, we return to language. Like young children, rhesus monkeys maximize in response to probabilistic cues, always selecting the most likely option (Treichler, 1967, Wilson & Rolling, 1959), and when combining probabilistic predictors in a task similar to ours, monkeys perform normatively (Yang & Shadlen, 2002). That is, like infants, monkeys do not show the dilution effect. But, unlike young children, these monkeys will not go on to acquire language.
One of the difficulties in learning natural language is dealing with exceptions. For instance, although conjugating an English verb most often involves appending ‘-ed,’ this is not always true. In fact, some of the most frequently encountered verbs have a different character (e.g., go becomes went). Learning irregular words turns out to be quite difficult for children, who often overregularize these words (e.g., turning go into goed; Brown, 1973). Although estimates of the rates of such regularization vary, they are known to be highest before the age of four and to drop significantly by seven or eight.(Marcus, Pinker, Ullman, Hollander, Rosen, & Xu, 1992; Maratsos, 2000; Maslen, Theakston, Lieven, & Tomasello, 2004). This seems to follow the same pattern found in the change from probability matching to maximizing. While single-mechanism accounts have been advanced which capture some of the regularities demonstrated by children in their rates and types of overregularization (e.g. Rumelhart & McClelland, 1986; Plunkett & Marchman, 1993), none successfully capture them all (MacWhinney, 1998, Pinker & Ullman, 2002). Following Elman (1993), we propose that what is missing from these accounts is developmental change. In order to deal with the regularities in language – regularities with exceptions – the cognitive system needs to represent predictors in proportion to their probabilities. Thus, it may be that for breaking into language, less is more. But, for mastering language and other complex systems, less must become more.
Acknowledgments
This research was supported by a NSF Graduate Research Fellowship to DY as well as NIH Grant R01HD056029 to CY. The authors are grateful to Celeste Kidd for help designing the stimuli, to Becca Baker, Kelsey Gibson, Amber Matthews, and Motomasa Tanioka for help with data collection, and to all of the members of the Yu, Smith, and Shiffrin labs for their feedback in discussions. We also thank Denis Mareschal and three anonymous reviewers for their feedback on this manuscript.
Appendix: Eye Tracking Details
Eye tracking for all participants began with a calibration procedure. Adult participants were calibrated using nine points, one at each point of a three by three grid. To expediate calibration, infant participants were calibrated using five points: the four corners and the center.
The Tobii eye tracker recorded participants’ distance from the screen and the location of both their left and right eyes at 50 Hz. Each participant’s sequence of gaze ps was derived from their recorded gaze samples. If the Tobii x and y coordinates for both eyes were on the screen, gaze was estimated to be at their midpoint. If the coordinates of only one eye were reliably recorded, those coordinates was estimated to be the point of gaze. Otherwise, the sample was marked as invalid. Distance was treated similarly. In order to correct for blinking or other sporadic tracking failures, we interpolated over short intervals of invalid samples. Up to three successive invalid samples between two valid samples were interpolated in equal steps. Larger blocks of invalid samples were not interpolated.
Finally, these time/x/y/distance tuples were used to estimate a series of fixations for each participant. Successive samples were considered part of the same fixation if they were within 1° of visual angle of each other (using the arctangent computation described by Kosslyn, 1978 to convert from on-screen distances to visual angle) and their summed durations was greater than 100 milliseconds. Table A1 shows the proportion of time during the 1.2s prediction window that participants’ fixation locations were on-screen.
Table A1.
Proportion of valid eye-tracking samples in the prediction window for participants in each Experiment. Boxes show mean (std err.).
| Participants | Exp 1: Adults | Exp 1: Infants | Exp 2: Infants |
|---|---|---|---|
| Prop. Valid Samples | .76 (.03) | .69 (.04) | .69 (.03) |
References
- Brockmole JR, Castelhano MS, Henderson JM. Contextual cueing in naturalistic scenes: Global and local contexts. Journal of Experimental Psychology: Learning, Memory, & Cognition. 2006;32:699–706. doi: 10.1037/0278-7393.32.4.699. [DOI] [PubMed] [Google Scholar]
- Brown R. A first language. Cambridge, MA: Harvard University Press; 1973. [Google Scholar]
- Bruner J. From communication to language: a psychological perspective. Cognition. 1975;3:255–287. [Google Scholar]
- Brunswik E. Organismic achievement and environmental probability. Psychological Review. 1943;50:255–272. [Google Scholar]
- Bulf H, Johnson SP, Valenza E. Visual statistical learning in the newborn infant. Cognition. 2011;121:127–132. doi: 10.1016/j.cognition.2011.06.010. [DOI] [PubMed] [Google Scholar]
- Butko NJ, Movellan JR. Detecting contingencies: An infomax approach. Neural Networks. 2010;23:973–984. doi: 10.1016/j.neunet.2010.09.001. [DOI] [PubMed] [Google Scholar]
- Chater N, Tenenbaum JB, Yuille A. Probabilistic models of cognition: Conceptual foundations. Trends in Cognitive Sciences. 2006;10:287–291. doi: 10.1016/j.tics.2006.05.007. [DOI] [PubMed] [Google Scholar]
- Clark A. Whatever Next? Predictive Brains, Situated Agents, and the Future of Cognitive Science. Behavioral and Brain Sciences. doi: 10.1017/S0140525X12000477. (in press) [DOI] [PubMed] [Google Scholar]
- Colunga E, Smith LB. From the lexicon to an expectation about kinds: a role for associative learning. Psychological Review. 2005;112:347–382. doi: 10.1037/0033-295X.112.2.347. [DOI] [PubMed] [Google Scholar]
- Cox DR. Regression models and life-tables. Journal of the Royal Statistical Society Series B. 1972;34:187–220. [Google Scholar]
- Derks PL, Paclisanu MI. Simple strategies in binary prediction by children and adults. Journal of Experimental Psychology. 1967;73:278–285. [Google Scholar]
- Elman JL. Learning and development in neural networks: the importance of starting small. Cognition. 1993;48:71–99. doi: 10.1016/0010-0277(93)90058-4. [DOI] [PubMed] [Google Scholar]
- Ernst MO, Banks MS. Humans integrate visual and haptic information in a statistical optimal fashion. Nature. 2002:429–433. doi: 10.1038/415429a. [DOI] [PubMed] [Google Scholar]
- Estes WK. The cognitive side of probability learning. Psychological Review. 1976;83:37–64. [Google Scholar]
- Engel KC, Anderson JH, Soechting JF. Oculomotor tracking in two dimensions. Journal of Neurophysiology. 1991;81:1597–1602. doi: 10.1152/jn.1999.81.4.1597. [DOI] [PubMed] [Google Scholar]
- Fiser J, Aslin RN. Statistical learning of new visual feature combinations by infants. Proceedings of the National Academy of Sciences. 2002;99:15822–15826. doi: 10.1073/pnas.232472899. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Frank MC, Slemmer JA, Marcus GF, Johnson SP. Information from multiple modalities helps 5-month-olds learn abstract rules. Developmental Science. 2009;12:504–509. doi: 10.1111/j.1467-7687.2008.00794.x. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Gaissmaier W, Schooler LJ, Rieskamp J. Simple predictions fueled by capacity limitations: When are they successful? Journal of Experimental Psychology: Learning, Memory and Cognition. 2006;32:966–982. doi: 10.1037/0278-7393.32.5.966. [DOI] [PubMed] [Google Scholar]
- Gaissmaier W, Schooler LJ. The smart potential behind probability matching. Cognition. 2008;109:416–422. doi: 10.1016/j.cognition.2008.09.007. [DOI] [PubMed] [Google Scholar]
- Gardner RA. Probability-learning with two and three choices. American Journal of Psychology. 1957;70:174–185. [PubMed] [Google Scholar]
- Gluck MA, Shohamy D, Myers C. How do people solve the “weather prediction” task?: Individual variability in strategies for probabilistic category learning. Learning & Memory. 2002;9:408–418. doi: 10.1101/lm.45202. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Griffiths TL, Tenenbaum JB. Optimal predictions in everyday cognition. Psychological Science. 2006;17:767–773. doi: 10.1111/j.1467-9280.2006.01780.x. [DOI] [PubMed] [Google Scholar]
- Hudson Kam CL, Newport EL. Regularizing unpredictable variation: The roles of adult and child learners in language formation and change. Language Learning and Development. 2005;1:151–195. [Google Scholar]
- Hudson Kam CL, Newport EL. Getting it right by getting it wrong: When learners change languages. Cognitive Psychology. 2009;59:30–66. doi: 10.1016/j.cogpsych.2009.01.001. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Johnson JS, Newport EL. Critical period effects in second language learning: The influence of maturational state on the acquisition of English as a second language. Cognitive Psychology. 1989;21:60–99. doi: 10.1016/0010-0285(89)90003-0. [DOI] [PubMed] [Google Scholar]
- Kail R. Processing time decreases exponentially during childhood and adolescence. Developmental Psychology. 1991;27:259–266. [Google Scholar]
- Kemp C, Perfors A, Tenenbaum JB. Learning overhypotheses with hierarchical Bayesian models. Developmental Science. 2007;10:307–321. doi: 10.1111/j.1467-7687.2007.00585.x. [DOI] [PubMed] [Google Scholar]
- Kersten D, Yuille A. Bayesian models of object perception. Current Opinion in Neurobiology. 2003;13:150–158. doi: 10.1016/s0959-4388(03)00042-4. [DOI] [PubMed] [Google Scholar]
- Kidd C, Piantadosi ST, Aslin RN. The Goldilocks effect: Human infants allocate attention to visual sequences that are neither too simple nor too complex. PLoS ONE. 2012;7:e36399. doi: 10.1371/journal.pone.0036399. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kirkham NZ, Slemmer JA, Johnson SP. Visual statistical learning in infancy: evidence for a domain general learning mechanism. Cognition. 2002;83:B35–B42. doi: 10.1016/s0010-0277(02)00004-5. [DOI] [PubMed] [Google Scholar]
- Knowlton BJ, Mangels JA, Squire LR. A neostriatal habit learning system in humans. Science. 1996;273:1399–1402. doi: 10.1126/science.273.5280.1399. [DOI] [PubMed] [Google Scholar]
- Kosslyn SM. Measuring the visual angle of the mind’s eye. Cognitive Psychology. 1978;10:356–389. doi: 10.1016/0010-0285(78)90004-x. [DOI] [PubMed] [Google Scholar]
- Kovács AM, Mehler J. Cognitive gains in 7-month-old bilingual infants. Proceedings of the National Academy of Sciences. 2009;106:6556–6560. doi: 10.1073/pnas.0811323106. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Körding KP, Wolpert DM. Bayesian decision theory in sensorimotor control. Trends in Cognitive Sciences. 2006;10:320–326. doi: 10.1016/j.tics.2006.05.003. [DOI] [PubMed] [Google Scholar]
- Lunn M, McNeil D. Applying Cox regression to competing risks. Biometrics. 1995;51:524–532. [PubMed] [Google Scholar]
- Maratsos M. More overregularizations after all: New data and discussion on Marcus, Pinker, Ullman, Hollander, Rosen & Xu. Journal of Child Language. 2000;27:183–212. doi: 10.1017/s0305000999004067. [DOI] [PubMed] [Google Scholar]
- Marcus G, Pinker S, Ullman M, Hollander M, Rosen T, Xu F. Overregularisations in language acquisition. Monographs of the society for research in child development. 1992;57 Serial no. 228. [PubMed] [Google Scholar]
- MacWhinney B. Models of the emergence of language. Annual Review of Psychology. 1998;49:199–227. doi: 10.1146/annurev.psych.49.1.199. [DOI] [PubMed] [Google Scholar]
- Maslen RJC, Theakston AL, Lieven EVM, Tomasello M. A dense corpus study of past tense and plural overregularization in English. Journal of Speech, Language, and Hearing Research. 2004;47:1319–1333. doi: 10.1044/1092-4388(2004/099). [DOI] [PubMed] [Google Scholar]
- McKenzie CR, Lee SM, Chen KK. When negative evidence increases confidence: change in belief after hearing two sides of a dispute. Journal of Behavioral Decision Making. 2002;15:1–18. [Google Scholar]
- McMurray B, Aslin RN. Anticipatory eye movements reveal infants’ auditory and visual categories. Infancy. 2004;6:203–229. doi: 10.1207/s15327078in0602_4. [DOI] [PubMed] [Google Scholar]
- Newport EL. Maturational constraints on language learning. Cognitive Science. 1990;14:11–28. [Google Scholar]
- Nisbett RN, Zuckier H, Lemley RE. The dilution effect: Nondiagnostic information weakens the implications of diagnostic information. Cognitive Psychology. 1981;13:248–277. [Google Scholar]
- Oliva A, Torralba A. The role of context in object recognition. Trends in Cognitive Sciences. 2006;11:520–527. doi: 10.1016/j.tics.2007.09.009. [DOI] [PubMed] [Google Scholar]
- Pinker S, Ullman MT. The past and future of the past tense. Trends in Cognitive Sciences. 2002;6:456–463. doi: 10.1016/s1364-6613(02)01990-3. [DOI] [PubMed] [Google Scholar]
- Plunkett K, Marchman V. From rote learning to system building: acquiring verb morphology in children and connectionist nets. Cognition. 1993;48:21–69. doi: 10.1016/0010-0277(93)90057-3. [DOI] [PubMed] [Google Scholar]
- Ramscar M, Yartlett D, Dye M, Denny K, Thorpe K. The effects of feature-label-order and their implications for symbol learning. Cognitive Science. 2010;34:909–957. doi: 10.1111/j.1551-6709.2009.01092.x. [DOI] [PubMed] [Google Scholar]
- Richardson DC, Kirkham NZ. Multimodal events and moving locations: Eye movements of adults and 6-month-olds reveal dynamic spatial indexing. Journal of Experimental Psychology: General. 2004;133:46–62. doi: 10.1037/0096-3445.133.1.46. [DOI] [PubMed] [Google Scholar]
- Rumelhart DE, McClelland JL. On learning the past tenses of English verbs. In: McClelland JL, Rumelhart DE, editors. Parallel Distributed Processing (Vol 2): Psychological and Biological Models. MIT Press; 1986. pp. 216–271. [Google Scholar]
- Saffran JR, Aslin RN, Newport EL. Statistical learning by 8-month-old infants. Science. 1996;274:1926–1928. doi: 10.1126/science.274.5294.1926. [DOI] [PubMed] [Google Scholar]
- Saffran JR, Pollack SD, Seibel RL, Shkolnik A. Dog is a dog is a dog: Infant rule learning is not specific to language. Cognition. 2007;105:669–680. doi: 10.1016/j.cognition.2006.11.004. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Shanteau J. Averaging versus multiplying combination rules of inference judgment. Acta Psychologica. 1975;39:83–89. [Google Scholar]
- Shiffrin RM, Steyvers M. A model for recognition memory: REM: Retrieving Effectively from Memory. Psychonomic Bulletin & Review. 1997;4:145–166. doi: 10.3758/BF03209391. [DOI] [PubMed] [Google Scholar]
- Smith LB, Yu C. Infants rapidly learn word-referent mappings via cross-situational statistics. Cognition. 2008;106:1558–1568. doi: 10.1016/j.cognition.2007.06.010. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Shukla M, White KS, Aslin RN. Prosody guides the rapid mapping of auditory word forms onto visual objects in 6-month-old infants. Proceedings of the National Academy of Sciences. 2011;108:6038–6043. doi: 10.1073/pnas.1017617108. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Téglás E, Vul E, Girotto V, Gonzalez M, Tenenbaum JB, Bonatti LL. Pure reasoning in 12-month-old infants as probabilistic inference. Science. 2011;332:1054–1059. doi: 10.1126/science.1196404. [DOI] [PubMed] [Google Scholar]
- Tenenbaum JB, Kemp C, Griffiths TL, Goodman ND. How to grow a mind: Statistics, structure, and abstraction. Science. 2011;331:1279–1285. doi: 10.1126/science.1192788. [DOI] [PubMed] [Google Scholar]
- Thiessen ED. Effects of visual information on adults’ and infants’ auditory statistical learning. Cognitive Science. 2010;34:1093–1106. doi: 10.1111/j.1551-6709.2010.01118.x. [DOI] [PubMed] [Google Scholar]
- Treichler FR. Reinforcer preference effects on probability learning by monkeys. Journal of Comparative and Physiological Psychology. 1967;64:339–342. doi: 10.1037/h0087997. [DOI] [PubMed] [Google Scholar]
- Vallabha GK, McClelland JL, Pons F, Werker JF, Amano S. Unsupervised learning of vowel categories from infant-direct speech. Proceedings of the National Academy of Sciences. 2007;104:13273–13278. doi: 10.1073/pnas.0705369104. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Xu F, Garcia V. Intuitive statistics by 8-month-old infants. Proceedings of the National Academy of Sciences of the United States of America. 2008;105:5012–5015. doi: 10.1073/pnas.0704450105. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Xu F, Tenenbaum JB. Word learning as Bayesian inference. Psychological Review. 2007;114:245–272. doi: 10.1037/0033-295X.114.2.245. [DOI] [PubMed] [Google Scholar]
- Wilson WA, Rollin RA. Two-choice behavior of rhesus monkeys in a noncontingent situation. Journal of Experimental Psychology. 1959;58:174–180. doi: 10.1037/h0043061. [DOI] [PubMed] [Google Scholar]
- Wolford G, Newman S, Miller MB, Wig G. Searching for patterns in random sequences. Canadian Journal of Experimental Psychology. 2004;58:221–228. doi: 10.1037/h0087446. [DOI] [PubMed] [Google Scholar]
- Yang T, Shadlen MN. Probabilistic reasoning by neurons. Nature. 2007;447:1075–1080. doi: 10.1038/nature05852. [DOI] [PubMed] [Google Scholar]
- Yoshida H, Smith LB. Linguistic cues enhance the learning of perceptual cues. Psychological Science. 2005;16:90–95. doi: 10.1111/j.0956-7976.2005.00787.x. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Yu AJ, Cohen JD. Sequential effects: Superstition or rational behavior? Advances in Neural Information Processing Systems. 2009;21:1873–1880. [PMC free article] [PubMed] [Google Scholar]
- Yuki M, Maddux WW, Masuda T. Are the windows to the soul the same in the East and West? Cultural differences in using the eyes and mouth as cues to recognize emotions in Japan and the United States. Journal of Experimental Social Psychology. 2007;43:303–311. [Google Scholar]
- Zhu X, Rogers TT, Gibson BR. Human Rademacher Complexity. Advances in Neural Information Processing Systems. 2009;21:2322–2330. [Google Scholar]
- Zosuls KM, Ruble DN, Tamis-LeMonda CS, Shrout PE, Bornstein MH, Greulich FK. The acquisition of gender labels in infancy: Implications for gender-typed play. Developmental Psychology. 2009;45:688–701. doi: 10.1037/a0014053. [DOI] [PMC free article] [PubMed] [Google Scholar]