Abstract
Soft tissues other than muscles are supposed to be of mechanical importance, yet they are rarely integrated into finite element models. Here, we investigate the functional role of the ischiopubic membrane for the loading of the pubis of the domestic fowl using 2D finite element analysis. For this purpose, a specimen of the domestic fowl was dissected and soft tissues attaching to the pubis were studied in great detail. Muscles were removed and measurements taken. For the 2D finite element model, the outline was taken from the dissected specimen. Two 2D finite element models were generated: one without and one with ischiopubic membrane. The same muscular loading based on own measurements and electromyographic data was applied to both models. The model without ischiopubic membrane shows anteroventral bending deformation of the scapus pubis, resulting in high compressive and tensile principal stresses at the level of ultimate bone stress values. The model with ischiopubic membrane shows low compressive principal stresses in the pubis consistent with the levels of steady state remodelling of bone. Based on these results, the ischiopubic membrane of the domestic fowl potentially establishes a physiological loading of the pubis and therefore might be of great mechanical significance for the loading of the bone.
Keywords: bending loading, collagen fibres, finite element analysis, membrana ischiopubica, passive tension chord, physiological loading
Introduction
The os pubis of Aves can be subdivided into two parts: the proximal end or corpus pubis that is fused to the os ilium and os ischium, and the thin, rod-like scapus pubis (Fig. 1A). The os pubis provides attachment for the muscles of the infrapubic and suprapubic abdominal wall (VandenBerge & Zweers, 1993; Vollmerhaus, 2004). The abdominal muscles of Aves are ventilatory muscles that are active during expiration (Fedde, 1987; Baumel et al. 1990; Vollmerhaus, 2004). The arrangement of the abdominal muscles clearly indicates that the scapus pubis is subject to high bending loading during contraction of the muscles during expiration (Fig. 1D). Bending loading results in high mechanical stresses which are not well addressed by a thin, rod-like bone such as the scapus pubis of Aves. Although bones are adapted to tolerate bending loading to some extent, excessive bending loading and high peak stresses are avoided (Currey, 2012). It has been shown in numerous studies that high bending strain levels lead to bone remodelling and consequently result in increasing bone cross-sections and more massive bones (Lišková & Hert, 1971; Rubin & Lanyon, 1987). Minimizing bending loading by muscle action, on the contrary, significantly reduces mechanical stresses in bones (Pauwels, 1965; Lu et al. 1997; Sverdlova & Witzel, 2010; Rantalainen & Kłodowsk, 2011). Thus, less bone material is required to withstand the mechanical loads and the development of delicate bone structures is induced. Therewith, the thin, rod-like scapus pubis of Aves calls for a structure that complies with this bending minimization principle. In fact, the scapus pubis of Aves is connected to the os ischium by the membrana ischiopubica (Fig. 1B). Membranes consist of elastic and collagen fibres embedded in an extracellular matrix. Due to the differing mechanical characteristics of elastin and collagen, the mechanical characteristics of a membrane depend on the composition of its components: elastic fibres confer flexibility and resilience to tissues (Midwood & Schwarzbauer, 2002); collagen fibres, in contrast, confer stability, toughness, and strength (Fratzl, 2010). The combination of the material properties of elastin and collagen are well suited for the transmission of tensile forces, and dense-fibred membranes increase the loading capacity of associated bony structures (Schwind, 2009). Thus, the membrana ischiopubica should be taken into account in the modelling of the mechanical loading of the os pubis of Aves.
Fig. 1.
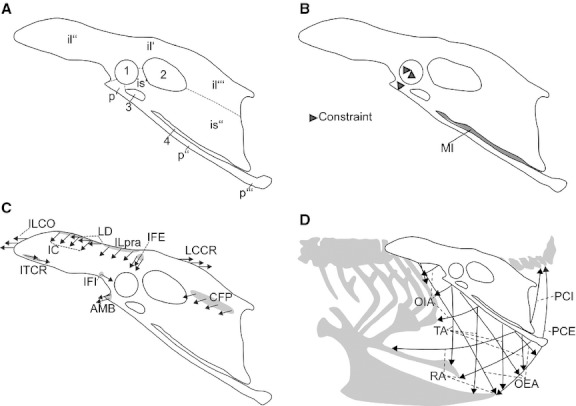
Lateral left view of the pelvis of Gallus gallus depicting (A) osteological features, (B) membrana ischiopubica and constraints, (C) schematic arrangement of the muscles attached to the pelvis and active during the chosen load case (excluding the abdominal muscles) indicated by arrows (grey areas indicate attachment site), (D) schematic arrangement of the muscles of the infrapubic and suprapubic abdominal wall indicated by arrows. (1) acetabulum with foramen acetabuli; (2) foramen ilioischiadicum, (3) foramen obturatum; (4) fenestra ischiopubica. il', ala praeacetabularis ilii; il'', corpus ilii; il''', ala postacetabularis ilii; is' corpus ischia; is'', Ala ischia; MI, membrana ischiopubica; p', corpus pubis; p'', scapus pubis; p''', Apex pubis. Abbreviations of muscles are listed in Table 1. Borders of the fused elements of the pelvis are indicated by dashed lines.
Although there is increasing evidence that soft tissue other than muscles (e.g. ligaments, tendons, fasciae) contribute to the loading regime of bones, they are only rarely included in studies (Rudman et al. 2006; Schwarz-Wings et al. 2010; Gößling, 2011). Most recently, Curtis et al. (2011) demonstrated the great potential of integrating non-muscular soft tissues into studies on the mechanical loading of bones. By investigating the effect of the inclusion of the fascia temporalis into their model of a primate skull, Curtis et al. (2011) showed that the fascia temporalis eliminated the high strain gradients in the zygomatic arch and adjacent structures. Additionally, the strains were found to be more uniform in magnitude than shown in previous studies on this subject.
In this study, we investigate the functional role of the membrana ischiopubica using 2D finite element analysis (FEA). We address: (i) stress and strain distribution in the os pubis of Gallus without membrana ischiopubica and (ii) stress and strain distribution in the os pubis of Gallus with membrana ischiopubica. We hypothesize that the membrana ischiopubica (i) compensates bending loading in the scapus pubis and leads to an even compressive stress distribution and reduces peak stress and strain magnitudes in the os pubis, and (ii) allows for delicate bone structures despite high mechanical loading.
Material and methods
A specimen of Gallus was dissected to study the gross anatomy of the os pelvis, the origin and insertion of muscles and fibre orientation and the presence of soft tissue other than muscle. The muscles were removed; muscle mass was measured with a digital scale and fibre length was measured using a digital calliper. Each step of the dissection procedure was documented with digital photographs.
To study the stress and strain distribution in the os pubis of Gallus without and with the membrana ischiopubica, an FE analysis was conducted. In the present FE analysis, a 2D FE model was generated. Using 2D FE models has the advantage of considerably reducing computing time. On the other hand, 2D FE models always implicate geometric abstraction of biological structures that will limit the model's potential to reflect the behaviour of the biological structure (Richmond et al. 2005; Rayfield, 2007). In the present study, which focuses on investigating the functional role of the membrana ischiopubica, a 2D FE model suits the purpose of this study. The mechanical loading of the membrane is mainly restricted to a single plane. Thus, the loading of the model can be projected into the parasagittal plane without introducing large distortions. The 2D FE model was generated based on the lateral outline of the os pelvis of the dissected specimen using ansys 12.0 Research Edition (ANSYS Inc., Canonsburg, PA, USA). The 2D plane stress FE model has a thickness of 1 mm and consists of 4724 PLANE2 elements and 9672 nodes. We used homogeneous material properties for the bone, with Young's modulus 17 GPa and a Poisson's ratio of 0.3 (e.g. Reilly & Burstein, 1974; Strait et al. 2005; Sverdlova & Witzel, 2010). A 2D FE model has two translational and one rotational degree of freedom (DOF) which have to be constrained. The two translational DOF were constrained at one node in the acetabulum (Fig. 1B). For the rotational DOF constraint at one node anteroventrally to the acetabulum, a second bearing was applied.
The simulated loading of the model is crucial for the accurate estimation of the stress and strain distribution in the model. Therefore, we based our loading conditions on own measurements as well as on published data on muscle anatomy and function. The loading of the 2D FE model was realized by nodal forces, which were distributed over a few nodes in accordance with anatomical data obtained during the dissection. In addition to weight forces, loads from 29 muscles were applied to the 2D FE model (Table 1). Six of those muscles (abdominal muscles) originate from or insert onto the os pubis (Fig. 1D; Table 1). For more detailed information on the anatomy of the muscles attached to the pelvis of Gallus, please refer to Vollmerhaus (2004). The maximum isometric muscle force (Fmax) of each muscle was calculated by multiplying the physiological cross-sectional area (PCSA) by the estimated maximum isometric stress of vertebrate skeletal muscle of 300 kN m–2 (Wells, 1965; Woledge et al. 1985; Medler, 2002). Muscular PCSA was based on measurements obtained from the dissection (Table 1). The magnitudes of the muscle forces applied to the models (FLC M1 and M2) were calculated using the ansys optimization tool (Table 1). The ansys optimization tool iteratively determines an optimal set of muscle forces that lie within the range of Fmax and satisfy the condition of physiological bone loading. This condition includes: (i) minimal absolute tensile stresses at several reference points in the FE model (as indication of minimized bending loading); (ii) physiological direction of the reaction force on the bearing in the acetabulum; (iii) reaction force of the second bearing approaching zero (as indication of force-balance around the hip joint). Information on which muscles were active was obtained from electromyographic (EMG) studies (Jacobson & Hollyday, 1982; Fedde, 1987; Baumel et al. 1990; Gatesy & Dial, 1993; Gatesy, 1999). For muscles for which EMG data were not available, Vollmerhaus (2004) was consulted. This muscle activity pattern, in turn, was used to determine the load cases for the FE analysis. According to the available data (Fedde, 1987; Baumel et al. 1990; Vollmerhaus, 2004), abdominal muscles are solely active during expiration. Therefore, one load case, expiration during gait (expiration/swing), was defined. The FE analysis was conducted on a model without (M1) and with simulated membrana ischiopubica (M2). The membrane was modelled using 1D linear tension-only elements LINK10 with Young's modulus of 3 GPa. The Young's modulus of 3 GPa for the membrana ischiopubica of Gallus was inferred from the assumption that the tensile deformation of a dense-fibred membrane or comparable structure should not exceed 5% (e.g. Fung, 1993; Schwind, 2009). Thirty-six LINK10 elements were modelled with a cross-sectional area of 1 mm2. The arrangement of the LINK10 elements in model M2 is not based on histological findings. As characteristic for a uniaxial transmission of tensile forces, the LINK10 elements are oriented perpendicular to the scapus pubis and Os ischium.
Table 1.
Muscular force values and maximal muscle force values. Listed are all muscles attached to the pelvis of Gallus gallus. Muscles attached to the os pubis are indicated in bold. – indicates muscles not active in the load case expiration/swing. Abbreviations are explained in the text
| Muscle | Mmusc (g) | Lfasc (mm) | Fibre angulation ϕ (°) | PCSA = (Vmusc/Lfasc) *cos ϕ (mm2) | Fmax = PCSA*ρmax (N) | FLC (M1 and M2) (N) |
|---|---|---|---|---|---|---|
| M. iliotibialis cranialis (IC) | 8.1 | 98.9 | 0 | 77.27 | 23.18 | 9.08 |
| M. iliotibialis lateralis pars praeacetabularis (ILpra) | 3.5 | 80.8 | 0 | 40.86 | 12.26 | 7.49 |
| M. iliotibialis lateralis pars postacetabularis (ILpos) | 14.6 | 109.4 | 30 | 109.03 | 32.71 | – |
| M. iliofemoralis externus (IFE) | 0.5 | 30.4 | 0 | 15.52 | 4.66 | 2.75 |
| M. iliotrochantericus caudalis (ITC) | 6.8 | 41.9 | 0 | 153.11 | 45.93 | – |
| M. iliotrochantericus medialis (ITM) | 0.48 | 26.3 | 0 | 17.22 | 5.17 | – |
| M. iliotrochantericus cranialis (ITCR) | 1.53 | 32.4 | 0 | 44.55 | 13.37 | 2.83 |
| M. iliofibularis (ILFB) | 10.51 | 80.9 | 0 | 122.56 | 36.77 | – |
| M. ambiens (AMB) | 0.78 | 50.8 | 0 | 14.49 | 4.35 | 0.84 |
| M. flexor cruris lateralis (FCL) | 9.36 | 80.1 | 10 | 110.54 | 33.16 | – |
| M. flexor cruris lateralis pars acc. (FCLacc) | 3.43 | 36.6 | 35 | 72.42 | 21.73 | – |
| M. flexor cruris medialis (FCM) | 2.95 | 65.3 | 10 | 41.97 | 12.59 | – |
| M. caudofemoralis pars pelvica (CFP) | 1.49 | 54.3 | 0 | 24.33 | 7.30 | 3.89 |
| M. ischiofemoralis (ISF) | 1.53 | 44.3 | 0 | 32.58 | 9.78 | – |
| M. puboischiofemoralis lateralis (PIFL) | 2.94 | 61.9 | 0 | 44.81 | 13.44 | – |
| M. puboischiofemoralis medialis (PIFM) | 4.48 | 55 | 0 | 76.84 | 23.05 | – |
| M. iliofemoralis internus (IFI) | 0.31 | 21.3 | 0 | 13.73 | 4.12 | 0.62 |
| M. obturator lateralis (OL) | 0.09 | 11.4 | 0 | 7.45 | 2.23 | – |
| M. obturator medialis (OM) | 3.92 | 51.2 | 10 | 71.13 | 21.34 | – |
| M. longissmus dorsi (LD) | 0.63 | 31 | 0 | 19.17 | 5.75 | 3.54 |
| M. iliocostalis (ILCO) | 1.35 | 59.5 | 0 | 21.40 | 6.42 | 0.74 |
| M. levator caudae pars cranialis (LCCR) | 0.49 | 36.1 | 0 | 12.80 | 3.81 | 2.83 |
| M. pubocaudalis externus et internus (PCE. PCI) | 1.14 | 49.8 | 0 | 21.60 | 6.48 | 1.64 |
| M. obliquus externus abdominis (OEA) | 2.35 | 89.6 | 0 | 24.74 | 7.42 | 3.06 |
| M. obliquus internus abdominis (OIA) | 1.15 | 21.95 | 0 | 49.43 | 14.83 | 8.48 |
| M. transversus abdominis (TA) | 2.3 | 85.03 | 0 | 25.52 | 7.66 | 0.64 |
| M. rectus abdominis (RA) | 2.2 | 72.32 | 0 | 32.25 | 9.67 | 8.10 |
Results
2D FEA of the pelvis of Gallus gallus without membrana ischiopubica
In M1, both the compressive and tensile principal stress plots show highly uneven stress distribution, with stress increasing towards the margins of the scapus pubis (Fig. 2). The highest compressive principal stresses with a peak at −140 MPa occur along the ventral margin of the greater part of the scapus pubis (Fig. 2A). The compressive principal stresses of the distal end of scapus pubis and along the entire dorsal margin of the scapus pubis are considerably lower, with values not exceeding −1.8 MPa. The corpus pubis shows relatively high compressive principal stresses, with a maximum at −20 MPa. The tensile principal stresses are also high and localize along the dorsal margin of the proximal end of the scapus pubis (Fig. 2C), with a maximum at 223 MPa. The distribution of compressive principal stress and tensile principal stress in the scapus pubis are indicative of bending loading of the scapus pubis, with a maximal bending loading at the proximal end of the scapus pubis. The bending deformation is in the anteroventral direction (Fig. 2A,C). The compressive principal strain (Fig. 3A) and tensile principal strain (Fig. 3B) distribution in the os pubis shows that the magnitude of strain levels exceeds 3000 microstrain each.
Fig. 2.
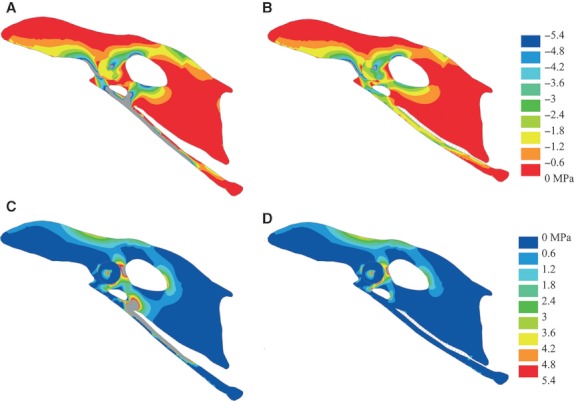
Principal stress plots and deformation of the pelvis of Gallus gallus. (A) Compressive principal stress plot without membrane; (B) compressive principal stress plot with membrane; (C) tensile principal stress plot without membrana ischiopubica, (D) tensile principal stress plot without membrana ischiopubica. Deformations are scaled by a factor of 1. Grey areas are in excess of 5.4 MPa.
Fig. 3.
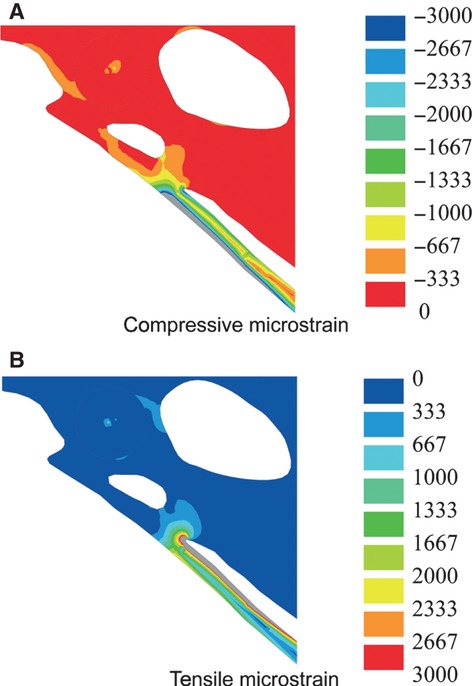
Detail of the strain plot of the pelvis of Gallus gallus without membrana ischiopubica. (A) Compressive strain plot and (B) tensile strain plot. Deformations are scaled by a factor of 1. Grey areas are in excess of 3000 microstrain.
2D FEA of the pelvis of Gallus gallus with membrana ischiopubica
In M2, the compressive principal stress plot shows an even stress distribution in the entire scapus pubis, with peak values of −3 MPa (Fig. 2B). In the corpus pubis, the compressive principal stress values do not exceed −5.4 MPa. The maximum compressive principal stress of −12.5 MPa is found in the ala praeacetabularis ilii. The tensile principal stresses do not exceed 1.8 MPa in the scapus pubis, with a local marginal rise at the distal third of the bone (Fig. 2D). The maximum tensile principal stress of 13.4 MPa is localized in the ala praeacetabularis ilii. The compressive strains vary between −66.7 and −133 microstrain, with peak value of −233 microstrain, and the tensile strains vary between 0 and 33.3 microstrain, with peak value of 100 microstrain for the greater part of the scapus pubis (Fig. 4A,B). In the corpus pubis, peak compressive strains of −300 microstrain are obtained (Fig. 4A). The LINK10 elements of the membrana ischiopubica show strain ranging between 0 and 0.0021, corresponding to a tensile deformation of up to 2.1%.
Fig. 4.
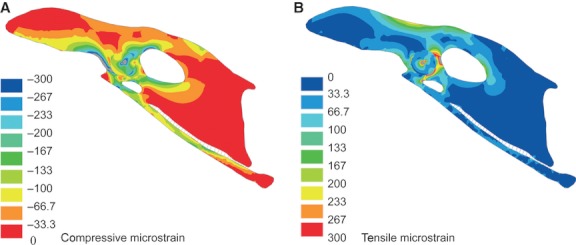
Strain plot of the pelvis of Gallus gallus with membrana ischiopubica. (A) Compressive strain plot and (B) tensile strain plot. Deformations are scaled by a factor of 1. Grey areas are in excess of 300 microstrain.
Discussion
The functional role of the membrana ischiopubica in Gallus gallus
The aim of this study was to investigate whether the membrana ischiopubica has the potential to fulfil the criteria of a bending minimization mechanism. In fact, the 2D FE model without (M1) and the 2D FE model with membrana ischiopubica (M2) show major differences in the mechanical loading of the os pubis. In M1, the obtained maximal stress values of both the compressive principal stress (−140 MPa) and the tensile principal stress (223 MPa) are at the level of the cortical bone mechanical strength. The values of the mechanical strength of bone have been measured at −133 to −237 MPa for compressive principal stress and 27–271 MPa for tensile principal stress (Currey, 2002, and references cited therein; Martin et al. 2010, and references cited therein). The wide-ranged values are explained not only by different animals and bones chosen in the studies (Currey, 2002; Martin et al. 2010) but also by differences in experimental settings, such as strain rate (Carter, 1976; Hansen et al. 2008). Unfortunately, the values of bone mechanical strength for the bones of Gallus are not available; however, they most likely lie within these ranges. Nonetheless, the bone mechanical strength is the ultimate stress the material is able to withstand and it seems unlikely that mechanical loading of a bone during ventilation causes stresses at the level of the ultimate stress of the material. The upper limit of the functional stress in bone during everyday activities is more likely linked to the yield stress of bone (Curtis et al. 2011) or to the fatigue strength of bone (Taylor, 2000; Taylor et al. 2003); both values are lower than the ultimate stress of bone. Furthermore, the functional stress in bone is subject to a safety factor; this is not strictly defined in the literature but can lead to a 1.4–6 times reduction of functional stress values in vivo (Biewener, 1993; Robling et al. 2006; Turner, 2006). In addition to that, both compressive and tensile strain levels in a major part of the scapus pubis and parts of the corpus pubis exceed 3000 microstrain (Fig. 3). In the overload range above 3000 microstrain, the bone formation exceeds the bone resorption, leading to net bone mass gain or bone cross-sectional growth (Frost, 2003; Robling et al. 2006; Turner, 2006). In these areas excessive bone remodelling due to overload is expected. However, the levels of functional strain observed in the corpus pubis are above the normally accepted modelling threshold. Thus, loading of the os pubis in M1 does not fully reflect physiological loading conditions of the bone.
In M2, in which the membrana ischiopubica is included, a physiological level of bone loading is re-established by compensating bending loading and subsequently reducing high principal stress values. Here, the maximal compressive principal stress in the os pubis (−12.5 MPa) is much lower than the mechanical strength of bone material and the tensile principal stress (< 0.6 MPa) is virtually absent. It is not sensible to draw conclusions about the safety factor because of the missing data on bone strength in this particular case and limitations of the study discussed below. However, our results for M2 show that the compressive strain levels in most of the os pubis lie between −66.7 and −133 microstrain, corresponding to the lower range of physiological loading. In a bone adapted to everyday loading, e.g. during ventilation and locomotion, strains ranging between 50 and 1500 microstrain are expected (Martin, 2000; Frost, 2003). In this physiological range, the bone resorption equals bone formation. Thus, our results show that the loading during expiration is well suited to maintain the bone structure of the scapus pubis. Nonetheless, the loading of the scapus pubis of Gallus simulated in M2 is in a low physiological range. This shows that the membrana ischiopubica allows for even higher mechanical loading of the os pubis, which can take place during hopping or fluttering, without bringing the bone dangerously close to the ultimate stress.
The compensation of the bending loading in the scapus pubis is explained by the mechanical characteristics of the membrana ischiopubica. The membrana ischiopubica of Gallus is a dense-fibred interosseus membrane (R. Fechner, pers. obs.). The membrana ischiopubica transfers the tensile loading produced by the infrapubic and suprapubic abdominal muscles onto the os ischium and probably os ilium, and at the same time restrains the bending deformation of scapus pubis. With elimination of the tensile principal stresses, the peak compressive principal stresses are reduced and the scapus pubis is strikingly evenly loaded under compression. Additionally, the reduction of the compressive principal stresses on the corpus pubis shows that the mechanical function of the membrana ischiopubica also influences the loading of adjacent structures.
The membrana ischiopubica follows the tension chord principle established by Pauwels (1965). Systematic investigations by Pauwels (1965) showed that bending loading in bones initiates adaptive bone remodelling processes and is minimized in two major ways: (i) using bone remodelling, which leads to the inhomogeneous structure of bones and (ii) using the action of soft tissues or the so-called tension chord principle. Usually, only bone adaptation mechanisms are considered as a bone reaction to the external loading (e.g. Hart, 2001). However, the importance of tension chords cannot be underestimated (Sverdlova & Witzel, 2010; Curtis et al. 2011; Gößling, 2011). In fact, the stimulus to avoid bending loading using both mechanisms culminates in the optimization of bones and muscular architecture for certain loading conditions. Tension chords can be realized by muscles (i.e. active tension chords) or by other soft tissue structures, such as ligaments, tendons, fasciae, and membranes (i.e. passive tension chords). The membrana ischiopubica of Gallus represents a passive tension chord. A passive tension chord has advantages for the musculoskeletal system. Muscle activity is the most costly activity for an organism (Conley & Lindstedt, 2002). Reducing muscle mass by developing membranes or other passive structures can be seen not only as an energy-saving mechanism but also as a weight-saving mechanism (Biewener, 2010). Combining passive soft tissue structures and optimizing bones in terms of minimizing mass has the potential to reduce total energy and weight requirements considerably.
As mentioned above, the arrangement of the collagen fibres in model M2 is not based on histological findings. In model M2, the collagen fibres are oriented perpendicular to the scapus pubis and os ischium, an arrangement characteristic for an uniaxial transmission of tensile forces. The modelled membrane with the uniaxially oriented collagen fibres is close to the behaviour of a real membrane. The tensile deformation of up to 2.1% in the modelled membrana ischiopubica lies within the range expected for a dense-fibred membrane (up to 5%; Schwind, 2009) or a comparable structure, such as a tendon (2–5%; Fung, 1993).
Summarizing, the bending minimization mechanism that controls the loading regime of the os pubis in Gallus is a membranous passive tension chord. The mechanical properties of the membrana ischiopubica allow tensile forces to be transmitted to adjacent bone structures. Thereby, bending loading exerted on the os pubis by contraction of the abdominal muscles during expiration is compensated, and high stresses and strains reduced. This bending minimization mechanism enables the development of delicate bone structures, such as the scapus pubis, despite relatively high mechanical loading.
The mechanical significance of the membrana ischiopubica for the anatomy of the ventral pelvis of Aves
As outlined above, passive tension chords have the advantage of reducing energy and weight requirements. However, the employment of passive tension chords is not possible if active control is required (i.e. joints). In Gallus, the corpus pubis is fused to the os ilium and os ischium and thus a passive structure such as the membrana ischiopubica suffices to oppose the forces exerted on the os pubis. A membrana ischiopubica is present not only in Gallus but is characteristic for most birds. In some neognath birds, the membrana ischiopubica is reduced or lost with the reduction of the fenestra ischiopubica. Nonetheless, it can be expected that the functional role of the membrana ischiopubica of the remaining neognath birds resembles the functional role investigated in Gallus. In ratite birds, this is different. The fenestra ischiopubica is comparatively large. In addition to a dense-fibred membrana ischiopubica covering the greater part of the fenestra ischiopubica (R. Fechner, pers. obs.; Vollmerhaus, 2004), a muscle attaches to the ventral aspect of the ala ischii and the dorsal aspect of the scapus pubis (R. Fechner pers. obs.; McGowan, 1979; Gangl et al. 2004; Picasso, 2010). This muscle, m. obturatorius medialis, functions as an active tension chord opposing the abdominal muscles. Most likely, the membrana ischiopubica assists the m. obturatorius medialis. As yet, the functional reasons for this arrangement in ratite birds has not been identified. Nonetheless, it is interesting to note that there is a relationship between the functional role of the membrana ischiopubica and the organization of m. obturatorius medialis. It appears that the moment m. obturatorius medialis is released from its function as an active tension chord, the origin of this muscle moves to the medial aspect of the ala ischii, as is characteristic for neognath birds. The limitations of a membranous passive tension chord as well as the evolution of the functional role of the membrana ischiopubica within reptiles should be the subject of future studies.
Conclusions
In this study the functional role of the membrana ischiopubica was studied using a 2D FE analysis. The results show that the membrana ischiopubica is potentially of great mechanical significance for the loading of the scapus pubis. In accordance with the principle of a passive tension chord, the membrana ischiopubica provides a bending minimization mechanism that establishes an even compressive stress distribution and reduces peak stress and strain magnitudes in the os pubis. Although non-muscular soft tissues are very common in the musculoskeletal system of tetrapods, they are rarely integrated in FE models. The consequences resulting from such a deficit have been demonstrated in this study. The absence of non-muscular soft tissues in FE models may lead to inaccurate loading of the structures and overestimation of non-physiological peak stresses and strains.
The mechanical characteristics of membranes and other non-muscular soft tissues strongly depend on the composition of collagen and elastin. The variation in the composition of non-muscular soft tissues suggests differences in their functional roles. Differences in the functional roles, however, imply that findings about the functional role of a structure cannot be transferred to other structures without careful analysis.
Acknowledgments
The authors thank U. Witzel and H. Preuschoft for helpful advice and discussion on biomechanical principles and soft tissue functional anatomy, and C. Distler-Hoffmann and N. Poschmann for helping with dissections. The authors are grateful to two anonymous reviewers for their constructive and helpful suggestions and to the editors of the Journal of Anatomy E. Fenton and T. Gillingwater for their support. This research was supported by DFG (Deutsche Forschungsgemeinschaft) grant FE 1115/1-1.
References
- Baumel JJ, Wilson JA, Bergren DR. The ventilatory movements of the avian pelvis and tail: function of the muscles of the tail region of the pigeon (Columba livia. J Exp Biol. 1990;151:263–277. doi: 10.1242/jeb.151.1.263. [DOI] [PubMed] [Google Scholar]
- Biewener AA. Safety factors in bone strength. Calcif Tissue Int. 1993;53(Suppl 1):S68–S74. doi: 10.1007/BF01673406. [DOI] [PubMed] [Google Scholar]
- Biewener AA. Tendons and ligaments: structure, mechanical behavior and biological function. In: Fratzl P, editor. Collagen: structure and mechanics. New York: Springer Verlag; 2010. pp. 269–284. [Google Scholar]
- Carter D. Bone compressive strength: the influence of density and strain rate. Science. 1976;194:1174–1176. doi: 10.1126/science.996549. [DOI] [PubMed] [Google Scholar]
- Conley KE, Lindstedt SL. Energy-saving mechanisms in muscle: the minimization strategy. J Exp Biol. 2002;205:2175–2181. doi: 10.1242/jeb.205.15.2175. [DOI] [PubMed] [Google Scholar]
- Currey JD. Bones. Princeton: Princeton University Press; 2002. [Google Scholar]
- Currey JD. The structure and mechanics of bone. J Mater Sci. 2012;47:41–54. [Google Scholar]
- Curtis N, Witzel U, Fitton L, et al. The mechanical significance of the temporal fasciae in Macaca fascicularis: an investigation using finite element analysis. Anat Rec. 2011;294:1178–1190. doi: 10.1002/ar.21415. [DOI] [PubMed] [Google Scholar]
- Fedde M. Respiratory muscles. In: Seller T, editor. Bird respiration. Boca Raton: CRC Press; 1987. pp. 3–94. [Google Scholar]
- Fratzl P. Collagen: structure and mechanics, an introduction. In: Fratzl P, editor. Collagen: structure and mechanics. New York: Springer Verlag; 2010. pp. 1–13. [Google Scholar]
- Frost H. Bone's mechanostat: a 2003 update. Anat Rec. 2003;275:1081–1101. doi: 10.1002/ar.a.10119. [DOI] [PubMed] [Google Scholar]
- Fung Y-C. Bioviscoelastic solids. In: Fung Y-C, editor. Biomechanics. Mechanical properties of living tissues. New York: Springer Verlag; 1993. pp. 242–319. [Google Scholar]
- Gangl D, Weissengruber G, Egerbacher M, et al. Anatomical description of the muscles of the pelvic limb in the ostrich (Struthio camelus. Anat Histol Embryol. 2004;33:100–114. doi: 10.1111/j.1439-0264.2003.00522.x. [DOI] [PubMed] [Google Scholar]
- Gatesy S. Guineafowl hind limb function. II. Electromyographic analysis and motor pattern evolution. J Morphol. 1999;240:127–142. doi: 10.1002/(SICI)1097-4687(199905)240:2<127::AID-JMOR4>3.0.CO;2-Q. [DOI] [PubMed] [Google Scholar]
- Gatesy SM, Dial KP. Tail muscle activity patterns in walking and flying pigeons (Columba livia. J Exp Biol. 1993;176:55–76. [Google Scholar]
- Gößling R. Biologische Vorteile und mechanische Probleme der langen Schnauze am Beispiel Plateosaurus. Bochum: Dr. Hut Verlag; 2011. [Google Scholar]
- Hansen U, Zioupos P, Simpson R, et al. The effect of strain rate on the mechanical properties of human cortical bone. J Biomech Eng. 2008;130:1–8. doi: 10.1115/1.2838032. [DOI] [PubMed] [Google Scholar]
- Hart R. Bone modeling and remodeling: theories and computation. In: Cowin S, editor. Bone mechanics handbook. Boca Raton: CRC Press; 2001. pp. 1–42. [Google Scholar]
- Jacobson RD, Hollyday M. A behavioral and electromyographic study of walking in the chick. J Neurophysiol. 1982;48:238–256. doi: 10.1152/jn.1982.48.1.238. [DOI] [PubMed] [Google Scholar]
- Lišková M, Hert J. Reaction of bone to mechanical stimuli. Part 2. Periosteal and endosteal reaction of tibial diaphysis in rabbit to intermittent loading. Folia Morphol. 1971;19:310–317. [PubMed] [Google Scholar]
- Lu TW, Taylor SJ, O'Connor JJ, et al. Influence of muscle activity on the forces in the femur: an in vivo study. J Biomech. 1997;30:1101–1106. doi: 10.1016/s0021-9290(97)00090-0. [DOI] [PubMed] [Google Scholar]
- Martin RB. Toward a unifying theory of bone remodeling. Bone. 2000;26:1–6. doi: 10.1016/s8756-3282(99)00241-0. [DOI] [PubMed] [Google Scholar]
- Martin RB, Burr DB, Sharkey NA. Skeletal tissue mechanics. New York: Springer Verlag; 2010. [Google Scholar]
- McGowan C. The hind limb musculature of the brown kiwi, Apteryx australis mantelli. J Morphol. 1979;160:33–73. doi: 10.1002/jmor.1051600105. [DOI] [PubMed] [Google Scholar]
- Medler S. Comparative trends in shortening velocity and force production in skeletal muscles. Am J Physiol Regul Integr Comp Physiol. 2002;283:368–378. doi: 10.1152/ajpregu.00689.2001. [DOI] [PubMed] [Google Scholar]
- Midwood K, Schwarzbauer J. Elastic fibers: building bridges between cells and their matrix. Curr Biol. 2002;12:R279–R281. doi: 10.1016/s0960-9822(02)00800-x. [DOI] [PubMed] [Google Scholar]
- Pauwels F. Gesammelte Abhandlungen zur funktionellen Anatomie des Bewegungsapparates. Berlin: Springer Verlag; 1965. [Google Scholar]
- Picasso M. The hindlimb muscles of Rhea americana (Aves, Palaeognathae, Rheidae) Anat Histol Embryol. 2010;39:462–472. doi: 10.1111/j.1439-0264.2010.01017.x. [DOI] [PubMed] [Google Scholar]
- Rantalainen T, Kłodowsk A. Estimating lower limb skeletal loading. In: Klika V, editor. Theoretical biomechanics. Rijeka: Intech; 2011. pp. 243–266. [Google Scholar]
- Rayfield E. Finite element analysis and understanding the biomechanics and evolution of living and fossil organisms. Annu Rev Earth Planet Sci. 2007;35:541–576. [Google Scholar]
- Reilly DT, Burstein AH. The mechanical properties of cortical bone. J Bone Joint Surg Am. 1974;56A:1001–1022. [PubMed] [Google Scholar]
- Richmond BG, Wright BW, Grosse I, et al. Finite element analysis in functional morphology. Anat Rec. 2005;283A:259–274. doi: 10.1002/ar.a.20169. [DOI] [PubMed] [Google Scholar]
- Robling AG, Castillo AB, Turner CH. Biomechanical and molecular regulation of bone remodeling. Annu Rev Biomed Eng. 2006;8:455–498. doi: 10.1146/annurev.bioeng.8.061505.095721. [DOI] [PubMed] [Google Scholar]
- Rubin CT, Lanyon LE. Osteoregulatory nature of mechanical stimuli: function as a determinant for adaptive remodeling in bone. J Orthop Res. 1987;5:300–310. doi: 10.1002/jor.1100050217. [DOI] [PubMed] [Google Scholar]
- Rudman K, Aspden R, Meakin J. Compression or tension? The stress distribution in the proximal femur. Biomed Eng Online. 2006;5:1–7. doi: 10.1186/1475-925X-5-12. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Schwarz-Wings D, Meyer CA, Frey E, et al. Mechanical implications of pneumatic neck vertebrae in sauropod dinosaurs. Proc Biol Sci. 2010;277:11–17. doi: 10.1098/rspb.2009.1275. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Schwind P. Faszien- und Membrantechnik. 2nd. Munich: Urban & Fischer; 2009. [Google Scholar]
- Strait, DS, Wang Q, et al. Modelling elastic properties in finite-element analysis: how much precision is needed to produce an accurate model? Anat Rec. 2005;283A:275–287. doi: 10.1002/ar.a.20172. [DOI] [PubMed] [Google Scholar]
- Sverdlova NS, Witzel U. Principles of determination and verification of muscle forces in the human musculoskeletal system: muscle forces to minimise bending stress. J Biomech. 2010;43:387–396. doi: 10.1016/j.jbiomech.2009.09.049. [DOI] [PubMed] [Google Scholar]
- Taylor D. Scaling effects in the fatigue strength of bones from different animals. J Theor Biol. 2000;206:299–306. doi: 10.1006/jtbi.2000.2125. [DOI] [PubMed] [Google Scholar]
- Taylor D, O'Reilly P, Vallet L, et al. The fatigue strength of compact bone in torsion. J Biomech. 2003;36:1103–1109. doi: 10.1016/s0021-9290(03)00104-0. [DOI] [PubMed] [Google Scholar]
- Turner C. Bone strength: current concepts. Ann NY Acad Sci. 2006;1068:429–446. doi: 10.1196/annals.1346.039. [DOI] [PubMed] [Google Scholar]
- VandenBerge JC, Zweers GA. Myologia. In: Baumel J, editor. Handbook of avian anatomy: nomina anatomica avium. Cambridge: Publications of the Nuttall Ornithological Club; 1993. pp. 189–247. [Google Scholar]
- Vollmerhaus B. Lehrbuch der Anatomie der Haustiere. Band 5. Stuttgart: Parey Verlag; 2004. [Google Scholar]
- Wells J. Comparison of mechanical properties between slow and fast mammalian muscles. J Physiol. 1965;178:252–269. doi: 10.1113/jphysiol.1965.sp007626. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Woledge R, Curtin N, Homsher E. Energetic aspects of muscle contraction. Monogr Physiol Soc. 1985;41:1–357. [PubMed] [Google Scholar]


