VALIDITY OF THE TIMPSI FOR ESTIMATING CONCURRENT PERFORMANCE ON THE TEST OF INFANT MOTOR PERFORMANCE

Abstract

The TIMPSI is a short version of the Test of Infant Motor Performance (TIMP) for use in screening. The purposes of this project were to compare concurrent results on the TIMPSI with those on the TIMP and recommend cutscores for clinical decision-making. 990 infants were recruited to reflect the race/ethnicity of U.S. low birthweight infants. From 67–97 infants were tested in 2-week age groups ranging from 34–35 weeks postmenstrual age through 16–17 weeks post-term. Rasch analysis of raw scores was used. TIMPSI cutscores ranging from the mean to −1.00 standard deviation (SD) were compared with performance above/below −.5 SD on the TIMP to assess accuracy of classification. The TIMPSI was a valid screening instrument when compared with concurrent performance on the TIMP. A cutscore of −.25 SD appeared useful in predicting the best combination of false negatives (5.8%) and false positives (12.5%) with an overall accuracy of classification of 81.7%.

The Test of Infant Motor Performance (TIMP) is a comprehensive assessment of the postural and selective control of movement needed by infants less than five months of age for functional activity in the early months of life.¹ The TIMP takes an average of 33 minutes to administer and score.² A shorter screening version of the TIMP would be useful for testing 1) infants who are deemed too fragile or irritable to withstand the full assessment, 2) large numbers of infants in a Neonatal Intensive Care Unit (NICU) to determine who should be followed or assessed more thoroughly, and 3) infants in a developmental follow up clinic in which time is limited and numerous professionals must see the babies. To that end, the Test of Infant Motor Performance Screening Items test or TIMPSI was derived from the full TIMP test and assessed in a large national sample of infants recruited to represent the range of race/ethnicity in the U.S. population of low birthweight infants. Our hypothesis for the present study was that scores on the TIMPSI would predict performance on the full TIMP with the accuracy necessary for the TIMPSI to be useful as a screening test. The specific aims of this research were to 1) compare results on the TIMPSI based on Rasch analysis of test performance with those on the full TIMP completed within a 3-day period and 2) develop recommended cutscores on the TIMPSI for use in clinical decision making. The cutscore of interest on the TIMPSI is defined as the threshold score below which there is the highest probability that the infant’s score on the TIMP would suggest delayed motor development. We assessed four different cutscores on the TIMPSI for comparison to scores obtained on the full TIMP after Rasch measures for performance on both tests were derived from raw scores.

Background

The TIMP has been standardized for two-week age groups from 34–35 weeks postmenstrual age (PMA) through 4 months post term³ (all ages adjusted for premature birth, when necessary) and evaluated for ability to diagnose and predict delayed motor development.^4,5 Based on this research a cutscore below −.5 standard deviation (SD) from the mean at 3 months corrected age was determined to produce the most accurate prediction of long-term motor outcome. Items on the TIMP reflect demands for movement placed on infants by their caregivers during naturalistic interactions,⁶ and TIMP scores have been used to document the effectiveness of both nursery and home-based intervention for infants born prematurely.^7,8

The TIMPSI is a shortened version of the TIMP, designed to be completed in about half the time for the purpose of screening for delayed motor development. During the development and assessment of content validity of the TIMP, item responses from two different samples were subjected to Rasch psychometric analysis.⁹ Based on these analyses, the first step in deriving a screening version of the TIMP was a review of the item statistics to determine which items 1) provided a wide range of age-related responses and difficulty, 2) together provided for assessment of postural control of all parts of the body, and 3) had strong psychometric characteristics, including good fit to the Rasch model and high item-to-total test score correlations. Based on this analysis 11 items were used to form a screening set to be administered to all infants in the age range from 34 weeks postmenstrual age through 17 weeks post term. Next, two additional sets of items were identified to use as a second stage of assessment: one a relatively easier set of 10 items, the other relatively harder (8 items) than the screening set based on 1) their average degree of difficulty from the Rasch analysis and 2) the goal of testing all parts of the body. Infants with low scores on the screening set are administered the second easier set of items while infants with high scores on the screening set receive the harder set next. Scores from the 2 sets are added to derive a final TIMPSI test score.²

Pilot data on the TIMPSI were subsequently collected on 25 infants tested on two occasions, first with the TIMPSI and then, within three days, on the full TIMP. The Pearson product moment correlation between the TIMPSI raw score and age in days was .66 (p<.0001) and between the TIMP and TIMPSI raw scores was .75 (p<.0001).² These correlations were deemed satisfactory for a screening test and the items were used in the present study without revision.

Methods

Sample

The sample for this study was intended to reflect the racial/ethnic distribution of the population of low birthweight (i.e., <2500 g at birth, LBW) infants in the U.S. based on 1996 census statistics,¹⁰ with 1) stratification based on age at testing and degree of risk for poor developmental outcome, and 2) geographic variability. A sample of 120 infants from each of 10 geographic locations (an 11^th was added partway through the project when one site dropped out) was planned for inclusion in this study based on a search for sites with special care nurseries and associated developmental follow up clinics to represent the diverse regions of the U.S. and willingness of professionals in each location to participate. Study sites were hospitals in Birmingham, AL; Boston, MA; Chicago, IL (two hospitals); Cleveland, OH; Los Angeles, CA (three hospitals); Omaha, NE; Pensacola, FL; Philadelphia, PA; Portland, OR; Raleigh, NC; and Sioux Falls, SD. Although no specific criteria were used to define the populations served by each site, represented were large urban health science centers as well as smaller hospitals serving regional, including rural, populations. A complete description of the sampling frame for the study has been previously published.³

Procedures

Recruitment

Subjects were recruited for the study for matching with a subject selection grid at each site based on the reported distribution of race/ethnicity in that center for the previous calendar year. When combined across sites, the plan called for 100 subjects in each of 12 two-week age groups from 34–35 weeks PMA through 16–17 weeks post term corrected age. Five race/ethnicity groupings were used according to National Center for Health Statistics definitions;¹⁰ mixed race infants were excluded. Risk for poor developmental outcome was estimated by scores from a modified version of the Problem-Oriented Perinatal Risk Assessment System Newborn Form.³ Scores >90 indicated high risk, scores 61–90 medium risk, and scores <61 low risk; infants with bronchopulmonary dysplasia, periventricular leukomalacia, hypoxic-ischemic encephalopathy, or a grade III or IV intraventricular hemorrhage were considered high risk regardless of score.

Following identification of a match with a grid assignment for age/ethnicity/risk at a testing site, infants were assigned by the recruiter for testing with the TIMP approximately one hour before a scheduled feeding during the two-week age window for which they were selected and for testing with the TIMPSI within 3 days in the same age window. Subjects were cleared by their physician as medically stable enough for testing, were off mechanical ventilation (but could be receiving oxygen by nasal canula, reside in an isolette, or both), and had a signed parental consent to participate. The infant’s age and medical history were masked to testers. To further avoid development of expectations for total test scores, all tests were forwarded with only individual item scores marked to the data analysis site for final calculation of total raw scores.

Rater Reliability

One to three testers were trained in each site. The testers followed previously reported procedures for rater reliability analysis.³ Testers scored items from videotapes of four actual tests of infants from the researchers’ databank of tests scored by reliable raters. The scores were analyzed with the FACETS computer program (V. 3.20) for Rasch analysis of rater consistency and severity/leniency.¹¹ Fewer than 5% misfitting ratings were required in order to be considered a reliable rater.

Instrumentation

Version 5 of the TIMP has 42 items, 13 dichotomously scored items rating observed behaviors and 29 items with 5–7 point scales for rating behaviors elicited by handling and positioning. The TIMPSI screening set consists of 11 items from the TIMP with 5–7 point rating scales; the easy set has 4 dichotomously scored items and 6 items with 5 or 6 point rating scales; and the hard set has 8 items with 5 dichotomously scored and 3 with 5 point rating scales. The average time to complete the TIMPSI was 22 minutes with a range from 12–32 minutes.

Analysis

Rasch model and equating

Methods based in Rasch measurement^12,13,14 were used to calibrate the response data from all 42 items on the TIMP and from the shorter TIMPSI version of the instrument. Data were analyzed using the WINSTEPS software package.¹⁵ The specific Rasch model used was the Rasch partial-credit model (PCM).^13,16 The PCM is suitable for the TIMP data as this model allows each item to have its own unique rating scale structure as required by the design of the test. The Rasch PCM describes the probability of a particular response for an infant to a particular item in terms of a log-odds ratio as shown in equation (1) below:

$$\text{ln}\left(\frac{P_{nij}}{P_{ni(j-1)}}\right)=B_n-D_i-F_{ij},$$ 1

where

• P_nij is the probability that infant n, being observed on item i, receives a score in category j,

• P_ni(j-1) is the probability that infant n, being observed on item i, receives a score in category j-1,

• B_n is the infant measure along the latent continuum (higher measures indicate higher or more advanced development),

• D_i is the difficulty of endorsement for item i,

• and F_ij is the threshold parameter for item i and response category j.

The threshold parameter (F_ij) can be interpreted as the point on the latent continuum at which a response is equally likely to be either category j or category j-1. These parameters are estimated via iterative joint maximum likelihood estimation (JMLE) as part of the Rasch analysis as implemented in Winsteps.¹⁵

The scores from the full version and the TIMPSI versions of the TIMP were equated through a common item anchoring approach,¹⁷ where the phrase “common item” refers to the set of items that appear on both versions of the TIMP. The response data for the 42 items of the TIMP were first calibrated with WINSTEPS. Then the responses from the TIMPSI version were calibrated, with the item endorsement difficulties (D_i) and threshold parameters (F_ij) corresponding to the common items anchored to those values obtained during the calibration of the full instrument. Performing this equating step places the infant measures on a common metric. Being on a common metric allows for the direct comparison of the infant measures from both the TIMP and the TIMPSI.

Development and evaluation of cutscores

For the full TIMP, a cutscore of −.5 SD below the mean for corrected age has been found to yield the optimal combination of specificity for predicting typical development and sensitivity for predicting delayed development.² We refer to this cutscore on the TIMP as AtRisk0. To compare the consistency of the decisions (delayed development versus not delayed) based on the measures from the full TIMP cutscores for each age group and the same decisions based on the TIMPSI, a series of potential cutscores was determined for each age group for the TIMPSI. In total, four sets of cutscores were explored for the TIMPSI in each two-week age group: AtRisk1 (cutscore = mean infant Rasch measure for an age group of -1 SD), AtRisk2 (cutscore = mean infant measure for an age group of −.5 SD), AtRisk3 (cutscore = mean infant measure for an age group of −.25 SD), and AtRisk4 (cutscore = mean infant measure for an age group).

Using AtRisk0 on the TIMP as the gold-standard, the classification of infants into at risk (below a cutscore) versus not at risk (at or above a cutscore) based on the potential TIMPSI cutscores (AtRisk1, AtRisk2, AtRisk3, and AtRisk4) were assessed by the percentage of false negatives and false positives. A classification can be considered a false negative if the infant was classified as delayed based on the full TIMP, but not at risk for delay based on the specific cutscore for the TIMPSI. Likewise, a false positive occurred if the infant was classified as not delayed on the TIMP, but at risk based on the TIMPSI score. Cohen’s Kappa, which adjusts the percentage agreement for chance level agreement, was also computed for each potential cutscore.

Prediction accuracy

To evaluate the prediction accuracy of the infant measures from the TIMPSI version of the instrument compared to the infant measures based on the TIMP for each age group, three separate indices were calculated. First, the root mean squared difference (RMSD) was calculated according to equation (2) below:

$$\mathit{\text{RMSD}}=\sqrt{\frac{1}{N}\sum _{j=1}^N{(b_i-e_i)}^2},$$ (2)

where

• b_i refers to infant i’s estimate on all 42 items of the full TIMP,

• e_i refers to infant i’s estimate based on either 19 or 21 TIMPSI items, depending on the infant’s initial responses to the screening set,

• and N is the number of infants in each two-week age group.

This index is analogous to the standard error of an estimate in a regression analysis used for evaluating the accuracy of a given prediction. Therefore, with respect to the measures from the two versions of the instrument, the smaller the RMSD, the more accurately the TIMPSI estimates predict the measures on the TIMP. Another index of accuracy, the mean signed difference (MSD), was calculated according to equation (3):

$$\mathit{\text{MSD}}=\frac{1}{N}\sum _{j=1}^N(b_i-e_i),$$ (3)

where b_i, e_i and N have the same meaning as described earlier for the RMSD. The MSD can be used to evaluate whether a systematic over- or underestimation bias may exist for the TIMPSI for each age group. Therefore, with values of MSD closer to zero, the smaller the error in the TIMPSI estimate compared to the estimate based on the full TIMP. Finally, the correlation between the TIMP and TIMPSI measures for all infants was calculated as an assessment of whether the rank ordering of the infants’ performance remains stable across the TIMP and the TIMPSI.

Results

Subjects

The total sample obtained was 990 infants (83% of the goal of 1200) with a range of 67–97 per two-week age group (Table 1). Thus, the smallest group (14–15 weeks AA) consisted of a sample 67% of the size intended. Reasons for failure to attain the planned sample size included loss of trained staff, end of funding, and difficulty identifying infants for the final hard-to-fill slots, e.g., a low risk infant of a specified ethnicity in the youngest age group, or inability to locate a child for testing who had been recruited while in the hospital for testing at a much later age. Finally, results of a preliminary analysis of the TIMP data after recruitment of 600 subjects were compared to results with 990. Because the relevant descriptive statistics were virtually identical, the study was terminated.

TABLE 1.

Sample Frequencies by Risk and Age Group

Age Group	Low risk (% in this age group)	Medium risk (% in this age group)	High risk (% in this age group)	Total (% of goal)	Goal
PCA 34–35 wks*	16 (18.6)	30 (34.9)	40 (46.5)	86	100
PCA 36–37 wks	23 (28.4)	27 (33.3)	31 (38.3)	81	100
PCA 38–39 wks	29 (34.1)	30 (35.3)	26 (30.6)	85	100
PCA 40–41 wks	23 (24.0)	30 (31.3)	43 (44.8)	96	100
2–3 wks AA**	32 (33.0)	27 (27.8)	38 (39.2)	97	100
4–5 wks AA	35 (42.2)	26 (31.2)	22 (26.5)	83	100
6–7 wks AA	32 (36.0)	21 (23.6)	36 (40.4)	89	100
8–9 wks AA	30 (35.7)	22 (26.2)	32 (38.1)	84	100
10–11 wks AA	33 (46.5)	21 (29.6)	17 (23.9)	71	100
12–13 wks AA	23 (32.9)	20 (28.6)	27 (38.6)	70	100
14–15 wks AA	31 (46.3)	18 (26.9)	18 (26.9)	67	100
16–17 wks AA	36 (44.4)	25 (30.9)	20 (24.7)	81	100
Total (%)	343 (34.6)	297 (30)	350 (35.4)	990 (82.58)	1200

^*wks PCA = postconceptional age in weeks

^**wks AA = post term age in weeks, adjusted for prematurity

Of the total sample of 990, 688 (69.5%) of the infants were born at a gestational age less than 37 weeks. For babies under 40 weeks PMA at the time of testing (N = 254), the mean chronologic age at testing was 5 weeks (SD = 3 weeks).

The sample was composed of 517 males (52%) and 473 females (48%). The total sample was 58% white, 25% black, 15% Hispanic, 2.3% Asian and .5% Native American.³ As a result, a sample resembling the 1996 U.S. distribution of race/ethnicity in LBW infants was substantially achieved. The total sample was 35% high risk, 30% medium risk, and 35% low risk (Table 1).

Descriptive Statistics

Calibration and equating of the response data yielded Rasch infant measures for both the TIMP (person reliability, analogous to Cronbach alpha¹³, of .96) and the TIMPSI (person reliability of .94) on a common logit scale. These measures, along with the total raw score from the full version are displayed in Table 2. Also included in the table are the standard deviations, minimum score, maximum score and range for each of the measures disaggregated by age group.

Table 2.

Descriptive Statistics by Age Group for Total Raw Score, TIMP Score (logits) and TIMPSI Score (logits)

		Total Raw Score					TIMP Score (Logits)					TIMPSI Score (Logits)
Age Group	N	Mean	Std. Dev.	Min	Max	Range	Mean	Std. Dev.	Min	Max	Range	Mean	Std. Dev.	Min	Max	Range
PCA 34–35 wks*	86	48.9	15.1	15	89	74	−0.67	0.77	−2.84	1.07	3.91	−1.03	1.10	−4.21	0.92	5.13
PCA 36–37 wks	81	54.1	13.1	15	80	65	−0.39	0.64	−2.84	0.72	3.56	−0.46	0.78	−3.23	1.25	4.48
PCA 38–39 wks	85	60.2	14.2	31	107	76	−0.10	0.60	−1.59	1.85	3.44	−0.26	0.75	−2.31	1.90	4.21
PCA 40–41 wks	96	65.1	16.3	27	109	82	0.10	0.71	−1.85	1.95	3.80	0.08	0.77	−1.96	2.16	4.12
2–3 wks AA**	97	69.3	15.1	38	111	73	0.30	0.63	−1.18	2.05	3.23	0.25	0.68	−1.21	2.56	3.77
4–5 wks AA	83	80.0	15.4	43	112	69	0.75	0.61	−0.86	2.10	2.96	0.65	0.72	−1.65	2.16	3.81
6–7 wks AA	89	84.9	17.2	39	116	77	0.93	0.71	−1.12	2.32	3.44	0.92	0.77	−1.27	2.56	3.83
8–9 wks AA	84	93.1	17.5	42	123	81	1.30	0.76	−0.96	2.78	3.74	1.28	0.79	−1.37	3.34	4.71
10–11 wks AA	71	98.9	20.7	45	132	87	1.60	0.97	−0.80	3.63	4.43	1.48	0.88	−0.69	3.52	4.21
12–13 wks AA	70	107.8	18.6	46	137	91	2.05	0.97	−0.75	4.46	5.21	2.10	1.06	−1.27	4.55	5.82
14–15 wks AA	67	113.2	22.2	25	137	112	2.43	1.17	−1.99	4.46	6.45	2.46	1.26	−2.07	5.00	7.07
16–17 wks AA	81	119.6	15.7	52	139	87	2.82	1.06	−0.46	5.02	5.48	2.73	1.08	0.30	5.68	5.38

^*wks PCA = postconceptional age in weeks

^**wks AA = post term age in weeks, adjusted for prematurity

As would be expected, the raw scores and linear Rasch measures all increase with age supporting the fact that older children are expected to be more developmentally proficient than younger children. There also seems to be a general trend for more variability in the scores and measures as the infants progress in age, a trend commonly seen in data from other developmental tests, e.g., the Alberta Infant Motor Scale.¹⁸

Cutscores Analysis

The series of cutscores determined for each two-week age group (in the Rasch logit metric) are shown in Table 3. Based on these cutscores on the TIMPSI, infants were classified as either at risk of failing the TIMP, i.e., falling below −.5 SD (for measures below a cutscore), or not at risk (for measures at or above a cutscore). The classifications based on the four cutscores associated with the TIMPSI (i.e., AtRisk1, AtRisk2, AtRisk3 and AtRisk4) were each compared to the classification based on the cutscore associated with the TIMP (AtRisk0). Table 4 shows the percentage of false negatives and false positives for each of the potential cutscores for the TIMPSI version (aggregated across all age groups); Table 5 provides the same information by two-week age group. A classification is a false negative if the infant was classified as delayed on the TIMP, but not at risk for delay based on the specific cutscore for the TIMPSI; a false positive occurred if the infant was classified as not delayed on the TIMP, but at risk for delay based on the TIMPSI. As expected, a cutscore at the mean produces the fewest false negatives across all age groups combined while a cutscore of -1 SD produces the lowest number of false positives. The most consistent classification of all children occurs with a cutscore of −.5 SD (83.7% correctly classified) while the cutscore of −.25 SD appears to produce the best combination of a low rate of false negatives (5.8%) with an acceptable rate of false positives of 12.5%.

Table 3.

Cutscores by Age Group

Age Group	AtRisk0 Cutscore	AtRisk1 Cutscore	AtRisk2 Cutscore	AtRisk3 Cutscore	AtRisk4 Cutscore
PCA 34–35 wks*	−1.052	−2.129	−1.578	−1.302	−1.026
PCA 36–37 wks	−0.707	−1.238	−0.849	−0.654	−0.459
PCA 38–39 wks	−0.406	−1.016	−0.640	−0.452	−0.265
PCA 40–41 wks	−0.255	−0.694	−0.307	−0.113	0.080
2–3 wks AA**	−0.020	−0.438	−0.095	0.076	0.247
4–5 wks AA	0.449	−0.070	0.291	0.471	0.651
6–7 wks AA	0.580	0.146	0.531	0.723	0.916
8–9 wks AA	0.920	0.491	0.887	1.086	1.284
10–11 wks AA	1.110	0.600	1.041	1.261	1.482
12–13 wks AA	1.563	1.044	1.574	1.839	2.104
14–15 wks AA	1.845	1.193	1.825	2.141	2.457
16–17 wks AA	2.292	1.651	2.191	2.461	2.731

^*wks PCA = postconceptional age in weeks

^**wks AA = post term age in weeks, adjusted for prematurity

Table 4.

Count and Percent of False Classifications by TIMPSI Cutscore Aggregated Across Age Groups

	False Negative		False Positive
TIMPSI Cutscore	N	%	N	%
AtRisk1	163	16.5%	19	1.9%
AtRisk2	88	8.9%	73	7.4%
AtRisk3	57	5.8%	124	12.5%
AtRisk4	33	3.3%	211	21.3%

Table 5.

Percent of False Classifications by TIMPSI Cutscore and Age Group

	AtRisk1		AtRisk2		AtRisk3		AtRisk4
Age Group	False Negative	False Positive	False Negative	False Positive	False Negative	False Positive	False Negative	False Positive
PCA 34–35 wks*	15.1%	2.3%	11.6%	7.0%	8.1%	10.5%	5.8%	15.1%
PCA 36–37 wks	14.8%	3.7%	9.9%	11.1%	6.2%	18.5%	3.7%	29.6%
PCA 38–39 wks	21.2%	2.4%	14.1%	8.2%	5.9%	14.1%	3.5%	22.4%
PCA 40–41 wks	18.8%	0.0%	14.6%	3.1%	12.5%	8.3%	5.2%	21.9%
2–3 wks AA**	15.5%	6.2%	8.2%	12.4%	4.1%	21.6%	3.1%	27.8%
4–5 wks AA	19.3%	2.4%	6.0%	13.3%	6.0%	15.7%	3.6%	21.7%
6–7 wks AA	12.4%	1.1%	5.6%	5.6%	3.4%	10.1%	3.4%	16.9%
8–9 wks AA	15.5%	2.4%	10.7%	4.8%	4.8%	10.7%	2.4%	19.0%
10–11 wks AA	16.9%	1.4%	5.6%	7.0%	2.8%	11.3%	2.8%	15.5%
12–13 wks AA	22.9%	0.0%	11.4%	2.9%	10.0%	5.7%	4.3%	14.3%
14–15 wks AA	11.9%	0.0%	6.0%	4.5%	3.0%	10.4%	0.0%	29.9%
16–17 wks AA	13.6%	0.0%	1.2%	7.4%	1.2%	11.1%	1.2%	21.0%

^*wks PCA = postconceptional age in weeks

^**wks AA = post term age in weeks, adjusted for prematurity

Table 6 display’s Cohen’s Kappa for classifications based on each of the cutscores by age group. A plus sign (+) next to a value of Kappa marks the highest value within the age group (across the four cutscores). In agreement with the results in Table 4, the cutscore labeled AtRisk2 (−.5 SD) seems to show the highest level of agreement with the decisions based on the full TIMP as it returns the highest value of Kappa for 9 of the 12 age groups.

Table 6.

Cohen’s Kappa by Cutscore and Age Group

Age Group	AtRisk1	AtRisk2	AtRisk3	AtRisk4
PCA 34–35 wks*	0.51	0.53	0.56+	0.54
PCA 36–37 wks	0.38	0.43+	0.42	0.33
PCA 38–39 wks	0.38	0.47	0.57+	0.49
PCA 40–41 wks	0.52	0.57+	0.53	0.46
2–3 wks AA**	0.36	0.49+	0.45	0.39
4–5 wks AA	0.36	0.56+	0.52	0.48
6–7 wks AA	0.59	0.71+	0.68	0.55
8–9 wks AA	0.51	0.61	0.65+	0.56
10–11 wks AA	0.50	0.71+	0.69	0.62
12–13 wks AA	0.37	0.65+	0.63	0.61
14–15 wks AA	0.54	0.68+	0.64	0.41
16–17 wks AA	0.63	0.81+	0.73	0.55

^*wks PCA = postconceptional age in weeks

^**wks AA = post term age in weeks, adjusted for prematurity

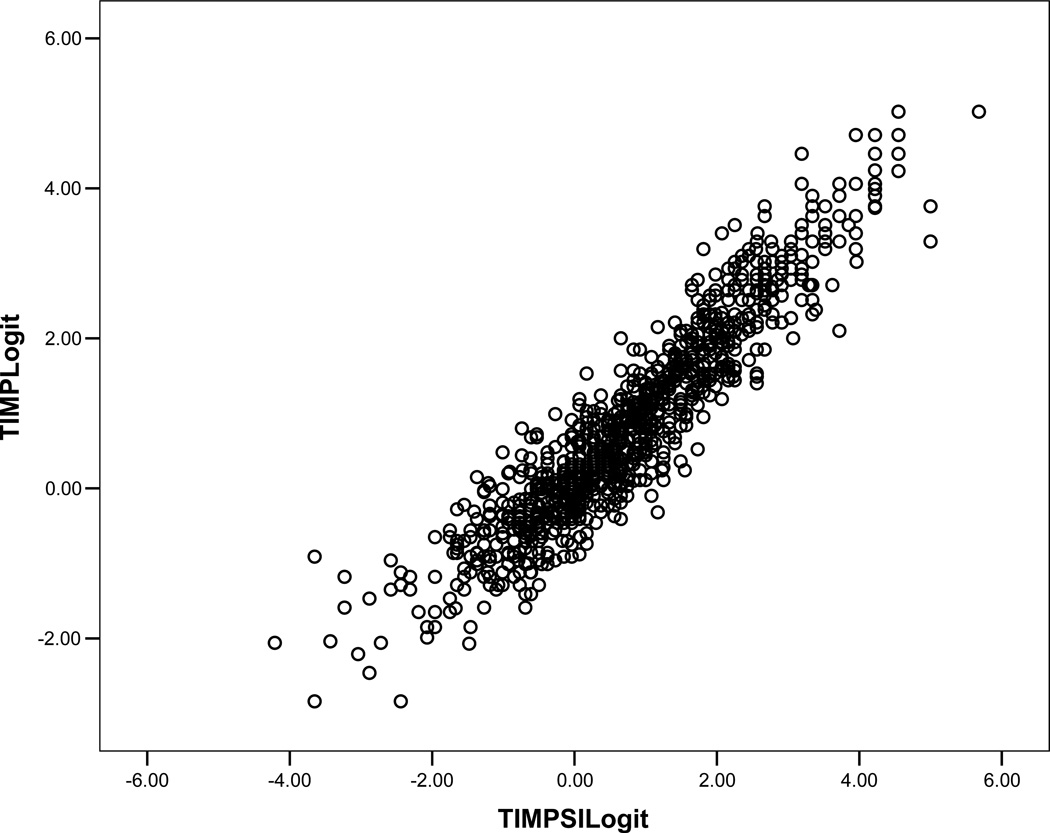
Figure 1 plots the infant measures on the TIMP versus measures from the TIMPSI. The two sets of measures are highly correlated (r = .93) indicating the rank ordering of the infants is very stable across the two versions. The TIMPSI version does produce more variation in the measures, particularly at the lower end of the distribution. The higher dispersion among the lower measures is likely due to the construction of the TIMPSI. The TIMPSI is composed of items with an average item difficulty of .22 logits (SD = 1.43); for the full TIMP the average item difficulty is 0 logits (SD = 1.53). Therefore, the greater lack of precision at the lower end of the distribution may be due to targeting issues in which infants with low performance measures are not being adequately evaluated with items targeted to their ability level on the TIMP.

Figure.

Plot of TIMPSI Versus Full TIMP Scores (Logit Metric)

The MSD and RMSD for each age group are provided in Table 7. For the RMSD there does not appear to be a systematic pattern of better or worse prediction of the full TIMP measures from the TIMPSI measures with increasing age, although the overall pattern suggests a slight increase in accuracy beginning at 6–7 weeks corrected age. The relatively larger RMSD for the PMA 34–35 weeks group indicates the least accurate prediction of full TIMP measures based on TIMPSI measures for these infants. This is noticeable in the lower left quadrant in Figure 1 as larger errors in prediction for very low TIMP measures from the TIMPSI measures. The MSD column in Table 7 shows that for all but two age groups (12–13 weeks and 14–15 weeks), the TIMPSI estimates tend to be lower than those based on the full TIMP. This systematic underestimation appears minimal except for the PMA 34–35 weeks age group. For this age group the TIMPSI measures are noticeably lower, on average, than the corresponding measures from the full TIMP indicating that the screening test will underestimate infants’ ability at 34–35 weeks PMA.

Table 7.

MSD and RMSD by Age Group

Age Group	MSD	RMSD
PCA 34–35 wks*	0.359	0.766
PCA 36–37 wks	0.071	0.532
PCA 38–39 wks	0.161	0.499
PCA 40–41 wks	0.022	0.463
2–3 wks AA**	0.048	0.492
4–5 wks AA	0.101	0.508
6–7 wks AA	0.019	0.464
8–9 wks AA	0.014	0.503
10–11 wks AA	0.114	0.397
12–13 wks AA	−0.054	0.523
14–15 wks AA	−0.025	0.574
16–17 wks AA	0.090	0.481

^*wks PCA = postconceptional age in weeks

^**wks AA = post term age in weeks, adjusted for prematurity

Discussion

The 29 items on the TIMPSI were extracted from the full TIMP in order to provide a quick screen to reduce the testing time and physical demand on infants in comparison with administration of the full 42-item test. The high correlation between outcomes on the two tests demonstrates that a short version of the test essentially ranks infants in the same order as does the TIMP. Figure 1 and the RMSD and MSD indices demonstrate, however, that estimates based on the TIMPSI vary in accuracy across the two-week age groups for which the TIMP has been normed. Prediction tends to be less accurate at 34–35 weeks PMA than at other ages and TIMPSI scores for this age group tend to be underestimated compared to the corresponding TIMP scores. As mentioned in the results section, this appears to be because the easy set of TIMPSI items is not well targeted to capture the performance of the youngest infants because the average item difficulty level is higher, i.e., items are harder to pass, than that of the TIMP items as a whole. This finding is disappointing because an important purpose of the TIMPSI is to lessen the physical demand of testing for the youngest, most fragile infants. Revision of the TIMPSI in the future should identify easier items to include in the screening test. In the meantime, testers should be aware that use of the TIMPSI with infants in the age range of 34–35 weeks PMA estimates TIMP scores less accurately than at other ages.

In an analysis of various cutscores on the TIMPSI using raw scores rather than Rasch logit measures, we previously reported the correlation between TIMP total raw scores and TIMPSI raw scores to be .88 (N=990, p<.0001), similar to the findings here from use of Rasch measures. The correlation between corrected age at testing and the TIMPSI was .72.² Selecting a cutscore for clinical use always represents a decision regarding what to maximize: overall correct classification from screening, sensitivity to avoid missing any delayed infants, or specificity to keep the number of follow up tests as low as possible. After analyzing several cutscores between the mean and −2.00 SD on the TIMPSI raw scores against a cutscore on the TIMP of −.5 SD, we reported use of −.25 SD below the mean to produce the best combination of sensitivity (72%) and specificity (84%) for clinical use, while the best sensitivity for identifying more of the low performers on the TIMP (82%) was obtained using the mean as the cutscore on TIMPSI raw scores. The best overall classification of children was obtained using the raw cutscore at −.5 SD (82% correct) but at the cost of missing 38% of low performers on the TIMP. In a clinical setting in which screening test results below the cutscore lead to assessment with the gold standard to confirm or rule out the first impression, we believe that it is more important to over-identify children in the screening process who must be tested further rather than rule out further assessment more often in favor of making fewer overall mistakes. Thus we recommended when using raw scores at −.25 SD as the cutscores that screening should be repeated before releasing children from further close scrutiny.

The findings from this study also reflect the tradeoffs involved in using various cutscores. Cohen’s Kappa results agree with the raw score analysis in suggesting that the most accurate classification of the children across all age groups occurs when using a cutscore based on Rasch measures of −.5 SD on the TIMPSI. Cohen’s Kappa, however, is a pure measure of agreement beyond chance and does not take into account the clinical consequences of false positive and false negative decisions. The cutscore of −.5 SD on the TIMPSI Rasch measures would miss 6–14.6% of low scorers on the TIMP because such children would not be followed up with the comprehensive test in clinical practice. To maximize the rate of false negative results to less than 6% across all age groups, one would choose a cutscore of the mean on the TIMPSI but at the cost of false positive rates ranging from 14.3% at 12–13 weeks corrected age to 29.9% at 14–15 weeks. As a result, using this cutscore would result in much more expensive TIMP testing to confirm or refute positive TIMPSI results.

The best compromise seems once again to be use of −.25 SD as the cutscore for Rasch measures to maximize identification of delayed infants (1.2–12.5% false negatives) while minimizing unnecessary follow up testing (5.7–21.6% false positives with rates for most age groups in the 10–11% range). We again suggest that repeat screening with the TIMPSI before testing with the TIMP might reduce the ultimate false positive rate, especially as children get older and the screening test gets more accurate. The ultimate decision regarding which cutscore to use rests with the individual setting, taking into account resources, frequency of clinical visits, and family considerations, such as travel time.

Another approach to clinical decision making could involve using different cutscores for different age groups. Clearly whichever cutscore is used, accuracy of the TIMPSI for predicting concurrent scores suggesting delay on the TIMP becomes greater as children become older, i.e., from about 6–7 weeks corrected age on, making the TIMPSI most accurate for use in developmental follow up clinics to reduce testing time. Similarly, prediction of later developmental outcome from TIMP scores becomes better as children reach 3 months corrected age.^4,5

In summary, the TIMPSI is a set of screening items with strong psychometric characteristics drawn from the TIMP which shows a strong correlation with full test results obtained concurrently. The positive and negative consequences of using various cutscores for clinical decision making were discussed with emphasis on the better accuracy obtained as children get older. The TIMPSI should be used with caution in infants at 34–35 weeks PMA because scores consistently underestimate TIMP performance. Future research should explore the addition of easier items to the TIMPSI because inclusion of additional items in the TIMPSI “easy” item set may increase the precision of screening at the lower end of the continuum.