Basilar-membrane responses to clicks at the base of the chinchilla cochlea

Abstract

Basilar-membrane responses to clicks were measured, using laser velocimetry, at a site of the chinchilla cochlea located about 3.5 mm from the oval window (characteristic frequency or CF: typically 8–10 kHz). They consisted of relatively undamped oscillations with instantaneous frequency that increased rapidly (time constant: 200 µs) from a few kHz to CF. Such frequency modulation was evident regardless of stimulus level and was also present post-mortem. Responses grew linearly at low stimulus levels, but exhibited a compressive nonlinearity at higher levels. Velocity-intensity functions were almost linear near response onset but became nonlinear within 100 µs. Slopes could be as low as 0.1–0.2 dB/dB at later times. Hence, the response envelopes became increasingly skewed at higher stimulus levels, with their center of gravity shifting to earlier times. The phases of near-CF response components changed by nearly 180 degrees as a function of time. At high stimulus levels, this generated cancellation notches and phase jumps in the frequency spectra. With increases in click level, sharpness of tuning deteriorated and the spectral maximum shifted to lower frequencies. Response phases also changed as a function of increasing stimulus intensity, exhibiting relative lags and leads at frequencies somewhat lower and higher than CF, respectively. In most respects, the magnitude and phase frequency spectra of responses to clicks closely resembled those of responses to tones. Post-mortem responses were similar to in vivo responses to very intense clicks.

INTRODUCTION

The basilar membrane of the mammalian cochlea responds nonlinearly to stimulation with tones (e.g., Rhode, 1971; Sellick et al., 1982; Robles et al., 1986; Cooper and Rhode, 1992; Nuttall and Dolan, 1996; Russell and Nilsen, 1997; reviewed by Ruggero, 1992b; and Patuzzi, 1996). Since, for nonlinear systems, the responses to tones cannot generally be used to predict the responses to arbitrary stimuli, a thorough understanding of basilar-membrane behavior requires the use of other stimuli, such as tone complexes, noise and clicks. Clicks are especially useful because, being punctate and wide-band in nature, they permit precise timing of a system’s responses while simultaneously testing it over a wide range of frequencies. In the case of linear systems, the Fourier transform of the unit impulse response is identical to the system’s transfer function. Departures from such identity in the case of nonlinear systems may provide clues about the nature of the nonlinearities.

The first in vivo study of basilar-membrane responses to clicks was carried out in the 8-kHz region of the squirrel monkey cochlea (Rhode and Robles, 1974; Robles et al., 1976). Although hampered by substantial waveform distortion introduced by the Mössbauer technique, this pioneering investigation established that basilar-membrane responses to clicks consisted of a brief and low-frequency initial segment, which grew linearly with stimulus intensity, and a longer-lasting segment with periodicity corresponding to the characteristic frequency (CF) measured using single tones, which grew at compressive rates with stimulus level. Mildly nonlinear growth of basilar-membrane responses to clicks was also measured with a capacitive probe at the basal region of guinea pig cochleae that had been severely traumatized by the experimental procedures (LePage and Johnstone, 1980). More recently, laser methodology and improved surgical techniques have made it possible to obtain undistorted recordings of responses to clicks in the basal region of relatively healthy cochleae of chinchilla (Ruggero and Rich, 1990, 1991a, b; Ruggero et al., 1991, 1992a, b, 1993, 1996) and guinea pig (Nuttall and Dolan, 1993; de Boer and Nuttall, 1997), as well as near the apex of guinea pig and chinchilla cochleae (Cooper and Rhode, 1996). To date, however, reports of these recordings (including those from our laboratory) have been very limited in scope and detail.

The present paper provides an extensive description of basilar-membrane responses to clicks for the 8–10 kHz region of the chinchilla cochlea. At this site, responses to clicks are frequency modulated, exhibiting a low-to-high-frequency glide both in vivo and post-mortem. In vivo, the responses to clicks grow at compressive rates within 100 µs of response onset, and accurately predict the main features of responses to tones. Taking the frequency glide into account, nonlinear feedback appears to accompany, nearly instantaneously, the CF spectral components of basilar-membrane vibration.

I. METHODS

A. Animal preparation

Male chinchillas, weighing about 0.5 kg, were anesthetized with an initial dose of Ketamine (100 mg/kg, S.C.) and supplementary doses of sodium pentobarbital (I.P.), or with Ketamine (20 mg/kg, I.M.) and Dial (50 mg/kg) in urethane (200 mg/kg, I.P.) and supplementary doses of Dial in urethane. They were tracheotomized and intubated but forced ventilation was rarely used. Core body temperature, measured using a rectal probe, was maintained at 38 °C using a servo-controlled electrical heating pad. The left pinna was resected, the bulla was widely opened, the tensor tympani was cut and the stapedius was detached from its anchoring. A silver-wire electrode was placed on the round window to record compound action potentials (CAPs) evoked by tone bursts. A small hole was made in the basal turn of the otic capsule by first thinning and drilling the bone using a dental bur and then chipping away bone fragments with a metal pick. The hole allowed direct visualization of the basilar membrane and placement on it of a few glass microbeads (10–30 µm in diameter), which served as reflecting targets for the laser beam. In most experiments, the otic-capsule hole was left open. In six experiments, basilar-membrane recordings were made after the hole was covered with a window fashioned from slide coverslip glass (to minimize motion of the perilymph meniscus overlying the recording site; see section A of Discussion). In these experiments, the basilar-membrane recordings were complemented by vibration measurements from the stapes or the incus, near the incudostapedial joint (without using reflecting beads).

B. Acoustic stimulation

Acoustic stimuli were produced by exciting a Beyer DT-48 earphone with electrical signals from a custom-built digital waveform generator (Ruggero and Rich, 1983) or from a commercial system (Tucker-Davis Technologies). Electrical clicks, which had durations of 50-µs or 10-µs (up to and following experiment L131, respectively), were presented with repetition periods of 20–53 ms (usually 25 ms). Single-tone stimuli were modulated at onset and offset by 1/2 period of a raised cosine waveform (1.16 ms rise/fall time). The tone bursts had durations of 5, 10, 25 or, exceptionally, 3 ms and repetition periods of 25, 50, 100 or 15 ms, respectively. At the beginning of each experiment, the probe tip of a calibrated miniature microphone (Knowles 1842 or 1785) was placed within 2 mm of the tympanic membrane. Using this microphone, the transfer function of the electroacoustic stimulus system was measured for 100 Hz–24 kHz tones, with 100-Hz resolution. The amplitude and phase spectra of the transfer function were stored digitally and were later used to compute the acoustic-click waveform by Fourier synthesis. A simulated electrical click was convolved with the transfer function in the frequency domain to obtain the spectrum of the acoustic click. Inverse Fourier transformation of this spectrum yielded the time waveform of the acoustic click. Throughout this paper click levels are given as the peak pressures of the synthesized clicks, expressed relative to 20 µPa.

C. Laser velocimetry

Basilar-membrane vibrations were recorded using a laser velocimeter, which measures the velocity of a vibrating object by detecting the Doppler frequency shift of light reflected from it. In our application, the laser beam was reflected from glass microbeads placed on the basilar membrane. The velocimeter consisted of a 20 mW He–Ne laser (Spectra Physics 106-1), a fiber vibrometer (Dantec 41X60) and a Doppler frequency tracker (Dantec 55n20). The velocimeter was coupled to a compound microscope (Olympus BHMJ) equipped with 5X and 20X ultralong working-distance objectives (Mitutoyo Plan Apo 5X, N.A. 0.14, and 20X, N.A. 0.42). The electrical output of the Doppler frequency tracker, a voltage proportional to the velocity, was filtered with a bandpass frequency response (1–15 000 Hz). The output of the filter was sampled by a computer at a rate of 40 kHz (up to L131) or 100 kHz (after L131).

D. Data analysis

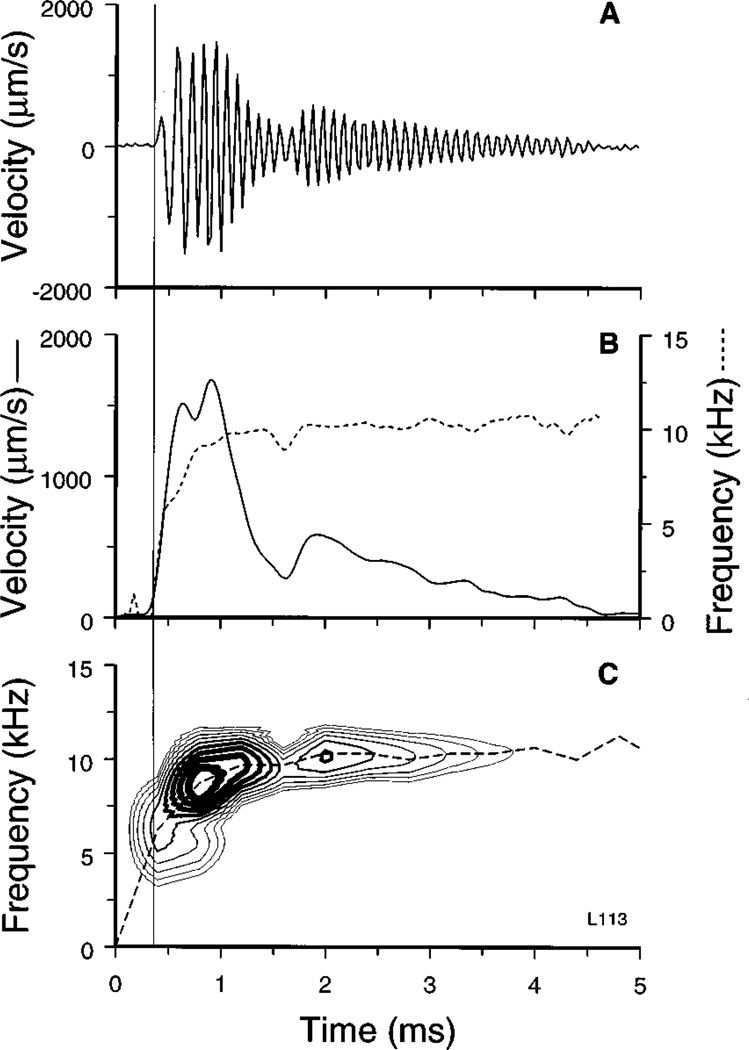
Responses to clicks or tones were averaged over 512, 1024 or 2048 stimulus repetitions. The magnitude and phase spectra of the average-response waveforms were routinely calculated by Fourier transformation using time windows of 12.8 or 10.24 ms (i.e., 512 25-µs bins or 1024 10-µs bins). In addition, short-term Fourier transforms (STFTs; see Fig. 5(C) were computed using 0.8-ms Hanning windows centered at each delay and zero padded to an overall duration of 3.2 ms. Consecutive STFTs were computed at 0.4-ms intervals. The envelope and instantaneous frequency of the responses to clicks were estimated using their analytic signal representation (Bennett, 1970). The analytic signal of a waveform is a complex quantity whose real part is the wave- form itself and whose imaginary part is the Hilbert transform of the real part. The envelope of the waveform is equal to the magnitude of the analytic signal and the instantaneous frequency corresponds to the derivative of the phase of the analytic signal.

FIG. 5.

Instantaneous frequency and envelope of basilar-membrane responses to 84-dB clicks. (A) Original response waveform. (B) Envelope (continuous line) and instantaneous frequency (dashed line) of the waveform depicted in A. (C) Magnitude of short-time Fourier transforms (STFTs; see Methods) of the same waveform, displayed as a function of time (abscissa) and frequency (ordinate). The thickness of the contour lines indicates the STFT amplitude, expressed relative to the ensemble maximum. The thickest line indicates a relative amplitude of −2 dB and the thinner lines correspond to lower levels, in steps of −2 dB. The frequency of the STFT maximum is also shown as a function of time (dashed line). The thin vertical line indicates the onset of middle-ear ossicular vibration.

II. RESULTS

Basilar-membrane responses to clicks were recorded at a region of the chinchilla cochlea located about 3.5 mm from the oval window. Data from two representative cochleae (L13 and L113) are highlighted throughout the paper. Responses from these cochleae were selected for presentation because: (1) they were exceptionally stable (remaining invariant over several hours of recording); (2) they were collected in near-normal ears (judging from surgically induced CAP threshold elevations at CF of 6–12 dB); (3) they were especially sensitive; and (4) extensive samples of responses to tones in the same cochleae are available for comparison (Ruggero et al., 1997).

A. Main features of basilar-membrane responses to clicks

Figure 1 allows a comparison of velocity responses to identical intense acoustic clicks measured in a single chinchilla ear from the incus (top panel) and from a basilar-membrane site located about 3.5 mm from the oval window (bottom panel). The response of the incus consisted of a short oscillation, consistent with the untuned, wide-band nature of middle-ear vibrations. The basilar-membrane response, much larger (note ordinate scales) and longer lasting than the incus response, was relatively undamped, displaying the characteristic “ringing” of a well-tuned bandpass system. In the overwhelming majority of experiments, rarefaction clicks evoked basilar-membrane responses whose first peak (“P1” in Fig. 1) was in the direction of scala vestibuli. Complementary measurements of incus and basilar-membrane motion, using intense clicks and 100-kHz sampling frequency, were performed in 7 ears. In 6 of these, the basilar-membrane recordings were carried out after covering the otic capsule hole with a glass window. Defining response onset as the time at which oscillations first reached 20% of their maximum value, the cochlear delay of the basilar-membrane response was computed as the interval between the onset of motion at the incus and at the basilar membrane. The cochlear delay measured in these 6 ears was 29.8±12.4 µs (mean±standard deviation).

FIG. 1.

Responses to intense rarefaction clicks recorded from the incus (top) and a basal site of the basilar membrane (bottom) in a single chinchilla ear. The thin vertical line intersects the incus response at the time it reaches 20% of its maximum value and may be taken as marking the onset of the input to the cochlea. Click peak pressure was 102 dB re: 20µPa.

Figure 2 presents basilar-membrane responses to clicks plotted with uniform scales of velocity (left column) and velocity normalized to stimulus pressure (right column). If the basilar membrane vibrated linearly, neither the response wave shapes nor their normalized magnitudes would vary as a function of stimulus level. In fact, increases in click level were accompanied both by changes in response wave shape and by decreases in normalized velocity (right column). Compressive growth was obvious at all stimulus levels but it became less evident at the very highest levels.

FIG. 2.

Basilar-membrane responses to rarefaction clicks presented at several intensities. The responses are displayed with uniform scales of velocity (left column) and normalized velocity (velocity divided by peak click pressure, right column). The thin vertical lines indicate the onset of middle ear ossicular vibration. Response polarity as in Fig. 1. The parameter next to each trace indicates the peak click pressure, expressed relative to 20 µPa.

Figure 3 shows a more complete series of basilar-membrane responses to rarefaction clicks (from the same cochlea of Fig. 2) with scales chosen to facilitate comparison of the wave shapes without regard to their magnitudes: the scales are compressed by a factor of 2 (6 dB) for every 10-dB increase of stimulus intensity. For most click intensities, the envelopes of the responses consisted of two adjacent spindle-shaped lobes. This “two-lobe” wave shape was characteristic of cochleae that were in good physiological state, it was absent in cochleae that were surgically traumatized and disappeared after death (Fig. 13) or acoustic overstimulation (Figs. 6 and 8 of Ruggero et al., 1996). The early response peaks grew with stimulus intensity at faster rates than later ones, giving rise to a systematic skewing of the envelope toward earlier times. For example, at low stimulus levels (14–24 dB SPL), the response maximum corresponded to the ninth positive peak (P9) but the maximum shifted to earlier peaks with increases of stimulus level: P8 at 34 dB, P6 at 54 dB, and P2 at 94 and 104 dB. The time elapsed between the response onset (0.38 ms) and the maximum of the response envelope decreased from 0.97 ms for 24-dB clicks to 0.25 ms for 104-dB clicks.

FIG. 3.

Basilar-membrane responses to rarefaction clicks. The responses are displayed with scales that are systematically compressed by a ratio of 2 (i.e., 6 dB) for every increment of 10 dB in stimulus intensity. Such scaling, which de-emphasizes intensity-dependent changes in response magnitude, allows for easier comparison of the response wave shapes.

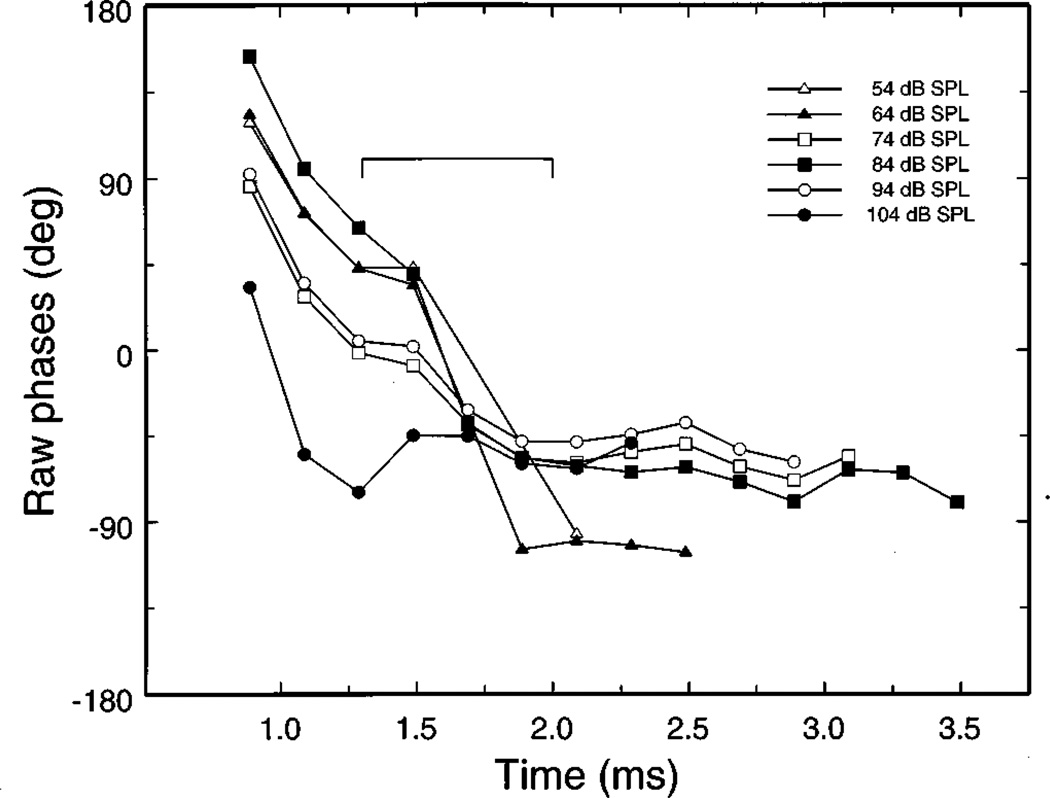
FIG. 13.

The variation of response phase at the notch frequency (10.23 kHz) as a function of time. Phases were computed by Fourier transformation of 200-µs segments of the responses to clicks of cochlea L113, including the waveform of the inset of Fig. 12A. The bracket indicates the times of the transitions between the time-domain lobes (see Fig. 3).

FIG. 6.

Instantaneous frequency (A) and envelope (B) of basilar-membrane responses to clicks as a function of time and stimulus level. The thick dashed line in panel A corresponds to responses recorded post-mortem (94-dB clicks). The vertical continuous line in panel B indicates the onset time of middle-ear vibration. The vertical dashed lines indicate the times of the first and second positive peaks and the first negative peak. The ordinate in panel B has units of micrometer/s and are normalized to 104-dB (i.e., the velocities of responses to 84- and 64-dB clicks are magnified 10 and 100 times, respectively). Data are those represented in Figs. 2 and 3.

FIG. 8.

Average slopes of the magnitude-intensity functions for the responses to clicks of 4 sensitive cochleae. The average slopes of curves such as those depicted in Fig. 7 were computed over 50-dB ranges (54–65 to 103–115 dB SPL). The thin vertical line indicates the onset time of basilar-membrane vibration (325 µs, averaged across the 4 cochleae).

Figure 4 shows responses to condensation clicks recorded in an exceptionally sensitive preparation. Apart from the long-lasting ringing, with duration longer than in any other cochlea in our sample, these responses share the same characteristics observed in Figs. 1–3, including initial response polarity (i.e., responses to condensation and rarefaction clicks, respectively, begin with motion toward scala tympani and scala vestibuli), compressive growth, and skewing of the envelope toward earlier times as a function of increasing stimulus level.

FIG. 4.

Basilar-membrane responses to condensation clicks. All details as for Fig. 3.

B. Frequency modulation in basilar-membrane responses to clicks

Close inspection of the waveforms of responses to clicks (e.g., Fig. 2, 104 dB SPL) reveals that their periodicity or instantaneous frequency changed as a function of time. To quantify this frequency modulation, we computed the instantaneous frequency and the envelope of the response waveforms using the “analytic signal” representation (Bennett, 1970; see Methods). Figure 5 shows the response to a click presented at 84 dB SPL (panel A), as well as its envelope (continuous line, panel B) and its instantaneous frequency (dashed line, panel B), plotted against time. The instantaneous frequency increased rapidly within several hundreds of microseconds: it was initially about 1 kHz, surpassed 5 kHz by the time of the first positive peak and saturated at about 10 kHz. An exponential fit had a time constant of 0.2 ms.

The variation of frequency with time was also measured using short-term Fourier transforms (STFTs; see Methods). Panel C of Fig. 5 displays the magnitude part of the STFTs for the response of panel A as a family of contour lines spaced at 2-dB intervals relative to the ensemble peak, with the thicker contour lines indicating higher spectral magnitudes. Also indicated is the frequency at which the peak magnitude of the STFT occurs as a function of time (dashed line). Both the STFT contours and the peak instantaneous frequency show that the frequency content glides from low to high (≈CF). The increase in response frequency was accompanied by a narrowing of the bandwidth. This may be ascertained from the STFT contours of Fig. 5C by measuring the frequency range encompassed by a fixed number of contour lines along any given time “slice.” The equivalent rectangular bandwidth and the 10- and 20-dB bandwidths were 3.9, 4.0 and 8.3 kHz, respectively, at 0.8 ms and decreased to 2.8, 3.3, and 4.4 kHz at 2 ms.

Instantaneous frequency was influenced by stimulus level but its time trajectory retained its main features even at the highest levels and post-mortem (Fig. 6A). Thus, it is clear that the frequency modulation is not a byproduct of nonlinear or “active” cochlear processing. In contrast, the response envelopes were highly dependent on stimulus intensity. Figure 6B shows the envelopes of responses to clicks with peak pressure of 64-, 84- and 104-dB, normalized to 104-dB. Had responses grown linearly, the normalized envelopes would be identical throughout their extent. In fact, due to the compressive growth of responses, the envelopes coincide only at the onset (where responses grow linearly).

C. Growth of responses as a function of click intensity

The initial peaks of responses to clicks grew with intensity at faster rates than later peaks (Figs. 2–4). To quantify these rates, peak times were determined in the responses to high-intensity clicks and the corresponding magnitudes (measured in the response envelopes) were plotted against click intensity (Fig. 7). With the exception of animal L13, the magnitudes measured were those corresponding to velocity maxima toward scala vestibuli (i.e., positive peaks in responses to rarefaction clicks). At low levels of stimulation (peak pressure: <30–40 dB re: 20 µPa), all peaks grew linearly or nearly so. The initial oscillation, P1, grew in an almost linear fashion at all levels. Peaks 3–7 grew compressively at intermediate levels but tended to become linear again at the highest levels of stimulation. Later peaks grew nonlinearly (at rates as low as 0–0.2 dB/dB) throughout the range of moderate and high stimulus levels.

FIG. 7.

The magnitudes of selected positive peaks of the responses to clicks, plotted against stimulus level. Also indicated are lines with slopes of 1 dB/dB and 0.2 dB/dB. Each panel represents data from one sensitive cochlea.

To further explore the development of compressive nonlinearity as a function of time, we computed the slopes of the velocity-intensity functions for the positive peaks and averaged the slopes over 50-dB ranges encompassing the highest stimulus levels. Figure 8 displays such averages for the four cochleae represented in Fig. 7. Nonlinear growth was evident within 100 µs (i.e., 1 CF period) of response onset (vertical line). In a sample of 8 sensitive cochlea (including the 4 of Fig. 8) the first positive and negative peaks, respectively, grew at rates of 0.950±0.035 and 0.883±0.053 dB/dB (over 40-dB ranges). Such slopes differed significantly from 1 dB/dB (p<0.005, one-tailed t test).

Slopes diminished rapidly as a function of time, from values approaching linearity immediately after response onset, to minima as low as 0.1–0.2 dB/dB at 1.3–1.9 ms. At later times, growth slopes waxed and waned and exhibited local maxima as high as 0.5–0.6 dB/dB and minima as low as 0.1 dB/dB. Inspection of the curves for cochleae L13 and L113 in Fig. 8 indicates that the slope maxima (i.e., compression minima) were approximately synchronous with the constrictions that demarcate adjacent lobes of the time-domain response waveforms (Figs. 3 and 4). This was also true for the other cochleae represented in Fig. 8.

D. The magnitude-frequency spectra of basilar-membrane responses to clicks

Figure 9 shows the magnitude of the Fourier transforms of the waveforms depicted in Figs. 3 and 4 (computed using 12.8-ms windows). At low spectral frequencies, the responses grew linearly: for 10-dB increments in click level, the responses grew by a factor of 3.1 (10 dB). At frequencies around CF, response growth was linear at the lowest stimulus levels but quite compressive at high intensities. The response bandwidth changed systematically with click intensity: for low stimulus levels, responses were largely confined to frequencies near CF, whereas at high stimulus levels responses encompassed a broad range of frequencies. The change in bandwidth was accompanied by an overall frequency shift toward lower frequencies. At the highest click intensities, the frequency of the spectral maximum was about −0.5 octave relative to CF. The Q₁₀ (peak frequency divided by 10-dB bandwidth) decreased substantially as a function of click intensity. In cochlea L113, for example, Q₁₀ was 4.06 for 44-dB clicks and 1.08 for 104-dB clicks. At frequencies near CF, some of the frequency spectra included sharp notches. These were seen only in the most sensitive and nonlinear preparations, and disappeared as the state of the preparation deteriorated with the passage of time, after death [note notches at 8.48 kHz in in vivo responses of L13 (Figs. 9 and 10) and their absence post-mortem (Fig. 10)] or after acoustic overstimulation (Fig. 9 of Ruggero et al., 1996).

FIG. 9.

Magnitude-frequency spectra for the velocity responses to clicks in two sensitive cochleae. Clicks were presented at levels of 24 or 26 dB up to 104 or 106 dB, in steps of 10 dB. Data are those represented in Figs. 2 and 3.

FIG. 10.

Gain-frequency spectra for the responses to clicks in two cochleae. Gains were computed by dividing, frequency by frequency, velocity magnitudes (shown in Fig. 9) by the peak click pressure (parameter). The thick lines indicate the gains of responses recorded 10–20 minutes post-mortem; dashed lines: 94 dB (L113) and 96 dB (L13); continuous lines: 104 dB (L113) and 106 dB (L13). Curves were smoothed using a 3-point running average.

The intensity-dependent nonlinear growth of responses is best visualized by normalizing the spectra of Fig. 9, frequency by frequency, to stimulus pressure (using the acoustic calibration tables; see Methods), thus producing estimates of basilar-membrane gain (Fig. 10). [In a linear system, such a procedure eliminates entirely the effects of irregularities in the stimulus spectrum. The usefulness of the correction is less certain in the case of a nonlinear system.] For clarity, the gains have been smoothed using a 3-point running average. At frequencies lower than 1/2 octave below CF, the curves coincided, indicating linear growth. Nonlinear behavior was evident at higher frequencies (>6 kHz), specially near CF (9 or 10 kHz), where gains became smaller with increases of stimulus level. Compressive growth persisted even at the highest levels of stimulation (compare the curves for 104 or 106 dB with those for 94 or 96 dB).

E. The phase-frequency spectra of basilar-membrane responses to clicks

Figure 11A displays the phases of responses to clicks in one cochlea, obtained by Fourier transformation of some of the waveforms of Fig. 3. The curves represent the phases of basilar-membrane displacement toward scala tympani relative to maximum condensation at the eardrum. The curves show a monotonically increasing phase lag, interrupted in some cases by abrupt shifts at frequencies corresponding to notches in the magnitude spectrum (Fig. 9A). Slopes were shallower at frequencies lower than 7 kHz than at higher frequencies and were steepest near 11 kHz, a frequency somewhat higher than the CF (estimated from responses to low-level clicks). [Slopes were steepest at CF only in the cases in which there were abrupt phase changes near this frequency (64–94 dB; see Fig. 13B).] In the range 3–7 kHz, the average slope was −250 µs. In the 8–10 kHz region, the slopes varied between about −560 µs for the responses to clicks presented at 104 dB SPL (both in vivo and post-mortem) and −826 µs for 24-dB clicks (not illustrated).

FIG. 11.

Phase-vs-frequency curves for basilar-membrane responses to clicks. (A) The ordinate indicates the phases of displacement toward scala tympani (ST) referred to peak positive pressure (condensation) at the eardrum. Phases were obtained by Fourier transformation of the data depicted in Figs. 2 and 3 (cochlea L113). The thick dashed line indicates post-mortem responses to intense clicks (94-dB SPL). The symbols indicate the phases of responses to tones. (B) Phase-vs-frequency curves for basilar-membrane responses to clicks in 8 cochleae, including L113 (identified by an open circle). The symbols indicate phases at CF (measured in responses to low-level clicks). The phase curves are presented relative to inward stapes motion. In one case (L163, indicated by a triangle), basilar-membrane and stapes response phases were measured in the same ear; in the other cases, basilar-membrane phases were normalized to previously published average stapes data for chinchilla (Fig. 9 of Ruggero et al., 1990). Clicks had peak pressures of 82–88 dB.

Figure 11B shows a representative sample of phase-vs-frequency curves, normalized to inward stapes displacement, for responses to clicks recorded in several cochleae. The basilar-membrane sites had CFs in the range 8–12 kHz and the clicks were presented at comparable levels (82–88 dB SPL). The low-frequency segments (<6–7 kHz) had slopes confined to a relatively narrow range, −137 to −269 µs, irrespective of CF. The high-frequency segments diverged increasingly at frequencies higher than 1/2 octave below CF. In general, the phase-frequency slopes were steepest near CF. At CF, the phase lags amounted to 1.5–2 cycles. Average group delays were measured over 1-kHz ranges centered at CF in responses to low-level clicks. [Phase-vs-frequency curves for responses to more intense clicks (such as those of Fig. 11B) included irregularities at frequencies near CF which rendered the measurement of group delays unreliable.] The cochleae represented in Fig. 11B had near-CF group delays averaging 779±147 µs (mean±s.d.). Group delays measured between 7 kHz and 1 kHz below CF (or somewhat smaller ranges if limited by the noise floor) averaged 410±109 µs.

The dependence of response phases on stimulus intensity (shown in Fig. 15B) re-plots the data of Fig. 11A after normalization to the phases of responses to 64-dB clicks. For low frequencies (<5–6 kHz) the phases varied little with stimulus intensity, consistent with the linearity of response growth in that frequency region. For frequencies (6–9 kHz) just below CF, the phases of responses exhibited increasing lags as a function of increasing click level. The lags were small except at levels higher than 74 dB. For frequencies just higher than CF, the response phases showed increasing leads as a function of increasing intensity. A similar intensity dependence of phase (lags and leads, respectively, for frequencies lower and higher than CF, as a function of increasing intensity) could be usually demonstrated in the responses of all sensitive cochleae.

FIG. 15.

Comparison of basilar-membrane responses to clicks (curves) and tones (symbols) recorded in the same cochlea. (A) Gain-vs-frequency spectra as a function of stimulus intensity. (B) Phase-vs-frequency spectra as a function of stimulus intensity. At each level, the phases responses to clicks are expressed relative to the phases of responses to 64-dB clicks. The phases of responses to tones are expressed relative to the phases of responses to 50-dB tones, whose magnitudes closely matched the spectral responses to 64-dB clicks (panel A). Positive values indicate relative phase leads

F. Relation between time-domain lobes and magnitude notches and phase jumps in the frequency domain

To explore the spectral notches observed in the CF region (Fig. 9), as well as the associated phase jumps (Fig. 11), the responses to clicks were studied using Fourier analysis of selected time windows. Figure 12 shows such an analysis for the response waveform shown in the inset. The waveform was divided into two nonoverlapping segments (B and C, inset in Fig. 12A). Segment B spans the first 1.6 ms of the response and extends to the transition between the two response lobes. Segment C, encompassing the second lobe, starts at 1.6 ms and ends at 6.4 ms. The magnitude spectra for these two segments are shown in Fig. 12A (B: dotted line; C: long-dash line), together with the spectrum of the entire original waveform (solid line). The magnitude spectrum of segment C (long-dash line) is sharply tuned to frequencies centered at 10.234 kHz, the frequency of the spectral notch of the original waveform. The notch is absent from segments B and C, which suggests that its presence in the original waveform resulted from destructive interference between early and late out-of-phase spectral components.Figures 12B and 13 illustrate this.

FIG. 12.

Time-dependent variation of the magnitude- and phase-frequency spectra of responses to clicks. Top panel: magnitude spectra. The continuous line shows the variation of magnitude as a function of frequency for the entire waveform (6.4 ms) of averaged responses to 74-dB clicks in cochlea L113 (inset). The other curves depict the magnitude-frequency spectra of the waveform segments indicated in the inset (A: 0–0.7 ms, short-dash line; B: 0–1.7 ms, dotted-line; C: 1.7–6.4 ms, long-dash line). Bottom panel: phase spectra. The continuous line indicates the variation of phase with frequency for the entire waveform. The dotted and long-dash lines depicts phases for segments B and C, respectively.

Figure 12B shows the origin of the 360-degree phase jumps (Fig. 11). At frequencies lower than that of the notch, the phase-vs-frequency curve of the entire response was dominated by the phase spectrum of segment B, whereas at higher frequencies it was dominated by the phase spectrum of segment C. At the notch frequency, the phases of segments B and C differed by 174 degrees (i.e., they were essentially in phase opposition). Figure 13 demonstrates that the response phases at the notch frequency exhibited a monotonically increasing lag in the time interval of 1–2 ms (i.e., straddling the constriction between the two lobes; indicated by the bracket in Fig. 13). Phases became stable within the second lobe, after accumulating a phase lag of nearly 180 degrees. Thus, it is clear that the notch in the magnitude spectrum was generated by a phase cancellation at the notch frequency between response components in the two lobes.

Figure 12A also shows the amplitude spectrum of segment A (short-dash line), which indicates that most of the low-frequency (<7 kHz) response components of the original waveform are confined to the response onset (consistent with the analytic-signal representation and the short-term Fourier transform: Fig. 5).

G. Effects of death on basilar-membrane responses to clicks

Figure 14 illustrates the effects of death on responses to clicks presented at 84 and 104 dB SPL. [The scale for the responses to 104-dB clicks is compressed by a factor of 10 (i.e., 20 dB) relative to the scale for responses to 84-dB clicks. Therefore, response features that grew linearly have identical magnitudes in the 84- and 104-dB traces.] When the cochlea was healthy (left column), all but the earliest peaks grew at highly compressive rates, so that wave shapes were skewed toward earlier times and gains became smaller as a function of increasing stimulus intensity. Post-mortem, the amplitude of all but the earliest response peaks were drastically reduced relative to the in vivo responses, with the responses to the weaker stimuli being more strongly affected (right column of Fig. 14; see also Figs. 7 and 8 of Ruggero and Rich, 1991a, and Figs. 1 and 3 of Ruggero et al., 1992a). After death, responses grew almost linearly, so that responses at all stimulus levels resembled scaled versions of a single wave shape, similar to that of in vivo responses to intense clicks. However, post-mortem responses (recorded within 10–20 minutes after death) were not completely stable and exhibited vestiges of nonlinearity (note the late oscillations in the traces of Fig. 14 and the post-mortem magnitude spectra of Fig. 10).

FIG. 14.

The effect of death on basilar-membrane responses to clicks. Responses to clicks, presented at 84 and 104 dB SPL, were recorded in vivo (left column) and about 10 minutes post-mortem (right column).

Post-mortem, the response gains (thick lines in Fig. 10) were reduced by 3–4 orders of magnitude at CF, relative to in vivo responses to low-level clicks (by 58–64 dB in L113 and 78–91 dB in L13), the bandwidths were broadened and the peaks of the gain spectra shifted down to frequencies about 0.5 octave lower than CF. Post-mortem, the Q₁₀’s (peak frequency divided by bandwidth) were reduced to 1.12–1.21 (L113) and 1.42–1.53 (L13). Overall, the post-mortem gain spectra were very similar to (but somewhat lower than) the spectra of in vivo responses to intense (104- or 106-dB) clicks.

In relation to in vivo responses to low-level clicks, post-mortem responses exhibited phase lags and leads, respectively, at frequencies lower and higher than CF (thick-dash lines in Figs. 11 and 15B; see also Fig. 2 of Ruggero, 1994). Death abolished the phase jumps evident in vivo at near-CF frequencies (compare in vivo and post-mortem responses to 94-dB clicks in Figs. 11A and 15B). The phase effects of death could not be assessed with any precision at frequencies higher than CF, at which responses were buried in the background noise.

H. Comparison of basilar-membrane responses to clicks and tones

As described in the preceding sections, the features of basilar-membrane responses to clicks varied systematically as a function of time: (1) the initial oscillation was nearly linear, whereas later oscillation peaks grew at compressive rates that waxed and waned as a function of time (Figs. 7 and 8); (2) the instantaneous frequency increased (Figs. 5–6 and 12A); and (3) the phases of near-CF components shifted by nearly 180 degrees (Figs. 12B and 13). We investigated how these time-varying features of basilar-membrane vibration relate to steady-state behavior by recording responses to tones and clicks in the same cochleae in close temporal proximity.

Responses to clicks and tones were compared in the frequency domain by plotting their gains and phases as a function of frequency and stimulus level (Fig. 15). There was an excellent match between the gains (Fig. 15A) of responses to clicks (replotted from Fig. 10) and to tones (from Fig. 9 of Ruggero et al., 1997) not only at low frequencies (below 6–7 kHz), where responses were linear, but also at frequencies around CF, where responses were strongly compressive. Figure 15A is representative of many other comparisons (not illustrated) in that they demonstrate a close correspondence between the gains of basilar-membrane responses to tones and clicks at the 3.5-mm site of the chinchilla cochlea (see also Fig. 3 of Ruggero et al., 1992a and Fig. 6 of Ruggero et al., 1992b). Such close correspondence was evident regardless of the health of the cochlea and/or the strength of the basilar-membrane nonlinearities and could be demonstrated whenever responses to both types of stimulus (click or tones) were recorded over a wide range of stimulus intensity. For the data of Fig. 15A, for example, the magnitude spectrum of responses to clicks with peak pressure of 104 dB matched accurately the magnitude of responses to 90-dB tones; responses to 94-dB clicks matched responses to 80-dB tones; and so on down to 24- and 34-dB clicks, which matched responses to 10- and 20-dB tones. In other words, over wide ranges of frequency and level, the spectrum of responses to clicks presented at a given level predicted accurately the responses to tones presented at a constant level. Furthermore, once the appropriate correspondence was ascertained for one click level (for example: in the case of cochlea L113, 60-dB tones corresponded to 74-dB clicks), all other levels were simultaneously determined.

Figures 11A and 15B allow comparison of the phases of responses to clicks (lines) and tones (symbols) recorded in the same cochlea. As in the case of the gain functions (Fig. 15A), there is a good match between the response phases for the two types of stimulus for frequencies lower than CF. The response phases for click and tone stimuli (lines and symbols, respectively, in Figs. 11A and 15B) vary as a function of increasing stimulus intensity in a qualitatively similar fashion. Phases tend to lag for frequencies (e.g., 8.5–9 kHz) lower than CF and to lead for frequencies (e.g., 10.3–10.8 kHz) higher than CF. There is little phase variation at CF or at frequencies lower than 5–6 kHz. Comparable matches between the phases of responses to tones and clicks were also obtained for other cochleae (not illustrated here; see Fig. 4 of Ruggero et al., 1992a).

III. DISCUSSION

A. Methodological considerations

In analyzing basilar-membrane recordings using laser velocimetry, it is important to take into account an artifact due to stapes-driven motion of the fluid meniscus overlying the recording site (Cooper and Rhode, 1992). Such motion changes the effective path length of the laser beam and mimics the Doppler shifts due to basilar-membrane motion. The artifact principally affects low-frequency measurements, when ossicular motion is largest and basilar-membrane motion is small (Cooper and Rhode, 1992; Ruggero et al., 1997).

We were especially concerned that motion of the fluid meniscus could introduce a spurious low-frequency oscillation, mimicking an early-onset basilar-membrane response to clicks. To control for this possibility, basilar-membrane responses were measured in 6 cochleae before and after placement of a small window (made up of slide coverslip glass) on the otic-capsule hole overlying the basilar-membrane recording site, a procedure that diminishes the motion of the fluid meniscus (Cooper and Rhode, 1996). [For illustration purposes, we present here responses to intense clicks, for which near-CF basilar-membrane response gains are lowest (e.g., Fig. 10) and therefore the effects of fluid-meniscus motion (which grow linearly with stimulus intensity) are relatively large. In the case of low-level stimulation, the effects of fluid-meniscus motion are negligible.] The window altered the recorded waveforms consistently (Figs. 16–17). In 5 of the 6 cochleae, the initial oscillation (as usual, toward scala vestibuli for rarefaction clicks) grew larger after placement of the glass window (e.g., Fig. 16, left panel). In one exceptional cochlea (Fig. 16, right panel) the initial oscillation was originally negative and became positive after the glass window was installed. Significantly, the onset delays were only minimally changed. Placement of the glass win- dow reduced the cochlear delays (relative to the onset of incus motion) from 43.0±21.1 µs to 29.8±12.4 µs (mean ±s.d., N56). Cochlea L163 was exceptional in that the delay increased, from 14 to 36 µs.

FIG. 16.

Basilar-membrane responses to clicks recorded in open and closed cochleae. The dashed and continuous lines, respectively, identify responses recorded before and after covering the otic-capsule hole with a glass window. The clicks had peak pressures of 78 dB (L157) and 92 dB (L163).

FIG. 17.

The effects on basilar-membrane responses to clicks of covering the otic capsule hole with a glass window. Upper panels: magnitude-frequency spectra of the responses of Fig. 16. Lower panel: phase effects. Positive phases indicate leads relative to responses before placement of the glass window.

The effects of covering the otic-capsule hole were especially obvious in the frequency domain (Fig. 17). The upper panels of Fig. 17, depicting the magnitude spectra of the waveforms of Fig. 16, show that the response components above 2–3 kHz were largely unaltered but those at lower frequencies decreased in magnitude by as much as 20 dB. Correspondingly, after the placement of the window response phases (lower panel of Fig. 17) increasingly lagged (by as much as 90 degrees) those measured with the open otic capsule as the frequency decreased below 3–4 kHz. These results indicate that fluid-meniscus motion typically does not alter drastically the polarity, magnitude or onset time of the initial oscillation of responses to clicks, whose dominant spectral components have frequencies higher than 2–3 kHz (Figs. 5–6 and 12A).

In the course of measuring responses to clicks at the apex of the cochlea, Cooper and Rhode (1996) found evidence for another artifact, also related to the opening of the otic capsule but still present after placement of a glass window. This artifact, which produced an initial oscillation lasting 1–1.5 ms and a spectral magnitude notch, was abolished by restoring the hydraulic seal of the cochlea. [In our preparations, placement of a glass window on the otic capsule hole also failed to abolish the spectral notches (not illustrated) but increased the magnitude of the initial oscillation (Fig. 16).] We did not attempt to fully restore the hydraulic seal and, therefore, we cannot rule out that our measurements were affected by a similar artifact. Nevertheless, we deem this an unlikely possibility. The apical preparation of Cooper and Rhode (1996) involved opening scala vestibuli. In contrast, in our preparation the cochlea is opened near its basal end, overlying scala tympani. Although the round window does influence pressure at nearby scala tympani sites (Nedzelnitsky, 1980), the differential pressure across the cochlear partition is dominated by pressure in scala vestibuli, which substantially exceeds that in scala tympani (Dancer and Franke, 1980; Nedzelnitsky, 1980). The implication is that opening a hole in the otic capsule near the round window should not have significantly altered the differential pressure, which is the driving force to basilar-membrane motion (Voss et al., 1996).

B. Basilar-membrane responses to clicks at the base of the chinchilla cochlea compared with measurements in other species and other cochlear locations

The present results are generally consistent with the main findings of the pioneering Mössbauer study of Robles et al. (1976; Rhode and Robles, 1974) at a site of the squirrel monkey cochlea with CF of 6–7.8 kHz. At that site, basilar-membrane responses to clicks consisted of two segments. The initial segment was of short duration, exhibited a relatively low frequency of oscillation and grew linearly with stimulus intensity. The second segment was a relatively undamped oscillation with frequency corresponding to CF, which grew at compressive rates. Nonlinear growth of basilar-membrane responses to clicks has also been demonstrated at the base of the cochleae of chinchilla (Ruggero et al., 1992a,b) and guinea pig (LePage and Johnstone, 1980; de Boer and Nuttall, 1997). Frequency modulation has been described in basilar-membrane responses to clicks at the base of the guinea-pig cochlea (de Boer and Nuttall, 1997). At the base of the chinchilla cochlea, both the frequency of oscillation and the extent of the nonlinearity increase continuously over several hundreds of microseconds (Figs. 5–8). The frequency modulation is not abolished by death (Fig. 6A) and, therefore, must be viewed as a “passive” feature of both linear and nonlinear basilar-membrane responses. Thus, it is not surprising that frequency modulation can be mimicked by some linear models of basilar-membrane vibration (Nilsson and Møller, 1977; Møller and Nilsson, 1979; Lyon, 1997; de Boer and Nuttall, 1997).

Mechanical responses to clicks at the apex of guinea pig cochleae grow linearly with stimulus intensity (Cooper and Rhode, 1996). It is likely that the linearity of such responses reflects surgically induced cochlear damage. Responses to clicks at the apex of chinchilla cochleae do exhibit a mild compressive nonlinearity, with output/input slopes no lower than 0.76 dB/dB (Cooper and Rhode, 1996), which contrast with slopes as low as 0.2 dB/dB at the cochlear base (e.g., Figs. 7–8). It is not clear whether this quantitative discrepancy reflects greater surgical damage in apical preparations or a genuine difference in the extent of nonlinearity between the apex and the base of the cochlea. The latter possibility merits consideration because some properties of auditory-nerve responses suggest, in fact, that compressive nonlinearity is less salient in low-CF than in high-CF cochlear regions (e.g., Cooper and Yates, 1994; Sewell, 1984; Temchin et al., 1997).

Responses to clicks at the apex of the chinchilla cochlea also differ from those at the base in that they apparently lack a (nearly) linear initial segment (Cooper and Rhode, 1996). We suppose that this difference reflects the distinct manner in which nonlinearities are distributed at the two recording sites as a function of time and in the corresponding frequency spectra. At basal locations, the initial (almost linear) oscillation has a spectral content heavily weighted by frequencies well below CF (Figs. 5–6), at which responses grow linearly, whereas nonlinear compressive growth is confined to later oscillations (Figs. 7–8) and to frequencies near CF (the “tip” of tuning curves; Fig. 11). At apical locations, compressive growth occurs over a wide frequency region (so that there is no distinction between nonlinear “tip” and linear “tail”) and the spectral content of the initial oscillation of responses to clicks falls within the frequency range of nonlinear growth, which spans more than 3 octaves (Rhode and Cooper, 1996).

C. Polarity and latency of the onset of basilar-membrane responses to clicks

At the base of the chinchilla cochlea, the initial basilar-membrane response to rarefaction clicks consists of motion toward scala vestibuli (Figs. 1–2, 4, and 16) and, appropriately, responses to condensation clicks begin with motion toward scala tympani (Fig. 3). Other investigations of basilar-membrane responses to clicks at the cochlear base (Rhode and Robles, 1974; Robles et al., 1976; LePage and Johnstone, 1980; Nuttall and Dolan, 1993; de Boer and Nuttall, 1997) did not report the polarity of responses. At the apex of chinchilla and guinea pig cochleae (at locations approximately 14 and 16.5 mm, respectively, from the stapes), the responses to clicks (recorded from the scala-media surfaces of Claudius cells, Hensen’s cells or the tectorial membrane) contain a “fast” (short-latency) component, which is presumably artifactual (see Discussion Section III A), and a “slow” component, which begins as late as 1.5 ms after the onset of ossicular motion (Cooper and Rhode, 1996). The polarity of the onset oscillation of this slow component (i.e., motion toward scala vestibuli for rarefaction clicks) is the same as we found at the cochlear base. This suggests that the same onset polarity holds throughout the cochlea.

At the 3.5-mm site of the chinchilla cochlea, basilar-membrane responses to clicks begin approximately 30 µs after the onset of ossicular motion. This delay is smaller than a previous preliminary estimate from our laboratory (90 µs; Ruggero et al., 1992a). The latter were not based on middleear and basilar-membrane responses to clicks recorded in the same ears and probably underestimated delays in the stimulus system.

Reports of responses to clicks at basal locations of guinea pig cochleae (LePage and Johnstone, 1980; Nuttall and Dolan, 1993; de Boer and Nuttall, 1997) did not provide estimates of onset delay. A cochlear delay of 300–390 µs was measured at a squirrel monkey basilar-membrane site with CF of 6–7.8 kHz (Robles et al., 1976). According to a CF-distance map proposed by Greenwood (1990), such CFs correspond to a distance of 8.3–9.5 mm from the oval window. The difference between the delays at the 3.5-mm basilar-membrane site of chinchilla and the 8.3–9.5-mm site of squirrel monkey probably reflects the slowing down of the basilar-membrane wave as it travels from base to apex.

D. Is there a traveling wave on the basilar membrane?

The mechanical responses to clicks at the base of the chinchilla cochlea (the present work), at apical sites of the guinea pig and chinchilla cochleae (Cooper and Rhode, 1996), as well as those at an intermediate cochlear location in squirrel monkey (Robles et al., 1976), imply that there is a progressive phase accumulation or increasing delay as a function of distance from the oval window. Responses to identical stimuli at closely spaced basilar-membrane locations in individual cochleae also show phase accumulation or increasing delay as a function of distance from the oval window (Rhode, 1971; Kohllöffel, 1972; Cooper and Rhode, 1996; Russell and Nilsen, 1997). Thus, the bulk of the basilar-membrane data on cochlear delays provide strong support for the classical view of the traveling wave (von Békésy, 1960). Indirect estimates of traveling-wave delays based on cochlear microphonic responses to low-frequency tones (Tasaki et al., 1952; Dallos and Cheatham, 1971; Dancer et al., 1997) do not differ greatly from the latencies of responses to clicks at the basilar membrane of squirrel monkeys, chinchillas and guinea pigs (Robles et al., 1976; Cooper and Rhode, 1996, and the present work). At sites located about 4, 9 and 14 mm from the oval window in the guinea pig cochlea, such delays amount to 25, 250 and 1000 µs, respectively (Dancer et al., 1997).

The latency of responses to clicks of auditory-nerve fibers increases systematically as a function of decreasing CF (Kiang et al., 1965; Kim and Molnar, 1979; Siegel et al., 1982; Ruggero and Rich, 1983, 1987; Ruggero, 1992a). In the chinchilla, latencies for rarefaction clicks range from about 1 ms for fibers with CFs higher than 3–4 kHz to about 2.7 ms for fibers with CF of 320 Hz (Ruggero and Rich, 1983, 1987; Salvi et al., 1979). If synaptic and neural delays account for a 1-ms delay, regardless of CF (discussed by Ruggero and Rich, 1987), the neural data imply that mechanical travel time is almost nil at basal cochlear locations and 1.7 ms near the apex. These delays are fairly consistent with those measured on the basilar membrane or the organ of Corti at basal (e.g., Fig. 1) and apical (Cooper and Rhode, 1996) sites of the chinchilla cochlea.

Dancer has suggested that the basilar membrane does not sustain a traveling wave (Dancer, 1992; see also Dancer et al., 1997). He offered two main arguments. The first was that the onset latencies of cochlear responses are shorter than those predicted by Zwislocki’s (1948) model of basilar-membrane vibration. We do not view this quantitative discrepancy between measurements and one particular mathematical model as evidence against the very existence of a traveling wave. The onset latencies of basilar-membrane and auditory-nerve responses to clicks increase systematically as a function of distance from the oval window, as expected for a mechanical wave that propagates from base to apex (Ruggero, 1994). Further, Zwislocki (1974) has shown that his model can be adjusted (by increasing stiffness) to yield latencies that closely match in vivo empirical data for the guinea pig cochlea (see his Fig. 5). Dancer’s second argument was that the substantial phase accumulations exhibited by basilar-membrane responses at near-CF frequencies (equivalent to 1–2 CF periods at both basal and apical sites of the chinchilla cochlea: the present work and Cooper and Rhode, 1996) are due mostly to “active” cochlear processes and should not be taken as evidence for the existence of a (“passive”) traveling wave. Our data on the effects of death on the phases of basilar-membrane responses clearly contradict this argument: the phases of post-mortem responses are fully within the range of those observed in vivo (Figs. 11A and 15B).

E. Nonlinear phase shifts in responses to clicks and their relation to gain spectra

A striking aspect of the phases of post-mortem responses to clicks, as well as in vivo responses to intense clicks, is that they did not differ substantially from in vivo responses to low-level clicks. Although death, as well as increases in click level in vivo, did cause phase changes (and abolished the phase jumps), the changes (Fig. 15B) were small in comparison to the accumulated phase lags exhibited by in vivo responses at CF, regardless of stimulus level. This is somewhat paradoxical, in view of the substantial broadening of the bandwidth of response gain that accompanies either death or increases in stimulus level in vivo (Fig. 10). Since, in general, sharper frequency tuning requires longer response delays (Bode, 1946; Goldstein et al., 1971; Geisler and Rhode, 1982), the large increases in bandwidth observed post-mortem (or at intense click levels in vivo) might have been expected to result in correspondingly large decreases of phase lag or group delay at frequencies near CF. In fact, the phases of post-mortem and in vivo responses to intense clicks did not change at CF and group delays decreased by only small amounts or not at all (Figs. 11A and 15B).

Basilar-membrane responses to clicks in healthy chinchilla cochleae often have two- (or even multiple-) lobed waveforms (e.g., Figs. 2–4; also see Fig. 6 of Ruggero and Rich, 1991a, and Fig. 6 of Ruggero et al., 1996) and their spectra may include a notch (e.g., Figs. 9, 10, and 12; also see Fig. 9 of Ruggero et al., 1996). Two-lobed mechanical responses to clicks and/or spectral notches have also been observed at a basal cochlear site in guinea pig (Nuttall and Dolan, 1993; de Boer and Nuttall, 1997) and at the apex of guinea pig and chinchilla cochleae (Cooper, 1997).

At the base of the chinchilla the spectral notches arise from cancellations due to phase opposition between same-frequency components in the (time-domain) lobes of the responses to clicks (Figs. 12 and 13). The phase modulation of basilar-membrane responses to clicks may be related to the asymmetry of their magnitude spectra, given that the impulse responses of asymmetrical filters generally exhibit such modulation (Papoulis, 1977, p. 123). However, the origin of the notches and the underlying phase modulation is obscure and we are uncertain about their significance. We doubt that they are solely artifacts (e.g., due to opening the otic capsule: Cooper, 1997; see Section III A of Discussion), since such artifacts should be relatively invulnerable to physiological deterioration and should exhibit linear properties. In contrast, notches and phase shifts were present only in sensitive cochleae, at or near CF at certain stimulus levels (i.e., their presence was CF-specific and intensity dependent) and disappeared post-mortem. All these features indicate that the phase modulation and associated notches are linked to nonlinear and physiologically vulnerable processes. Most importantly, the notches occurred at levels at which response growth was highly compressive (see Fig. 7, L113), thus ruling out such linear artifacts as motion of the fluid-meniscus (see Section A of Discussion). However, we cannot rule out that these phenomena arise from an interaction between cochlear nonlinearities and stimulus artifacts (such as ringing in the acoustic click waveform).

F. Interpretation of the close resemblance between basilar-membrane responses to tones and clicks: Linearlike correspondences in spite of nonlinear growth

Robles et al. (1976) noted that at the basilar membrane of the squirrel monkey, responses to clicks could be mimicked to a fair extent by a Fourier synthesis based on magnitude-vs-frequency spectra measured with tones and derived phase-vs-frequency functions (computed from the magnitude data on the assumption of minimum-phase behavior). Our present findings show that, indeed, basilar-membrane responses to clicks and tones are generally well matched (Fig. 15; see also Figs. 3 and 4 of Ruggero et al., 1992a, and Fig. 6 of Ruggero et al., 1992b), so that responses to tones can be predicted, with good accuracy, from responses to clicks, and vice versa.

It seems remarkable that reasonably accurate cross-stimulus predictions are possible for such a highly nonlinear system as the one underlying basilar-membrane vibration at the base of the cochlea. We surmise that the system properties that make such predictions possible are the same that severely restrict the prominence of basilar-membrane harmonic distortion and other nonlinearities, especially when stimulation is confined to a single spectral level (e.g., Evans, 1989; de Boer and Kruidenier, 1990; Zwislocki et al., 1997). (1) The magnitude- and phase-frequency spectra of responses to a given type of stimulus (click or tone) presented at any one level accurately predicts responses to the other type of stimulus only at a single, specific level. In the case of Fig. 15A, for example, responses to 54-dB clicks predict accurately the magnitudes of responses to 40-dB tones but grossly overestimate the responses to 70-dB tones. (2) Basilar-membrane responses to single tones at the base of the cochlea exhibit no dc components (Cooper and Rhode, 1992) and contain little (perhaps negligible) harmonic distortion (Cooper and Rhode, 1992; Ruggero et al., 1992c, 1997). (3) Responses to white noise can be accurately predicted by first-order Wiener kernels (Recio et al., 1996, 1997). (4) The magnitude of odd-order distortion products elicited by pairs of equal-level tones rarely exceeds 10% of the responses to the primary tones (Robles et al., 1991, 1997; Nuttall et al., 1990; Rhode and Cooper, 1993).

G. Frequency modulation, the extent of nonlinearity as a function of time, and the speed of the “cochlear amplifier”

Nonlinear compressive growth at the 3.5-mm site of the chinchilla basilar membrane is evident within 100 µs states of response onset (Figs. 6 and 8). By implication, the organ of Corti feedback that boosts basilar membrane vibrations (“the cochlear amplifier”) starts its operation within 1 CF period following the arrival of the traveling wave at the recording site. The strength of the feedback (as indicated by the magnitude of compressive nonlinearity) varies significantly as a function of time, increasing rapidly from a minimum at onset to a maximum 1–1.6 ms later but waxing and waning thereafter (Fig. 8). One plausible interpretation of the initial variation is that the feedback is tuned to CF and thus merely follows the “passive” frequency glide, which is present both in vivo and post-mortem (Figs. 5 and 6). Taking the frequency glide into account, the onset of nonlinearity appears to be an almost instantaneous response to the CF spectral components of the “passive” vibrations.

However, the time course of the frequency glide cannot fully account for the time course of the compressive nonlinearity. The frequency glide consists of a roughly monotonic saturating-exponential increase, whereas the magnitude of the compressive nonlinearity undergoes waxing and waning, with compression minima (i.e., slope maxima) corresponding approximately to the wave shape constrictions. The nearly synchronous occurrence of the constrictions and the compression minima suggests that response sensitivity and nonlinear growth are tightly linked, which is consistent with the operation of a (nearly) instantaneous nonlinear “cochlear amplifier.”

H. Comparison between responses to clicks at the basilar membrane and auditory-nerve responses to clicks and noise

The responses to clicks of the basilar-membrane site with CF of 9–10 kHz cannot be compared in any detail with those of auditory-nerve fibers with similar CFs because such neurons do not phase lock at near-CF frequencies. Except for rectification (presumably due to synaptic processes), the responses to clicks of low-CF neurons resemble qualitatively the high-CF basilar-membrane responses in several respects. First, low-CF auditory-nerve fibers respond to rarefaction clicks with shorter latencies [by about 1/(2*CF)] than to condensation clicks (Kiang et al., 1965; Goblick and Pfeiffer, 1969; Pfeiffer and Kim, 1972; Kim and Molnar, 1979; Siegel et al., 1982; Ruggero and Rich, 1983, 1987). This is consistent with the onset polarity of basilar membrane responses (the present work and Cooper and Rhode, 1996) on the assumption that, in apical cochlear regions, auditory-nerve excitation occurs when the basilar membrane is deflected or in motion toward scala vestibuli (Ruggero and Rich, 1983, 1987). Second, neural responses exhibit nonlinear properties reminiscent of those at the basilar membrane, including a skew of their envelope toward earlier times as a function of increasing stimulus intensity (e.g., Kiang et al., 1965; Pfeiffer and Kim, 1972) and an amplitude nonlinearity in responses to paired clicks (Goblick and Pfeiffer, 1969). This amplitude nonlinearity may reflect directly the nonlinear growth of responses at the basilar membrane. The envelope skew, on the other hand, probably reflects mixed contributions from both basilar-membrane nonlinearities (Figs. 2–4,7 and 8) and neural and synaptic processes (e.g., Gray, 1967; Schoonhoven et al., 1994). Third, the responses to clicks of 7% of low-CF fibers exhibit lobes reminiscent of those (Figs. 3 and 4) characterizing basilar-membrane responses at the cochlear base (Pfeiffer and Kim, 1972). However, it is puzzling that such lobes should be only present in a small minority of fiber responses, if in fact they reflect basilar-membrane vibrations.

Revcors (de Boer, 1967; de Boer and de Jongh, 1978) for responses to noise of low-CF auditory-nerve fibers resemble basilar-membrane responses to clicks even more closely than do auditory-nerve fiber responses to clicks. This is because the first-order cross-correlation between the spike train and the noise stimulus removes rectification and other even-order nonlinearities, which are largely (but not entirely: Rhode and Cooper, 1996) of synaptic and/or neural origin (Recio et al., 1996, 1997). Revcors of neural responses to noise (Møller and Nilsson, 1979) exhibit a frequency modulation very much like that seen in basilar-membrane responses (Figs. 5–6). They also show a deterioration of frequency tuning and a spectral shift toward lower frequencies with increasing stimulus intensity (Evans, 1977; de Boer and de Jongh, 1978; Møller, 1978). Again, it is likely that these nonlinearities reflect both basilar-membrane and more central (synaptic and neural) contributions.