Combination of Multichannel Single-Voxel MRS Signals Using Generalized Least Squares

Abstract

Purpose

To propose using the generalized least square (GLS) algorithm for combining multichannel single-voxel MRS signals.

Materials and Methods

Phantom and in vivo brain MRS experiments on a 7 T scanner equipped with a 32-channel receiver coil, as well as Monte Carlo simulations, were performed to compare the coefficient of variation (CV) of the GLS method with those of two recently reported spectral combination methods.

Results

Compared to the two existing methods, the GLS method significantly reduced CV values for the simulation, phantom, and in vivo experiments.

Conclusion

The GLS method can lead to improved precision of peak quantification.

INTRODUCTION

Multichannel receiver coils (1,2) are widely used in anatomical imaging and spectroscopic imaging for shortening scan time or improving signal-to-noise ratio (SNR). In recent years, the use of multichannel receiver coils in single-voxel magnetic resonance spectroscopy (MRS) has become increasingly popular. However, it remains somewhat unclear how to optimally combine multichannel signals to produce the combined spectrum.

A simple way to combine multichannel signals is to individually phase the spectrum obtained from each channel and then add them to give the single combined spectrum. For better SNR performance, various methods have been proposed for combining multichannel signals (3–13). Most of these methods ignore noise correlation between different coil elements when calculating the weighting factors for each channel. Two recent methods, nd-comb (noise decorrelated combination) (12) and WSVD (Whitened Singular Value Decomposition) (13), take into account the noise correlation between different channels to further improve the SNR of the combined spectra. In both methods, a linear transformation of the multichannel signals is performed to remove the noise correlation and standardize the noise level. The transformation matrix is obtained by eigen decomposition of the noise covariance matrix. In nd-comb, the transformed signals are individually phased and then weighted averaged where the weighting factor for each channel is the SNR of the largest metabolite peak in the spectrum. In WSVD, the combined spectrum is computed from the transformed signals by singular value decomposition. Both methods offer improved SNR performance compared to other methods that ignore the noise correlation between different channels. However, both methods have room for improvement in terms of the precisions of the measurements.

In this work, we propose to combine multichannel MRS signals using a generalized least squares (GLS) (14,15) method. The GLS algorithm has been used in parallel imaging and spectroscopic imaging by Pruessmann (16) and Dydak (17), respectively. Recently, the GLS algorithm was used in a multi-compartment spectroscopic imaging technique (18). Single-voxel MRS using a multichannel receiver coil can be considered as a special case of the multi-compartment spectroscopic imaging technique where the total number of compartments is 1. Therefore, it is natural to adopt the GLS approach for combining multichannel single-voxel MRS signals. However, to our best knowledge, there is no reported work that uses the exact GLS algorithm to combine multichannel single-voxel MRS signals. Through simulation, phantom, and in vivo experiments, we will demonstrate that the GLS method performs better than the nd-comb and WSVD methods for combining multichannel single-voxel MRS signals.

MATERIALS AND METHODS

Let the integrated sensitivity of the mth coil element over the voxel of interest be S_m, the free induction decay (FID) signals in the mth channel, D_m(t), can be expressed as

$$D_m(t)=S_{m}C(t)+{\epsilon }_m(t),$$ [1]

where C(t) represents the FID of the voxel measured by a hypothetical homogeneous coil and ε_m(t) is the random noise in the mth channel. In matrix form, Eq. 1 becomes

$$\mathit{D}=\mathit{SC}+\mathit{\epsilon },$$ [2]

where D and ε are M x P matrices with M being the total number of coil elements and P the number of digitized data points in the FIDs; S is an M-element column vector and C a P-element row vector. The best linear unbiased estimate (BLUE) of C is given by the GLS solution (16)

$$\mathit{C}={({\mathit{S}}^{†}{\mathit{\Psi }}^{-1}\mathit{S})}^{-1}{\mathit{S}}^{†}{\mathit{\Psi }}^{-1}\mathit{D},$$ [3]

where Ψ is the noise covariance matrix of the coil elements, given by Ψ = εε^†, and ‘†’ denotes conjugate transpose. All variables in Eq. 3 have complex values. Note that S^†Ψ⁻¹S is a 1 × 1 scalar, so (S^†Ψ⁻¹S)⁻¹ is equivalent to 1/(S^†Ψ⁻¹S). Fourier transform of C(t) gives the combined spectrum. Alternatively, equations 1–3 can be equivalently expressed in the frequency domain. The multichannel FIDs can be individually Fourier transformed into frequency domain and subsequently combined using Eq. 3 to give the combined spectrum.

Simulations

Monte Carlo simulations were performed to compare the precision and lack of bias of the three different methods, i.e. nd-comb, WSVD, and GLS. Thirty-two channel metabolite FIDs were simulated based on a four-peak (N-acetylaspartate (NAA), creatine (Cr), choline (Cho), and residual water peak) spectral model and realistic coil sensitivity values obtained from an in vivo experiment. Correlated multivariate Gaussian noise was generated based on a noise covariance matrix obtained from an in vivo experiment and was added to the synthetic metabolite FIDs. These noise-added multichannel FIDs were individually Fourier transformed into the frequency domain and then combined to give the combined spectrum using the three different methods. For the nd-comb and GLS methods, the NAA peak was used as the reference signal for computing the weighting factor or coil sensitivity of each channel. In the nd-comb method, the noise-whitened multichannel spectra were phased and weighted summed to give the combined spectrum. The phase correction term for each channel is determined by iteratively changing its value until the real part of the NAA peak in the spectrum has maximum area. This maximum NAA peak area was used as the magnitude of the weighting factor for each channel. In GLS, the integral of the complex-valued spectral signal over the NAA peak was used as the coil sensitivity S_m for each channel and the combined spectrum was computed according to Eq. 3. The noise level in the multichannel FIDs was programmed to step through 50 different values with the noise correlations keeping the same. At each noise level, the noise-added FIDs were simulated 200 times. The combined spectrum was computed each time using the three different methods, and the Cr peak area in the combined spectrum was computed. The averaged value and the coefficient of variation (CV) of the Cr peak area over the 200 repetitions was computed for each method at each noise level. The averaged Cr peak area values at different noise levels were divided by the ideal Cr peak area determined from noise free data to give the normalized Cr peak area values.

In the above simulation experiment, all metabolite signals in each channel were made to be proportional to the integrated coil sensitivity of that channel. There were no other errors except the Gaussian noise. In reality, however, small amount of water and lipid signals could be present over the whole range of metabolite resonance frequencies. These water and lipid signals are generally not proportional to the integrated coil sensitivities at the voxel of interest because they could come from outside the voxel of interest due to imperfect RF profiles for localization and extremely inhomogeneous B₀ field near tissue-air interface. Water suppression and outer volume suppression (OVS) cannot fully eliminate the water and lipid signal contaminations due to inhomogeneous B₀ and B₁ fields outside the voxel of interest. This is especially true for high field scanners.

The second simulation experiment was designed to test the tolerance of the three spectral combination methods to a simple small baseline error. A constant baseline error that is equal to 2% of the NAA peak amplitude in the most sensitive channel was added to the simulated spectrum of each channel. Similar to the first simulation experiment, multichannel FIDs were simulated 200 times for each of the 50 noise levels. The three different methods were used to compute the combined spectra. The averaged value and CV of the Cr peak area were computed at each noise level. The averaged Cr peak area values at different noise levels were divided by the ideal Cr peak area to give the normalized Cr peak area values.

Phantom Experiment

A phantom experiment was performed on a Siemens 7 T scanner equipped with a 32-channel receiver head coil. A phantom containing 12.5 mM N-acetylaspartate (NAA), 10 mM creatine (Cr), 3 mM choline (Cho), 7.5 mM myo-inositol (mI), 12.5 mM glutamate (Glu), and 5 mM lactate (Lac) was scanned with a point resolved spectroscopy (PRESS) sequence. The parameters of the sequence were TR = 2.5 s, TE₁ = 37 ms, TE₂ = 63 ms, voxel size = 2 × 2 × 2 cm³, spectral width = 4000 Hz, number of data points = 2048, and number of acquisitions = 128. The values of the sub-TEs were optimized for measuring the Glu peak (19). The water signal was suppressed by eight sinc-gauss RF pulses with 350 Hz FWHM (full width at half maximum) bandwidth.

Raw signals from each channel were processed offline. The FIDs were zero padded to 16384 data points and multiplied by an exponential function of 1 Hz linewidth. These filtered FIDs were individually Fourier transformed into frequency domain and then used to compute the combined spectrum for each of the 128 acquisitions using the three different methods. For all three methods, the noise covariance matrix was computed using the spectral signal of each channel between 9 and 11.4 ppm where no metabolite peaks were detected. For both the nd-comb and GLS methods, the NAA peak was used as the reference signal for computing the weighting factor or coil sensitivity of each channel. After the combined spectra were obtained, the CV values of the Glu, Cr, and Cho peak areas were computed from the 128 acquisitions.

In Vivo Experiments

Two normal volunteers, consented in accordance with procedures approved by our institutional review board, were scanned on a Siemens 7 T scanner equipped with a 32-channel receiver head coil. For the first volunteer, two MRS scans were performed on the same voxel with size of 3 × 3 × 3 cm³ located in the occipital lobe. Shimming of the B₀ field was performed before each scan. The pulse sequence was similar to the one used in the phantom experiment except the difference in voxel size. The data post-processing procedure was identical to that of the phantom experiment. For the second volunteer, three MRS scans were performed on the same voxel (3 × 3 × 3 cm³) located in the occipital lobe. B₀ shimming was performed before each scan. The pulse sequence for the first two MRS scans were the same as the one used to scan the first volunteer. For the third MRS scan, a six slab (thickness = 5 cm) OVS using hyperbolic secant RF pulses was added to the pulse sequence. The TR value had to be increased to 4.3 s to satisfy the specific absorption rate (SAR) limit. All other pulse sequence parameters and the postprocessing procedure were kept unchanged.

RESULTS

Simulations

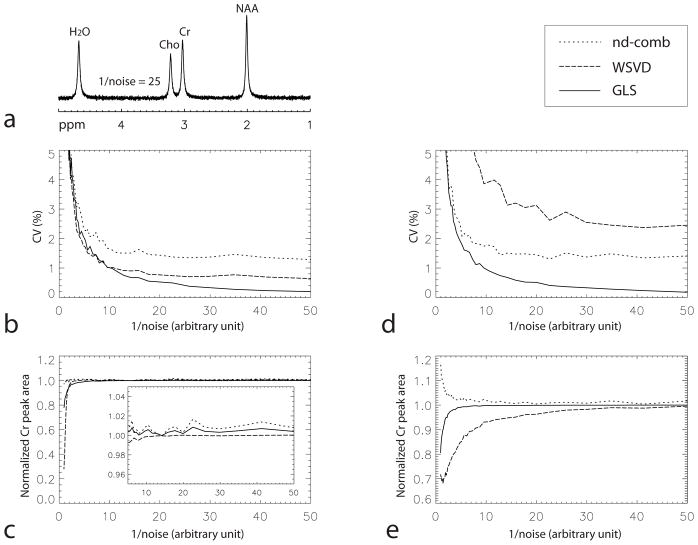
The results for the first simulation experiment are presented in Figs. 1a–c. A representative combined spectrum computed using the GLS method at one noise level (1/noise = 25) is displayed in Fig. 1a, where 1/noise is the reciprocal of the level of noise added to the simulated multichannel FIDs in an arbitrary unit. The same arbitrary unit was used in both simulation experiments. The CV values of the Cr peak area at different noise levels for the three different methods are plotted against 1/noise in Fig. 1b. This plot shows that the GLS method has significantly lower CV values than the nd-comb and WSVD methods when the noise levels are not too high, i.e. 1/noise > 13 or CV for the GLS method < 0.75. The values of the normalized Cr peak area for the three different methods are plotted against 1/noise in Fig. 1c. The values of the three curves are not far from 1 when the noise levels are not very high. This means that there is very little bias in peak quantification when the noise levels are not very high.

Fig. 1.

Comparisons of precision and lack of bias of the three spectral combination methods using Monte Carlo simulations. a: One combined spectrum computed using the GLS method for the first simulation experiment. There were no input baseline errors in the multichannel FIDs except random noise with 1/noise = 25 which was in an arbitrary unit. The same arbitrary unit was used in both simulation experiments. b: CV of the Cr peak area as a function of 1/noise for the first simulation experiment. c: Normalized Cr peak area as a function of 1/noise for the first simulation experiment. d: CV of the Cr peak area as a function of 1/noise for the second simulation experiment, in which a constant baseline error being equal to 2% of the NAA peak amplitude in the most sensitive channel was added to the simulated spectrum of each channel. e: Normalized Cr peak area as a function of 1/noise for the second simulation experiment.

The results for the second simulation experiment, in which a small constant baseline was added to the simulated multichannel spectra, are presented in Figs. 1d–e. The CV values of the Cr peak area for the three different methods are plotted against 1/noise in Fig. 1d. Comparing Fig. 1d with Fig. 1b, it is clear that the CV values at different noise levels for the WSVD method become much larger in the second simulation experiment while the CV values for the nd-comb and GLS methods do not change much. The GLS method has significantly lower CV values than the nd-comb and WSVD methods when the noise levels are not too high, i.e. 1/noise > 3.5 or CV for the GLS method < 2.6. The normalized Cr peak area values for the three different methods are plotted against 1/noise in Fig. 1e. The values for the nd-comb and GLS methods are close to 1 when the noise levels are not very high, but the values for the WSVD method start to drop at relatively low noise levels. This indicates that the nd-comb and GLS methods have less bias in peak quantification than the WSVD method in the presence of small baseline errors.

Phantom Experiment

One combined spectrum of the phantom experiment computed using the GLS method is plotted in Fig. 2. The spectrum was computed using data from the first of the 128 acquisitions. The voxel of interest is depicted on the gradient-echo image in Fig. 2. The CV values of the Glu, Cr, and Cho peak areas for the nd-comb, WSVD, and GLS methods were computed from the 128 acquisitions and are listed in Table 1. The CV values for the GLS method are significantly lower (F-test, p < 0.01) than those of the nd-comb and WSVD methods. In the spectrum, the negative peak around 2.05 ppm comes from ³CH₂ of glutamate (2.04 and 2.12 ppm). The peak is negative due to J-coupling effects. The negative peak around 3.5 ppm comes from ¹CH and ³CH of myo-inositol (3.52 ppm).

Fig. 2.

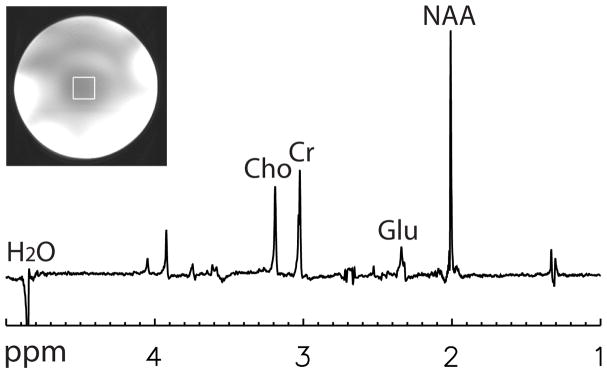
One combined spectrum of the phantom computed using the GLS method, where 32-channel data from the first acquisition were used. Voxel size = 2 × 2 × 2 cm³, TR = 2.5 s, TE₁ = 37 ms, TE₂ = 63 ms, spectral width = 4000 Hz, number of samples = 2048, number of acquisitions = 128.

Table 1.

Coefficient of variation values of the Glu, Cr, and Cho peaks in the combined spectra.

	nd-comb	WSVD	GLS
Phantom
Glu	6.33%	5.37%	2.57%
Cr	6.03%	5.78%	1.37%
Cho	6.24%	6.25%	1.47%
Volunteer 1
Scan 1
Glu	7.49%	4.97%	3.83%
Cr	7.14%	4.31%	2.63%
Cho	8.00%	5.33%	3.85%
Scan 2
Glu	7.53%	4.96%	3.62%
Cr	7.49%	4.54%	2.57%
Cho	8.00%	5.21%	3.86%
Volunteer 2
Scan 1
Glu	7.76%	5.20%	3.90%
Cr	7.58%	4.47%	2.59%
Cho	7.71%	4.71%	3.34%
Scan 2
Glu	7.94%	5.10%	3.83%
Cr	7.54%	4.24%	2.25%
Cho	7.36%	4.48%	3.17%
Scan 3
Glu	7.58%	5.09%	3.36%
Cr	7.13%	4.25%	2.53%
Cho	7.63%	4.88%	3.38%

Glu, glutamate

Cr, creatine

Cho, choline

nd-comb, noise-decorrelated combination

WSVD, whitened singular value decomposition

GLS, generalized least squares

In vivo Experiments

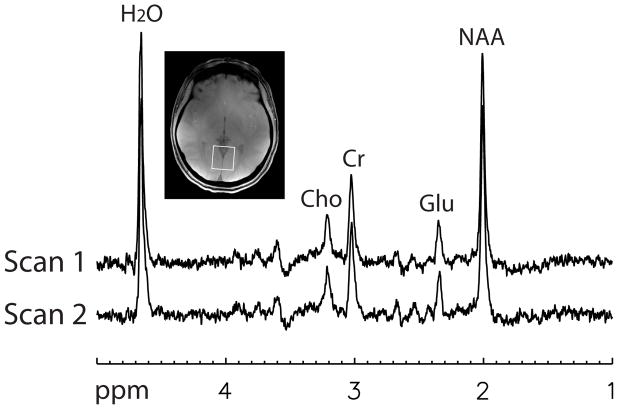
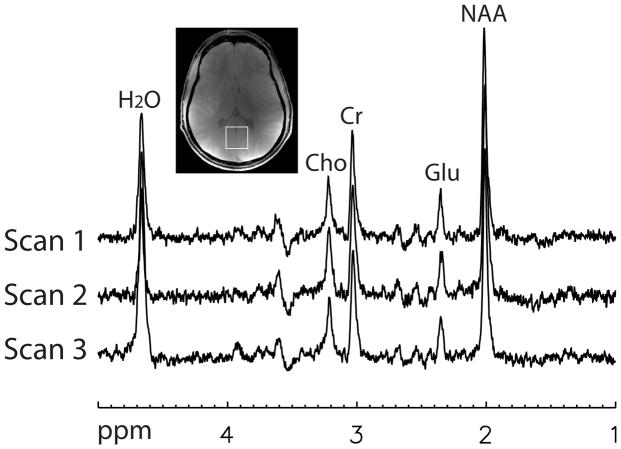
Two combined spectra, one for each of the two MRS scans performed on the first volunteer, are plotted in Fig. 3. The two spectra were computed using the GLS method and data from the first of the 128 acquisitions. The voxel of interest is depicted on the gradient-echo image in Fig. 3. Three combined spectra, one for each of the three MRS scans performed on the second volunteer, are plotted in Fig. 4. The three spectra were computed using the GLS method and data from the first of the 128 acquisitions.

Fig. 3.

Two combined spectra, one for each scan, of the first normal volunteer computed using the GLS method. Each combined spectrum was computed using the 32-channel data from the first acquisition. Voxel size = 3 × 3 × 3 cm³, TR = 2.5 s, TE₁ = 37 ms, TE₂ = 63 ms, spectral width = 4000 Hz, number of samples = 2048, number of acquisitions = 128.

Fig. 4.

Three combined spectra, one for each scan, of the second normal volunteer computed using the GLS method. Voxel size = 3 × 3 × 3 cm³, TE₁ = 37 ms, TE₂ = 63 ms, spectral width = 4000 Hz, number of samples = 2048, number of acquisitions = 128. For the first and second scans, no OVS was applied and TR = 2.5 s. For the third scan, OVS with six slabs were added to the pulse sequence and TR = 4.3 s.

For all five MRS scans performed on the two volunteers, the CV values of the Glu, Cr, and Cho peak areas for the nd-comb, WSVD, and GLS methods were computed from the 128 acquisitions in each scan and are listed in Table 1. The CV values for the GLS method are all significantly lower (F-test, p < 0.01) than those of the nd-comb and WSVD methods.

DISCUSSION

It has long been proved that the GLS solution is the best linear unbiased estimate of an unknown vector in a linear regression model when the error vector has a non-scalar covariance matrix (14,15). Our simulation, phantom, and in vivo experiments demonstrate that the GLS method performs better than the nd-comb and WSVD methods in terms of reducing CV values.

The second simulation experiment indicates that the WSVD method is more sensitive than the GLS method to baseline errors originated from water or lipid signals from outside the voxel of interest. The WSVD method decomposes the noise-whitened multichannel signals into a series of contributions of increasing rank and selects the best rank-1 decomposition in terms of two vectors: a column vector containing the coil sensitivities and a row vector containing the combined signals. The baseline errors which are not proportional to coil sensitivities can cause relatively large errors in this rank-1 decomposition. The second simulation experiment also indicates that the WSVD method tends to underestimate the metabolite peak areas when there are baseline errors. On the other hand, the GLS method gives an unbiased estimate of the peak areas for most noise levels. When the noise level becomes very high, the GLS method starts to underestimate the peak areas as well. This problem could be solved by using the unsuppressed water signals as the coil sensitivity reference signals (8). However, care must be taken when doing experiments on high field scanners (e.g. 7 T or 11.7 T) with large voxel sizes for detecting low concentration metabolites. The large unsuppressed water signals could induce radiation damping (20), which could cause the computed coil sensitivities to have large errors from the true coil sensitivity values in the water-suppressed data acquisitions.

For the nd-comb method, the magnitudes of the weighting factors are not optimized for minimizing multi-measurement variations. It would become optimal if the weighting factors were divided by the sum of squares of the SNR values of the reference peak. This small imperfection results in relatively large multi-measurement variations.

When comparing the performances of the three different methods, CV is used instead of one of the frequently used definitions of SNR, i.e. the ratio of peak amplitude to background noise. This is because that background noise is not equivalent to standard deviation of peak amplitude when other inter-measurement variations are involved. In repeated MRS experiments, the residual water signals, the computed coil sensitivities, and the computed noise covariance matrices will vary in general. Therefore, 1/CV is a truer measure of SNR than the ratio of peak amplitude to background noise because CV is computed using data from different acquisitions.

The CV values of the NAA peak are not given in Table 1. because comparing the CV values of the NAA peak for the three different methods would not be appropriate as NAA is already used as the reference signal for computing weighting factors or coil sensitivities in the nd-comb and GLS methods.

Because a relatively long TE of 100 ms is used in our experiments, signals from macromolecules are very small. In addition, the residual water signals in our experiments are very small due to the effective water suppression pulses. Therefore, a direct measurement of the peak areas for Glu, Cr, and Cho is good enough for the purpose of comparing the CV values of the three spectral combination methods. For pulse sequences with shorter TE values, LCModel (21) may become necessary for computing the peak areas.

In conclusion, this work proposes to use the GLS algorithm to combine multichannel single-voxel MRS signals when the noise correlations between different channels are not negligible. Results from simulation, phantom, and in vivo experiments show that the combined spectra computed using the GLS method have lower CV values than those of the nd-comb and WSVD methods. Therefore, the GLS method can lead to improved precision of peak quantification compared to the existing methods.