Abstract
The purpose of this investigation is to utilize a computational model to compare a synchronized valveless pulsatile left ventricular assist device to continuous flow left ventricular assist devices at the same level of device flow, and to verify the model with in vivo porcine data. A dynamic system model of the human cardiovascular system was developed to simulate support of a healthy or failing native heart from a continuous flow left ventricular assist device or a synchronous, pulsatile, valveless, dual piston positive displacement pump. These results were compared to measurements made during in vivo porcine experiments. Results from the simulation model and from the in vivo counterpart show that the pulsatile pump provides higher cardiac output, left ventricular unloading, cardiac pulsatility, and aortic valve flow as compared to the continuous flow model at the same level of support. The dynamic system model developed for this investigation can effectively simulate human cardiovascular support by a synchronous pulsatile or continuous flow ventricular assist device.
Introduction
Mathematical models designed to simulate the hemodynamics of the human cardiovascular system are versatile and cost-effective platforms to conduct studies comparing the hemodynamics resultant from various types of ventricular assist device (VAD) support. A popular way to represent a human cardiovascular system model employs electric circuit analogs, where variables such as systemic pressures and flows are represented as voltages and currents. Critical physical properties such as arterial and venous inertia, compliance, and friction are modeled as inductive, capacitive, and resistive elements. Heart valves can be represented by either ideal diodes or more complex dynamic models.1 There are multiple ways to model dynamic ventricular myocardial function; most relevant to this study are time-varying elastance functions.2 In this approach, ventricles and atria are described as contracting chambers with a time-varying pressure-volume relationship. Both chambers have passive and active elastance components that can be parameterized to simulate heart failure. Uncertainty exists with regards to predicting the hemodynamic response to VADs, especially when new modes and methods of support are introduced. Simulation models can provide a suitable testing platform to investigate device design and operation before actual prototyping and implantation into animal or human subjects.3,4
Several cardiovascular simulation models for studying the hemodynamic effect of VADs have been reported in the literature5-11 and describe different levels of verification against in vivo animal and human clinical data. For example, Morley et al. verified a cardiovascular model of partial continuous flow VAD support by comparing modeled relationships between VAD flow and cardiac output and between VAD flow and left atrial pressure to the same relationships obtained during an acute failure experiment in a bovine model.12 The present study describes simulation of experiments reported by Letsou et al.13, in which both a continuous flow device and a valveless pulsatile flow VAD are directly compared during in vivo animal experiments. Letsou et al. demonstrated that synchronous pulsatile left ventricular assistance produces higher left ventricular unloading and circulatory support as compared to continuous flow left ventricular assist at the same flow rates in an acute porcine model. While absolute values of the porcine and human cardiovascular systems differ, we anticipate similar results from the simulation study.
The purpose of this investigation is to verify that a computational model can be used to predict cardiovascular hemodynamics with ventricular assist device support using in vivo porcine data, and to compare continuous to synchronous pulsatile support at the same level of device flow.
Materials and Methods
A simulation model was developed that solves for key hemodynamic metrics based on clinically defined parameters, allowing it to simulate a wide range of cardiac physiology. Cardiac function is supported either by a synchronous, valveless, pulsatile device or a continuous flow VAD. The model equations were implemented in and solved using the commercial software program Matlab (The MathWorks, Inc., Natick, MA). All in vivo data was obtained from the experiments described in a porcine acute ischemic heart failure model by Letsou et al.13
Cardiovascular System Model
An electrical circuit analog of the human cardiovascular system model used in this study is shown in Figure 1. The closed circuit model includes the heart, systemic circulation, and pulmonary circulation. Both systemic and pulmonary circulations include arteries, arterioles, capillaries and veins. The analogous elements are indicated as fluid resistive effects in vessels as electrical resistors, fluid inertial effects as inductors, and vessel compliance as capacitors. Flow from the VAD runs in parallel to the aortic valve, aspirating blood from the left ventricle and ejecting it into the aortic sinus.
Figure 1.
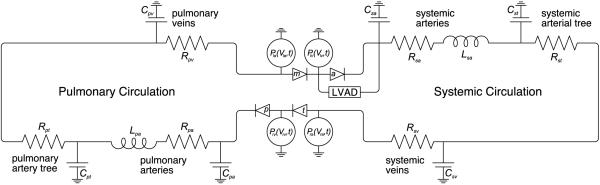
Electrical circuit analog of the cardiovascular system model.
The tricuspid, pulmonary, mitral and aortic valves are represented by electronic diodes.6,7,11,14-16 The four heart chambers are modeled as independent dynamic volumes. The pulsatile dynamics of the myocardium in the ventricles and atria are approximated using passive and active elastance components.17,18 Clinically derived parameters are used to simulate the model in a healthy condition and in end-stage heart failure.19-22 Critical hemodynamic information such as aortic pressure, cardiac output, coronary flow and cardiac workload, for example, can be derived from the outputs of the simulation model, as described in the following sections. The model parameter values for both healthy and end-stage heart failure as well as the parameter units and abbreviation definition are provided in Table 1.
Table 1.
Values of model parameters for the cardiovascular system in a healthy state and in heart failure. Values used to simulate heart failure are designated by parenthesis.
| Parameter | Description | Value | Units | |
|---|---|---|---|---|
| Valves | Rt | Valve resistance | 0.0025 | mmHg/mL |
| Left | Ela | Elastance | 0.25 | mmHg/mL |
| atria | Vla 0 | Unstressed volume | 10 | mL |
| Ala | Left atria exponential constant | 0.45 | mmHg | |
| Bla | Left atria exponential constant | 0.05 | 1/mL | |
| Ta | Atrial ejection time | 0.09 | sec | |
| Left | Elv | Left ventricular elastance | 3.25 (0.30) | mmHg/mL |
| ventricle | Vlv 0 | Unstressed left ventricular volume | 5 | mL |
| Alv | Left ventricle exponential constant | 0.03 (0.18) | mmHg | |
| Blv | Left ventricle exponential constant | 0.05 (0.016) | 1/mL | |
| Right | Era 0 | Right atria elastance | 0.25 | mmHg/mL |
| atria | Vra 0 | Unstressed right atrial volume | 10 | mL |
| Ara | Right atria exponential constant | 0.45 | mmHg | |
| Bra | Right atria exponential constant | 0.05 | 1/mL | |
| Ta | Atrial ejection time | 0.09 | sec | |
| Right | Erv | Right ventricular elastance | 0.75 (0.45) | mmHg/mL |
| ventricle | Vlv 0 | Unstressed right ventricular volume | 5 | mL |
| Ara | Right ventricle exponential constant | 0.04 | mmHg | |
| Brv | Right ventricle exponential constant | 0.05 | 1/mL | |
| Systemic | Rsa | Systemic artery resistance | 0.15 | mmHg s/mL |
| circulation | Csa | Systemic artery compliance | 1.25 (0.65) | mL/mmHg |
| Lsa | Systemic artery inertia | 0.0022 | mmHg s2/mL | |
| Rst | Systemic arterial tree resistance | 0.8 (0.9) | mmHg s/mL | |
| Cst | Systemic arterial tree compliance | 2.0 (1.5) | mL/mmHg | |
| Rsv | Systemic venous resistance | 0.025 (0.020) | mmHg s/mL | |
| Csv | Systemic venous compliance | 20 | mL/mmHg | |
| Pulmonary | Rpa | Pulmonary artery resistance | 0.07 | mmHg s/mL |
| circulation | Cpa | Pulmonary artery compliance | 7.5 | mL/mmHg |
| Lpa | Pulmonary artery inertia | 0.0018 | mmHg s2/mL | |
| Rpt | Pulmonary arterial tree resistance | 0.04 | mmHg s/mL | |
| Csp | Pulmonary arterial tree compliance | 0.5 | mL/mmHg | |
| Rpv | Pulmonary venous resistance | 0.003 | mmHg s/mL | |
| Cpv | Pulmonary venous compliance | 20 | mL/mmHg | |
| Cannulas | Ro | Cannula resistance | 0.0054 | mmHg s/mL |
| Lo | Cannula fluid inertia | 0.0122 | mmHg s2/mL |
Cardiac Elastance and Chamber Flow Equations
Each heart chamber is modeled individually with its own elastance, pressure, and volume. Assuming blood to be incompressible, conservation of mass defines the rate of change of volume as follows,
| (1) |
In the case of the left ventricle, the flow in (Qtm) is the mitral valve flow (Qm) and the flow out (Qout) is the aortic valve flow (Qa) plus the VAD flow (QVAD). Modeling for the remaining chambers (left atria, right ventricle, and right atria) is accomplished in a similar fashion.
To determine pressure (P) as a function of volume, elastance must be defined. This function describes the active time-varying contractile and relaxation states of the ventricular or atrial myocardium. The following elastance function23 for the ventricles is used:
| (3) |
where time (t) is normalized to the cardiac cycle with value zero at the R-wave. The ventricular contraction time (Tvc), with unit seconds, is a function of heart rate HR (in bpm):
| (3) |
The atria are modeled in a similar manner but with their own elastance functions24:
| (4) |
where time (t) is the same as above, the atrial contraction time (Ta) is define in Table 1, and the R-R interval (RR), with unit seconds, is inversely proportional to heart rate.
Atrial and ventricular pressure are functions of the active elastance e(t), a passive elastance exponential25, and the atrial or ventricular volume (V). With values for the exponential constants (A,B), unstressed volume (V0), and elastance (E) defined in Table 1, the pressure functions are defined by,
| (5) |
A non-linear orifice model with unidirectional flow is used to determine flow through the heart valves24. For example, flow through the mitral valve is computed as follows:
| (6) |
where Rv is the valve resistance. Modeling the remaining valves (aortic, tricuspid, and pulmonary) is done in a similar fashion.
Systemic and Pulmonic Circulation
The systemic and pulmonic vasculature is modeled by a dynamic fluid circuit, based on the unsteady Bernoulli equation, with fluid resistances and inertias in series and capacitors in parallel. The systemic circulation involves mathematical models relating pressure and flow for arteries, arterioles, the capillary tree and veins.24 The dynamic equations for pressure in the systemic arteries, arterial tree with arterioles and capillaries, and veins are functions of vessel compliance and flow:
| (7) |
| (8) |
| (9) |
The dynamic equations for flow through the systemic arteries, arterial tree, and veins are functions of vessel pressure, frictional fluid resistance, and blood inertia,
| (10) |
| (11) |
| (12) |
Dynamic equations for finding the pressure and flows on the pulmonic side of the circulatory system are formulated in a similar manner.
Simulating Heart Failure
In this study the primary mode of cardiac failure is congestive heart failure (HF). Normal physiological response to HF involves arterial and venous vasoconstriction, increased blood volume and decreased cardiac output. Structural changes to the left ventricle such as dilation and wall thinning leading to decreased contractility occur. To simulate the physiological response to HF in the computational model, parameters governing the left ventricle and systemic vasculature were modified to mimic disease states.12,26 Values for these parameters are in parenthesis next to the healthy parameters in Table 1. The model approximates the structural changes seen in end-stage heart failure by altering passive and active elastance. Passive elastance of the left ventricle, defined as the myocardium’s pressure response to a volume change, will decrease and the ventricles will dilate. Active elastance, defined as the sarcomeric development of force during systole, will decrease and the ability of the left ventricle to contract will diminish. Heart rate is increased in the model from 75 bpm to 90 bpm. Vascular changes include increasing resistance of systemic veins and arterioles as well as decreasing artery compliance. The physiological differences in these two modes can be seen in the left ventricular pressure-volume loops in Figure 2.
Figure 2.
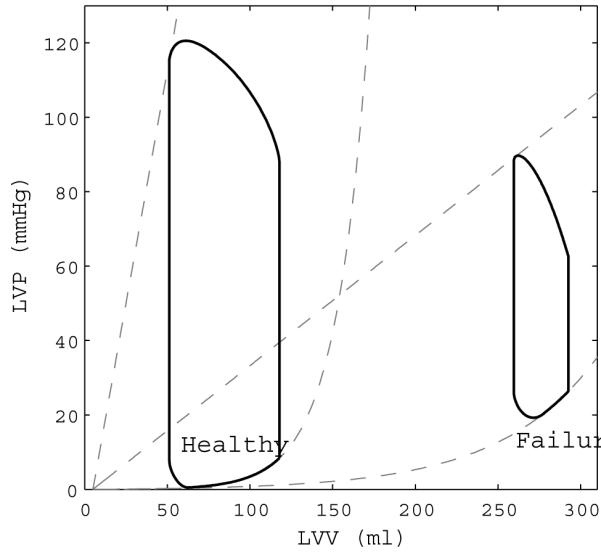
Left ventricular pressure-volume loops for the healthy state and failing state in the computational model. Note the increase in ventricular volume and decrease in contractility from healthy to failure.
Synchronous Valveless Pulsatile VAD Model
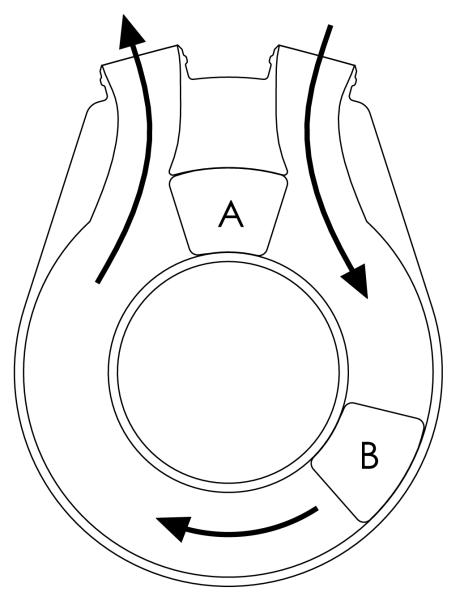
The pulsatile VAD used in the simulation produces flow similar to the TORVAD™ ventricular assist device (Windmill Cardiovascular Systems, Inc., Austin, TX). The TORVAD™ is a valveless positive-displacement pulsatile flow pump that can be synchronized with the cardiac cycle based on the signal measured from epicardial electrocardiogram leads, or can be run asynchronously up to 8 L/min. In synchronous mode, the ejection pulse of the VAD is programmable to eject at any point in the cardiac cycle. Figure 3 is a simplified representation of the TORVAD™ pump configuration.13 Two pistons are independently driven, by position-controlled motors and magnetic couplings, within a torodial pumping chamber to produce pulsatile flow. Pumping is achieved by driving one piston around the chamber while holding the other piston between the inlet and outlet ports. After each stroke the pistons exchange roles, eliminating the need for valves.
Figure 3.
A simplified schematic of the TORVAD™. Two pistons are independently driven, by position-controlled motors and magnetic couplings (not shown), within a torodial pumping chamber to produce pulsatile flow. Pumping is achieved by driving one piston (B) around the chamber while holding the position of the other piston (A) between the inlet and outlet ports. After each stroke the pistons exchange roles, eliminating the need for valves.
To model the pulsatile flow induced by the TORVAD™ for the purposes of this study, the simulation uses an ideal piece-wise sinusoidal flow rate profile, synchronized to the simulated cardiac cycle:
| (13) |
where SV is the stroke volume of the TORVAD™, time (t) is normalized to the cardiac cycle with value zero at the R-wave, synchronous phase delay (TD) is the programmable time delay from the R-wave to the beginning of ejection, and TST is the ejection time for a single bolus of fluid. In the healthy and failing states with TORVAD™ support simulated in this model, the device delivers a 35 ml bolus of blood in 0.30 seconds starting 0.24 seconds into a 0.800 (healthy) or 0.667 (failing) second RR interval. By starting 0.24 seconds into the cardiac cycle, the TORVAD™ pauses during systole and allows the ventricle to eject through the aortic valve, the TORVAD™ then augments the flow and pressure during early diastole, increasing cardiac output and arterial pressure.
Continuous Flow VAD Model
The continuous flow pump model is based on a generic axial flow design with a single impeller capable of speeds between 6,000 and 15,000 rpm.27 The term “continuous flow” is a misnomer, since flow produced by the pump actually varies as the pressure differential across the device fluctuates throughout the cardiac cycle. In simulations where the pump is placed across a healthy heart and pump rpm is low, pressure differentials between the aorta and left ventricle during diastole are high enough across the pump to drop flow to zero, or even reverse flow completely. In cases where the continuous flow pump completely overrides native cardiac output and flow across the aortic valve is zero, inlet pressure to the pump and pump output varies with the cyclic pressures of systole and diastole. Blood flow across the continuous flow device is modeled by,
| (14) |
with dependence on aortic pressure, left ventricular pressure, cannula resistance, and inertial energy of blood within the cannula.6 Cannula resistance and inertia, Rc and Lc respectively, are dependent on cannula length and radii as well as blood density and viscosity6, the values used can be found in Table 1. P(QVAD) is the functional relationship between pressure and flow for the device. Figure 4 shows pressure flow curves for the HeartMate II, which are used in the model to define this functional relationship for a range of pump speeds.28,29 Pressure flow curves based on the HeartMate II were used because it is the only commercially approved continuous flow device in the US and has accessible and verified specifications. An axial flow model is used here, however a centrifugal flow device has been used in animal experiments. The pressure flow (pump) curves for an axial flow device are functionally similar to those of centrifugal devices, and the overall hemodynamics induced would not be significantly different. In previous in vivo porcine experiments described by Letsou et al13, averaged flow rates for both devices were matched to make side-by-side physiologic comparisons. Similarly in the computational model, averaged flow rates for the continuous flow VAD were tuned to match those of the valveless pulsatile flow VAD to allow for physiologic comparisons between the in vivo experiment and computer model. Flow rates needed to support a healthy or failing heart using synchronous pulsatile assistance are significantly lower than flow rates created by the continuous flow pump when run at clinically normal speeds of approximately 9,000 rpm (8,600-9,800 rpm is the typical operation range).30 Consequently, the continuous flow VAD was run at slower than normal speeds to produce similar pump outputs. The pulsatile flow VAD, at a synchronized 35 mL stroke volume in the healthy heart, has a pump output of 2.63 L/min for a heart rate of 75 beats per minute. In the failing heart with a heart rate of 90 beats per minute, pump output reaches 3.15 L/min. To match these outputs, the continuous flow VAD was run at 8,400 rpm for the healthy and at 7,300 rpm in the failing heart.
Figure 4.
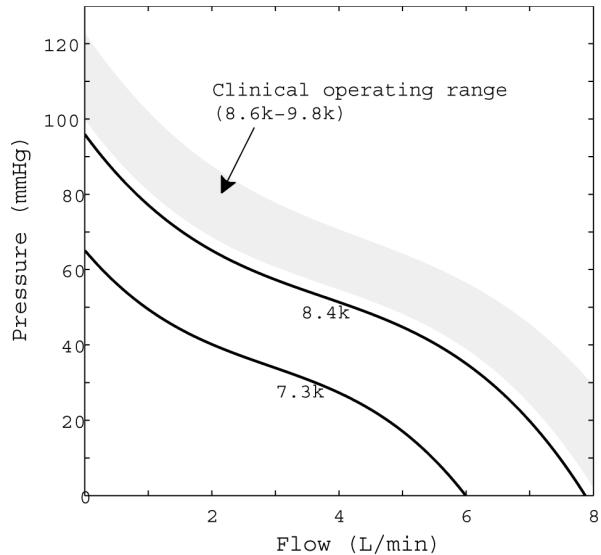
Pressure-flow curves for the HeartMate II axial flow pump at 7,300 rpm, used in the failure model, and 8,400 rpm, used in the healthy model. The typical clinical operating range is between 8,600 and 9,800 rpm, and is represented by the shaded region on the plot.
Calculating SHE and PVA
Surplus hemodynamic energy (SHE), energy generated by flow pulsation above the mean arterial pressure (MAP), and pressure-volume area (PVA), an index of myocardial work, are two metrics important to this study. SHE is defined as the difference between MAP and the energy equivalent pressure (EEP), which is the ratio of the integrated hemodynamic power curve to the integrated hemodynamic flow curve in the systemic arteries.31 SHE approaches zero as the pulsatile nature of the flow diminishes.
| (15) |
PVA is calculated from the summation of external work (EW) and potential energy (PE). EW is the area within a pressure-volume loop, as shown in Figure 2, and PE is the area contained by the isovolumetric relaxation curve and the ventricular passive and active elastance curves. PVA is calculated by a stepwise integration method.
In Vivo Data Collection
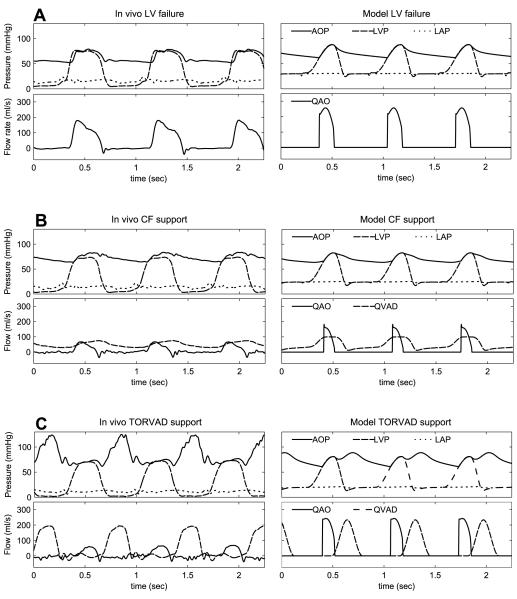
Six porcine experiments were conducted with left ventricular assistance from the TORVAD™ and Bio-Medicus BPX-80® continuous flow device. General anesthesia was used and animals were instrumented via a median sternotomy. The inflow was attached to the left ventricular apex and the outflow to the brachiocephalic artery. Y-connectors were used to allow each pump to be temporarily isolated from the circuit, providing a direct comparison between pulsatile and continuous assistance in each animal. To simulate heart failure, the left anterior descending artery was ligated and hemodynamic measurements were recorded after 15 minutes of stable left ventricular failure. The hemodynamic recordings from the in vivo experiments shown in Figure 5 were obtained from a single pig and the data in Table 2 and Table 3 are averaged data from the six experiments.
Figure 5.
Hemodynamics obtained from in-vivo experiments and the computational model during left ventricular failure (A), support with a continuous flow (CF) device (B), and counterpulse support with the TORVAD™ (C).
Table 2.
Hemodynamic metrics from the computational model and from the in vivo porcine experiment for the baseline healthy state and with TORVAD™ and continuous flow support.
| Computational Model |
In Vivo Porcine Experiment |
|||||
|---|---|---|---|---|---|---|
| Baseline | TORVAD™ | CF | Baseline | TORVAD™ | CF | |
| HR (bpm) | 75 | 75 | 75 | 90 | 89 | 88 |
| CO (L/m) | 5.75 | 6.51 | 6.06 | 4.49 | 5.87 | 5.42 |
| QAO (L/m) | 5.75 | 3.89 | 3.38 | 4.49 | 2.60 | 2.15 |
| QVAD (L/m) | 0 | 2.62 | 2.68 | 0 | 3.27 | 3.27 |
| MAP (mmHg) | 98.1 | 114.3 | 104.3 | 73.1 | 82.0 | 74.2 |
| SBP (mmHg) | 120.1 | 124.7 | 122.6 | 96.0 | 100.5 | 92.0 |
| DBP (mmHg) | 82.7 | 99.6 | 90.5 | 56.7 | 62.7 | 61.5 |
| PP (mmHg) | 37.4 | 25.1 | 32.1 | 39.3 | 37.8 | 30.5 |
| LAP (mmHg) | 5.9 | 2.0 | 4.4 | 18.4 | 11.6 | 13.2 |
| SHE (mmHg) | 8.6 | 3.7 | 6.9 | 14.3 | 7.4 | 5.9 |
| PVA (ml mmHg) | 10391 | 8404 | 9811 | 6945 | 5697 | 6254 |
CF; continuous flow support (HeartMate II at 8,400 rpm in the computational model); HR, heart rate; CO, cardiac output; QAO, averaged aortic flow; QVAD, averaged VAD flow; MAP, mean arterial pressure; SBP, systolic blood pressure; DBP, diastolic blood pressure; PP, pulse pressure; LAP, mean left atrial pressure; SHE, surplus hemodynamic energy; PVA, pressure volume area
Table 3.
Hemodynamic metrics from the computational model and from the in vivo porcine experiment for the baseline heart failure state and with TORVAD™ and continuous flow support.
| Computational Model |
In Vivo Porcine Experiment |
|||||
|---|---|---|---|---|---|---|
| Baseline | TORVAD™ | CF | Baseline | TORVAD™ | CF | |
| HR (bpm) | 90 | 90 | 90 | 86 | 91 | 88 |
| CO (L/m) | 2.83 | 5.38 | 4.29 | 3.54 | 5.58 | 5.12 |
| QAO (L/m) | 2.83 | 2.24 | 1.16 | 3.54 | 2.19 | 1.77 |
| QVAD (L/m) | 0 | 3.14 | 3.13 | 0 | 3.39 | 3.36 |
| MAP (mmHg) | 71.2 | 74.8 | 70.1 | 54.6 | 67.8 | 60.2 |
| SBP (mmHg) | 87.8 | 88.7 | 82.7 | 75.8 | 89.1 | 74.9 |
| DBP (mmHg) | 61.9 | 60.7 | 63.5 | 41.8 | 48.9 | 51.7 |
| PP (mmHg) | 26.0 | 28.0 | 19.2 | 34.0 | 40.2 | 23.2 |
| LAP (mmHg) | 30.0 | 19.8 | 24.2 | 18.9 | 11.5 | 13.9 |
| SHE (mmHg) | 7.4 | 4.4 | 3.3 | 13.5 | 7.6 | 3.8 |
| PVA (ml mmHg) | 13378 | 11541 | 12071 | 4926 | 4229 | 4560 |
CF; continuous flow support (HeartMate II at 7,300 rpm in the computational model); HR, heart rate; CO, cardiac output; QAO, averaged aortic flow; QVAD, averaged VAD flow; MAP, mean arterial pressure; SBP, systolic blood pressure; DBP, diastolic blood pressure; PP, pulse pressure; LAP, mean left atrial pressure; SHE, surplus hemodynamic energy; PVA, pressure volume area
Results
A simulation model was developed by compiling the previously described ordinary differential equation sets, and six unique scenarios were studied. The baseline healthy and failing states did not include ventricular assistance. The pulsatile flow scenarios simulated support from a VAD similar to the TORVAD™, and the continuous flow scenarios simulated support from a VAD similar to the HeartMate II. For all scenarios, the basic model of the cardiovascular system and beating heart were the same. Time dependent tracings of pressures in the left ventricle, left atria, and systemic arteries and blood flow trough the aortic valve and VAD (when present) are presented in Figure 5 for baseline heart failure and heart failure with either pulsatile or continuous support. Derived values for metrics such as cardiac output, average VAD flow, and SHE (for example) are presented in Table 2 for the healthy state and Table 3 for the failing state alongside the corresponding measured values from the in vivo porcine experiments. In Table 2 and Table 3 systolic (SBP) and diastolic blood pressure (DBP) are presented as the absolulte maximum and minimum pressures, respectively, during one cardiac cycle. This distinction is important because in select instances peak pressure occurs during diastolic relaxation of the heart due to the counter-pulse nature of the pulsatile pump. The pulse pressure (PP) is calculated by subtracting DBP from SBP.
Hemodynamics in the Healthy State
Values presented in Table 2 for the baseline healthy simulation agree well with typical healthy hemodynamics. The heart rate is 75 bpm, producing a cardiac output (CO) of 5.75 L/min. Mean arterial pressure (MAP) is 98.1 mmHg and PP is 37.4 mmHg. PVA is 10,391 mL mmHg, left atrial pressure (LAP) is 5.9 mmHg, and SHE is 8.6 mmHg. These values correspond to published averages of CO (5-6 L/min), left atrial pressure (2-10 mmHg), and MAP (90-100 mmHg)3.
With initiation of simulated left ventricular support from the valveless pulsatile flow VAD in the healthy state, CO increases to 6.51 L/min with 3.89 L/min of this coming from the native heart and 2.62 L/min coming from the VAD. Similarly, CO is 6.06 L/min upon initiation of the continuous flow pump with 3.38 L/min from the native heart and 2.68 L/min from the device (Table 2). Flow rates from both devices are matched to allow comparisons to be made regarding pulsatile versus continuous flow support independent of device output. PVA is lowered to 8,404 mL mmHg with support from the pulsatile flow versus 9,811 mL mmHg with continuous flow, driven mainly by the increase in cardiac output.
Hemodynamics in the Failing State
The computational model simulates congestive heart failure by decreasing passive and active elastance and increasing left ventricular volumes. In the failing state, heart rate increases to 90 bpm and CO decreases to 2.83 L/min. MAP falls to 71.2 mmHg, and PP falls to 26.0 mmHg. LAP in the failing state rises to 30 mmHg. Due to increased left ventricular volumes (Figure 2), PVA increases to 13,378 mL mmHg (Table 3). These values correspond to clinically published averages of CO (3 L/min), left atrial pressure (20-30 mmHg), and MAP (65-75 mmHg)3.
Ventricular flow support is simulated and flow rates from both devices are again matched to allow comparisons to be made regarding pulsatile versus continuous flow support independent of device output. CO increases to 5.38 L/min with pulsatile flow support, while CO with continuous flow support is 4.29 L/min. Pulsatile flow support induces a higher flow through the aortic valve of 2.24 L/min versus 1.16 L/min with continuous flow support (Table 3). Flow through the aortic valve is important because it maintains normal physiologic function of the heart and aortic valve. MAP increased with valveless pulsatile flow support to 74.8 mmHg compared with 70.1 mmHg with continuous flow support, and LAP decreased with valveless pulsatile flow support to 19.8 mmHg compared with 24.2 mmHg with continuous flow support. In addition, with pulsatile flow support systolic blood pressure (SBP) increases from 87.7 mmHg at baseline failure to 88.7 mmHg, but falls to 82.7 with continuous flow support. Figure 5B shows that during failure the continuous flow VAD generates flow throughout the cardiac cycle, assisting maximally during systole and greatly reducing native left-ventricular output. The valveless pulsatile flow VAD ejects only during diastole allowing aortic valve flow to remain high, as seen in Figure 5C.
Verification Using In Vivo Porcine Data
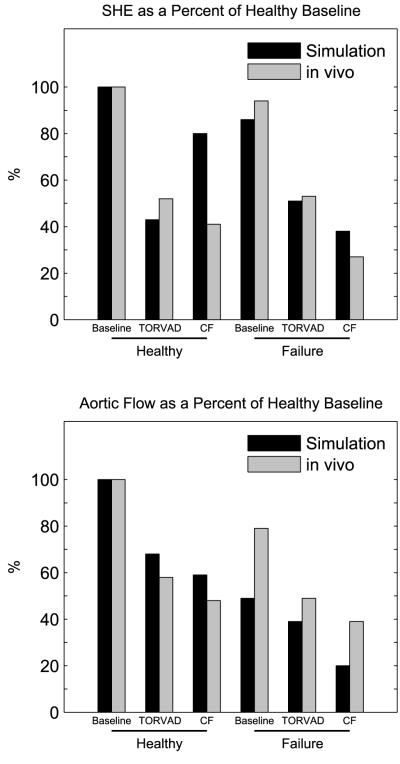
Comparisons are made between a computational model of the human cardiovascular system and a porcine experiment, therefore verification for the purposes of this study will be defined as agreement in relative increases or decreases of metrics and relative performance between baseline, TORVAD™ support, and continuous flow support. Data comparing SHE and aortic valve flow on a normalized scale are seen in Figure 6. For both metrics, data from the computational model and in vivo experiment were normalized on a percentage scale relative to their respective baselines. This allowed relative comparisons between the simulations and in vivo data showing that in healthy and failing states the outputs from the simulation are directional and scalable. According to data in Table 2 and Table 3, all metrics agree in the healthy state except SHE and PP and all relative performances of the three scenarios agree except SHE, PP and SBP. In the failing state, all metrics agree and all relative performances of the three scenarios agree except DBP.
Figure 6.
Percent differences from healthy baseline in surplus hemodynamic energy (SHE) and aortic valve flow for the computational model and in vivo porcine experiments. Data is presented for the healthy and failure state at baseline and with TORVAD™ and continuous flow support.
Discussion
Ventricular assist devices serve as a viable option for patients in end-stage heart failure as a bridge to transplantation, bridge to recovery or destination therapy. Clinical evidence demonstrates the value of mechanical cardiac assistance as compared with maximum medical therapy in multiple research trials.32,33 Currently 35% of heart transplant patients receive some form of mechanical support before their transplant.34 Successful outcomes using VAD technology largely depend on patient selection and device selection.35 First generation pulsatile sac pumps with mechanical or tissue values were prone to various durability and functional issues. Second and third generation devices are continuous flow, eliminating the need for valves and allowing the pumps to be smaller, but produce non-physiologic flow which cannot synchronize to the cardiac cycle. While both flow types improve patient quality of life and functional capacity, patient outcomes of continuous flow VADs are associated with decreased mortality and fewer device failures.36 However, despite their initial design issues, in many aspects pulsatile VADs are physiologically superior to continuous flow VADs.13,37 Due to this contradiction, continuous and pulsatile VADs deserve continued robust comparative studies to identify the specific hemodynamic advantages of each pump type.
An economical and verified method for performing studies on the human cardiovascular system and its response to mechanical assistance involves the use of computational models which allow simulation of assist devices in various patient conditions. Numerous studies published in the literature take advantage of computational models to investigate interactions between the human cardiovascular system and mechanical assistance. In a study performed by Cox et al.38 based on a one-fiber heart contraction computer model, left ventricular support was simulated using a HeartMate II VAD model in pulsatile and constant speed modes at the same mean pump speed. In pulsatile operation, coronary blood flow was greater since during ventricular contraction pump speed is decreased and during ventricular relaxation pump speed is increased. Also, left ventricular stroke work decreased during pulsatile support. In two different papers,1,39 Shi and colleagues show that with simulated pulsatile flow support, pulsatility and cardiac output similar to healthy conditions was achieved in a failing heart model. Also, Shi discusses the merits of in-series pulsatile VADs by demonstrating that they preserve native heart pulsatility and prevent stasis of blood near the aortic valve. In this study, we contribute to these efforts by presenting a model of the human cardiovascular system having either a healthy or failing heart. This model can simulate support by either a continuous flow VAD, similar to the HeartMate II, or a synchronous valveless pulsatile flow VAD, similar to the TORVAD™.
Study Limitations
To make definitive comparisons of the TORVAD™ to continuous flow VADs such as the HeartMate II using this computational model, further investigations with the continuous flow device operated at flow rates similar to those used clinically are currently being performed by the authors. The comparisons between the derived metrics from the computational model and the measured metrics from the in vivo porcine experiments do not merit further extrapolative conclusions since the cardiovascular physiology of the two systems are different.
Conclusions
In vivo data has been used to verify a computational model comparing synchronous valveless pulsatile and continuous flow assistance in a heart failure model. Using this model we demonstrated improved cardiac output, aortic valve flow, left ventricular unloading, and higher pulsatility for a failed heart supported by a pulsatile flow device similar to the TORVAD™ compared with a continuous flow device similar to the HeartMate II and at the same levels of VAD flow.
Footnotes
This is a PDF file of an unedited manuscript that has been accepted for publication. As a service to our customers we are providing this early version of the manuscript. The manuscript will undergo copyediting, typesetting, and review of the resulting proof before it is published in its final citable form. Please note that during the production process errors may be discovered which could affect the content, and all legal disclaimers that apply to the journal pertain.
References
- 1.Shi Y, Korakianitis T. Numerical simulation of cardiovascular dynamics with left heart failure and in-series pulsatile ventricular assist device. Artif Organs. 2006;30:929–48. doi: 10.1111/j.1525-1594.2006.00326.x. [DOI] [PubMed] [Google Scholar]
- 2.Suga H, Sagawa K. Instantaneous pressure-volume relationships and their ratio in the excised, supported canine left ventricle. Circ Res. 1974;35:117–26. doi: 10.1161/01.res.35.1.117. [DOI] [PubMed] [Google Scholar]
- 3.Gohean JR. M.S. Thesis, Mechanical Engineering. 2007. A Closed-Loop Multi-Scale Model of the Cardiovascular System for Evaluation of Ventricular Assist Devices. [Google Scholar]
- 4.Gohean JR, Pate TD, Longoria RG, Smalling RW, Kurusz M. Comparison of a Valveless Pulsatile Assist Device with Continuous Flow in a Computational Model of the Cardiovascular System; 57th Annual Conference of the American Society for Artificial Internal Organs; Washington, DC. 2011. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 5.Arndt A, Nusser P, Graichen K, Muller J, Lampe B. Physiological control of a rotary blood pump with selectable therapeutic options: control of pulsatility gradient. Artif Organs. 2008;32:761–71. doi: 10.1111/j.1525-1594.2008.00628.x. [DOI] [PubMed] [Google Scholar]
- 6.Vandenberghe S, Segers P, Meyns B, Verdonck PR. Effect of rotary blood pump failure on left ventricular energetics assessed by mathematical modeling. Artif Organs. 2002;26:1032–9. doi: 10.1046/j.1525-1594.2002.07105.x. [DOI] [PubMed] [Google Scholar]
- 7.Vandenberghe S, Segers P, Meyns B, Verdonck P. Unloading effect of a rotary blood pump assessed by mathematical modeling. Artif Organs. 2003;27:1094–101. doi: 10.1111/j.1525-1594.2003.07198.x. [DOI] [PubMed] [Google Scholar]
- 8.Korakianitis T, Shi Y. Numerical comparison of hemodynamics with atrium to aorta and ventricular apex to aorta VAD support. ASAIO J. 2007;53:537–48. doi: 10.1097/MAT.0b013e318142bfce. [DOI] [PubMed] [Google Scholar]
- 9.De Lazzari C, Darowski M, Ferrari G, Clemente F, Guaragno M. Computer simulation of haemodynamic parameters changes with left ventricle assist device and mechanical ventilation. Comput Biol Med. 2000;30:55–69. doi: 10.1016/s0010-4825(99)00026-8. [DOI] [PubMed] [Google Scholar]
- 10.Lim E, Dokos S, Cloherty SL, et al. Parameter-optimized model of cardiovascular-rotary blood pump interactions. IEEE Trans Biomed Eng. 2010;57:254–66. doi: 10.1109/TBME.2009.2031629. [DOI] [PubMed] [Google Scholar]
- 11.Vollkron M, Schima H, Huber L, Wieselthaler G. Interaction of the cardiovascular system with an implanted rotary assist device: simulation study with a refined computer model. Artif Organs. 2002;26:349–59. doi: 10.1046/j.1525-1594.2002.06870.x. [DOI] [PubMed] [Google Scholar]
- 12.Morley D, Litwak K, Ferber P, et al. Hemodynamic effects of partial ventricular support in chronic heart failure: results of simulation validated with in vivo data. J Thorac Cardiovasc Surg. 2007;133:21–8. doi: 10.1016/j.jtcvs.2006.07.037. [DOI] [PubMed] [Google Scholar]
- 13.Letsou GV, Pate TD, Gohean JR, et al. Improved left ventricular unloading and circulatory support with synchronized pulsatile left ventricular assistance compared with continuous-flow left ventricular assistance in an acute porcine left ventricular failure model. J Thorac Cardiovasc Surg. 2010;140:1181–8. doi: 10.1016/j.jtcvs.2010.03.043. [DOI] [PubMed] [Google Scholar]
- 14.Danielsen M, Ottesen JT. Describing the pumping heart as a pressure source. J Theor Biol. 2001;212:71–81. doi: 10.1006/jtbi.2001.2348. [DOI] [PubMed] [Google Scholar]
- 15.Ha R, Qian J, Wang D, Zwischenberger JB, Bidhani A, Clark JW., Jr. A closed-loop model of the ovine cardiovascular system. Conf Proc IEEE Eng Med Biol Soc. 2004;5:3781–4. doi: 10.1109/IEMBS.2004.1404060. [DOI] [PubMed] [Google Scholar]
- 16.Smith BW, Chase JG, Nokes RI, Shaw GM, David T. Velocity profile method for time varying resistance in minimal cardiovascular system models. Phys Med Biol. 2003;48:3375–87. doi: 10.1088/0031-9155/48/20/008. [DOI] [PubMed] [Google Scholar]
- 17.Zhong L, Ghista DN, Ng EY, Lim ST. Passive and active ventricular elastances of the left ventricle. Biomed Eng Online. 2005;4:10. doi: 10.1186/1475-925X-4-10. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 18.Zhong L, Ghista DN, Ng EY, Lim ST, Tan RS, Chua LP. Explaining left ventricular pressure dynamics in terms of LV passive and active elastances. Proc Inst Mech Eng H. 2006;220:647–55. doi: 10.1243/09544119JEIM123. [DOI] [PubMed] [Google Scholar]
- 19.Lu K, Clark JW, Jr., Ghorbel FH, Ware DL, Bidani A. A human cardiopulmonary system model applied to the analysis of the Valsalva maneuver. Am J Physiol Heart Circ Physiol. 2001;281:H2661–79. doi: 10.1152/ajpheart.2001.281.6.H2661. [DOI] [PubMed] [Google Scholar]
- 20.Ursino M. Interaction between carotid baroregulation and the pulsating heart: a mathematical model. Am J Physiol. 1998;275:H1733–47. doi: 10.1152/ajpheart.1998.275.5.H1733. [DOI] [PubMed] [Google Scholar]
- 21.Ursino M. A mathematical model of the carotid baroregulation in pulsating conditions. IEEE Trans Biomed Eng. 1999;46:382–92. doi: 10.1109/10.752935. [DOI] [PubMed] [Google Scholar]
- 22.Heldt T, Shim EB, Kamm RD, Mark RG. Computational modeling of cardiovascular response to orthostatic stress. J Appl Physiol. 2002;92:1239–54. doi: 10.1152/japplphysiol.00241.2001. [DOI] [PubMed] [Google Scholar]
- 23.Ottesen JT, Danielsen M. Modeling ventricular contraction with heart rate changes. J Theor Biol. 2003;222:337–46. doi: 10.1016/s0022-5193(03)00040-7. [DOI] [PubMed] [Google Scholar]
- 24.Korakianitis T, Shi Y. A concentrated parameter model for the human cardiovascular system including heart valve dynamics and atrioventricular interaction. Med Eng Phys. 2006;28:613–28. doi: 10.1016/j.medengphy.2005.10.004. [DOI] [PubMed] [Google Scholar]
- 25.Ferrari G, De Lazzari C, Mimmo R, Tosti G, Ambrosi D. A modular numerical model of the cardiovascular system for studying and training in the field of cardiovascular physiopathology. J Biomed Eng. 1992;14:91–107. doi: 10.1016/0141-5425(92)90014-c. [DOI] [PubMed] [Google Scholar]
- 26.Ferrari M, Kadipasaoglu KA, Croitoru M, et al. Evaluation of myocardial function in patients with end-stage heart failure during support with the Jarvik 2000 left ventricular assist device. J Heart Lung Transplant. 2005;24:226–8. doi: 10.1016/j.healun.2003.09.044. [DOI] [PubMed] [Google Scholar]
- 27.Thunberg CA, Gaitan BD, Arabia FA, Cole DJ, Grigore AM. Ventricular assist devices today and tomorrow. J Cardiothorac Vasc Anesth. 2010;24:656–80. doi: 10.1053/j.jvca.2009.11.011. [DOI] [PubMed] [Google Scholar]
- 28.Griffith BP, Kormos RL, Borovetz HS, et al. HeartMate II left ventricular assist system: from concept to first clinical use. Ann Thorac Surg. 2001;71:S116–20. doi: 10.1016/s0003-4975(00)02639-4. discussion S114-6. [DOI] [PubMed] [Google Scholar]
- 29.Frazier OH, Khalil HA, Benkowski RJ, Cohn WE. Optimization of axial-pump pressure sensitivity for a continuous-flow total artificial heart. J Heart Lung Transplant. 2010;29:687–91. doi: 10.1016/j.healun.2009.12.017. [DOI] [PubMed] [Google Scholar]
- 30.Slaughter MS, Pagani FD, Rogers JG, et al. Clinical management of continuous-flow left ventricular assist devices in advanced heart failure. J Heart Lung Transplant. 2010;29:S1–39. doi: 10.1016/j.healun.2010.01.011. [DOI] [PubMed] [Google Scholar]
- 31.Shepard RB, Simpson DC, Sharp JF. Energy equivalent pressure. Arch Surg. 1966;93:730–40. doi: 10.1001/archsurg.1966.01330050034005. [DOI] [PubMed] [Google Scholar]
- 32.Rose EA, Gelijns AC, Moskowitz AJ, et al. Long-term use of a left ventricular assist device for end-stage heart failure. N Engl J Med. 2001;345:1435–43. doi: 10.1056/NEJMoa012175. [DOI] [PubMed] [Google Scholar]
- 33.Rogers JG, Butler J, Lansman SL, et al. Chronic mechanical circulatory support for inotrope-dependent heart failure patients who are not transplant candidates: results of the INTrEPID Trial. J Am Coll Cardiol. 2007;50:741–7. doi: 10.1016/j.jacc.2007.03.063. [DOI] [PubMed] [Google Scholar]
- 34.Starling RC, Naka Y, Boyle AJ, et al. Results of the post-U.S. Food and Drug Administration-approval study with a continuous flow left ventricular assist device as a bridge to heart transplantation: a prospective study using the INTERMACS (Interagency Registry for Mechanically Assisted Circulatory Support) J Am Coll Cardiol. 2011;57:1890–8. doi: 10.1016/j.jacc.2010.10.062. [DOI] [PubMed] [Google Scholar]
- 35.Lietz K, Long JW, Kfoury AG, et al. Outcomes of left ventricular assist device implantation as destination therapy in the post-REMATCH era: implications for patient selection. Circulation. 2007;116:497–505. doi: 10.1161/CIRCULATIONAHA.107.691972. [DOI] [PubMed] [Google Scholar]
- 36.Slaughter MS, Rogers JG, Milano CA, et al. Advanced heart failure treated with continuous-flow left ventricular assist device. N Engl J Med. 2009;361:2241–51. doi: 10.1056/NEJMoa0909938. [DOI] [PubMed] [Google Scholar]
- 37.Bartoli CR, Giridharan GA, Litwak KN, et al. Hemodynamic responses to continuous versus pulsatile mechanical unloading of the failing left ventricle. ASAIO J. 2010;56:410–6. doi: 10.1097/MAT.0b013e3181e7bf3c. [DOI] [PubMed] [Google Scholar]
- 38.Cox LG, Loerakker S, Rutten MC, de Mol BA, van de Vosse FN. A mathematical model to evaluate control strategies for mechanical circulatory support. Artif Organs. 2009;33:593–603. doi: 10.1111/j.1525-1594.2009.00755.x. [DOI] [PubMed] [Google Scholar]
- 39.Shi Y, Korakianitis T, Bowles C. Numerical simulation of cardiovascular dynamics with different types of VAD assistance. J Biomech. 2007;40:2919–33. doi: 10.1016/j.jbiomech.2007.02.023. [DOI] [PubMed] [Google Scholar]