BOX SPLINE BASED 3D TOMOGRAPHIC RECONSTRUCTION OF DIFFUSION PROPAGATORS FROM MRI DATA

Abstract

This paper introduces a tomographic approach for reconstruction of diffusion propagators, P(r), in a box spline framework. Box splines are chosen as basis functions for high-order approximation of P(r) from the diffusion signal. Box splines are a generalization of B-splines to multivariate setting that are particularly useful in the context of tomographic reconstruction. The X-Ray or Radon transform of a (tensor-product B-spline or a non-separable) box spline is a box spline – the space of box splines is closed under the Radon transform.

We present synthetic and real multi-shell diffusion-weighted MR data experiments that demonstrate the increased accuracy of P(r) reconstruction as the order of basis functions is increased.

1. INTRODUCTION

Diffusion weighted MRI is sensitive to the in vivo Brownian motion of water molecules. Since this motion is constrained by the biological structure of the tissue, water molecules exhibit directional diffusion characteristics, which can be used to sense the connectivity pattern of the tissue. Studying such micro-structures has various clinical applications [1, 2].

One of the major goals of diffusion MRI is the reconstruction of the 3-D diffusion propagator P(r), characterizing the diffusion process of water molecules within a fibrous tissue. P(r) is the probability density function (PDF) that specifies the probability for a water molecule to displace by a given distance along a direction r. Clinical MR scanners cannot measure P(r) directly. Instead, they can measure the diffusion-based echo attenuation E(q), hereafter referred to as the diffusion signal. Under the narrow pulse assumption (i.e., the duration of the applied diffusion sensitizing gradients, δ, is much shorter than the time between the two gradient pulses Δ), the diffusion signal E(q) in q-space and the diffusion propagator P(r) in distance space are related through the Fourier transform [3] as:

$$P(\mathit{r})=\int E(\mathit{q})exp(-2\pi i\mathit{q}·\mathit{r})\text{d}\mathit{q}$$ (1)

where E(q) = S(q)/S₀, S₀ is the diffusion signal with zero diffusion gradient (q = 0), r is the displacement vector, q = γδG/2π is the reciprocal space vector, γ is the gyro-magnetic ratio and G is the gradient vector.

A number of techniques have been proposed to reconstruct the diffusion propagator from samples of the diffusion signal, E(q). Diffusion tensor imaging (DTI) [4] is a simple yet commonly used one. It assumes the diffusion propagator function can be represented with an oriented Gaussian probability density function (i.e., a second order tensor model). This model has only 7 coefficients and can be determined with 7 diffusion weighted images of different orientations. The drawback in this model is that it is difficult to capture complex geometries caused by crossing, kissing or splaying fibers that result in orientational heterogeneity in a voxel [5]. Thus, the high angular-resolution diffusion imaging (HARDI) method, which acquires the signal in an increased number of orientations, was introduced. In [5], the diffusion signal is assumed to have independent exponential decay along different orientations. Based on the same acquisitions, researchers proposed several techniques such as generalization of DTI using higher order tensors [6], modeling the diffusion signal using a mixture of Gaussian densities [5] or tensor distribution model [7], and the diffusion orientation transform (DOT) [8] that analytically evaluates the Fourier relation in spherical coordinates assuming the diffusion signal being a mixture of exponential decay functions. All these techniques fit certain models on the diffusion signal samples and estimate the diffusion propagator through analytical inverse Fourier transform of the model functions. They are resistant to noise but carry the bias of the model. q-Ball imaging (QBI) [9, 10] estimates the radial integral of the diffusion propagator through spherical Funk-Radon transform. It is model-free, but it only captures diffusion orientation distribution function (ODF) [11, 12] which is a compromised version of P(r).

On the other hand, diffusion space imaging (DSI) (i.e., q-space imaging (QSI)), starts from dense diffusion signal samples on 3-D Cartesian lattice and reconstructs the diffusion propagator on the reciprocal lattice through the fast Fourier transform. This reconstruction technique is supported by the Shannon sampling theorem, but the heavy burden of time-intensive sampling process limits its widespread application. To address this problem, computerized tomography principles were applied to reconstruct P(r) from diffusion signal samples distributed on radial lines [13]. The sampling efficiency can be further improved through introducing optimal sampling lattices [14] which can lead to lower acquisition time.

In this paper, we introduce a box spline based tomographic scheme for reconstruction of diffusion propagators. The key property of box splines that makes them particularly suitable for the tomographic reconstruction is that they are closed under X-Ray and Radon transforms [15]. In other words, a signal which is represented in box spline basis can be represented exactly (i.e., with no approximation or discretization of the forward model) in the sinogram space. Therefore, from the X-Ray or Radon data one can formulate the tomographic reconstruction process exactly. The box spline approach offers an exact inversion of X-Ray or Radon transform, similar to Filtered Back Projection algorithm; however, the box spline approach achieves the exact inversion process with finite amount of computation and data, in contrast to the FBP solution. From the approximation-theoretic point of view, the box spline approach can be considered as a generalization of the (square) pixel basis approach that allows for basis functions with higher approximation order (than the pixel basis). The increase in approximation order offered by the compactly supported box splines can lead to significant savings in the computational cost of reconstruction.

2. BOX SPLINES AND RADON TRANSFORM

A box spline is a smooth piecewise polynomial, compactly-supported, function (defined on ℝ², ℝ³ or generally in ℝ^d), that is associated with a set of vectors that are usually gathered in a matrix: Ξ = [ξ₁ … ξ_N] [16]. From the signal processing point of view, box splines are constructed by repeated convolution of elementary line-segment distributions along each vector in Ξ. Specifically, we have:

$$M_{\mathbf{\Xi }}(\mathit{x})=(M_{{\mathit{\xi }}_1}\ast \cdots \ast M_{{\mathit{\xi }}_N})(\mathit{x}),$$ (2)

where the elementary box splines, M_ξn, are Dirac-like line distributions supported over x = tξ_n with t ∈ [0, 1]. These elementary box splines are in direct geometric correspondence (via a rotation and a proper scaling) with the primary box spline

$$M_{{\overrightarrow{e}}_1}(\mathit{x})=\text{box}(x_1)\delta (x_2,\cdots ,x_d)$$

where δ(x₂,···, x_d) is the (d − 1)-dimensional Dirac distribution and

$$\text{box}(x)=\{\begin{array}{cc}1& 0\le x\le 1\\ 0& \text{otherwise}\end{array}.$$

Moreover, they integrate to 1 which is a property that is shared by all box splines (and also preserved through convolution).

Based on (2), one directly infers that the box splines are positive, compactly-supported functions. Their support is a zonotope, which is the Minkowski sum of N vectors in Ξ.

For instance, in a 3-D setting, a pixel basis (i.e., voxel basis) can be represented by a box spline whose direction matrix, Ξ = I₃ is the 3 × 3 identity matrix. More generally, an n^th-order tensor-product B-spline can be represented as a box spline whose direction matrix contains the directions in I₃, each of which is repeated by n-times.

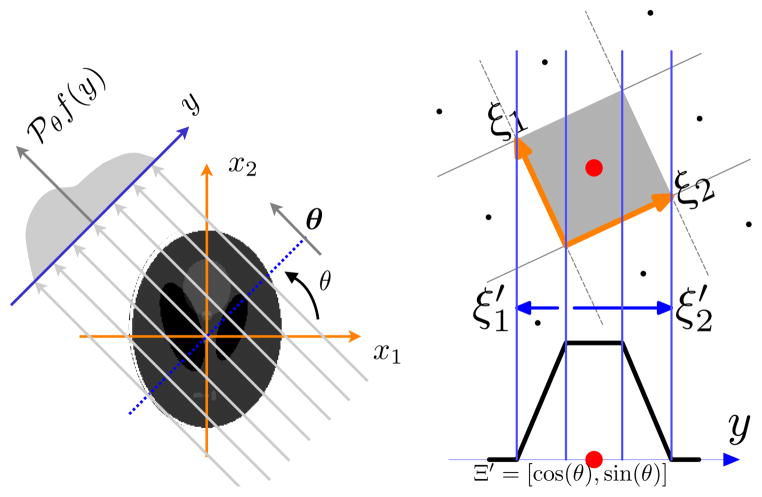
The key property of box splines that is used in our tomographic approach is that the Radon transform of a box spline along a particular direction specified by (θ, φ) is a univariate (1-D) box spline whose direction vectors are the geometric projection of the original box spline directions [15]. Let P_{(θ, φ)} denote the projection matrix that geometrically projects a point ℝ³ to the line specified by the direction (θ, φ). Then, the Radon transform of a trivariate box spline associated with a matrix Ξ is a 1-D box spline specified by Ξ′ = P_{(θ, φ)}Ξ (see Figure 1).

Fig. 1.

A 2-D illustration of Radon transform geometry. On the right: Radon transform of a pixel (tensor-product first-order B-spline) leads to a 1-D box spline whose directions are the geometric projection of the directions of the source box spline. This property directly generalizes to 3-D for voxel or higher-order basis.

This property suggests that for tomographic reconstruction applications, box splines are suitable basis functions for representing the source signal. This choice of representation of the source signal, leads to an exact forward-model that can be used to match the sinogram data. This property is exploited in the following section for our reconstruction algorithm.

3. ALGORITHM

In practice, diffusion propagator P(r) is reconstructed from samples of diffusion signal E(q). The q-space samples usually lie on radial lines through the origin of different orientations. According to the Fourier transform relationship in Equation 1 and the Fourier slice theorem, the 1-D inverse Fourier transform of the restriction of E(q) to a radial line equals to the Radon transform of P(r) along line in r space of the same orientation. Hence, the reconstruction problem is equivalent to inverting the Radon transform that translates into reconstructing the P(r) from its projections, (i.e., Radon data). This problem problem has widely been studied in the tomographic reconstruction literature. Our contribution is that we generalize the natural pixel basis, which is the first order tensor product B-spline, to basis functions of high approximation power using the framework of non-separable box splines. The more general class of box splines include higher-order tensor-product B-splines as a special case, but also include non-separable basis functions. This generalization significantly simplifies the inversion of Radon transform since the more general class of box splines happen to be closed under X-Ray and Radon transform.

We assume that P(r) can be represented in box spline basis:

$$P(\mathit{r})=c\ast M_{\mathbf{\Xi }}=\sum _{\mathit{k}\in {\mathbb{Z}}^3}{c}_{\mathit{k}}{M}_{\mathbf{\Xi }}(\mathit{r}-\mathit{k}).$$ (3)

When Ξ is the 3 × 3 identity matrix, the box spline corresponds to the cube voxel basis and we have a piecewise-constant approximation of P(r). However, a higher order tensor-product B-spline or generally a non-separable box spline can be used in the above approximation to achieve a higher-order approximation to the true P(r). The reconstruction problem is now the task of finding suitable coefficients c_k in Equation 3 such that P(r) agrees with the given data (i.e., samples of diffusion signal E(q)). According to the discussion in Section 2, the Radon transform of P(r) for a given direction (θ, φ) is:

$$\begin{array}{l}{P}_{(\theta ,\phi )}(r)=\sum _{\mathit{k}\in {\mathbb{Z}}^3}{c}_{\mathit{k}}{M}_{{\mathbf{\Xi }}^{\prime }}(r-{\mathit{P}}_{(\theta ,\phi )}\mathit{k})\\ {\mathbf{\Xi }}^{\prime }={\mathit{P}}_{(\theta ,\phi )}\mathbf{\Xi }\end{array}$$ (4)

where P_{(θ, φ)} is the 3-D to 1-D projection matrix onto the direction (θ, φ). Note that the Cartesian grid shifts k ∈ ℤ³, are also transformed by P_{(θ, φ)}. In other words, the Radon-transform data can be represented by P_{(θ, φ)} k shifts of the 1-D box spline which is associated with the matrix Ξ′ = P_{(θ, φ)}Ξ.

Denoting the samples of real projected data as d_{(θ, φ)}(r) and enforce d_{(θ, φ)} (r) = P_{(θ, φ)} (r) at all the sample points, we can build a linear equation set expressed as Ac = d where c is the vector composed of coefficients c_k in Equation 4, d is the vector of sampled data and each row of A is the evaluations of M_{P(θ, φ)} Ξ (r) at each sample position. In our application, the number of samples is usually smaller than the number of shifted box splines, so the linear system is under-determined. In order to get reasonable solution of coefficients, we introduce a smoothness regularization and search for the least square solution. Hence, we solve the following optimization problem:

$$\underset{\mathit{c}}{min}{\left|\right|\mathit{Ac}-\mathit{d}\left|\right|}^2+\lambda {\left|\right|\mathit{Lc}\left|\right|}^2$$ (5)

where L is the matrix of 3-D discrete Laplacian operator on c, λ is the weights for the smoothness regularization term ||Lc||².

4. EXPERIMENTS

We first evaluated our algorithm using synthetic data. We generated samples from a mixture of two Gaussian functions in 3-D q-space simulating the diffusion signal of two- fiber crossings. Crossing angles of 90° and 60° as shown in Figure 2 were tested. The data samples are uniformly distributed on radial lines specified by spherical coordinates (r, θ, φ) with 0 ≤ r ≤ 35. We picked 19 points on each radial line and 81 directions that correspond to vertices of a subdivided icosahedron approximating a unit hemisphere. The basis function of choice were tensor-product B-splines shifted on a 25×25×25 Cartesian lattice.

Fig. 2.

The desired isosurface of P(r): (a) of 90° crossing (b) of 60° crossing

Figure 3 show the isosurfaces of the reconstructed P(r) with different B-spline basis orders. We observe that the reconstruction becomes smoother and more accurate as the order of the basis function increases. Increasing the approximation order above the third order leads to less significant improvement as the approximation error becomes very small for this particular dataset. Numerical comparisons with different noise level δ_n are shown in Table 1. The mean square error (MSE) normalized by the energy of the desired signal was used as the measurement. The numerical results also support the expected advantages of higher order basis functions.

Fig. 3.

Reconstruction results for the synthetic data. First row, 90° crossing. Second row, 60° crossing. (a) first order box spline, (b) second order box spline, (c) third order box spline, (d) fourth order box spline.

Table 1.

MSE in percentage of the reconstructions for the synthetic data. α is the crossing angle. δ_n is the noise level. n is the order of the box spline.

α	δn	n = 1	n = 2	n = 3	n = 4
90°	0	16.03	7.02	3.34	2.80
	.04	19.16 ± .79	10.17 ± .25	5.25 ± .15	4.53 ± .14
	.08	27.87 ± 1.31	19.88 ± .62	11.34 ± .46	10.38 ± .31
60°	0	11.67	7.42	3.57	2.95
	.04	15.05 ± .54	10.45 ± .26	5.37 ± .16	4.66 ± .14
	.08	22.97 ± .85	19.99 ± .80	11.38 ± .33	10.56 ± .39

We also tested our algorithm on real multi-shell data consisting of mid-sagittal mouse brain scans acquired at different b values. 16 orientations and 5 different b values, including b = 0, were used. All magnetic resonance imaging was performed on a 600MHz (14.1 Tesla) Bruker imaging spectrometer, using a conventional diffusion weighted spin echo pulse sequence. The dataset was acquired with: slice thickness = 0.35mm, 1.8 × 0.9cm² field-of-view, 256 × 128 data matrix, and 70.3mm in-plane resolution, Δ = 12msec, δ = 1msec, and b-values of 187, 750, 1687, and 3000 s/mm². The nonuniform spacing between b-values was chosen to provide roughly equal spacing between q-values (||q|| = 20.2, 40.3, 60.5, and 80.7 mm⁻¹).

Figure 4 shows the reconstructed P(r) for a small region of the real data set with different box spline orders. We can observe the smoothness improvement going from the first order one to the third order. For the first order box spline basis (i.e., voxel basis), the reconstructed P(r) is discontinuous; hence, the P(r) values (evaluated on the sphere for visualization) appear spiky as shown in Figure 4 Order 1.

Fig. 4.

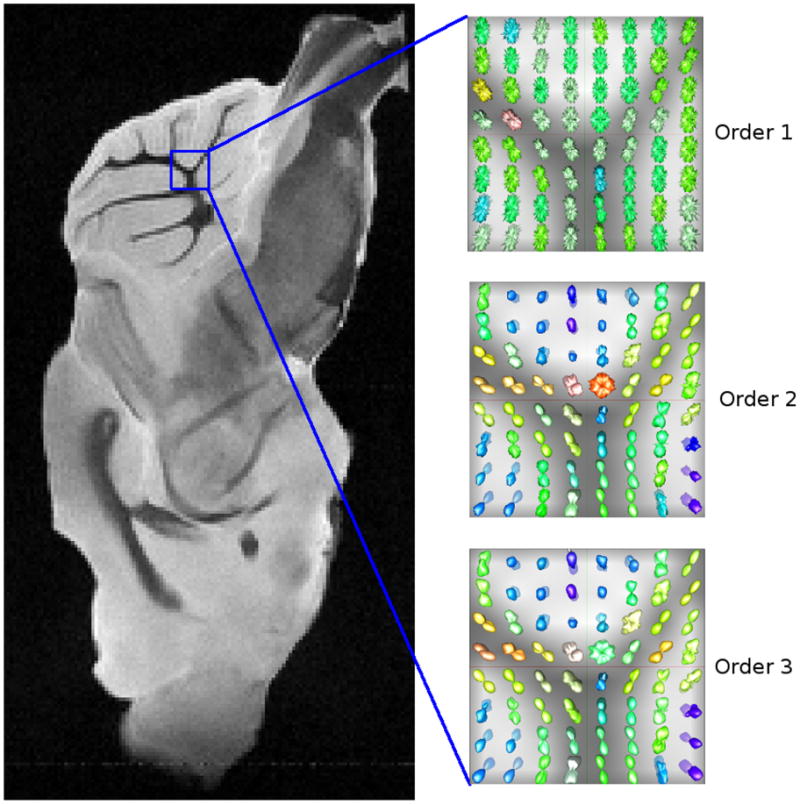
Reconstruction results for a region of the multi-shell mouse brain data with different box spline basis orders.

5. CONCLUSIONS

We presented a box spline framework for tomographic reconstruction of diffusion propagators, P(r), from diffusion-based echo attenuation signal, E(q). The simple voxel (cube) basis achieves a first order approximation in the context of tomgoraphic reconstruction. Our framework allows one to employ higher-order basis functions that significantly increase the accuracy of reconstruction. The theoretical expectation of increased accuracy was validated by synthetic and multi-shell diffusion-weighted MR data experiments.