A SIMULTANEOUS CONFIDENCE BAND FOR SPARSE LONGITUDINAL REGRESSION

Abstract

Functional data analysis has received considerable recent attention and a number of successful applications have been reported. In this paper, asymptotically simultaneous confidence bands are obtained for the mean function of the functional regression model, using piecewise constant spline estimation. Simulation experiments corroborate the asymptotic theory. The confidence band procedure is illustrated by analyzing CD4 cell counts of HIV infected patients.

1. Introduction

Functional data analysis (FDA) has in recent years become a focal area in statistics research, and much has been published in this area. An incomplete list includes Cardot, Ferraty, and Sarda (2003), Cardot and Sarda (2005), Ferraty and Vieu (2006), Hall and Heckman (2002), Hall, Müller, and Wang (2006), Izem and Marron (2007), James, Hastie, and Sugar (2000), James (2002), James and Silverman (2005), James and Sugar (2003), Li and Hsing (2007), Li and Hsing (2009), Morris and Carroll (2006), Müller and Stadtmüller (2005), Müller, Stadtmüller, and Yao (2006), Müller and Yao (2008), Ramsay and Silverman (2005), Wang, Carroll, and Lin (2005), Yao and Lee (2006), Yao, Müller, and Wang (2005a), Yao, Müller, and Wang (2005b), Yao (2007), Zhang and Chen (2007), Zhao, Marron, and Wells (2004), and Zhou, Huang, and Carroll (2008). According to Ferraty and Vieu (2006), a functional data set consists of iid realizations {ξ_i (x), x ∈ χ}, 1 ≤ i ≤ n, of a smooth stochastic process (random curve) {ξ (x), x ∈ χ} over an entire interval χ. A more data oriented alternative in Ramsay and Silverman (2005) emphasizes smooth functional features inherent in discretely observed longitudinal data, so that the recording of each random curve ξ_i(x) is over a finite number of points in χ, and contaminated with noise. This second view is taken in this paper.

A typical functional data set therefore has the form {X_ij, Y_ij}, 1 ≤ i ≤ n, 1 ≤ j ≤ N_i, in which N_i observations are taken for the i^th subject, with X_ij and Y_ij the j^th predictor and response variables, respectively, for the i^th subject. Generally, the predictor X_ij takes values in a compact interval χ = [a, b]. For the i^th subject, its sample path {X_ij, Y_ij} is the noisy realization of a continuous time stochastic process ξ_i(x) in the sense that

$$Y_{\mathit{ij}}={\xi }_i(X_{\mathit{ij}})+\sigma (X_{\mathit{ij}}){\epsilon }_{\mathit{ij}},$$ (1.1)

with errors ε_ij satisfying E (ε_ij) = 0, $E({\epsilon }_{\mathit{ij}}^2)=1$, and {ξ_i(x), x ∈ χ} are iid copies of a process {ξ(x), x ∈ χ} which is L², i.e., E ∫_χ ξ²(x)dx < +∞.

For the standard process {ξ(x), x ∈ χ}, one defines the mean function m(x) = E{ξ(x)} and the covariance function G(x, x′) = cov {ξ(x), ξ(x′)}. Let sequences ${\left\{{\lambda }_k\right\}}_{k=1}^{\infty },{\{{\psi }_k(x)\}}_{k=1}^{\infty }$ be the eigenvalues and eigenfunctions of G(x, x′), respectively, in which λ₁ ≥ λ₂ ≥ ⋯ ≥ 0, ${\sum }_{k=1}^{\infty }{\lambda }_k<\infty ,{\left\{{\psi }_k\right\}}_{k=1}^{\infty }$ form an orthonormal basis of L² (χ) and $G(x,x^{\prime })={\sum }_{k=1}^{\infty }{\lambda }_k{\psi }_k(x){\psi }_k(x^{\prime })$, which implies that ∫ G(x, x′) ψ_k (x′) dx′ = λ_kψ_k(x).

The process {ξ_i(x), x ∈ χ} allows the Karhunen-Loève L² representation

$${\xi }_i(x)=m(x)+{\sum }_{k=1}^{\infty }{\xi }_{\mathit{ik}}{\varphi }_k(x),$$

where the random coefficients ξ_ik are uncorrelated with mean 0 and variances 1, and the functions ${\varphi }_k=\sqrt{{\lambda }_k}{\psi }_k$. In what follows, we assume that λ_k = 0, for k > κ, where κ is a positive integer, thus $G(x,x^{\prime })={\sum }_{k=1}^{\kappa }{\varphi }_k(x){\varphi }_k(x^{\prime })$ and the data generating process is now written as

$$Y_{\mathit{ij}}=m(X_{\mathit{ij}})+{\sum }_{k=1}^{\kappa }{\xi }_{\mathit{ik}}{\varphi }_k(X_{\mathit{ij}})+\sigma (X_{\mathit{ij}}){\epsilon }_{\mathit{ij}}.$$ (1.2)

The sequences ${\left\{{\lambda }_k\right\}}_{k=1}^{\kappa },{\{{\varphi }_k(x)\}}_{k=1}^{\kappa }$ and the random coefficients ξ_ik exist mathematically, but are unknown and unobservable.

Two distinct types of functional data have been studied. Li and Hsing (2007), and Li and Hsing (2009) concern dense functional data, which in the context of model (1.1) means min_1≤i≤n N_i → ∞ as n → ∞. On the other hand, Yao, Müller, and Wang (2005a), Yao, Müller, and Wang (2005b), and Yao (2007) studied sparse longitudinal data for which N_i’s are i.i.d. copies of an integer-valued positive random variable. Pointwise asymptotic distributions were obtained in Yao (2007) for local polynomial estimators of m(x) based on sparse functional data, but without uniform confidence bands. Nonparametric simultaneous confidence bands are a powerful tool of global inference for functions, see Claeskens and Van Keilegom (2003), Fan and Zhang (2000), Hall and Titterington (1988), Härdle (1989), Härdle and Marron (1991), Huang, Wang, Yang, and Kravchenko (2008), Ma and Yang (2010), Song and Yang (2009), Wang and Yang (2009), Wu and Zhao (2007), Zhao and Wu (2008), and Zhou, Shen, and Wolfe (1998) for its theory and applications. The fact that a simultaneous confidence band has not been established for functional data analysis is certainly not due to lack of interesting applications, but to the greater technical difficulty in formulating such bands for functional data and establishing their theoretical properties. Specifically, the strong approximation results used to establish the asymptotic confidence level in nearly all published works on confidence bands, commonly known as “Hungarian embedding”, are unavailable for sparse functional data.

In this paper, we present simultaneous confidence bands for m(x) in sparse functional data via a piecewise-constant spline smoothing approach. While there exist a number of smoothing methods for estimating m(x) and G(x, x′) such as kernels (Yao, Müller and, Wang (2005a); Yao, Müller, and Wang (2005b); Yao (2007)), penalized splines (Cardot, Ferraty, and Sarda (2003); Cardot and Sarda (2005); Yao and Lee (2006)), wavelets Morris and Carroll (2006), and parametric splines James (2002), we choose B splines (Zhou, Huang, and Carroll (2008)) for simple implementation, fast computation and explicit expression, see Huang and Yang (2004), Wang and Yang (2007), and Xue and Yang (2006) for discussion of the relative merits of various smoothing methods.

We organize our paper as follows. In Section 2 we state our main results on confidence bands constructed from piecewise constant splines. In Section 3 we provide further insights into the error structure of spline estimators. Section 4 describes the actual steps to implement the confidence bands. Section 5 reports findings of a simulation study. An empirical example in Section 6 illustrates how to use the proposed confidence band for inference. Proofs of technical lemmas are in the Appendix.

2. Main results

For convenience, we denote the supremum norm of a function r on [a, b] by ∥r∥_∞ = sup_x∈[a,b] |r(x)|, and the modulus of continuity of a continuous function r on [a, b] by ω (r, δ) = max_{x,x′∈[a,b],|x−x′|≤δ} |r(x) − r(x′)|. Denote by ∥g∥₂ the theoretical L² norm of a function g on [a, b], ${\parallel g\parallel }_2^2=E\{g^2(X)\}={\mathit{\int }}_a^b{g}^2(x)f(x)\mathit{dx}$, where f(x) is the density function of X, and the empirical L² norm as ${\parallel g\parallel }_{2,N_{\mathrm{T}}}^2=N_{\mathrm{T}}^{-1}{\sum }_{i=1}^n{\sum }_{j=1}^{N_i}{g}^2(X_{\mathit{ij}})$, where we denote the total sample size by $N_{\mathrm{T}}={\sum }_{i=1}^n{N}_i$. Without loss of generality, we take the range of X, χ = [a, b], to be [0, 1]. For any β ∈ (0, 1], we denote the collection of order β Hõlder continuous function on [0, 1] by

$$C^{0,\beta }[0,1]=\left\{\varphi :{\parallel \varphi \parallel }_{0,\beta }=\underset{x\ne x^{\prime },x,x^{\prime }\in [0,1]}{\sup }\frac{|\varphi (x)-\varphi (x^{\prime })|}{{|x-x^{\prime }|}^{\beta }}<+\infty \right\},$$

in which ∥ϕ∥_0,β is the C^0,β-seminorm of ϕ. Let C [0, 1] be the collection of continuous function on [0, 1]. Clearly, C^0,β [0, 1] ⊂ C [0, 1] and, if ϕ ∈ C^0,β [0, 1], then ω (ϕ, δ) ≤ ∥ϕ∥_0,β δ^β.

To introduce the spline functions, divide the finite interval [0, 1] into (N_s+1) equal subintervals χ_J = [t_J, t_J+1), J = 0, …., N_s − 1, χ_Ns = [t_Ns, 1]. A sequence of equally-spaced points ${\left\{t_J\right\}}_{J=1}^{N_{\mathrm{s}}}$, called interior knots, are given as

$$t_0=0<t_1<\cdots <t_{N_{\mathrm{s}}}<1=t_{N_{\mathrm{s}}+1},t_J={\mathit{Jh}}_{\mathrm{s}},0\le J\le N_{\mathrm{s}}+1,h_{\mathrm{s}}=1/(N_{\mathrm{s}}+1),$$

in which h_s is the distance between neighboring knots. We denote by G⁽⁻¹⁾ = G⁽⁻¹⁾ [0, 1] the space of functions that are constant on each χ_J. For any x ∈ [0, 1], define its location index as J(x) = J_n(x) = min {[x/h_s], N_s} so that t_Jn(x) ≤ x < t_Jn(x)+1, ∀x ∈ [0, 1]. We propose to estimate the mean function m(x) by

$$\widehat{m}(x)=\underset{g\in G^{(-1)}}{\mathrm{argmin}}{\sum }_{i=1}^n{\sum }_{j=1}^{N_i}{\{Y_{\mathit{ij}}-g(X_{\mathit{ij}})\}}^2.$$ (2.1)

The technical assumptions we need are as follows

• (A1)The regression function m(x) ∈ C^0,1 [0, 1].
• (A2)The functions f(x), σ(x), and ϕ_k(x) ∈ C^0,β [0, 1] for some β ∈ (2/3, 1] with f(x) ∈ [c_f, C_f], σ(x) ∈ [c_σ, C_σ], x ∈ [0, 1], for constants 0 < c_f ≤ C_f < ∞, 0 < c_σ ≤ C_σ < ∞.
• (A3)The set of random variables ${(N_i)}_{i=1}^n$ is a subset of ${(N_i)}_{i=1}^{\infty }$ consisting of independent variables N_i, the numbers of observations made for the i-th subject, i = 1, 2, …, with N_i ~ N, where N > 0 is a positive integer-valued random variable with $E\left\{N^{2r}\right\}\le r!c_N^r$, r = 2, 3, … for some constant c_N > 0. The set of random variables ${(X_{\mathit{ij}},Y_{\mathit{ij}},{\epsilon }_{\mathit{ij}})}_{i=1,j=1}^{n,N_i}$ is a subset of ${(X_{\mathit{ij}},Y_{\mathit{ij}},{\epsilon }_{\mathit{ij}})}_{i=1,j=1}^{\infty ,\infty }$ in which ${(X_{\mathit{ij}},{\epsilon }_{\mathit{ij}})}_{i=1,j=1}^{\infty ,\infty }$ are iid. The number κ of nonzero eigenvalues is finite and the random coefficients ξ_ik, k = 1, …, κ, i = 1, …, ∞ are iid N (0, 1). The variables ${(N_i)}_{i=1}^{\infty },{({\xi }_{\mathit{ik}})}_{i=1,k=1}^{\infty ,\kappa },{(X_{\mathit{ij}})}_{i=1,j=1}^{\infty ,\infty },{({\epsilon }_{\mathit{ij}})}_{i=1,j=1}^{\infty ,\infty }$ are independent.
• (A4)As n → ∞, the number of interior knots N_s = o (n^ϑ) for some ϑ ∈ (1/3, 2β − 1) while $N_{\mathrm{s}}^{-1}=o\left\{n^{-1/3}{(\log n)}^{-1/3}\right\}$. The subinterval length $h_{\mathrm{s}}~N_{\mathrm{s}}^{-1}$.
• (A5)There exists r > 2/ {β − (1 + ϑ) /2} such that E |ε₁₁|^r < ∞.

Assumptions (A1), (A2), (A4) and (A5) are similar to (A1)–(A4) in Wang and Yang (2009), with (A1) weaker than its counterpart. Assumption (A3) is the same as (A1.1), (A1.2), and (A5) in Yao, Müller, and Wang (2005b), without requiring joint normality of the measurement errors ε_ij.

We now introduce the B-spline basis of G⁽⁻¹⁾, the space of piecewise constant splines, as ${\{b_J(x)\}}_{J=0}^{N_{\mathrm{s}}}$, which are simply indicator functions of intervals χ_J, b_J(x) = I_χJ (x), J = 0, 1, …, N_s. Define

$$\begin{array}{c}{c}_{J,n}={\parallel b_J\parallel }_2^2={\mathit{\int }}_0^1{b}_J(x)f(x)\mathit{dx},J=0,\dots ,N_{\mathrm{s}},\\ {\sigma }_Y^2(x)=\mathrm{var}(Y\mid X=x)=G(x,x)+{\sigma }^2(x),\forall x\in [0,1],\end{array}$$ (2.2)

$${\sigma }_n^2(x)=c_{J(x),n}^{-2}{\{\mathit{nE}(N_1)\}}^{-1}\left\{\frac{E\{N_1(N_1-1)\}}{{\mathit{EN}}_1}\sum _{k=1}^{\kappa }{\left({\mathit{\int }}_{{\chi }_{J(x)}}{\varphi }_k(u)f(u)\mathit{du}\right)}^2+{\mathit{\int }}_{{\chi }_{J(x)}}{\sigma }_Y^2(u)f(u)\mathit{du}\right\}.$$ (2.3)

In addition, define $Q_{N_{\mathrm{s}}+1}(\alpha )=b_{N_{\mathrm{s}}+1}-a_{N_{\mathrm{s}}+1}^{-1}\log \{-(1/2)\log (1-\alpha )\}$,

$$a_{N_{\mathrm{s}}+1}={\{2\log (N_{\mathrm{s}}+1)\}}^{1/2},b_{N_{\mathrm{s}}+1}=a_{N_{\mathrm{s}}+1}-\frac{\log (2\pi a_{N_{\mathrm{s}}+1}^2)}{2a_{N_{\mathrm{s}}+1}},$$ (2.4)

for any α ∈ (0, 1). We now state our main results.

Theorem 1

Under Assumptions (A1)-(A5), for any α ∈ (0, 1),

$$\begin{array}{c}\underset{n\to \infty }{\lim }P\left\{{\sup }_{x\in [0,1]}|\widehat{m}(x)-m(x)|/{\sigma }_n(x)\le Q_{N_{\mathrm{s}}+1}(\alpha )\right\}=1-\alpha ,\\ \underset{n\to \infty }{\lim }P\left\{|\widehat{m}(x)-m(x)|/{\sigma }_n(x)\le Z_{1-\alpha /2}\right\}=1-\alpha ,\forall x\in [0,1],\end{array}$$

where σ_n(x) and Q_Ns+1 (α) are given in (2.3) and (2.4), respectively, while Z_1−α/2 is the 100 (1 − α/2)^th percentile of the standard normal distribution.

The definition of σ_n(x) in (2.3) does not allow for practical use. The next proposition provides two data-driven alternatives

Proposition 1

Under Assumptions (A2), (A3), and (A5), as n → ∞,

$$\underset{x\in [0,1]}{\sup }\left\{|{\sigma }_n^{-1}(x){\sigma }_{n,\mathrm{IID}}(x)-1|+|{\sigma }_n^{-1}(x){\sigma }_{n,\mathrm{LONG}}(x)-1|\right\}=O\left(h_{\mathrm{s}}^{\beta }\right),$$

in which for x ∈ [0, 1], σ_n,IID (x) ≡ σ_Y (x) {f(x)h_snE(N₁)}^−1/2 and

$${\sigma }_{n,\mathrm{LONG}}(x)\equiv {\sigma }_{n,\mathrm{IID}}(x){\left\{1+\frac{E\{N_1(N_1-1)\}}{{\mathit{EN}}_1}{h}_{\mathrm{s}}\frac{G(x,x)f(x)}{{\sigma }_Y^2(x)}\right\}}^{1/2}.$$

Using σ_n,IID(x) instead of σ_n(x) means to treat the (X_ij, Y_ij) as iid data rather than as sparse longitudinal data, while using σ_n,LONG(x) means to correctly account for the longitudinal correlation structure. The difference of the two approaches, although asymptotically negligible uniformly for x ∈ [0, 1] according to Proposition 1, is significant in finite samples, as shown in the simulation results of Section 5. For similar phenomenon with kernel smoothing, see Wang, Carroll, and Lin (2005).

Corollary 1

Under Assumptions (A1)-(A5), for any α ∈ (0, 1), as n → ∞, an asymptotic 100 (1 − α) % simultaneous confidence band for m(x), x ∈ [0, 1] is

$$\widehat{m}(x)\pm {\sigma }_n(x)Q_{N_{\mathrm{s}}+1}(\alpha ),$$

while an asymptotic 100 (1 − α) % pointwise confidence interval for m(x), x ∈ [0, 1], is m̂(x) ± σ_n(x)Z_1−α/2.

3. Decomposition

In this section, we decompose the estimation error m̂(x) − m(x) by the representation of Y_ij as the sum of m (X_ij), ${\sum }_{k=1}^{\kappa }{\xi }_{\mathit{ik}}{\varphi }_k(X_{\mathit{ij}})$, and σ (X_ij) ε_ij.

We introduce the rescaled B-spline basis ${\{B_J(x)\}}_{J=0}^{N_{\mathrm{s}}}$ for G⁽⁻¹⁾, which is $B_J(x)\equiv b_J(x){\parallel b_J\parallel }_2^{-1}$, J = 0, …, N_s. Therefore,

$$B_J(x)\equiv b_J(x){\left\{c_{J,n}\right\}}^{-1/2},J=0,\dots ,N_{\mathrm{s}}.$$ (3.1)

It is easily verified that ${\parallel B_J\parallel }_2^2=1$, J = 0, 1, …, N_s, 〈B_J, B_J′〉 ≡ 0, J ≠ J′.

The definition of m̂(x) in (2.1) means that

$$\widehat{m}(x)\equiv {\sum }_{J=0}^{N_{\mathrm{s}}}{\widehat{\lambda }}_J^{\prime }{b}_J(x),$$ (3.2)

with coefficients ${\left\{{\widehat{\lambda }}_0^{\prime },\dots ,{\widehat{\lambda }}_{N_{\mathrm{s}}}^{\prime }\right\}}^{\mathrm{T}}$ as solutions of the least squares problem

$${\left\{{\widehat{\lambda }}_0^{\prime },\dots ,{\widehat{\lambda }}_{N_{\mathrm{s}}}^{\prime }\right\}}^{\mathrm{T}}=\underset{\{{\lambda }_0,\dots ,{\lambda }_{N_{\mathrm{s}}}\}\in R^{N_{\mathrm{s}}+1}}{\mathrm{argmin}}{\sum }_{i=1}^n{\sum }_{j=1}^{N_i}{\left\{Y_{\mathit{ij}}-{\sum }_{J=0}^{N_{\mathrm{s}}}{\lambda }_J{b}_J(X_{\mathit{ij}})\right\}}^2.$$

Simple linear algebra shows that $\widehat{m}(x)\equiv {\sum }_{J=0}^{N_{\mathrm{s}}}{\widehat{\lambda }}_J{B}_J(x)$, where the coefficients {λ̂₀, …, λ̂_Ns}^T are solutions of the least squares problem

$${\left\{{\widehat{\lambda }}_0^{\prime },\dots ,{\widehat{\lambda }}_{N_{\mathrm{s}}}^{\prime }\right\}}^{\mathrm{T}}=\underset{\{{\lambda }_0,\dots ,{\lambda }_{N_{\mathrm{s}}}\}\in R^{N_{\mathrm{s}}+1}}{\mathrm{argmin}}{\sum }_{i=1}^n{\sum }_{j=1}^{N_i}{\left\{Y_{\mathit{ij}}-{\sum }_{J=0}^{N_{\mathrm{s}}}{\lambda }_J{B}_J(X_{\mathit{ij}})\right\}}^2.$$ (3.3)

Projecting the relationship in model (1.2) onto the linear subspace of $R^{N_{\mathrm{T}}}$ spanned by {B_J (X_ij)}_{1≤j≤Ni,1≤i≤n,0≤J≤Ns}, we obtain the following crucial decomposition in the space G⁽⁻¹⁾ of spline functions:

$$\widehat{m}(x)=\stackrel{\sim }{m}(x)+\stackrel{\sim }{e}(x)=\stackrel{\sim }{m}(x)+\stackrel{\sim }{\epsilon }(x)+{\sum }_{k=1}^{\kappa }{\stackrel{\sim }{\xi }}_k(x),$$ (3.4)

$$\stackrel{\sim }{m}(x)={\sum }_{J=0}^{N_{\mathrm{s}}}{\stackrel{\sim }{\lambda }}_J{B}_J(x),\stackrel{\sim }{\epsilon }(x)={\sum }_{J=0}^{N_{\mathrm{s}}}{\stackrel{\sim }{a}}_J{B}_J(x),{\stackrel{\sim }{\xi }}_k(x)={\sum }_{J=0}^{N_{\mathrm{s}}}{\stackrel{\sim }{\tau }}_{k,J}{B}_J(x).$$ (3.5)

The vectors {λ̃₀, …, λ̃_Ns}^T, {ã₀, …, ã_Ns}^T, and {τ̃_k,0, …, τ̃_k,Ns}^T are solutions to (3.3) with Y_ij replaced by m(X_ij), σ (X_ij) ε_ij, and ξ_ikϕ_k (X_ij), respectively. We cite next an important result concerning the function m̃(x). The first part is from de Boor (2001), p. 149, and the second is from Theorem 5.1 of Huang (2003).

Theorem 2

There is an absolute constant C_g > 0 such that for every ϕ ∈ C [0, 1], there exists a function g ∈ G⁽⁻¹⁾ [0, 1] that satisfies ∥g − ϕ∥_∞ ≤ C_gω (ϕ, h_s). In particular, if ϕ ∈ C^0,β [0, 1] for some β ∈ (0, 1], then ${\parallel g-\varphi \parallel }_{\infty }\le C_g{\parallel \varphi \parallel }_{0,\beta }{h}_{\mathrm{s}}^{\beta }$. Under Assumptions (A1) and (A4), with probability approaching 1, the function m̃(x) defined in (3.5) satisfies ∥m̃(x) − m(x)∥_∞ = O (h_s).

The next proposition concerns the function ẽ(x) given in (3.4).

Proposition 2

Under Assumptions (A2)-(A5), for any τ ∈ R, and σ_n(x), a_Ns+1, and b_Ns+1 as given in (2.3) and (2.4),

$$\underset{n\to \infty }{\lim }P\{{\sup }_{x\in [0,1]}|{\sigma }_n{(x)}^{-1}\stackrel{\sim }{e}(x)|\le \tau /a_{N_{\mathrm{s}}+1}+b_{N_{\mathrm{s}}+1}\}=\exp (-2e^{-\tau }).$$

4. Implementation

In this section, we describe procedures to implement the confidence bands and intervals given in Corollary 1. Given any data set ${(X_{\mathit{ij}},Y_{\mathit{ij}})}_{j=1,i=1}^{N_i,n}$ from model (1.2), the spline estimator m̂(x) is obtained by (3.2), and the number of interior knots in (3.2) is taken to be $N_{\mathrm{s}}=[c{N}_{\mathrm{T}}^{1/3}(\log n)]$, in which [a] denotes the integer part of a and c is a positive constant. When constructing the confidence bands, one needs to evaluate the function ${\sigma }_n^2(x)$ by estimating the unknown functions f(x), ${\sigma }_Y^2(x)$, and G (x, x), and then plugging in these estimators: the same approach is taken in Wang and Yang (2009).

The number of interior knots for pilot estimation of f(x), ${\sigma }_Y^2(x)$, and G (x, x) is taken to be $N_{\mathrm{s}}^{\ast }=\left[n^{1/3}\right]$, and $h_{\mathrm{s}}^{\ast }=1/(1+N_{\mathrm{s}}^{\ast })$. The histogram pilot estimator of the density function f(x) is

$$\widehat{f}(x)=\{{\sum }_{i=1}^n{\sum }_{j=1}^{N_i}{b}_{J(x)}(X_{\mathit{ij}})\}/\{({\sum }_{i=1}^n{N}_i)h_{\mathrm{s}}^{\ast }\}.$$

Defining the vector $\mathbf{R}={\left\{R_{\mathit{ij}}\right\}}_{1\le j\le N_i,1\le i\le n}^{\mathrm{T}}={\left\{{(Y_{\mathit{ij}}-\widehat{m}(X_{\mathit{ij}}))}^2\right\}}_{1\le j\le N_i,1\le i\le n}^{\mathrm{T}}$, the estimation of ${\sigma }_Y^2(x)$ is ${\widehat{\sigma }}_Y^2(x)={\sum }_{J=0}^{N_{\mathrm{s}}^{\ast }}{\widehat{\rho }}_J{b}_J(x)$, where the coefficients ${\{{\widehat{\rho }}_0,\dots ,{\widehat{\rho }}_{N_{\mathrm{s}}^{\ast }}\}}^{\mathrm{T}}$ are solutions of the least squares problem:

$${\{{\widehat{\rho }}_0,\dots ,{\widehat{\rho }}_{N_{\mathrm{s}}^{\ast }}\}}^{\mathrm{T}}=\underset{\{{\widehat{\rho }}_0,\dots ,{\widehat{\rho }}_{N_{\mathrm{s}}^{\ast }}\}\in R^{N_{\mathrm{s}}+1}}{\mathrm{argmin}}{\sum }_{i=1}^n{\sum }_{j=1}^{N_i}{\left\{R_{ij}-{\sum }_{j=0}^{N_{\mathrm{s}}^{\ast }}{\rho }_J{b}_J\left(X_{ij}\right)\right\}}^2.$$

The pilot estimator of covariance function G (x, x′) is

$$\widehat{G}(x,x^{\prime })=\arg \underset{g\in G^{(-1)}\otimes G^{(-1)}}{\min }{\sum }_{i=1}^n{\sum }_{j,j^{\prime }=1,j\ne j^{\prime }}^{N_i}{\{C_{{\mathit{ijj}}^{\prime }}-g(X_{\mathit{ij}},X_{{\mathit{ij}}^{\prime }})\}}^2,$$

where C_ijj′ = {Y_ij − m̂ (X_ij)} {Y_ij′ − m̂ (X_ij′)}, 1 ≤ j, j′ ≤ N_i, 1 ≤ i ≤ n. The function σ_n(x) is estimated by either σ̂_n,IID(x) ≡ σ̂_Y(x) {f̂(x)h_sN_T}^−1/2 or

$${\widehat{\sigma }}_{n,\mathrm{LONG}}(x)\equiv {\widehat{\sigma }}_{n,\mathrm{IID}}(x){\left\{1+\left({\sum }_{i=1}^n{N}_i^2/N_{\mathrm{T}}-1\right)\frac{\widehat{G}\left(x,x\right)}{{\widehat{\sigma }}_Y^2(x)}\widehat{f}\left(x\right)h_{\mathrm{s}}\right\}}^{1/2}.$$

We now state a result. That is easily proved by standard theory of kernel and spline smoothing, as in Wang and Yang (2009).

Proposition 3

Under Assumptions (A1)-(A5), as n → ∞

$${\sup }_{x\in \left[0,1\right]}\left\{\left|{\widehat{\sigma }}_{n,\mathrm{IID}}\left(x\right){\widehat{\sigma }}_{n,\mathrm{IID}}^{-1}\left(x\right)-1\right|+\left|{\widehat{\sigma }}_{n,\mathrm{LONG}}\left(x\right){\widehat{\sigma }}_{n,\mathrm{LONG}}^{-1}\left(x\right)-1\right|\right\}=O_{a.s}\left(h_{\mathrm{s}}^{\beta }+n^{-1/2}{N}_{\mathrm{s}}^{-1}{\left(\mathit{logn}\right)}^{1/2}\right).$$

Proposition 1, about how σ_n,IID(x) and σ_n,LONG(x) uniformly approximate σ_n(x), and Proposition 3 together imply that both σ̂_n,IID(x) and σ̂_n,LONG(x) approximate σ_n(x) uniformly at a rate faster than (n^−1/2+1/3 (logn)^1/2−1/3), according to Assumption (A5). Therefore as n → ∞, the confidence bands

$$\widehat{m}\left(x\right)\pm {\widehat{\sigma }}_{n,\mathrm{IID}}\left(x\right)Q_{N_{\mathrm{s}}+1}\left(\alpha \right),$$ (4.1)

$$\widehat{m}\left(x\right)\pm {\widehat{\sigma }}_{n,\mathrm{LONG}}\left(x\right)Q_{N_{\mathrm{s}}+1}\left(\alpha \right),$$ (4.2)

with Q_Ns+1 (α) given in (2.4), and the pointwise intervals m̂(x) ± σ̂_n,IID(x)Z_1−α/2, m̂(x) ± σ̂_n,LONG(x)Z_1−α/2 have asymptotic confidence level 1 − α.

5. Simulation

To illustrate the finite-sample performance of the spline approach, we generated data from the model

$$Y_{\mathit{ij}}=m(X_{\mathit{ij}})+{\sum }_{k=1}^2{\xi }_{\mathit{ik}}{\varphi }_k(X_{\mathit{ij}})+\sigma {\epsilon }_{\mathit{ij}},1\le j\le N_i,1\le i\le n,$$

with X ~ Uniform[0, 1], ξ_k ~ Normal(0, 1), k = 1, 2, ε ~ Normal(0, 1), N_i having a discrete uniform distribution from 25, … , 35, for 1 ≤ i ≤ n, and $m\left(x\right)=\sin \left\{2\pi \left(x-1/2\right)\right\},{\varphi }_1\left(x\right)=-2\cos \left\{\pi \left(x-1/2\right)\right\}/\sqrt{5},{\varphi }_2\left(x\right)=\sin \left\{\pi \left(x-1/2\right)\right\}/\sqrt{5}$, thus λ₁ = 2/5, λ₂ = 1/10. The noise levels were σ = 0.5, 1.0, the number of subjects n was taken to be 20, 50, 100, 200, the confidence levels were 1 − α = 0.95, 0.99, and the constant c in the definition of N_s in Section 4 was taken to be 1, 2, 3. We found that the confidence band (4.1) did not have good coverage rates for moderate sample sizes, and hence in Table 1 we report the coverage as the percentage out of the total 200 replications for which the true curve was covered by (4.2) at the 101 points {k/100, k = 0, …, 100}.

Table 1.

Uniform coverage rates from 200 replications using the confidence band (4.2). For each sample size n, the first row is the coverage of a nominal 95% confidence band, while the second row is for a 99% confidence band.

σ	n	1 − α	c = 1	c = 2	c = 3
0.5	20	0.950	0.920	0.930	0.800
		0.990	0.990	0.990	0.900
	50	0.950	0.960	0.965	0.910
		0.990	0.995	0.995	0.965
	100	0.950	0.955	0.955	0.955
		0.990	1.000	1.000	0.985
	200	0.950	0.950	0.965	0.975
		0.990	0.985	0.985	0.990
1.0	20	0.950	0.935	0.930	0.735
		0.990	0.990	0.990	0.870
	50	0.950	0.975	0.960	0.895
		0.990	0.995	0.995	0.980
	100	0.950	0.950	0.940	0.935
		0.990	0.995	0.990	0.990
	200	0.950	0.940	0.965	0.960
		0.990	0.985	0.995	0.995

At all noise levels, the coverage percentages for the confidence band (4.2) are very close to the nominal confidence levels 0.95 and 0.99 for c = 1, 2, but decline for c = 3 when n = 20, 50. The coverage percentages thus depend on the choice of N_s, and the dependency becomes stronger when sample sizes decrease. For large sample sizes n = 100, 200, the effect of the choice of N_s on the coverage percentages is insignificant. Because N_s varies with N_i, for 1 ≤ i ≤ n, the data-driven selection of some “optimal” N_s remains an open problem.

We next examine two alternative methods to compute the confidence band, based on the observation that the estimated mean function m̂(x) and the confidence intervals are step functions that remain the same on each subinterval χ_J, 0 ≤ J ≤ N_s. Follwing an associate editor’s suggestion, locally weighted smoothing was applied to the upper and lower confidence limits to generate a smoothed confidence band. Following a referee’s suggestion to treat the number (N_s + 1) of subintervals as fixed instead of growing to infinity, a naive parametric confidence band was computed as

$$\widehat{m}(x)\pm {\widehat{\sigma }}_{n,\mathrm{LONG}}(x)Q_{1-\alpha .N_{\mathrm{s}}+1}$$ (5.1)

in which Q_1−α.Ns+1 = Z_{{1+(1−α)^1/(Ns+1)}/2} is the (1 − α) quantile of the maximal absolute values of (N_s + 1) iid N (0, 1) random variables. We compare the performance of the confidence band in (4.2), the smoothed band and naive parametric band in (5.1). Given n = 20 with N_s = 8, 12, and n = 50 N_s = 44 (by taking c = 1 in the definition of N_s in Section 4), σ = 0.5, 1.0, and 1 − α = 0.99, Table 2 reports the coverage percentages P̂, P̂_naive, P̂_smooth and the average maximal widths W, W_naive, W_smooth of N_s + 1 intervals out of 200 replications calculated from confidence bands (4.2), (5.1), and the smoothed confidence bands, respectively.

Table 2.

Uniform coverage rates and average maximal widths of confidence intervals from 200 replications using the confidence bands (4.2), (5.1), and the smoothed bands respectively, for 1 − α = 0.99.

n	σ	Ns	P̂	P̂naive	P̂smooth	W	Wnaive	Wsmooth
20	0.5	8	0.820	0.505	0.910	1.490	1.210	1.480
		12	0.930	0.765	0.955	1.644	1.363	1.628
	1.0	8	0.910	0.655	0.970	1.725	1.401	1.721
		12	0.960	0.820	0.985	1.937	1.606	1.928
50	0.5	44	0.990	0.960	0.990	1.651	1.522	1.609
	1.0	44	0.990	0.975	1.000	2.054	1.893	2.016

In all experiments, one has P̂_smooth > P̂ > P̂_naive and W > W_smooth > W_naive. The coverage percentages for both the confidence bands in (4.2) and the smoothed bands are much closer to the nominal level than those of the naive bands in (5.1), while the smoothed bands perform slightly better than the constant spline bands in (4.2), with coverage percentages closer to the nominal and smaller widths. Based on these observations, the naive band is not recommended due to poor coverage. As for the smoothed band, although it has slightly better coverage than the constant spline band, its asymptotic property has yet to be established, and the second step smoothing adds to its conceptual complexity and computational burden. Therefore with everything considered, the constant spline band is recommended for its satisfactory theoretical property, fast computing, and conceptual simplicity.

For visualization of the actual function estimates, at σ = 0.5 with n = 20, 50, Figure 1 depicts the simulated data points and the true curve, and Figure 2 shows the true curve, the estimated curve, the uniform confidence band, and the pointwise confidence intervals.

Figure 1.

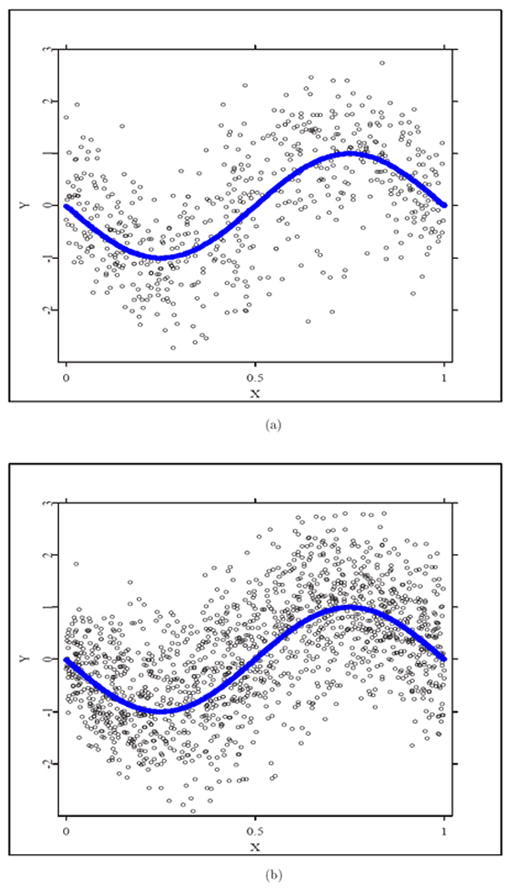
Plots of simulated data scatter points at σ = 0.5: (a) n = 20, (b) n = 50, and the true curve.

Figure 2.

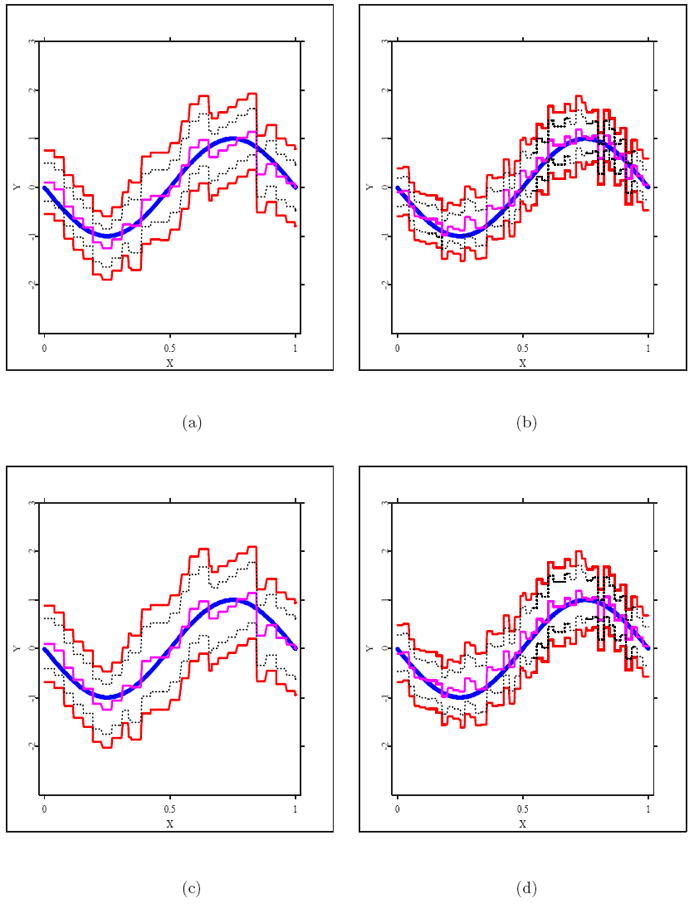
Plots of confidence bands (4.2) (upper and lower solid lines), pointwise confidence intervals (upper and lower dashed lines), the spline estimator (middle thin line), and the true function (middle thick line): (a) 1 − α = 0.95, n = 20, (b) 1 − α = 0.95, n = 50, (c) 1 − α = 0.99, n = 20,(d) 1 − α = 0.99, n = 50.

6. Empirical example

In this section, we apply the confidence band procedure of Section 4 to the data collected from a study by the AIDS Clinical Trials Group, ACTG 315 (Zhou, Huang, and Carroll (2008)). In this study, 46 HIV 1 infected patients were treated with potent antiviral therapy consisting of ritonavir, 3TC and AZT. After initiation of the treatment on day 0, patients were followed for up to 10 visits. Scheduled visit times common for all patients were 7, 14, 21, 28, 35, 42, 56, 70, 84, and 168 days. Since the patients did not follow exactly the scheduled times and/or missed some visits, the actual visit times T_ij were irregularly spaced and varied from day 0 to day 196. The CD4+ cell counts during HIV/AIDS treatments are taken as the response variable Y from day 0 to day 196. Figure 3 shows that the data points (dots) are extremely sparse between day 100 and 150, thus we first transform the data by $X_{\mathit{ij}}=T_{\mathit{ij}}^{1/3}$. A histogram (not shown) indicates that the X_ij-values are distributed fairly uniformly. The number of interior knots in (3.2) is taken to be N_s = 6, so that the range for visit time T, which is [0, 196], is divided into seven unequal subintervals, and in each subinterval, the mean CD4+ cell counts and the confidence bands remain the same. Table 3 gives the mean CD4+ cell counts and the confidence limits on each subinterval at simultaneous confidence level 0.95. For instance, from day 4 to 14, the mean CD4+ cell counts is 241.62 with lower and upper limits 171.81 and 311.43 respectively.

Figure 3.

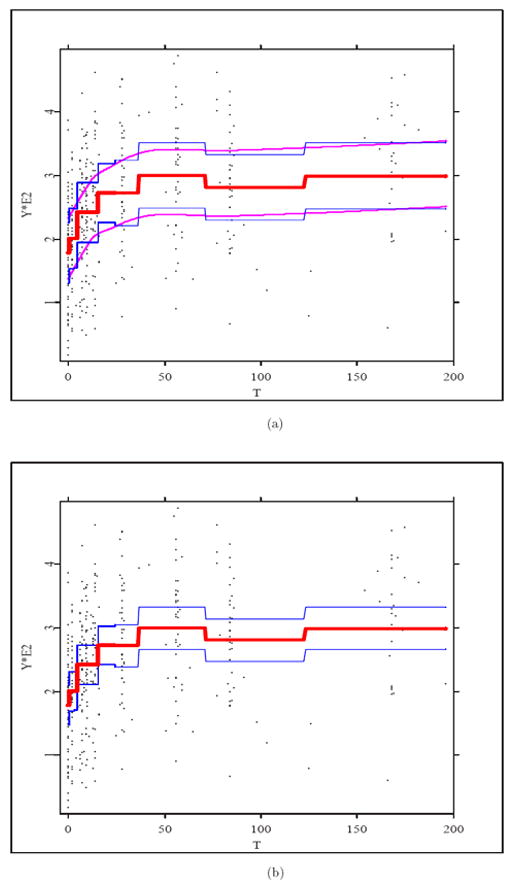
Plots of the piecewise-constant spline estimator (thick line), the data (dots), and (a) confidence band (4.2) (upper and lower solid lines), the smoothed band (upper and lower thin lines), (b) pointwise confidence intervals (upper and lower thin lines) at confidence level 0.95.

Table 3.

The mean CD4+ cell counts and the confidence limits on each subinterval at simultaneous confidence level 0.95.

Days	Mean CD4+ cell counts	Confidence limits
[0, 1)	178.23	[106.73, 249.72]
[1, 4)	20.32	[130.51, 270.13]
[4, 15)	24.62	[171.81, 311.43]
[15, 36)	27.87	[194.70, 349.04]
[36, 71)	299.51	[222.34, 376.68]
[71, 123)	280.78	[203.50, 358.06]
[123, 196]	299.27	[221.99, 376.55]

Figure 3 depicts (a) the 95% simultaneous (smoothed) confidence band according to (4.2) in (median) thin lines, and (b) the pointwise 95% confidence intervals in thin lines. The center thick line is the piecewise-constant spline fit m̂(x). It can be seen that the pointwise confidence intervals are of course narrower than the uniform confidence band by the same ratio. Figure 3 is essentially a graphical representation of Table 3; both confirm that the mean CD4+ cell counts generally increases over time as Zhou, Huang, and Carroll (2008) pointed out. The advantage of the current method is that such inference on the overall trend is made with predetermined type I error probability, in this case 0.05.

7. Discussion

In this paper, we have constructed a simultaneous confidence band for the mean function m(x) for sparse longitudinal data via piecewise-constant spline fitting. Our approach extends the asymptotic results in Wang and Yang (2009) for i.i.d. random designs to a much more complicated data structure by allowing dependence of measurements within each subject. The proposed estimator has good asymptotic behavior, and the confidence band had coverage very close to the nominal in our simulation study. An empirical study for the mean CD4+ cell counts illustrates the practical use of the confidence band.

Clearly the simultaneous confidence band in (4.2) can be improved in terms of both theoretical and numerical performance if higher order spline or local linear estimators are used. Constant piecewise spline estimators are less appealing and have sub-optimal convergence rates in the sense of Hall, Müller, and Wang (2006), which uses local linear approaches. Establishing the asymptotic confidence level for such extensions, however, requires highly sophisticated extreme value theory, for sequences of non-stationary Gaussian processes over intervals growing to infinity. That is much more difficult than the proofs of this paper. We consider the confidence band in (4.2) significant because it is the first of its kind for the longitudinal case with complete theoretical justification, and with satisfactory numerical performance for commonly encountered data sizes.

Our methodology can be applied to construct simultaneous confidence bands for other functional objects, such as the covariance function G(x, x′) and its eigenfunctions, see Yao (2007). It can also be adapted to the estimation of regression functions in the functional linear model, as in Li and Hsing (2007). We expect further research along these lines to yield deep theoretical results with interesting applications.

Appendix

Throughout this section, a_n ~ b_n means $\underset{n\to \infty }{\lim }{b}_n/a_n=c$, where c is some nonzero constant, and for functions a_n(x), b_n(x), a_n(x) = u {b_n(x)} means a_n(x)/b_n(x) → 0 as n → ∞ uniformly for x ∈ [0, 1].

A.1. Preliminaries

We first state some results on strong approximation, extreme value theory and the classic Bernstein inequality. These are used in the proofs of Lemma A.7, Theorem 1, and Lemma A.6.

Lemma A.1

(Theorem 2.6.7 of Csőrgő and Révész (1981)) Suppose that ξ_i, 1 ≤ i ≤ n are iid with E(ξ₁) = 0, $E({\xi }_1^2)=1$, and H(x) > 0 (x ≥ 0) is an increasing continuous function such that x^−2−γ H(x) is increasing for some γ > 0 and x⁻¹ logH (x) is decreasing with EH (|ξ₁|) < ∞. Then there exists a Wiener process {W (t), 0 ≤ t < ∞} that is a Borel function of ξ_i, 1 ≤ i ≤ n, and constants C₁, C₂, a > 0 which depend only on the distribution of ξ₁, such that for any ${\left\{x_n\right\}}_{n=1}^{\infty }$ satisfying H⁻¹ (n) < x_n < C₁ (nlogn)^1/2 and $S_k={\sum }_{i=1}^k{\xi }_i$,

$$P\left\{\underset{1\le k\le n}{\max }|S_k-W(k)|>x_n\right\}\le C_{2}n{\{H({\mathit{ax}}_n)\}}^{-1}.$$

Lemma A.2

Let ${\xi }_i^{(n)}$, 1 ≤ i ≤ n, be jointly normal with ${\xi }_i^{(n)}~N(0,1)$. Let $r_{\mathit{ij}}^{(n)}=E{\xi }_i^{(n)}{\xi }_j^{(n)}$ be such that for γ > 0, C_r > 0, $\left|r_{\mathit{ij}}^{(n)}\right|<C_r/n^{\gamma }$, i ≠ j. Then for τ ∈ R, as n → ∞, P{M_n,ξ ≤ τ/a_n + b_n} → exp (−2e^−τ), in which $M_{n,\xi }=\max \left\{\left|{\xi }_1^{(n)}\right|,\dots ,\left|{\xi }_n^{(n)}\right|\right\}$ and a_n, b_n are as in (2.4) with N_s + 1 replaced by n.

Proof

Let ${\left\{{\eta }_i\right\}}_{i=1}^n$ be i.i.d. standard normal r.v.’s, $\mathbf{u}={\left\{u_i\right\}}_{i=1}^n,\mathbf{v}={\left\{{\upsilon }_i\right\}}_{i=1}^n$ be vectors of real numbers, and ω = min (|u₁|,…, |u_n| , |υ₁|,…, |υ_n|). By the Normal Comparison Lemma (Leadbetter, Lindgren and Rootzén (1983), Lemma 11.1.2),

$$\begin{array}{c}\left|P\left\{-{\upsilon }_j<{\xi }_j^{(n)}\le u_j\mathrm{for}j=1,\dots ,n\right\}-P\{-{\upsilon }_j<{\eta }_j\le u_j\mathrm{for}j=1,\dots ,n\}\right|\\ \le \frac{4}{2\pi }{\sum }_{1\le i<j\le n}\left|r_{\mathit{ij}}^{(n)}\right|{\left(1-{\left|r_{\mathit{ij}}^{(n)}\right|}^2\right)}^{-1/2}\exp \left(\frac{-{\omega }^2}{1+r_{\mathit{ij}}^{(n)}}\right).\end{array}$$

If u₁ = ⋯ = u_n = υ₁ = ⋯ = υ_n = τ/a_n + b_n = τ_n, it is clear that ${\tau }_n^2/(2\log n)\to 1$, as n → ∞. Then ${\tau }_n^2>(2-\epsilon )\log n$, for any ε > 0 and large n. Since $1-r_{\mathit{ij}}^{(n)2}\ge 1-{(C_r/n^{\gamma })}^2\to 1$ as n → ∞, i ≠ j, for i ≠ j, ∃C_r2 > 0 such that $1-r_{\mathit{ij}}^{(n)2}\ge C_{r2}>0$ and $1+r_{\mathit{ij}}^{(n)}<1+\epsilon$ for any ∊ > 0 and large n. Let M_n,η = max {|η₁|,…, |η_n|}. By Leadbetter, Lindgren and Rootzén (1983), Theorem 1.5.3, P {M_n,η ≤ τ_n} → exp (−2e^−τ) as n → ∞, while the above results entail

$$\begin{array}{c}|P(M_{n,\xi }\le {\tau }_n)-P(M_{n,\eta }\le {\tau }_n)|\le \frac{4}{2\pi }\sum _{1\le i<j\le n}\left|r_{\mathit{ij}}^{(n)}\right|{\left(1-{\left|r_{\mathit{ij}}^{(n)}\right|}^2\right)}^{-1/2}\exp \left(\frac{-{\omega }^2}{1+r_{\mathit{ij}}^{(n)}}\right)\\ \le \frac{4}{2\pi }{\sum }_{1\le i<j\le n}{C}_r{n}^{-\gamma }{C}_{r2}^{-1/2}\exp \left\{\frac{-(2-\epsilon )\log n}{1+\epsilon }\right\}\le C_r^{\prime }{n}^{2-\gamma -(2-\epsilon ){(1+\epsilon )}^{-1}}\to 0\end{array}$$

as n → ∞. Hence P {M_n,ξ ≤ τ_n} → exp (−2e^−τ), as n → ∞.

Lemma A.3

(Theorem 1.2 of Bosq (1998)) Suppose that ${\left\{{\xi }_i\right\}}_{i=1}^n$ are iid with E(ξ₁) = 0, ${\sigma }^2=E{\xi }_1^2$, and there exists c > 0 such that for r = 3, 4, …, $E{|{\xi }_1|}^r\le c^{r-2}r!E{\xi }_1^2<+\infty$. Then for each n > 1, t > 0, $P(|S_n|\ge \sqrt{n}\sigma t)\le 2\exp \left(-t^2{(4+2\mathit{ct}/\sqrt{n}\sigma )}^{-1}\right)$, in which $S_n={\sum }_{i=1}^n{\xi }_i$.

Lemma A.4

Under Assumption (A2), as n → ∞ for c_J,n defined in (2.2), c_J,n = f (t_J) h_s (1 + r_J,n), 〈b_J, b_J′〉 ≡ 0, J ≠ J′, where max_0≤J≤Ns |r_J,n| ≤ Cω (f,h_s). There exist constants C_B > c_B > 0 such that $c_B{h}_{\mathrm{s}}^{1-r/2}\le E{\{B_J(X_{\mathit{ij}})\}}^r\le C_B{h}_{\mathrm{s}}^{1-r/2}$ for r = 1, 2, … and 1 ≤ J ≤ N_s + 1, 1 ≤ j ≤ N_i, 1 ≤ i ≤ n.

Proof

By the definition of c_J,n in (2.2),

$$c_{J,n}=\mathit{\int }{b}_J\left(x\right)f\left(x\right)\mathit{dx}={\mathit{\int }}_{[t_J,t_{J+1}]}f\left(x\right)\mathit{dx}=f\left(t_J\right)h_{\mathrm{s}}+{\mathit{\int }}_{[t_J,t_{J+1}]}\left\{f\left(x\right)-f\left(t_J\right)\right\}\mathit{dx}.$$

Hence for all J = 0, …, N_s, |c_J,n − f (t_J) h_s| ≤ ∫_{[tJ, tJ+1]}| f(x) − f (t_J)| dx ≤ ω (f, h_s) h_s, or |r_J,n| = |c_J,n − f (t_J) h_s| {f (t_J) h_s}⁻¹ ≤ Cω (f, h_s), J = 0, …, N_s. By (3.1), $E{\{B_J(X_{\mathit{ij}})\}}^r={(c_{J,n})}^{-r/2}\mathit{\int }{b}_J\left(x\right)f\left(x\right)\mathit{dx}={(c_{J,n})}^{1-r/2}~h_{\mathrm{s}}^{1-r/2}$.

Proof of Proposition 1

By Lemma A.4 and Assumption (A2) on the continuity of functions ${\varphi }_k^2\left(x\right)$, σ²(x) and f(x) on [0, 1], for any x ∈ [0, 1]

$$\begin{array}{c}\left|{\mathit{\int }}_{{\chi }_{J\left(x\right)}}{\varphi }_k\left(x\right)f\left(x\right)\mathit{du}-{\mathit{\int }}_{{\chi }_{J\left(x\right)}}{\varphi }_k\left(u\right)f\left(u\right)\mathit{du}\right|\le \omega \left({\varphi }_{k}f,h_{\mathrm{s}}\right)h_{\mathrm{s}}=O\left(h_{\mathrm{s}}^{1+\beta }\right),\\ \left|{\mathit{\int }}_{J\left(x\right)}\{{\sigma }_Y^2\left(x\right)f\left(x\right)-{\sigma }_Y^2\left(u\right)f\left(u\right)\}\mathit{du}\right|\le \omega \left({\sigma }_Y^{2}f,h_{\mathrm{s}}\right)h_{\mathrm{s}}=O\left(h_{\mathrm{s}}^{1+\beta }\right).\end{array}$$

Hence,

$$\begin{array}{c}{\sigma }_n^2\left(x\right)=c_{J\left(x\right),n}^{-2}{\left(n{\mathit{EN}}_1\right)}^{-1}{\mathit{\int }}_{J\left(x\right)}{\sigma }_Y^2\left(u\right)f\left(u\right)\mathit{du}\times \left\{1+\frac{E\left\{N_1\left(N_1-1\right)\right\}}{{\mathit{EN}}_1}\sum _{k=1}^{\kappa }{\left({\mathit{\int }}_{{\chi }_{J\left(x\right)}}{\varphi }_k\left(u\right)f\left(u\right)\mathit{du}\right)}^2{\left\{{\mathit{\int }}_{J\left(x\right)}{\sigma }_Y^2\left(u\right)f\left(u\right)\mathit{du}\right\}}^{-1}\right\}\\ ={\left\{f\left(x\right)h_{\mathrm{s}}+U\left(h_{\mathrm{s}}^{1+\beta }\right)\right\}}^{-2}{\left(n{\mathit{EN}}_1\right)}^{-1}\left\{{\sigma }_Y^2\left(x\right)f\left(x\right)h_{\mathrm{s}}+U\left(h_{\mathrm{s}}^{1+\beta }\right)\right\}\times \left\{1+\frac{E\left\{N_1\left(N_1-1\right)\right\}}{{\mathit{EN}}_1}\sum _{k=1}^{\kappa }{\left\{{\varphi }_k\left(x\right)f\left(x\right)h_{\mathrm{s}}+U\left(h_{\mathrm{s}}^{1+\beta }\right)\right\}}^2{\left\{{\sigma }_Y^2\left(x\right)f\left(x\right)h_{\mathrm{s}}+U\left(h_{\mathrm{s}}^{1+\beta }\right)\right\}}^{-1}\right\}\\ ={\left(f\left(x\right)h_{\mathrm{s}}n{\mathit{EN}}_1\right)}^{-1}{\sigma }_Y^2\left(x\right)\left\{1+\frac{E\left\{N_1\left(N_1-1\right)\right\}}{E{N}_1}\frac{{\sum }_{k=1}^{\kappa }{\varphi }_k^2\left(x\right)f\left(x\right)h_{\mathrm{s}}}{{\sigma }_Y^2\left(x\right)}\right\}\left\{1+U\left(h_{\mathrm{s}}^{\beta }\right)\right\}={\sigma }_{n,\mathrm{LONG}}^2\left(x\right)\left\{1+U\left(h_{\mathrm{s}}^{\beta }\right)\right\}={\sigma }_{n,\mathrm{IID}}^2\left(x\right)\left\{1+U\left(h_{\mathrm{s}}^{\beta }\right)\right\}.\end{array}$$

A.2. Proof of Theorem 1

Note that $B_{J(x)}(x)\equiv c_{J(x),n}^{-1/2},x\in [0,1]$, so the terms ξ̃_k(x) and ε̃(x) defined in (3.5) are

$$\begin{array}{c}{\widehat{\xi }}_k(x)=\sum _{J=0}^{N_{\mathrm{s}}}{N}_{\mathrm{T}}^{-1}{B}_J(x){\parallel B_J\parallel }_{2,N_{\mathrm{T}}}^{-2}\sum _{i=1}^n\sum _{j=1}^{N_i}{B}_J(X_{\mathit{ij}}){\varphi }_k(X_{\mathit{ij}}){\xi }_{\mathit{ik}}\\ =c_{J(x),n}^{-1/2}\parallel B_{J(x)}{\parallel }_{2,N_{\mathrm{T}}}^{-2}{N}_{\mathrm{T}}^{-1}\sum _{i=1}^n\sum _{j=1}^{N_i}{B}_{J(x)}(X_{\mathit{ij}}){\varphi }_k(X_{\mathit{ij}}){\xi }_{\mathit{ik}},\\ \stackrel{\sim }{\epsilon }(x)=c_{J(x),n}^{-1/2}\parallel B_{J(x)}{\parallel }_{2,N_{\mathrm{T}}}^{-2}{N}_{\mathrm{T}}^{-1}\sum _{i=1}^n\sum _{j=1}^{N_i}{B}_{J(x)}(X_{\mathit{ij}})\sigma (X_{\mathit{ij}}){\epsilon }_{\mathit{ij}}.\end{array}$$

Let

$$\begin{array}{r}{\widehat{\xi }}_k(x)={\parallel B_{J(x)}\parallel }_{2,N_{\mathrm{T}}}^2{\stackrel{\sim }{\xi }}_k(x)=c_{J(x),n}^{-1/2}{N}_{\mathrm{T}}^{-1}{\sum }_{i=1}^n{R}_{\mathit{ik},\xi ,J(x)}{\xi }_{\mathit{ik}},\\ \widehat{\epsilon }(x)={\parallel B_{J(x)}\parallel }_{2,N_{\mathrm{T}}}^2\stackrel{\sim }{\epsilon }(x)=c_{J(x),n}^{-1/2}{N}_{\mathrm{T}}^{-1}{\sum }_{i=1}^n{\sum }_{j=1}^{N_i}{R}_{\mathit{ij},\epsilon ,J(x)}{\epsilon }_{\mathit{ij}},\end{array}$$ (8.1)

where

$$R_{\mathit{ik},\xi ,J}={\sum }_{j=1}^{N_i}{B}_J(X_{\mathit{ij}}){\varphi }_k(X_{\mathit{ij}}),R_{\mathit{ij},\epsilon ,J}=B_J(X_{\mathit{ij}})\sigma (X_{\mathit{ij}}),0\le J\le N_{\mathrm{s}}.$$ (8.2)

Lemma A.5

Under Assumption (A3), for ẽ(x) given in (3.4) and ξ̂_k(x), ε̂(x) given in (8.1), we have

$$\left|\stackrel{\sim }{e}(x)-\left\{\sum _{k=1}^{\kappa }{\widehat{\xi }}_k(x)+\widehat{\epsilon }(x)\right\}\right|\le A_n{(1-A_n)}^{-1}\left|\sum _{k=1}^{\kappa }{\widehat{\xi }}_k(x)+\widehat{\epsilon }(x)\right|,x\in [0,1],$$

where $A_n={\sup }_{0\le J\le N_{\mathrm{s}}}\left|{\parallel B_J\parallel }_{2,N_{\mathrm{T}}}^2-1\right|$. There exists C_A > 0, such that for large n, $P\left(A_n\ge C_A\sqrt{\mathit{log}(n)/({\mathit{nh}}_{\mathrm{s}})}\right)\le 2n^{-3}$. $A_n=O_{a.s.}\left(\sqrt{\mathit{log}(n)/({\mathit{nh}}_{\mathrm{s}})}\right)$ as n → ∞.

See the supplement of Wang and Yang (2009) for a detailed proof.

Lemma A.6

Under Assumptions (A2) and (A3), for R_1k,ξ,J, R_{11, ε,J} in (8.2),

$$\begin{array}{l}{\mathit{ER}}_{1k,\xi ,J}^2=c_{J,n}^{-1}\left[E(N_1)\mathit{\int }{b}_J(u){\varphi }_k^2(u)f(u)\mathit{du}+E\{N_1(N_1-1)\}{\left(\mathit{\int }{b}_J(u){\varphi }_k(u)f(u)\mathit{du}\right)}^2\right],\\ {\mathit{ER}}_{11,\epsilon ,J}^2=c_{J,n}^{-1}\mathit{\int }{b}_J(u){\sigma }^2(u)f(u)\mathit{du},0\le J\le N_{\mathrm{s}},\end{array}$$

there exist 0 < c_R < C_R < ∞, such that ${\mathit{ER}}_{1k,\xi ,J}^2,{\mathit{ER}}_{11,\epsilon ,J}^2\in [c_R,C_R]$ for 0 ≤ J ≤ N_s, ${\sup }_{0\le J\le N_{\mathrm{s}}}|n^{-1}{\sum }_{i=1}^n{R}_{ik,\xi ,J}^2-{\mathit{ER}}_{1k,\xi ,J}^2|=O_{a.s.}\left(\sqrt{\mathit{logn}/({\mathit{nh}}_{\mathrm{s}})}\right),1\le k\le \kappa ,\underset{0\le J\le N_{\mathrm{s}}}{\sup }|N_{\mathrm{T}}^{-1}{\sum }_{i=1}^n{\sum }_{j=1}^{N_i}{R}_{\mathit{ij},\epsilon ,J}^2-{\mathit{ER}}_{11,\epsilon ,J}^2|=O_{a.s.}\left(\sqrt{\mathit{logn}/{\mathit{nh}}_{\mathrm{s}})}\right)$ as n → ∞.

Proof

By independence of X_1j, 1 ≤ j ≤ N₁ and N₁ and (3.1),

$$\begin{array}{c}{\mathit{ER}}_{1k,\xi ,J}^2=E\left\{{\sum }_{j,j\prime =1}^{N_1}E\{B_J(X_{1j})B_J(X_{1j\prime }){\varphi }_k(X_{1j}){\varphi }_k(X_{1j\prime })\mid N_1\}\right\}\\ =E\left\{{\sum }_{j=1}^{N_1}E\{B_J^2(X_{1j}){\varphi }_k^2(X_{1j})\mid N_1\}\right\}+E\left\{{\sum }_{j\ne j\prime }^{N_1}E\{B_J(X_{1j})B_J(X_{1j\prime }){\varphi }_k(X_{1j}){\varphi }_k(X_{1j\prime })\mid N_1\}\right\}\\ =c_{J(x),n}^{-1}\left\{E(N_1)\mathit{\int }{b}_J(u){\varphi }_k^2(u)f(u)\mathit{du}+E\{N_1(N_1-1)\}{\left(\mathit{\int }{b}_J(u){\varphi }_k(u)f(u)\mathit{du}\right)}^2\right\}.\end{array}$$

It is easily shown that ∃ 0 < c_R < C_R < ∞ such that $c_R\le {\mathit{ER}}_{1k,\xi ,J}^2\le C_{R,}0\le J\le N_{\mathrm{s}}$. Let ${\zeta }_{i,J}={\zeta }_{i,k,J}=R_{\mathit{ik},\xi ,J}^2,{\zeta }_{i,J}^{\ast }={\zeta }_{i,J}-E({\zeta }_{1,J})$ for r ≥ 1 and large n,

$$\begin{array}{c}E{({\zeta }_{i,J})}^r=E{\left\{{\sum }_{j=1}^{N_i}{B}_J(X_{\mathit{ij}}){\varphi }_k(X_{\mathit{ij}})\right\}}^{2r}\le C_{\varphi }^{2r}E{\left\{{\sum }_{j=1}^{N_i}{B}_J(X_{\mathit{ij}})\right\}}^{2r}\\ =C_{\varphi }^{2r}E\left\{\sum _{0\le {\nu }_1\cdots {\nu }_{N_i}\le 2r}^{{\nu }_1+\cdots +{\nu }_{N_i}=2r}\left(\begin{array}{c}2r\\ {\nu }_1\cdots {\nu }_{N_i}\end{array}\right)\prod _{j=1}^{N_i}E{\{B_J(X_{\mathit{ij}})\}}^{{\nu }_j}\right\}\\ \le C_{\varphi }^{2r}E\left\{N_1^{2r}\max \left\{\prod _{j=1}^{N_i}E{\{B_J(X_{\mathit{ij}})\}}^{{\nu }_j}\right\}\right\}\le C_{\varphi }^{2r}({\mathit{EN}}_1^{2r})C_B{h}_{\mathrm{s}}^{1-r}\le C_{\varphi }^{2r}{C}_B{c}_N^{r}r!h_{\mathrm{s}}^{1-r}=C_{\zeta }r!h_{\mathrm{s}}^{1-r},\\ E{({\zeta }_{i,J})}^r\ge c_{\varphi }^{2r}E\left\{{\sum }_{j=1}^{N_i}E{\{B_J(X_{\mathit{ij}})\}}^{2r}\right\}\ge c_{\varphi }^{2r}({\mathit{EN}}_1)c_B{h}_{\mathrm{s}}^{1-r},\end{array}$$

by Lemma A.4. So {E(ζ_1,J)}^r ~ 1, E (ζ_i,J)^r ≫ {E(ζ_1,J)}^r for r ≥ 2, and $\exists C_{\zeta }^{\prime }>c_{\zeta }^{\prime }>0$ such that $C_{\zeta }^{\prime }{h}_{\mathrm{s}}^{-1}\ge {\sigma }_{\zeta \ast }^2\ge c_{\zeta }^{\prime }{h}_{\mathrm{s}}^{-1}$, for ${\sigma }_{\zeta \ast }={\left\{E{\left({\zeta }_{i,J}^{\ast }\right)}^2\right\}}^{1/2}$. We obtain $E{|{\zeta }_{i,J}^{\ast }|}^r\le c_{\ast }^{r-2}r!E{\left({\zeta }_{i,J}^{\ast }\right)}^2$ with $c_{\ast }={\left(C_{\zeta }/c_{\zeta }^{\prime }\right)}^{\frac{1}{r-2}}{h}_{\mathrm{s}}^{-1}$, which implies that ${\left\{{\zeta }_{i,J}^{\ast }\right\}}_{i=1}^n$ satisfies Cramér’s condition. Applying Lemma A.3 to ${\sum }_{i=1}^n{\zeta }_{i,J}^{\ast }$, for r > 2 and any large enough δ > 0, $P\left\{n^{-1}|{\sum }_{i=1}^n{\zeta }_{i,J}^{\ast }|\ge \delta \sqrt{\log n/({\mathit{nh}}_{\mathrm{s}})}\right\}$ is bounded by

$$2\exp \left\{\frac{-{\delta }^2{(C_{\zeta }^{\prime })}^{-1}(\log n)}{4+2{(C_{\zeta }/c_{\zeta }^{\prime })}^{\frac{1}{r-2}}\delta {(c_{\zeta }^{\prime })}^{-1}{h}_{\mathrm{s}}^{1/2}{(\log n)}^{1/2}{n}^{-1/2}}\right\}\le 2\exp \left\{\frac{-{\delta }^2(\log n)}{4C_{\zeta }^{\prime }}\right\}\le 2n^{-3}.$$

Hence $\sum _{n=1}^{\infty }P\left\{\underset{0\le J\le N_{\mathrm{s}}}{\sup }\left|\frac{1}{n}\sum _{i=1}^n{R}_{\mathit{ik},\xi ,J}^2-{\mathit{ER}}_{1k,\xi ,J}^2\right|\ge \delta \sqrt{\log n/({\mathit{nh}}_{\mathrm{s}})}\right\}\le \sum _{n=1}^{\infty }\frac{2N_{\mathrm{s}}}{n^3}<\infty$. Thus, ${\sup }_{0\le J\le N_{\mathrm{s}}}\left|n^{-1}{\sum }_{i=1}^n{R}_{\mathit{ik},\xi ,J}^2-{\mathit{ER}}_{1k,\xi ,J}^2\right|=O_{\mathrm{a}.\mathrm{s}.}\left(\sqrt{\log n/({\mathit{nh}}_{\mathrm{s}})}\right)$ as n → ∞ by Borel-Cantelli Lemma. The properties of R_ij,ε,J are obtained similarly.

Order all X_ij, 1 ≤ j ≤ N_i, 1 ≤ i ≤ n from large to small as X_(t), X₍₁₎ ≥ … ≥ X_(NT), and denote the ε_ij corresponding to X_(t) as ε_(t). By (8.1),

$$\begin{array}{ll}\widehat{\epsilon }(x)& =c_{J(x),n}^{-1}{N}_{\mathrm{T}}^{-1}{\sum }_{t=1}^{N_{\mathrm{T}}}{b}_{J(x)}(X_{(t)})\sigma (X_{(t)}){\epsilon }_{(t)}\\ & =c_{J(x),n}^{-1}{N}_{\mathrm{T}}^{-1}{\sum }_{t=1}^{N_{\mathrm{T}}}{b}_{J(x)}(X_{(t)})\sigma (X_{(t)})\{S_t-S_{t-1}\},\end{array}$$

where $S_q={\sum }_{t=1}^q{\epsilon }_{(t)},q\ge 1$ and S₀ = 0.

Lemma A.7

Under Assumptions (A2)-(A5), there is a Wiener process {W (t), 0 ≤ t < ∞} independent of {N_i, X_ij, 1 ≤ j ≤ N_i, ξ_ik, 1 ≤ k ≤ κ, 1 ≤ i ≤ n}, such that as n → ∞, $\underset{x\in [0,1]}{\sup }\left|{\widehat{\epsilon }}^{(0)}(x)-\widehat{\epsilon }(x)\right|=o_{a.s.}(n^t)$ for some t < − (1 − ϑ) /2 < 0, where ε̂⁽⁰⁾ (x) is

$${(c_{J(x),n}{N}_{\mathrm{T}})}^{-1}{\sum }_{t=1}^{N_{\mathrm{T}}}{b}_{J(x)}(X_{(t)})\sigma (X_{(t)})\{W(t)-W(t-1)\},x\in [0,1].$$ (8.3)

Proof

Define M_NT = max_1≤q≤NT |S_q − W (q)|, in which {W (t), 0 ≤ t ≤ ∞} is the Wiener process as in Lemma A.1 that as a Borel function of the set of variables {ε_(t) 1 ≤ t ≤ N_T} is independent of {N_i, X_ij, 1 ≤ j ≤ N_i, ξ_ik, 1 ≤ k ≤ κ, 1 ≤ i ≤ n} since {ε_(t) 1 ≤ t ≤ N_T} is. Further,

$$\begin{array}{l}\underset{x\in [0,1]}{\sup }\left|{\widehat{\epsilon }}^{(0)}(x)-\widehat{\epsilon }(x)\right|=\underset{x\in [0,1]}{\sup }{c}_{J(x),n}^{-1}{N}_{\mathrm{T}}^{-1}\left|b_{J(x)}(X_{(N_{\mathrm{T}})})\sigma (X_{(N_{\mathrm{T}})})\{W(N_{\mathrm{T}})-S_{N_{\mathrm{T}}}\}+{\sum }_{t=1}^{N_{\mathrm{T}}-1}\{b_{J(x)}(X_{(t)})\sigma (X_{(t)})-b_{J(x)}(X_{(t+1)})\sigma (X_{(t+1)})\}\{W(t)-S_t\}\right|\\ \le \underset{0\le J\le N_{\mathrm{s}}+1}{\max }{c}_{\mathit{Jn}}^{-1}{N}_{\mathrm{T}}^{-1}\{b_J(X_{(N_{\mathrm{T}})})\sigma (X_{(N_{\mathrm{T}})})+{\sum }_{t=1}^{N_{\mathrm{T}}-1}\left|b_J(X_{(t)})\sigma (X_{(t)})-b_J(X_{(t+1)})\sigma (X_{(t+1)})\right|\}{M}_{N_{\mathrm{T}}}\\ \le \underset{0\le J\le N_{\mathrm{s}}+1}{\max }{c}_{J,n}^{-1}{N}_{\mathrm{T}}^{-1}{M}_{N_{\mathrm{T}}}\left\{3C_{\sigma }+\sum _{1\le t\le N_{\mathrm{T}}-1,X_{(t)}\in b_J}\left|\sigma (X_{(t)})-\sigma (X_{(t+1)})\right|\right\}\end{array}$$

which, by the Hölder continuity of σ in Assumption (A2), is bounded by

$$\begin{array}{c}{N}_{\mathrm{T}}^{-1}{M}_{N_{\mathrm{T}}}\underset{0\le J\le N_{\mathrm{s}}+1}{\max }{c}_{J,n}^{-1}\left\{3C_{\sigma }+{\parallel \sigma \parallel }_{0,\beta }\sum _{1\le t\le N_{\mathrm{T}}-1,X_{(t)}\in b_J}{\left|X_{(t)}-X_{(t+1)}\right|}^{\beta }\right\}\le \\ N_{\mathrm{T}}^{-1}{M}_{N_{\mathrm{T}}}\underset{0\le J\le N_{\mathrm{s}}+1}{\max }{c}_{J,n}^{-1}\left\{3C_{\sigma }+{\parallel \sigma \parallel }_{0,\beta }{n}_J^{1-\beta }{\left(\sum _{1\le t\le N_{\mathrm{T}}-1,X_{(t)}\in b_J}\left|X_{(t)}-X_{(t+1)}\right|\right)}^{\beta }\right\}\\ \le N_{\mathrm{T}}^{-1}{M}_{N_{\mathrm{T}}}\left(\underset{0\le J\le N_{\mathrm{s}}+1}{\max }{c}_{J,n}^{-1}\right)\left\{3C_{\sigma }+{\parallel \sigma \parallel }_{0,\beta }{h}_{\mathrm{s}}^{\beta }{\left(\underset{0\le J\le N_{\mathrm{s}}+1}{\max }{n}_J\right)}^{1-\beta }\right\}\end{array}$$

where $n_J={\sum }_{t=1}^{N_{\mathrm{T}}}I(X_{(t)}\in {\chi }_J)$, 0 ≤ J ≤ N_s + 1, has a binomial distribution with parameters (N_T, p_J,n), where p_J,n = ∫_χJ f (x) dx. Simple application of Lemma A.3 entails ${\max }_{0\le J\le N_{\mathrm{s}}+1}{n}_J=O_{\mathrm{a}.\mathrm{s}.}\left(N_{\mathrm{T}}{N}_{\mathrm{s}}^{-1}\right)$. Meanwhile, by letting H(x) = x^r, x_n = n^t′, t′ ∈ (2/r, β − (1 + ϑ) /2), the existence of which is due to the Assumption (A4) that r > 2/ {β − (1 + ϑ) /2}. It is clear that ${\left\{{\epsilon }_{(t)}\right\}}_{t=1}^{N_{\mathrm{T}}}$ satisfies the conditions in Lemma A.1. Since $\frac{n}{H({\mathit{ax}}_n)}=a^{-r}{n}^{1-r{t}^{\prime }}=O(n^{-{\gamma }_1})$ for some γ₁ > 1, one can use the probability inequality in Lemma A.1 and the Borel-Cantelli Lemma to obtain M_NT = O_a.s. (x_n) = O_a.s. (n^t′). Hence Lemma A.4 and the above imply

$$\begin{array}{c}\underset{x\in [0,1]}{\sup }\left|{\widehat{\epsilon }}^{(0)}(x)-\widehat{\epsilon }(x)\right|=O_{\mathrm{a}.\mathrm{s}.}\left(N_{\mathrm{s}}{n}^{t^{\prime }-1}\right)\left\{1+N_{\mathrm{s}}^{-\beta }{\left(N_{\mathrm{T}}{N}_{\mathrm{s}}^{-1}\right)}^{1-\beta }\right\}\\ =O_{\mathrm{a}.\mathrm{s}.}\left(N_{\mathrm{s}}{n}^{t^{\prime }-1}+N_{\mathrm{s}}{n}^{t^{\prime }-1}\times N_{\mathrm{s}}^{-1}{n}^{1-\beta }\right)\\ =O_{\mathrm{a}.\mathrm{s}.}\left(N_{\mathrm{s}}{n}^{t^{\prime }-1}+N_{\mathrm{s}}{n}^{t^{\prime }-\beta }\right)=o_{\mathrm{a}.\mathrm{s}.}\left(n^{t^{\prime }-\beta +\vartheta }\right)\end{array}$$

since t′ < β − (1 + ϑ) /2 by definition, implying t′ − 1 ≤ t′ − β < − (1 + ϑ) /2. The Lemma follows by setting t = t′ − β + ϑ.

Now

$$\begin{array}{l}{\widehat{\epsilon }}^{(0)}(x)=c_{J(x),n}^{-1}{N}_{\mathrm{T}}^{-1}{\sum }_{t=1}^{N_{\mathrm{T}}}{b}_{J(x)}\left(X_{(t)}\right)\sigma \left(X_{(t)}\right)Z_{(t)}\\ =c_{J(x),n}^{-1}{N}_{\mathrm{T}}^{-1}{\sum }_{i=1}^n{\sum }_{j=1}^{N_i}{b}_{J(x)}\left(X_{\mathit{ij}}\right)\sigma \left(X_{\mathit{ij}}\right)Z_{\mathit{ij},}\end{array}$$ (8.4)

where Z_(t) = W (t) − W (t − 1), 1 ≤ t ≤ N_T, are i.i.d N (0, 1), ξ_ik, Z_ij, X_ij, N_i are independent, for 1 ≤ k ≤ κ, 1 ≤ j ≤ N_i, 1 ≤ i ≤ n, and ξ̂_k(x), ε̂⁽⁰⁾(x) are conditional independent of X_ij, N_i, 1 ≤ j ≤ N_i, 1 ≤ i ≤ n. If the conditional variances of ξ̂_k(x), ε̂⁽⁰⁾(x) on (X_ij, N_i)_{1≤j≤Ni,1≤i≤n} are ${\sigma }_{{\xi }_k,n}^2(x),{\sigma }_{\epsilon ,n}^2(x)$, we have

$$\begin{array}{c}{\sigma }_{{\xi }_k,n}(x)={\left\{c_{J(x),n}^{-1}{N}_{\mathrm{T}}^{-2}{\sum }_{i=1}^n{R}_{\mathit{ik},\xi ,J(x)}^2\right\}}^{1/2}\\ {\sigma }_{\epsilon ,n}(x)={\left\{c_{J(x),n}^{-1}{N}_{\mathrm{T}}^{-2}{\sum }_{i=1}^n{\sum }_{j=1}^{N_i}{R}_{\mathit{ij},\epsilon ,J(x)}^2\right\}}^{1/2},\end{array}$$ (8.5)

where R_ik,ξ,J(x), R_ij,ε,J(x), and c_J(x),n are given in (8.2) and (2.2).

Lemma A.8

Under Assumptions (A2) and (A3), let

$$\eta (x)={\left\{\sum _{k=1}^{\kappa }{\sigma }_{{\xi }_k,n}^2(x)+{\sigma }_{\epsilon ,n}^2(x)\right\}}^{-1/2}\left\{\sum _{k=1}^{\kappa }{\widehat{\xi }}_k(x)+{\widehat{\epsilon }}^{(0)}(x)\right\},$$ (8.6)

with σ_ξk,n(x), σ_ε,n(x), ξ̂_k(x), ε̂⁽⁰⁾(x), and c_J(x),n given in (8.5), (8.1), (8.3), and (2.2). Then η(x) is a Gaussian process consisting of (N_s + 1) standard normal variables ${\{{\eta }_J\}}_{J=0}^{N_{\mathrm{s}}}$ such that η(x) = η_J(x) for x ∈ [0, 1], and there exists a constant C > 0 such that for large n, sup_{0≤J≠J′≤Ns} |Eη_Jη_J′| ≤ Ch_s.

Proof

It is apparent that ℒ {η_J |(X_ij, N_i), 1 ≤ j ≤ N_i, 1 ≤ i ≤ n} = N (0, 1) for 0 ≤ J ≤ N_s, so ℒ {η_J} = N (0, 1), for 0 ≤ J ≤ N_s. For J ≠ J′, by (8.2) and (3.1), R_ij,ε,J R_ij,ε,J′ = B_J (X_ij) B_J′ (X_ij) σ² (X_ij) = 0, along with (8.4), (8.3), the conditional independence of ξ̂_k(x), ε̂⁽⁰⁾(x) on X_ij, N_i, 1 ≤ j ≤ N_i, 1 ≤ i ≤ n, and independence of ξ_ik, Z_ij, X_ij, N_i, 1 ≤ k ≤ κ, 1 ≤ j ≤ N_i, 1 ≤ i ≤ n, E (η_Jη_J′) is

$$\begin{array}{l}E\{{\left\{{\sum }_{i=1}^n\left\{{\sum }_{k=1}^{\kappa }{R}_{\mathit{ik},\xi ,J}^2+{\sum }_{j=1}^{N_i}{R}_{\mathit{ij},\epsilon ,J}^2\right\}\right\}}^{-1/2}{\left\{{\sum }_{i=1}^n\left\{{\sum }_{k=1}^{\kappa }{R}_{\mathit{ik},\xi ,J^{\prime }}^2+{\sum }_{j=1}^{N_i}{R}_{\mathit{ij},\epsilon ,J^{\prime }}^2\right\}\right\}}^{-1/2}E\{{\sum }_{k=1}^{\kappa }\left\{{\sum }_{i=1}^n{R}_{\mathit{ik},\xi ,J}{\xi }_{\mathit{ik}}\right\}\left\{{\sum }_{i=1}^n{R}_{\mathit{ik},\xi ,J^{\prime }}{\xi }_{\mathit{ik}}\right\}+\\ \left\{{\sum }_{i=1}^n{\sum }_{j=1}^{N_i}{R}_{\mathit{ij},\epsilon ,J}{Z}_{\mathit{ij}}\right\}\left\{{\sum }_{i=1}^n{\sum }_{j=1}^{N_i}{R}_{\mathit{ij},\epsilon ,J^{\prime }}{Z}_{\mathit{ij}}\right\}\mid {(X_{\mathit{ij}},N_i)}_{1\le j\le N_i,1\le i\le n}\}\}={\mathit{EC}}_{n,J,J^{\prime }}\end{array}$$

in which $C_{n,J,J^{\prime }}={\left\{N_{\mathrm{T}}^{-1}\sum _{i=1}^n\left\{\sum _{k=1}^{\kappa }{R}_{\mathit{ik},\xi ,J}^2+{\sum }_{j=1}^{N_i}{R}_{\mathit{ij},\epsilon ,J}^2\right\}\right\}}^{-1/2}\times {\left\{N_{\mathrm{T}}^{-1}\sum _{i=1}^n\left\{\sum _{k=1}^{\kappa }{R}_{\mathit{ik},\xi ,J^{\prime }}^2+\sum _{j=1}^{N_i}{R}_{\mathit{ij},\epsilon ,J^{\prime }}^2\right\}\right\}}^{-1/2}\left\{N_{\mathrm{T}}^{-1}\sum _{k=1}^{\kappa }\sum _{i=1}^n{R}_{\mathit{ik},\xi ,J}{R}_{\mathit{ik},\xi ,J^{\prime }}\right\}$.Note that according to definitions of R_ik,ξ,J, R_ij,ε,J, and Lemma A.5,

$$N_{\mathrm{T}}^{-1}{\sum }_{i=1}^n\left\{{\sum }_{k=1}^{\kappa }{R}_{\mathit{ik},\xi ,J}^2+{\sum }_{j=1}^{N_i}{R}_{\mathit{ij},\epsilon ,J}^2\right\}$$

$\ge c_{\sigma }^2{N}_{\mathrm{T}}^{-1}{\sum }_{i=1}^n{\sum }_{j=1}^{N_i}{B}_J^2(X_{\mathit{ij}})=c_{\sigma }^2{\parallel B_J\parallel }_{2,N_{\mathrm{T}}}^2\ge c_{\sigma }^2(1-A_n)$, for 0 ≤ J ≤ N_s,

$$P\left\{\underset{0\le J\ne J^{\prime }\le N_{\mathrm{s}}}{\inf }\{N_{\mathrm{T}}^{-1}\sum _{i=1}^n\left(\sum _{k=1}^{\kappa }{R}_{\mathrm{ik},\xi ,J}^2+\sum _{j=1}^{N_i}{R}_{\mathit{ij},\epsilon ,J}^2\right)\right\}\times \left\{N_{\mathrm{T}}^{-1}\sum _{i=1}^n\left(\sum _{k=1}^{\kappa }{R}_{\mathit{ik},\xi ,J^{\prime }}^2+\sum _{j=1}^{N_i}{R}_{\mathit{ij},\epsilon ,J^{\prime }}^2\right)\right\}\ge c_{\sigma }^4{\left(1-C_A\sqrt{\frac{\log \left(n\right)}{{\mathit{nh}}_{\mathrm{s}}}}\right)}^2]\ge 1-2n^{-3},$$

by Lemma A.5. Thus for large n, with probability ≥ 1 − 2n⁻³, the numerator of C_n,J,J′ is uniformly greater than $c_{\sigma }^2/2$. Applying Bernstein’s inequality to $N_{\mathrm{T}}^{-1}\left\{{\sum }_{k=1}^{\kappa }{\sum }_{i=1}^n{R}_{\mathit{ik},\xi ,J}{R}_{\mathit{ik},\xi ,J^{\prime }}\right\}$, there exists C₀ > 0 such that, for large n,

$$P\left(\underset{0\le J\ne J^{\prime }\le N_{\mathrm{s}}}{\sup }\left|N_{\mathrm{T}}^{-1}{\sum }_{k=1}^{\kappa }{\sum }_{i=1}^n{R}_{\mathit{ik},\xi ,J}{R}_{\mathit{ik},\xi ,J^{\prime }}\right|\le C_0{h}_{\mathrm{s}}\right)\ge 1-2n^{-3}.$$

Putting the above together, for large n, $C_1=C_0{(c_{\sigma }^2/2)}^{-1}$,

$$P\left({\sup }_{0\le J\ne J^{\prime }\le N_{\mathrm{s}}}\mid C_{n,J,J^{\prime }}\mid \le C_1{h}_{\mathrm{s}}\right)\ge 1-4n^{-3}.$$

Note that as a continuous random variable, sup_{0≤J≠J′≤Ns}|C_n,J,J′| ∈ [0, 1], thus

$$E\left({\sup }_{0\le J\ne J^{\prime }\le N_{\mathrm{s}}}\mid C_{n,J,J^{\prime }}\mid \right)={\mathit{\int }}_0^{1}P\left({\sup }_{0\le J\ne J^{\prime }\le N_{\mathrm{s}}}\mid C_{n,J,J^{\prime }}\mid >t\right)\mathit{dt}.$$

For large n, C₁h_s < 1 and then E (sup_{0≤J≠J′≤Ns} |C_n,J,J′|) is

$$\begin{array}{c}{\mathit{\int }}_0^{C_1{h}_{\mathrm{s}}}P\left\{{\sup }_{0\le J\ne J^{\prime }\le N_{\mathrm{s}}}\mid C_{n,J,J^{\prime }}\mid >t\right\}\mathit{dt}+{\mathit{\int }}_{C_1{h}_{\mathrm{s}}}^{1}P\left\{{\sup }_{0\le J\ne J^{\prime }\le N_{\mathrm{s}}}\mid C_{n,J,J^{\prime }}\mid >t\right\}\mathit{dt}\\ \le {\mathit{\int }}_0^{C_1{h}_{\mathrm{s}}}1\mathit{dt}+{\mathit{\int }}_{C_1{h}_{\mathrm{s}}}^{1}4n^{-3}\mathit{dt}\le C_1{h}_{\mathrm{s}}+4n^{-3}\le {\mathit{Ch}}_{\mathrm{s}}\end{array}$$

for some C > 0 and large enough n. The lemma now follows from

$${\sup }_{0\le J\ne J^{\prime }\le N_{\mathrm{s}}}|E(C_{n,J,J^{\prime }})|\le E({\sup }_{0\le J\ne J^{\prime }\le N_{\mathrm{s}}}|C_{n,J,J^{\prime }}|)\le {\mathit{Ch}}_{\mathrm{s}}.$$

By Lemma A.8, the (N_s + 1) standard normal variables η₀, …, η_Ns satisfy the conditions of Lemma A.2 Hence for any τ ∈ R,

$$\underset{n\to \infty }{\lim }P\left({\sup }_{x\in \left[0,1\right]}\mid \eta \left(x\right)\mid \le \tau /a_{N_{\mathrm{s}}+1}+b_{N_{\mathrm{s}}+1}\right)=\exp \left(-2e^{-\tau }\right).$$ (8.7)

For x ∈ [0, 1], R_ik,ξ,J, R_ij,ε,J given in (8.2), define the ratio of population and sample quantities as r_n(x) = {nE (N₁) / N_T}^1/2 {R̄_n(x) / R̄(x)}^1/2, with

$$\begin{array}{c}{\overline{R}}_n(x)=N_{\mathrm{T}}^{-1}\{{\sum }_{i=1}^n({\sum }_{k=1}^{\kappa }{R}_{\mathit{ik},\xi ,J(x)}^2+{\sum }_{j=1}^{N_i}{R}_{\mathit{ij},\epsilon ,J(x)}^2)\}\\ \overline{R}(x)={\left({\mathit{EN}}_1\right)}^{-1}{\sum }_{k=1}^{\kappa }{\mathit{ER}}_{1k,\xi ,J(x)}^2+{\mathit{ER}}_{11,\epsilon ,J(x)}^2.\end{array}$$

Lemma A.9

Under Assumptions (A2), (A3), for η(x), σ_n(x) in (8.6), (2.3),

$$\mid {\sigma }_n{(x)}^{-1}\left\{{\sum }_{k=1}^{\kappa }{\widehat{\xi }}_k(x)+{\widehat{\epsilon }}^{(0)}(x)\right\}-\eta (x)\mid =\mid r_n(x)-1\mid \mid \eta (x)\mid$$ (8.8)

as n → ∞, ${\sup }_{x\in [0,1]}\{a_{N_{\mathrm{s}}+1}\mid r_n(x)-1\mid \}=O_{a.\mathrm{s}.}\left(\sqrt{\{\mathit{log}(N_{\mathrm{s}}+1)\}(\mathit{logn})/({\mathit{nh}}_{\mathrm{s}})}\right)$.

Proof

Equation (8.8) follows from the definitions of η(x) and σ_n(x). By Lemma A.6, ${\sup }_{x\in [0,1]}\mid N_{\mathrm{T}}^{-1}\sum _{i=1}^n\sum _{j=1}^{N_i}{R}_{\mathit{ij},\epsilon ,J(x)}^2-{\mathit{ER}}_{11,\epsilon ,J(x)}^2\mid =O_{\mathrm{a}.\mathrm{s}.}\left(\sqrt{\log n/({\mathit{nh}}_{\mathrm{s}})}\right),$,

$$\begin{array}{c}{\sup }_{x\in [0,1]}\mid N_{\mathrm{T}}^{-1}{\sum }_{k=1}^{\kappa }{\sum }_{i=1}^n{R}_{\mathit{ik},\xi ,J(x)}^2-{({\mathit{EN}}_1)}^{-1}{\sum }_{k=1}^{\kappa }{\mathit{ER}}_{1k,\xi ,J(x)}^2\mid \\ \le {\sup }_{x\in [0,1]}{\left({\mathit{EN}}_1\right)}^{-1}{\sum }_{k=1}^{\kappa }\mid n^{-1}{\sum }_{i=1}^n{R}_{\mathit{ik},\xi ,J(x)}^2-{\mathit{ER}}_{1k,\xi ,J(x)}^2\mid \\ +{\sup }_{x\in [0,1]}{\left({\mathit{EN}}_1\right)}^{-1}{\sum }_{k=1}^{\kappa }|n({\mathit{EN}}_1)N_{\mathrm{T}}^{-1}-1|\mid n^{-1}{\sum }_{i=1}^n{R}_{\mathit{ik},\xi ,J(x)}^2\mid \\ =O_{\mathrm{a}.\mathrm{s}.}\left(\sqrt{\log n/({\mathit{nh}}_{\mathrm{s}})}\right)+O_{\mathrm{a}.\mathrm{s}.}=\left(n^{-1/2}\right)=O_{\mathrm{a}.\mathrm{s}.}\left(\sqrt{\log n/({\mathit{nh}}_{\mathrm{s}})}\right),\end{array}$$

and there exist constants 0 < c_R̄ < C_R̄ < ∞ such that for all x ∈ [0,1], c_R̄ < R̄(x) < C_R̄. Thus, sup_x∈[0,1] |R̄_n(x) − R̄(x)| is bounded by

$$\begin{array}{c}{\sup }_{x\in [0,1]}\mid N_{\mathrm{T}}^{-1}{\sum }_{k=1}^{\kappa }{\sum }_{i=1}^n{R}_{\mathit{ik},\xi ,J(x)}^2-{({\mathit{EN}}_1)}^{-1}{\sum }_{k=1}^{\kappa }{\mathit{ER}}_{1k,\xi ,J(x)}^2\mid +\\ {\sup }_{x\in [0,1]}\mid N_{\mathrm{T}}^{-1}{\sum }_{i=1}^n{\sum }_{j=1}^{N_i}{R}_{\mathit{ij},\epsilon ,J(x)}^2-{\mathit{ER}}_{11,\epsilon ,J(x)}^2\mid =O_{\mathrm{a}.\mathrm{s}.}\left(\sqrt{\log n/({\mathit{nh}}_{\mathrm{s}})}\right).\end{array}$$

Thus $\underset{x\in [0,1]}{\sup }\mid {\left\{{\overline{R}}_n(x)\right\}}^{1/2}-{\left\{\overline{R}(x)\right\}}^{1/2}\mid \le \underset{x\in [0,1]}{\sup }\mid {\overline{R}}_n(x)-\overline{R}(x)\mid \underset{x\in [0,1]}{\sup }{\left\{\overline{R}(x)\right\}}^{-1/2}=O_{\mathrm{a}.\mathrm{s}.}\left(\sqrt{\log n/({\mathit{nh}}_{\mathrm{s}})}\right)$. Then sup_x∈[0,1] {a_Ns+1 |r_n(x) − 1|} is bounded by

$$\begin{array}{l}{a}_{N_{\mathrm{s}}+1}\left\{{\{\mathit{nE}(N_1)/N_{\mathrm{T}}\}}^{1/2}\underset{x\in [0,1]}{\sup }\mid {\{{\overline{R}}_n(x)/\overline{R}(x)\}}^{1/2}-1\mid +\mid 1-{\{\mathit{nE}(N_1)/N_{\mathrm{T}}\}}^{1/2}\mid \right\}\\ \le a_{N_{\mathrm{s}}+1}\left\{{\{\mathit{nE}(N_1)/N_{\mathrm{T}}\}}^{1/2}\underset{x\in [0,1]}{\sup }{\{\overline{R}(x)\}}^{-1/2}\underset{x\in [0,1]}{\sup }\mid {\left\{{\overline{R}}_n(x)\right\}}^{1/2}-{\left\{\overline{R}(x)\right\}}^{1/2}\mid +\mid 1-{\{\mathit{nE}(N_1)/N_{\mathrm{T}}\}}^{1/2}\mid \right\}=O_{\mathrm{a}.\mathrm{s}.}\left(\sqrt{\{\log (N_{\mathrm{s}}+1)\}(\log n)/({\mathit{nh}}_{\mathrm{s}})}\right).\end{array}$$

Proof of Proposition 2

The proof follows from Lemmas A.5, A.7, A.9, (8.7), and Slutsky’s Theorem.

Proof of Theorem 1

By Theorem 2, ∥m̃(x) − m(x)∥_∞ = O_p (h_s), so

$$\begin{array}{c}{a}_{N_{\mathrm{s}}+1}\left(\underset{x\in [0,1]}{\sup }{\sigma }_n^{-1}(x)|\stackrel{\sim }{m}(x)-m(x)|\right)=O_p\left\{{({\mathit{nh}}_{\mathrm{s}})}^{1/2}\sqrt{\log (N_{\mathrm{s}}+1)h_{\mathrm{s}}}\right\}=o_p(1),\\ a_{N_{\mathrm{s}}+1}\left(\underset{x\in [0,1]}{\sup }{\sigma }_n^{-1}(x)|\widehat{m}(x)-m(x)|-\underset{x\in [0,1]}{\sup }{\sigma }_n^{-1}(x)\left|\sum _{k=1}^{\kappa }{\stackrel{\sim }{\xi }}_k(x)+\stackrel{\sim }{\epsilon }(x)\right|\right)=o_p(1).\end{array}$$

Meanwhile, (3.4) and Proposition 2 entail that, for any τ ∈ R,

$$\underset{n\to \infty }{\lim }P\left\{a_{N_{\mathrm{s}}+1}\left(\underset{x\in [0,1]}{\sup }{\sigma }_n^{-1}(x)\mid \sum _{k=1}^{\kappa }{\stackrel{\sim }{\xi }}_k(x)+\stackrel{\sim }{\epsilon }(x)\mid -b_{N_{\mathrm{s}}+1}\right)\le \tau \right\}=\exp (-2e^{-\tau }).$$

Thus Slutsky’s Theorem implies that

$$\underset{n\to \infty }{\lim }P\left\{a_{N_{\mathrm{s}}+1}\left(\underset{x\in [0,1]}{\sup }{\sigma }_n^{-1}(x)\mid \widehat{m}(x)-m(x)\mid -b_{N_{\mathrm{s}}+1}\right)\le \tau \right\}=\exp (-2e^{-\tau }).$$

Let $\tau =-\log \left\{-\frac{1}{2}\log (1-\alpha )\right\}$, definitions of a_Ns+1, b_Ns+1, and Q_Ns+1 (α) in (2.4) entail

$$\begin{array}{c}\underset{n\to \infty }{\lim }P\left\{m(x)\in \widehat{m}(x)\pm {\sigma }_n(x)Q_{N_{\mathrm{s}}+1}(\alpha ),\forall x\in [0,1]\right\}\\ =\underset{n\to \infty }{\lim }P\left\{Q_{N_{\mathrm{s}}+1}^{-1}(\alpha )\underset{x\in [0,1]}{\sup }{\sigma }_n^{-1}(x)\mid \stackrel{\sim }{e}(x)+\stackrel{\sim }{m}(x)-m(x)\mid \le 1\right\}=1-\alpha .\end{array}$$

by (3.4). That σ_n(x)⁻¹ {m̂(x) − m(x)} →_d N (0, 1) for any x ∈ [0, 1] follows by directly using η(x) ~ N (0, 1), without reference to sup_x∈[0,1] |η(x)|.