Bayesian Spatial Quantile Regression

Abstract

Tropospheric ozone is one of the six criteria pollutants regulated by the United States Environmental Protection Agency under the Clean Air Act and has been linked with several adverse health effects, including mortality. Due to the strong dependence on weather conditions, ozone may be sensitive to climate change and there is great interest in studying the potential effect of climate change on ozone, and how this change may affect public health. In this paper we develop a Bayesian spatial model to predict ozone under different meteorological conditions, and use this model to study spatial and temporal trends and to forecast ozone concentrations under different climate scenarios. We develop a spatial quantile regression model that does not assume normality and allows the covariates to affect the entire conditional distribution, rather than just the mean. The conditional distribution is allowed to vary from site-to-site and is smoothed with a spatial prior. For extremely large datasets our model is computationally infeasible, and we develop an approximate method. We apply the approximate version of our model to summer ozone from 1997–2005 in the Eastern U.S., and use deterministic climate models to project ozone under future climate conditions. Our analysis suggests that holding all other factors fixed, an increase in daily average temperature will lead to the largest increase in ozone in the Industrial Midwest and Northeast.

1. INTRODUCTION

Beginning in 1970, the United States Clean Air Act (CAA) directed the U.S. Environmental Protection Agency (EPA) to consider the best available science on exposure to and effects of several ambient air pollutants, emitted by a wide array of sources. National Ambient Air Quality Standards (NAAQS) were set for pollutants to which the public was widely exposed. Since the inception of NAAQS, EPA has determined that photochemical-oxidant air pollution, formed when specific chemicals in the air react with light and heat, is of sufficient public-health concern to merit establishment of a primary NAAQS. EPA has since 1979 identified ozone, a prominent member of the class of photochemical oxidants, as an indicator for setting the NAAQS and tracking whether areas of the country are in compliance with the standards. To attain the current ozone standard, the three-year average of the fourth-highest daily maximum eight-hour average ozone concentrations measured at each monitor within an area over each year must not exceed 0.075 ppm (standard effective since May 27, 2008).

Most ozone in the troposphere is not directly emitted to the atmosphere, although there are minor sources of such ozone, including some indoor air cleaners. Rather, it is formed from a complex series of photochemical reactions of the primary precursors: nitrogen oxides (NOx), volatile organic compounds (VOCs), and to a smaller extent other pollutants, such as carbon monoxide (CO). Since the reactions that form ozone are driven by sunlight, ambient ozone concentrations exhibit both diurnal variation (they are typically highest during the afternoon) and marked seasonal variation (they are highest in summer). Ambient concentrations are highest during hot, sunny summer episodes characterized by low ventilation (a result of low winds and low vertical mixing).

Due to the strong dependence on weather conditions, ozone levels may be sensitive to climate change (Seinfeld and Pandis 2006). There is great interest in studying the potential effect of climate change on ozone levels, and how this change may affect public health (Bernard et al. 2001; Haines and Patz 2004; Knowlton et al. 2004; Bell et al. 2007). In this article we also study the potential changes in ozone due to climatic change. This type of work is needed to address the impact of climate change on emission control strategies designed to reduce air pollution. Using future numerical climate model forecasts of meteorological conditions, we forecast potential future increases or decreases in ozone levels. In particular, based on current relationships between temperature, cloud cover, wind speed, and ground-level ozone, we predict the percent change in ozone given future temperature and cloud cover levels.

The objective of the article is to develop an effective statistical model for the daily tropospheric ozone distribution as a function of daily meteorological variables. The daily model is then used to study trends in ozone levels over space and time, and to forecast yearly summaries of ozone under different climate scenarios. We build our model using spatial methods to borrow strength across nearby locations. Several spatial models have been proposed for ozone (Guttorp, Meiring, and Sampson 1994; Carroll et al. 1997; Meiring, Guttorp, and Sampson 1998; Huang and Hsu 2004; Huerta, Sanso, and Stroud 2004; Gilleland and Nychka 2005; Sahu, Gelfand, and Holland 2007). These models assume normality for either untransformed ozone or for the square root of ozone. Exploratory analysis suggests that ozone data are non-Gaussian even after a square root transformation. Ozone is often right-skewed (Lee et al. 2006; Zhang and Fan 2008) in which case Gaussian models may underestimate the tail probability. Correctly estimating the tail probability is critically important in studying the health effects of ozone exposure, and has policy implications because EPA standards are based on the fourth highest day of the year (approximately the 99th percentile). A further challenge is that the relationship between meteorological predictors and the ozone response can be nonlinear and the meteorological effects are not restricted to the mean. The variance and skewness of the response varies depending on location and meteorological conditions. Recently several methods have been developed for non-Gaussian spatial modeling (Gelfand, Kottas, and MacEachern 2005; Griffin and Steel 2006; Reich and Fuentes 2007; Dunson and Park 2008). These methods treat the conditional distribution of the response given the spatial location and the covariates as an unknown quantity to be estimated from the data. We follow this general approach to model the conditional ozone density.

Although these models are quite flexible, one drawback is the difficulty in interpreting the effects of each covariate. For example, many of these models are infinite mixtures, where the spatial location and/or covariates affect the mixture probabilities. In this very general framework, it is difficult to make inference on specific features of the conditional density, for example, whether there is an interaction between cloud cover and temperature, or whether there is a statistically significant time trend in the distribution’s upper tail probability. As a compromise between fully-general Bayesian density regression and the usual additive mean regression, we propose a Bayesian spatial quantile regression model. Quantile regression models the distribution’s quantiles as additive functions of the predictors. This additive structure permits inference on the effect of individual covariates on the response’s quantiles.

There is a vast literature on quantile regression (e.g., Koenker 2005), mostly from the frequentist perspective. The standard model-free approach is to estimate the effect of the covariates separately for a few quantile levels by minimizing an objective function. This approach is popular due to computational convenience and theoretical properties. Sousa et al. (2008) applied the usual quantile regression method to ozone data and found it to be superior to multiple linear regression, especially for predicting extreme events. An active area of research is incorporating clustering into the model-free approach (Jung 1996; Lipsitz et al. 1997; Koenker 2004; Wang and He 2007; Wang and Fygenson 2008). Recently, Hallin, Lu, and Yu (2009) propose a quantile regression model for spatial data on a grid. They allow the regression coefficients to vary with space using local regression. This approach, and most other model-free approaches, perform separate analyses for each quantile level of interest. As a result, the quantile estimates can cross, that is, for a particular combination of covariates the estimated quantile levels are nonincreasing, which causes problems for prediction. Several post-hoc methods have been proposed to address this problem (He 1997; Yu and Jones 1998; Takeuchi et al. 2006; Dette and Volgushev 2008) for nonspatial data.

Incorporating spatial correlation may be more natural in a Bayesian setting, which necessarily specifies a likelihood for the data. Model-based Bayesian quantile regression methods for independent (Kottas and Gelfand 2001; Yu and Moyeed 2001; Hjort and Walker 2009; Kottas and Krnjajic 2009) and clustered (Geraci and Bottai 2007) data that focus on a single quantile level have been proposed. Dunson and Taylor (2005) propose a method to simultaneously analyze a finite number of quantile levels for independent data. To our knowledge, we propose the first model-based approach for spatial quantile regression.

Rather than focusing on a single or finite number of quantile levels, our approach is to specify a flexible semiparametric model for the entire quantile process across all covariates and quantile levels. We assume the quantile function at each quantile level is a linear combination of the covariates and model the quantile functions using a finite number of basis functions with constraints on the basis coefficients to ensure that the quantile function is noncrossing for all covariate values. An advantage of this approach is that we can center the prior for the conditional density on a parametric model, for example, multiple linear regression with skew-normal errors. Our model is equipped with parameters that control the strength of the parametric prior. Also, the quantile function, and thus the conditional density, is allowed to vary spatially. Spatial priors on the basis coefficients are used to allow the quantile process to vary smoothly across space.

The article proceeds as follows. Section 2 proposes the spatial quantile regression model. While this model is computationally efficient for moderately sized datasets, it is not feasible for very large datasets. Therefore Section 3 describes an approximate model which is able to handle several years of daily data for the entire Eastern U.S. Section 4 conducts a brief simulation to compare our model with other methods and examine sensitivity to hyperprior choice. In Section 5 we analyze a large spatiotemporal ozone dataset. We discuss meteorologically adjusted spatial and temporal trends for different quantile levels and use the estimated conditional densities to forecast future ozone levels using deterministic climate model output. Section 6 concludes.

2. BAYESIAN QUANTILE REGRESSION FOR SPATIOTEMPORAL DATA

Let y_i be the observed eight-hour maximum ozone for space/time location (s, t)_i, and denote the day and spatial location of the ith observation as t_i and s_i, respectively. Our interest lies in estimating the conditional density of y_i as a function of s_i and covariates X_i = (X_i1, … , X_ip)′, where X_i1 = 1 for the intercept. In particular, we would like to study the conditions that lead to extreme ozone days. Extreme events are often summarized with return levels. The n-day return level is the value c_n so that P(y_i > c_n) = 1/n. Given our interest in extreme events and return levels, we model y_i’s conditional density via its quantile (inverse CDF) function q(τ|X_i, s_i), which is defined so that P{y_i < q(τ|X_i, s_i)} = τ ∈ [0, 1]. We model q(τ|X_i, s_i) as

$$q(\tau \mid {\mathbf{X}}_i,{\mathbf{s}}_i)={\mathbf{X}}_i^{\prime }\beta (\tau ,{\mathbf{s}}_i),$$ (1)

where β(τ, s_i) = (β₁(τ, s_i), … , β_p(τ, s_i))′ are the spatially varying coefficients for the τth quantile level. Directly modeling the quantile function makes explicit the effect of each covariate on the probability of an extreme value.

Several popular models arise as special cases of Model (1). For example, setting β_j(τ, s) ≡ β_j for all τ, s, and j > 1 gives the usual linear regression model with location shifted by ${\sum }_{j=2}^p{X}_{ij}{\beta }_j$ and residual density determined by β₁(τ, s). Also, setting β_j(τ, s) ≡ β_j(s) for all τ and j > 1 gives the spatially varying coefficients model (Gelfand et al. 2003) where the effect of X_j on the mean varies across space via the spatial process β_j(s). Allowing β_j(τ, s) to vary with s and τ relaxes the assumption that the covariates simply affect the mean response, and gives a density regression model where the covariates are allowed to affect the shape of the response distribution. In particular, the covariates can have different effects on the center (τ = 0.5) and tails (τ ≈ 0 and τ ≈ 1) of the density.

2.1 Model for the Quantile Process

We begin modeling the quantile function by ignoring spatial location and assuming the intercept-only model with X_i = 1. In this case, the quantile function in (1) reduces to q(τ) = β(τ). The process β(τ) must be constructed so that q(τ) is nondecreasing in τ. Let

$$\beta \left(\tau \right)=\sum _{m=1}^M{\mathit{B}}_m\left(\tau \right){\alpha }_m,$$ (2)

where M is the number of basis functions, B_m(τ) is a known basis function of τ, α_m are unknown coefficients that determine the shape of the quantile function. We use Bernstein basis polynomials

$${\mathit{B}}_m\left(\tau \right)=\left(\begin{array}{c}\hfill M\hfill \\ \hfill m\hfill \end{array}\right){\tau }^m{(1-\tau )}^{M-m}.$$ (3)

An attractive feature of these basis functions is that if α_m ≥ α_m−1 for all m > 1, then β(τ), and thus q(τ), is an increasing function of τ. This reduces the complicated monotonicity constraint to a sequence of simple constraints δ_m = α_m − α_m−1 ≥ 0, for m = 2, … , M. These constraints are sufficient, but not necessary, to ensure an increasing function. As is typical for semiparametric models, for finite M this model does not span the entire class of continuous monotonic functions. However, as M increases, the Bernstein polynomials basis with these constraints induces a prior with dense support on the space of continuous monotone functions from $[0,1]\to \mathcal{R}$ (Chang et al. 2007).

Since the constraints on α = (α₁, … , α_M) are expressed in terms of the difference between adjacent terms, we reparameterize to δ₁ = α₁ and δ_m = α_m − α_m−1 for m = 2, … , M. The original basis function coefficients are then ${\alpha }_m={\sum }_{l=1}^m{\delta }_l$. Following Cai and Dunson (2007), we ensure the quantile constraint by introducing a latent unconstrained variable ${\delta }_m^{\ast }$ and taking ${\delta }_1={\delta }_1^{\ast }$ and

$${\delta }_m=\{\begin{array}{cc}{\delta }_m^{\ast },\hfill & {\delta }_m^{\ast }\ge 0\hfill \\ 0,\hfill & {\delta }_m^{\ast }<0\hfill \end{array}\phantom{\}}$$ (4)

from m > 1.

The ${\delta }_m^{\ast }$ have independent normal priors ${\delta }_m^{\ast }~\mathrm{N}\left({\stackrel{‒}{\delta }}_m\right(ϴ),{\sigma }^2)$, with unknown hyperparameters Θ. We pick ${\stackrel{‒}{\delta }}_m\left(ϴ\right)$ to center the quantile process on a parametric distribution f₀(y|Θ), for example, a $\mathrm{N}({\mu }_0,{\sigma }_0^2)$ random variable with Θ = (μ₀,σ₀). Letting q₀(τ|Θ) be the quantile function of f₀(y|Θ), the ${\stackrel{‒}{\delta }}_m\left(ϴ\right)$ are then chosen so that

$$q_0(\tau \mid ϴ)\approx \sum _{m=1}^M{\mathit{B}}_m\left(\tau \right){\stackrel{‒}{\alpha }}_m\left(ϴ\right),$$ (5)

where ${\stackrel{‒}{\alpha }}_m\left(ϴ\right)={\sum }_{l=1}^m{\stackrel{‒}{\delta }}_l\left(ϴ\right)$. The ${\stackrel{‒}{\delta }}_m\left(ϴ\right)$ are chosen to correspond to the following ridge regression estimator:

$$\begin{array}{cc}\hfill & {\left({\stackrel{‒}{\delta }}_1\right(ϴ),\dots ,{\stackrel{‒}{\delta }}_M(ϴ\left)\right)}^{\prime }\hfill \\ \hfill & =\underset{d}{\arg \min }\sum _{k=1}^K{\left(q_0({\tau }_k\mid ϴ)-\sum _{m=1}^M{\mathit{B}}_m\left({\tau }_k\right)\left[\sum _{l=1}^m{d}_l\right]\right)}^2\hfill \\ \hfill & +\lambda \sum _{m=1}^M{d}_m^2,\hfill \end{array}$$ (6)

where d_m ≥ 0 for m > 1, {τ₁, … , τK} is a dense grid on (0, 1). We find that simple parametric quantile curves can often be approximated almost perfectly with fewer than M terms. Therefore several combinations of d give essentially the same fit, including some undesirable solutions with negative values for elements of $\stackrel{‒}{\delta }$. For numerical stability we add the ridge penalty $\lambda {\sum }_{m=1}^M{d}_m^2$. Setting the tuning constant λ to zero gives the unpenalized fit and setting λ to infinity gives $\stackrel{‒}{\delta }=0$ for all terms. We pick λ = 1 because this allows the parametric quantile curve to be approximated well and gives $\stackrel{‒}{\delta }$ values that vary smoothly from term to term. As σ → 0, the quantile functions this resembles are increasing shrunk towards the parametric quantile function q₀(τ|Θ), and the likelihood is similar tof f₀(y|Θ).

2.2 Model for the Spatial Quantile Process With Covariates

Adding covariates, the conditional quantile function becomes

$$q(\tau \mid {\mathbf{X}}_i)={\mathbf{X}}_i^{\prime }\beta \left(\tau \right)=\sum _{j=1}^p{X}_{ij}{\beta }_j\left(\tau \right).$$ (7)

As in Section 2.1, the quantile curves are modeled using Bernstein basis polynomials

$${\beta }_j\left(\tau \right)=\sum _{m=1}^M{\mathit{B}}_m\left(\tau \right){\alpha }_{jm},$$ (8)

where α_jm are unknown coefficients. The processes β_j (τ) must be constructed so that q(τ|X_i) is nondecreasing in τ for all X_i. Collecting terms with common basis functions gives

$${\mathbf{X}}_i^{\prime }\beta \left(\tau \right)=\sum _{m=1}^M{\mathit{B}}_m\left(\tau \right){\theta }_m\left({\mathbf{X}}_i\right),$$ (9)

where ${\theta }_m\left({\mathbf{X}}_i\right)={\sum }_{j=1}^p{X}_{ij}{\alpha }_{jm}$. Therefore, if ${\theta }_m\left({\mathbf{X}}_i\right)\ge {\theta }_{m-1}\left({\mathbf{X}}_i\right)$ for all m > 1, then ${\mathbf{X}}_i^{\prime }\beta \left(\tau \right)$, and thus q(τ|X_i), is an increasing function of τ.

To specify our prior for the β_jm to ensure monotonicity, we assume that X_i1 = 1 for the intercept and the remaining covariates are suitably scaled so that X_ij ∈ [0, 1] for j > 1. Since the constraints are written in terms of the difference between adjacent terms, we reparameterize to δ_j1 = α_j1 and δ_jm = α_jm − α_jm−1 for m = 2, … , M. We ensure the quantile constraint by introducing latent unconstrained variable ${\delta }_{jm}^{\ast }~\mathrm{N}\left({\stackrel{‒}{\delta }}_{jm}\right(ϴ),{\sigma }_j^2)$ and taking

$${\delta }_{jm}=\{\begin{array}{cc}{\delta }_{jm}^{\ast },\hfill & {\delta }_{1m}^{\ast }+\sum _{j=2}^p\mathit{I}({\delta }_{jm}^{\ast }<0){\delta }_{jm}^{\ast }\ge 0\hfill \\ 0,\hfill & \text{otherwise}\hfill \end{array}\phantom{\}}$$ (10)

for all j = 1, … , p and m = 1, … , M. Recalling X_i1 = 1 and X_ij ∈ [0, 1] for j = 2, … , p, and thus X_ijδ_jm ≥ X_ijI(δ_jm < 0)δ_jm ≥ I (δ_jm < 0)δ_jm for j > 1,

$$\begin{array}{cc}\hfill {\theta }_m& \left({\mathbf{X}}_i\right)-{\theta }_{m-1}\left({\mathbf{X}}_i\right)\hfill \\ \hfill & =\sum _{j=1}^p{\mathit{X}}_{ij}{\delta }_{jm}\ge {\delta }_{1m}+\sum _{j=2}^p{\mathit{X}}_{ij}\mathit{I}({\delta }_{jm}<0){\delta }_{jm}\hfill \\ \hfill & \ge {\delta }_{1m}+\sum _{j=2}^p\mathit{I}({\delta }_{jm}<0){\delta }_{jm}\ge 0\hfill \end{array}$$ (11)

for all X_i, giving a valid quantile process. As in Section 2.1 we center the intercept curve on a parametric quantile function q₀(Θ). The remaining coefficients have ${\stackrel{‒}{\delta }}_{jm}\left(ϴ\right)=0$ for j > 1.

Although this model is quite flexible, we have assumed that the quantile process is a linear function of the covariates, simplifying interpretation. In some applications the linear quantile relationship may be overly restrictive. In this case, transformations of the original predictors such as interactions or basis functions can be added to give a more flexible model. However, (10) may be prohibitive if quadratic or higher-order terms are added to the model since (10) unnecessarily restricts the quantile function for combinations of the covariates that can never occur, for example, the linear term being zero and the quadratic term being one. Also, the linear relationship between the predictors and the response is not invariant to transformations of the response. To alleviate some sensitivity to transformations, it may be possible to develop a nonlinear model for q(τ|X_i), so that q(τ|X_i) and T(q(τ|X_i)) span the same class of functions (and therefore response distributions) for a class of transformations T.

For spatial data, we allow the quantile process to be different at each spatial location,

$${\beta }_j(\tau ,\mathbf{s})=\sum _{m=1}^M{\mathit{B}}_m\left(\tau \right){\alpha }_{jm}\left(\mathbf{s}\right),$$ (12)

where α_jm(s) are spatially varying basis-function coefficients. We enforce the monotonicity constraint at each spatial location by introducing latent Gaussian parameters ${\delta }_{jm}^{\ast }\left(\mathbf{s}\right)$. The latent parameters relate to the basis-function coefficients as ${\alpha }_{jm}\left(\mathbf{s}\right)={\sum }_{l=1}^m{\delta }_{jl}\left(\mathbf{s}\right)$ and

$${\delta }_{jm}\left(\mathbf{s}\right)=\{\begin{array}{cc}{\delta }_{jm}^{\ast }\left(\mathbf{s}\right),\hfill & {\delta }_{1m}^{\ast }\left(\mathbf{s}\right)+\sum _{j=2}^p\mathit{I}\left({\delta }_{jm}^{\ast }\right(\mathbf{s})<0){\delta }_{jm}^{\ast }\left(\mathbf{s}\right)\ge 0\hfill \\ 0,\hfill & \text{otherwise}\hfill \end{array}\phantom{\}}$$ (13)

for all j = 1, … , p and m = 1, … , M.

To encourage the conditional density functions to vary smooth across space we model the ${\delta }_{jm}^{\ast }\left(\mathbf{s}\right)$ as spatial processes. The ${\delta }_{jm}^{\ast }\left(\mathbf{s}\right)$ are independent (over j and m) Gaussian spatial processes with mean $E\left({\delta }_{jm}^{\ast }\right(\mathbf{s}\left)\right)={\stackrel{‒}{\delta }}_{jm}\left(ϴ\right)$ and exponential spatial covariance $\mathrm{Cov}\left({\delta }_{jm}^{\ast }\right(\mathbf{s}),{\delta }_{jm}^{\ast }({\mathbf{s}}^{\prime }\left)\right)={\sigma }_j^2\exp (-\mid \mid \mathbf{s}-{\mathbf{s}}^{\prime }\mid \mid ∕{\rho }_j)$, where ${\sigma }_j^2$ is the variance of ${\delta }_{jm}^{\ast }\left(\mathbf{s}\right)$ and ρ_j determines the range of the spatial correlation function.

3. APPROXIMATE METHOD

Section 2’s spatial quantile regression model can be implemented efficiently for moderately sized datasets. However, it becomes computationally infeasible for Section 5.3’s analysis of several years of daily data for the Eastern U.S. To approximate the full Bayesian analysis, we propose a two-stage approach related to that of Daniels and Kass (1999). We first perform separate quantile regression at each site for a grid of quantile levels to obtain estimates of the quantile process and their asymptotic covariance. In a second stage, we analyze these initial estimates using the Bayesian spatial model for the quantile process.

The usual quantile regression estimate (Koenker 2005) for quantile level τ_k and spatial location s is

$$\begin{array}{cc}\hfill & ({\widehat{\beta }}_1{({\tau }_k,\mathbf{s}),\dots ,{\widehat{\beta }}_p({\tau }_k,\mathbf{s}))}^{\prime }\hfill \\ \hfill & =\underset{\beta }{\arg \min }\sum _{s_i=s,y_i>{\mathbf{X}}_i^{\prime }\beta }{\tau }_k\mid y_i-{\mathbf{X}}_i^{\prime }\beta \mid \hfill \\ \hfill & +\sum _{s_i=s,y_i<{\mathbf{X}}_i^{\prime }\beta }({\tau }_k-1)\mid y_i-{\mathbf{X}}_i^{\prime }\beta \mid .\hfill \end{array}$$ (14)

This estimate is easily obtained from the quantreg package in R and is consistent for the true quantile function and has asymptotic covariance (Koenker 2005)

$$\mathrm{Cov}\left[\sqrt{n_s}\right({\widehat{\beta }}_1({\tau }_k,\mathbf{s}),\dots ,{\widehat{\beta }}_p({\tau }_k,\mathbf{s})),\sqrt{n_s}({\widehat{\beta }}_1({\tau }_l,\mathbf{s}),\dots ,{\widehat{\beta }}_p({\tau }_l,\mathbf{s})\left)\right]=H{\left({\tau }_k\right)}^{-1}J({\tau }_k,{\tau }_l)H{\left({\tau }_l\right)}^{-1},$$ (15)

where n_s is the number of observations at site s, $H\left(\tau \right)={\lim }_{n_s\to \infty }{n}_{\mathbf{s}}^{-1}{\sum }_{i=1}^{n_{\mathbf{s}}}{\mathbf{X}}_i{\mathbf{X}}_i^{\prime }{f}_i\left({\mathbf{X}}_i^{\prime }\widehat{\beta }\right(\tau \left)\right),f_i\left({\mathbf{X}}_i^{\prime }\widehat{\beta }\right(\tau \left)\right)$ is the conditional density of y_i evaluated at ${\mathbf{X}}_i^{\prime }\widehat{\beta }\left(\tau \right)$, and $J({\tau }_k,{\tau }_l)=[{\tau }_k\wedge {\tau }_l-{\tau }_k{\tau }_l]n_{\mathbf{s}}^{-1}\sum {\mathbf{X}}_i{\mathbf{X}}_i^{\prime }$.

Although consistent as the number of observations at a given site goes to ∞, these estimates are not smooth over space or quantile level, and do not ensure a noncrossing quantile function for all X. Therefore we smooth these initial estimates using the spatial model for the quantile process proposed in Section 2. Let $\widehat{\beta }\left({\mathbf{s}}_i\right)={\left[{\widehat{\beta }}_1\right({\tau }_1,{\mathbf{s}}_i),\dots ,{\widehat{\beta }}_1({\tau }_K,{\mathbf{s}}_i),{\widehat{\beta }}_2({\tau }_1,{\mathbf{s}}_i),\dots ,{\widehat{\beta }}_p({\tau }_K,{\mathbf{s}}_i\left)\right]}^{\prime }$ and $\mathrm{Cov}\left(\widehat{\beta }\right({\mathbf{s}}_i\left)\right)={\Sigma }_i$ [with elements defined by (15)]. We fit the model

$$\widehat{\beta }\left({\mathbf{s}}_i\right)~N\left(\beta \right({\mathbf{s}}_i),{\Sigma }_i),$$ (16)

where the elements of β(s_i) = [β₁(τ₁, s_i), … , β₁(τ_K, s_i), β₂(τ₁, s_i), … , β_p(τ_K, s_i)]′ are functions of Bernstein basis polynomials as in Section 2.2. This approximation provides a dramatic reduction in computational time because the dimension of the response is reduced from the number of observations at each site to the number of quantile levels in the approximation, and the posteriors for the parameters that define β are fully conjugate allowing for Gibbs updates and rapid convergence.

The correlation between initial estimates is often very high. To avoid numerical instability we pick the number of quantile levels in the initial estimate, K, so that the estimated correlation is no more than 0.95. For the simulated and real data, we use K = 10. Also, our experience with this approximation suggests that this approximation has coverage probability below the nominal level. Therefore, we inflate the estimated variance by a factor of c² and fit the model $\widehat{\beta }\left({\mathbf{s}}_i\right)~\mathrm{N}\left(\beta \right({\mathbf{s}}_i),c^2{\Sigma }_i)$. We pick c by first fitting the model with c = 1. We then generate R datasets from the fitted model, analyze each dataset with c = {0.5, 0.75, 1, 1.25, 1.5}, and compute the proportion (averaged over space, quantile level, and covariate) of the 90% intervals that cover the coefficients used to generate the data. We pick the smallest c with 90% coverage. For large datasets with many locations and several covariates we find R = 1 is sufficient to give reasonable coverage probabilities.

This simplification may permit extensions to more sophisticated spatial models for the basis coefficients, such as nonstationary and non-Gaussian spatial models. Details of the MCMC algorithm for this model and the full model are given in the Appendix. It may also be possible to develop an EM-type algorithm or a constrained optimization routine, although MCMC is well suited as described above.

4. SIMULATION STUDY

In this section we analyze simulated data to compare our method with standard quantile regression approaches, and to examine the performance of Section 3’s approximate method. For each of the S = 50 simulated datasets we generate n = 20 spatial locations s_i uniformly on [0, 1]². The p = 3 covariates are generated as X₁ ≡ 1 and $X_{i2},X_{i3}\stackrel{\mathrm{iid}}{~}\mathrm{U}(0,1)$, independent over space and time. The true quantile function is

$$q(\tau \mid {\mathbf{X}}_i,{\mathbf{s}}_i)=2s_{i2}+(\tau +1){\Phi }^{-1}\left(\tau \right)+\left(5s_{i1}{\tau }^2\right)X_{i3},$$ (17)

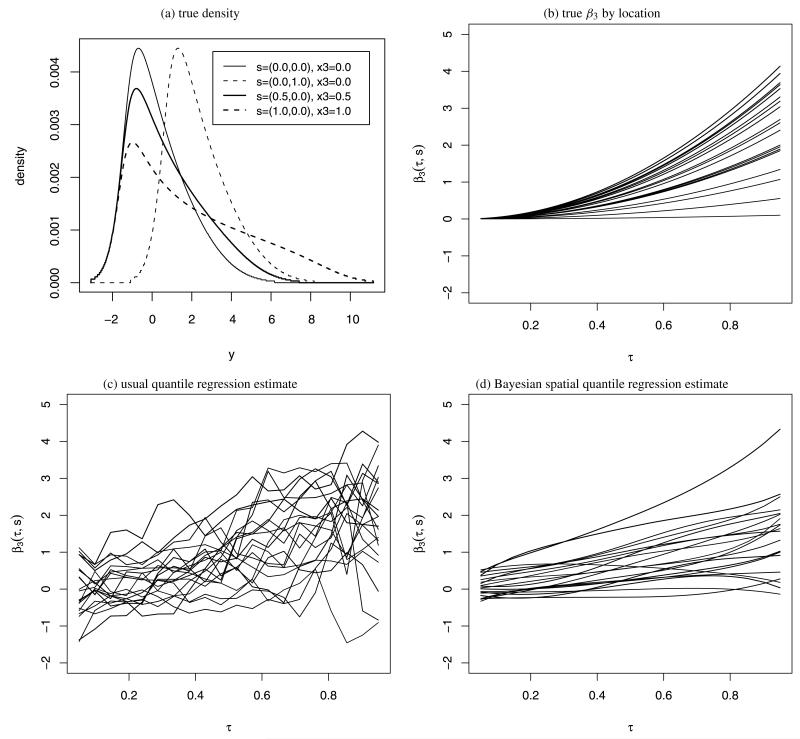
which implies that β₁(τ, s_i) = 2s_i2+(τ+1)Φ⁻¹(τ), β₂(τ, s_i) = 0, and β₃(τ, s_i) = 5s_i1τ², where Φ is the standard normal distribution function. Figure 1(a) plots the density corresponding to this quantile function for various covariates and spatial locations. The density is generally right-skewed to mimic ozone data. The second spatial coordinate simply shifts the entire distribution by increasing the intercept function β₁. The first predictor X₂ has no effect on the density because β₂(τ, s) = 0. The second predictor X₃ has little effect on the left tail because β₃(τ, s) is near zero for small τ, but increasing X₃ adds more mass to the density’s right tail.

Figure 1.

True and estimated quantile curves for the simulation study. Panel (a) gives the true density as a function of space and covariates, panel (b) plots the true quantile function β₃(s,τ), panel (c) plots the usual quantile estimate for one dataset, and panel (d) plots the posterior mean from spatial quantile regression for one dataset.

Each dataset contains 100 replicates at each spatial location. We first consider the situation where the replicates are independent over space and time. We also generate data with spatially and temporally correlated residuals using a Gaussian copula. To generate spatially correlated residuals, we first generate U_i as independent (over time) Gaussian processes with mean zero and exponential spatial covariance exp(−||s − s′||/ρ_Z), and then transform using the marginal quantile function $y_i=q_o\left[\Phi \right(U_i\left)\right]+{\sum }_{m=1}^M{B}_m\left[\Phi \right(U_i\left)\right]{\theta }_m({\mathbf{X}}_i,{\mathbf{s}}_i)$. We assume the spatial range of the residuals is ρ_Z = 0.5. We also generate data with no spatial correlation, but temporal correlation at each site. The latent Gaussian process at each site has mean zero and exponential covariance Cor(U_i, U_j) = exp(−|i − j′|/ρ_U), where ρ_U = −1/ log(0.5) so the correlation between subsequent sites is 0.5.

For each simulated dataset we fit three Bayesian quantile methods: the full model described in Section 2, the model in Section 2 without spatial modeling [i.e., ${\delta }_{jk}^{\ast }\stackrel{\mathrm{iid}}{~}\mathrm{N}\left({\stackrel{‒}{\delta }}_{jk}\right(ϴ),{\sigma }_j^2)$], and Section 3’s approximate method. For the Bayesian quantile regression models (full and approximate) we use M = 10 knots and vague yet proper priors for the hyperparameters that control the prior covariance of the quantile function, ${\sigma }_j^2$ ~ InvGamma(0.1, 0.1) and ρ_j ~ Gamma(0.06, 0.75). The prior for the ρ_j is selected so the effective range −ρ_j log(0.05), that is, the distance at which the spatial correlation equals 0.05, has prior mean 0.25 and prior standard deviation 1. The centering distribution f₀ was taken to be skew-normal (Azzalini 1985) with location μ₀ ~ N(0, 10²), scale ${\sigma }_0^2$ ~ InvGamma(0.1, 0.1), and skewness ψ₀ ~ N(0, 10²). We also compare our methods with the usual frequentist estimates in (14), computed using the quantreg package in R. Of course these estimates do not smooth over quantile level or spatial location, so they may not be directly comparable in this highly-structured setting.

For each simulated dataset and each method we compute point estimates (posterior means for Bayesian methods) and 90% intervals for β_j(τ_k, s_i) for j = 1, 2, 3, τ_k ∈ {0.05, 0.10, … , 0.95}, and all spatial locations s_i. We compare methods using mean squared error, coverage probability, and power (i.e., the proportion of times in repeated samples under the alternative that the 90% interval excludes zero) averaged over space, quantile levels, and simulated dataset. Specifically, mean squared error for the jth quantile function is computed as

$$MSE=\frac{1}{SnK}\sum _{sim=1}^S\sum _{i=1}^n\sum _{k=1}^K{({\widehat{\beta }}_j{({\tau }_k,s_i)}^{\left(sim\right)}-{\beta }_j({\tau }_k,s_i\left)\right)}^2,$$ (18)

where $\widehat{\beta }{({\tau }_k,s_i)}^{\left(sim\right)}$ is the point estimate for the simulation number sim. Coverage and power are computed similarly.

Table 1 presents the results. We first discuss the results without residual correlation. By borrowing strength across quantile level and spatial location all three Bayesian methods provide smaller mean squared error and higher power than the usual quantile regression approach. Figure 1(b) shows the true quantile curve for β₃ for each spatial location for one representative dataset with line width proportional to the first spatial coordinate. The usual estimates in Figure 1(c) fluctuate greatly across quantile levels compared to the smooth curves produced by the Bayesian spatial quantile regression model in Figure 1(d).

Table 1.

Simulation study results. MSE and coverage probabilities are averaged over spatial location, simulated dataset, and quantile level. Power is evaluated only for the 95th quantile level for β₃ and is averaged over space and simulated data set

Method	Corr. resids	MSE			Coverage			Power
		β 1	β 2	β 3	β 1	β 2	β 3	β 3
Quantreg	None	0.51 (0.06)	0.99 (0.11)	1.02 (0.11)	0.89	0.89	0.88	0.35
Bayes–approx.		0.09 (0.01)	0.13 (0.01)	0.23 (0.03)	0.87	0.91	0.88	0.44
Bayes–full nonspatial		0.31 (0.04)	0.21 (0.02)	0.62 (0.08)	0.82	0.93	0.85	0.57
Bayes–full spatial		0.13 (0.02)	0.12 (0.01)	0.27 (0.04)	0.86	0.93	0.88	0.79
Quantreg	Space	0.53 (0.06)	1.02 (0.11)	1.03 (0.11)	0.89	0.88	0.88	0.36
Bayes–approx.		0.10 (0.01)	0.11 (0.01)	0.21 (0.03)	0.83	0.92	0.88	0.45
Bayes–full nonspatial		0.32 (0.05)	0.20 (0.01)	0.65 (0.08)	0.82	0.92	0.84	0.58
Bayes–full spatial		0.14 (0.02)	0.10 (0.01)	0.23 (0.03)	0.84	0.93	0.88	0.81
Quantreg	Time	0.56 (0.06)	0.94 (0.10)	1.03 (0.11)	0.89	0.88	0.88	0.36
Bayes–approx.		0.13 (0.01)	0.11 (0.01)	0.27 (0.03)	0.85	0.91	0.88	0.49
Bayes–full nonspatial		0.33 (0.04)	0.16 (0.01)	0.63 (0.08)	0.79	0.93	0.84	0.30
Bayes–full spatial		0.15 (0.02)	0.10 (0.01)	0.23 (0.03)	0.72	0.86	0.79	0.59

The approximate method which smooths the initial estimates from usual quantile regression reduces mean squared error. In fact, in this simulation the approximate method often has smaller mean squared error than the full model. Therefore, the approximate model appears to provide a computationally efficient means to estimate the true quantile function to be used for predicting future observations. However, the full model gives higher power for the nonnull coefficient β₃.

Adding residual correlation does not affect mean square error. Spatial correlation in the residuals has a small effect on the coverage probabilities, perhaps because the spatially varying regression parameters absorb some of the residual correlation. However, adding temporal correlation reduces the coverage probability below 0.8. Therefore, strong residual correlation should be accounted for, perhaps using a copula model as discussed in Section 6.

In this simulation we assumed M = 10 basis functions, ${\sigma }_j^2$ ~ InvGamma(0.1, 0.1), and the prior standard deviation of the effective range was one. We reran the simulation (with independent residuals) with S = 10 datasets using the full model three times, each varying one of these assumptions. The alternatives were M = 25 basis functions, σ_j) ~ InvGamma(0.001, 0.001), and the prior standard deviation of the effective range set to five. The results of the simulation were fairly robust to these changes; the mean squared error varied from 0.06 to 0.11 for X₁, from 0.07 to 0.12 for X₂, and from 0.18 to 0.26 for X₃, and the average coverage probability was at least 0.86 for all fully Bayes models and all covariates. The prior for the effective range was most influential. Altering this prior affected the posterior of the spatial range, but had only a small effect on the mean squared errors and coverage probabilities.

5. ANALYSIS OF EASTERN U.S. OZONE DATA

In this section we analyze monitored ozone data from the Eastern U.S. from the summers of 1997–2005 and climate model output from 2041–2045. Section 5.1 describes the data. Sections 5.2 and 5.3 analyze monitored ozone data from 1997–2005, first using the full model and a subset of the data, and then using Section 3’s approximate model and the complete data. Sections 5.4 and 5.5 analyze the computer model output.

5.1 Description of the Data

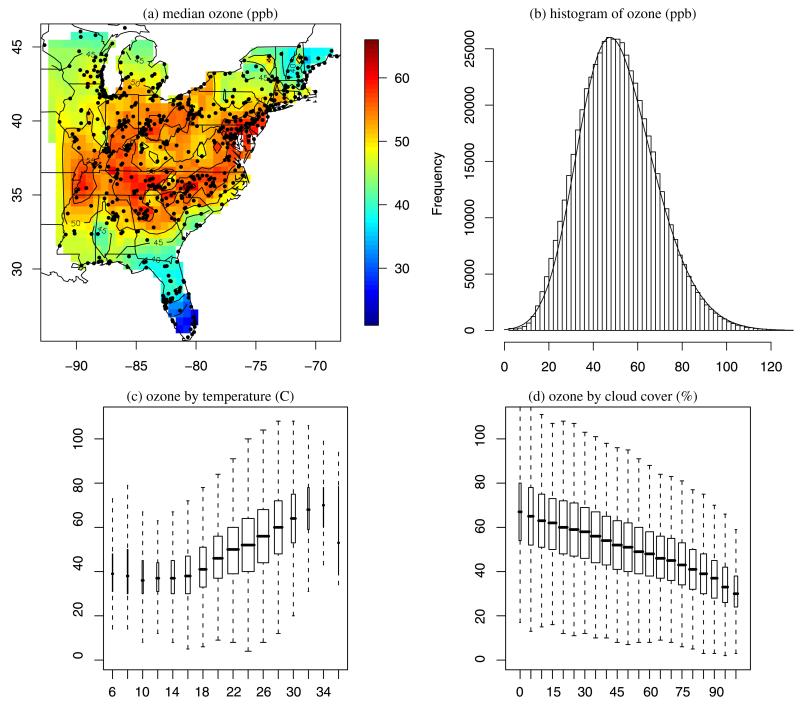
Meteorological data were obtained from the National Climate Data Center (NCDC; http://www.ncdc.noaa.gov/oa/ncdc.html). We obtained daily average temperature and daily maximum wind speed for 773 monitors in the Eastern U.S. from the NCDC’s Global Summary of the Day Database. Daily average cloud cover for 735 locations in the Eastern U.S. was obtained from the NCDC’s National Solar Radiation Database.

Maximum daily eight-hour average ozone was obtained from the US EPA’s Air Explorer Database (http://www.epa.gov/airexplorer/index.htm). We analyze daily ozone concentrations measured at 631 locations in the Eastern U.S. during the summers (June–August) of 1997–2005 (470,239 total observations), plotted in Figure 2(a). Meteorological and ozone data are not observed at the same locations. Therefore we imputed meteorological variables at the ozone locations using spatial Kriging. Spatial imputation was performed using SAS version 9.1 and the MIXED procedure with spatial exponential covariance function, with covariance parameters allowed to vary by variable and year. We treat these predictors as fixed. Li, Tang, and Lin (2009) discuss the implications of ignoring uncertainty in spatial predictors. Temperature and cloud cover are fairly smooth across space and thus have small interpolation errors, however there is more uncertainty in the wind speed interpolation. Accounting for uncertainty in the predictors using a spatial model for the meteorological variables warrants further consideration.

Figure 2.

Panel (a) maps the sample median ozone concentration; the points are the 631 monitoring locations. Panel (b) plots the skew-normal(34.5, 24.3, 1.8) over the histogram of ozone concentrations, pooled over spatial location. Panels (c) and (d) plot ozone by daily average temperature and cloud cover proportion, respectively; the data are pooled over space and the width of the boxplots are proportional to the number of observations in the bins. The online version of this figure is in color.

The final source of data is time slice experiments from the North American Regional Climate Change Assessment Program (http://www.narccap.ucar.edu/data/). These data are output from the Geophysical Fluid Dynamics Laboratory’s (GFDL) deterministic atmospheric computer model (AM2.1) with three hour × 50 km resolution. We use data from two experiments. The first provides modeled data from 1968 to 2000 using observed sea surface temperature and sea-ice extent. These data are a reanalysis using boundary conditions determined by actual historical data. The second provides modeled data for 2038 to 2070 using deviations in sea surface temperature and sea-ice extent from the GFDL’s CM2.1 A2 scenario. From these experiments we obtain modeled daily average temperature, maximum wind speed, and average cloud cover fraction. These gridded data do not have the same spatial support as ozone and meteorology data obtained from point-reference monitors. Throughout we use the ozone monitoring locations as the spatial unit, and we match modeled climate data with ozone data by extracting climate data from the grid cell containing the ozone monitor.

5.2 Atlanta Substudy

We begin by comparing several models using only data from the 12 stations in the Atlanta area. The continuous variables temperature and wind speed are standardized and transformed to the unit interval (as assumed in the monotonicity constraints described in Section 2) by the normal CDF

$$X_j=\Phi \left(\right[temp-m\left(temp\right)]∕s(temp\left)\right),$$ (19)

where m(temp) and s(temp) are the sample mean and standard deviation of daily temperature over space and time. Cloud cover proportion naturally falls on the unit interval. We also include the year to investigate temporal trends in the quantile process. The year is transformed as X_j (year − 1997)/8. We also include the interaction X_jX_l between temperature and cloud cover and quadratic effects 4(X_j − 0.5)².

We fit the full and approximate model with and without quadratic terms and compare these models with the fully Gaussian spatial model with spatially varying coefficients,

$$y(\mathbf{s},t)=\sum _{j=1}^p{X}_j(\mathbf{s},t){\beta }_j\left(\mathbf{s}\right)+\mu (\mathbf{s},t)+\epsilon (\mathbf{s},t),$$ (20)

where β_j(s) are spatial Gaussian processes with exponential covariance, μ(s, t) are independent (over time) spatial Gaussian processes with exponential covariance, and $\epsilon (\mathbf{s},t)\stackrel{\mathrm{iid}}{~}\mathrm{N}(0,{\sigma }^2)$ is the nugget effect. For both the full and approximate Bayesian quantile regression models, the centering distribution f₀ is taken to be skew-normal with location μ₀ ~ N(0, 10²), scale ${\sigma }_0^2$ ~ InvGamma(0.1, 0.1), and skewness ψ₀ ~ N(0, 10²). Figure 2(b) shows that this distribution is flexible enough to approximate the ozone distributions. However, the parametric mean regression model with parametric skew-normal errors would not allow for the shape of the right tail to depend on covariates. We note that the quantile regression models do not explicitly model spatial or temporal association in the daily ozone values. Effects of residual correlation are examined briefly in Section 5.5 and alternative models are discussed in Section 6. We use M = 10 knots and priors ${\tau }_{jm}^2$ ~ InvGamma(0.1, 0.1) and) ρ_j ~ Gamma(0.5, 0.5), which gives ) prior 95% intervals (0.00, 0.99) and (0.00, 0.80) for the correlation between the closest and farthest pairs of points, respectively.

To compare models we randomly removed all observations for 10% of the days (N = 910 total observations), with these test observations labeled $y_1^{\ast },\dots ,y_N^{\ast }$. For each deleted observation we compute the posterior predictive mean ${\widehat{y}}_i^{\ast }$ and the posterior predictive 95% equal-tailed intervals. Table 2 gives the root mean squared prediction error $RMSE=\sqrt{{\sum }_{i=1}^N{(y_i^{\ast }-{\widehat{y}}_i^{\ast })}^2∕N}$, mean absolute deviation $MAD={\sum }_{i=1}^N\mid y_i^{\ast }-{\widehat{y}}_i^{\ast }\mid ∕N$, and the coverage probabilities and average (over i) width of the prediction intervals. Note that the RMSEs reported here are larger than those reported by other spatial analyses of ozone data, for example, Sahu, Gelfand, and Holland (2007), that withhold all observations for some sites, rather than all observations for some days. In contrast, we withhold all observations on a subset of days, and therefore our predictions rely entirely on correctly modeling the relationship between meteorology and ozone, and do not use spatial interpolation. Since ozone shows a strong spatial pattern, this results in higher RMSE. We feel this approach to cross-validation is more relevant for our goal of prediction for future days without any observed values.

Table 2.

Cross-validation results for the Atlanta substudy

Model	Covariates	Coverage prob. 95% interval	Average width 95% interval	RMSE	MAD
Gaussian	Linear	0.965	60.4	14.3	9.34
Gaussian	Quadratic	0.969	59.8	14.2	9.07
QR–approx.	Linear	0.959	50.4	13.1	7.76
QR–approx.	Quadratic	0.947	47.3	12.9	7.62
QR–full	Linear	0.987	70.1	13.2	7.87
QR–full	Quadratic	0.986	69.6	13.0	7.64

The coverage probabilities of the 95% intervals are near or above the nominal rate for all models in Table 2. The Gaussian models have the highest RMSE and MAD. To test for a possible transformation to normality, we also fitted the Gaussian model using the square root of ozone as the response. RMSE and MAD are compared by squaring the draws from the predictive distribution. RMSE (14.4 for linear predictors, 14.2 for quadratic predictors) and MAD (9.6 for linear predictors, 9.2 for quadratic predictors) were similar to the untransformed response, so we use the untransformed response for ease of interpretation. The approximate method with quadratic terms minimizes both RMSE and MAD, has good coverage probability, justifying its use for prediction.

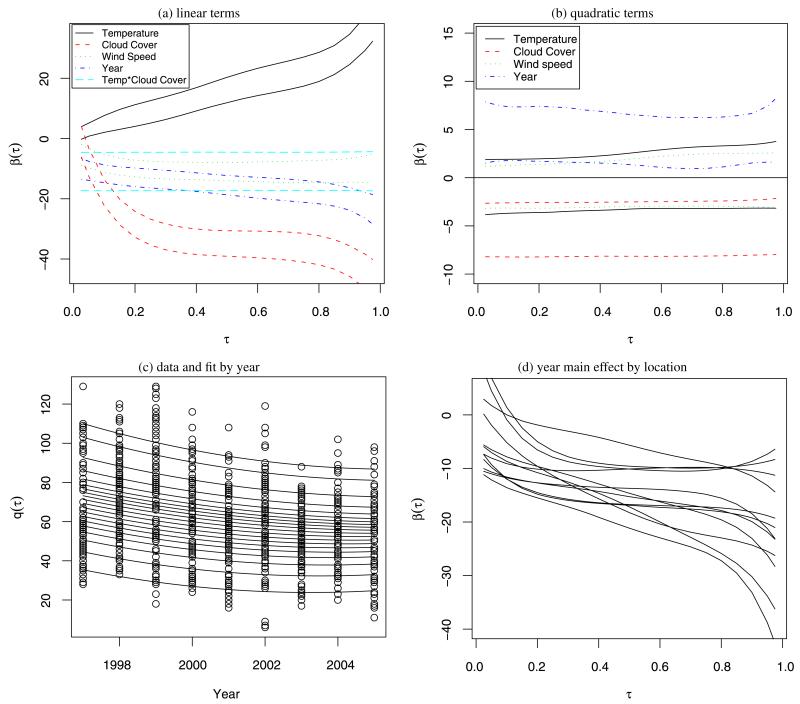
Figure 3 summarizes the posterior for the full Bayesian spatial quantile regression model with quadratic terms. Panels (a)–(c) plot the quantile curves for one representative location. The main effects are all highly significant, especially for the upper quantile levels. As expected ozone concentration increases with temperature and decreases with cloud cover and wind speed. Figure 3 reveals a complicated relationship between ozone and temperature. The linear temperature effect is near zero for low quantile levels and increases with τ.

Figure 3.

Results for Atlanta substudy. Panels (a)–(c) plot the results for one location. Panels (a) and (b) give posterior 95% intervals for main effect and second-order quantile curves. Panel (c) plots the data by year, along with the posterior mean quantile curves for several quantile levels ranging from τ = 0.05 to τ = 0.95 with all covariates fixed at 0.5 expect year. Panel (d) plots the posterior mean of the year main effect for each location. The online version of this figure is in color.

Figure 3(c) plots the data and several fitted quantile curves (τ ranging from 0.05 to 0.95) by year with the transformed meteorological variables fixed at 0.5. All quantile levels decrease from 1997 to 2002; after 2002 the lower quantiles plateau while the upper quantiles continue to decline. Note that in this plot more than 5% of the observations fall above the 95% quantile level. This is the result of plotting the quantile functions without regard to variability in the meterological variables (i.e., fixing them at 0.5). To give a sense of the spatial variability in the quantile curves, Figure 3(d) plots the posterior mean of the main effect for year for all locations. All sites show a decreasing trend, especially for upper quantile levels. The decreasing trends are adjusted for meteorology, and may be explained by other factors, such as emission reductions. There is considerable variation from site to site. The posterior 95% interval for the difference between the year main effect at τ = 0.8 for the sites with largest and smallest posterior mean is (10.4, 25.0).

5.3 Analysis of Eastern U.S. Ozone Data

Analyzing data for the entire Eastern U.S. using the full Bayesian spatial quantile regression model is not computationally feasible, so we use only the approximate model. We selected variance inflation c = 1. We considered other values of c, but the estimates were nearly identical so we pick c = 1 for simplicity. Based on Section 5.2’s results, we include quadratic terms for all predictors. Also, we use the same priors as in Section 5.2. The posterior median (95% interval) for the skewness parameter ψ₀ of the skew-normal base distribution is 3.76 (1.12, 10.54), supporting a non-Gaussian analysis. To justify that this model fits well, we randomly removed observations for 2% of the days (N = 12,468 observations) and the out-of-sample coverage probability of the 95% prediction intervals was 93.4%.

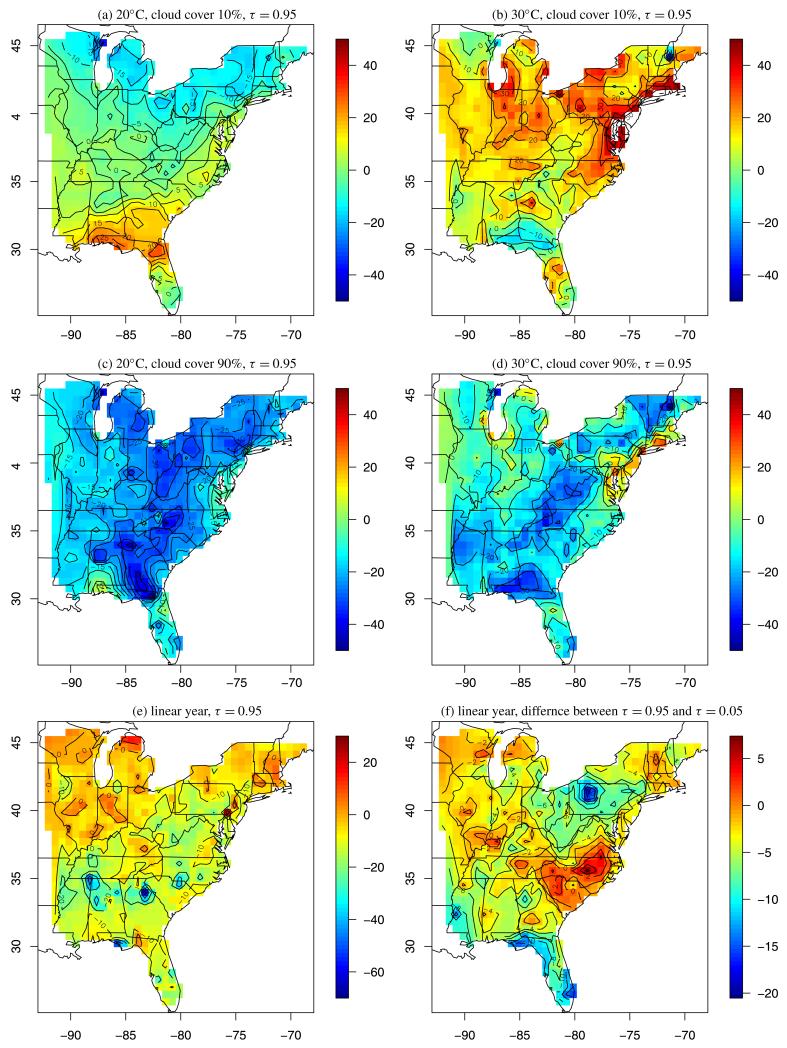
Figure 4 maps the posterior means of several quantile functions. The two strongest predictors are temperature and cloud cover. The model includes interaction and quadratic terms, so to illustrate the effects, we plot linear combinations of all terms involving these predictors,

$$X_1{\beta }_1(\tau ,\mathbf{s})+X_2{\beta }_2(\tau ,\mathbf{s})+4{(X_1-0.5)}^2{\beta }_3(\tau ,\mathbf{s})+4{(X_2-0.5)}^2{\beta }_4(\tau ,\mathbf{s})+X_1{X}_2{\beta }_5(\tau ,\mathbf{s}),$$ (21)

where X₁ and X₂ are temperature and cloud cover values, respectively, and β₁–β₅ are the corresponding quantile curves. Figure 4(a)–(d) plot the posterior means of linear combinations using X₁ that correspond to 20°C and 30°C and X₂ that correspond to 10% and 90% cloud cover.

Figure 4.

Summary of the posterior mean of β_j(τ, s). Panels (a)–(d) plot linear combinations of β_j(τ, s) as discussed in (21). Panels (e) and (f) plot the posterior mean of β_j(0.95, s) and β_j(0.95, s) − β_j(0.05, s), respectively. The units are parts per billion in all plots. The online version of this figure is in color.

For both temperature values ozone concentrations are generally higher when cloud cover is low. For clear days with 10% cloud cover temperature has a strong effect on ozone in the north, but only a weak effect in the south. For cloudy days with 90% cloud cover, temperature has less effect overall, but remains significant in the northeast.

The linear time trend for the 95th quantile in Figure 4(e) is generally decreasing, especially in the south. This agrees with Chan (2009). To compare the rate of decrease in the upper and lower tails, Figure 4(f) plots the difference between the linear time trend for the 95th and 5th quantile [β_j(0.95, s) − β_j(0.05, s)]. In the Middle Atlantic (red) the negative trend is stronger in the lower tail than the upper tail; in contrast in Florida the trend is stronger in the upper tail.

5.4 Calibrating Computer Model Output

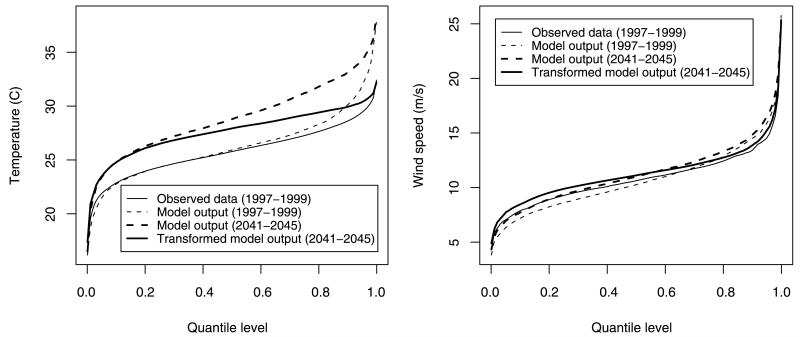
Before applying our statistical model to project ozone levels, we must calibrate the climate model with the observed data. For example, calibration is necessary to account for systematic differences between grid cell averages and point measurements. Figure 5 plots the sample quantile function for the observed and modeled temperature and wind speed for all days in 1997–1999 in Georgia. The distribution of daily average temperature agrees quite well below the median, however the modeled temperature has a heavier right tail than the observed temperature. The standard approach to calibration is to simply shift and scale the computer model output by matching the sample mean and standard deviation. However, in light of the differences in the tail of the distributions and our desire to accurately model extreme events, a more sophisticated approach is warranted.

Figure 5.

Calibration plots for meteorological data in Georgia.

We use nonlinear monotonic regression on the sample quantile functions to calibrate these distributions. Let ${\widehat{q}}_o\left({\tau }_k\right)$ and ${\widehat{q}}_m\left({\tau }_k\right)$ be the τ_kth sample quantiles of the observed and modeled 1997–1999 data, respectively. These distributions are standardized by the nonlinear model $E\left[{\widehat{q}}_o\right(\tau \left)\right]=g\left[{\widehat{q}}_m\right(\tau \left)\right]$ using sample quantiles on the grid τ_k ∈ {0.01, 0.02, … , 0.99}. We model g using M = 20 Bernstein polynomial basis functions with monotonicity constraints (fitted using restricted least squares) as in Section 2 to ensure that g is an increasing function. Figure 5 shows the transformed temperature for Georgia. Model outputs for 2041–2045 with large temperatures are reduced to resolve the discrepancy between observed and modeled 1997–1999 data. The meteorological predictors are transformed separately by state to account for spatial variation in the calibration.

We compare this calibration method to the simple method of adjusting each site by the state mean and variance using five-fold cross-validation. We randomly divided the observed temperature data into five groups. For each group we used the observations from the remaining four groups to calibrate the computer model output for the group. For each site, we computed the squared difference between the mean observed temperature and the mean of the calibrated computer output, as well as the Kolmogorov–Smirnov test statistic for the test that the observed temperature and calibrated computer model output follow the same distribution. The quantile calibration method has smaller squared error (average of 3.26 compared to 3.31, smaller at 56% of sites) and KS-statistic (average of 0.139 compared to 0.149, smaller at 59% of sites) than the mean/variance calibration method.

5.5 Projecting Ozone Levels Under Different Climate Scenarios

The additive structure of the quantile regression model gives the effect of each covariate on the maximum daily eight-hour average ozone in closed form. In addition, policy makers are often interested in the effect of covariates on the yearly ozone distribution. For example, in this section we explore the relationship between temperature and yearly median and 95th percentile of ozone. Here we use Section 5.3’s estimate of the conditional density of daily ozone to simulate several realizations of the ozone process to forecast yearly summaries under different climate scenarios. These simulations vary temperature, wind speed, and cloud cover and assume all other factors (emissions, land use, etc.) are fixed. Certainly other factors will change in the future (e.g., emissions may decline in response to new standards) so these projections are not meant to be realistic predictions. Rather, they are meant to isolate the effect of climate change on future ozone levels.

Two factors contribute to the effect of climate changes on ozone levels at a given location: the magnitude of the climate change and the strength of the association of meteorology and ozone. To quantify spatial variability in the effect of temperature increase on yearly summaries, we generate 500 replicates of the ozone process at the data points under different climate scenarios. The first scenario is no change in the meteorological variables. In this case, replicates are generated by simulating the ozone concentration each day at each spatial location from the Section 5.3’s conditional daily ozone distribution given the observed meteorological values for that location on that day. For this and all other simulations we fix the year variable to 2005 for all observations to represent the most recent ozone distribution. The rth replicate at location s and day t, y^(r)(s, t), is generated by first drawing u_st) ~ U(0, 1) independent over space and time and then transforming to

$$y^{\left(r\right)}(\mathbf{s},t)=\sum _{j=1}^p{X}_j(\mathbf{s},t){\widehat{\beta }}_j(u_{st},\mathbf{s}),$$ (22)

where ${\widehat{\beta }}_j(u_{st},\mathbf{s})$ is the posterior mean of β_j(u_st, s). For each replication we calculate the yearly summaries $Q_1^{\left(r\right)}(\mathbf{s},\tau )$, the τth quantile of {y^(r)(s, 1), … , y^(r)(s, n_t)}, and $T_1^{\left(r\right)}\left(\mathbf{s}\right)$, the three-year (2003–2005) average of the fourth-highest daily maximum eight-hour average ozone concentrations.

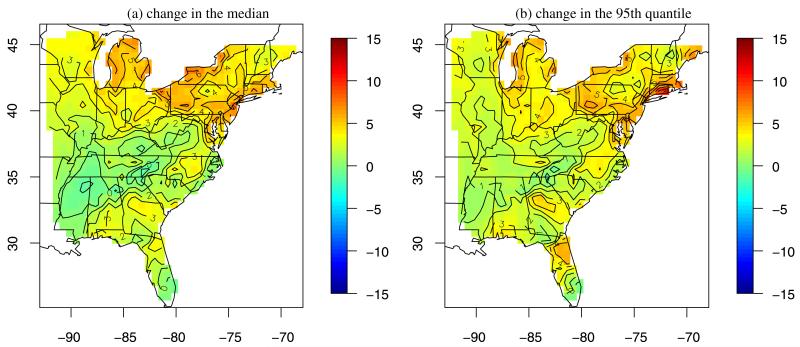
The second scenario increases the daily average temperature by 2°C every day at every location and keeps all other variables fixed. Denote $Q_2^{\left(r\right)}(\mathbf{s},\tau )$ and $T_2^{\left(r\right)}\left(\mathbf{s}\right)$ as the yearly summaries for replication r from this scenario. Figure 6 plots the mean (over r) of $Q_2^{\left(r\right)}(\mathbf{s},\tau )-Q_1^{\left(r\right)}(\mathbf{s},\tau )$ for τ = 0.5 and τ = 0.95 to illustrate the effect of a shift in daily temperature holding all other variables fixed. The change in median and 95th quantile of yearly ozone are both the largest in Michigan and Northeast U.S. The current (as of 2008) EPA ozone standard is that the three-year average of the fourth-highest daily maximum eight-hour average ozone concentrations is less than 0.075 ppm.

Figure 6.

Estimates of the change (ppb) in yearly median and 95th quantile due to shifting each daily average temperature by 2°C (standard errors are less than 3 ppb for all sites and quantiles). The online version of this figure is in color.

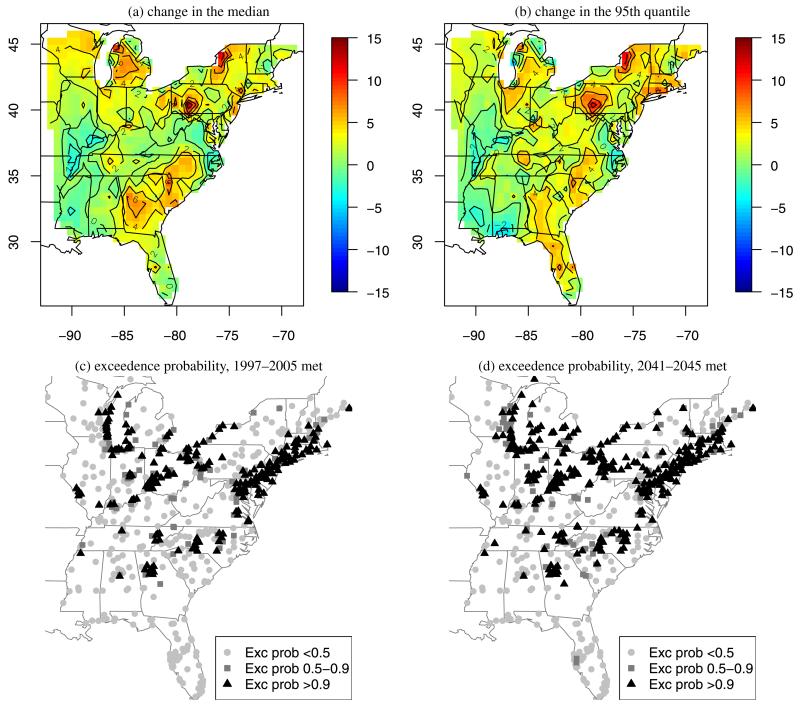
The third scenario uses the calibrated GFDL projected temperature, wind speed, and cloud cover for 2041–2045. The projected temperature change from the observed 1997–2005 temperatures and calibrated 2041–2045 temperatures varies spatially, but is generally between 1-4°C and is largest in the Midwest. As an example of the analysis that can be conducted using the rich output of the Monte Carlo simulation, Figures 7(c) and 7(d) plot the probability of the three-year (2041–2043) average of the fourth-highest daily maximum eight-hour average ozone concentrations is greater than 0.075 ppm under the current and future climate scenarios, respectively. Also, Table 3 shows the mean and standard deviation of the Monte Carlo samples for the stations with the largest projected difference in fourth-highest daily maximum eight-hour average ozone. The largest increases are in the Northeast and Midwest.

Figure 7.

Panels (a) and (b) plot estimates of the change in yearly median and 95th quantile under the future and current climate scenarios. Panels (c) and (d) give the probability that the three-year (2041–2043) average of the fourth-highest daily maximum eight-hour average ozone concentrations exceeds 75 ppb for current and future climate scenarios, respectively. The online version of this figure is in color.

Table 3.

Mean (standard deviation) of the 500 Monte Carlo simulations of the fourth-highest daily maximum eight-hour average ozone (ppb) using current (1997–2005) and projected (2041–2045) meteorology, and the difference between fourth-highest daily maximum eight-hour average ozone using projected and current meteorology for the stations with largest projected increase

County, State	Longitude	Latitude	Current	Projected	Difference
New London, CT	−72.06	41.32	79.13 (3.27)	99.21 (4.03)	20.09 (5.41)
New Haven, CT	−72.55	41.26	88.62 (3.06)	105.51 (3.93)	16.88 (4.80)
Schoolcraft, MI	−85.95	46.29	67.43 (2.36)	82.26 (2.27)	14.83 (3.34)
Fairfield, CT	−73.34	41.12	88.18 (3.15)	101.41 (3.52)	13.23 (4.76)
Wake, NC	−78.62	35.79	66.49 (2.09)	79.71 (2.54)	13.22 (3.31)
Fairfield, CT	−73.44	41.40	88.72 (3.38)	101.64 (3.14)	12.92 (4.74)
New Castle, DE	−75.49	39.76	80.13 (1.91)	92.72 (2.57)	12.59 (3.25)
Blair, PA	−78.37	40.54	73.25 (2.29)	85.76 (2.30)	12.51 (3.24)
Cambria, PA	−78.92	40.31	73.60 (1.99)	86.07 (1.91)	12.47 (2.64)
Lincoln, ME	−69.73	43.80	61.25 (2.36)	73.41 (2.45)	12.16 (3.49)
Bristol, MA	−70.88	41.63	82.54 (2.89)	94.18 (2.76)	11.64 (3.96)
Jefferson, NY	−75.97	44.09	77.57 (2.94)	88.91 (2.50)	11.34 (3.88)
Northampton, NC	−77.62	36.48	67.36 (1.84)	78.69 (2.00)	11.33 (2.65)
Rockingham, NH	−70.81	42.79	76.21 (3.11)	87.48 (3.12)	11.28 (4.51)
Putnam, TN	−85.40	36.21	69.36 (1.53)	80.40 (2.11)	11.04 (2.57)

To test for sensitivity to modeling assumptions, we also make projections under the future climate scenario without calibration of the computer model and with temporal correlation in the Monte Carlo samples. The results were quite different without calibration. For example, the projected average (over space) change in median and 95th percentile yearly ozone, respectively, is 3.54 and 5.43 without calibration, compared to 2.29 and 2.26 with calibration. To test for sensitivity to correlation in the Monte Carlo samples, we generate the latent u_st as u_st = Φ(U_st), where U_st are independent across space, and mean zero, Gaussian, with temporal covariance Cov(U_st, U_st+h) = 0.4^h, where the correlation 0.4 was chosen to match a lag-1 residual autocorrelation of a typical location. The projected average (over space) change in median and 95th percentile yearly ozone with correlated draws are 2.29 and 2.21, respectively. Therefore the projections are not sensitive to residual autocorrelation.

6. DISCUSSION

In this article we propose a Bayesian spatial quantile method for tropospheric ozone. Our model does not assume the response is Gaussian and allows for complicated relationships between the covariates and the response. Working with a subset of data from the Atlanta area we found that temperature, cloud cover, and wind speed were all strongly associated with ozone, and that the effects are stronger in the right tail than the center of the distribution. Working with the entire Eastern U.S. dataset we found a decreasing time trend, especially in the South. Applying the model fit under different climate scenarios suggests that the effect of a warmer climate on ozone levels will be strongest in the Industrial Midwest and Northeast, and that a warmer climate will increase the probability of exceeding the EPA ozone standard in these areas.

Our model accounts for spatial variability by modeling the conditional distribution as a spatial process. However, we do not directly account for the correlation of two nearby observations on the same day or two observations at the same location on consecutive days. A spatial copula (Nelsen 1999) could be used to account for this source of correlation while preserving the marginal distribution specified by the quantile function. We experimented with a spatial Gaussian copula and found it dramatically improved prediction of withheld observations when several observations on the same day were observed. However, when all observations on a day were withheld, prediction did not improve substantially. Since our objective is to predict ozone on days with no direct observations, and MCMC convergence and run times are slower using a copula, we elect to present results from the independent model. An efficient way to account for residual correlation is an area of future work.

In addition to projecting ozone levels, the analysis in this article could be combined with health effects estimates to study changes in ozone health risks. The Monte Carlo simulation in Section 5.5 produces samples of the joint spatiotemporal distribution of ozone and meteorology. For each sample, we could generate a realization of the mortality time series, and compare the distributions of mortality rates across climate scenarios. In this analysis, it would be important to account for spatially varying health effects as well as interactions between ozone and meteorology.

APPENDIX: MCMC DETAILS

MCMC sampling is carried out using the software package R. Different sampling schemes for the full and approximate models are used to update the regression coefficients ${\delta }_{jm}^{\ast }\left(\mathbf{s}\right)$; all other parameters are updated identically for both methods. For Section 2.2’s full model, the ${\delta }_{jm}^{\ast }\left(\mathbf{s}\right)$ are updated individually using Metropolis sampling. This requires computing the likelihood for each observation. This likelihood is approximated by computing q(τ_k|X_i, s_i) on a grid of 100 equally spaced τ_k from 0 to 1, and taking p(y_i|X_i, δ(s_i)) ≈ 1/[q(τ_j+1|X_i, s_i) − q(τ_j|X_i, s_i)], where τ_j is the quantile level so that q(τ_j|X_i, s_i) ≤ q(τ_j+1|X_i, s_i).

Using Section 3’s approximate model, the latent ${\delta }_{jm}^{\ast }\left(\mathbf{s}\right)$ have conjugate full conditionals and are updated using Gibbs sampling. Denote the quantile process at location s_i evaluated on the grid of τ in (16) as β(s_i) = Ωδ(s_i), where Ω is the appropriate matrix of basis functions, δ(s_i) the vector of δ_jm(s_i), and δ*(s_i) the vector of ${\delta }_{jm}^{\ast }\left({\mathbf{s}}_i\right)$. The full joint posterior for δ*(s_i) is the product of the Gaussian likelihood $\widehat{\beta }\left({\mathbf{s}}_i\right)~\mathrm{N}\left(\Omega \delta \right({\mathbf{s}}_i),{\Sigma }_i)$ and the Gaussian spatial prior for δ*(s_i). However, in this normal/normal model δ*(s_i) does not have a Gaussian full conditional since δ(s_i), a truncated version of δ*(s_i), appears in the likelihood instead of δ*(s_i). However, the individual components ${\delta }_{jm}^{\ast }\left({\mathbf{s}}_i\right)$ do have conjugate full conditionals, given below.

Define ${\delta }_{jm}^{\ast }\left({\mathbf{s}}_i\right)\mid {\delta }_{jm}^{\ast }\left({\mathbf{s}}_k\right),k\ne i~\mathrm{N}(m_1,s_1^2)$ as the conditional prior from the Gaussian spatial model, Ω_jm as the column of Ω that corresponds to δ_jm(s_i), ${\mathbf{r}}_1=\widehat{\beta }\left({\mathbf{s}}_i\right)-\Omega \delta \left({\mathbf{s}}_i\right)+{\sum }_{l=1}^p{\Omega }_{lm}{\delta }_{lm}\left({\mathbf{s}}_i\right)$ as the residuals not accounting for the terms corresponding to δ_1m(s_i), … , δ_pm(s_i), and ${\mathbf{r}}_2=\widehat{\beta }\left({\mathbf{s}}_i\right)-\Omega \delta \left({\mathbf{s}}_i\right)+{\Omega }_{jm}{\delta }_{jm}\left({\mathbf{s}}_i\right)$ as the residuals not accounting for the term corresponding to δ_jm(s_i). Then twice the negative log of the full conditional of ${\delta }_{jm}^{\ast }\left({\mathbf{s}}_i\right)$ is the sum of a constant that does not depend on ${\delta }_{jm}^{\ast }\left({\mathbf{s}}_i\right)$ and

$$\{\begin{array}{cc}{\mathbf{r}}_1^{\prime }{\Sigma }_i^{-1}{\mathbf{r}}_1+s_1^{-2}{\left({\delta }_{jm}^{\ast }\right({\mathbf{s}}_i)-m_1)}^2,\hfill & {\delta }_{jm}\left(\mathbf{s}\right)=0\hfill \\ {[{\mathbf{r}}_2-{\Omega }_{jm}{\delta }_{jm}^{\ast }({\mathbf{s}}_i\left)\right]}^{\prime }{\Sigma }_i^{-1}[{\mathbf{r}}_2-{\Omega }_{jm}{\delta }_{jm}^{\ast }({\mathbf{s}}_i\left)\right]+s_1^{-2}{\left({\delta }_{jm}^{\ast }\right({\mathbf{s}}_i)-m_1)}^2,\hfill & {\delta }_{jm}\left(\mathbf{s}\right)>0,\hfill \end{array}\phantom{\}}$$ (A.1)

where ${\delta }_{jm}\left(\mathbf{s}\right)=0\text{if}{\delta }_{1m}^{\ast }\left(\mathbf{s}\right)+{\sum }_{l=2}^p\mathit{I}\left({\delta }_{lm}^{\ast }\right(\mathbf{s})<0){\delta }_{lm}^{\ast }\left(\mathbf{s}\right)\le 0$. In both cases of (A.1), the full conditional is proportional to a Gaussian distribution. Therefore, the full conditional of ${\delta }_{jm}^{\ast }\left({\mathbf{s}}_i\right)$ is a mixture of two truncated normal densities

$$\pi \ast N_{[-\infty ,c]}(m_1,s_1^2)+(1-\pi )N_{[c,\infty ]}(m_2,s_2^2),$$ (A.2)

where N_A(m, s²) is the truncated normal density with location m, scale s, and domain A. The first truncated normal density corresponds to δ_jm(s) = 0 and the mth term dropping from the likelihood, and so the parameters of the truncated normal are the prior mean and variance. The second term corresponds to ${\delta }_{jm}\left(\mathbf{s}\right)={\delta }_{jm}^{\ast }\left(\mathbf{s}\right)\ne 0$, and has parameters m₂ and $s_2^2$, where $s_2^{-2}=1∕s_1^2+{\Omega }_{jm}^{\prime }{\Sigma }_i^{-1}{\Omega }_{jm}$, $m_2=s_2^2[m_1∕s_1^2+{\Omega }_{jm}^{\prime }{\Sigma }_i^{-1}{\mathbf{r}}_2]$.

The probability π and cutpoint c depend on j and m. The first term is unconstrained, so if m = 1 then π = 0 and c = −∞. Terms with m > 1 are constrained. For these terms if j = 1 then $c=-{\sum }_{j=2}^p\mathit{I}\left({\delta }_{jm}^{\ast }\right(\mathbf{s})<0){\delta }_{jm}^{\ast }\left(\mathbf{s}\right)$ and

$$\pi =\Phi \left(\frac{c-m_1}{s_1}\right)∕\left(\Phi \left(\frac{c-m_1}{s_1}\right)+\frac{s_2}{s_1}\left(1-\Phi \left(\frac{c-m_2}{s_2}\right)\right)\times \exp (-[r_2^{\prime }{\Sigma }_i^{-1}{r}_2+m_1^2{s}_1^2-m_2^2∕s_2^2-r_1^{\prime }{\Sigma }_i^{-1}{r}_1]∕2)\right).$$ (A.3)

Finally, we give the full conditional for terms with m > 1 and j > 1. For these terms, if $c^{\ast }=-{\delta }_{1m}^{\ast }\left(\mathbf{s}\right)-{\sum }_{k>1,k\ne j}\mathit{I}\left({\delta }_{km}^{\ast }\right(\mathbf{s})<0){\delta }_{km}^{\ast }\left(\mathbf{s}\right)\ge 0$ then π = 1 and c = ∞ and if c* < 0 then c = c* and π is given by (A.3).

For both full and approximate methods, the spatial variances ${\tau }_j^2$ have conjugate inverse gamma priors and are updated using Gibbs sampling. The spatial ranges ρ_j and centering distribution parameters Θ are updated individually using Metropolis sampling with Gaussian candidate distributions.

For all analyses we generate 20,000 MCMC samples and discard the first 10,000 as burn-in. Convergence is monitored using trace plots of the deviance and several representative parameters.