Alchemical prediction of hydration free energies for SAMPL

Abstract

Hydration free energy calculations have become important tests of force fields. Alchemical free energy calculations based on molecular dynamics simulations provide a rigorous way to calculate these free energies for a particular force field, given sufficient sampling. Here, we report results of alchemical hydration free energy calculations for the set of small molecules comprising the 2011 Statistical Assessment of Modeling of Proteins and Ligands (SAMPL) challenge. Our calculations are largely based on the Generalized Amber Force Field (GAFF) with several different charge models, and we achieved RMS errors in the 1.4-2.2 kcal/mol range depending on charge model, marginally higher than what we typically observed in previous studies^1-5. The test set consists of ethane, biphenyl, and a dibenzyl dioxin, as well as a series of chlorinated derivatives of each. We found that, for this set, using high-quality partial charges from MP2/cc-PVTZ SCRF RESP fits provided marginally improved agreement with experiment over using AM1-BCC partial charges as we have more typically done, in keeping with our recent findings⁵. Switching to OPLS Lennard-Jones parameters with AM1-BCC charges also improves agreement with experiment. We also find a number of chemical trends within each molecular series which we can explain, but there are also some surprises, including some that are captured by the calculations and some that are not.

1 Introduction

Hydration free energies based on molecular simulations have amassed numerous applications over the last decade^1-15. This widespread interest is grounded in the fact that hydration free energies provide a rigorous test of force field accuracy, to the extent that all system degrees of freedom are adequately sampled. By extension, these calculations are believed to provide a proxy for the accuracy that can reasonably be expected in binding free energy calculations. Though these expectations may be well-founded, systematic tests of hydration free energies were typically limited to amino acid sidechain analogs until very recently (i.e. beginning around 2007¹), with few tests on diverse sets of small molecules. Perhaps as a consequence, hydration free energies, which yield just a single number potentially influenced by all of the force field parameters, have not been directly incorporated into force field development.

The relationship between hydration free energies and ligand-receptor binding free energies is complex, but not to be over-looked. Binding of a ligand to a receptor partially removes the ligand from solvent, and partially desolvates the receptor binding site. If, in the best case scenario, bound state interactions between the ligand, protein, and environment are well predicted, then the error in computed binding free energies will be dominated by any error in the hydration free energy. If errors in modeling hydration free energies are consistent within a chemical series, binding free energy calculations may still yield accurate relative free energy predictions. However, to predict binding of individual compounds, accurate absolute hydration free energies are necessary as well. In either of these general scenarios, the accuracy of hydration free energies, relative or absolute, sets a lower bound on the total error of predicted binding affinities (in the absence of fortuitous cancellation of error between hydration and binding calculations). Indeed, RMS errors in calculated binding free energies have proven comparable to or slightly larger than errors observed in hydration free energy calculations^16-20.

While hydration free energies are important, the experimental data is still somewhat limited: the largest test sets typically span 200-500 small molecules covering a relatively narrow range of chemical space^3,5,14,21 for which the molecules have been studied extensively. However, pharmaceuticals often have a variety of functional groups which are only sparsely represented in these sets, fostering interest in new benchmarks. Several hydration free energy “prediction”¹ challenges have focused on more diverse sets of small molecules^2,4,22,23. Depending on the nature of the test set, performance can be substantially worse on the diverse, polyfunctional molecules in these test sets than on more typical test sets^2,4,12. In some cases, these tests provide new insights – for example, the Generalized Amber Force Field (GAFF)^24,25 does not properly model hypervalent sulfur compounds and shows systematic errors in alcohols which grow with the number of hydroxyl groups¹².

Here, we report our results from the latest SAMPL hydration free energy challenge, which in this case focuses on three molecules and their chlorinated derivatives. This data set is more focused than those of previous SAMPL challenges, providing an especially good opportunity to gain new insight. In these calculations, we applied our “standard” hydration free energy approach based on AM1-BCC partial charges^26,27 with the GAFF small molecule parameter set^24,25, but we also took several other approaches. We tested an alternate set of partial charges from MP2/cc-PVTZ SCRF RESP²⁸ fits following the success of our recent work⁵. Alternatively, we tried a new set of QM-based charges calculated using explicit solvent simulations of each molecule to develop a solvent reaction field used in performing a fit of charges. We also took another approach for assigning GAFF or GAFF-like parameters, using OEAnte²⁹. Further, we tested some newly developed aromatic carbon Lennard-Jones parameters. Finally, after seeing the correct hydration free energies for the molecules in the SAMPL challenge, we generated new estimates using OPLS³⁰ Lennard-Jones parameters for two of our submitted charge models, as well as a third charge model augmented with virtual sites to improve the molecular mechanics fit of MP2/cc-pvTZ SCRF calculations. These numerous approaches help to answer three fundamental questions about molecular mechanical hydration free energies. First, which charge model excels? Second, which van der Waals model excels? Third, given a specific quantum mechanical description of the electrostatics, does the quality of the molecular mechanics approximation to the quantum data matter?

2 Method

2.1 Overview

Our approach for hydration free energy calculations uses molecular dynamics simulations based on a classical atomistic force field to sample small molecules in water and in the gas phase, as well as at a variety of partially interacting intermediate “alchemical” states spanning between these end states. Using data collected from these simulations (specifically, potential energy differences evaluated between pairs of simulations) we are able to compute hydration free energies, in this case using the Multistate Bennett Acceptance Ratio (MBAR) approach for analysis³¹. This approach gives correct free energies for the particular parameter set given adequate simulation time and sufficient phase space overlap between neighboring alchemical states. This is the same approach in spirit as that in our previous work^1-5,12, with minor and mostly insignificant changes relating to software versions.

Here, we briefly detail our general protocol for free energy calculations, then discuss setup differences between the different approaches considered, and conclude with some analysis details.

2.2 General “standard” protocol

We used a pre-release version of GROMACS 4.6² containing free energy modifications implemented by Michael Shirts (University of Virginia) to allow energy evaluations for MBAR to be done within the code rather than needing to store trajectory snapshots for later evaluation. This was used both for simulation setup and data analysis. The small molecule set was taken as provided by the SAMPL organizers, and then the OpenEye OEChem Python toolkit and Omega were used to generate likely solvated conformations for each molecule and assign AM1-BCC partial charges, unless otherwise noted. (As is relatively common with AM1-BCC charge calculations, the charges were not based on the wave function of a structurally optimized configuration.) These final conformations and charges were stored to mol2 files and then the AmberTools 1.4 version of Antechamber was used to assign GAFF atom types. AmberTools’ tleap was used to convert these to AMBER prmtop and crd files, which were converted to GROMACS format using acpype. Small molecules were then set up in GROMACS and, for the solute-in-water case, solvated in TIP3P³² water in a dodecahedral simulation box with at least 1.2 nm from the solute to the nearest box edge. The number of water molecules was approximately 510 for typical ethane systems, 875 for typical biphenyl systems, and 890 for typical dioxin systems. AMBER combination rules (arithmetic average for σ and geometric for ε) were used.

Simulations were run using Langevin dynamics, as previously^1,3, and a timestep of 2 fs. Van der Waals interactions were gradually switched off between 0.9 and 1.0 nm, and an analytical correction was applied to the energy and pressure³³. PME was used for electrostatics, as previously, with a real-space cutoff of 1.2 nm. LINCS³⁴ was used to constrain bonds to hydrogen. Each system and λ value (where λ is a parameter ranging between 0 and 1, where 0 corresponds to the unmodified system, and 1 corresponds to the end-state of the transformation where the solute has no partial charges and no Lennard-Jones interactions) were independently minimized for up to 1000 steps of steepest-descents minimization, followed by 10 ps of constant volume equilibration, then 100 ps of constant pressure equilibration (for the solvated case). Following constant pressure equilibration, box sizes were adjusted at each λ value by an affine transformation to ensure each λ value had the correct volume for the target pressure. After this, we conducted an additional 5 ns of constant volume production simulation at each λ, discarding the first 100 ps as additional “equilibration”, as previously³.

The parameter λ controls the transformation between end states. In this version of GROMACS, we use two separate λ values, one controlling modification of partial charges (turning solute partial charges to zero) and the second controlling modification of Lennard-Jones interactions (turning solute LJ interactions to zero). Here, λ_chg = [0.0 0.25 0.5 0.75 1.0 1.00 1.0 1.0 1.0 1.0 1.0 1.0 1.0 1.0 1.0 1.0 1.0 1.0 1.0 1.0] and λ_LJ = [0.0 0.00 0.0 0.00 0.0 0.05 0.1 0.2 0.3 0.4 0.5 0.6 0.65 0.7 0.75 0.8 0.85 0.9 0.95 1.0]¹. Hence, partial charges are first turned off and then LJ interactions are turned off separately. Hydration free energies are calculated by first computing the free energy of turning of solute-environment interactions in gas (vacuum) and then subtracting the free energy of turning these off in water.

The above constitutes our “standard” protocol. However, we also tested a number of deviations from this protocol which focused mainly in three areas: (a) alternate partial charge models; (b) alternate Lennard-Jones parameters; and (c) alternate software for assigning parameters.

2.3 MP2/SCRF charge model

In addition to AM1-BCC partial charges, we tried an alternate charge model (as suggested by our previous work⁵) based on MP2/cc-pVTZ calculations done in Gaussian03³⁵ with a self-consistent reaction field (SCRF) continuum electrostatic model to represent solvent (particularly, the Integral Equation Formalism Polarizable Continuum Model (IEF-PCM)^36,37 where the cavity is represented by a united atom topological model applied on atomic radii from the UFF force field (UA0)). Geometry optimization was done at the same level of theory. Charges were fitted using RESP²⁸ as implemented in Antechamber, taking Gaussian output files as input. Here, we refer to this charge model as “MP2/SCRF” for brevity.

We used this charge model with the same Lennard-Jones parameters as in the “standard” approach. To obtain hydration free energies with this charge model, we used the Lennard-Jones component of solvation (which is calculated without partial charges on the solute) from the “standard” protocol above and repeated the charging component of the calculations with the new charge model.

2.4 Solvent background charge QM

In addition to fitting charges to reproduce the electrostatics calculated by MP2 quantum calculations in a polarizable continuum solvent, we fitted charges to reproduce electrostatics of similar MP2-level quantum calculations in an explicit solvent reaction field generated by time-averaged densities of TIP4P-Ew³⁸ water around each target molecule in a variety of conformations. This approach, to be described in detail in a later publication, follows the conclusions of Karamertzanis et al.³⁹: a non-polarizable model of a molecule should produce an electrostatic field which is precisely the average of the electrostatic fields produced by the unpolarized molecule in vacuum and by the polarized molecule in solvent. The derivation rests on a fundamental assumption that a change in the molecular dipole and the solvent reaction field which induced it are consistent, but it provides some rationalization of why the existing fixed-charge water models all have dipoles roughly halfway between the solution-phase dipole of 2.6-3.0D and the vacuum dipole of 1.85D⁴⁰. Although the fitting method was complex and will require extensive scripting in order to be convenient, the result is simply an alternative set of charges for each molecule which enter into the same molecular mechanics energy function as existing force fields. These charges will be referred to as ”MP2/ExpSQ” for ”explicit solvent charge” denoting the reaction field potential employed in MP2 calculations.

2.5 Updated LJ Parameters for GAFF

Relatively little work has been done on optimizing GAFF parameters based on simulations of small molecules, so the recent suggestion of new aromatic carbon Lennard-Jones parameters for GAFF was intriguing⁴¹. Hence, for the molecules in the set containing those parameters (all but the ethane series) we repeated our hydration free energy calculations for the AM1-BCC (“standard”) charge model with these new parameters. We call this approach “Standard-newLJ”.

2.6 OEAnte Parameterization

We typically assign GAFF parameters using Antechamber. However, there is some interest in developing a more easily-extensible and open tool for atom typing and parameter assignment, which led Richard Dixon at Vertex Pharmaceuticals to release “OEAnte”²⁹, a Python tool based on the OpenEye libraries which handles atom typing and parameter assignment. Currently, it can either assign some rough guess parameters based on internal rules, or GAFF parameters after being passed a GAFF parameter file. We tested OEAnte in both modes, expecting that the rough guess parameters might give marginally worse results than standard GAFF, and expecting the GAFF mode to agree nearly perfectly with results from GAFF parameters assigned by Antechamber. Essentially, this last test amounts to validating parameter assignments by testing on hydration free energies. We tested these two sets of parameter assignments with AM1-BCC partial charges as in our standard approach. We call these “OEAnte-GAFF” and “OEAnte-Default”.

2.7 OPLS Results

After submitting our SAMPL predictions, discussions with Charles Kehoe at the University of California, San Francisco^42,43 suggested that OPLS parameters might yield better results for this series than GAFF parameters. Motivated by this discussion, we replaced Lennard-Jones parameters for the few atom types in our study with OPLS Lennard-Jones parameters and modified the combination rules (geometric for OPLS). We maintained GAFF bonded parameters, expecting that hydration free energies would be relatively insensitive to these. Our goal was mainly to test whether the OPLS LJ parameters performed better here. Along those same lines, we maintained the AMBER 1-4 scaling parameters (0.5 for LJ and 0.8333 for Coulomb interactions) rather than switching to the OPLS values (0.5 for each) since we minted the AMBER bonded parameters. With this modification, we repeated both our standard and MP2/SCRF calculations with OPLS LJ parameters. We will call these methods “Standard-OPLS” and “MP2/OPLS”.

At a philosophical level, this swapping of parameters between AMBER and OPLS should perhaps be taken with a grain of salt. Computed hydration free energies are of course correct given the model that we use, but they may not be representative of what we would obtain from the true OPLS force field. Particularly, torsional parameters are typically derived after LJ parameters and partial charges are assigned, and depend on the charge model and LJ parameters. This coupling in some respects impedes the ability to use OPLS LJ parameters with AMBER bonded terms, and vise versa. That said, there has been considerable interpollination of the AMBER and OPLS force fields, as a reading of the AMBER parameter files will show, and occasionally, adopting OPLS LJ parameters straight into AMBER leads to marked improvements in computed observables, such as for alkynes³.

2.8 Error analysis

Uncertainties in computed free energies were taken as the standard error in the mean from the MBAR estimator³¹ and took into account the autocorrelation time of the potential energies being evaluated. Uncertainties in statistics such as the RMS error, R², Kendall τ and average errors were computed using a bootstrapping procedure, wherein new hydration free energy datasets were constructed from the original datasets by choosing random entries, with replacement. Uncertainties were estimated for these as 95% confidence intervals computed from looking at the variation of these statistics over a minimum of 1000 bootstrap trials (bootstrapping was repeated until confidence interval estimates converged to a tolerance of less than 1% of their values when averaged over 20 bootstrap trials).

3 Results

3.1 Accuracy of blind predictions

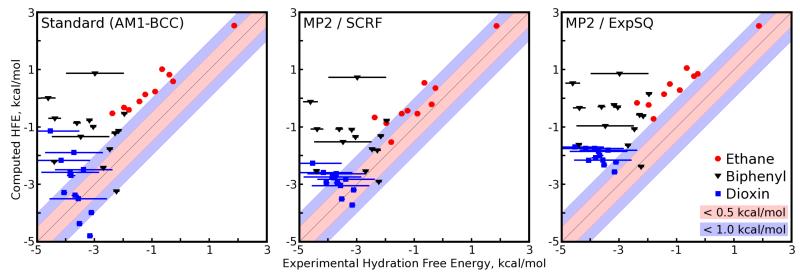
Blind predictions submitted for the SAMPL challenge, based on GAFF bonded and van der Waals parameters and three different charge models, are summarized in Figure 1 and statistics are shown in Table 1³ (the table includes all methods used, not just those applied predictively). Previously, we reported hydration free energies with RMS errors relatively near 1 kcal/mol^1-3,5, but test sets containing third-row elements or atypical organic functional groups have been much more challenging^4,12. Here, depending on the charge model, our submissions had RMS errors from 1.4 to 2.2 kcal/mol. The combination of narrow target ranges, particularly among compounds in the dioxin and biphenyl series, and larger errors made this set difficult in terms of rank ordering. Kendall τ values, measuring the fraction of compound pairs with correct rank orderings, ranged from 0.38±0.04 to 0.43±0.04 for these predictions. This is low, but nonzero, so some trends are correctly predicted. Overall, the RMS error is particularly poor given the range of free energies – as was noted at the meeting following the SAMPL challenge, predicting a constant hydration free energy equal to the average of all compounds (if that value were known) would have yielded an RMS error of 1.4 kcal/mol⁴⁴. However, this would also have led to a Kendall τ value and correlation coefficients which were substantially lower (zero).

Fig. 1.

Computed versus experimental hydration free energies for several of the approaches and charge models tested here. Methods are discussed in the text and compounds are color coded by chemical series. Plots for additional approaches are shown in the Supporting Information. Inner gray bars denote 0.5 kcal/mol error, and outer gray bars denote 1.0 kcal/mol error.

Table 1.

Statistics for different methods computing hydration free energies for SAMPL, with methods abbreviated as described in the text. We compare the RMS error, the Pearson correlation coefficient (R²), the average error, the average unsigned (absolute) error (AUE), and the Kendall τ value.

Method	RMS (kcal/mol)	R2 (kcal/mol)	Avg. err (kcal/mol)	AUE (kcal/mol)	Kendall τ
Standard	1.88 ± 0.07	0.64 ± 0.04	−1.34 ± 0.07	1.59 ± 0.06	0.43 ± 0.04
MP2/SCRF	1.59 ± 0.07	0.69 ± 0.04	−1.14 ± 0.06	1.22 ± 0.06	0.38 ± 0.04
MP2/ExpSQ	2.18 ± 0.07	0.70 ± 0.04	−1.92 ± 0.06	1.93 ± 0.06	0.40 ± 0.04
Standard-newLJ	1.90 ± 0.07	0.63 ± 0.04	−1.35 ± 0.07	1.59 ± 0.06	0.41 ± 0.04
OEAnte-GAFF	1.88 ± 0.07	0.64 ± 0.04	−1.34 ± 0.07	1.60 ± 0.05	0.42 ± 0.04
OEAnte-Default	2.02 ± 0.07	0.64 ± 0.04	−1.51 ± 0.07	1.71 ± 0.06	0.41 ± 0.04
Standard-OPLS	1.40 ± 0.05	0.74 ± 0.03	−0.87 ± 0.06	1.16 ± 0.04	0.46 ± 0.04
MP2/OPLS	1.48 ± 0.04	0.30 ± 0.07	−0.28 ± 0.08	1.26 ± 0.04	0.04 ± 0.04
MP2/ExpSQ-Q	1.33 ± 0.06	0.81 ± 0.03	−0.99 ± 0.05	1.06 ± 0.04	0.58 ± 0.03

Overall, all charge models approaches did relatively well at predicting trends within the ethane derivatives, but appear to have predicted the wrong trend in the dioxin derivatives (the narrow range of the experimental HFEs, coupled with the large experimental uncertainties on many of these values, give some uncertainty as to what the experimental trend truly is). No charge model predicted a discernable trend in the biphenyl derivatives, even though the experimental HFEs in this group are more certain and their range is more broad than that of the dioxins.

None of our SAMPL submissions is clearly superior. The MP2/SCRF charge fitting approach performed marginally better than our standard AM1-BCC charge assignment approach, as was expected (R² of 0.69 ± 0.04 kcal/mol and RMS error 1.59±0.07 kcal/mol for the former versus 0.64±0.04 kcal/mol and 1.88 ± 0.07 kcal/mol, respectively, for the latter). Kendall τ values were essentially within uncertainty of one another for all approaches. The MP2/ExpSQ charge fitting approach performed as well as the MP2/SCRF approach in predicting the overall trend in HFEs (R² = 0.70 ± 0.04) but it consistently estimated the HFEs to be less favorable than in the experiment, leading to the highest overall RMS error (2.18 ± 0.07 kcal/mol). In fact, all of the SAMPL submissions, and also the other methods we tested after the competition, estimated hydration free energies with an unfavorable bias. This is consistent with our previous work (for example, across 504 molecules, the mean error was 0.67 kcal/mol in the same direction³) and clearly contributes to the RMS errors.

We also tested a new set of aromatic carbon Lennard-Jones parameters for GAFF⁴¹which had been informed by hydration free energy calculations. However, on this set (Standard-newLJ), these parameters did not result in a statistically significant change in the quality of calculated hydration free energies. Further, we applied the OEAnte package for assigning small molecule parameters as a substitute for Antechamber. The default set of parameters for this package are relatively crude and use far fewer atom types than GAFF (OEAnte-Default). The default parameter set in fact contained a misprint in the Lennard-Jones well depth for hydrogens which initially led to clearly incorrect hydration free energies. This was fixed and incorporated into the package prior to SAMPL. OEAnte can also be used to assign GAFF parameters, and we tested this approach as well (OEAnte-GAFF). When combined with AM1-BCC charges, the default approach resulted in marginally worse performance in terms of average error and RMS error (but comparable R² values) to our standard approach, while the GAFF parameter set produced results that were statistically indistinguishable from our standard approach, validating the package’s parameter assignments.

3.2 Accuracy in follow-up testing after SAMPL

Several additional sets of hydration free energy calculations were performed after receiving the results of the SAMPL challenge. While many of our submissions to SAMPL tested different charge models, a significant focus in this follow-up testing was different Lennard-Jones parameters. As noted above, the Dill group found that OPLS Lennard-Jones parameters yielded better results than those with GAFF⁴³. Combining these parameters with AM1-BCC partial charges improved the agreement with experiment (Standard-OPLS): RMS error of 1.4 ± 0.05 kcal/mol and an R² of 0.74 ± 0.03, though this is almost statistically indistinguishable from the MP2/SCRF approach. In contrast, combining OPLS Lennard-Jones parameters with charges assigned by MP2/SCRF (resulting in MP2/OPLS) decreased the RMS error slightly to 1.48 ± 0.04 kcal/mol but, by placing a favorable bias on the HFEs of the ethane derivatives in general and a severe favorable bias on the HFE of ethane itself, reduced R² to 0.30 ± 0.07. The Kendall τ value was also dramatically reduced in this case, from 0.46 ± 0.04 to 0.04 ± 0.04.

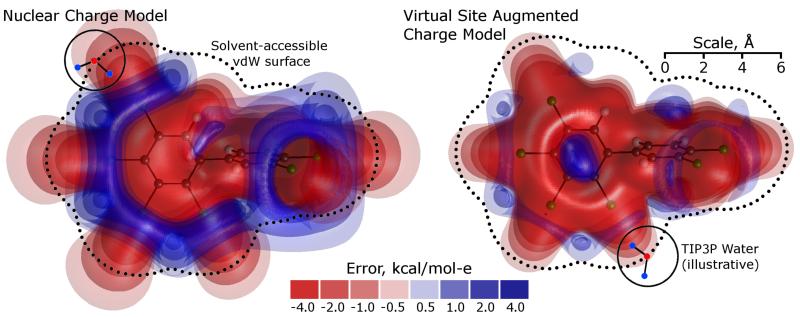
Finally, we looked at another possible source of error: the quality of the molecular mechanics approximation to electrostatic potentials derived from quantum-mechanical calculations. We repeated MP2/SCRF calculations on all molecules with chlorine substituents, saved the final checkpoint files containing the electron density, and then used the Gaussian cubegen utility to compute the electrostatic potential on rectangular grids around each molecule. The electrostatic potential created by a fitted charge model and the actual, target potential can then be directly compared, as shown in Figure 3. The RESP procedure is designed to minimize overall mean squared differences between the molecular mechanics potential and the quantum mechanical potential (subject to certain constraints) at a specified set of points, typically chosen at or near the molecular surface. As shown in Figure 3, the RESP-fitted charges may create localized regions of excess negative or excess positive potential, many of which are accessible to solvent molecules and particularly to solvent protons. By reviewing plots from chlorinated derivatives of ethanes, biphenyls, and dioxins, it became clear that the ”knob” of excess negative potential and the “ring” of excess positive potential are typical features of RESP-fitted, atom-centered charges on organic chlorine. We therefore extended the charge model to include virtual sites attached to each chlorine atom, distal to the backbone carbon atoms and along the carbon-chlorine bond axis at a distance 30% of the carbon-chlorine bond length (roughly 0.54Å). Forces on the (massless) virtual sites can be computed during a typical molecular mechanics step and reassigned to atoms with mass by chain rules. We call this approach, with added charges at virtual sites, MP2/ExpSQ-Q.

Fig. 3.

Errors in the electrostatic potential inherent in using point-charge models to approximate electron density derived from MP2 calculations. A set of point charges cannot perfectly reproduce the electrostatic field implied by quantum mechanical calculations. Some amount of error is due to the constraint that a set of fixed charges mimic the electrostatic potential for all molecular conformations, but a set of monopoles on atomic nuclei has more fundamental limitations. The two plots show differences between a quantum mechanical model and two fitted molecular mechanics approximations. The quantum mechanical model is a set of MP2 calculations performed in the context of the Gaussian SCRF continuum solvent model. The molecular mechanics approximation at left entails only charges at nuclear sites fitted with a RESP protocol. Significant errors in the electrostatic potential arise in solvent-accesible regions (the dotted line shows the boundary at which a TIP3P water molecule begins to experience a repulsive Lennard-Jones potential, and the illustrated water molecules show how TIP3P protons can sample regions even closer to the solute). The approximation at right adds additional sites not at nuclear positions (virtual sites) to better fit the potential near the chlorine atom as described in the text; the result in this case is a roughly two-fold reduction in the error over all space, most significantly near the solute surface. Including such virtual sites on all chlorinated compounds made a modest improvement to the computed hydration free energies.

By adding virtual sites to chlorine atoms and repeating the RESP fit, errors in the molecular mechanics approximation to the electrostatic potential were reduced by 40-50%, as shown in Table 3 of the Supporting Information. The virtual sites were pure charge sites with no Lennard-Jones interactions; in such cases it is always a concern that the unshielded charges may interact adversely with unshielded water protons. However, the charges on the virtual sites were always positive, reflecting the uniformity of the electrostatic potential defects around organic chlorine groups in atomcentered charge models, implying no risk of electrostatic singularities during the simulations. Overall, adding the extra points increased the negative charges on the chlorine atoms themselves, creating a stronger dipole along the carbon-chlorine bond than would have been fitted by an atom-centered charge model. While the fitted charges on chlorines did not always follow expected trends (see below) and the carbon-chlorine bonds were often modeled with small dipoles, these results can be understood as products of the RESP fit rather than the quantum-mechanical calculation.

The error in the molecular mechanics electrostatic approximation is readily quantifiable, but its effect on the computed hydration free energies is much less certain. We therefore performed additional free energy calculations (here with thermodynamic integration (TI)) to quantify the hydration free energy change implied by changing the atomic charges from the original atom-centered MP2/SCRF model to the new set augmented with virtual sites. A pre-release version of the mdgx program (part of the Amber software package⁴⁵), augmented to run simulations involving virtual sites, was used to perform the TI. As shown in Table 2 of the supporting information, the ΔΔG values implied by changing the charges were generally modest, but the overall effect of adding the virtual sites was to reduce the RMS error to 1.33 ± 0.06 kcal/mol and improve R² to 0.81 ± 0.03 (correspondingly, the Kendall τ increased to 0.58 ± 0.03).

3.3 Key trends in hydration free energies

Overall, we expected that molecules in our series which are more highly chlorinated ought to be more favorably solvated, for two main reasons. First, adding a relatively electronegative chlorine tends to increase the overall polarity of the solute, and, in general, more polar molecules are more favorably solvated. Within the force field, this is typically represented by partial charges which become larger in magnitude (and typically negative on the chlorine atoms). Second, (for reasons which are related physically), chlorine atoms have stronger dispersion interactions with their environment than hydrogen atoms. Within the force field, this is seen by a substantially larger well depth for chlorine atoms as compared to hydrogen atoms (ε = 0.0150 to 0.0157 kcal/mol for hydrogen, here in GAFF, versus ε = 0.2650 for chlorine). These stronger dispersion interactions, we believed, would result in favorable nonpolar interactions with the surrounding solute that would more than offset the increased cavity volume due to the increased size of chlorine.

Both of these trends were generally borne out in our computed hydration free energies, though there are exceptions. Focusing on our MP2/SCRF results, and looking at a series of ethane derivatives, we find the expected trend generally holds up (Table 2). Adding chlorines does generally make solvation more favorable (Table 2(a)-(d)) in terms of both electrostatic and Lennard-Jones components of solvation. Because the effects contributing to this are largely local effects and strongly dependent on the first solvation shell, the solvent accessibility of the chlorines also makes a difference (Table 2(e)) – with an equal number of chlorines, the solute with the more solvent-accessible chlorines is preferentially solvated. In this specific case, there is also a dipole moment contribution – the overall dipole moment of the molecule is substantially higher in the case where the chlorines are at opposite ends, as well.

Table 2.

Changes in hydration free energy on adding a chlorine, or moving chlorines, for selected pairs of ethane derivatives. Shown are calculated and experimental hydration free energy changes, as well as the portion of the calculated change due to electrostatics (ΔΔG_calc,e) and the portion due to changing Lennard-Jones interactions (ΔΔG_calc,LJ). All calculated values are from the MP2/SCRF set.

	Transformation	ΔΔGexpt	ΔΔGcalc	ΔΔGcalc,e	ΔΔGcalc,LJ
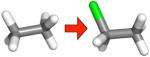
(a)		−2.25 ± 0.14	−2.74 ± 0.01	−2.31 ± 0.01	−0.42 ± 0.01
(b)		−0.49 ± 0.14	−0.32 ± 0.01	−0.08 ± 0.01	−0.24 ± 0.01
(C)		− 1.09 ± 0.14	−0.34 ± 0.05	−0.06 ± 0.01	−0.29 ± 0.04
(d)		−0.40 ±0.14	0.21 ± 0.05	0.40 ± 0.01	−0.20 ± 0.03
(e)		−0.92 ±0.14	−1.00 ± 0.01	−0.81 ± 0.01	−0.19 ± 0.01
(f)		0.62 ±0.14	0.88 ± 0.01	1.0 ± 0.01	−0.14 ± 0.01
(g)		−0.57 ± 0.14	0.87 ± 0.02	1.16 ± 0.01	−0.29 ± 0.02

Dipole moment and charge distribution alone can make a substantial difference as well. Going from 1,1-dichlorethane to 1,1,1-trichloroethane results in a substantial overall decrease in dipole moment, and solvation becomes less favorable (Table 2(f)), both in our calculations and experimentally. Partial charges on the chlorine atoms are dramatically reduced, presumably because no nearby hydrogen atom donates electrons.

This isn’t to say that the calculations correctly capture every trend. The 1,1-dichloroethane to 1,1,2,2,tetrachloroethane pair (Table 2(g)) is a mystery. Our computed charge sets (and the MP2 density itself) have the dipole moment here staying roughly constant and partial charges on the chlorine atoms undergoing a dramatic reduction. Overall, this means adding these two additional chlorine atoms is actually calculated to be unfavorable by nearly 1 kcal/mol, while experimentally it is favorable to add these. We are unclear why this is, as this discrepancy is robust across all the approaches we tried.

Thus, the key trends observed in ethanes (both with calculation and experiment) are that adding chlorines generally improves solvation, and improving solvent accessibility of chlorines also improves solvation. Increasing the dipole moment or polarity of the overall molecule tends to improve solvation, and there can be subtle effects depending on chlorine placement that play a role in this.

These trends are much harder to see, if they are present at all, in the data for the other two series. The experimental values may show some evidence for these for some of the compounds, but we see little sign of these trends in the calculated values. This is not necessarily a problem – it may be that as molecular complexity grows, other factors such as the details of the electron distribution (particularly, the pi systems present in these molecules) and structure become much more important than the number of chlorine atoms.

3.4 Observations for specific charge models and methods

As seen in Figure 1 and Figure 1 of the Supporting Information, most of the approaches we tried show rather similar trends. However, some specific observations are warranted. First, while our standard approach does well overall, it also exhibits a clear and incorrect trend for the dioxins. While the dioxin trend is incorrect across all our methods, the error is particularly pronounced in approaches using AM1-BCC partial charges (the standard, OEAnte-GAFF, OEAnte-Default, standard-newLJ, and standard-OPLS approaches).

Second, all the approaches we tested agree in computing hydration free energies for a number of compounds which are substantially too positive. This is moderated somewhat in the MP2/ExpSQ-Q case, where addition of virtual sites shifts the hydration free energies of many of these polychlorinated compounds to be somewhat more favorable, probably because these sites capture stronger C-Cl bond dipoles even while the overall polarity of the molecule remains weak. Still, even for this charge model free energies are still too positive on average. In some cases, there is some question about the quality of the experimental data⁴⁶. This is denoted by large error bars (estimated by J. Peter Guthrie). The belief is that in these cases, if the experimental value is in error, it will typically be in error by being too negative. This could result because some of the specific experiments reported observing solubilities higher than the true value, which would yield hydration free energy estimates that are too negative⁴⁶. Given the consistency across all of the approaches we tried, we are particularly concerned that this may be the case for 1,2,4,5-tetrachloro-3-(3,4-dichlorophenyl)-benzene, 1,2,3,4-tetrachloro-5-(2,3,4,6-tetrachlorophenyl)-benzene, and the base dioxin, dibenzo-p-dioxin. Computed free energies are consistently too positive for some other members of the dioxin series as well, but the consistency and magnitude in those cases is not as pronounced. Given the consistency of this observation even across different Lennard-Jones parameters (including OPLS parameters) it seems likely the experimental data needs reevaluation.

Of the models we tested, the MP2/ExpSQ charges yielded the worst overall RMS error in absolute hydration free energies, but nearly the best overall correlation between predicted and experimental hydration free energies across all classes of compounds. As shown in Figure 1, the MP2/ExpSQ charges showed behavior similar to the AM1-BCC and MP2/SCRF charge sets: strong performance in predicting relative hydration free energies of ethane derivatives, prediction of the wrong trend in hydration free energies of the dioxin derivatives, and inability to predict any trends in the biphenyl derivatives. While the overall correlations with experimental hydration free energies were not high for any charge model, hydration free energies produced by all of the charge models are strongly correlated, particularly the MP2/SCRF and MP2/ExpSQ models as shown in Table 3.

Table 3.

Correlation coefficients (R²) between MP2/SCRF results and results obtained with various other approaches.

Method	R2 with MP2/SCRF
Standard	0.96±0.01
MP2/ExpSQ	0.99±0.01
Standard-newLJ	0.96±0.01
OEAnte-GAFF	0.95±0.01
OEAnte-Default	0.93±0.01
Standard-OPLS	0.94±0.01
MP2/OPLS	0.75±0.03
MP2/ExpSQ-Q	0.95±0.01

As noted in Methods, after submission of our SAMPL results we also tried OPLS Lennard-Jones parameters. With AM1-BCC charges, these actually substantially improve the overall quality of the computed hydration free energies, increasing the R² and decreasing the average and RMS error relative to other charge models. As seen in Figure 1, most of the improvement comes from the biphenyls, where scatter is substantially reduced for a number of the compounds and error relative to experiment is reduced to less than 0.5 kcal/mol; the Kendall τ value is also just slightly increased for this set. This does not hold up, however, when OPLS Lennard-Jones parameters are used with MP2/SCRF partial charges – the average and RMS error again increase somewhat. (The R² and Kendall τ also decrease markedly, apparently chiefly because of a poor value for ethane, the single compound in this set with a hydration free energy that is very different from the rest.)

4 Discussion and conclusions

This test set, three different chemical series involving chlorinated derivatives of a common scaffold, represents an interesting and challenging set, especially given the relatively narrow range of experimental hydration free energies. While most of the approaches we tried gave reasonable agreement with experiment in terms of RMS and average errors (with RMS errors in the 1.4-2.0 kcal/mol range), this was actually somewhat less than satisfactory in this set given the narrow range of experimental values (with the RMS difference in experimental values also around 1.4 kcal/mol). Thus, essentially all approaches we tried do not do a good job at capturing experimental trends in hydration free energies, except for the ethane derivatives, where trends are typically captured reasonably well. Typically around 40% of pairs of compounds are correctly ranked (as measured with Kendall τ).

Our results suggest that, overall, current force fields still need substantial improvement in the area of accurately treating chlorinated derivatives of common scaffolds. While modifying the charge model (going from AM1-BCC to our approach) or switching Lennard-Jones parameters (from GAFF to OPLS) can yield modest improvement on this particular test set, even in the best cases, trends remain poorly captured, except for ethane derivatives. Perhaps these results are indicating that we can do no better for these compounds without going beyond an atom-centered partial charge model or atom types that are more dependent on the chemical environment, or perhaps Lennard-Jones parameters would need to be reoptimized in a charge-model-dependent way to improve agreement with experiment.

We also find, generally, that computed hydration free energies from our different approaches are strongly correlated (R² from 0.93 to 0.99 relative to MP2/SCRF, except for the MP2/OPLS set, with R² = 0.75, with much of the difference in this last case being due to substantial changes for ethane). In most of the sets we tried, the Lennard-Jones parameters are identical, which may be one major source of this correlation. However, even results with OPLS Lennard-Jones parameters remain fairly highly correlated. This is likely because the charge models themselves share numerous similarities that deserve examination. The strongest correlation in predicted hydration free energies occurs between charge sets fitted against MP2 calculations with similar basis sets (R²=0.99); in one charge model, the aqueous solvent environment was mimicked by a dielectric boundary akin to Poisson-Boltzmann calculations, whereas in the other the aqueous solvent environment was represented by a time-averaged solvent charge density. As has been shown before, these two treatments actually create strikingly similar reaction fields within the solute⁴⁷, implying that the influence of each field on the solute charge density determined by MP2 calculations may have been very similar. Subsequent RESP fitting merely attempted to reproduce the field due to the solute charge density, not the field due to the solvent. No matter the charge model, the distribution of atomic partial charges was also similar: non-polarizable point charges placed at all atomic nuclei. Even in the AM1-BCC case, charges are parameterized to be like those from RESP fits. The process of RESP fitting naturally creates regions near the solute surface where the electrostatic potential is over- or under-estimated. While RESP fitting seeks to minimize mean square error in the potential, these regions of error might have been qualitatively similar across different models. Finally, another strong determinant of hydration free energies, the solvent model used during the thermodynamic calculations, was consistently set to TIP3P. No matter the charge model, water arrangements around the solute will be similar due to identical or at least extremely similar Lennard-Jones parameters. And the arrangement of water molecules will be a substantial contribution to the overall hydration free energy, especially since most of these compounds are not extremely polar.

Extension of the monopole basis set used in RESP fitting by massless virtual sites (in the MP2/ExpSQ-Q case) did substantially improve the fit to the quantum-mechanical electrostatic potential in regions accessible to solvent. In most cases, this extension of the charge model does not drastically change the hydration free energy. However, in polychlorinated biphenyl and dioxin compounds the virtual sites do appear to have a more pronounced effect in making the hydration free energies more favorable. None of these compounds showed strong overall dipoles, but the virtual sites permitted local dipoles along C-Cl bonds which models with only atomic nuclear charges could not fit. Although the solubilities of some of these compounds are uncertain, local dipoles may contribute to the unexpectedly high values reported in the literature.

Although the virtual site charge model afforded some success, it is noteworthy that all of the non-nuclear virtual sites took on positive values while driving the chlorine nuclear charges more negative. While numerically convenient for avoiding singularities in the simulations, this result underscores the artificial nature of the molecular mechanics charge model. Experience with modeling other compounds using the mdgx virtual site capabilities suggests that more virtual sites are of decreasing marginal value to improving the RESP fit. Complicated pi systems in the biphenyl and dioxin compounds likely cannot be modeled by simply adding virtual sites with fixed partial charges; although this treatment can create static dipole and quadrupole moments, polarization would likely be necessary to capture the physics of aromatic systems.

Despite the overall similarity of computed free energies across all of the different approaches, there are enough differences that when all approaches are wrong in a consistent way, it stands out. Particularly, there are three compounds identified above for which there is some question about the quality of the experimental data, and all of our tested approaches show substantial deviations from experiment. For these compounds, we believe our results suggest experimental follow-up is warranted.

Overall, agreement between calculated hydration free energies and experiment is decent in terms of average error, but there is considerable room for improvement in how classical molecular mechanics force fields capture hydration free energies for chlorinated derivatives in these three chemical series.

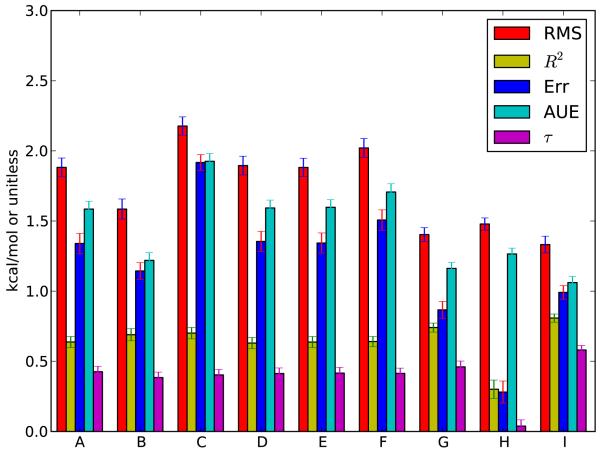
Fig. 2.

Statistics for the different approaches tested here. Shown are the RMS error, correlation coefficient R², average error (“Err”), average unsigned error (AUE), and Kendall τ (τ). Methods are (A) Standard; (B) MP2/SCRF; (C) MP2/ExpSQ; (D) Standard-newLJ; (E) OEAnte-Standard; (F) OEAnte-Default; (G) Standard-OPLS; (H) MP2/OPLS; (I) MP2/ExpSQ-Q; as discussed in the text. Error bars denote 95% confidence intervals. Data also in Table 1.