On the use of orientational restraints and symmetry corrections in alchemical free energy calculations

Abstract

Alchemical free energy calculations are becoming a useful tool for calculating absolute binding free energies of small molecule ligands to proteins. Here, we find that the presence of multiple metastable ligand orientations can cause convergence problems when distance restraints alone are used. We demonstrate that the use of orientational restraints can greatly accelerate the convergence of these calculations. However, even with this acceleration, we find that sufficient sampling requires substantially longer simulations than are used in many published protocols. To further accelerate convergence, we introduce a new method of configuration space decomposition by orientation which reduces required simulation lengths by at least a factor of 5 in the cases examined. Our method is easily parallelizable, well suited for cases where a ligand cocrystal structure is not available, and can utilize initial orientations generated by docking packages.

I. Introduction

Alchemical free energy methods can calculate binding free energies of small molecule ligands to proteins. In these methods, a binding free energy calculation is decomposed into steps in which the ligand is either annihilated^1–5 or decoupled ^6,7 from its bound state in the complex. The process is then reversed in solvent to complete a thermodynamic cycle equivalent to dissociating the ligand from the protein.

Previous work^1–3,8,9 introduced a restraining potential to keep the ligand in the binding site during this process so that the ligand need not sample the entire simulation volume during this process. In published protocols, the restraining free energy is computed by a series of short simulations—often only 20 or 40 ps in length, including equilibration—at a series of different restraint strengths and initiated from the same starting configuration.^1–4

Here, we find two problems with these protocols. First, they prescribe an equilibration stage that can be far too short, leading to computed free energies that are sensitive to the initial orientation⁶⁰ of the ligand. Second, in some cases, multiple ligand orientations contribute to the binding affinity, but present methods can fail to sample these alternate orientations sufficiently.

In order to obtain correct results with these calculations, all of the component simulations (which can often number up to 30) must have both equilibrated and converged. That is, each simulation must have time not only to leave its initial configuration and find the most important region of configuration space (equilibrate) but also to make a substantial number of visits to all of the relevant regions of configuration space so that thermodynamic averages will be accurate (converge). Signs of equilibration^10–12 must be carefully monitored and nonequilibrated data must be discarded. Likewise, careful examination of simulations and calculation of autocorrelation times^13–16 can give indications that too few transitions are observed and averages may not be converged. Similar indications can sometimes be detected by the use of multiple independent simulations.¹⁷ However, of particular concern are simulations that are so short that they do not even visit other relevant regions of configuration space. This can happen if the system is trapped in a metastable state. In such cases, correlation times may appear short and computed free energies may appear reproducible but still be wrong.^18,19

In some alchemical free energy calculations, results depend on the ligand starting orientation.⁷ Some workers have even suggested that an accurate crystallographic structure of the protein-ligand complex is a requirement.^4,5 Such observations indicate that these simulations may not have been equilibrated or converged. Both are undesirable, because alchemical free energy calculations will be most useful if they do not require knowledge of a crystal structure of the ligand already bound to the protein. For example, it would be valuable to predict binding affinities using putative bound conformations of small molecules identified by computational docking.^20,21 This will be possible only if the simulations are properly equilibrated and the free energy estimates converged, because only then will the calculated binding free energy be insensitive to the starting orientation and a cocrystal structure be not needed.

To study potential convergence problems, we examine the binding of several small ligands to a model protein binding site—the L99A/M102Q mutant of T4 lysozyme.²² Previously, the apolar cavity in the L99A mutant of this protein was studied extensively with alchemical free energy methods.^1,3,4 The L99A/M102Q binding site we consider here is quite similar, except that a carbonyl group has been introduced in the periphery of the binding site, allowing the binding of polar ligands such as phenol and catechol. We focus here on the problem of convergence—that is, on obtaining the correct free energy for the force field and partial charges used—rather than on comparison with experimental binding free energies. While the calculation of a protein-ligand binding affinity actually requires two separate sets of calculations—one in which the free energy of transforming the ligand to a noninteracting reference state is computed in its complex with the protein and another in which the process is repeated for the ligand in solvent—we discuss the first exclusively, since this is the problematic one here due to the large number of frustrated degrees of freedom present. Also, here we focus on ligand orientational degrees of freedom only, as the binding site is fairly rigid and protein rearrangement is relatively minor. In more complex systems, protein side chain degrees of freedom could present convergence problems as well.

In this system, the ligands can sample multiple long-lived metastable orientations. For example, catechol binds in two distinct orientations.²³ In our simulations, these multiple orientations lead to convergence problems. Short simulations can be especially problematic for the ligand restraining step, where simulations can easily fail to sufficiently sample all of the relevant regions of configuration space. With orientational restraints, this is precisely the step that must be sampled most thoroughly. We find that restraining simulations must be orders of magnitude longer than those sometimes employed in order to obtain converged results.

The existence of these multiple favorable binding orientations can be due to true symmetries or pseudosymmetries of the ligand or its substituents. For pseudosymmetries, several orientations may contribute comparably to the free energy of binding, and all must be sampled to ensure convergence. True symmetries, on the other hand, can be identified and need not be explicitly sampled if symmetry number corrections are used.^1,3,4 We clarify below how and when these should be applied.

We also show how to improve equilibration and convergence by decomposing the full binding free energy into the component free energies for several different orientations. This eliminates the need to sample the slow transitions between different orientations. Our method is applicable even when given only the apo structure of the protein, or the structure of the protein bound to a different ligand, provided no significant conformational rearrangements of the protein occur upon binding of various ligands.

Finally, we demonstrate that alchemical free energy calculations performed without orientational restraints (using only simple distance restraints between the protein and the ligand) are substantially more difficult to converge for this system. Additionally, strong orientational restraints allow discharging and Lennard-Jones decoupling simulations to be shorter, because the need to sample alternate binding orientations is confined to the restraining step.

II. Theory

A. Alchemical binding free energy calculations

The binding of a ligand to a protein can be described by the reaction

$$P+L\stackrel{\mathrm{\Delta }{G}^o}{⟶}PL,$$ (1)

where P+L represents the uncomplexed, solvated protein and ligand at a standard reference concentration, and PL the solvated complex. On the left, P and L are both fully solvated; on the right, the ligand is bound to the protein and the compound is solvated. ΔG^o represents the free energy of forming the complex under these conditions, and is negative if binding is favorable.

This binding free energy is related to the dissociation constant K_d or binding affinity K_a by

$$\mathrm{\Delta }{G}_{\text{bind}}^o={\beta }^{-1}ln\left(k_d{V}^o\right)=-{\beta }^{-1}ln\left(k_a/V^o\right).$$ (2)

Here, V^o denotes the standard volume, which is 1660 ų for a 1M standard state, and β=(k_BT)⁻¹, where k_B is the Boltzmann constant and T is the absolute temperature. For a more detailed discussion of issues relating to the standard state, see Refs. 3, 9, and 24.

While it is possible in principle to estimate the free energy of binding (or the dissociation constant) from a long molecular dynamics trajectory that samples many association and dissociation events, ²⁴ this approach is generally impractical because of computational limitations. However, since the free energy is a function of state, we are free instead to choose an arbitrary path connecting the bound and unbound states, even if it is unphysical, and use some form of importance sampling to compute the free energy change along this path. In practice, this is often done by perturbing the Hamiltonian in a series of alchemical steps that gradually eliminate the interactions between the ligand and the solvated protein, effectively disappearing the ligand. In subsequent steps, the perturbation is reversed in solvent, restoring the ligand to a fully solvated environment and completing the thermodynamic cycle (Fig. 1).

FIG. 1.

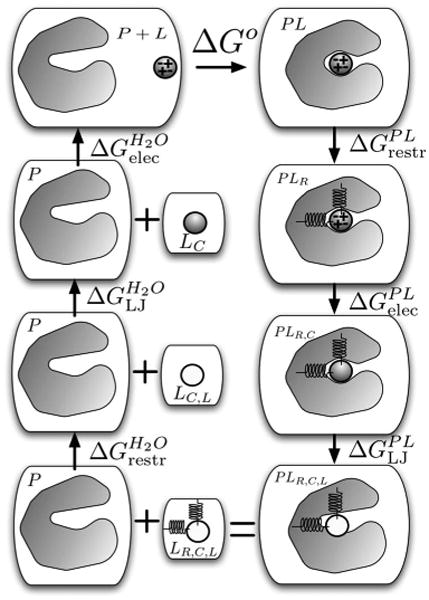
The thermodynamic cycle for alchemical binding free energy calculations. Beginning with the complex (PL, top right), the ligand is first restrained in the complex (PL_R), its electrostatic interactions (shown schematically by + and − signs) eliminated (PL_R,C), and then its Lennard-Jones interactions (PL_R,C,L) turned off (shown by the unshaded ligand). This state is equivalent to having the ligand separate from the protein, in water (L_R,C,L still restrained and with no interactions (bottom left). In a subsequent leg of the cycle, its Lennard-Jones and electrostatic interactions are turned back on in water, and the free energy of removing the restraints is computed analytically, closing the cycle.

To obtain standard free energies of binding (for a ligand concentration of 1M), a correction term should be applied to the computed binding free energy based on the size of the simulation cell.^3,9 However, convergence is difficult when weakly interacting ligands must sample the entire simulation volume. Several groups have proposed that restraints first be imposed between the ligand and the protein to improve convergence.^1,3,8,9

In the resulting thermodynamic cycle (Fig. 1) the ligand is first restrained in the binding site of the protein with the transformation

$$PL\stackrel{\mathrm{\Delta }{G}_{\text{restr}}^{PL}}{⟶}P{L}_R,$$ (3)

where PL is the solvated complex and PL_R is the solvated complex with the ligand restrained. $\mathrm{\Delta }{G}_{\text{restr}}^{PL}$ is the free energy of restraining the ligand in the binding site, and will depend on the details of the choice of restraint.³ Next, the ligand electrostatic interactions are either turned off entirely (annihilated)^1,3 or its electrostatic interactions with the environment are turned off (decoupled)^6,7 in the transformation

$$P{L}_R\stackrel{\mathrm{\Delta }{G}_{\text{elec}}^{PL}}{⟶}P{L}_{R,C}.$$ (4)

Here, PL_RC denotes the complex where the ligand has been restrained and the charge interactions involving the ligand have been turned off and $\mathrm{\Delta }{G}_{\text{elec}}^{PL}$ the free energy of this transformation. The ligand Lennard-Jones interactions are subsequently either turned off entirely (annihilated) or only its interactions with its environment are turned off (decoupled):

$$P{L}_{R,C}\stackrel{\mathrm{\Delta }{G}_{\text{LJ}}^{PL}}{⟶}P{L}_{R,C,L}.$$ (5)

PL_R,C,L denotes the restrained ligand in the complex with no electrostatic or Lennard-Jones interactions at all (annihilated) or no such interactions with its environment (decoupled). (Note that we use the terms decoupling and annihilation to refer exclusively to the modification of nonbonded interactions in these alchemical calculations, a terminology that differs from some previous literature but avoids confusion.⁶¹) Since the ligand is no longer interacting with its environment, PL_R,C,L is equivalent to P+L_R,C,L; a noninteracting ligand in the complex is the same as a noninteracting ligand in vacuum or water. Now it remains to compute the free energy of releasing the ligand to the standard volume ( $\mathrm{\Delta }{G}_{\text{restr}}^{{\text{H}}_2\text{O}}$ in Fig. 1), then to turn its Lennard-Jones and electrostatic interactions back on in water (giving $\mathrm{\Delta }{G}_{\text{LJ}}^{{\text{H}}_2\text{O}}$ and $\mathrm{\Delta }{G}_{\text{elec}}^{{\text{H}}_2\text{O}}$ in Fig. 1). Moving clockwise around the cycle of Fig. 1, beginning from the bound state and ending with the unbound state, the sum of the free energies equals the negative of the standard free energy of binding.

B. Choice of restraints

The simplest restraint is a single distance restraint between the ligand and protein.⁷ In that case, it is easy to analytically compute the free energy of releasing the restraint on the noninteracting ligand.^3,7,9 To facilitate convergence, orientational restraints have also been used to restrict the ligand's orientation relative to the protein.^1,3–5 The form, stiffness, and equilibrium geometry for these restraints are arbitrary, and they will not affect the asymptotic estimate of the binding free energy. Here, we use the orientational restraints suggested by Boresch et al.:³ One distance (r_aA), two angles (θ_A and θ_B), and three torsions (ϕ_A, ϕ_B, and ϕ_C) determine the orientation of three atoms in the ligand relative to three in the protein.

To use an orientational restraint, we must choose a reference orientation that gives the values (θ_A0, …, r_aA,0). Previous work extracts these parameters from the ligand orientation in the crystal structure.^1,3–7,25 In this work, we choose reference orientations by docking the ligand into the binding site of the apo structure of the protein (discussed in detail in Sec. III E).

C. Equilibration and convergence

The free energy differences above can be computed with thermodynamic integration (TI) or free energy perturbation (FEP) methods.¹¹ Both methods involve simulating a number of alchemical intermediates between two physical end states. For example, for annihilating the ligand electrostatics, simulations can be run at a series of intermediate states where the ligand electrostatic potential energy is scaled by a factor (1−λ), resulting in a fully interacting state at λ=0, a state without ligand charge interactions at λ=1, and a series of alchemical intermediates in between. The free energy of turning off the electrostatics entirely is the sum of the free energy differences from λ=0 to λ=1.

Regardless of whether TI or FEP is used, the free energy change of the alchemical transformation is computed from one or more averages computed from simulations of each intermediate state. Here, using small aryl ligands binding to a model site as an illustration, we show how convergence of these averages can be frustrated by the presence of multiple favorable binding orientations.

Convergence can also be affected by the choice of restraints. Without restraints, the ligand must sample all favorable orientations and regions of the simulation volume in every simulation. This means it must sample all relevant orientations when interactions with the protein are strong, and leave and reenter the binding site multiple times when interactions with the protein are weak. When only the protein-ligand distance is restrained (as in Refs. 6 and 7) the ligand must at least remain near the binding site, but all relevant orientations must still be sampled in every simulation.

However, if the ligand orientation is also restrained, the probability of alternate conformations can vanish for the sets of simulations in which the electrostatic and Lennard-Jones interactions are eliminated, aiding convergence. In other words, orientational sampling problems can be confined to the restraining step. When there is only one dominant binding orientation, the resulting savings of simulation time may be minimal. However, when there are multiple binding orientations, the savings can be tremendous.

D. Orientational decomposition of the configuration integral

One way to facilitate convergence of the total binding free energy is to decompose it into individual free energies for the different orientations of the ligand.

Following roughly the notation of Gilson et al.,⁹ we express the free energy as

$$\mathrm{\Delta }{G}^o=-{\beta }^{-1}ln\left[\frac{C^o}{8{\pi }^2}\frac{{\sigma }_P{\sigma }_L}{{\sigma }_{PL}}\frac{Z_{PL}{Z}_0}{Z_P{Z}_L}\right]+P^o\mathrm{\Delta }{V}_{PL}.$$ (6)

Here, subscripts P, L, and PL refer to the protein, ligand, and complex, respectively. Z denotes the configuration integral and σ the symmetry number, discussed in more detail in Sec. II E below. The final term, P^oΔV_PL, represents the standard pressure times the change in equilibrium volume on complex formation, which is negligible at standard pressure,⁹ so will be neglected here.

The configuration integral for the complex, Z_PL, is given by

$$Z_{PL}={{\int }_{\text{bound}}d{\mathbf{\text{r}}}_{\mathit{\text{pls}}}d\mathit{\xi }}_{L}J({\mathit{\xi }}_L)exp[-\beta U({\mathbf{\text{r}}}_{\mathit{\text{pls}}},{\mathit{\xi }}_L)].$$ (7)

ξ_L denotes the ligand's six degrees of freedom relative to the protein, and r_pls denotes the rest of the degrees of freedom in the system (protein and ligand internal degrees of freedom and solvent degrees of freedom). J(ξ_L) is the Jacobian determinant for the rotation of the ligand relative to the protein, as given elsewhere.³U(r_pls,ξ_L) is the potential energy as a function of the degrees of freedom of the system. The integral runs over the entire bound state, including all of the possible ligand orientations relative to the protein in the binding site. Similar expressions describe the configuration integrals for the isolated protein in solvent, Z_P, the isolated ligand in solvent, Z_L, and so on. Finally, in Eq. (6), the integral Z₀ runs only over the solvent degrees of freedom.

Equation (7) can be divided up into substates by defining indicator functions which run over only some portion of the bound state. For example, we consider the case of two substates. We define an indicator function I(ξ_L) which equals 1 for the entire bound state and is zero otherwise. Then, we define a decomposition

$$I\left({\mathit{\xi }}_L\right)\equiv I_1\left({\mathit{\xi }}_L\right)+I_2\left({\mathit{\xi }}_L\right)$$ (8)

into two indicator functions I₁ and I₂ that form a complete decomposition of the bound state, each including some contiguous region of the binding site. We are free to choose the bounds of each indicator function so long as the sum includes the entire binding site. We now define

$$Z_{1,PL}=\int d{\mathbf{\text{r}}}_{\mathit{\text{pls}}}d{\mathit{\xi }}_{L}J\left({\mathit{\xi }}_L\right)I_1\left({\mathit{\xi }}_L\right)exp[-\beta U({\mathbf{\text{r}}}_{\mathit{\text{pls}}},{\mathit{\xi }}_L)],$$ (9)

and similarly for the integral involving I₂, which becomes Z_2,PL. Thus we have, from Eq. (6),

$$\mathrm{\Delta }{G}^o=-{\beta }^{-1}ln\left[\frac{C^o}{8{\pi }^2}\frac{{\sigma }_P{\sigma }_L}{{\sigma }_{PL}}\frac{(Z_{1,PL}+Z_{2,PL})Z_0}{Z_P{Z}_L}\right].$$ (10)

Now, we need to evaluate the sum of the configuration integrals in the numerator. Each integral is restricted to some portion of the binding site. It is useful to define an effective free energy of ligand binding to just one part of the binding site. For Z_1,PL, we define

$$\mathrm{\Delta }{G}_1^o=-{\beta }^{-1}ln\left[\frac{C^o}{8{\pi }^2}\frac{{\sigma }_P{\sigma }_L}{{\sigma }_{PL}}\frac{(Z_{1,PL})Z_0}{Z_P{Z}_L}\right].$$ (11)

This quantity, $\mathrm{\Delta }{G}_1^o$, is easily computed with standard free energy methods provided that we restrict the simulation to the region defined by I₁(ξ_L). $\mathrm{\Delta }{G}_2^o$, for the second region, is computed similarly. Finally, we can combine Eqs. (10) and (11) to obtain

$$\mathrm{\Delta }{G}^o=-{\beta }^{-1}ln\left[exp\left(-\beta \mathrm{\Delta }{G}_1^o\right)+exp\left(-\beta \mathrm{\Delta }{G}_2^o\right)\right].$$ (12)

Thus, we can decompose the integral over the binding site into two (or more) integrals over portions of the binding site for which we compute “effective” binding free energies $\mathrm{\Delta }{G}_1^o$ and $\mathrm{\Delta }{G}_2^o$ for binding specifically in these orientations. Then, we combine these to compute the overall free energy of binding, allowing all orientations in the binding site. If both orientations have the same effective binding free energy, the contribution of the second orientation will be around −β⁻¹ ln 2 ≈ −0.41 kcal/mol at 300 K. The contribution of the less favorable orientation is smaller than typical statistical uncertainties by the time the free energy difference is 2 kcal/mol.

With this method, we are free to identify dominant energy minima in the binding site which are separated by large barriers and compute the effective binding free energy in the region of each minimum in separate calculations, then combine our results to get the overall free energy. We show below that this strategy improves convergence.

It is worth noting that the problem of multiple relevant binding modes is essentially equivalent to the problem of multiple relevant conformational substates. Related theoretical background was laid out early on, along with an analogous expression to the one presented here.²⁶ Also, a similar expression was developed for treating multiple rotational isomeric states and used in several earlier computational studies which pointed out some problems with slow degrees of freedom in free energy calculations.^18,27

E. Symmetry number corrections

In many alchemical binding free energy calculations, symmetry number corrections are applied to correct the computed free energy for certain symmetric ligands.^1,3,4,9 These corrections account for equivalent regions of configuration space that have been excluded from sampling, either intentionally or by large kinetic barriers. The binding free energy is determined by a ratio of partition functions [Eq. (6)] where the integral over the bound state Z_PL runs over all equivalent orientations [Eq. (7)]. So, restriction of this integral to only one of these orientations will underestimate the ratio of partition functions Z_PL/(Z_PZ_L) by a factor of the ligand symmetry number σ_L, and the binding free energy ΔG^o by an additive offset of −β⁻¹ ln σ_L. For example, benzene has D_6h symmetry and 12 equivalent orientations. While all orientations are readily sampled when the ligand is in solvent, only one of its orientations might be sampled when it is in a binding site due to large kinetic barriers, necessitating the use of a correction factor. If all its orientations were sampled a number of times, no correction factor would be necessary. In addition to molecular symmetry, some ligands contain symmetric substituents, such as a phenyl group, attached via rotatable bonds. The rotation of these groups can be slowed by large barriers in the binding site, but not in the solvent, again requiring the use of a correction factor.

The use of the symmetry correction factor is only straightforward when the equivalent orientations in the binding site are never sampled. However, if the simulations are long enough that a few (but not all) of these configurations are well sampled in the complex and/or solvent, the correction factor must be modified appropriately. Since there are actually a number of simulations conducted in the complex at different protein-ligand interaction strengths, there is the additional possibility that some equivalent orientations are sampled in some of these simulations (such as when the ligand is weakly interacting) but not others. In this case, the symmetry factor correction would have to be applied to each pair of neighboring intermediate simulations, which can be complicated. Alternatively, we can use orientational restraints to confine the ligand to only one of these orientations. If this is done only in the complex, a correction term is needed, but not if it is done both in the complex and in solvent.⁵

A further complication arises for molecules that share similar interactions with the binding site in one of several different orientations but are not truly symmetric. Good examples are 2-aminophenol and indene, as are larger molecules with these groups attached as substituents via a rotatable bond. In these cases, convergence will require sampling the pseudosymmetric orientations. When these orientations are separated by large energy barriers, the method of phase space decomposition introduced above may prove useful, as may the potential of mean force method suggested by Woo and Roux²⁵ and the biasing method discussed elsewhere.¹⁹

III. Methods

To test the convergence of alchemical binding affinity calculations subject to restraints, we initiated independent free energy calculations from multiple different initial ligand orientations in a polar binding pocket engineered into T4 lysozyme. The ligand was first docked into the preequilibrated apo structure to obtain various initial orientations, free energy calculations were performed, and convergence was tested by ensuring the computed free energies were independent of the initial ligand orientation. Details are given below.

A. Ligand preparation

Here, we study the small molecule ligands phenol and catechol (Fig. 2), both of which have been crystallized in the engineered binding site considered here,^22,23 although these structures (PDB accession codes ILI2 and 1XEP) are only used for comparison purposes. The binding affinity for phenol has been experimentally determined to be in the high micromolar range, and catechol binds with an affinity of millimolar or better (possibly also in the high micromolar range).²³

FIG. 2.

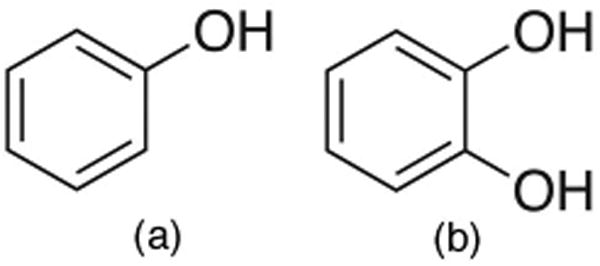
Ligands used in this study. Phenol and catechol, the ligands studied here, have both been crystallized in the binding site of the L99A/M102Q double mutant of T4 lysozyme.

The ligands were assigned parameters from the general AMBER force field (GAFF) for small molecules²⁸ using the ANTECHAMBER package²⁹ version 1.2.4. In earlier versions (such as those distributed with AMBER version 8), the ANTECHAMBER program PARMCHK would occasionally omit improper torsions for some ligands. Ligand partial charges were obtained by the AM1-CM2 method³⁰ computed using AMSOL version 6.5.3 (Ref. 31) and were used for both docking and molecular dynamics simulations. Ligands were converted to GROMACS topology and coordinate files using a Perl script that can be obtained from the Pande group.³²

B. Protein preparation

Rather than begin our simulations from cocrystal structures of the ligand bound to the protein, we start instead from the apo structure of the protein. Thus, protein coordinates were taken from the X-ray apo structure of the T4 lysozyme engineered double-mutant L99A/M102Q (PDB accession code 1LGU).²⁷ In this structure, the buried binding pocket is occupied by one water molecule and β-mercaptoethanol, which we removed before further preparation. Hydrogens, counterions, crystallographic waters, and cosolvents were removed manually. Default protonation states for pH 7 were assigned to titratable residues.

Protons were added and parameters assigned using the GROMACS (Refs. 33 and 34) utility PDB2GMX with the AMBER-96 force field³⁵ as ported to GROMACS.³⁶ The protein was then placed in a dodecahedral simulation box and solvated with TIP3P water³⁷ using GENBOX, with box dimensions chosen to ensure a minimum of 5 Å from the protein to the box boundaries. Even though the amount of clearance around the protein is small, trial free energy calculations (results not shown) indicated that the computed free energies of binding were insensitive to increasing the simulation volume. To prevent placing water molecules in the binding site during the solvation step, we used a modified solvent culling cutoff, forbidding waters within 3 Å of protein atom centers. This solvation step resulted in a box of volume of 142 000 ų containing 6120 water molecules. Because the protein in this protonation state has a net charge of +8, eight water molecules were replaced by chloride ions using the GROMACS utility GENION.

After solvation and minimization, we equilibrated the water around the protein, with the protein held rigidly in its crystal structure, using a molecular dynamics simulation (around 1.1 ns, in the standard protocol described below).

C. System preparation

Ligands were docked into the binding site of the equilibrated apo structure with DOCK 3.5.54 in single mode³⁸ using the same protocol as Graves et al.²³ to generate several thousand poses per ligand. In this protocol, the protein structure is held fixed and ligand conformations are generated from a conformer library. The resulting poses were subjected to K-medoid clustering³⁹ in root mean squared deviation (RMSD) using a Python script to recover a number of clusters determined by experimentation, typically 3–5. We then selected the best-scoring pose from each cluster to use as the initial geometry for free energy calculations and unrestrained molecular dynamics simulations.

A more general and robust way to identify conformation-ally distinct orientations is to sort the poses by their docking scores and identify the top-scoring orientations that differ from each other by more than 2 Å in RMSD, as in Dock 5.0.⁴⁰

D. General simulation parameters

All molecular dynamics simulations were performed with the GROMACS program MDRUN compiled in single-precision mode. We used GROMACS version 3.3 with a number of critical bug fixes that corrected the behavior of the dihedral and angle restraints and the -RERUN flag. These changes were incorporated into the CVS version of GROMACS by February 10, 2006, and into version 3.3.1.

Short-range interactions were evaluated using a neighbor list of 10 Å updated every ten steps, and the Lennard-Jones interactions smoothly switched off between 8 and 9 Å. A long-range analytical dispersion correction ^10,41 was applied to the energy and pressure to account for the truncation of the Lennard-Jones interactions. Electrostatic interactions were evaluated with a real space cutoff of 9 Å, and the particle mesh Ewald (PME) method⁴² was used to evaluate long-ranged electrostatic interactions, using a spline order of 4, a Fourier spacing of 1.2 Å, and relative tolerance between long- and short-range energies of 10^−8.62 In all simulations, thermostatting was performed using Langevin dynamics⁴³ with a reference temperature of 300 K and a friction constant of 10 ps⁻¹ in order to avoid problems with ergodicity when the ligand is fully decoupled from the rest of the system. Simulations conducted with Nosé-Hoover showed similarly slow switching between ligand orientations, suggesting that the friction constant was sufficiently small that its effect on convergence properties was minor. In all simulations, all bonds to hydrogen were constrained with LINCS (Ref. 44) (with an order of 12), and a time step of 2 fs was used for dynamics.

After preparation, the systems were minimized using up to 5000 steps of L-BFGS (Broyden-Fletcher-Goldfarb-Shanno) minimization,^45,46 with default termination criteria. Because the minimizer would sometimes terminate after fewer than 10 steps, this step was followed by 500 steps of steepest descent minimization to ensure adequate minimization.

To equilibrate the systems, velocities were assigned from a Maxwell-Boltzmann distribution at 300 K and the system was subjected to 10 ps of isothermal molecular dynamics. This was followed by 100 ps of isothermal-isobaric dynamics using the Berendsen barostat⁴⁷ with a time constant of 0.5 ps, a reference pressure of 1.0 atm, and an isothermal compressibility of 4.5 × 10⁻⁵ bar.

After equilibration, we fixed the simulation cell and ran all production simulations with isothermal dynamics using the Langevin integrator. Energies were written to disk every 0.2 ps during production, and trajectory snapshots every 1 ps. All production simulations were 1 ns in length, unless otherwise specified.

E. Unrestrained simulations to identify reference orientations

The ligand reference orientation is arbitrary if results are converged, but restraining the ligand to extremely unfavorable orientations may cause large forces and numerical instabilities. Thus it is useful to choose a reference orientation that is low energy and relatively free from steric clashes. There is no guarantee that the docking poses selected with K-medoid clustering (Sec. III C) are reasonable in this sense. Therefore, we allowed the system to relax by initiating 1 ns molecular dynamics trajectories from each of these starting orientations. From these simulations, histograms in the six relative ligand-protein degrees of freedom were constructed and used to resolve conformationally distinct orientations. In all cases, the ligand found orientations that were stable for a substantial fraction of 1 ns, several of which were kinetically distinct in that trajectories initiated from other orientations obtained from the clustering step converted to one of these dominant orientations within 1 ns. This procedure identified two kinetically distinct orientations for phenol, one of which, as we will discuss below, includes suborientations which are separated by only minimal energy barriers. The procedure also identified two kinetically distinct orientations for catechol.

From these probability distributions in each of the six degrees of freedom, we picked the most probable value of each degree of freedom independently to construct the reference orientation.

In this particular binding site, most of the relevant ligand motion occurs by rotation in the plane of the aromatic ring, so there are relatively few relevant ligand orientations, all of which can be easily identified from docking. Docking seems to do well at identifying orientations which are sterically reasonable in this binding site.

F. Imposition and removal of restraints

For orientational restraints, we imposed harmonic restraints of the form

$$U\left(\xi ;\lambda \right)=\frac{K_0\lambda }{2}{\left(\xi -{\xi }_0\right)}^2$$ (13)

in either the ligand-protein distance alone or all six relative protein-ligand degrees of freedom (described in Sec. II above). The free energy of imposing these restraints was computed by performing a number of simulations in parallel. ξ denotes the degree of freedom being restrained, ξ₀ the reference value, and K₀ the base spring constant, here chosen to be 10 kcal mol⁻¹ Å⁻² for distance restraints or 10 kcal mol⁻¹ rad⁻² for angular or torsional restraints. To prevent large forces, distance restraints grow only linearly if the distance exceeds the reference distance by more than 0.2 Å, with the slope chosen to ensure continuous first derivatives. Fourteen values of λ were employed, with simulations conducted at λ={0.01, 0.025, 0.05, 0.075, 0.1, 0.15, 0.2, 0.3, 0.4, 0.5, 0.6, 0.7, 0.85, 1}.

The three reference atoms in the protein were the same as those used in previous work on the apolar version of this binding site:³ the C, C_α, and N in residue Y88. For phenol, the reference atoms were C1, C2, and O, and for catechol, they were C4, C5, and O1.

The free energy of removing the restraints, $\mathrm{\Delta }{G}_{\text{restr}}^{{\text{H}}_2\text{O}}$, is computed analytically using the expression of Boresch et al.³

G. Charge annihilation

The free energy of discharging the ligand is computed by scaling the ligand electrostatic potential energy by (1−λ) over a series of simulations (λ={0, 0.25, 0.5, 0.75, 1}) performed in parallel, such that at λ=0 the ligand is fully charged and at λ= 1 the ligand has no electrostatic interaction with itself or its environment.

H. Lennard-Jones decoupling

Lennard-Jones interactions with the protein were eliminated after the ligand had been discharged using a method similar to that of Shirts.⁷ Only the Lennard-Jones interactions of the ligand with its environment were eliminated, a process called decoupling, rather than removing all Lennard-Jones interactions entirely. This was done to avoid unphysical conformations that can occur when annihilating the ligand Lennard-Jones interactions entirely, which can increase the uncertainty in the estimated free energy. Soft core potentials were used at intermediate values of λ in order to avoid problems with simple scaling schemes.^48,49 We used the modified functional form of Shirts and Pande⁵⁰ with a soft core exponent of 1.0 and α=0.5, and 16 lambda values, with λ={0,0.05, 0.1, 0.2, 0.3, 0.4, 0.5, 0.6, 0.65, 0.7, 0.75, 0.8, 0.85, 0.9, 0.95, 1}.

I. Computing free energies by BAR

We computed free energy differences between Hamiltonians at different values of λ using the Bennett acceptance ratio (BAR) method.^51,52 At each value of λ, for each configuration stored from the production simulation, we must compute the instantaneous work required to change the Hamiltonian to that at a neighboring value of λ. Because the standard GROMACS molecular dynamics program MDRUN does not provide the facility to compute this work during the simulation, we use an approach that does not involve source code modifications. For the charging and restraining calculations, the instantaneous work can be computed from the reported values of the potential energy U and its derivative with respect to λ, ∂U/∂λ. In these cases, the dependence of the potential U on λ is quite simple:

$$U\left(\lambda \right)=\left(1-\lambda \right)U_0+\lambda U_1,$$ (14)

where U₀ is the potential energy at λ = 0 and U₁ is the potential energy at λ=1. Most simulation packages, including GROMACS, output U and ∂U/∂λ each time the energy is output, which gives us two equations we can solve for U₀ and U₁. We find

$$U_0=-\lambda \frac{\partial U}{\partial \lambda }+U,U_1=\left(1-\lambda \right)\frac{\partial U}{\partial \lambda }+U.$$ (15)

Thus, given a trajectory at λ_i, we can compute U₀ and U₁ and use these and Eq. (14) to evaluate what the potential energy of that trajectory would have been at λ_i−1 and λ_i+1, exactly the potential energies needed to apply BAR.

However, there is no similar simple way to obtain the soft core Lennard-Jones energies at different lambda values from derivatives of the potential energy. Therefore, we computed these using the -RERUN option of GROMACS, which allows snapshots from a trajectory to be reprocessed using an alternate Hamiltonian.

Uncertainties were computed using the block bootstrap method.⁵³ Blocks are taken to be the length of the statistical inefficiency g, computed as described elsewhere. ^16,54

J. Decomposition of the partition function by orientation

As discussed above in Sec. II D, our method of decomposition of the partition function involves separating the integral over the binding site into integrals over subregions of the binding site. These regions are arbitrary, because the integral may be broken up in whatever ways are most convenient. Here, we do this at the data analysis stage by discarding snapshots from a given trajectory if they leave the subregion of interest. A more effective means would be to introduce restraints to keep the ligand in the subregion of interest during the simulation, such that no configurations need to be discarded. Assuming that a sufficient number of regions can be identified that cover all of the relevant phase space (which in general may be difficult), this may be the most effective approach for more complicated systems.

Here, our approach at the analysis stage is to identify the one of the six ligand-protein relative degrees of freedom that best separates the different orientations being considered. For our particular choice of reference atoms, this turns out to be θ_B, which measures in-plane rotation of the aromatic ring in the binding site. The unoccupied volume of the empty binding site is disk shaped, so most ligand motion can be described by this rotation.

Our method of partitioning is best illustrated by example. For the simulations beginning from and restraining to a given reference orientation, called orientation 1, we include a given simulation snapshot in the thermodynamic average over orientation 1 only if it falls closer (in θ_B) to orientation 1 than to the other reference orientation (orientation 2); the remaining snapshots are discarded. Likewise, for simulations beginning from and restraining to orientation 2, we retain only those snapshots which are closer to orientation 2 than to orientation 1.

Other partitionings of phase space are also possible.

K. Symmetry number corrections

In this binding site, it is easier for aryl groups to rotate in plane than to flip out of plane. Therefore, it is difficult for symmetric molecules such as phenol and catechol to swap to their symmetric orientations during the course of the simulation. Such events were never observed on our simulation time scales. Thus, the ligand is effectively unable to sample its symmetric orientation. Therefore, we applied a symmetry correction (with symmetry number 2) to the free energy of transfer to vacuum for each ligand.

L. Reported free energies

Our interest here is only in the free energy of transfer of the ligand from the protein to vacuum, ΔG_trans, rather than full binding free energies, since our focus is on the convergence of simulations of the complex. This free energy of transfer to vacuum is given by

$$\mathrm{\Delta }{G}_{\text{trans}}=\mathrm{\Delta }{G}_{\text{restr}}^{PL}+\mathrm{\Delta }{G}_{\text{elec}}^{PL}+\mathrm{\Delta }{G}_{\text{LJ}}^{PL}+\mathrm{\Delta }{G}_{\text{restr}}^{H_{2}O}+\mathrm{\Delta }{G}_{\text{sym}}+\mathrm{\Delta }{G}_{\text{elec}}^{\text{vac}},$$ (16)

where the first four terms are as in Fig. 1, the fifth is the symmetry number correction, and the final term is the free energy of turning the ligand charges back on in vacuum. This is added purely for convenience, so that −ΔG^o = ΔG_trans +ΔG_hyd, where ΔG_hyd is the ligand hydration free energy. If we were computing binding free energies, or if we decoupled the ligand electrostatic interactions rather than annihilated them, this additional free energy component would not be needed.

In principle, water can replace the ligand in the binding site as the ligand interactions are eliminated. However, the binding site is buried, and we observed no such events. If the absolute free energy of binding were to be computed, the free energy of allowing the appropriate number of waters to enter the binding site would need to be computed in a separate step, possibly using standard methods.^8,55

IV. Results

In this section, we compute free energies of transfer from the protein complex to vacuum for two small ligands, phenol and catechol.

A. Phenol

K-medoid clustering of DOCK poses identified three main clusters of configurations for phenol in the binding pocket (Fig. 3). Two of these orientations have been noted previously.²² Unrestrained simulations show that phenol remains stable in one of these orientations [orientation I, Fig. 4(a)] for substantially longer than 1 ns, but can switch between the other two orientations [orientation 2, Figs. 4(b), and orientation 3, not shown] several times in the course of a 1 ns simulation. To determine the length of simulation necessary for convergence of the free energy estimate in the presence of these multiple orientational states, we initiated separate free energy calculations from orientations 1 and 2. The results are shown in Table I.

FIG. 3.

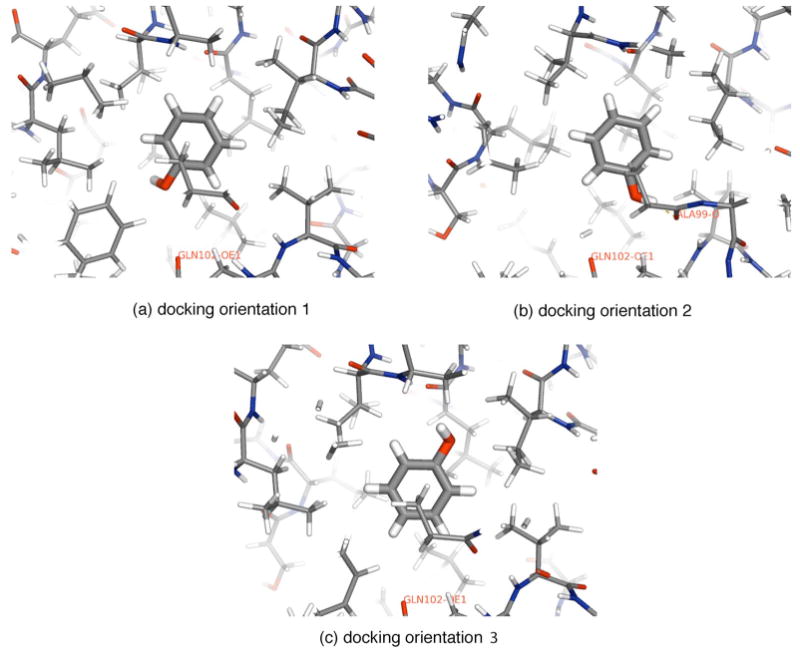
Orientations of bound phenol identified from clustering DOCK poses. When dynamics simulations are initiated from these orientations, we find that interconversion between orientations (b) and (c) is fast compared to our simulation time scales of 1–5 ns, but interconversion from (a) to either (b) or (c) is very slow.

FIG. 4.

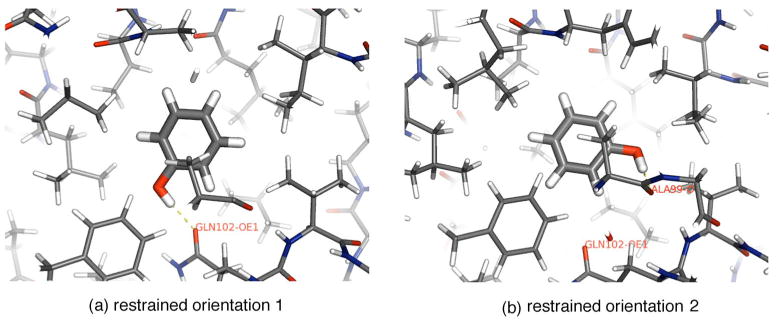
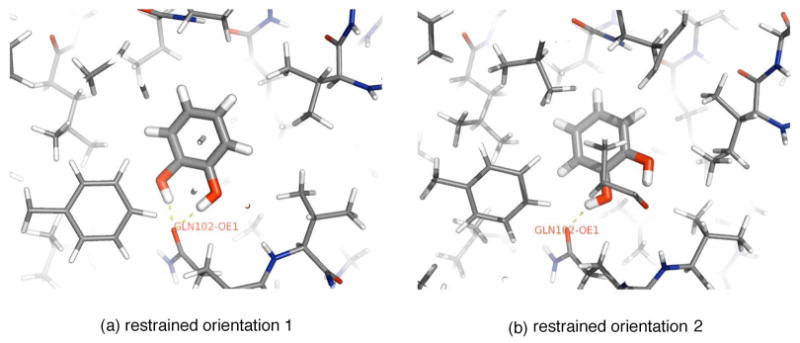
Reference configurations chosen for restraints. From the unrestrained simulations initiated from the three orientations obtained by clustering DOCK poses, we identify two orientations [(a) and (b)] between which sampling is slow compared to 1 ns. Separate free energy calculations are conducted using each of these as a reference orientation for restraint. The final snapshots from the molecular dynamics trajectories run with full-strength restraints on the ligand are shown.

Table I.

Computed free energies of transfer from binding pocket to vacuum for phenol. All free energies are listed in kcal/mol. Uncertainties listed represent one standard deviation of the mean, estimated by the block bootstrap procedure described in Sec. III I. The different orientations are explained in the text, and denote the ligand initial orientation as well as the orientation to which the ligand was restrained. For the orientational restraint calculations, listed times indicate the simulation length at each lambda value in the restraining portion of the calculation. The 1 and 5 ns calculations for this portion were separate sets of simulations. All the other portions employed simulations 1 ns in length for each lambda value, except the vacuum calculation, which was 5 ns in length. For the calculations with no orientational restraints, times denote the time spent on each portion of the calculation. The values reported here are explained in Sec. III L. ΔG_tans values shown in bold are those we believe to be converged (within statistical uncertainty of the best estimate).

	$\mathrm{\Delta }{G}_{\text{restr}}^{PL}$	$\mathrm{\Delta }{G}_{\text{elec}}^{PL}$	$\mathrm{\Delta }{G}_{\text{LJ}}^{PL}$	$\mathrm{\Delta }{G}_{\text{restr}}^{{\text{H}}_2\text{O}}$	ΔGsym	$\mathrm{\Delta }{G}_{\text{elec}}^{\text{vac}}$	ΔGtans
Standard approach
Orientation 1
1 ns	0.65±0.01	18.95±0.05	9.37±0.04	−6.58	0.41	−12.82±0.01	9.98±0.06
Orientation 2
1 ns	2.90±0.12	16.34±0.03	8.44±0.06	−6.73	0.41	−12.82±0.01	8.54±0.14
5 ns	4.31±0.16						9.95±0.18
Orientation decomposition
Orientation 1
1 ns	0.65±0.01	19.00±0.02	9.37±0.04	−6.58	0.41	−12.82±0.01	10.03 ±0.05
Orientation 2
1 ns	0.34±0.01	16.32±0.03	8.44±0.07	−6.73	0.41	−12.82±0.01	5.96±0.07
Combined
1 ns							10.03±0.05
No orientatinal restraints
1 ns	0.28±0.01	18.98±0.04	4.36±0.08	−5.26	0.41	−12.82±0.01	5.95±0.09
5 ns	0.28±0.01	18.85±0.02	3.93±0.07			−12.82±0.01	5.39±0.09

1. Assessing convergence

The computed free energy of transfer ΔG_trans will be insensitive to the choice of initial (and restrained) ligand orientation if all individual simulations are sufficiently long. In such cases, the ligand has time to sample all relevant orientations within the binding site, and if the restrained orientation is not the optimal binding orientation, the restraining free energy will be larger.

As can be seen from Table I, for simulations only 1 ns in length, ΔG_trans changes by 1.4±0.1 kcal/mol depending on the initial orientation. We obtain agreement to within statistical uncertainty only with 5 ns of sampling at each λ value for the restraining portion of the calculation (and 1 ns for each of the other portions).

Convergence is slow because the two main orientations of Fig. 4 are separated by large energy barriers, causing slow barrier crossings. Even in the 5 ns simulations, phenol only switches between orientations of Figs. 4(a) and 4(b) once or twice at most λ values, and most 1 ns simulations contain no switching events. This suggests that even the 5 ns calculations may not be completely converged, since they fail to sample the relevant regions of phase space several times in each simulation. Figure 5 shows sample time series and distributions illustrating this.

FIG. 5.

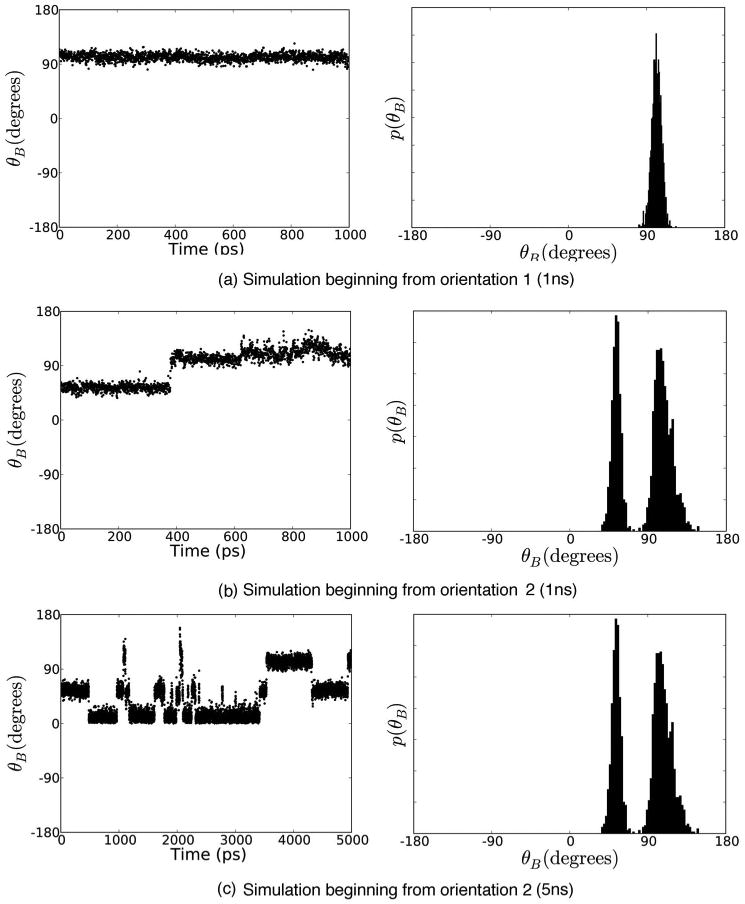
Time series and probability distributions for θ_B, the degree of freedom which describes in-plane rotation of the aromatic ring in the binding site, for simulations with the weakest restraints. (a) shows a 1 ns simulation restraining to orientation 1 [Fig. 4(a)], (b) shows a 1 ns simulation restraining to orientation 2 [Fig. 4(b)], and (c) shows a 5 ns simulation restraining to orientation 2. In order for estimates computed by simulations restraining to the two orientations to be converged, both simulations must sample the same regions of phase space, but it is apparent from (a) and (b) that they have not done so on 1 ns time scales, since the distribution shown in (b) includes a region of phase space never sampled in (a). Here, in (c), it is obvious that phenol spends time in at least three different orientations. Shown here are the simulations with the weakest restraints, where the restraints were sufficiently small that the distribution of angles sampled was essentially the same as in the unrestrained case.

It is worth noting that the restraints used here are relatively weak, so phenol is actually observed to change orientations up to restraint strengths around λ=0.5 in these calculations (data not shown). With much stronger restraints (such as those used by Roux and co-workers^4,5) the region where sampling alternate orientations is possible corresponds to only one or several λ values and may be even more likely to be missed.

We can assess convergence by examining the six protein-ligand relative degrees of freedom as a function of time. In Fig. 5(b), for example, it is clear that phenol has not sampled the relevant regions of configuration space sufficiently, since it mostly remains trapped in its starting orientation [Fig. 4(b)]. An alternate approach would be to compute the autocorrelation time and ensure that every simulation is long enough—perhaps 20 times the correlation length—to give sufficient statistics.

In either case, the difficulty is knowing whether other orientations have simply not been seen or whether they really are not relevant. One test may be that if the ligand never even samples alternate orientations, it is certainly not safe to assume the calculations are converged: The ligand could simply be trapped in a metastable orientation that is different from the dominant binding mode.

2. Configuration space decomposition

Alternatively, with the method of configuration space decomposition described above, we can combine the results of simulations beginning from (and restraining to) orientations 1 and 2 (Fig. 4) by the method described in Sec. II D. Applying this method to 1 ns simulations beginning from each orientation, we get 10.03±0.05 kcal/mol for the free energy of transfer to vacuum, consistent with that obtained from the 5 ns simulations restraining to orientation 2 [Fig. 4(b)] and the simulations beginning from orientation 1 [Fig. 4(a)]. Of this total, the region of phase space containing orientation 2 contributes negligibly; thus in this case free energies would have been correct had the correct starting structure been known a priori (see Table I).

It is also worth noting that this decomposition method does not require any particular decomposition of states; the choice of decomposition is arbitrary, though it will affect the duration of simulations necessary for convergence and the resulting uncertainty.

B. Catechol

Catechol is especially an interesting case, since X-ray diffraction electron density shows two distinct orientations.²³ We examine whether transitions between these two orientations are rapid enough that standard free energy calculations will include contributions from both orientations.

Clustering of docked ligand poses identified three main clusters. Unrestrained (1 ns) simulations initiated from these clusters identified two main stable orientations, between which no transitions were observed. The third orientation can interconvert reasonably quickly with one of the other two. Separate free energy calculations were therefore initiated from each of the two orientations, as shown in Fig. 6. These initial orientations were quite similar to those observed in the crystal structure.²³

FIG. 6.

Stable orientations of catechol observed from unrestrained simulations initiated from docking clusters. From the unrestrained simulations, we identify two main stable orientations for catechol, shown in (a) and (b), between which we see no transitions, so we conduct separate simulations restraining to each of these orientations, as for phenol. Shown are final snapshots from the 5 ns molecular dynamics trajectories run with full restraints on the ligand.

1. Convergence tests

We see no transitions between the two orientations of catechol (Fig. 6) in any of the 5 ns restraining simulations beginning from (and restraining to) orientation 1 [Fig. 6(a)], and only one transition in a single restraining simulation from simulations initiated from orientation 2 [Fig. 6(b)]. Figure 7 illustrates the absence of transitions at the weakest restraint strength for catechol, even in 5 ns simulations. Averages computed from these simulations will clearly not be converged. Thus, the computed free energies of transfer to vacuum depend on the choice of the reference orientation for restraint (Table II). The differences are 0.5±0.1 kcal/mol (1 ns) and 0.7±0.1 kcal/mol (5 ns), with orientation 1 being less favorable for binding in both cases. Table II shows computed free energies and components. Convergence would apparently require simulations that are substantially longer than 5 ns at each λ value for the restraining portion of the calculation, an extremely high computational cost for even these simple ligands.

FIG. 7.

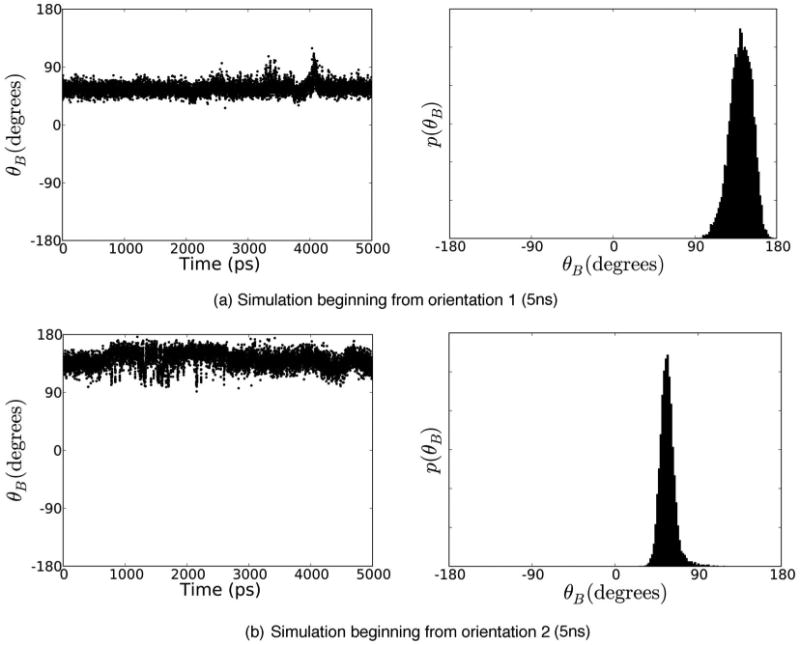
Time series and histogram of in-plane rotation for weakly restrained catechol. Time series (left) and histograms (right) for θ_B, the degree of freedom which describes in-plane rotation of the aromatic ring in the binding site, for simulations at the weakest restraints, λ = 0.01. (a) shows a 5 ns simulation beginning from orientation 1 and (b) shows a 5 ns simulation beginning from orientation 2. Clearly, there is no interchange between the two orientations here, as would be required for convergence.

Table II.

Computed free energies of transfer from binding pocket to vacuum for catechol. All free energies are listed in kcal/mol and are as explained in Table I and in Sec. III L. ΔG_trans value shown in bold is the one we believe to be converged (within statistical uncertainty of the best estimate).

	$\mathrm{\Delta }{G}_{\text{restr}}^{PL}$	$\mathrm{\Delta }{G}_{\text{elec}}^{PL}$	$\mathrm{\Delta }{G}_{\text{LJ}}^{PL}$	$\mathrm{\Delta }{G}_{\text{restr}}^{{\text{H}}_2\text{O}}$	ΔGsym	$\mathrm{\Delta }{G}_{\text{elec}}^{\text{vac}}$	ΔGtrans
Standard approach
Orientation 1
1 ns	0.73±0.01	13.17±0.08	9.54±0.05	−7.08	0.41	−7.66±0.01	9.11 ±0.10
5 ns	0.86±0.01						9.24±0.10
Orientation 2
1 ns	1.09±0.01	14.78±0.08	8.30±0.04	−7.25	0.41	−7.66±0.01	9.67±0.09
5 ns	1.35±0.10						9.93±0.14
Orientation decomposition
Orientation 1
1 ns	0.73±0.01	13.23±0.04	9.54±0.05	−7.08	0.41	−7.66±0.01	9.17±0.06
5 ns	0.86±0.01						9.30±0.06
Orientation 2
1 ns	1.19±0.02	14.85±0.04	8.30±0.05	−7.25	0.41	−7.66±0.01	9.84±0.07
5 ns	1.35±0.11					−7.66±0.01	10.00±0.13
Combined
1 ns							10.00±0.09
5 ns							10.16±0.14

2. Configuration space decomposition

We find that our method of phase space decomposition is more efficient at obtaining the free energies including contributions from both of the relevant orientations. Free energy estimates for the 1 and 5 ns simulations agree roughly within statistical uncertainty, as shown in Table II, and both orientations contribute comparably to the total free energy of transfer. This gives us a benchmark to compare with the unconverged results discussed above. We find that simulations initiated from and restrained to orientation 1 would have neglected at least 1 kcal/mol of the binding free energy. Restraining to orientation 2 would have underestimated the binding free energy by at least 0.4 kcal/mol for 1 ns restraining calculations, and would have come fairly close for the 5 ns restraining calculations (fortuitously, both due to cancellation of errors and the fact that the contribution from each of the two orientations is fairly similar). This agreement beginning from orientation 2 [of Fig. 6(b)] is clearly fortuitous, because even in these 5 ns restraining calculations, the simulation manages to sample the alternate orientation to a substantial degree only at a single λ value, so the free energy estimates are not converged.

C. Phenol with no orientational restraints

To examine the convergence properties of using only a distance restraint (as in Ref. 7) instead of full orientational restraints, we computed ΔG_trans for phenol in which the only restraint was between the phenol C1 and the N of residue Y88. The simulations were initiated from the orientation of Fig. 4(a), since it is most similar to the orientation in the cocrystal structure.

The computed free energy (see Table I) is 5.95±0.09 kcal/mol with 1 ns at each λ value, and is 5.39±0.09 with 5 ns at each λ value (for every λ value, not just for the restraining step). No conformations were discarded in calculating these values. If computed transfer free energies are converged, they should be the same whether orientational restraints or only distance restraints are used. This is not the case here. Even with substantially increased sampling during the discharging and Lennard-Jones decoupling steps, this is an error of approximately 4 kcal/mol. This suggests that the use of orientational restraints greatly improves the ease of convergence of these calculations.

Interestingly, we find that, even without orientational restraints, phenol remains in orientation 1 during the discharging portion of the cycle; thus the free energy of turning off the electrostatics is the same within statistical uncertainty as in the calculations with orientational restraints (18.95±0.04 kcal/mol with orientational restraints; 18.98±0.05 kcal/mol without orientational restraints). Thus, the difference in the computed transfer free energies with and without orientational restraints comes almost entirely from the Lennard-Jones portion of the cycle. Of this difference, almost all of it comes from three λ values (λ = {0.8, 0.85,and 0.9}) (data not shown). In other words, without orientational restraints, the favorable contribution of Lennard-Jones interactions to ΔG_trans seems to be substantially underestimated, especially at three λ values, which would lead to an underestimate of the binding free energy.

V. Discussion And Conclusions

A major goal of computational biology is to compute accurate free energies of binding of small molecule ligands to proteins. It would be a significant drawback to need an experimental cocrystal structure of the complex as input for these calculations. Rather, it would significantly aid drug discovery if binding affinities could be predicted using only the structure of the apo form of the protein. Currently, this cannot be done reliably even for relatively rigid binding sites. The primary difficulty has been that convergence of free energies estimated from simulations started far from the optimal binding mode can be quite difficult.

A. Convergence of free energies of restraint

Here, following others, we apply orientational restraints to keep the ligand close to a reference orientation (usually a favorable binding orientation) in the binding site. Convergence of this restraining step is essential for calculations to be predictive and insensitive to the ligand initial and reference orientations. Published protocols have employed simulations of only 20–40 ps at each λ value during this step,^1,3–5 which our results indicate is insufficient to sample all orientations adequately. We find here that, even for several simple ligands, simulation lengths of at least 5 ns are necessary to obtain convergence.

The basic problem is that a ligand may occupy multiple metastable orientations within a binding site, separated by kinetic barriers which hinder sampling and require long simulations to ensure an adequate number of barrier crossing events. One good example of this is catechol in the lysozyme binding site studied here. It has two orientations which contribute comparably to the binding affinity, separated by a large kinetic barrier. Characteristic barrier crossing times can be in excess of 5 ns.

To overcome this problem, we introduced a method of configuration space decomposition that allows potential ligand orientations to be considered independently, without requiring simulations to directly sample transitions between these orientations. For the systems considered here, the method performs well with substantially shorter simulations than are necessary for the brute force approach. The observed speedup was more than a factor of 5 for catechol. With larger barriers, the speedup can be even greater, since typical barrier crossing times depend exponentially on the barrier height, and this method bypasses the need to sample barrier crossing events entirely.

In parallel to this work, another group has simultaneously developed a similar approach to deal with multiple ligand orientations.⁵⁶ Their work is complementary in suggesting that considering multiple ligand orientations (for which calculations can be carried out independently) can substantially improve agreement with experiment. Also, it, too, allows initial structures to easily be generated with docking methods. One significant difference, however, is that the method does not use any restraints between the protein and the ligand, which probably necessitates sampling of the entire simulation volume.

B. Convergence of free energy calculations using only distance restraints

Some investigators have suggested that the use of orientational restraints improves convergence of alchemical free energy calculations.^1,3 Others have used only a single distance restraint between the protein and the ligand.⁷ Here, we tested whether orientational restraints improve convergence by computing the free energy of transfer from the binding site to vacuum for phenol using only such a distance restraint.

Using 1 ns per simulation at each λ value for every portion of the calculation, the computed ΔG_trans underestimates binding strength by 4.0±0.1 kcal/mol compared to the converged binding free energies obtained using orientational restraints. Interestingly, both studies using this method report an excellent correlation between the computed binding free energies and experiment,^6,7 but with 3 kcal/mol (Ref. 6) to 4 kcal/mol (Ref. 7) offset towards weaker binding, close to the 4 kcal/mol offset we observe here. In our study, we find that increasing the simulation time at each λ value (to 5 instead of 1 ns) actually led to an increased deviation from the converged estimate of ΔG_trans, further underestimating the binding affinity by an additional 0.5±0.1 kcal/mol. As discussed in Sec. IV C, the difference is mostly in the Lennard-Jones decoupling portion of the cycle, where the contribution to the binding free energy is substantially underestimated.

What is the origin of the discrepancy? We believe our data suggest an explanation. If only the ligand-protein distance is restrained, the ligand can still sample a spherical shell about the point of restraint on the protein, at least when its interactions with the protein are weak. For some range of the λ values where the interactions are weak, the ligand will be able to permeate the protein and must sample all favorable regions on this shell, including some buried within the protein, to achieve convergence. Unfortunately, there can be multiple pockets of favorable interactions within the protein, separated by relatively large barriers. This is especially problematic at the λ value(s) where the ligand is interacting just weakly enough that it begins to permeate the protein. Here, correlation times become very long (500 ps or more) as the ligand gets trapped in various regions within the protein. Thus, as discussed above, the error seems to come essentially from only three λ values around λ = 0.85.

It is interesting to note that very short simulations may not allow time for this permeation. Thus, as simulations are lengthened, computed binding free energies may actually get worse as this permeation begins, before they finally get better when convergence is achieved. Apparently the time scale for convergence here is substantially longer than 5 ns.

Regardless of whether the 3–4 kcal/mol offset reported elsewhere^6,7 comes entirely from this effect, without orientational restraints, substantially more sampling is required. This raises serious concerns about simulations conducted without orientational restraints and suggests that workers using that approach should explicitly demonstrate that sampling is adequate. In view of these results, it seems unlikely that alchemical binding free energy calculations in typical protein systems will produce converged results using distance restraints only or no restraints, at least with current simulation protocols.

C. Implications

As already pointed out, our results demonstrate that adequate sampling of the restraining step in free energy calculations is essential for obtaining precise free energies. However, our results have implications beyond the use of orientational restraints. They suggest that the brute force approach to convergence can require an unreasonable amount of computational effort, even for small molecules. We expect these problems to be even worse with larger molecules, where steric barriers to orientational change can be even larger.

Although phenol and catechol are not very interesting as biological ligands, they are relatively similar to substituents of many molecules of pharmaceutical and biological interest, so it seems likely that the sampling problems we see here will be transferred to the internal ligand degrees of freedom for many larger molecules, as suggested by early work on rotational isomeric states²⁷ as well as some more recent work.¹⁹ If energy barriers are sufficiently large, results can appear quite reproducible without being correct,^18,19 as observed here for catechol.

Our approach of configuration space partition can help with such sampling problems, as it can be applied to ligand orientational as well as internal degrees of freedom. The essential idea is the same: Compute effective binding free energies from a number of different substrates to a shared reference state and then combine these to obtain the correct free energy of transfer. In this sense, it could be applied in a similar way to the mining minima algorithm of Gilson and collaborators:⁵⁷ If the most important regions of conformation space can be identified by some fast algorithm, whether by docking or some other approach, free energy calculations can be carried out to evaluate the contributions from each of these minima to the free energy of binding without the need to sample transitions between them.

Our results also have implications for the calculations of relative binding free energies by mutating one molecule into another. For example, here, had we computed the free energy difference between phenol and catechol by mutating phenol into catechol in the binding site, calculations would have needed to be long enough to sample all of the potential orientations of both molecules at every λ value. Based on our results here, this would have required substantially longer than 5 ns per λ, since catechol could remain trapped in a single orientation for substantially longer than 5 ns. Failure to run simulations of sufficient length would underestimate the binding free energy for catechol relative to phenol, because it would miss the contribution of at least one of catechol's two orientations.

Our results also suggest a convergence test for free energy calculations: At the very least, the computed free energies should be shown to be independent of the starting orientation of the ligand. Better still, these results should be demonstrated to be independent of the choice of reference orientation for restraint. This is a more stringent test than simply examining correlation times, which can appear short if the ligand never leaves its starting orientation, regardless of whether there are other favorable orientations. If the computed free energies are not independent of these orientations, at best, they represent the free energy of some subregion of the binding site, and at worst, they are completely wrong.

Although in this work we have focused on slow sampling of ligand degrees of freedom, it is very likely that some of the same problems may plague protein side chain degrees of freedom, or even backbone degrees of freedom when protein flexibility is more important. For example, crystal structures of the L99A mutant (which instead has a completely hydrophobic binding site) show that a valine side chain in the binding site rotates to accommodate some of the larger ligands.⁵⁸ Side chain rotation time scales may present similar sampling problems to those discussed here, so further method development will likely be necessary.

Convergence problems may actually be even worse in such cases if the relevant side chain rotations cannot be easily sampled on simulation time scales. For example, even if correct bound protein conformations can be identified in advance (perhaps with flexible docking protocols), the free energy of changing the protein conformation will also need to be computed, perhaps with enhanced sampling methods such as umbrella sampling.⁵⁹ These issues need to be examined carefully to determine whether molecular dynamics is capable of sampling protein flexibility sufficiently on accessible simulation time scales.

D. Generalizing the method

In case where protein flexibility is not important, this method can be easily generalized to handle more realistic ligands. Work done in parallel to this has already suggested one such approach.⁵⁶ Likewise, a natural way of generalizing the work done here would be to dock ligands into a target protein. For larger ligands, a larger number of potential bound orientations (perhaps on the order of 100) should be retained from docking. A decomposition of configuration space can then be defined using these starting orientations (or unrestrained simulations ran from each of these orientations), and then separate free energy calculations can be carried out for each region of configuration space. In our opinion, the best way to do this would be to prevent the ligand from making large excursions from its assigned orientation with restraints, and thus transitions between regions need not be considered. Ensuring that all relevant ligand orientations are included may, however, be a very difficult task, even without protein flexibility, especially since the number of potential ligand orientations grows very rapidly when ligand internal degrees of freedom are also relevant. It is worth noting that approaches which do not begin with a wide variety of docking poses face the same problem: Any one of the many possible ligand orientations could contribute significantly to binding, so it will be difficult to be certain that all of the relevant orientations have been included in computed binding free energies.