A Simulation Study of Permutation, Bootstrap, and Gene Dropping for Assessing Statistical Significance in the Case of Unequal Relatedness

Abstract

We used simulations to evaluate methods for assessing statistical significance in association studies. When the statistical model appropriately accounted for relatedness among individuals, unrestricted permutation tests and a few other simulation-based methods effectively controlled type I error rates; otherwise, only gene dropping controlled type I error but at the expense of statistical power.

DETERMINING statistical significance thresholds is an essential part of quantitative trait locus (QTL) mapping. Computationally efficient methods have been proposed to obtain significance thresholds via approximating the test statistic by an Ornstein–Uhlenbeck diffusion process (Lander and Botstein 1989; Dupuis and Siegmund 1999; Zou et al. 2001) or Davis’ approximation (Davis 1987; Rebaï 1994; Piepho 2001) or by estimating the effective number of independent tests (Cheverud 2001; Moskvina and Schmidt 2008). However, these methods may not provide satisfactory results (Zou et al. 2001; Dudbridge and Gusnanto 2008). Simulation-based tests are still recommended (Lander and Schork 1994) and have been used extensively in QTL mapping. Permutation tests (Fisher 1935) have been a standard method with which to estimate significance thresholds in QTL mapping since they were introduced for this purpose by Churchill and Doerge (1994). Problems may arise when complex mapping populations or complicated statistical analyses are used (Zou et al. 2006; Churchill and Doerge 2008). In these situations, naive application of unrestricted permutation tests may lead to invalid inference because the fundamental assumption of exchangeability is violated. This problem typically occurs in mapping populations where individuals share varying degrees of genetic relatedness and has raised questions about whether permutation tests should be applied in such situations (Abney et al. 2002; Zou et al. 2005; Peirce et al. 2008; Cheng et al. 2010).

In this study, we performed extensive simulations to evaluate the permutation test as well as several other simulation-based methods: parametric bootstrapping (Efron 1979), gene dropping and genome reshuffling for advanced intercross permutation (GRAIP), for assessing significance using linear mixed effect models and advanced intercross lines (AIL) (Darvasi and Soller 1995), where individuals are known to be genetically unequally related. The primary purpose of this work was to investigate the performance of these methods with respect to type I error rates and statistical power in the context of statistical modeling and to provide useful insight in the choice of methods for estimating significance thresholds when subjects are genetically unequally related. In contrast to Valdar et al. (2009), which focused on modeling, our study focuses on methods for determining significance thresholds when relatedness is a concern. We report our main findings while leaving the details in Supporting Information, File S1, File S2, and File S3.

Simulation Results

We generated an AIL pedigree and sampled 576 individuals from F₂₆ (Table S1). The phenotype was generated such that polygenic variation approximately accounted for 56, 46, or 32% of the total phenotypic variation, corresponding to the standard deviation 0.7, 1, or 1.5 of the residual effect.

Type I error

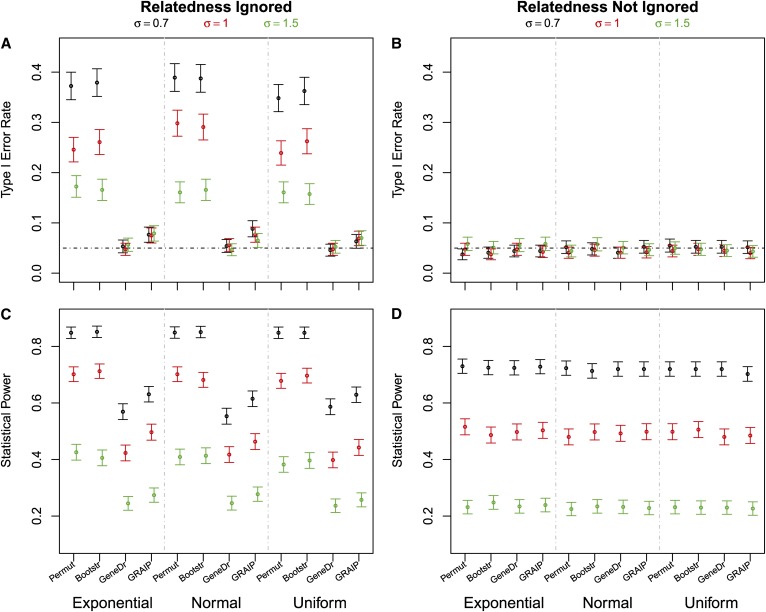
First, we ignored polygenic variation. Only the gene-dropping method effectively controlled the type I error rates; all other methods produced inflated type I error rates (Figure 1A). The larger the polygenic variation was relative to the environmental variation, the more seriously the type I error rates were inflated. GRAIP performed much better than either bootstrap or permutation but was still not able to control false positives at the expected significance level.

Figure 1.

Type I error rates and statistical power. Type I error rates (A and B) and statistical power (C and D) estimated at genome-wide significance level 0.05 by each of the following methods: permuting genotypic data (Permut), bootstrapping phenotypic data (Bootstr), gene dropping (GeneDr), and GRAIP. The distribution of the residual was exponential, normal, or uniform, each with a standard deviation 0.7, 1, or 1.5.

Next we took polygenic variation into account. All the methods controlled type I error rates at the expected levels (Figure 1B). Misspecification of the residuals produced somewhat overly conservative results, but had little impact overall (Table S2).

Statistical power

One QTL was generated with a heritability of ∼2.8, 2.3, or 1.6%, corresponding to the standard deviation 0.7, 1, or 1.5 of the residual effect. Figure 1C reports power even when type I error is not controlled (e.g., permutation, bootstrapping). This reflects a combination of both true and false positives. The power was comparable for all of the four methods when polygenic variation was accounted for in the model (Figure 1D). Notably, gene dropping has a higher statistical power when the relatedness was accounted for (Figure 1, C and D).

Simulations with different family sizes and subpopulation structure

We performed additional simulations by randomly choosing 288 individuals from the F₂₆ sample and 288 individuals from a real data set (see below). The results were similar (data not shown), suggesting that variable family size did not negatively affect the procedures. We then considered different allele (A/a) frequencies at the founder generation: 3/1 for F₂₆ vs. 1/3 for F₃₄. Under these conditions both permutation and bootstrap failed to control type I error when the residual was exponentially distributed and permutation also failed to control type I error when the residual was uniformly distributed (Table 1). This is broadly consistent with our main point, which is that when the model used to analyze the data are correctly chosen, permutation is an effective strategy for analyzing the data.

Table 1. Estimated Type I Error Rate and Statistical Power.

		Type I error rate			Statistical power
Distra	Methodb	α = 0.10	α = 0.05	α = 0.01	α = 0.10	α = 0.05	α = 0.01
Exp	Permut	0.191***	0.113***	0.028***	0.493	0.387	0.235
	Bootstr	0.145***	0.078***	0.022***	0.451	0.360	0.235
	GeneDr	0.108	0.045	0.009	0.402	0.312	0.164
	GRAIP	0.116*	0.052	0.012	0.416	0.315	0.164
Norm	Permut	0.129***	0.059	0.012	0.478	0.379	0.241
	Bootstr	0.090	0.048	0.007	0.409	0.343	0.223
	GeneDr	0.090	0.051	0.010	0.416	0.355	0.239
	GRAIP	0.086*	0.044	0.010	0.418	0.342	0.217
Unif	Permut	0.136***	0.079***	0.014	0.488	0.397	0.241
	Bootstr	0.104	0.057	0.011	0.435	0.352	0.219
	GeneDr	0.104	0.062*	0.011	0.429	0.351	0.220
	GRAIP	0.105	0.060	0.011	0.430	0.352	0.246

Allele (A/a) frequencies at the founder generation: 3/1 for F₂₆ vs. 1/3 for F₃₄. Estimated from 1200 simulations at genome-wide significance level α = 0.10, 0.05 or 0.01. *, **, and *** indicate that the estimated type I error rate is significantly different from the expected significance levels 0.10, 0.05, and 0.01, respectively.

^aResidual distribution: exponential (Exp), normal (Norm), or uniform (Unif).

^bPermuting marker data (Permut), bootstrapping phenotypic data (Bootstr), or gene dropping (GeneDr).

Real data example

We used a data set from a 34th generation of a mouse AIL, which consisted of body weight measurements and genotypes for 688 mice at 3105 SNPs (Cheng et al. 2010; Parker et al. 2011). We did not perform the exact GRAIP procedure; instead, we shuffled simulated F₃₃ haplotype pairs within sex and then simulated F₃₄ genotypes. This simplified the analysis while maintaining the key property of GRAIP, i.e., its ability to retain relatedness solely for full sibship. The estimated thresholds were similar when polygenic variation was accounted for in the model (Table S3). Both permutation and bootstrap produced similar thresholds regardless of whether polygenic variation was ignored or accounted for in the model. In contrast, both gene dropping and GRAIP yielded significantly larger thresholds when polygenic variation was ignored.

Discussion

There has been widespread concern about the use of permutation tests in complex mapping designs (Abney et al. 2002; Zou et al. 2005; Churchill and Doerge 2008; Peirce et al. 2008). In a previous publication we observed that permutation and gene dropping produced similar thresholds in the analysis of an AIL when polygenic variation was incorporated in the model (Cheng et al. 2010); however, that article did not explore the finding, consider alternative methods, or explore statistical power. Here we studied four simulation-based methods for obtaining empirical significance thresholds: permuting genotypes, bootstrapping phenotypes, gene dropping, and GRAIP. The permutation test has been a standard simulation-based method in QTL mapping, the bootstrap test is among the most useful empirical methods in statistics and has been recommended in mixed effect models (Pinheiro and Bates 2000; Valdar et al. 2009), and gene dropping is appropriate when pedigree information is available. We found that all these methods worked well when polygenic variation was appropriately taken into account in the model; however, when polygenic variation was ignored, only gene dropping was able to control type I error rates and this came at the expense of statistical power (Figure 1, C and D). Thus, it is important to specify an appropriate statistical model in QTL mapping, especially in complex populations such as AIL; an inappropriate model can invalidate statistical inference. These principles should extend to general cases where unequal relatedness or a population structure exists.

We found that the estimated distribution of the test statistic under the null hypothesis (no real QTL) was similar whether or not polygenic variation was accounted for in the model for some of the methods we examined but not for others (Table S4). In particular, the estimated distribution was significantly different when using gene dropping and GRAIP but not when using bootstrap or permutation. The take-home message is that if the model is appropriate for a genome-wide scan, we may ignore the random polygenic effect to reduce computation when performing permutation tests to estimate the significance threshold. We also found that when the polygenic variation was accounted for in the model, the estimated distributions of the test statistic for all the four methods were not significantly different from one another. One possible explanation for this is that the trait values of genetically related individuals tend to be similar and thus the test statistic is inflated because of the confounding effect between the genotype and the phenotype adjusted for other effects in the model when the polygenic variation is ignored. Gene dropping (or to a lesser extent GRAIP) retains the relationship and is therefore capable of controlling the false-positive rate regardless of the inclusion of polygenic variation. The permutation (or bootstrap) test largely dissolves the confounding and therefore provides similar thresholds regardless of whether or not the polygenic variation is accounted for in the model, and it cannot control the false-positive rate if the polygenic variation is ignored.

Our observations were mainly based on AIL data. It is worth pointing out that the permutation test, as well as the bootstrap test, should be used with caution. Model appropriateness such as independency, normality, and constancy of residuals is a general concern in statistical modeling. We showed that the permutation test was not robust to misspecification of the residual distribution when the population was structured with different allele frequencies (Table 1). In addition, a major QTL (or a polygene with relatively large effects) may result in false positives due to uncontrolled confounding between the QTL (or polygene) and a scanning locus. In such a case, incorporating major QTL and possibly a few loci with relatively large effects as covariates in the model may address this concern (Valdar et al. 2009; Segura et al. 2012).