Membrane protein native state discrimination by implicit membrane models

Abstract

Four implicit membrane models (IMM1, GBSAIM, GBSW, HDGB) were tested for their ability to discriminate the native conformation of five membrane proteins from 450 decoys generated by the Rosetta-Membrane program. The energy ranking of the native state and Z-scores were used to assess the performance of the models. The effect of membrane thickness was examined and was found to be substantial. Quite satisfactory discrimination was achieved with the all-atom IMM1 and GBSW models at 25.4 Å thickness and with the HDGB model at 28.5 Å thickness. The energy components by themselves were not discriminative. Both van der Waals and electrostatic interactions contributed to native state discrimination, to a different extent in each model. Computational efficiency of the models decreased in the order: extended-atom IMM1 > all-atom IMM1 > GBSAIM > GBSW » HDGB. These results encourage the further development and use of implicit membrane models for membrane protein structure prediction.

Introduction

Membrane proteins are crucial for many cell processes including intercellular communication, molecular transport, and energy transduction. About 8000 membrane proteins are encoded in the human genome^[1] and constitute about 60% of the targets for currently available drugs^[2]. Hence their structure is of utmost importance in the biological and pharmacological sciences. Despite their significance, the number of solved structures in the Protein Data Bank (PDB) is limited due to difficulties in expression, purification and crystallization^[3,4]. It has been estimated that about 1700 membrane protein structures are needed to account for each structural family^[5], which at the current level of technology may take about 30 years^[6].

Given the experimental difficulties, computational approaches to membrane protein structure prediction would be highly appealing. Methods for structure prediction have so far mostly focused on aqueous proteins and can be divided into four groups: homology modeling that is applied in cases of sequence similarity^[7,8] or known structural similarity, as in the case of GPCRs^[9–11]; fold recognition methods^[12,13], motivated by the notion that structure is evolutionarily more conserved than sequence; fragment-based methods^[14,15], which assemble the biomolecule by comparing short amino acid subsequences of a target to fragments of known structures; and ab initio methods^[16–23], which do not rely on previously known structures but attempt to identify the structure with minimum free energy. The most popular methods for ab initio prediction use evolutionary or knowledge-based information for collecting spatial restraints^[19,24] or for identifying local structural building blocks^[16,25–27]. ]The last step of ab initio structure prediction - high-resolution structural refinement^[28,29], is crucial for achieving predictions of good accuracy and is computationally more demanding, especially when the surrounding solvent/medium has to be taken into account.

Membrane protein structure prediction is more challenging^[30] because membrane proteins are typically longer than 200 residues and exist in a highly anisotropic solvent. A number of studies have shown that the lipids play an important role in modulating membrane protein structure and function.^[31–33] Therefore, the membrane environment needs to be taken into account in structure prediction studies. A number of approaches have been developed to address specific aspects of membrane protein structure ^[30,34]: helical pairwise interfacial propensity^[35], inter-residue interactions^[36], lipid exposure propensity^[37]; prediction of the tertiary fold of α-helix pairs^[38], scoring function for modeling TM-helix oligomer structures^[39], hidden Markov model based prediction of membrane spanning helices in proteins^[40]; and surface accessibility prediction^[41]. A membrane-specific version of the Rosetta program was developed for prediction of entire membrane protein structures^[42,43], which relied on knowledge-based residue–residue and residue–environment interaction potentials. Further improvements included an all-atom physical energy function that described intraprotein and protein–solvent interactions^[44] and inclusion of experimental constraints^[45]. Some ab initio methods, such as PREDICT^[46,47], FOLDGPCR^[48], MembStruk^[49], TASSER^[50], target specifically prediction of GPCR structures.

Explicit representation of the lipid and water molecules is impractical for structure prediction studies, unless special hardware is used.^[51] Implicit membrane models offer a promising alternative.^[52] In such models a mean field approach is used to account for solute-solvent interactions. Implicit models can be statistics-based or physics-based. Statistics-based models use data derived from proteins of known structure. One example uses the distributions of all residues along the membrane normal and potentials of mean force, calculated for each amino acid by fitting Gaussian functions to the residue distributions^[53]. Rosetta-Membrane represents the bilayer as parallel planes which define hydrophobic, interface and polar layers and derives one and two-body potentials based on known structures.^[42]

Physics-based implicit membrane models try to reproduce membrane-biomolecule interactions based on known physicochemical principles. They do not use any information on protein structures, but may use experimental data on the solvation of small molecules. Some models focus on obtaining the transfer free energy of fixed protein conformations from water into the membrane using solvation parameters or energy functions derived from those data.^[54–57] Others describe the free energy of different conformations in homogeneous membrane-mimetic environments.^[58] More recent models are complete energy functions that can describe the free energy difference between different conformations in a heterogeneous environment. For example, IMM1^[59] is an extension of the EEF1^[60] implicit solvation model for proteins in solution. Another group of models obtains the electrostatic contribution from the generalized Born (GB) model, and the nonpolar contribution from a term proportional to the solvent-accessible surface area (SASA).^[61–64]

The first requirement of ab initio structure prediction is the availability of a function that can discriminate the native state from incorrect conformations. This paper aims to compare the performance of four physics-based membrane energy functions in doing this for membrane proteins. We consider four models available in the CHARMM program: IMM1 and three GB models. A version of IMM1 based on the all-atom CHARMM36 force field (IMM1-p36) was also considered. We studied in total 450 decoys, generated by the Rosetta-Membrane program^[42], for 5 transmembrane proteins of different length and biological function. We explored the influence of the membrane thickness on distinguishing the native from non-native conformations using the IMM1 energy function. Advantages and disadvantages of the models are discussed as well as their suitability for transmembrane protein structure prediction.

Methods

In this work we considered 5 transmembrane proteins examined by Yarov-Yarovoy et al.^[42] V-ATPase (VATP) is a vacuolar-type sodium ion-pumping adenosine triphosphatase consisting of 10 NtpK subunits.^[65] One of these subunits, consisting of four transmembrane helices, is considered here. Fumarate reductase (fmr5) is the terminal enzyme of fumarate respiration, a complex consisting of three subunits. It contains two haem b groups bound by the transmembrane subunit C, and two hydrophilic subunits A and B.^[66] The transmembrane subunit C is considered here. Lactose permease (ltpA) is a membrane transport protein that transduces free energy stored in electrochemical ion gradients into a concentration gradient by lactose/proton symport. It is composed of 12 transmembrane helices: the N- and C-terminal six helices (N6 and C6, respectively) form two distinct helical bundles connected by a long loop between helices VI and VII. The N6 and C6 have the same topology and are related by an approximate two-fold symmetry.^[67] The N6 domain is considered here. Bacteriorhodopsin (BRD7) and rhodopsin (RHOD) are prokaryotic and animal opsins, respectively, which are light-sensitive membrane-bound receptors consisting of seven transmembrane α-helical domains connected by three extra-cellular and three cytoplasmic loops. BRD7 acts as a proton pump, capturing light energy and using it to move protons across the membrane out of the cell.^[68,69] RHOD is a G protein-coupled receptor that activates visual phototransduction. The entire sequence of BRD7 and RHOD is considered here. The decoys were obtained from the Baker lab^[42], 100 each for one subunit of VATP, transmembrane domain (subunit C) of fmr5, N6 domain of ltpA, BRD7^[70] and 50 for RHOD^[71] (Table 1, Figure 1). The native structures (VATP, fmr5, RHOD) were truncated (N- and/or C-terminus residues) to match exactly the sequence of the corresponding decoys and were subjected to the same computational protocol as the decoys. This truncation did not expose any polar residues to the membrane hydrocarbon core.

Table 1.

Membrane proteins tested using implicit membrane models.

No	Protein name	PBD ID	Code	Resolution (Å)	Nr of TM helices	Nr of residues	Residue Nrs in chain
1	Subdomain of V-type Na+-ATPase	2BL2	VATP	2.1	4	145	12–156
2	Subdomain of fumarate reductase complex	1QLA	fmr5	2.2	5	217	21–237
3	Subdomain of lactose permease transporter	1PV6	ltpA	3.5	6	190	1–190
4	Bacteriorhodopsin	1PY6	BRD7	1.8	7	227	5–231
5	Rhodopsin	1U19	RHOD	2.2	7	278	33–310

Figure 1.

The native structures of tested transmembrane proteins

All native structures and decoys were subjected to short molecular dynamics simulations (MD) using the program CHARMM^[72] version C36a4 or C37a1 (for IMM1-p36 only). The coordinates of all hydrogen atoms in the decoys were generated by the CHARMM HBUILD routine. The initial structures were oriented perpendicular to the membrane surface. The thickness (T) of the hydrocarbon core of the membrane was set to 23.1, 25.4, 27.0, 28.5 and 30.4 Å. HDGB model was tested only with T=28.5 Å.^[63] The initial minimization was carried out with all backbone atoms fixed (except for GBSAIM which does not allow fixed atoms) using the adopted basis Newton-Raphson algorithm (ABNR) for 1000 steps. The constraints were subsequently released for the MD simulations (0.1 ns) with the Verlet integrator and a time step of 1 fs. All bonds involving hydrogen atoms were fixed using SHAKE^[74]. The temperature was 310 K. The nonbonded interactions were truncated at 12 Å, with gradual switching from 10 Å. We tried several approaches to obtain energy from the MD trajectories. The first approach was to extract the average energy from the second half of the trajectory. The remaining approaches aimed to extract a conformation for further minimization from the MD trajectory: the structure of the last frame, the average structure from the second half of the trajectory, or the lowest energy structure from the second half of the trajectory. The latter gave higher correlation and better discrimination when comparing the final results, hence, we used this approach for the remaining decoys. The selected structure was subjected to an ABNR minimization for 1000 steps.

For all obtained values of the energy and its components we calculated relative values by subtracting the corresponding value of the native structure from the one of its decoy. Hence the energy values of all the native proteins plotted correspond to 0.

We computed Z-scores^[75] according to eq. 1:

$$Z=\frac{\langle E_{\mathit{\text{decoys}}}\rangle -E_{\mathit{\text{native}}}}{{\sigma }_{\mathit{\text{decoys}}}}$$ (1)

where 〈E_decoys〉 is the average energy of the ensemble of decoys, σ_decoys is the standard deviation of the energy in that ensemble, and E_native is the energy of the native structure of a protein. A larger Z-score means higher discriminative ability.

IMM1

IMM1 employs an empirical Gaussian exclusion solvation model and solvation parameters derived from experimental data for small molecule transfer from the gas phase to water and cyclohexane. It also adjusts the dielectric screening depending on position within the membrane^[59]. CHARMM version C36a4 was used with the IMM1 energy function on neutral membranes ^[59]. IMM1 is based on the polar hydrogen force field CHARMM19^[76]. The standard nonbonded options (ctonnb 7, ctofnb 9, cutnb 10) were found to yield inferior results (Fig. S1) than longer cutoffs (ctonnb 10, ctofnb 12, cutnb 16). Therefore, these longer cutoffs were used in this work, unless stated otherwise.

IMM1-p36

We recently discovered that interactions between certain transmembrane helices in IMM1 are too strong and adapted IMM1 for use with the all-atom CHARMM36 force field (to be published). CHARMM36 is essentially the CHARMM22 all-atom force field^[77] incorporating an improved treatment of backbone torsions^[78] and other smaller refinements.

GBSAIM

The generalized Born-surface area-implicit membrane model (GBSAIM)^[61] is a two-dielectric membrane model with electrostatic contribution calculated using an older version of the GB model^[79]. The nonpolar part is approximated by a term proportional to the SASA. The surface-tension parameter was set to 25.0 cal/mol•Å². The value of the dielectric constant was set to ε_m=2 for the solute and membrane interior and to ε_slv=80 for the solvent. The CHARMM19^[76] force field was used, as it is the one for which parameters are available.

GBSW

GB with a simple switching (GBSW) model^[62] is similar to GBSAIM but implements a recent GB model and a higher-order correction to the Coulomb field approximation^[80]. It uses overlapping van der Waals spheres with a smoothing function instead of the molecular surface to represent the dielectric interface. The nonpolar contribution is calculated in the same way as GBSAIM. The CHARMM22^[77] force field was used with CMAP φ/ψ torsion potential^[78,81]. The parameter msw (half of membrane switching length) was set to 1.5 Å. The nonpolar surface tension coefficient was set to 5 cal/mol•Å², as recommended for folding studies.^[62]

HDGB

The heterogeneous dielectric GB (HDGB)^[63,64] implicit membrane is an extension of the homogeneous GB with molecular volume (GBMV) method^[82,83]. This method is similar to GBSW, but HDGB incorporates a sharp molecular surface. The membrane is represented by multiple layers with dielectric constants different from that of the solute cavity.^[63] The dielectric environment of the bilayer is computed by solving the Poisson equation for the monovalent spherical ion transfer across the implicit membrane and is sensitive to membrane thickness. The nonpolar contribution is calculated as in GBSAIM and additionally incorporates the variation of the surface tension along the membrane normal obtained from the free energy of O₂ insertion into a DPPC bilayer^[84]. The CHARMM22^[77] parameter set and CMAP φ/ψ torsion potential^[78,81] with surface area coefficient of 15 cal/mol•Å² were used. Parameters for the switching function for the nonpolar energy were set to ZS=0.5, ZM=9.2, ZT=25, ST0=0.32 and correspond to membrane thickness of 28.5 Å.^[63]

Results

A crucial test of an effective energy function is to compare the energy of misfolded conformations (decoys) to that of the native conformation. Assuming the validity of the thermodynamic hypothesis^[85], the native structure should have the lowest effective energy. In addition, if the energy landscape is "funnel-like"^[86], we expect to see some correlation between effective energy and the proximity to the native state. Such a property of folding free energy landscapes is consistent with experimental protein folding data and is a main postulate of protein folding theories.^[87–91] We tested four implicit membrane models – IMM1 (extended-atom and all-atom)^[59], GBSAIM^[61], GBSW^[62,80] and HDGB^[63] for their ability to discriminate the native structure from ab initio generated decoys. We also analyzed electrostatic, nonpolar and solvation energy contributions to examine their discriminative power and obtain insights into their contributions to membrane protein stability.

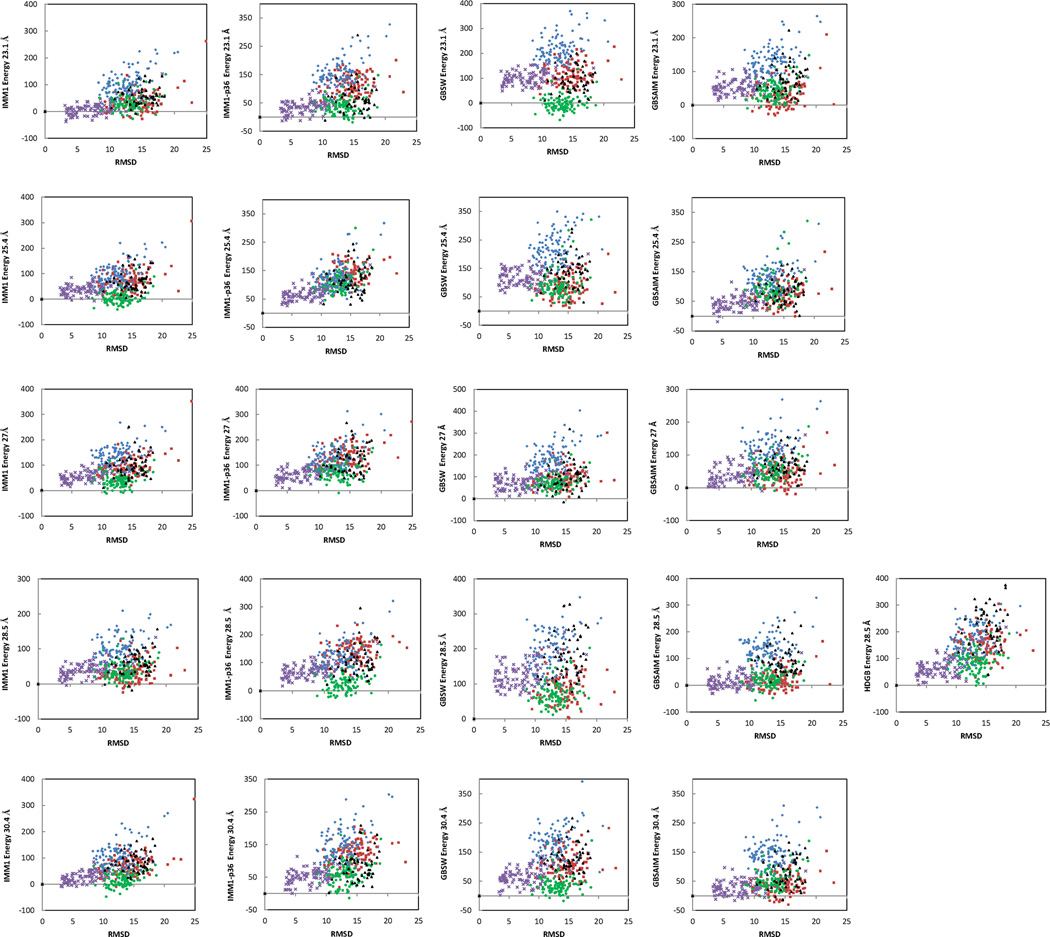
To test the effect of hydrocarbon thickness, we performed simulations with five membrane thicknesses: 23.1, 25.4, 27.0, 28.5 and 30.4 Å. Only T=28.5 Å was tested with HDGB, which is the thickness corresponding to the available parameters. Figure 2 shows the energy of all decoys relative to the corresponding native state. Tables 2 and S1 show the number and the identity, respectively, of the discriminated proteins for each membrane thickness. Table 3 shows the Z scores in each case. It can be seen that membrane thickness has a significant effect on native state discrimination. Different membrane models perform best at different thicknesses. IMM1 performs best at 27 Å, where it discriminates all native states except ltpA. IMM1-p36 performs best at 25.4 Å and GBSW at 25.4 or 28.5 Å, where they discriminate all five proteins. GBSAIM performs best for thinner membranes, but it only discriminates three proteins. At T=28.5 Å HDGB performed comparably to GBSW with only one ltpA decoy having lower energy than the native conformation. IMM1 with the standard nonbonded cutoffs did not perform as well as with the longer cutoffs (Fig. S1). It should be noted that the lowest energy decoys were not the same for different implicit membrane models and no clear trend was observed for any property of the lowest energy decoy that might be contributing to that state.

Figure 2.

Relative energy in kcal/mol of the decoys obtained using five implicit membrane models vs relative RMSD. Purple crosses – VATP; red squares – fmr5; green dots – ltpA; blue diamonds –BRD7; black triangles –RHOD.

Table 2.

Number of discriminated native structures for each width and membrane model

T, Å	IMM1	IMM1-p36	GBSAIM	GBSW	HDGB
23.1	1	2	3	4
25.4	3	5	3	5
27.0	4	4	1	4
28.5	1	4	2	5	4
30.4	2	4	1	4

Table 3.

Z-scores for each membrane width and protein.

T, Å	IMM1	IMM1-p36	GBSW	GBSAIM	HDGB
23.1	1.4	2.1	2.5	2.0
25.4	1.7	3.0	2.9	2.0
27.0	2.4	2.8	2.3	1.9
28.5	1.9	2.5	2.9	1.5	2.8
30.4	1.8	2.6	2.4	1.8

The ranking of the models according to average Z-score (Table 3) depends on membrane thickness. If one uses the best thickness for each model where thickness varies, the ranking is:

• IMM1-p36 (3.0) > GBSW (2.9) > IMM1 (2.4) > GBSAIM (2.0)

Comparing all five models at T=28.5 Å, the ranking is

• GBSW (2.9) ≈ HDGB (2.8) > IMM1-p36 (2.5) > IMM1 (1.9) > GBSAIM (1.5)

Overall, the best discrimination was achieved using IMM1-p36 model with membrane thickness 25.4 Å.

CPU times (in hours) for 0.1 ns of an MD simulation can be used to rank the models according to computational efficiency:

• IMM1 (0.7) < IMM1-p36 (3.5) < GBSAIM (4.5) < GBSW (5.8) « HDGB (25.8)

Analysis of the electrostatic, van der Waals and solvation components could provide insights into the factors that stabilize membrane protein structure^[92]. For the optimal membrane thicknesses for each model those components are shown in Table 4, Figures S2, S3 and S4 (T=25.4, 27 and 28.5 Å, respectively). One can see that none of these components alone can discriminate the native state as well as the total effective energy (Table 5). For IMM1, based on computed averages (Table 4) and Z-scores (Table 5), the largest contribution to the difference in total effective energy between the native structure and the decoys comes from van der Waals (VDW) interactions, followed by the electrostatic (ELEC) contribution. For IMM1-p36, the largest contribution comes from ELEC interactions, followed by VDW. The solvation free energy (SFE) shows the least discriminatory power, especially for IMM1-p36. For the GB models, the ELEC and GB energy (GBEN) terms are closely connected, therefore it is best that they be combined. The combined term displayed good discriminative ability (Table 5, Fig. S2 – S4). The total nonpolar component, VDW interactions and nonpolar solvation energy (ASP), also contributed to the discrimination, albeit to a smaller extent. The above results suggest that both electrostatic and nonpolar contributions are important for membrane protein stability.

Table 4.

Average relative energy and contributions (in kcal/mol) of the decoys.

	IMM1			IMM1-p36			GBSAIM		GBSW				HDGB
T, Å	25.4	27	28.5	25.4	27	28.5	25.4	27	28.5	25.4	27	28.5	28.5
Energy	57.5	84.5	54.7	112.2	106.2	95.0	72.6	66.2	57.4	130.4	106.2	127.3	132.0
VDW	53.0	42.3	43.7	77.0	53.6	50.7	32.3	30.8	17.5	36.0	47.2	51.2	36.6
ELEC	26.3	37.2	23.2	79.6	98.6	75.1	30.5	−10.6	23.0	195.5	160.7	158.5	306.8
SFE/ASP	−24.9	5.3	−13.7	−41.2	−46.6	−36.7	5.7	4.6	3.2	1.4	4.0	5.3	11.5
GBEN							−1.4	33.2	3.0	−96.7	−95.7	−77.2	−203.6
ELEC+GBEN							29.1	22.5	26.0	98.8	64.9	81.2	103.2
VDW+ASP							38.0	35.4	20.8	37.3	51.2	56.5	48.1

Table 5.

Average Z-scores of the energy components of the implicit membrane potentials.

	IMM1			IMM1-p36			GBSAIM			GBSW			HDGB
T, Å	25.4	27	28.5	25.4	27	28.5	25.4	27	28.5	25.4	27	28.5	28.5
VDW	1.6	1.4	1.6	2.6	1.5	1.6	1.2	1.2	0.7	1.3	1.6	1.8	1.3
ELEC	1.0	1.3	0.8	1.8	2.2	1.6	0.5	0.0	0.4	1.2	1.0	1.0	1.5
SFE/ASP	−1.1	0.2	−0.5	−1.5	−1.4	−1.0	0.7	0.6	0.4	0.4	1.1	1.4	1.7
GBEN							−0.2	0.2	−0.2	−0.8	−0.7	−0.5	−1.2
ELEC+GBEN							1.6	1.2	1.2	3.1	2.0	2.5	2.3
VDW+ASP							1.2	1.2	0.7	1.2	1.6	1.8	1.4

Discussion

Anfinsen showed that the biologically active structure of a protein was also the most thermodynamically stable under in vivo conditions.^[85,93] Later experiments provided direct evidence that the amino acid sequence determines all other higher order structure, function, and stability.^[94] These findings imply that, in principle, protein structure can be predicted if a model of the free energy is available, and if the global minimum of this function can be identified. Many computational approaches for protein structure prediction have been developed using this principle.^[16–23] Folding studies on bacteriorhodopsin provided the first evidence that the thermodynamic hypothesis is also valid for TM proteins.^[95–99] Since then, many membrane proteins have been refolded in detergent micelles or lipid vesicles^[100–103] Structure prediction for membrane proteins is more complex because they exist in a heterogeneous solvent environment that is not as well characterized as aqueous solution.

Lipid composition, specifically the acyl chain length of phospholipids, is important for determining the thickness of a lipid bilayer. Bilayers that are too thick or too thin to accommodate the hydrophobic region of the protein may result in improper folding, low stability and lower levels of inclusion.^{[31,104–106]} It is not surprising then that membrane thickness affects the ability of the tested energy functions to discriminate the native state. IMM1 performed best at 27 Å discriminating four out of five proteins (Tables 2 and S1). Discrimination became worse at smaller or larger thicknesses (Tables 2, 3, Fig. 2). 25.4 Å was the best thickness for the other tested models: IMM1-p36, GBSW and GBSAIM. 28.5 Å was equally good for GBSW. HDGB model performed comparably to GBSW at that thickness (Table 2, 3, Fig. 2). Comparing the best performance of all models, GBSW, HDGB and IMM1-p36 performed about the same, followed by IMM1 and GBSAIM.

The least discriminated native structure was ltpA (Fig. 2, Table S1), which according to the experimental studies may adopt a somewhat different fold in the absence of the C-terminal helices^[107]. We analyzed the interaction between the N6- and C6-terminal subdomains of ltpA and found that the interaction energy between them is large enough (~150 kcal/mol) to provide stabilization of the native state. Decoys of fmr5 were often found having marginal or lower than the native structure energy. This can be attributed to the fact that naturally fmr5 has two haem molecules bound and they could impact the overall packing of the TM helices (the interaction energy between fmr5 and heme molecules is also quite substantial). Although decoys of VATP were overall well discriminated, their discrimination was often found marginal (Fig. 2, Table S1). This observation may be associated with the fact that VATP forms a 10 subunit rotor ring and oligomerization may influence helix packing and exposure to membrane lipids. Despite their larger size, BRD7 and RHOD were discriminated better than the smaller proteins.

Compatibility of IMM1 with both CHARMM19 and 22 force fields allows assessment of the effect of the force field on native state discrimination. Unlike CHARMM19, CHARMM22 models aliphatic hydrogens explicitly and provides a more accurate account of packing interactions. In addition it has been more thoroughly parameterized and in various instances it has been shown to give results closer to experimental data compared to CHARMM19.^[108] From our results, IMM1 performed almost equally well with CHARMM19 as with CHARMM22 (Fig. 2). The difference was more pronounced with T=25.4 Å where IMM1 discriminated only one protein and IMM1-p36 discriminated all with a larger energy gap between the native structures and lowest energy decoys. IMM1-p36, compared to IMM1, also showed higher Z-scores (Table 3) and better discrimination with all membrane thicknesses (Fig. 2). CHARMM22-based GBSW and HDGB energy functions discriminated native structures much better than the CHARMM19-based GBSAIM (Table 2, 3 and Fig. 2) with none (GBSW T=25.4 and 28.5 Å) or only one decoy (GBSW T=27 Å, HDGB) having lower energy than the native conformation. Membrane thickness has stronger impact on the discriminative ability of GBSAIM than GBSW. While GBSW performs comparably well in the range of T=25.4 – 30.4 Å, GBSAIM shows moderate discrimination only with T=25.4 Å (Fig. 2). It is not clear, however, whether this is mostly attributed to the force field or to the algorithms used to evaluate the energy.

Electrostatic effects have been shown to play an important role and contribute to the low energies of the native structures in sets of alternative conformations.^[109] The native structure does not necessarily need to possess the lowest electrostatic energy, although it is reasonable to assume that the native conformation should be found among decoys with the lowest value of electrostatic interactions. The Coulomb energy term by itself displayed higher discriminative ability in IMM1-p36 than in IMM1. This suggests that the all-atom representation of the protein for this energy function might provide better description of electrostatic interactions. The Coulomb energy term in the GB models was increasingly discriminative in the order GBSAIM, GBSW, HDGB (Table 5). Despite the fact that HDGB uses a more sophisticated representation of the membrane as three dielectric slabs, accounting for the headgroup region, a simple two-dielectric slab representation of the bilayer, as in the case of GBSW, seems to be sufficient. Since the accuracy of the GB models depends strongly on the evaluation of the Born radii (α), it is important to use as precise a method as possible.^[110] All models use the Coulomb field approximation (CFA)^[111] as a basis for the estimation of α with the difference that GBSAIM uses a simple empirical function derived from the initial CFA^[61], while GBSW and HDGB implement higher-order correction terms to the CFA^[82,83]. GBSAIM uses a slightly modified older and less accurate version of GB method than the one implemented in GBSW and HDGB. Further, GBSW uses the van der Waals-based surface with a smooth dielectric boundary^[112] to estimate the integral over the volume, while HDGB uses a molecular surface with sharp boundary between solute and solvent^[113]. The latter was shown to give a higher degree of realism for macromolecules^[114], however no benefit from this in native state discrimination is apparent (Table 5, Fig. S4).

The van der Waals term showed higher discriminative power than the ELEC component in the IMM1 models, especially IMM1-p36 (Table 5, Fig. S2 – S4). This term computed using GB models was less discriminative (Fig. S1 – S4). It was also much less discriminative than the ELEC+GBEN component. Combination with the nonpolar solvation term did not improve the discrimination. The solvation terms ASP and SFE show the least discriminative power. In fact, in most cases they tend to be lower in the decoys (Tables 4, 5, Fig. S2 – S4). It should be noted that the SFE term in IMM1 corresponds to the sum of ASP and GBEN terms in the GB models. The ASP term in the GB models should be a measure of how much protein area is buried in the membrane. This term does show some discriminative power in the GBSW and HDGB models (Fig. S4).

It should be noted that the decoys examined in this work are quite far from the native state: for four proteins the RMSDs are in the range 8–25 Å and for VATP in the range 3–11 Å. For the most part, they represent gross misfolding and not small deviations from the native state. Thus, the conclusions from the present study are relevant to low-resolution structure prediction. It would be interesting to repeat this work for decoys closer to the native state to explore the utility of these implicit membrane models in high-resolution refinement.

Summarizing, we have tested four implicit membrane models for their ability to discriminate the native state of membrane proteins from misfolded decoys. Membrane thickness was found to play a substantial role in performance. All-atom force fields performed better than extended-atom ones, at the cost of some computational efficiency. Combining performance and computational efficiency one could derive "value" rankings depending on the relative importance of one or the other factor. For example, IMM1 would be a reasonable choice for very large systems, and IMM1-p36 or GBSW would be the method of choice for smaller systems demanding higher accuracy. Our results encourage the use of implicit membrane energy functions as scoring functions in membrane protein structure prediction, at least at low resolution. Additional improvements may be achieved through incorporation of additional physics, such as the membrane dipole potential^[115], membrane elasticity effects^[116] and specific headgroup-protein interactions.