A Valence Bond Model for Aqueous Cu(II) and Zn(II) Ions in the AMOEBA Polarizable Force Field

Abstract

A general molecular mechanics (MM) model for treating aqueous Cu²⁺ and Zn²⁺ ions was developed based on valence bond (VB) theory and incorporated into the AMOEBA polarizable force field. Parameters were obtained by fitting molecular mechanics energies to that computed by ab initio methods for gas phase tetra- and hexa-aqua metal complexes. Molecular dynamics (MD) simulations using the proposed AMOEBA-VB model were performed for each transition metal ion in aqueous solution and solvent coordination was evaluated. Results show the AMOEBA-VB model generates the correct square-planar geometry for gas phase tetra-aqua Cu²⁺ complex and improves the accuracy of MM model energetics for a number of ligation geometries when compared to quantum mechanical (QM) computations. On the other hand, both AMOEBA and AMOEBA-VB generate results for Zn²⁺-water complexes in good agreement with QM calculations. Analyses of the MD trajectories revealed a 6-coordination first solvation shell for both Cu²⁺ and Zn²⁺ ions in aqueous solution, with ligation geometries falling in the range reported by previous studies.

Introduction

Transition metal (TM) ions are involved in a wide range of important catalytic species and biomolecular structures,^[1–6] and numerous computational studies have modeled these compounds in silico.^[7,8] However, it remains challenging to formulate a scalable model that can satisfactorily describe a range of TM species and coordination conditions in an efficient manner.^[9] In order to accurately account for interactions between a TM ion and its ligands, it is crucial to capture the local ligand-field effects as described by the valence orbitals on TM centers and ligands,^[10,11] as well as other long-range energetics. Currently, the most common approaches to capture these effects are quantum mechanical (QM) methods, usually based on density functional theory (DFT),^[12,13] hybrid QM/molecular mechanics (MM) calculations in which a QM region is applied in the immediate vicinity of the TM center while other regions of the complex are described by MM,^[14] or semi-empirical molecular orbital (MO) methods^[15,16]. Nevertheless, most ab initio methods are computationally expensive and can prohibit modeling of large biomolecular systems over long time-scales, especially those with multiple TM binding sites. Although application of linear-scaling electron correlation techniques^[17,18] significantly speeds up MO calculations, its sampling efficiency is still inferior to MM. Therefore, it is of great interest to develop a MM force field model for TM ions, which is significantly more efficient computationally than QM/MM methods. An outstanding question is whether MM models can achieve accuracy comparable to established QM-based methods.

The traditional approach to describe TM-ligand interactions is to fit classical force field energy terms such as bonding, angular and torsional potentials to some combination of experimental and QM results. However, the parameters for one TM complex are not easily transferable to a different system, and distinct parameters maybe necessary for the same type of ligand depending on ligation geometry. Extensive a priori data is often needed to produce a satisfactory parameter set. These shortcomings limit the predictive capability of the methodology.^[7] One way of addressing these issues is to forgo the classical force field model in favor of a “reactive” framework that allows atoms to respond chemically to their environment. Models such as ReaxFF, which allows dynamic changes in bond order and charge transfer, have demonstrated this paradigm is applicable to various TM complexes.^[19,20] Alternatively, classical force fields can be supplemented with terms for d-electron effect derived directly from QM theory to improve their accuracy. In recent years, several “semi-classical” MM models based on valence bond (VB) theory^[21,22] and the angular overlap model (AOM)^[23] have been developed for TM complexes. The main difference between the classical and semi-classical methods lies in the derivation of ligand angular potentials. Unlike angular potentials commonly used in force fields for organic compounds, a functional form dependent on a reference value for each ligand-metal-ligand angle is not a general, transferable approach for TM-ligand interactions because the details of ligation geometry vary dynamically with the overall ligand arrangement. The angular energies for ligands in force fields such as VALBOND^[24–27] are derived from a simplified version of VB theory. TM ions are described as resonance centers and angular terms are developed from geometrical overlap between sdⁿ hybridized bonding metal-ligand orbitals. On the other hand, DommiMOE developed by Deeth, et al.^[28] and previous work by Carlsson, et al.,^[29] are based on AOM in which the metal-ligand angular term arises from the explicit diagonalization of a ligand field potential matrix. Both approaches avoid the use of reference ligation geometries in their angular potentials and have shown to provide favorable results when compared to experimental data and QM-based calculations across a range of different coordination geometries and ligation states.^[9]

Previous work on semi-classical force fields has focused on modeling the effects of local metal-ligand binding on the geometry of TM complexes. However, electrostatic interactions are also a major component in TM complex energetics. At distances beyond direct ligation, TM ions behave similarly to main group cations and polarization becomes an important contributing factor. To date, most semi-classical models developed for TM ions use a fixed charge model for electrostatic interactions, which is inadequate in treating systems with high charge density.^[30] In the present study, we seek to develop a semi-classical force field for TM ions incorporating explicit treatment of both metal-ligand binding effects and polarization. Specifically, a ligand angular potential is developed for aqueous Cu²⁺ and Zn²⁺ ions based on VB theory in conjunction with the AMOEBA (Atomic Multipole Optimized Energetics for Biomolecular Applications) polarizable force field.^[31] In light of the extensive MM studies based on the AOM carried out by Deeth, et al., ^{[9,28,32–36]} we investigate a alternative TM complex model that is built upon the chemical principles of hybridization and resonance in the spirit of Pauling’s theory. We believe that the VB approach provides a complimentary model to the AOM approach if one, for example, is interested in interpreting TM binding in terms of its resonance constructs. Furthermore, the development of VALBOND by Landis, et al. suggests that VB theory may be incorporated into MM through relatively simple algebraic functions that are computationally efficient.

It has been shown that AMOEBA produces excellent results for main group aqueous dications^[37,38] and therefore provides a suitable basis for modeling TM dications. In this initial report, we limit our scope to Cu²⁺ and Zn²⁺ in order to reduce the number of spin states and the complexity of model development. Parameters are determined against energies calculated with QM methods for metal-water complexes in the gas phase and validated against experimental data for the aqueous ions. Additionally, previous work shows that the AMOEBA force field provides a satisfactory description for the aqueous Zn²⁺ ion.^[39] We have pursued further investigation to see if modeling the covalency explicitly between water ligands and Zn²⁺ can improve the accuracy of the existing AMOEBA model. In the following sections, we present the AMOEBA-VB framework for Cu²⁺ and Zn²⁺ ions and document the procedures for obtaining force field parameters. Results from energy computations for gas phase ion-water complexes and molecular dynamics simulations for aqueous ion solutions are reported and compared against QM and previously published data.

Methods

AMOEBA-VB Framework

The general interatomic AMOEBA potential energy can be expressed as:

$$U_{\text{AMOEBA}}=U_{\text{bond}}+U_{\text{angle}}+U_{\text{b}-\text{a}}+U_{\text{oop}}+U_{\text{torsion}}+U_{\text{vdW}}+U_{\text{ele}}^{\text{perm}}+U_{\text{ele}}^{\text{ind}}$$ (1)

where the first five terms represent bond stretch, angle bend, bond-angle cross-term, out-of-plane bend and torsion potentials to describe local valence contributions. The last three terms are handle nonbonded interactions, including the van de Waals (vdW), permanent electrostatic and induced electrostatic potentials.^[31,40,41] Additional potentials for TM centers based on VB theory are added to the overall energy:

$$U_{\text{total}}=U_{\text{AMOEBA}}+U_{\text{VB}}$$ (2)

In the context of aqueous TM ions, only the nonbonded interactions from AMOEBA are applied between the metal center and water molecules.

Nonbonded Intermolecular Potentials

The basic AMOEBA potential terms use energy expressions from previous published reports.^[31,40,41] A buffered 14-7 potential ^[42] is used to model vdW interactions, and takes the following form:

$$U_{ij}^{\text{vdW}}={\epsilon }_{ij}{\left(\frac{1+\delta }{{\rho }_{ij}+\delta }\right)}^{n-m}\left(\frac{1+\gamma }{{\rho }_{ij}^m+\gamma }-2\right)$$ (3)

where ${\rho }_{ij}=R_{ij}/R_{ij}^0$, and R_ij represents the separation between atoms i and j. The values of n, m, δ and γ are set to 14, 7, 0.07 and 0.12 respectively, while ε_ij and $R_{ij}^0$ correspond to the potential energy well-depth and minimum energy distance. For heterogeneous atom pairs, mixing rules are applied to determine ε_ij and $R_{ij}^0$:

$$\begin{array}{l}{R}_{ij}^0=\frac{{(R_{ii}^0)}^3+{(R_{jj}^0)}^3}{{(R_{ii}^0)}^2+{(R_{jj}^0)}^2}\\ {\epsilon }_{ij}=\frac{4{\epsilon }_{ii}{\epsilon }_{jj}}{{({\epsilon }_{ii}^{1/2}+{\epsilon }_{ij}^{1/2})}^2}\end{array}$$ (4)

The electrostatic potential is described as having a permanent and an induced component. The permanent electrostatic component is represented by atom-centered monopole, dipole and quadruple moments. The parameters are determined via Stone’s distributed multipole analysis^[43] followed by refinement against QM-derived electrostatic potentials. Polarization is accounted for self-consistent induced dipoles computed from:

$${\mu }_{i,\alpha }^{\text{ind}}={\alpha }_i{E}_{i,\alpha }$$ (5)

where α_i is the atomic polarizability and E_i,α is the total electric field generated by permanent multipoles and induced dipoles. A Thole damping factor is applied at short interaction distances, corresponding to use of a smeared charge representation that takes the form:

$$\rho =\frac{3a}{4\pi }{e}^{-{au}^3}$$ (6)

where α is a dimensionless factor controlling the strength of damping and u= R_ij/(α_i α_j) ^1/6 is the effective separation between polarizable sites i and j. The Thole mechanism serves to avoid the well-known polarization catastrophe at small separations,^[44] and yields reasonable reasonable anisotropic molecular polarizabilities starting from isotropic atomic polarizability values.^[41]

Water Model

The AMOEBA water model has been previously reported,^[40] and tested in a variety of different environments.^[45] The standard intermolecular and intramolecular energy terms for water are retained in the AMOEBA-VB model. The water force field parameters for nonbonded and valence potentials are reported in Table 1 and Table 2, respectively.

Table 1.

Intermolecular (vdW and electrostatic) potential parameters for AMOEBA water;

	ε (kcal/mol)	R0 (Å)	M* (a.u.)	α (Å3)	a
O	0.1100	3.405	$$\left[\begin{array}{cccc}\hfill -0.51966& \cdots & \hfill & \\ \hfill 0.00000& \hfill 0.00000& \hfill -0.14279& \cdots \\ \hfill 0.37928& \hfill 0.00000& \hfill 0.00000& \cdots \\ \hfill 0.00000& \hfill -0.41809& \hfill 0.00000& \cdots \\ \hfill 0.00000& \hfill 0.00000& \hfill 0.03881& \end{array}\right]$$	0.837	0.39
H	0.0135	2.655	$$\left[\begin{array}{cccc}\hfill 0.25983& \cdots & \hfill & \hfill \\ \hfill -0.03859& \hfill 0.00000& \hfill -0.05818& \cdots \\ \hfill -0.03673& \hfill 0.00000& \hfill -0.00203& \cdots \\ \hfill 0.00000& \hfill -0.10739& \hfill 0.00000& \cdots \\ \hfill -0.00203& \hfill 0.00000& \hfill 0.14412& \end{array}\right]$$	0.496	0.39

^*M=[q,μ₁,μ₂,μ₃,Q₁₁,Q₁₂,…,Q₃₃]^T.

Table 2.

Intramolecular potential parameters for AMOEBA water.

Potential	Force Constant	Ideal Length/Angle
Bond Stretching	Kb = 529.6 kcal/mol/Å2	b0 = 0.9572 Å
Angle Bending	Kθ = 34.05 kcal/mol/radian2	θ0 = 108.5°
Urey-Bradley	Kl = 38.25 kcal/mol/Å2	l0 = 1.5537 Å (H…H)

Transition Metal Ion Model

In addition to the usual AMOEBA vdW and electrostatic potentials, VB terms are applied between each TM ion and ligand water oxygen atom, as water molecules interact with TM ions predominately through lone pair p-orbital electrons on the oxygen atoms. As a first approximation, a TM-water complex is modeled by its principle field, with water interacting with TM ions through σ bonding only.^[11] The VB component is expressed as:

$$U_{\text{VB}}=\sum _k^{\mathit{resonance}}{W}_k{U}_{\mathit{resonance},k}$$ (7)

where the total VB potential is the summation of individual energy contributions from the resonance structures corresponding to the TM complex. W_k is an empirical function that mimics the weighting for resonance structure k in natural resonance theory.^[46]

For Cu²⁺ and Zn²⁺ water complexes, the principle resonance structure corresponds to the Lewis structure, as shown in Figure 1a, where the TM interacts with water molecules via ionic interactions. The intermolecular energy of the principle resonance structure corresponds to the regular AMOEBA non-bonded potentials. The d-electron effect can then be explained by considering minor non-Lewis resonance species where 3-center-4-electron (3c4e) bonds are formed between the TM center and ligand atoms.^[46] This represents the donation of electron density from oxygen to the metal, and delocalized ionic-covalent bonding stabilizes the hypervalent TM center. Using this description, the molecular orbitals of Cu²⁺-water complexes can be decomposed into the contributions from Lewis and non-Lewis resonance structures. Its 3c4e bonds have predominantly d character since the d⁹ configuration of Cu²⁺ 3d valence orbitals can accept electron density more readily than the 4s orbital. On the other hand, the 3d orbitals of Zn²⁺ are fully filled and the resonance hybrids are mainly due to overlap with the Zn²⁺ 4s orbital. Hence Cu²⁺ has greater resonance stabilization energy than Zn²⁺. The overall hypervalent resonance scheme for the TM ions is shown in Figure 1b. The angle formed by a 3c4e bond will be referred to as the resonance angle henceforth.

Figure 1.

Resonance scheme for [M(H₂O)₄]²⁺ complex where M = Cu or Zn. a) Principle resonance that corresponds to the Lewis structure of the complex. b) Non-Lewis minor hypervalent resonance structures with a single 3c4e bond per resonance; the number of such resonance structures is equal to $C_{\text{2}}^n$ where n is the number of ligands.

The intermolecular energy between a TM ion and ligand water molecules for an individual resonance construct k can be expressed as:

$$U_{\text{resonance},k}=U_{\text{VB}-\text{bond},k}+U_{\text{VB}-\text{angle},k}$$ (8)

where U_VB-bond,k and U_VB-angle,k are the two bonding terms and one angular term used to describe a single 3c4e bond. Since the number of resonance structures is equal to the number of angles formed by the TM-water complex, the overall energy contribution from the VB component becomes:

$$U_{\text{VB}}=\sum _k^{\mathit{angles}}{W}_k(U_{\text{VB}-\text{bond},k}+U_{\text{VB}-\text{angle},k})$$ (9)

VB angular potential is based on Pauling’s principle of angular overlap for a pair of sp^mdⁿ hybrid orbitals.^[21,22,47] The overlap integral associated with the presence of two identical nonorthogonal sp^mdⁿ bonding orbitals is:

$$\begin{array}{c}\mathrm{\Delta }={\sigma }^2+{\pi }^2\text{cos}\theta +\frac{{\delta }^2}{2}\left(3{cos}^2\theta -1\right)\\ {\sigma }^2=\frac{1}{1+m+n},{\pi }^2=\frac{m}{1+m+n},{\delta }^2=\frac{n}{1+m+n}\end{array}$$ (10)

where θ is the angle between the orbitals. The terms σ ², π ² and δ ² represent the s, p and d contributions to the bond, respectively. Following Landis,^[25] we construct the angular potential for a 3c4e bond as:

$$\begin{array}{c}{U}_{\text{VB}-\text{angle},k}=K_{\text{VB}-\text{angle},k}\left(1-\mathrm{\Delta }{({\theta }_k+\pi )}^2\right)\prod _i^2{F}_{\text{VB}-\text{angle},k,i}\\ F_{\text{VB}-\text{angle},k,i}=e^{-{\alpha }_{k,i}{r}_{k,i}^2}\end{array}$$ (11)

where K_VB-angle,k is a constant scaling factor for angle k. The bond order term in Landis’ formulation is folded into K_VB-angle,k. We introduce an additional scaling factor, F _VB-angle,k,i, as a function of the metal-ligand distance r_k,i in bond i, and an empirical parameter α_k,i. This function is necessary to describe the overlap drop-off with increasing metal-ligand distance. The overall energy term has a linear geometrical preference that is suitable for describing 3c4e bonding involving Cu²⁺. The angular potential is not applicable to Zn²⁺ since the interacting 4s orbital is spherically symmetric. Previous data has shown AMOEBA satisfactorily describes aqueous Zn²⁺ ions without the addition of a potential term for d-electron effect.^[39] However, the bonding component is retained to investigate its impact on the AMOEBA model. Note the result from overlapping hybrid orbitals is destabilizing and therefore the VB angular term is always positive. A Gaussian-like function is adapted for the VB bonding potential:

$$\begin{array}{c}{U}_{\text{VB}-\text{bond},k}=-\sum _i^2{K}_{\text{VB}-\text{bond},k}{F}_{\text{VB}-\text{bond},k,i}\\ F_{\text{VB}-\text{bond},k,i}=e^{-{\beta }_{k,i}{r}_{k,i}^2}\end{array}$$ (12)

where the index i sums over the two ligands in a single 3c4e hypervalent bond. K_VB-bond,k,i is the scaling parameter for bond i of resonance angle k. In contrast to the angular term, the VB bonding contribution is purely stabilizing. Finally, we propose an empirical resonance weighting function for resonance structure k that is based on metal-ligand distances:

$$\begin{array}{c}{W}_k=\prod _i^2{F}_{\text{resonance},k,i}\sum _l^{\mathit{angles}}\left(c_l+\prod _j^2{F}_{\text{resonance},l,j}\right)\\ F_{\text{resonance},k,i}=e^{-{\gamma }_{k,i}{r}_{k,i}^2},F_{\text{resonance},l,j}=e^{-{\gamma }_{l,j}{r}_{l,j}^2}\end{array}$$ (13)

where c_l is a parameter for resonance angle l. The index l runs through all resonance angles including k. The subscripts i and j denote the two metal-ligand pairs in resonance angles k and l, respectively. According to this formulation, the weighting for resonance construct k depends on the positions of all water molecules in the TM complex. Note although the resonance weight function depends on the number of ligands, it is applicable to all coordination numbers and its value transitions smoothly as the coordination number changes.

Finally, it has been shown that Cu²⁺ complexes in octahedral geometries exhibit Jahn-Teller type distortions.^[48–50] Since the simplified AMOEBA-VB model presented does not compensate for this effect explicitly, we explored the effect of adding a harmonic first order component^[51] where the Jahn-Teller stabilization energy arises from the Q_θ distortion mode. The exact formulation used is:

$$\begin{array}{l}{E}_{\text{JT}}^{xy}=-(r-r_0)\mathrm{\Delta }/r_0\\ E_{\text{JT}}^z=-2(r-r_0)\mathrm{\Delta }/r_0\end{array}$$ (14)

where r is the metal-ligand distance, r₀ is the average bonding distance of the TM complex, and Δ is an empirical value to scale the strength of the Jahn-Teller effect. $E_{\text{JT}}^{xy}$ and $E_{\text{JT}}^z$ are applied to the in-plane and axial ligand molecules respectively.

Parameterization and Validation

The parameters for the AMOEBA-VB framework are based on fitting MM energy values to those obtained by ab initio methods for structural variants derived from common ligation geometries of TM complexes, including square-planar, tetrahedral and octahedral. These structures are generated in such way that they are easily accessible states during computational simulations. All electronic structure calculations were performed with the Gaussian 09 package.^[52] QM geometry optimizations were carried out with B3LYP^[53,54] DFT calculations using the 6-311G(d,p)^[55] basis set. Single-point energy were computed via MP2/aug-cc-pVTZ ^[56] on main group elements and MP2/cc-pVTZ ^[57] for the TM ions. An SCF convergence criterion of 10⁻⁹ a.u. was imposed, and a Fermi-broadening SCF method^[58] was used for Cu²⁺ complexes to improve convergence stability. The AMOEBA-VB potentials and Cartesian derivatives were implemented in the TINKER^[31] molecular modeling package used for all MM computations.

The [M(H₂O)₄]²⁺ and [M(H₂O)₆]²⁺ gas phase complexes were optimized using QM methods with angular constraints to yield idealized tetrahedral, square-planar and octahedral ligation geometries. Intramolecular optimization within water molecules was allowed. These structures serve as a starting point for generating further variations in geometry designed to assess different aspects of the MM model. Complex energies computed by AMOEBA were manually fit to QM data for each of the following procedures using a common set of parameters for a metal ion interacting with a single ligand molecule. AMOEBA parameters were optimized, and then fixed in value, prior to fitting the VB terms. Results with the Jahn-Teller distortion term were also computed when applicable.

Bond stretching

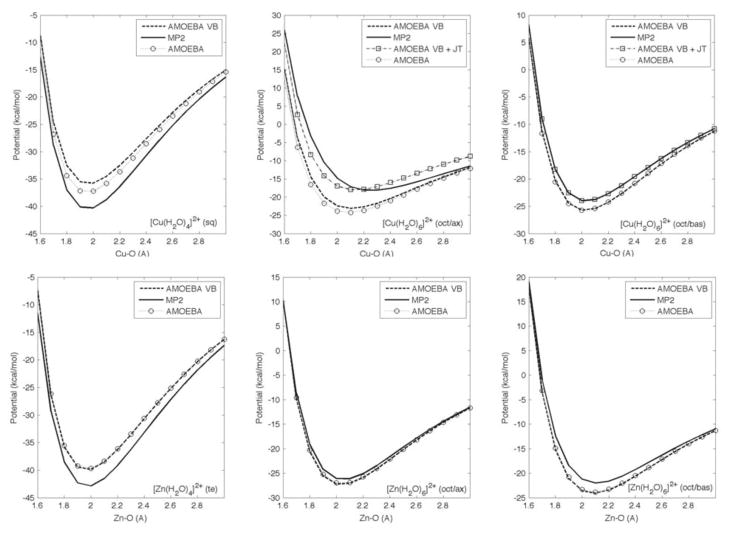
Starting from optimized structures with idealized bonding geometry for square-planar [Cu(H₂O)₄]²⁺, tetrahedral [Zn(H₂O)₄]²⁺ and octahedral [M(H₂O)₆]²⁺, single point energy calculations were performed with both QM and MM methods and plotted as a function of varying metal-oxygen distance (see Figure 2a). Water molecules remained rigid during the procedure. This protocol was designed to test the accuracy of MM model in describing bonding potentials for ideal ligation geometries.

Figure 2.

Methods for generating TM complex structural variations from idealized geometries that are used in AMOEBA-VB and QM gas phase calculations. a) a single TM-ligand distance is varied while other ligands are fixed at their QM-optimized coordinates. b) all TM-ligand distances are changed simultaneously from the optimized geometry and each ligand remains equidistance to the metal center during the process. c) perturbations are introduced to TM-water complexes by randomly changing the metal-ligand distances and rotating around the local metal-ligand vector and two axes orthogonal to the vector.

Hypervalent effect

Without the effect of hypervalent center, gas phase metal-water complexes adopt geometries that minimize ligand-ligand repulsion.^[7] Hence main group tetra-aqua complexes favor tetrahedral geometry over the corresponding square-planar configuration. The presence of strong 3c4e resonance hybrids for Cu²⁺ is predicted to stabilize the square-planar geometry according to VB theory. On the other hand, the lack of angular contribution from 3c4e bonding for Zn²⁺ leads it to prefer a tetrahedral water complex. Therefore, the energetic difference between tetrahedral and square planar offers a direct measurement to the hypervalent effect. Single point energies were computed by QM and MM methods for [M(H₂O)₄]²⁺ in both square-planar and tetrahedral coordination, and at varying metal-oxygen distances. All water molecules were kept equidistance from the TM center for each data point (see Figure 2b). Energy differences between the two geometries, after removing the water-water interaction energy in the absence of a metal ion, are calculated and plotted with respect to the metal-oxygen separation.

Random perturbation

We use a series of perturbed metal-ligand structures to gain insight into whether the MM models can reproduce the ab initio energy surface near the optimized structures. Small random perturbations were introduced to optimized ideal geometries by changing the metal-ligand distances and rotating the ligand around the metal-ligand vector and two orthogonal axes (Figure 2a). The maximum perturbation from optimized structure was 0.2Å for metal-ligand distance and 10 degrees for each rotation. Structures containing ligand-ligand contact distances less than 2.5Å were discarded, and a total of 100 random complex geometries were generated. The energy of each complex was computed by QM, and compared against values obtained from MM models. Structures with QM energies more than 15 kcal/mol higher than that of the idealized geometry were discarded since these high-energy structures are not readily accessible during routine MD simulations.

Molecular dynamics

Molecular dynamics simulations were performed for both aqueous Cu⁺² and Zn⁺² ions using the parameters derived above. A total of 8ns of canonical ensemble MD trajectory at 298K was collected for a single TM ion and 214 water molecules in a 18.6216 Å cubic box. Periodic boundary conditions were applied and particle-mesh Ewald summation was utilized to include long-range electrostatic interactions.^[59,60] The convergence criterion for self-consistent dipole polarization was set to a 0.01 Debye RMS change in atomic induced dipole moments. The correlation function, solvation shell properties and coordination number of each TM ion was computed from the trajectories and compared to published data.

Results and Discussions

Energy Components

The values for parameters obtained from the fitting procedures are shown in Table 3. The TM ions are assigned only a +2 permanent charge since it does not make sense for TM ions to possess higher-order multipoles in the absence of an external electric field. The polarizability and Thole damping factor are similar to those of main group dications in previously published studies.^[38,61] The vdW radii follow the general trend across third row transition metals in that Zn²⁺ ≥ Cu^2+.[62]

Table 3.

Force field parameters for TM ions; the second row for each TM ion represents values fitted without VB component.

	vdW		Electrostatics			VB-bond		VB-angle		Resonance		Jahn-Teller
	ε	R0	M*	a	α	KVB-bond	α	KVB-angle	β	γ	c	Δ#
Cu2+	0.24	2.88	2	0.16	0.12	5.49	0.20	9.01	0.22	0.22	2.00	0.40
	0.24	2.88	2	0.16	0.12	--	--	--	--	--	--	--
Zn2+	0.34	2.90	2	0.16	0.12	0.20	0.30	--	--	0.30	10.00	--
	0.34	2.90	2	0.16	0.12	--	--	--	--	--	--	--

^*TM ions are assigned only permanent monopole equal to their formal charge.

^# only applied to octahedral complexes.

The Cu²⁺ VB parameters are obtained with the 3c4e bond hybridization set to 10% s and 90% d (corresponding to σ ² = 0.1, π ² =0 and δ ² = 0.9 in Equation 10). We obtained this empirical ratio by recognizing that oxygen lone-pair electrons predominately interact with d orbitals of the Cu²⁺ ion, which has d⁹ configuration in its ground state. A small amount of s hybridization is modeled to take into account the effect of d-s mixing. Figure 3 shows the overall shape of the VB angular potential, which is similar to the corresponding function derived by Carlsson, et al.^[29,63] from AOM considerations. The main features of the potential function are the two local minima at ligand-metal-ligand angles of 180° and 90°, allowing tetra-aqua Cu²⁺ complexes to adopt the preferred square-planar geometry.

Figure 3.

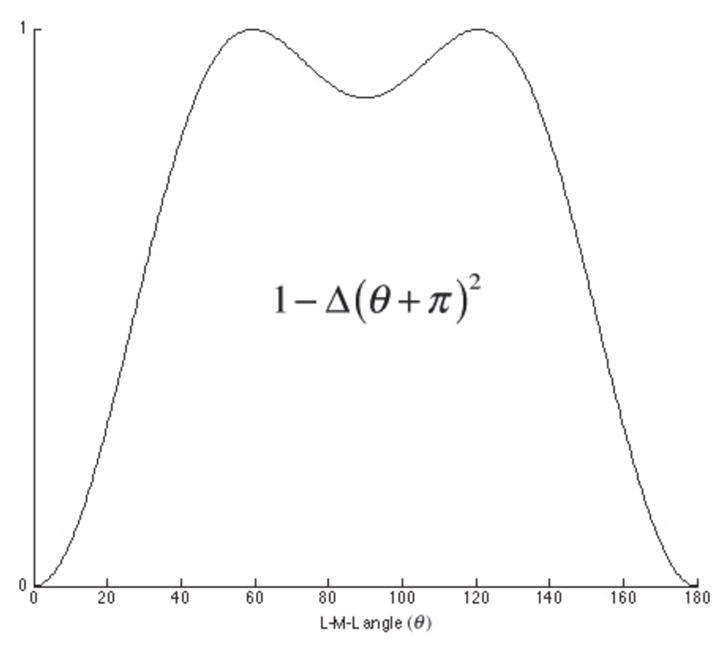
Schematic plot of VB angular potential for each 3c4e bond based on 10% s and 90% d hybridization.

The QM optimized metal-ligand distances for tetra- and hexa-aqua TM complexes are reported in Table 4. For tetra-aqua complexes, all four water molecules remain equidistance from the TM center, after bond relaxation under symmetry angular constraints. However, the axial and basal water molecules for hexa-aqua Cu²⁺ complexes adopt very different ligation distances as a result of Jahn-Teller distortion.^[50] The axial water molecules in [Cu(H₂O)₆]²⁺ are significantly elongated, and this presents a challenge for MM models lacking separate parameters for axial and basal water molecules as shown in the results below. The AMOEBA-VB energy breakdown for these optimized geometries is presented in Table 5. Note the VB bonding and angular components are reported in conjunction with resonance weighting as this reflects the final energy contributions from both 3c4e interactions and resonance as indicated in Equation 9. In terms of relative strength of the various energy components, the permanent electrostatic interaction makes the largest individual contribution, followed in order by polarization, vdW and VB potentials.

Table 4.

Metal-ligand distances in B3LYP/6-311G(1d,1p) optimized geometries for tetra- and hexa-aqua Cu²⁺ and Zn²⁺ gas phase clusters.

[Cu(H2O)4]2+ (sq)	4 × 1.93Å
[Zn(H2O)4]2+ (te)	4 × 1.98Å
[Cu(H2O)6]2+ (oct)	4 × 2.03Å + 2 × 2.33Å
[Zn(H2O)6]2+ (oct)	4 × 2.10Å + 2 × 2.16Å

Table 5.

AMOEBA-VB energy breakdown for QM optimized cluster geometries; Energy values are in kcal/mol;

	[Cu(H2O)4]2+ (sq)	[Zn(H2O)4]2+ (te)	[Cu(H2O)6]2+ (oct)	[Zn(H2O)6]2+ (oct)
Ubond	1.5069	0.5574	0.5539	0.5469
Uangle	2.3861	0.1349	0.4740	0.4196
Ub-a	0.2910	0.0002	0.1013	0.0363
UvdW	79.5473	79.3527	60.5484	56.7608
$U_{\text{ele}}^{\text{perm}}$	−226.2327	−218.6961	−271.6602	−266.6295
$U_{\text{ele}}^{\text{ind}}$	−107.7846	−111.7536	−97.6227	−91.7410
WUVB-bond	−17.5323	−0.3736	−36.7016	−0.5242
WUVB-angle	14.9848	--	36.8102	--

Abbreviations: sq = square planar, te = tetrahedral, oct = octahedral.

Bonding Potential

Bonding potential energies computed by QM and MM methods are shown in Figure 4. A single bond potential is constructed for tetra-aqua complexes since the water molecules are equidistant from the metal. However, axial and basal water molecules for octahedral complexes are plotted separately due to their differences in bonding distances and energies. In the case of [Cu(H₂O)₄]²⁺, both the AMOEBA and the AMOEBA-VB models arrive at minimum energy distances consistent with QM values, but the inclusion of the VB components produces a stronger binding interaction that better reflects QM results. For [Cu(H₂O)₆]²⁺, both MM models produce the correct bonding geometry for basal water molecules, with AMOEBA-VB again producing a more accurate interaction energy. Neither model was able to reproduce the full extent of the elongation of axial ligand to metal distances, resulting in 2.07Å and 2.09Å for AMOEBA and AMOEBA-VB respectively versus 2.33Å for QM. The interactions between axial water molecules and Cu²⁺ ion are also too strong (−23.07 kcal/mol for AMOEBA-VB, −24.23 kcal/mol for AMOEBA and −18.07 kcal/mol for QM), in general agreement with the distance discrepancies. Adding an explicit Jahn-Teller distortion term does not dramatically improve the ligand binding geometry (axial Cu-O distance at 2.12Å) but it does produce a more accurate binding energy (−17.94 kcal/mol). Results from the MM model with and without the VB term do not exhibit a significant difference for tetra-and hexa-aqua Zn²⁺ complexes. For Zn²⁺, both MM methods produce bonding potentials in agreement with QM calculations.

Figure 4.

Comparison of bond potentials between QM and MM methods; zero potential is set as the energy of complex at 5Å metal-oxygen distance to approximate dissociation; see supporting information Table 1 and 2 for numerical values. Abbreviations: sq = square-planar, te = tetrahedral, oct = octahedral, ax = axial, bas = basal, JT = Jahn-Teller distortion term.

Hypervalent Effect

The energy difference between gas phase square-planar and tetrahedral tetra-aqua complexes are plotted as a function of metal-ligand distance in Figure 5. Note that water-water interactions are subtracted to isolate the energetics between TM and water molecules. It is apparent from the figure that in the absence of a VB component, AMOEBA produces the wrong geometrical preference for [Cu(H₂O)₄]²⁺. The AMOEBA-VB framework is able to capture the correct trend of the hypervalent effect, even though the computed energy difference is still relatively small compared to QM data. As our final proposed model, we have settled on a set of parameters producing the most balanced performance across all aspects of the parameterization. Figure 5 also suggests the VB angular potential is not required to obtain the optimal tetrahedral geometry for [Zn(H₂O)₄]²⁺ complex.

Figure 5.

Energy difference between square-planar and tetrahedral tetra-aqua TM complexes; energy calculated by: (U_sq − U_sq/empty) − (U_te −U_te/empty); data points from AMOEBA and AMOEBA-VB methods for [Zn(H₂O)₄]²⁺ overlap each other since the differences in results are very small; see supporting information Table 3 and 4 for numerical values.

Energy Surface

To help assess the accuracy of the MM energy surface, we compare in figure 6 the energies computed using ab initio methods with that from MM for perturbed structures around idealized geometries. All energy values presented are relative to those of idealized coordination structures. Results obtained with the AMOEBA-VB framework show there is a 18–19% reduction in RMS deviation from QM values when compared with AMOEBA-only data for Cu²⁺ complexes. Addition of the Jahn-Teller distortion term does not materially change the results. On the other hand, the addition of the VB term to Zn²⁺ does not have a meaningful impact on correlation between QM and MM results. Both AMOEBA and AMOEBA-VB are able to generate accurate relative potential energies in comparison with to QM data.

Figure 6.

Comparisons of QM and MM energies for perturbed structures; results without VB components are on the left and that with VB terms are on the right.

Ions in Aqueous Solution

A series of canonical ensemble molecular dynamic simulations were performed for aqueous solutions containing a single Cu²⁺ or Zn²⁺ ion. Calculation for Cu²⁺ used the AMOEBA-VB model, but without application of the Jahn-Teller distortion term. Omission of the Jahn-Teller was necessary during MD because the simple first harmonic potential function does not provide a smooth energy transition when axial and basal ligands rearrange during the course of a simulation. The metal-oxygen correlation function and radial distribution function for water surrounding the TM ion is presented in Figure 7. The first solvation shell for both TM ions is found to contain six water molecules and the ligation geometries, along with data from previous studies, are reported in Table 6. Six-membered ligation states have been reported in the literature for Zn^{2+ [64–66]} and this agrees with our observation. However, there is a lack of general consensus regarding the optimal ligation geometry of aqueous Cu²⁺, and a variety of first solvation shell occupancies have been reported.^[67,68] A solvation number of 5–6 has been suggested for Cu²⁺ from numerous experimental and computational studies. ^[64,69–71] The 5-coordinate structure is generally attributed to a distortion from octahedral geometry due to the Jahn-Teller effect. We did not observe the “dual-peak” 6-coordinate Cu-O radial distribution obtained from simulation with the ReaxFF model.^[20]

Figure 7.

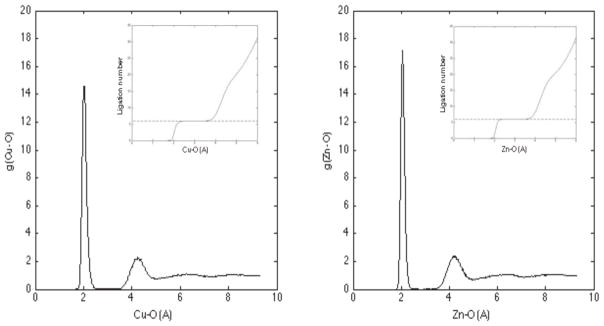
Metal-oxygen correlation function and radial distribution of water molecules surrounding a TM center (insert). The dashed line corresponds to a first solvation shell with 6 water molecules.

Table 6.

Metal-oxygen coordination for first solvation shell of aqueous TM ions; MD results for present work are taken from the first peak of M-O correlation function.

	Method	1st solvation shell M-O coordination number and geometry	Reference
Cu2+	MD (AMOEBA-VB)	6 × 2.005	Present work
	MD (REAX-FF)	4 × 1.94 + 2 × 2.27	[20]
	Neutron diffraction	6 × 1.97	[72]
	Neutron diffraction	5 × 1.96	[70]
	EXAFS	4 × 1.96 + 2 × 2.60	[73]
	EXAFS	4 × 2.04 + 2 × 2.29	[74]
	Car-Parrinello MD	5 × 1.96	[70]
	Car-Parrinello MD	4 × 2.00 + 1 × 2.45	[75]
Zn2+	MD	6 × 2.055	Present work
	X-Ray diffraction	6 × 2.04	[65]
	B3LYP/MD	6 × 2.05	[66]

Conclusions

The AMOEBA-VB framework presents a foundation on which a generalized transition metal force field can be built. The appeal of a MM model based on VB is that it is physically intuitive and avoids differential treatment of ligands of the same type based on coordination geometry. The results presented show addition of VB components to AMOEBA improves energetic accuracy when compared to QM data, while producing reasonable simulation results in aqueous solution. It is also clear that AMOEBA can satisfactorily describe the characteristics for aqueous Zn²⁺ without explicit modeling of the interaction between oxygen lone-pair electrons and TM orbitals.

An evident area of improvement for AMOEBA-VB is its treatment of Jahn-Teller distortion. The elongation of axial water molecules in octahedral Cu²⁺ complexes is not fully reproduced by the AMOEBA-VB model. An explicit description based on the harmonic first order approximation improves the results. However, this necessarily requires the energy function to be applied selectively based on geometry and ligand type. As a result, this solution cannot provide a smooth transition for dynamic Jahn-Teller effect and exchange between hexa and penta-aqua coordination. A possible remedy is to explore alternative forms of resonance weighting function to better describe the effects of Jahn-Teller distortion. This approach conforms to the tenets of VB theory and does not limit the generality of the model.

In addition to further optimization of the AMOEBA-VB aqueous TM model, future work should extend to more complex systems, especially cases with more than one type of ligand, as well as ligands with a significant π contribution. VB model can be generalized for such systems through developing hybridization-mixing rules. Modifications to the resonance weighting function may also be necessary for these more complex situations. In addition, we are currently exploring alternative TM models derived from AOM theory.