Preprocessing of Fluoresced Transmembrane Potential Signals for Cardiac Optical Mapping

Abstract

Fluorescence imaging of transmembrane voltage-sensitive dyes is used to study electrical activation in cardiac tissue. However, fluorescence signals typically have a low signal to noise ratio that can be contaminated with motion artifacts. We describe an alternative processing approach for fluoresced transmembrane potentials (fTmps) using the wavelet multiresolution analysis. We show that fTmp signals can be decomposed and reconstructed to form three sub-signals that contain signal noise (noise signal), the early depolarization phase of the action potential (rTmp signal), and motion artifact (rMA signal). Discrete wavelet transform is used with coiflet4 scaling and wavelet functions for fTmp decomposition and reconstruction of these sub-signals. Our results show that this type of analysis can be used to remove baseline drift, reduce noise, and reveal wavefronts. It streamlines the preprocessing of fTmps for subsequent measurement of activation times and conduction velocities. The approach is promising for studying wave fronts without aggressive mechanical tissue constraint or electromechanical uncoupling agents, and it is particularly useful for single camera systems that do not provide for ratiometric imaging.

I. BACKGROUND

FLUORESCENCE imaging of living myocardial tissue stained with a voltage sensitive dye is a powerful tool for studying cardiac electrophysiology. This technique is used with living animal heart preparations to record electrical activation sequences and provide high spatial resolution data compared to traditional electrode mapping techniques. However, one limitation of fluorescence imaging is its sensitivity to motion. Spatial registration between the imaging device and cardiac tissue is distorted during muscle contraction. As a result, fluorescence signals become contaminated with “motion artifact” [1].

The impact of contraction on the measurement of optical action potentials (OAPs) can be minimized pre- or post acquisition. Pre-acquisition approaches include mechanical constraint or pharmacological immobilization of the heart using electromechanical uncouplers. Post acquisition approaches include ratiometery [2] and image registration [3]. Ratiometery eliminates baseline drift due to photobleaching, but it does not completely remove the motion artifact. However, ratiometry can be combined with either gentle mechanical constraint or a low dose uncoupler to minimize the effect of a motion artifact. Furthermore, a modified subtraction method, based upon a linear model, can also be used to remove motion from ratiometric data [4, 5].

The conventional approach for identifying local tissue depolarization is to compute the first derivative of fluoresced transmembrane potential signals (fTmps) [1]. Differentiated fTmps reveal excitation wavefronts because phase-zero depolarization precedes motion in fTmps. However, since differentiation amplifies noise, the signals need to be aggressively filtered to reduce noise levels.

We present an alternative post-acquisition non-ratiometric approach to separate phase zero depolarization sequences from signal noise and motion artifact. Our main objective was to reveal wave front propagation. We hypothesized that this could be done using a wavelet analysis since phase zero depolarization and motion artifact occur at different temporal scales. The analysis is based upon the discrete wavelet transform, a signal-processing tool used for feature extraction. In one processing step fTmp signals were de-noised, baseline drift was removed, and OAP phase-zero depolarization was separated from motion artifact. The result is reconstructed transmembrane potentials (rTmps) from which measurements of activation times and conduction velocities can be derived.

II. METHODS

A. Heart preparations and optical imaging system

Adult Sprague-Dawley rats (300 – 400 g) were injected with sodium heparin and anesthetized with sodium pentobarbital. The heart was quickly excised and the aorta was cannulated. The heart was stained with the potentiometric dye RH237 (10 μM) by a bolus injection (5 mL) to the aorta and transferred to a Langendorff perfusion system where it was retrograde perfused at constant pressure (50 mmHg) with oxygenated Tyrode's solution. After a 15min stabilization period, RH237 was imaged during both endogeneous and paced rhythms. Pacing was set at twice the diastolic threshold (700ms cycle length) using a bipolar electrode placed on the anterior epicardial surface. RH237 was excited by illuminating the anterior epicardium with light from two light emitting diodes (LumiLEDs, 530/35 nm). Emitted light passed through a single lens system (Cosmicar 6 mm, F/1.0 with +27 closeup lenses), a dichroic mirror (610 nm), a long pass filter (680 nm), and was imaged with a CCD camera (Andor IXON DV860). Images were acquired at a frame rate of 650 fps. Background fluorescence was subtracted and signals were normalized at each pixel. Images were filtered with a 3×3 point spatial conical filter using a slope of one. All experimental procedures were approved by the GWU Institutional Animal Care and Use Committee.

B. Wavelet expansion series

Wavelets are mathematical constructs used to analyze signals according to scale or, equivalently, according to resolution (i.e., the reciprocal of scale). According to the theory of multiresolution [6] the difference of information between the approximation of a signal at different resolutions can be extracted by decomposing a signal with finite energy x(t)∈L2(R) using the discrete wavelet transform (DWT).

For a signal x(t), the orthogonal wavelet series expansion is

$$x\left(t\right)=\sum _{n=-\infty }^{\infty }{a}_{Mn}{\varphi }_{Mn}\left(t\right)+\sum _{m=-\infty }^M\sum _{n=-\infty }^{\infty }{d}_{mn}{\psi }_{mn}\left(t\right)$$ (1)

where a_Mn are the approximation coefficients that represent the coarse information of the signal at maximum scale M and shift 2^Mn. The detail coefficients, d_mn, represent the detailed features of the signal x(t) at scale m and shift parameter n. φ(t) and ψ(t) are prototype scaling and wavelet functions, respectively.

A multiresolution analysis for a basis function is implemented numerically using a hierarchical algorithm. An extended discussion of wavelet theory and its application to multiresolution analysis for signal decomposition is provided in [7]. In this report all signals were processed and analyzed using Matlab® (Mathworks, Natick, MA) and wavelet analyses were implemented using functions from the Matlab wavelet toolbox™ as described below.

C. Test signal synthesis, decomposition and reconstruction

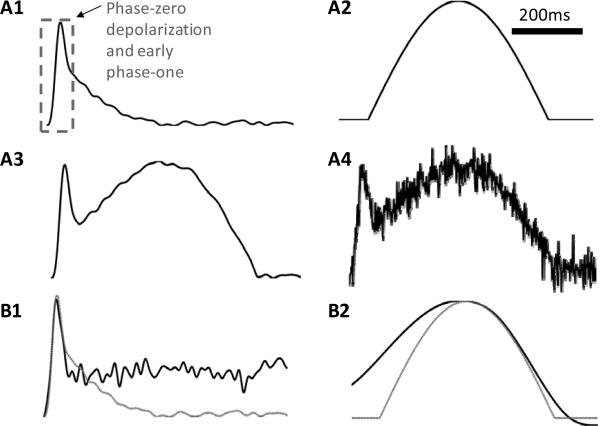
fTmp decomposition using a DWT was tested using idealized fTmp signals that represent those recorded from rat ventricular epicardial tissue. The idealized fTmps had three components: an idealized optical action potential (IOAP), simulated motion artifact, and simulated noise. The IOAP was generated by the ensemble average of fTmp signals acquired from the epicardial surface after the administration of blebbistatin (Fig1 A1). Blebbistatin is an inhibitor of myosin II isoforms and is used as an electro-mechanical uncoupler in optical mapping studies [8]. IOAPs did not have motion artifact. Motion artifact was simulated using a half-wave rectified sine wave (Fig 1 A2) and was added to the IOAP (Fig 1 A3). White noise was then added to the total signal using the Matlab function awgn.m. The signal to noise ratio of the final idealized fTmp signal was 20dB (Fig 1 A4). This signal was used for optimizing the multiwavelet resolution analysis of experimental fTmp signals.

Fig1. Idealized fTmp signals synthesis and analysis.

A1 IOAP: ensemble averaged fTmp signal acquired from the epicardial surface of a rat heart after the administration of blebbistatin. A2 Simulated motion artifact: a half-wave rectified sine wave . A3. Summation of signals in A1 and A2. A4 white noise was added to the signal shown in A3 B1. Rat IOAP (dotted gray) and reconstructed fTmp signal (rTmp) from detail coefficients at levels 4 to 7 (black). B2. Simulated motion artifact (dotted gray) and rMA from approximation coefficients at level 7 (black).

The idealized fTmp signal was decomposed up to scale level M=10 using the Matlab function wavdec.m. A wavelet decomposition of the idealized fluorescence signal using the coiflet4 wavelet is shown in Fig 2. The detail coefficients at levels 1 to m (d₁ to d_m) were then used to reconstruct the signals shown on the left while the approximation coefficients (a_m) were used to reconstruct the signals shown on the right.

Fig.2. Decomposition of idealized fTmp signal.

At each level m signals were reconstructed from detail coefficients d₁ to d_m (left panel) and approximation coefficients a_m (right panel). Lower level detail coefficients represent the noise signal (m=1 to3). Approximation coefficients at levels 6 or 7 represent the motion artifact. The RMSE of rMA to the simulated motion artifact (Fig 1 A1) was computed at each level m and are listed on the far left.

We identified the optimal level of decomposition (M) for the idealized fTmp signals that provided the best reconstruction of the simulated motion artifact. This was determined by computing the root mean squared error (RSME) at each scale level for the signal reconstructed using the approximation coefficients (a_m) and the original idealized motion artifact (Fig1 B2). For the idealized signal this corresponded to level 7, as shown in Fig 2.

A signal with phase zero depolarization and early repolarization of the IOAP was reconstructed using detail coefficients. Detail coefficients at low scale levels (1, 2 & 3) mainly contained noise information. A de-noised version of the IOAP (rTmp signals) was reconstructed using detail coefficients from levels 4 to 7. An example of rTmp signal is shown in Fig1 B1. Signals reconstructed using approximation coefficients at level M=7 (rMA signals) are shown in Fig1 B2.

D. An optimal wavelet

Using the decomposition and reconstruction approach described above, the idealized fTmp signal was analyzed using 35 wavelets of different classes to find an optimal wavelet basis function. The wavelets included orthogonal bases such as Daubechies, symlets, coiflets, Meyer wavelets and biorthogonal wavelets (using bior.m and rbio.m from the Matlab wavelet toolbox). At each level m, rTmp and rMA signals were compared (by computing RMSEs) to the IOAP and simulated motion artifact, respectively.

We found that the Coiflet4 provided lowest RMSE, best preserved the location of phase-zero depolarization, and least distorted the reconstructed signals.

III. RESULTS

A. fTmp decomposition and reconstruction of subsignals

fTmp signals at each pixel in fluorescence datasets were decomposed using the multiresolution wavelet analysis described above. Datasets were fTmp movies 4 to 5 sec in duration (650 fps). First, an appropriate level of reconstruction for rTmp and rMA sub-signals was deter-mined using the fTmp signal from one pixel. The signal was then decomposed and reconstructed in the same way as the idealized fTmp signals (Fig 1). Using these reconstructions, we identified the level at which all motion artifact was detected in the approximation coefficients, without leakage of motion artifact into rTmp signals. Similarly, the detail coefficients cutoff level for signal noise was identified as the level at which no information from the early phases of the OAP was present in reconstructed noise signals. The same levels were then used to reconstruct sub-signals at all other pixels in the dataset. Overall, we found that selection of the levels of reconstruction at one pixel provided adequate separation of motion artifact and the early phases of OAPs for all pixels.

An example of reconstruction of sub-signals (rTmp and rMA) from a fluorescence dataset is shown in Fig 3 (pacing, no blebbistatin). fTmp signal to noise ratio was 15.3 dB. Detail coefficients at levels 4 to 6 were used to reconstruct de-noised rTmp signals at each pixel which revealed the early phases of OAPs. rMA at each pixel was reconstructed using approximation coefficients at level 6. The rMA signal also contained the baseline drift that was present in the fTmp signal (see Fig 6 for additional information regarding baseline drift removal). Signal noise was reconstructed using detail coefficients at levels 1 to 3. Even during unsteady rhythms, phase zero depolarization of OAPs could be successfully reconstructed. A typical rTmp for an unsteady rhythm (2 S1s followed by a premature S2 and another premature S3) is shown in Fig 3 (right).

Fig3. Successful reconstructions of OAP phase zero using wavelet analysis.

fTmps and rTmps and rMA are shown during pacing (left S1: 700ms) and during an S1-S2-S3 pacing protocol (right). Signals are the average of a 3 pixel radius.

Fig6. Baseline drift reconstruction.

A. Spatially averaged fTmp signal using a 3 pixel radius. Baseline drift (gray line) was reconstructed using approximation coefficients at level 10. B. fTmp signal after subtracting the reconstructed baseline drift shown in A.

Wave fronts were clearly identified in the rTmps movies. Activation maps constructed from rTmps for a paced rhythm and during more complex wave propagation (reentrant wave) are shown in Fig4.

Fig4. Activation time maps.

for A. paced beat. Wave fronts reveal the elliptical wave originating from the pacing electrode. B. Reentry. Activation times measured from rTmps revealed the reentrant pathway and a slowly conducting zone near the base of the heart.

B. Spatial variation of motion artifact and baseline drift removal

Motion artifact in fTmp signals is the result of local tissue deformation, rigid body motion, and spatial variations of background fluorescence caused by anatomic features of tissue such as vessels and fat deposits. As such, the duration, magnitude, and morphology of motion artifact varied across the epicardial surface. Motion artifacts from six different epicardial sites in a typical dataset were reconstructed and compared to the original fTmp signals to determine whether motion artifact of different morphologies could be properly reconstructed. As shown in Fig 5, rMAs adequately represented motion artifacts of multiple morphologies. Approximation coefficients at higher scale levels (>7) mainly contained information related to fTmp baseline drift. Fig 6 shows an example of how approximation coefficients at a scale level of 10 can be used to remove baseline drift.

Fig5. Morphology of motion artifact.

Motion artifacts were reconstructed using approximation coefficients at level 6 from six different epicardial sites. A. An image of the heart during diastole. The locations of signals shown in B are labeled. B. rMA (gray) is shown on top of original fTmp signals (black) from the six locations marked in A.

IV. DISCUSSION

In this report we show how wavelet theory can be used to de-noise fTmps, remove baseline drift, and separate OAP phase-zero depolarization from motion artifact in one processing step. This is particularly useful for visualizing wave fronts using single camera fluorescence imaging systems where ratiometric imaging is not possible. Wavelet multiresolution analysis could be used instead of conventional Fourier-based filtering to remove noise and baseline drift and as an alternative to signal differentiation to reveal wave fronts. Unlike Fourier-based filtering, no a priori knowledge of the frequency content of the signal is necessary for the multiresolution based analysis. A time-frequency analysis of an OAP before and after application of blebbistatin is presented in Fig 7, reveals that the frequency content of the phase zero depolarization, the motion artifact and the repolarization phase is very similar. Accordingly, it is not trivial to discern distinct frequencies associated with the phase zero depolarization compared to the motion artifact or the repolarization phase. Using the wavelet multi-resolution analysis, the separation of phase-zero depolarization and motion artifact was achieved with accuracy using an optimal wavelet basis function (coiflet4) that best fit phase zero of the OAP.

Fig7. Discrete short time Fourier transform analysis of fTmp signals before and after the application of blebbstatin.

Spatially averaged fTmp signals (3 pixel radius) are shown above the spectrogram for each signal. A. Spectrogram of an fTmp signal after the administration of blebbistatin (no motion artifact). B. Spectrogram of an fTmp signal before the administration of blebbistatin (with motion artifact). Analysis parameters were window size=32, overlap=31 and NFFT = 1024.

A limitation of this technique is the inability to reconstruct the repolarization phase of the OAP. Signal components corresponding to the repolarization phase are represented by the approximation coefficients, along with motion artifact. In our studies fTmp signals were recorded from rat ventricles, which have little or no plateau phase and have an exponentially decaying repolarization phase. Wavelet basis functions that more closely mimic the shape of the entire OAP could potentially be used to remove motion artifact and reveal the repolarization phase.

Information provided by rMA signals could be useful for quantifying the effect of electro-mechanical uncoupling agents or alterations that influence contractility, such as ischemia. The synergistic combination of rMA and rTmp datasets could be useful for studying arrhythmia mechanisms in working heart preparations during acute local ischemia, reperfusion, or fibrillation.

V. CONCLUSION

Multilevel wavelet analysis is a powerful tool for the extraction of features from signals. We have shown that such an approach can be used as an alternative processing technique of fluoresced trasmembrane potentials to 1) remove noise from fTmp signals 2) remove baseline drift due to photobleaching and 3) separate the motion artifact (rMA) from optical action potential phase-zero depolarization. We conclude that this processing tool could expand the scope of applications for fluorescence imaging, so that it is applied to targets with limited or repetitive motion using a single camera.