On the Bias of Finite-View Interior Tomography Using Piecewise-Constant and Non-Negativity Constraints

Abstract

It has been widely believed that the non-negativity and the piecewise-constant constraints guarantee a unique solution to an interior tomographic problem. This letter points out that if the number of views is finite, the non-negativity and the piecewise-constant constraints do not guarantee a unique solution to an interior tomographic problem and the reconstruction could be biased by a constant polygon.

I. Introduction

Interior tomography is an underdetermined problem; solutions in general are not unique. Many constraints can be applied so that a useful solution can be obtained among these solutions (Natterer 1986, Pan at al 2005, Defrise et al 2006, Chen et al 2008). One way to select a useful solution is to impose the restrictions that i) the reconstructed image is non-negative, and ii) the reconstructed image is piecewise constant. The piecewise-constant constraint is encouraged usually by using an iterative algorithm to minimize an l₁ norm of the gradient or the total variation (TV) of the solution image.

In some recent papers (Yu and Wang 2009, Yu et al 2009) we learn that if the object is piecewise constant, the interior tomography problem is uniquely solvable by using total variation (TV) minimization. The above papers assume a continuous image domain, a continuous projection domain, and continuous angular sampling. This paper points out that if the number of views is finite, many different piecewise-constant images can generate the same set of projection data.

II. An Example of Finite Angular Sampling

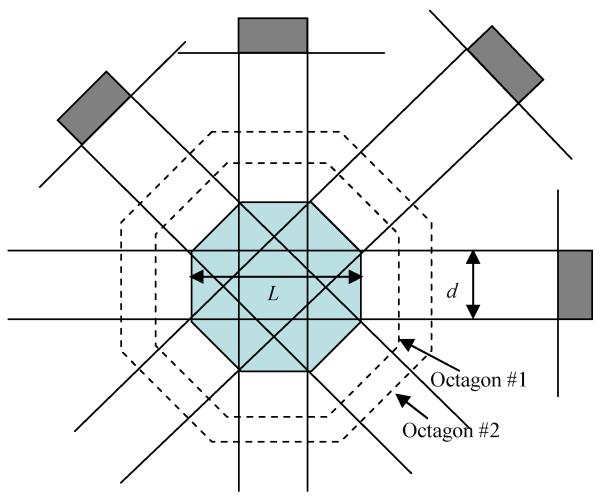
In this section, an example of finite angular sampling is presented to demonstrate that the reconstruction is not unique with truncated projections. The truncated projections are acquired at N (say, N=4) views uniformly sampled over 180°, as shown in Fig. 1. The projection values are equal to 1 in the untruncated central region for all views. The ROI (region-of-interest) is the common FOV (field-of-view) of all views.

Fig. 1.

An example of an octagon object with a varying size shows that the interior tomography problem is not unique with a finite number of views.

Many sizes of uniform octagons can be a solution of this problem (two of them, Octagon #1 and Octagon #2, are shown in Fig. 1 and any octagon larger than the shaded octagon is also a solution), as long as the linear density of the octagon is 1/L, and the side length d is at least the length of the detector. The image within ROI is identical to a constant 1/L. Those two octagons in Fig. 1 are both non-negative and piecewise-constant and both satisfy the same set of projection data. Therefore, the non-negativity and piecewise-constant constraints do not guarantee a unique solution. Extra information may be needed to ensure a unique solution. For example, if the average ROI value were given or a pixel value within the ROI were known, this information could be used (Kudo et al 2008).

If the data are truncated, the number of views is N over 180°, and the octagon side-length is d, the minimum flat-to-flat diameter L of the polygon is given by

$$L=\frac{d}{\tan \left(\frac{\pi }{2N}\right)}.$$ (1)

If the projection value is 1, any positive constant value less than or equal to 1/L can be a solution to the interior problem, and 1/L is defined as

$$\frac{1}{L}=\frac{1}{d}\tan \frac{\pi }{2N}.$$ (2)

Currently it is not clear whether there are other non-negative, piecewise-constant solutions than the uniform polygons satisfying the projections. Therefore, it is not guaranteed that the value 1/L given in (2) is the upper bound of the bias.

The potential bias value 1/L is related to the projection value. In this counter example, the projection value is assumed to be 1. If the projection value is p, then the upper bound of the bias will be p/L.

III. A Remedy for this polygon-type bias

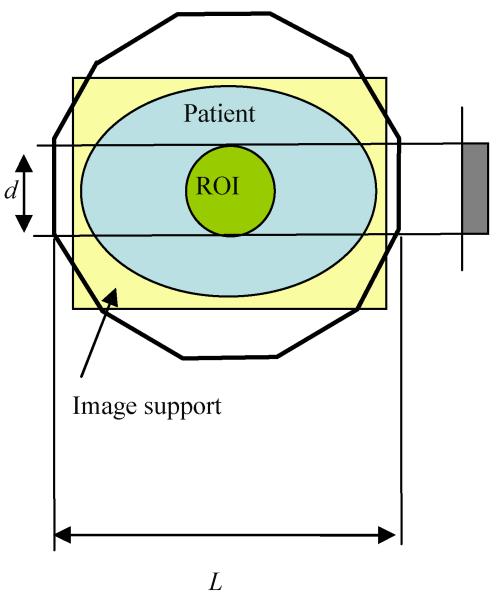
There may be many other (possibly even piecewise constant) null functions. The polygon-type constant bias can be easily removed. For example, one can choose a relatively large number N of view angles over 180°, and (1) implies that a large L is required to form the bias-causing polygon. If the image support is smaller than L, the bias-causing polygon (which is the large polygon shown in Fig. 2) cannot be formed. In fact, in practice this number N can be a very reasonable value. For example, if N = 30, (1) gives d/L= 5.2% This implies that even in the highly truncated situation where the detector width is 5.2% of the full image width with only 30 view angles, the polygon-type null space function can be forbidden.

Fig. 2.

If the number of angles is large enough, L will be large enough so that there exists an image support that contains the object (patient) but is within the polygon of diameter L. No bias-causing polygons are able to form within the image support.

The practical importance of this is that most applications of interior tomography would acquire a sufficient number of angles so that this non-uniqueness effect is never observed. However, one must be aware of the non-uniqueness problem if the number of views is small and/or the data are severely truncated (which results in a small ROI).

IV. Conclusions

The examples presented consider the uniqueness issue of the interior problem in tomography, with the non-negativity and piecewise-constant constraints. We must point out that the general non-uniqueness of a tomographic problem with finite views is well-known (Natterer 1986, Louis and Rieder 1989), and the general non-uniqueness issue (even without any data truncation) is due to the null-space function with high-frequency oscillation at the edge/boundary of an object. When we restrict that the objects and the solutions must be piecewise constant, the oscillation induced non-uniqueness phenomenon is ruled out. We claim that for a non-negative and piecewise-constant object, if the number of views is finite the solution to the interior problem is not unique even with the non-negative and piecewise-constant constraints. The presentation herein alerts the imaging engineers for potential image bias. The null-space functions may not be restricted to the constant polygons. However, the polygon-type bias can be removed easily by, for example, knowing one image value within the ROI, or using a sufficient number of views and a tight image support so that the polygon-type null space function cannot be formed.

This paper presents an example of null space functions that still exist with the non-negative and piecewise-constant constraints. This would mean that the result is applicable to arbitrary projections (not just constant projections). If a set of arbitrary truncated projections p(t,θ), with t and θ being linear and angular coordinates, can be decomposed into two parts: a constant “C” plus “p(t,θ)-C”, one can attempt to reconstruct two images, one by using “C” and the other one by using “p(t,θ)-C”. The final image is the sum image of these two reconstructions. It is clearly that the image reconstructed by using “C” is not unique.