Abstract
Two 13C-labeled isomers of the formal Diels−Alder adduct of acetylmethyloxirene to tetramethyl 1,2,4,5-benzenetetracarboxylate have been synthesized. Flash vacuum thermolysis of these adducts leads to various isotopic isomers of acetylmethylketene, the ratios of which have been determined by NMR. The surprising finding that the principal product comes from methylpyruvoyl carbene rather than its more stable isomer diacetylcarbene is explained by MPWB1K density functional calculations, which show that the reactant probably undergoes a unimolecular rearrangement to a norcaradiene derivative prior to its fragmentation. Coupled-cluster calculations on the methylpyruvoyl carbene show that it is capable of undergoing three unimolecular isomerizations. The fastest is 1,2-acetyl migration to give acetylmethylketene directly. The next is rearrangement via acetylmethyloxirene to diacetylcarbene and thence by Wolff rearrangement to acetylmethylketene. The least-favorable reaction is degenerate rearrangement via 1,3-dimethyl-2-oxabicyclo[1.1.0]butan-4-one (the epoxide of dimethylcyclopropenone). The combined experimental and computational results indicate that Wolff rearrangement of the diacetylcarbene occurs with a 2.5:1 ratio of the methyl groups despite the fact that they are related by a twofold axis of symmetry in the carbene. Preliminary molecular dynamics simulations are consistent with this conclusion. Taken together, the results suggest that the Wolff rearrangement is subject to the same kind of nonstatistical dynamical effects detected for other kinds of thermally generated reactive intermediates.
Introduction
This paper details a combined experimental and computational study designed to investigate the role, if any, of nonstatistical dynamics in the Wolff rearrangement of diacetylcarbene following its preparation from an oxirene precursor. The work is presented in a rather unorthodox narrative style. There are two reasons for this. First, the mechanistic picture at which we finally arrived is quite complex, and we believe that the reader will better appreciate the way in which this description evolved if it is presented with the missteps and corrections as they actually occurred along the way. Second, concern has been expressed recently about the unwillingness of some scientists to put in the time required to do a thorough job as peer reviewers.1 This story offers a reminder, in case one be needed, of how important good refereeing is to the advancement of science.
Discovery of Apparent Nonstatistical Dynamics for a Wolff Rearrangement
Design and Execution of the First Experiment
In recent years, experimental and computational evidence has revealed an important role for nonstatistical dynamics in the chemistry of several types of reactive intermediates.2 Thus far, the intermediates known to exhibit such behavior are singlet biradicals,3 radical cations,4 radicals,5 and carbocations.6 In the present study, we sought to investigate whether carbene chemistry might also be subject to these dynamical effects.
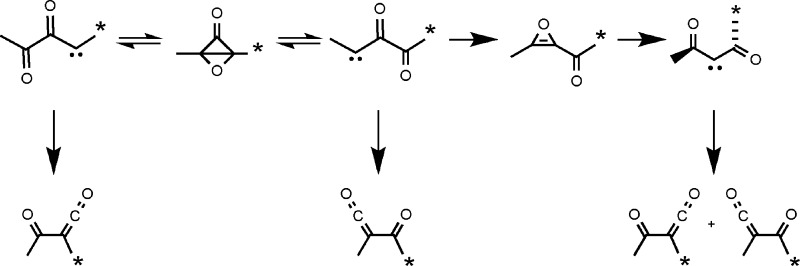
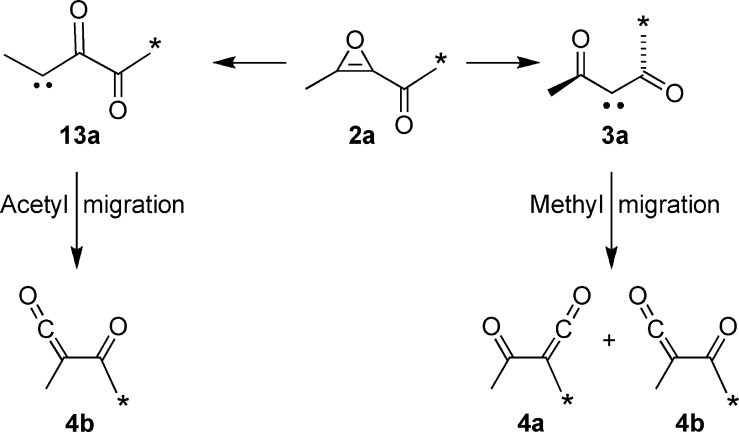
One criterion for the type of nonstatistical behavior7 seen in thermally generated organic intermediates has come from the application of a symmetry test.2 In this approach, one seeks to determine whether a new symmetry element generated by the formation of an intermediate from its precursor is expressed in the final product ratio, as statistical kinetic models would demand. Application of that test in the present study is illustrated by the formation of singlet diacetylcarbene 3a from acetylmethyloxirene 2a (Scheme 1), which in turn might be prepared by retro-Diels−Alder (rDA) fragmentation of precursor 1a. Aside from a small 13C isotope effect, statistical kinetic models would require that the ketene products 4a and 4b be formed in a 1:1 ratio because all of the electronic-structure methods examined give 3 exact or effective C2 symmetry in its minimum-energy conformation. (Here and in the following text, we use structure identifiers that include lower-case letters to indicate specific isotopomers and identifiers that are just numbers to indicate the unlabeled analogues or labeled compounds for which there is only a single isotopomer.) The hybrid density functional (DFT) models B3LYP/6-31+G(d,p)8 and O3LYP/6-31+G(d,p)9 found an exact C2 global minimum on the potential energy (PE) surface for 3, as did CCSD/cc-pVDZ calculations.10 The MPWB1K/6-31+G(d,p)11 DFT model found two equivalent C1 minima linked by the C2 structure as a transition state on the PE surface. However, the energy difference between the C2 and C1 geometries was only 0.09 kcal/mol, which was much less than the zero-point-energy (ZPE) difference between the two. Thus, with the ZPE correction, the C2 structure was also the minimum for the MPWB1K model.
Scheme 1. Precursor 1a, Whose Retro-Diels−Alder Reaction Was Designed To Release Oxirene 2a and Thence Carbene 3a (* Indicates the Site of a 13C Label).
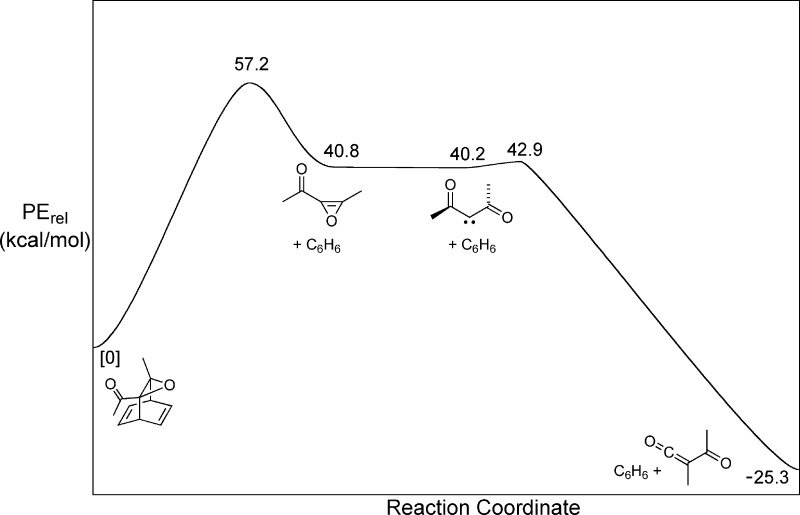
Precursor 1a was selected because the work of Lewars and Morrison12 provided good precedent for its synthesis and fragmentation and because MPWB1K/6-31+G(d,p) DFT calculations on a model for compound 1a lacking the carbomethoxy substituents suggested a PE profile (Figure 1) for the reaction sequence in Scheme 1 that might promote nonstatistical dynamics.13 In particular, the ∼16 kcal/mol drop in PE following the rate-determining step and the very small barriers for the ensuing unimolecular rearrangements suggested that the reactive intermediates involved could be generated with substantial selective excitation of certain vibrational modes and that formation of the final products might occur before energy relaxation by way of intramolecular vibrational redistribution (IVR) could reach completion.
Figure 1.
The MPWB1K/6-31+G(d,p) PE profile for retro-Diels−Alder fragmentation of an analogue of precursor 1a. A local minimum was found for the oxirene, but the barrier to its ring opening to the carbene was so low that no transition structure could be located.
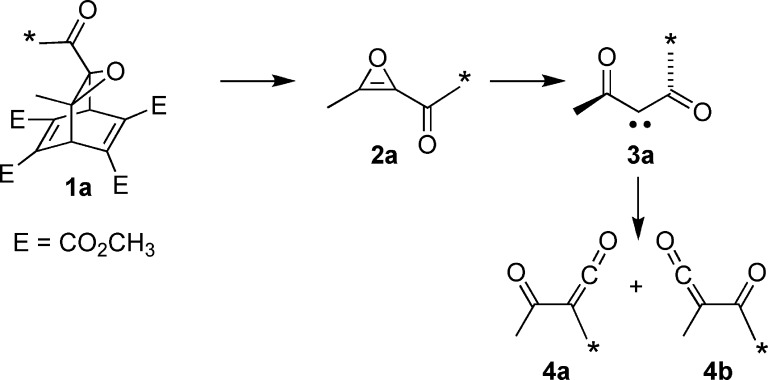
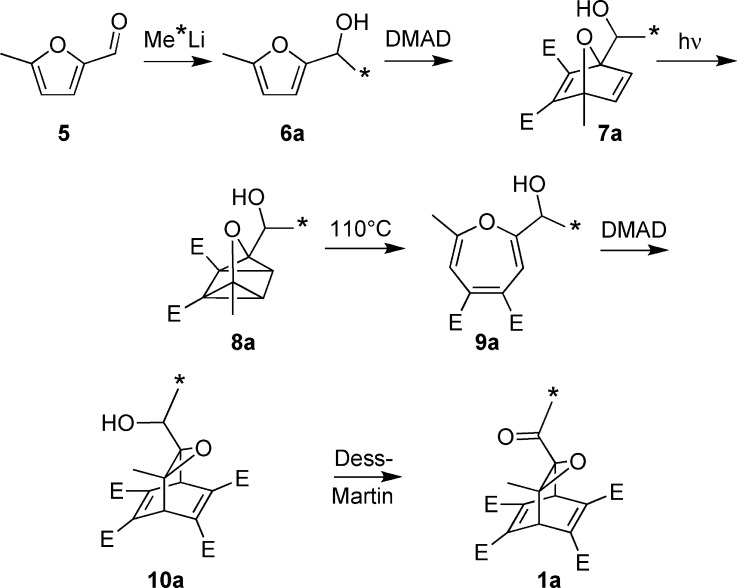
The synthesis of precursor 1a is summarized in Scheme 2 and described in detail in the Experimental Section. Compound 1a was subjected to flash vacuum thermolysis (650 °C, ∼0.3 Torr), and the resulting ketenes 4a and 4b were trapped by methanol to give the more stable methylacetoacetate isotopomers 11a and 11b (Scheme 3). Purification of the target compounds was facilitated by conversion of 11a and 11b to 12a and 12b, respectively, via pyridine reflux with methylhydroxylamine. The ratio of 12a to 12b was determined by proton and HSQC NMR experiments to be 1 to 4.5 ± 0.5.
Scheme 2. Synthesis of Precursor 1a (DMAD = Dimethylacetylenedicarboxylate; * Shows the Location of a 13C Label).
Scheme 3. Results of Thermolysis of Precursor 1a and Derivatization of the Resulting Ketenes (* Shows the Location of a 13C Label).
This result could be taken as evidence for nonstatistical dynamical behavior in the diacetylcarbene intermediate. However, it was recognized that the excess of 12b could in principle also be due to its parallel formation from asymmetric carbene 13a (Scheme 4). The MPWB1K calculations did not make the involvement of carbene 13 seem very likely, since its enthalpy was found to be 6.9 kcal/mol higher than that of carbene 3 at 25 °C. Nevertheless, since ketene 4b was seen to be the preferred product, it seemed prudent to carry out a control experiment to check for the involvement of carbene 13a.
Scheme 4. Possible Formation of Ketene 4b by Two Different Routes (* Shows the Location of a 13C Label).
Design and Execution of the Control Experiment
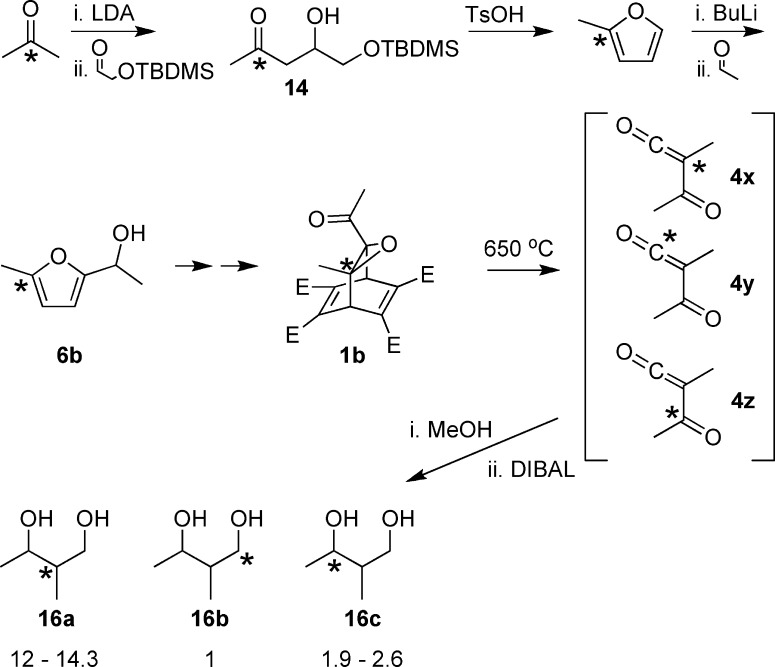
To determine whether the route via carbene 13 was a contributing factor in the ketene formation, a second isotopomer of the precursor (1b) was synthesized. The use of this precursor allowed discrimination among three distinct pathways to the products: the two symmetry-related routes through diacetylcarbene 3 as well as any that might occur via carbene 13. The second version of precursor 1 was synthesized in a similar fashion to the first. However, in this case, the 13C-methylfurfuryl alcohol 6b was generated by addition of the enolate of 13C-labeled acetone to (t-butyldimethylsilyloxy)acetaldehyde (Scheme 5). After acid-catalyzed removal of the protecting group and ring closure, the resultant methylfuran was deprotonated with butyllithium and added to acetaldehyde to give 6b.14 The remainder of the synthesis leading to 1b proceeded as for 1a.
Scheme 5. Synthesis and Thermolysis of a New Isotopomer of Precursor 1 (* Shows the Location of a 13C Label).
After the flash vacuum thermolysis experiment had been repeated with isotopomer 1b, the product methyl esters were reduced with DIBAL to 2-methylbutane-1,3-diol, allowing purification and analysis of 13C location by HSQC-AD NMR spectroscopy. As shown in Scheme 5, the remarkable result was that product 16a dominated, suggesting that the asymmetric carbene pathway was strongly favored over that via diacetylcarbene. However, discrimination between the two pathways derived from the symmetric diacetylcarbene 3 was still possible. The ratio of 16c to 16b was found to be 2.3 ± 0.4 to 1.
Interpretation of the Results from the Control Experiment
The finding that most of the ketene-derived products came from carbene 13 was a great surprise. The seeming discrepancy with the DFT calculations, which had predicted both kinetic and thermodynamic preferences for ring opening of oxirene 2 to diacetylcarbene 3, could not easily be explained away as a failure of the electronic-structure calculations because other methods gave similar results. For example, CCSD(T)/cc-pVTZ//CCSD/cc-pVDZ calculations placed carbene 13 8.7 kcal/mol above carbene 3 in enthalpy at 25 °C. Although the free energy difference at the reaction temperature was much smaller (0.5 kcal/mol in favor of 3), the calculations still did not explain the preference for reaction via 13.
One conceivable explanation could have been that following the rate-determining rDA transition state a bifurcation in the reaction path occurred,15 yielding branches leading monotonically down in PE to the two carbenes, as illustrated schematically in Figure 2. Under such circumstances, the yields of the carbenes need not be determined by their relative energies,16 although it had to be admitted that outside of an ill-defined dynamical effect, no obvious reason for preferential formation of carbene 13 could be offered.
Figure 2.
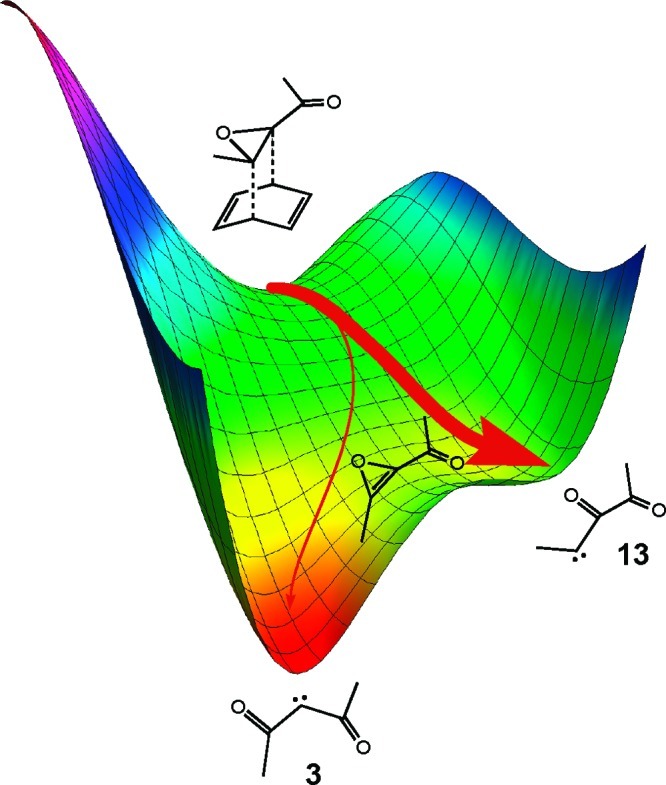
Schematic representation of a bifurcated potential energy surface that could in principle allow preferential reaction via the less-stable carbene.
Regardless of the explanation for the preferential formation of carbene 13, the ratio of products 16b and 16c seemed to require that the Wolff rearrangement of diacetylcarbene be subject to the nonstatistical dynamical effects that formed the basis for the whole study. Consequently, a communication was sent to this journal describing that result and using the bifurcation explanation for the unexpectedly favorable formation of the product from carbene 13.
Crucial Contribution from an Insightful Referee
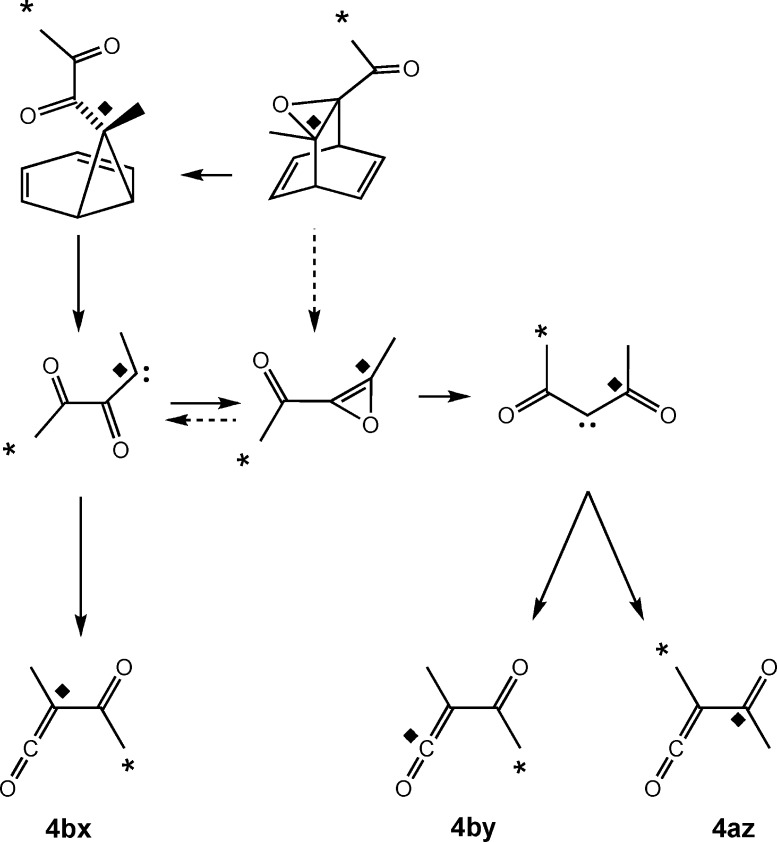
One of the reviewers for the manuscript of the intended communication, who subsequently identified himself as Professor Daniel Singleton of Texas A&M University, came up with an alternative explanation for the preferential formation of carbene 13. This explanation made the formation of 13 a necessary step in the formation of all of the label-isomeric ketenes and thereby elevated its importance from that assigned to it in our original explanation. Singleton’s mechanism involved a unimolecular rearrangement of the precursor 1 prior to its fragmentation. For the sake of clarity, the new mechanism is shown in Scheme 6 without the carbomethoxy substituents on the precursor or its rearrangement and fragmentation products.
Scheme 6. Singleton’s Mechanism for Rearrangement of Precursor 1 Prior to Fragmentation (The Curved Arrows Were Not Proposed by Singleton; Ester Substituents Have Been Omitted for Clarity).
If taken literally, the curved arrows in Scheme 6 (which were not proposed by Singleton) would imply that the first step was a poorly precedented σ2s + σ2s + π2s pericyclic reaction. Furthermore, the orbital alignment of the breaking C−O and C−C bonds would seem to be very unfavorable. Nevertheless, preliminary DFT calculations carried out by Singleton suggested a barrier for the rearrangement that was far lower that the one for the intended retro-Diels−Alder reaction of the precursor. We confirmed that conclusion with calculations at the MPWB1K/6-31+G(d,p) level. The computed enthalpies at 298 K are shown in Figure 3.
Figure 3.
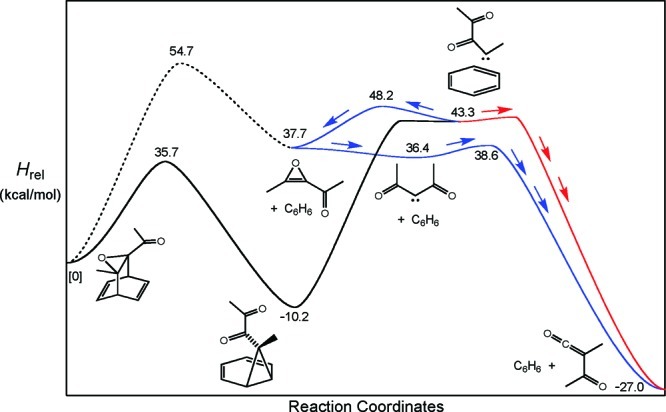
Summary of MPWB1K results comparing the originally intended retro-Diels−Alder reaction (dashed curve) with the Singleton rearrangement (solid black curve). The principal and secondary mechanisms for formation of acetylmethylketene are shown by the red and blue pathways, respectively.
In hindsight, one can perhaps rationalize the unexpected facility of the rearrangement by identifying it as a pseudopericyclic17 rather than a truly pericyclic reaction. The hypothetical electron transfers in the pseudopericyclic process are shown schematically in Figure 4. The implication is that for the C−C bond, σ and σ* orbitals are involved in the reaction, while the C=C bond uses π and π* orbitals. However, the C−O bond uses a p-type lone-pair orbital (np) and the σ* orbital instead of the σ and σ* orbitals. The orthogonality between np and σ* leads to the pseudopericyclic classification17a and circumvents the orbital-alignment problems that the truly pericyclic process would seem to face. The implication of this analysis is that the analogous rearrangement would be much more difficult if the reactant had a cyclopropane in place of the oxirane ring. That prediction has not been pursued.
Figure 4.
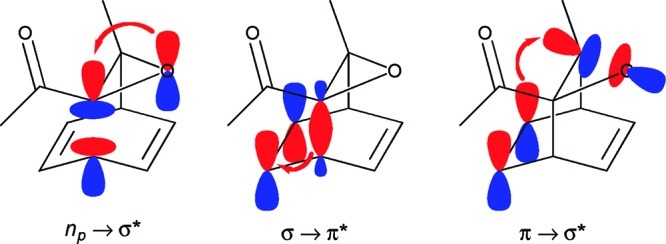
Decomposition of the Singleton rearrangement into three hypothetical electron-pair transfers. The np → σ* transfer identifies the reaction as a pseudopericyclic process.
The alternative sense of the Singleton rearrangement, leading to 7,7-diacetylnorcaradiene, was also investigated. The free energy of the transition state at the reaction temperature was found to be 9.8 kcal/mol higher than that for the rearrangement shown in Figure 3, so this pathway was not explored further.
The calculations strongly suggested that the originally intended rDA reaction of precursor 1 would not be able to compete with Singleton’s rearrangement. Initially that seemed not to be of great concern for the original purpose of the study, since the label distribution in the products still required that some of the ketenes be formed by methyl migration from diacetylcarbene. The diacetylcarbene could now be seen to have come from carbene 13, but the oxirene mediating that reaction would be exactly the same (including label positions in both experiments) as that from the original rDA reaction (Scheme 7).
Scheme 7. Summary of the Two Labeling Experiments and the Various Mechanisms for Formation of Acetylmethylketene 4.
The dashed arrows show the originally intended retro-Diels-Alder route from the precursor. The solid arrows show the route via the Singleton rearrangement. The separate 13C labels are shown by * and ◆ symbols.
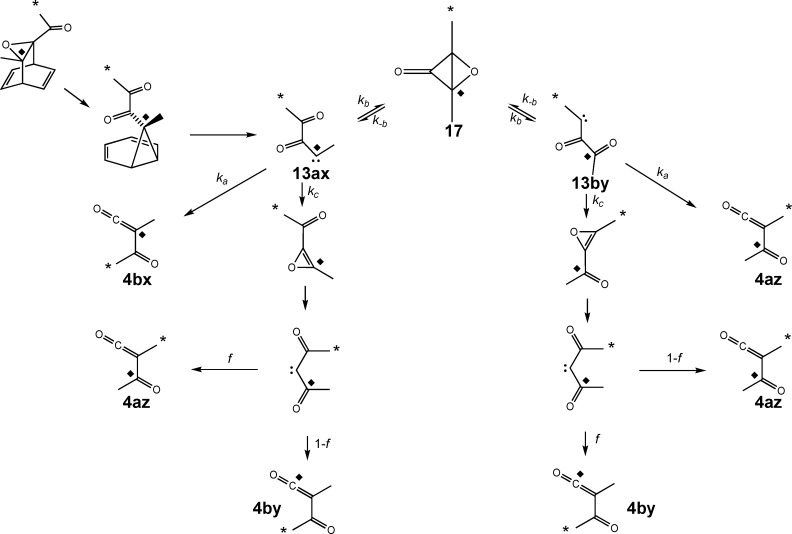
Nevertheless, the fact that carbene 13 now played a more central role than was originally believed made it seem worthwhile to explore its properties thoroughly using electronic-structure calculations. In particular, we became concerned that a prospective degenerate rearrangement of carbene 13 via intermediate 17 or 18 (Scheme 8) could lead to label scrambling that would further complicate the interpretation of the experiments.
Scheme 8. Potential Label Scrambling in Carbene 13 by an Additional Unimolecular Rearrangement (* and ◆ Show the Sites of 13C Labels in the Two Separate Experiments).
Kinetic Analysis and Computational Investigation of Unimolecular Rearrangements of Carbene 13
The isomerization of carbene 13 to diacetylcarbene 3 via oxirene 2 could be viewed as either an analogue of an intramolecular cyclopropanation reaction or as a nucleophilic addition by the carbonyl oxygen to the carbene carbon. But carbene 13 has two carbonyls. What would happen if the distal carbonyl were to be involved in similar reactions? The cyclopropanation would generate the epoxide of dimethylcyclopropenone (17), whereas the nucleophilic addition would generate the singlet oxyallyl 18. In either case, reversion of the reaction would lead to label scrambling and potential complication of the interpretation of the experiments (Scheme 8). MPWB1K/6-31+G(d,p) calculations (using a broken-symmetry unrestricted wave function for 18) showed a clear preference for 17 over 18, the enthalpy difference at 25 °C being 11.4 kcal/mol. This is consistent with the results from earlier calculations on bicyclo[1.1.0]butanone and its oxyallyl isomer.18 Consequently, in the higher-level calculations, only isomer 17 was considered.
The potential complicating consequences of isomerization via 17 are shown in Scheme 9. The experimental results from the two 13C-labeling studies place constraints on some of the rate-constant ratios in this mechanism and on the crucial fractionation factor, f, which defines the symmetry test described at the beginning of this paper. A value of 0.5 for f would mean statistical behavior of the diacetylcarbene, whereas other values would imply that the methyl groups had retained dynamical “memory” of their origins on the ring or on the acetyl group of the preceding oxirene.
Scheme 9. Consequences of the Potential Isomerization via Intermediate 17 for the Label Distribution in Ketene 4 (* and ◆ Show the Separate 13C Labels).
Simultaneous application of the steady-state approximation to the concentrations of carbene 13by and intermediate 17 allows one to write eq 1:
| 1 |
The results from the two experiments were simultaneously best fit by the conditions [4bx]/([4az]+[4by]) = 5.0 and [4az]/[4by] = 2.6. These constraints and the steady-state result lead to eqs 2 and 3,
 |
2 |
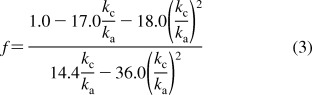 |
3 |
which are depicted graphically in Figures 5 and 6. These graphs show that the ratio of mechanistic rate constants kc/ka has an upper bound of 0.2 (above which the ratio kb/ka becomes negative) and a lower bound of ∼0.056 (below which f becomes negative).
Figure 5.

Experimental constraints on the relationship between the rate-constant ratios kb/ka and kc/ka. The dashed lines show the values required for these two ratios if the Wolff rearrangement of carbene 3 were to occur as expected by statistical kinetic models (i.e., with f = 0.5). The horizontal and vertical red lines, respectively, show the independently assessed values of kb/ka and kc/ka from coupled-cluster calculations.
Figure 6.

Experimental constraints on the relationship between the fractionation factor f and the rate-constant ratio kc/ka. The dashed lines show the values required for these two quantities if the Wolff rearrangement of carbene 3 were to occur as expected by statistical kinetic models (i.e., with f = 0.5). The red lines show the value of f associated with the estimate of kc/ka from coupled-cluster calculations.
If the Wolff rearrangement of diacetylcarbene were properly described by statistical kinetic models, then f = 0.5 (ignoring small 13C isotope effects, as mentioned above), which would imply that kc/ka = 0.102 and kb/ka = 0.215. Because this value of kc/ka lies within the previously defined bounds, the statistical interpretation of the data cannot be ruled out on purely experimental grounds. In order to assess its viability, we consequently set about calculating the barriers to the three unimolecular reactions of carbene 13 at the highest level of theory that was computationally feasible with the available resources. The model selected was CCSD(T)/cc-pVTZ//CCSD/cc-pVDZ with MPWB1K/6-31+G(d,p) evaluation of the ZPE and thermal corrections. A more complete description of the calculations is provided in Computational Details.
The computed free energy differences at 650 °C are depicted graphically in Figure 7. The calculations made possible independent estimates of kc/ka and kb/ka, indicated by the vertical and horizontal red lines, respectively, in Figure 5. The fact that these lines intersect close to the experimental curve provides some evidence that the calculations are reliable. The values found for kc/ka and kb/ka (0.194 and 0.024, respectively) were far from those required if f = 0.5. In fact, f was calculated to be 0.717, corresponding to a ratio of 2.5:1 for migration of the erstwhile acetyl and ring methyl groups.
Figure 7.
Free energy profiles at 650 °C for the unimolecular rearrangements of carbene 13, as obtained from CCSD(T)/cc-pVTZ//CCSD/cc-pVDZ calculations.
Preliminary Molecular Dynamics Simulations
An investigation employing molecular dynamics (MD) simulations to explore the rearrangement of carbene 13 to carbene 3 and thence to acetylmethylketene is currently underway. Although much more work is required before a thorough understanding of the reaction dynamics can be claimed, the preliminary results are reported here because they provide an interesting complement to the results of the experiments and electronic-structure calculations.
Direct dynamics calculations were carried out with quasiclassical normal-mode sampling from a canonical ensemble at 923 K (the experimental reaction temperature). Three different DFT models were used (B3LYP,8 O3LYP,9 and MPWB1K11a), all with a 3-21G basis set. The small basis set for these initial calculations was used in order to permit a reasonable number of trajectories to be run in a reasonable amount of time. Larger-scale calculations are currently in progress.
For each simulation, the starting point was located in the vicinity of the transition state for rearrangement of carbene 13 to carbene 3 via oxirene 2. A total of 300 trajectories were run, 100 for each DFT model. This is not a large enough sample to make quantitative predictions, but at this stage, our interest was only in detecting qualitative trends. Each trajectory was run for 500 fs. Four different outcomes were found. Some trajectories led to formation of carbene 3 followed by a shift of the C1 methyl group to make the final product. Some led to carbene 3 followed by a shift of the C5 methyl group. Some made it to carbene 3 but did not undergo the Wolff rearrangement in the allocated 500 fs time span. It was assumed that these trajectories would eventually have led to the ketene product with an equal probability of C1 and C5 methyl migrations. Finally, some of the trajectories underwent barrier recrossings, returning to carbene 13 and then in most cases undergoing an acetyl migration. In the calculation of the fractionation factor, f, the recrossing trajectories were ignored. The results of the calculations are summarized in Table 1.
Table 1. Results of Preliminary MD Simulations on the Rearrangement of Carbene 13 to Carbene 3 Followed by Wolff Rearrangementa.

| DFT model |
|||
|---|---|---|---|
| B3LYP | O3LYP | MPWB1K | |
| number of C1 shifts | 13 | 27 | 7 |
| number of C5 shifts | 69 | 54 | 79 |
| number failing to form product in 500 fs | 8 | 12 | 8 |
| number of recrossings | 10 | 7 | 6 |
| f | 4.3 | 1.8 | 7.6 |
All of the calculations used the 3-21G basis set.
Clearly, all three DFT models predict preferred migration of the C5 methyl, although the fractionation factors differ widely for the different descriptions of the PE surface. The ongoing work seeks to understand the reasons for the C5 preference and the factors that lead to the varying quantitative predictions. In addition, the dependence of the fractionation factor on the lifetime of carbene 3 is being explored.4 Although a fuller understanding of the dynamics must await the results from this additional work, it seems safe to conclude that the preliminary results are qualitatively consistent with the value of f = 2.5 deduced from the experimental studies and coupled-cluster calculations.
Computational Details
Most of the electronic-structure calculations used for the present work employed the MPWB1K density functional of Zhao and Truhlar11a with a 6-31+G(d,p) basis set.11 This functional has been reported to be superior to commonly used alternatives such as B3LYP for the calculation of activation barriers of typical organic reactions.11a
For the critical calculations on the unimolecular rearrangements of carbene 13, the coupled-cluster model CCSD(T)/cc-pVTZ//CCSD/cc-pVDZ was employed,10 although MPWB1K was used to compute the ZPE and thermal corrections. The suitability of the DFT model for the vibrational calculations was assessed by comparing its results with those from CCSD/cc-pVDZ for one case, namely, intermediate 17. Lack of analytical second derivatives for the coupled-cluster method made it too time-consuming to use for the vibrational calculations at each stationary point. The ratios of individual frequencies for 17 at the CCSD and DFT levels averaged 0.96, which we took to be the scale factor for use with the DFT method on the other species.
Because the experimental studies were conducted at a high temperature (650 °C), it was recognized that some of the internal rotational modes of the species involved might be poorly described by the default harmonic oscillator model. Those rotors for which the barrier was lower than kBT were treated separately with free-rotor partition functions. Their contributions to the energy of the system were set to RT/2 for each rotor, and their contributions to the entropy were calculated from the formula
| 4 |
where σi is the internal symmetry number for the rotor and Ir is its reduced moment of inertia. It is quite likely that the most accurate estimates of E and S for the two carbenes (3 and 13) would involve the use of hindered-rotor partition functions for internal rotations about the bonds to the divalent carbons. However, this was not pursued in the present work because the result would have no effect on the critical issue of the relative barrier heights for the three unimolecular rearrangements.
Experimental Section
General Considerations
Moisture-sensitive reactions were performed in flame-dried glassware under a dry nitrogen atmosphere. All of the reagents were purchased from Aldrich or Acros. All of the 13C-labeled compounds were obtained from Cambridge Isotope Laboratories. Solvents were purchased from Fisher Scientific. Dry THF was obtained by distillation from sodium benzophenone ketal or obtained dry from Glass Contour solvent purification columns. Anhydrous methanol was used as purchased for the flash vacuum thermolysis trials without any decrease in yield. Diisopropylamine was stored over 4 Å molecular sieves.
Proton NMR spectra were obtained using Varian Mercury-300, Inova-400, Inova-500, and Inova-600 spectrometers, and 13C NMR spectra were obtained using the Mercury-300, Inova-400, and Inova-500 instruments. All of the spectra were referenced to solvent peaks. Mass spectra were obtained on a JEOL GCMate II with EI+ ionization.
Photolysis reactions were performed using an Ace-Hanovia 450 W medium-pressure mercury arc lamp, cooled with a quartz water-flow jacket.
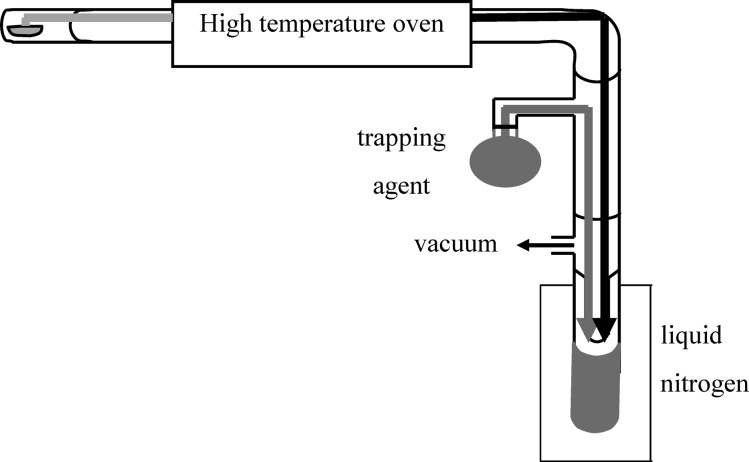
Flash Vacuum Thermolysis
The components of the system are shown in Figure 8. The sample chamber and the tube passing through the oven were both made of quartz. The oven was a Lindberg/Blue M Mini-Mite Tube Furnace. Before the cold trap region was an attachment that allowed trapping agent to flow through the latter part of the apparatus and cocondense with the thermolysate in the cold trap. All of the glass surfaces were silanized twice with triethylamine and trimethylsilyl chloride to prevent reactions at the surface. The top of the trap was connected to a vacuum pump.
Figure 8.
Flash vacuum thermolysis apparatus.
A flash vacuum thermolysis experiment began when precursor material was placed in the sample chamber. For each analysis, the thermolysates from two trials were grouped, each trial beginning with 0.35 g of precursor material. A large amount of material was necessary because of the large number of products formed. Trapping agent (anhydrous methanol, 105 mL) was placed in the trap, and an additional 15 mL was placed in a round-bottom flask on the attachment to flow through the system to the trap. The total amount of trapping agent was chosen to ensure that after the flow-through solvent had condensed into the cold trap, the solvent level would be just under the entry tube. The methanol in the trap was frozen using a Dewar flask containing liquid nitrogen. After ∼1 min, the vacuum pump was then turned on (∼300 mTorr). The trapping agent was left to flow through the system into the first cold trap for 1 h. The thermolysis oven was turned on and set to 650 °C during the latter part of this hour, and heating tape was wrapped around the sample chamber with care taken to cover all of the surfaces preceding entry into the oven. Once the first hour had elapsed, the heating tape was turned on through a Variac (set at 55 V to give a temperature of ∼170 °C) to slowly volatilize the precursor material so it could move through the oven. After 1 h of heating the sample, the oven, heating tape, and vacuum pump were turned off and the liquid nitrogen traps removed. The product mixture was left to slowly warm to room temperature (∼1 h), and volatile trapping material (solvent) was removed by rotary evaporation to give crude thermolysate product for analysis, purification, or derivatization.
Synthesis and Characterization
It should be noted that because of the use of 13C labeling, trace impurities often showed strong peaks in the 13C spectra. All of the peak assignments were made by comparison to unlabeled material.
1-(5-Methylfuran-2-yl)ethanol-2-13C (6a)
13C-labeled 6a, leading to precursor 1a, was synthesized by generating 13C-labeled methyllithium from n-butyllithium and methyl iodide. Two three-neck round-bottom flasks, one 100 mL and the other 250 mL, were flame-dried and placed under nitrogen. n-Butyllithium (1.2 M in hexanes, 38 mL, 45 mmol) was added to the 100 mL flask and cooled in an ice bath. 13C-labeled methyl iodide was slowly added to the n-butyllithium by syringe. Because of the high volatility of methyl iodide, it tended to leak out of the syringe. To prevent this, a syringe valve was placed between the syringe and the needle to prevent movement of fluid from the syringe into the needle before injection. The solution was stirred in the ice bath for 3 min and then at room temperature for 20 min. Freshly distilled methylfurfural (7.71 g, 70 mmol) was placed in the 250 mL flask with dry THF (50 mL), and the mixture was cooled in an acetone/dry ice bath. The synthesized 13C-methyllithium mixture from the 100 mL flask was slowly added to the 250 mL flask. The syringe valve was again useful in making this transfer. The reaction mixture was stirred in the gradually warming bath for 2.5 h. A saturated solution of sodium chloride (30 mL) was slowly added to quench the reaction. The aqueous layer was extracted three times with ethyl acetate (50 mL). The combined organic layers were briefly dried over magnesium sulfate, and after removal of the solvents, the crude material was immediately used in the following Diels−Alder reaction.
Dimethyl 1-(1-Hydroxyethyl-2-13C)-4-methyl-7-oxabicyclo[2.2.1]hepta-2,5-diene-2,3-dicarboxylate (7a)
The alcohol from the previous reaction (30.2 mmol for 100% yield) was placed in a 100 mL round-bottom flask with dimethylacetylene dicarboxylate (5.66 g, 39.0 mmol) and toluene (20 mL). The mixture was refluxed for 14 h. After removal of the solvent, the crude brown oil was purified by column chromatography (1:1 ether/pentane) to give 7a as an orange oil (7.14 g, 88.1% yield over two reactions).
1H NMR (500 MHz, CDCl3) for both diastereomers (present in a ratio of ∼3:2): δ 1.15−1.46 (2 × dd, J = 6.3, 27.4 and 6.3, 27.0 Hz, 3H for each diastereomer); 1.75 and 1.79 (2 × s, 3H for each); 3.78, 3.80, 3.82, and 3.83 (4 × s, 6H for each); 4.47−4.55 (m, 1H for each); 6.94−7.25 (m, 2H for each).
Dimethyl 2-(1-Hydroxyethyl-2-13C)-4-methyl-3-oxatetracyclo[3.2.0.02,7.04,6]heptane-1,5-dicarboxylate (8a)
Alcohol 7a (13.78 g, 51.4 mmol) was placed in dry THF (∼900 mL) in an immersion-well photolysis apparatus. The lamp was enclosed in a vycor-glass sleeve. The solution was degassed by bubbling argon through the solution for 90 min and continuously throughout the reaction. The solution was irradiated for 14 h at room temperature. As the product 8a was not stable to column chromatography, after solvent removal it was used for further reaction without purification.
Dimethyl 1-(1-Hydroxyethyl-2-13C)-7-methyloxepin-4,5-dicarboxylate (9a)
Alcohol 8a (51.4 mmol for 100% yield from the previous reaction) was placed in toluene (650 mL) and refluxed for 3 h. After removal of the solvent, the crude material was purified by column chromatography (3:2 ether/pentane), giving 9a as an orange-red oil (8.58 g, 62.3% yield over two reactions). Although the oxepin 9a was in equilibrium with the benzene oxide form, NMR information showed that the oxepin structure was favored at room temperature in chloroform.
1H NMR (500 MHz, CDCl3): δ 1.24−1.51 (dd, J = 6.8, 127.7 Hz, 3H), 1.97 (s, 3H), 2.46 (br s, 1H), 3.75 (s, 3H), 3.76 (s, 3H), 4.18 (br m, 1H), 5.60 (s, 1H), 5.92 (s, 1H). 13C NMR (75.4 MHz, CDCl3): δ 20.8 (highly intense), 21.6, 52.7, 52.8, 68.4 (d, J = 38.6 Hz), 109.3, 110.9, 132.9, 135.7, 158.0, 160.8, 167.4, 167.9.
Tetramethyl 2-(1-Hydroxyethyl-2-13C)-4-methyl-3-oxatricyclo[3.2.2.02,4]nona-6,8-diene-6,7,8,9-tetracarboxylate (10a)
Alcohol 9a (3.47 g, 12.9 mmol) was placed in toluene (20 mL) with dimethylacetylene dicarboxylate (2.57 g, 18.1 mmol) and refluxed for 38 h. After removal of the solvent, the material was purified by column chromatography (1:1 ethyl acetate/pentane) to give 10a as a yellow oil (3.74 g, 70.6%) that solidified on standing. Because of the viscous nature of the oil, care was taken in removing the solvent to prevent the oil from bumping and coating the rotary evaporator attachment. Both diastereomers (∼3:1 ratio) were visible by TLC and NMR.
1H NMR (300 MHz, CDCl3): δ 1.11 (dd, J = 6.7, 27.2 Hz, minor diastereomer, 3H), 1.35 (d, J = 6.4, 27.3 Hz, major diastereomer, 3H), 1.58 (s, minor diastereomer, 3H), 1.59 (s, major diastereomer, 3H), 3.80−3.88 (8 s but difficult to distinguish, 4 peaks each for the major and minor diastereomers, 3H per peak), 3.89−3.95 (m, 1H for each diastereomer), 4.34 (s, minor diastereomer, 1H), 4.38 (s, major diastereomer, 1H), 4.66 (s, major diastereomer, 1H), 4.83 (s, minor diastereomer, 1H). 13C NMR (75.4 MHz, CDCl3), presumed major diastereomer peaks only: δ 15.3, 19.0 (intense), 45.9, 51.9, 52.9, 53.0, 53.0, 53.1, 65.7, 66.8 (weak d), 68.2, 138.1, 139.0, 144.8, 145.8, 165.0, 165.0, 165.4, 165.6. HRMS (EI): calcd for C1813CH22O10, m/z 411.1246; measured, m/z 411.1241; fit, −1.2 ppm.
Tetramethyl 2-(Acetyl-2-13C)-4-methyl-3-oxatricyclo[3.2.2.02,4]nona-6,8-diene-6,7,8,9-tetracarbox-ylate (1a)
The Dess−Martin periodinane (5.00 g, 11.8 mmol) was placed in a 100 mL round-bottom flask with dry dichloromethane (50 mL) under nitrogen. Alcohol 10a (3.52 g, 8.58 mmol) in dichloromethane (15 mL) was added by syringe, and the solution was stirred for 70 min. Mild heat (∼30 °C) improved the reaction yield. The mixture was poured into an Erlenmeyer flask containing 50 mL of a 1:1 mixture of dilute sodium thiosulfate solution and saturated sodium bicarbonate solution, forming a milky solution. The liquid was vigorously stirred for 15 min, by which point the mixture no longer appeared milky. The organic layer was washed once with sodium thiosulfate/sodium bicarbonate solution (30 mL), once with water (30 mL), and once with brine (30 mL) and then dried for 30 min over sodium sulfate. After removal of the solvent, the product was purified by column chromatography (2:1 ether/pentane) with initial loading of the column done with a dichloromethane solution of the crude material. Upon removal of the solvent from the column fractions containing the product, a white powdery solid formed provided the rotary-evaporator water bath was kept fairly cool. This solid was rinsed from the flask with ether, filtered, and washed with cold ether to give precursor 1a as a white powder (2.99 g, 85.3%).
1H NMR (300 MHz, CDCl3): δ 1.68 (s, 3H), 2.19 (d, J = 129.2 Hz, 3H), 3.81 (s, 3H), 3.81 (s, 3H), 3.81 (s, 3H), 3.87 (s, 3H), 4.39 (s, 1H), 4.77 (s, 1H). 13C NMR (75.4 MHz, CDCl3): δ 15.8, 27.3 (intense), 47.7, 52.5, 53.0, 53.0, 53.0, 53.0, 68.7, 69.5 (d, J = 13.8 Hz), 138.9, 138.9, 144.4, 144.5, 164.2, 164.6, 164.7, 165.6, 204.0 (weak d). HRMS (EI): calcd for C1813CH20O10, m/z 409.1090; measured, m/z 409.1082; fit, −1.9 ppm.
5-(tert-Butyldimethylsilyloxy)-4-hydroxypentan-2-one-2-13C (14)
Diisopropylamine (3.60 g, 35.6 mmol) and dry THF (100 mL) were placed in a flame-dried 250 mL round-bottom flask under nitrogen. The solution was cooled in an acetone/dry ice bath. N-Butyllithium (22.25 mL, 1.6 M, 35.6 mmol) was added slowly, and the mixture was stirred for 10 min. A solution of acetone-2-13C (2.00 g, 33.9 mmol) in THF (6 mL) was then added by syringe pump over 10 min. After 30 min of stirring, (tert-butyldimethylsilyloxy)acetaldehyde (6.21 g, 35.6 mmol) was slowly added, and the mixture was stirred for an additional 40 min. While the mixture was still in the cold bath, the reaction was quenched with the addition of a saturated aqueous solution of ammonium chloride. The mixture was extracted three times with ethyl acetate, and the combined organic layers were washed once with a saturated aqueous solution of sodium chloride and dried over magnesium sulfate. After removal of the solvent, the crude product was purified by column chromatography (1:2 ether/pentane) to give 14 (5.50 g, 70%) as a colorless oil.
1H NMR (500 MHz, CDCl3): δ 0.07 (s, 3H), 0.07 (s, 3H), 0.90 (s, 9H), 2.20 (d, J = 5.9 Hz, 3H), 2.61 (t, J = 5.4 Hz, 2H), 2.86 (d, J = 4.4 Hz, 1H), 3.52−3.61 (m, 2H) 4.09 (m, 1H). 13C NMR (100 MHz, CDCl3): δ −5.2, −5.2, 18.5, 26.1, 30.0 (d, J = 41 Hz), 46.6 (d, J = 40 Hz), 66.4 (d, J = 1.9 Hz), 68.4 (d, J = 1.9 Hz), 208.7 (high intensity).
HRMS (EI) showed loss of the t-butyl group: calcd for C613CH15O3Si, m/z 176.0824; measured, m/z 176.0826; fit, 1.0 ppm.
2-Methylfuran-2-13C
Compound 14 (6.73 g, 28.8 mmol) was placed in a stoppered 250 mL round-bottom flask with diethyl ether (12 mL) and p-toluenesulfonic acid monohydrate (0.553 g, 2.91 mmol). The mixture was stirred overnight, after which 2 mL of hexanes was added and the solvents and product distilled into a round-bottom flask cooled in an acetone/dry ice bath (distillate up to 115 °C was collected). The distillate was dried over magnesium sulfate but was not further purified because of its volatility.
1-(5-Methylfuran-2-yl-5-13C)-ethanol (6b)
The distilled methylfuran (28.8 mmol for 100% yield) and ether from the previous step was placed in a flame-dried 100 mL three-necked round-bottom flask under nitrogen. Dry THF (4 mL) was added, bringing the total volume of the solution to ∼20 mL. The solution was cooled in an ice bath, and n-butyllithium (1.6 M in hexanes, 18.0 mL, 28.8 mmol) was added. The mixture stirred at room temperature for 3 h and then placed back into an ice bath, and a solution of acetaldehyde (1.50 g, 34.1 mmol) in dry THF (4 mL) was added. After the mixture was stirred at room temperature for 3 h, 10 mL of ammonium chloride solution was added. The aqueous layer was extracted three times with ethyl acetate (20 mL), and the combined organic extracts were washed with brine and briefly dried over magnesium sulfate.
As in the synthesis of the other isotopomer of 7, after removal of solvent, 6b was used immediately in a Diels−Alder reaction to generate 7b. This reaction gave 1.46 g of labeled product (20.5% over three steps). Subsequent synthetic steps were performed as described above. The analytical data for the resulting isotopomers 7b, 9b, 10b, and 1b are listed below.
Dimethyl 1-(1-Hydroxyethyl)-4-methyl-7-oxabicyclo[2.2.1]hepta-2,5-diene-2,3-dicarboxylate-4-13C (7b)
1H NMR (400 MHz, CDCl3) for both diastereomers (∼5:4 ratio): δ 1.25−1.31 (two sets of doublets, J = 6.4, 6.6 Hz, 3H for each diastereomer); 1.73 and 1.76 (2 × d, J = 5.5, 5.5 Hz, 3H for each); 3.75, 3.77, 3.79, and 3.80 (4 × s, 6H for each); 4.45−4.52 (m, 1H for each); 6.90−7.23 (m, 2H for each).
Dimethyl 2-Acetyl-7-methyl-7-oxepin-4,5-dicarboxylate-13C (9b)
1H NMR (500 MHz, CDCl3): δ 1.38 (d, J = 6.3 Hz, 3H), 1.97 (d, J = 7.3 Hz, 3H), 2.46 (br s, 1H), 3.75 (s, 3H), 3.75 (s, 3H), 4.18 (q, J = 6.8 Hz, 1H), 5.60 (d, J = 5.5 Hz, 1H), 5.92 (s, 1H). 13C NMR (125.7 MHz, CDCl3): δ 20.8, 21.6 (d, J = 51.9 Hz), 52.8, 52.8, 68.3, 109.2, 110.9 (d, J = 80.9 Hz), 132.9, 135.7, 158.0 (intense), 161.0, 167.4, 167.9.
Tetramethyl 2-(1-Hydroxyethyl)-4-methyl-3-oxatricyclo[3.2.2.02,4]nona-6,8-diene-6,7,8,9-tetra-carboxylate-4-13C (10b)
1H NMR (400 MHz, CDCl3): δ 1.11 (d, J = 6.7 Hz, minor diastereomer, 3H), 1.34 (d, J = 6.4 Hz, major diastereomer, 3H), 1.56 (d but partially buried, minor diastereomer, 3H), 1.58 (d, J = 5.7 Hz, major diastereomer, 3H), 3.80−3.88 (8 s but difficult to distinguish, 4 peaks each for the major and minor diastereomers, 3H per peak), 3.85−3.90 (m, 1H for each diastereomer), 4.32 (d, J = 2.5 Hz, minor diastereomer, 1H), 4.36 (d, J = 2.7 Hz, major diastereomer, 1H), 4.66 (d, J = 3.9 Hz, major diastereomer, 1H), 4.81 (d, J = 3.9 Hz, minor diastereomer, 1H). 13C NMR (75.4 MHz, CDCl3), presumed major diastereomer peaks only: δ 15.3 (d, J = 48.8 Hz), 19.0, 45.9, 51.9 (d, J = 36.0 Hz), 52.9, 53.0, 53.0, 53.1, 65.8 (intense), 68.2 (weak d), 138.1, 139.1, 144.8, 145.9, 165.0, 165.0, 165.4, 165.6. HRMS (EI): calcd for C1813CH22O10, m/z 411.1256; measured, m/z 411.1241; fit, 2.4 ppm.
Tetramethyl 2-Acetyl-4-methyl-3-oxatricyclo[3.2.2.02,4]nona-6,8-diene-6,7,8,9-tetracarboxylate-4-13C (1b)
1H NMR (500 MHz, CDCl3): δ 1.68 (d, J = 5.9 Hz, 3H), 2.19 (s, 3H), 3.80 (s, 3H), 3.80 (s, 3H), 3.81 (s, 3H), 3.86 (s, 3H), 4.38 (d, J = 2 Hz, 1H), 4.76 (d, J = 3.9 Hz, 1H). 13C NMR (125.7 MHz, CDCl3): δ 15.8 (d, J = 48 Hz), 27.3, 47.7, 52.5 (d, J = 35.8 Hz), 53.0, 53.0, 53.0, 53.0, 68.8 (highly intense), 69.7, 138.9, 139.0, 144.4, 144.5, 164.2, 164.6, 164.7, 165.6, 204.0. HRMS (EI): calcd for C1813CH20O10, m/z 409.1090; measured, m/z 409.1078; fit, −2.8 ppm.
2,3,4-Trimethyl-2H-isoxazol-5-one (12)
Derivatization of flash vacuum thermolysis products was performed by placing the thermolysate with N-methylhydroxylamine (0.058 g, 0.694 mmol) in pyridine (2 mL) and then refluxing the mixture for 14 h. Ether (3 mL) and a saturated solution of potassium carbonate (2 mL) were added and mixed, and the aqueous layer was extracted twice more with ether. The combined organic material was washed once with brine, and 1 mL of xylenes was added. Most of the solvent was removed by distillation. The material was partially purified by column chromatography (3:1 ether/pentane).
To ensure the most quantitative results for the integrations of the two methyl groups of interest, experiments were first performed on an unlabeled sample. The delay time was checked, and the transmitter offset and decoupler offset were centered between the peaks of interest. The experiment on the synthesized sample was also repeated five times to check reproducibility. Likely because these methyl protons were in similar environments, the relative integrations for these two peaks were within 5% of 1:1 in all cases. The experiment was then repeated on the derivatized thermolysis sample using the same parameters. The spectrum was simple enough that a one-dimensional spectrum was adequate. The ratio of the peaks at 2.16 ppm and 1.72 ppm was 4.0−5.0 to 1, with the range established by multiple experiments (1H and HSQC). On the basis of the HMBC spectrum, this ratio favored the methyl group closer to the nitrogen.
2-Methylbutane-1,3-diol (16)
The thermolysate was placed in a 25 mL round-bottom flask with dry THF (8 mL) under nitrogen. The flask was cooled in an acetone/dry ice bath, and DIBAL (1 M in THF, 5.2 mL, 5.2 mmol) was added slowly. The reaction mixture was stirred in the cold bath for 2 h. Stirring was continued as the cold bath was gradually warmed to room temperature over an additional 2 h. A small amount of ether was slowly added as an initial quench of the reaction, and then a low-water DIBAL workup consisting of the following additions was performed: water (0.21 mL), 15% aqueous NaOH (0.21 mL), water (0.53 mL). After this mixture was stirred for 15 min, the salts were removed by suction filtration and the solvents by rotary evaporation. The crude material was partially purified by column chromatography (5:1 ethyl acetate/pentane). All of the operations involving the diol were made with efforts to prevent evaporation. Both diastereomers were observed by NMR in a 2:1 ratio.
The HSQC-AD spectrum for the two diastereomers of 2-methylbutane-1,3-diol is described as follows: On the basis of the integrations of protons b and d, the ratio of 16a to 16b was 1.9−2.6 to 1, with the range of values expressing the results for each of the two diastereomers of the diol. The major diastereomer provided the larger ratio (2.6:1). To ensure maximum quantitative accuracy, efforts as described above for HSQC were performed. One of the peaks for the diasteromeric protons at position d in the major diastereomer overlapped one of the minor diastereomeric proton peaks, and thus, this peak is not listed.
Conclusion
This study turned out to be much more complex in interpretation than originally intended. Full analysis required contributions from both theory and experiment (and, of course, the crucial insight of Dan Singleton, as detailed above). In the end, the picture that is most consistent with the two independent isotopic labeling studies, the coupled-cluster calculations, and preliminary MD simulations is one in which the C2 symmetry of diacetylcarbene 3 fails to be expressed in the ratio of products from its Wolff rearrangements. The nominally symmetry-related methyl groups migrate in a ratio of 2.5:1, favoring the methyl that was on the acetyl substituent in the starting material. We find no indication that this result is due to formation of the carbene in a conformation favoring the migration of one methyl; instead, we take the results to be evidence that the Wolff rearrangment of carbene 3 is subject to the same kind of nonstatistical dynamical effects observed for unimolecular reactions of other transient intermediates.
Acknowledgments
Support of this work by the National Science Foundation (Grant CHE 516991 to B.K.C.) is gratefully acknowledged. A.E.L. thanks the National Science and Engineering Research Council of Canada for a Postgraduate Scholarship. Calculations were performed in part on the Cornell NanoScale Science and Technology Facility (CNF) computer cluster. The authors thank Professor Daniel Singleton for insightful discussions.
Supporting Information Available
1H and 13C NMR spectra of key compounds, Cartesian coordinates and energies of stationary points in the calculations, and complete refs (10) and (11b). This material is available free of charge via the Internet at http://pubs.acs.org.
Supplementary Material
References
- a Perrin W. F. Science 2008, 319, 32. [DOI] [PubMed] [Google Scholar]; b Zucker R. S. Science 2008, 319, 32. [DOI] [PubMed] [Google Scholar]
- Carpenter B. K. Angew. Chem., Int. Ed. 1998, 37, 3340. [DOI] [PubMed] [Google Scholar]
- a Reyes M. B.; Carpenter B. K. J. Am. Chem. Soc. 2000, 122, 10163. [Google Scholar]; b Doubleday C.; Li G.; Hase W. L. Phys. Chem. Chem. Phys. 2002, 4, 304. [Google Scholar]; c Singleton D. A.; Hang C.; Szymanski M. J.; Meyer M. P.; Leach A. G.; Kuwata K. T.; Chen J. S.; Greer A.; Foote C. S.; Houk K. N. J. Am. Chem. Soc. 2003, 125, 1319. [DOI] [PubMed] [Google Scholar]; d Doubleday C.; Suhrada C. P.; Houk K. N. J. Am. Chem. Soc. 2006, 128, 90. [DOI] [PubMed] [Google Scholar]; e Schmittel M.; Vavilala C.; Jaquet R. Angew. Chem., Int. Ed. 2007, 46, 6911. [DOI] [PubMed] [Google Scholar]; f Hamaguchi M.; Nakaishi M.; Nagai T.; Nakamura T.; Abe M. J. Am. Chem. Soc. 2007, 129, 12981. [DOI] [PubMed] [Google Scholar]
- Nummela J. A.; Carpenter B. K. J. Am. Chem. Soc. 2002, 124, 8512. [DOI] [PubMed] [Google Scholar]
- Bach A.; Hostettler J. M.; Chen P. J. Chem. Phys. 2006, 125, 024304. [DOI] [PubMed] [Google Scholar]
- a Ammal S. C.; Yamataka H.; Aida M.; Dupuis M. Science 2003, 299, 1555. [DOI] [PubMed] [Google Scholar]; b Ussing B. R.; Singleton D. A. J. Am. Chem. Soc. 2005, 127, 2888. [DOI] [PubMed] [Google Scholar]
- Carpenter B. K. Annu. Rev. Phys. Chem. 2005, 56, 57. [DOI] [PubMed] [Google Scholar]
- a Becke A. D. Phys. Rev. A 1988, 38, 3098. [DOI] [PubMed] [Google Scholar]; b Lee C.; Yang W.; Parr R. G. Phys. Rev. B 1988, 37, 785. [DOI] [PubMed] [Google Scholar]
- Cohen A. J.; Handy N. C. Mol. Phys. 2001, 99, 607. [Google Scholar]
- Coupled-cluster calculations were carried out using MOLPRO, version 2006.1:Werner H.-J.; et al. MOLPRO: A Package of Ab Initio Programs, version 2006.1; University College Cardiff Consultants Limited: Cardiff, U.K., 2006.
- a Zhao Y.; Truhlar D. G. J. Phys. Chem. A 2004, 108, 6908. [Google Scholar]; b DFT calculations were performed using the Gaussian 03 program:Frisch M. J.; et al. Gaussian 03, revision B.04; Gaussian, Inc.: Wallingford, CT, 2004.
- Lewars E. G.; Morrison G. Can. J. Chem. 1977, 80, 94.and references therein. [Google Scholar]
- Carpenter B. K. J. Phys. Org. Chem. 2003, 16, 858. [Google Scholar]
- Wu H.-J.; Lin S.-H.; Lin C.-C. Heterocycles 1994, 38, 1507. [Google Scholar]
- Valtazanos P.; Ruedenberg K. Theor. Chim. Acta 1986, 69, 281. [Google Scholar]
- a Singleton D. A.; Hang C.; Szymanski M. J.; Greenwald E. E. J. Am. Chem. Soc. 2003, 125, 1176. [DOI] [PubMed] [Google Scholar]; b Gonzalez-Lafont A.; Moreno M.; Lluch J. M. J. Am. Chem. Soc. 2004, 126, 13089. [DOI] [PubMed] [Google Scholar]
- a Ross J. A.; Seiders R. P.; Lemal D. M. J. Am. Chem. Soc. 1976, 98, 4325. [Google Scholar]; b Birney D. M. J. Org. Chem. 1996, 61, 243. [DOI] [PubMed] [Google Scholar]
- a Ichimura A. S.; Lahti P. M.; Matlin A. R. J. Am. Chem. Soc. 1990, 112, 2868. [Google Scholar]; b Hrovat D. A.; Rauk A.; Sorensen T. S.; Powell H. K.; Borden W. T. J. Am. Chem. Soc. 1996, 118, 4159. [Google Scholar]; c Hess B. A. Jr.; Smentek L. Eur. J. Org. Chem. 1999, 3363. [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.