Tight-frame based iterative image reconstruction for spectral breast CT

Abstract

Purpose: To investigate tight-frame based iterative reconstruction (TFIR) technique for spectral breast computed tomography (CT) using fewer projections while achieving greater image quality.

Methods: The experimental data were acquired with a fan-beam breast CT system based on a cadmium zinc telluride photon-counting detector. The images were reconstructed with a varying number of projections using the TFIR and filtered backprojection (FBP) techniques. The image quality between these two techniques was evaluated. The image's spatial resolution was evaluated using a high-resolution phantom, and the contrast to noise ratio (CNR) was evaluated using a postmortem breast sample. The postmortem breast samples were decomposed into water, lipid, and protein contents based on images reconstructed from TFIR with 204 projections and FBP with 614 projections. The volumetric fractions of water, lipid, and protein from the image-based measurements in both TFIR and FBP were compared to the chemical analysis.

Results: The spatial resolution and CNR were comparable for the images reconstructed by TFIR with 204 projections and FBP with 614 projections. Both reconstruction techniques provided accurate quantification of water, lipid, and protein composition of the breast tissue when compared with data from the reference standard chemical analysis.

Conclusions: Accurate breast tissue decomposition can be done with three fold fewer projection images by the TFIR technique without any reduction in image spatial resolution and CNR. This can result in a two-third reduction of the patient dose in a multislit and multislice spiral CT system in addition to the reduced scanning time in this system.

INTRODUCTION

Breast cancer is one of the most common cancers in women, resulting in about 39 000 deaths in 2011 from this disease in the United States. Many techniques, including mammography and computed tomography (CT), have been developed for early detection and diagnosis of breast cancer. Recent advances in solid state semiconductor materials allow photon-counting and energy discriminating imaging detectors to be used in a breast CT system to produce higher quality images.^{1, 2, 3, 4, 5, 6, 7, 8, 9} Cadmium zinc telluride (CZT) single crystal detectors have been investigated and implemented as x-ray detectors in current breast CT systems. These systems use CZT due to its large effective atomic number (49.6), high mass density (5.8 g/cm³), and higher quantum efficiency. CZT based spectral breast CT can potentially be applied in material decomposition to provide additional information for evaluating the risk of breast cancers. Compared to the two-material segmentation of glandular and adipose tissues in mammographic breast density measurement, three-material decomposition (water, lipid, and protein) can improve the capability of predicting breast cancers. It has been reported that measurement of the protein fraction can help to categorize a suspicious finding as either malignant or benign.¹⁰ Malignant tissues have a significantly higher water fraction compared to normal tissues.^{11, 12} Lipid content can be used to identify certain benign lesions.¹³ The feasibility of three-material decomposition for breast tissue with spectral breast CT system has been investigated in recent studies^{8, 14} in which the images were reconstructed using a filtered backprojection (FBP) technique. The FBP technique is widely used because it is computationally fast, accurate, and easily implemented.^{15, 16} However, the FBP technique has some disadvantages. For example, a large number of projections are required to reconstruct CT images. To reduce patient radiation dose, it is necessary to reduce the number of projections needed for reconstruction. This leads to undersampling and strong noise and streak artifacts in the reconstructed images using the FBP technique.¹⁷ Thus, it is desirable to find a technique to reconstruct the images with fewer projections, but without the reduction in image quality.

Many efforts have been made in the past decades to develop or find algorithms that can be used to reconstruct CT images with fewer projections. Algebraic reconstruction techniques (ART) (Ref. ¹⁸) and simultaneous algebraic reconstruction techniques (SART) (Ref. ¹⁹) are both possible algorithms that can be used for this purpose. These algorithms assume that projections through the object are modeled by a linear system of equations based on the discretization of the Radon transform, and then are solved iteratively. However, due to the highly demanding computation requirements, there has been no significant development in these algorithms until the past decade. The techniques utilizing these algorithms have been rediscovered^{20, 21, 22, 23, 24, 25} and applied to the image reconstruction of low-dose CT, such as total variation,^{26, 27, 28} dictionary learning,^{17, 29, 30, 31} and tight-frame or framelet techniques.^{32, 33, 34} The technique of total variation minimizes the total variation of the estimated images with the assumption that the image gradient is sparse and is widely used for low-dose, few-view, limited-angle, and truncated data. However, it may lead to undesirable biases and artifacts as well as loss of fine features, which may reduce the diagnostic values of reconstructed images. Dictionary learning is more specific to a particular application and more effective in terms of a sparse representation, which learns from a set of given samples and then processes the image patch by patch. Dictionary learning has been successfully applied to image processing and feature recognition areas. However, dictionary learning needs to acquire sample images to build dictionaries, and is not effective for a totally unknown object. On the other hand, tight frame offers a generally sparse representation of L1 norm and total variation with high-order differencing, and it also generalizes the wavelet with redundant representation. Overall, the flexibility and usefulness of tight frame renders it as a natural choice for sparsifying the CT image.

One potential application of the tight-frame iterative reconstruction (TFIR) technique is to reconstruct images for a breast CT system. In a previous study,¹⁴ the postmortem breast tissue samples were successfully decomposed into water, lipid, and protein contents based on acquired images with a CZT photon-counting detector and reconstructed using FBP with a large number of projections. TFIR can reconstruct images with fewer projections, while retaining image quality. The reconstructed images can also be used for three-material decomposition of breast tissue. Thus, the dose to patients can be reduced by implementing the TFIR technique in image reconstruction for future breast CT systems.

In this study, we investigate an iterative image reconstruction technique based on a tight-frame sparsity model for a spectral breast CT system using a CZT photon-counting detector and the feasibility of decomposing breast tissue with limited number of projections. In Sec. 2, we introduce the TFIR technique, the dedicated breast CT system in our laboratory, image acquisition and reconstruction techniques and the method for breast tissue decomposition. In Sec. 3, we report our results by comparing spatial resolution and contrast to noise ratio (CNR) of the images reconstructed from the FBP and TFIR techniques. We also compare the results of breast tissue decomposition with the images reconstructed by conventional FBP technique with a large number of projections and by the TFIR technique with a factor of 3 less number of projections. In Sec. 4, we discuss relevant issues and the possible application of the TFIR technique for a breast CT system.

METHODS AND MATERIALS

The TFIR technique

The image reconstruction problem via TFIR is formulated as the L1-type convex minimization

$$X=\underset{X}{\arg \min }{\Vert AX-Y\Vert }_2^2+\lambda {\Vert WX\Vert }_1.$$ (1)

In Eq. 1, A is the system matrix that corresponds to the x-ray transform of the breast CT system, a discretized Radon transform in 2D,³⁵X is the image to be reconstructed, Y is the acquired data after the log transform, and λ balances the data fidelity and the sparsity regularization.

In this study, W refers to the piecewise-linear tight-frame transform that can be constructed by the tensor product of the averaging mask, the first-order differencing mask, and the second-order differencing mask

$$w_0=\frac{1}{4}\left[121\right],w_1=\frac{\sqrt{2}}{4}\left[10-1\right],w_2=\frac{1}{4}\left[-12-1\right].$$ (2)

Therefore, the 2D refinement masks are

$$\begin{array}{ccc}\hfill w_{0,0}& =& {\displaystyle \frac{1}{16}\left[\begin{array}{ccc}\hfill 1& \hfill 2& \hfill 1\\ \hfill 2& \hfill 4& \hfill 2\\ \hfill 1& \hfill 2& \hfill 1\end{array}\right],}{\displaystyle w_{0,1}=\frac{\sqrt{2}}{16}\left[\begin{array}{ccc}\hfill 1& \hfill 0& \hfill -1\\ \hfill 2& \hfill 0& \hfill -2\\ \hfill 1& \hfill 0& \hfill -1\end{array}\right],}{\displaystyle w_{0,2}=\frac{1}{16}\left[\begin{array}{ccc}\hfill -1& \hfill 2& \hfill -1\\ \hfill -2& \hfill 4& \hfill -2\\ \hfill -1& \hfill 2& \hfill -1\end{array}\right]}\hfill \\ \hfill w_{1,0}& =& {\displaystyle \frac{\sqrt{2}}{16}\left[\begin{array}{ccc}\hfill 1& \hfill 2& \hfill 1\\ \hfill 0& \hfill 0& \hfill 0\\ \hfill -1& \hfill -2& \hfill -1\end{array}\right],}{\displaystyle w_{1,1}=\frac{1}{8}\left[\begin{array}{ccc}\hfill 1& \hfill 0& \hfill -1\\ \hfill 0& \hfill 0& \hfill 0\\ \hfill -1& \hfill 0& \hfill 1\end{array}\right],}{\displaystyle w_{1,2}=\frac{\sqrt{2}}{16}\left[\begin{array}{ccc}\hfill -1& \hfill 2& \hfill -1\\ \hfill 0& \hfill 0& \hfill 0\\ \hfill 1& \hfill -2& \hfill 1\end{array}\right]}.\hfill \\ \hfill w_{2,0}& =& {\displaystyle \frac{1}{16}\left[\begin{array}{ccc}\hfill -1& \hfill -2& \hfill -1\\ \hfill 2& \hfill 4& \hfill 2\\ \hfill -1& \hfill -2& \hfill -1\end{array}\right],}{\displaystyle w_{2,1}=\frac{\sqrt{2}}{16}\left[\begin{array}{ccc}\hfill -1& \hfill 0& \hfill 1\\ \hfill 2& \hfill 0& \hfill -2\\ \hfill -1& \hfill 0& \hfill 1\end{array}\right],}{\displaystyle w_{2,2}=\frac{1}{16}\left[\begin{array}{ccc}\hfill 1& \hfill -2& \hfill 1\\ \hfill -2& \hfill 4& \hfill -2\\ \hfill 1& \hfill -2& \hfill 1\end{array}\right]}\hfill \end{array}$$ (3)

These masks correspond to the discretized high-order partial derivatives, and therefore tight frame generalizes total variation. In addition, they provide rich multilevel redundancy in sparsifying the image, and therefore tight frame also generalizes the wavelet.

The multilevel tight-frame transform of X up to L levels is

$$WX=\left[\underset{\mathrm{Level}:1}{\underbrace{\begin{array}{ccc}{\left[WX\right]}_{0,1}^1& \cdots & {\left[WX\right]}_{2,2}^1\end{array}}}\cdots \underset{\mathrm{Level}:l}{\underbrace{\begin{array}{ccc}{\left[WX\right]}_{0,1}^l& \cdots & {\left[WX\right]}_{2,2}^l\end{array}}}\cdots \underset{\mathrm{Level}:L}{\underbrace{\begin{array}{ccc}{\left[WX\right]}_{0,1}^L& \cdots & {\left[WX\right]}_{2,2}^L\end{array}}}\begin{array}{c}{X}^L\end{array}\right],$$ (4)

with X⁰ = X and the following convolutions:

$$\begin{array}{ccc}\hfill X^l=w_{0,0}^l*X^{l-1},{\left[WX\right]}_{0,1}^l& =& w_{0,1}^l*X^l,...,{\left[WX\right]}_{2,2}^l\hfill \\ & =& w_{2,2}^l*X^l,1\le l\le L.\hfill \end{array}$$ (5)

In Eq. 5, considering computational efficiency, instead of downsampling X^l, we dilute the masks 3 so that

$$w_{i_1,i_2}^l=D^l{w}_{i_1,i_2},0\le i_1,i_2\le 2,$$ (6)

where D^l, w′, and s are (2^l+1+ 1) × (2^l+1 + 1) matrices with nine nonzero entries defined by

$$\begin{array}{ccc}\hfill D^{l}w& =& \left[\begin{array}{ccccc}\hfill w(1,1)& \hfill \cdots & \hfill w(1,2)& \cdots & w(1,3)\\ \hfill ⋮& \hfill ⋮& \hfill ⋮& ⋮& ⋮\\ \hfill w(2,1)& \hfill \cdots & \hfill w(2,2)& \cdots & w(2,3)\\ \hfill ⋮& \hfill ⋮& \hfill ⋮& ⋮& ⋮\\ \hfill w(3,1)& \hfill \cdots & \hfill w(3,2)& \cdots & w(3,3)\end{array}\right]\hfill \\ \hfill \mathrm{for}\\ \hfill w& =& \left[\begin{array}{ccc}\hfill w(1,1)& \hfill w(1,2)& \hfill w(1,3)\\ \hfill w(2,1)& \hfill w(2,2)& \hfill w(2,3)\\ \hfill w(3,1)& \hfill w(3,2)& \hfill w(3,3)\end{array}\right].\hfill \end{array}$$ (7)

On the other hand, the transpose of tight frame on Y = WX in the format of Eq. 4 is

$$W^T\left(Y\right)=Y^L+\sum _{l=1}^L\left({\left[Y\right]}_{0,1}^l+\cdots +{\left[Y\right]}_{2,2}^l\right).$$ (8)

And we have W^T(WX) = X. Now, we can give the definition of the isotropic tight-frame norm in Eq. 1 as

$$\begin{array}{ccc}\hfill {\Vert WX\Vert }_1& =& \Vert X^L{\Vert }_1+\sum _{l=1}^L\{\Vert {\left[WX\right]}_1^l{\Vert }_1+\Vert {\left[WX\right]}_2^l+\Vert {\left[WX\right]}_3^l\hfill \\ & & +\Vert {\left[WX\right]}_4^l{\Vert }_1\},\hfill \end{array}$$ (9)

with

$$\begin{array}{ccc}\hfill {\left[WX\right]}_1^l& =& \sqrt{{\left({\left[WX\right]}_{0,1}^l\right)}^2+{\left({\left[WX\right]}_{1,0}^l\right)}^2},\hfill \\ \hfill {\left[WX\right]}_2^l& =& \sqrt{{\left({\left[WX\right]}_{0,2}^l\right)}^2+{\left({\left[WX\right]}_{1,1}^l\right)}^2+{\left({\left[WX\right]}_{2,0}^l\right)}^2,}\hfill \\ \hfill {\left[WX\right]}_3^l& =& \sqrt{{\left({\left[WX\right]}_{1,2}^l\right)}^2+{\left({\left[WX\right]}_{2,1}^l\right)}^2},\hfill \\ \hfill {\left[WX\right]}_4^l& =& {\left[WX\right]}_{2,2}^l,\hfill \end{array}$$ (10)

which corresponds to isotropic first-ordering differencing, second-order differencing, third-order differencing (partial), and fourth-order differencing (partial), respectively.

The solution of this nondifferentiable L1 problem (1) can be solved through the split Bregman method.^{36, 37} The details of Bregman algorithm for solving Eq. 1 have been previously reported.^{38, 39}

Here, we propose the following three-step simple-to-implement new algorithm that seems to be faster than split Bregman method from our numerical experience. However, the rigorous justification of the algorithm will be reported in future

$$\left\{\begin{array}{c}{X}^{n+1/2}=\underset{X}{\arg \min }{\Vert AX-Y+f^n\Vert }_2^2\hfill \\ X^{n+1}=\underset{WX=Z}{\arg \min }\frac{1}{2}\Vert W{X}^{n+1/2}{-Z\Vert }_2^2+\lambda {\Vert Z\Vert }_1\hfill \\ f^{n+1}=f^n+AX-Y\hfill \end{array}\right.,$$ (11)

where f ⁿ and the third step come from the Bregman iteration.⁴⁰

The first step of Eq. 11 is a least-square problem that can be solved, e.g., by ART and SART. For our 2D problem, A can be either explicitly computed and saved or computed on-the-fly. Here, we use the conjugate gradient method, i.e.,

$$A^{T}A{X}^{n+1/2}=A^T(Y-f^n),$$ (12)

in which AX, A^TX are evaluated instead of forming A^TA. Note that a few conjugate gradient iterations for Eq. 12 are sufficient since it is not necessary to get an accurate intermediate solution during the iterative scheme (12), and also an accurate solution is difficult to obtain when A is ill-posed in the case with incomplete projections.

Due to W^TW = I, the second step of Eq. 11 has the explicit solution formula, the so-called shrinkage formula,

$$X^{n+1}=W^{T}S(W{X}^{n+1/2},\lambda ).$$ (13)

The exact form of Eq. 13 depends on the definition ‖WX‖₁. With our definitions 9, 10 and Z = WX, the shrinkage formula S in Eq. 11 consists of

$$\begin{array}{ccc}& & {\left[Z^{n+1}\right]}^L=\max \left(\right|{\left[Z^{n+1/2}\right]}^L|-\lambda /2^L,0)·\mathrm{sgn}\left({\left[Z^{n+1/2}\right]}^L\right),\hfill \\ & & {\displaystyle ({\left[Z^{n+1}\right]}_{0,1}^l,{\left[Z^{n+1}\right]}_{1,0}^l)=\max ({\left[Z^{n+1/2}\right]}_1^l-\lambda /2^l,0)·\frac{({\left[Z^{n+1/2}\right]}_{0,1}^l,{\left[Z^{n+1/2}\right]}_{1,0}^l)}{{\left[Z^{n+1/2}\right]}_1^l},}\hfill \\ & & {\displaystyle ({\left[Z^{n+1}\right]}_{0,2}^l,{\left[Z^{n+1}\right]}_{1,1}^l,{\left[Z^{n+1}\right]}_{2,0}^l)=\max ({\left[Z^{n+1/2}\right]}_2^l-\lambda /2^l,0)·\frac{({\left[Z^{n+1/2}\right]}_{0,2}^l,{\left[Z^{n+1/2}\right]}_{1,1}^l,{\left[Z^{n+1/2}\right]}_{2,0}^l)}{{\left[Z^{n+1/2}\right]}_2^l},}\hfill \\ & & {\displaystyle ({\left[Z^{n+1}\right]}_{1,2}^l,{\left[Z^{n+1}\right]}_{2,1}^l)=\max ({\left[Z^{n+1/2}\right]}_3^l-\lambda /2^l,0)·\frac{({\left[Z^{n+1/2}\right]}_{1,2}^l,{\left[Z^{n+1/2}\right]}_{2,1}^l)}{{\left[Z^{n+1/2}\right]}_3^l},}\hfill \\ & & {\left[Z^{n+1}\right]}_{2,2}^l=\max \left(\right|{\left[Z^{n+1/2}\right]}_{2,2}^l|-\lambda /2^l,0)·\mathrm{sgn}\left({\left[Z^{n+1/2}\right]}_{2,2}^l\right),\hfill \end{array}$$ (14)

with

$$\mathrm{sgn}\left(x\right)=\left\{\begin{array}{c}\hfill 1,\\ \hfill -1,\end{array}\begin{array}{c}x>0\hfill \\ x\le 0\hfill \end{array}\right..$$ (15)

Breast CT system

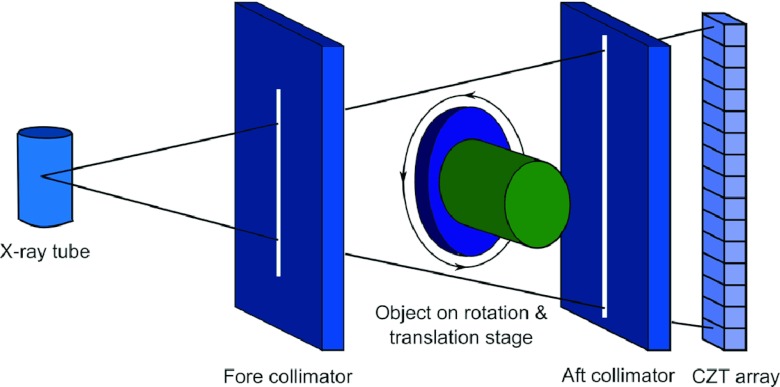
The breast CT system studied in this paper consisted of an x-ray tube, fore and aft collimators, rotation and translation stage platform and CZT photon-counting detector, shown in Fig. 1.⁴¹ The x-ray tube (Dynamax 78E) used a tungsten target and was coupled to a constant potential x-ray generator (Phillips Optimus M200). A total of 2 mm Al and 0.15 mm Cu were used as prefiltration. The fore and aft collimators were made of 3 mm thick lead sheets to minimize x-ray scatter, and the collimator slit widths were 0.3 and 0.8 mm, respectively. The rotation and translation stage platform consisted of a high precision direct drive rotary (DDR) motor (Kollmorgen Goldline DDR D062M, Danaher Motion, Wood Dale, IL) and a translation stage, not only providing both vertical and horizontal translations to extend the field of view beyond the size limitation of the detector, but also serving as the rotation platform for the object. The CZT photon-counting detector (eV2500, eV Microelectronics, Inc., Saxonburg, PA) was composed of a linear row of four CZT crystals with length of 12.8 mm, width of 3 mm, and depth of 3 mm. Each crystal consisted of 16 pixels, yielding a total of 64 pixels with an effective pitch of 0.8 mm in each pixel. The entrance beam to the detector was shaped by a brass collimator and collimated at the height of each pixel to 0.8 mm.⁴¹

Figure 1.

Schematic drawing of the spectral CT system with a CZT photon-counting detector (Ref. ⁴¹).

The CZT detector was placed 1.35 m from the x-ray tube and the rotation and translation stage platform was placed 0.95 m away from the x-ray tube, which resulted in an approximate distance of 0.93 m between the source and the isocenter. A field programmable gate array (FPGA) chip was used to count the trigger pulses generated by five comparators from each pixel over a user-defined collection period (frame, selectable from 1 to 50 ms). Then each frame was sent to the workstation over a USB interface for data processing, storage, and visualization.^{42, 43} The peaking time of the detector was set at 160 ns. The energy resolution of the detector was calibrated up to 140 keV by the manufacturer (Endicott Interconnect Detection & Imaging Systems). The acquired photons were sorted into five user-definable energy bins via the energy resolving capability of the detector. The maximum count rate of the detector was calibrated to approximately 2.3 × 10⁶ cps/mm². The linear count rate range was less than 1.2 × 10⁶ cps/mm². The detector itself did not experience pulse pileup and charge sharing correction mechanisms.⁴¹ During the scan, the rotation and translation stage platform rotated the object as well as translated the object's height, resulting in a helical scan. A helical scan was performed with a pitch of 2 in the experiment. The measured helical sinogram was first interpolated to generate 2D sinograms for each slice, which were used for the following CT reconstructions. Therefore, all reconstructions were based on 2D fan beam geometry.

The CZT detector was operated in Ohmic mode with a bias voltage of 1000 V across the CZT crystal. As a photon interacted with the CZT crystal, an electron hole pair was created for any energy above 4.64 eV deposited in the crystal. Electrons generated from this interaction of photons within the crystal were collected at the back of the electrode and formed a pulse by application-specific integrated circuit (ASIC) with its height proportional to the energy of the incoming photon. A count was registered if the pulse height was higher than the given threshold value. The lower boundaries of the energy bins were defined by five user-definable thresholds, therefore, the count within an energy bin could be easily obtained by subtracting the count from its two adjacent thresholds.⁴¹

Image acquisition and reconstruction

A high-resolution phantom, motivated by a previous study,⁴⁴ was designed to compare spatial resolution of images reconstructed by FBP and TFIR. This phantom was also used in a previous study.⁴⁵ In this phantom, a cylinder with diameter of 13 cm and length of 2 cm was constructed of resin as the phantom base. The phantom also included an insert with 5 fine Al wires of various diameters (643, 813, 1020, 1290, and 1630 μm) and a cylinder of Delrin with diameter of 2.5 cm and length of 3 cm (Fig. 2). The resin was chosen as the phantom base because of its similar x-ray attenuation to breast tissue (0.2076 cm²/g for resin and 0.2186 cm²/g for breast tissue at 50 keV) (Ref. ⁴⁶) as well as the low cost and convenience of fabricating the phantom base for inserting Al wires. The Al wires in the insert were orientated vertically and arranged with enough space between each of them to minimize reconstruction artifacts between wires. Image spatial resolution was studied by extracting the profiles of Al wires from reconstructed CT images. Postmortem breast samples were obtained from the willed body program at the University of California, Irvine's School of Medicine and sealed in plastic bags. Five postmortem breasts were used in this study whose mass varied from 326 to 434 g and breast density varied from 34% to 72%. These samples were placed in a cylindrical high-density polyethylene plastic container of approximately 10 cm in diameter.

Figure 2.

(a) Layout and (b) picture of high resolution phantom with the Al wire insert (the ruler is in unit of inch).

During the image acquisition, the object was placed on a translation stage platform shown in Fig. 1 and was rotated at approximately 0.977 rpm. With the frame rate of 20 frames per second, a total of 1229 frames were acquired for a scan that covered 360° of rotation. The tube potential was set at 100 kVp and the tube current was set 1.00 mA. The total entrance skin air kerma (ESAK) without back scattering under the current setting was estimated to be 2.4 mGy. By setting the lowest energy threshold at 22 keV to optimally eliminate electronic noise, all x-ray photons interacting with the CZT detector with the energy above the lowest threshold were acquired. Another threshold of 42 keV was selected to split the photons into low and high energy bins. These settings were kept during image acquisition. All data acquired with the CZT detector were corrected for nonuniformity across pixels, using a previously reported flat field correction technique⁸ with an open source image processing software package.⁴⁷ Resultant images were reconstructed using a conventional FBP technique with the software package from the University of Michigan⁴⁸ and by TFIR with various number of projections.

Image analysis

The image quality, including spatial resolution and CNR, between the TFIR and FBP techniques was compared to evaluate the performance of the TFIR technique. For spatial resolution comparison, the CT images of the high-resolution phantom were reconstructed by TFIR with 204 projections and by FBP with 614 projections, which were downsampled from the original dataset of 1229 projections. Two line profiles of an Al wire were extracted from the image in the crossed directions, which were specifically selected to avoid beam hardening. Then the average of these two line profiles were fitted with a Gaussian function to evaluate the full width at half maximum (FWHM).^{22, 49} For CNR comparison, the region of interest (ROI) was selected from glandular or adipose tissue of the postmortem breast sample images to calculate CNR using the following equation:

$$\mathrm{CNR}=\frac{M_G-M_A}{\sqrt{{\sigma }_G^2+{\sigma }_A^2}},$$ (16)

where M_i and σ_i are the average mean gray value and the standard deviation of the glandular (G) tissue and adipose (A) tissue from the selected ROI, respectively. The size of the ROI was determined by selecting a region as large as possible within pure glandular tissue or pure adipose tissue.

Breast tissue decomposition

With dual-energy CT imaging technology, three equations and three unknowns were used to calculate the tissue compositions based on the measured linear attenuation.^{10, 50} The natural logarithm of the ratio of the measured attenuated photon intensity I over the nonattenuated photon intensity I₀ is defined as $U=\ln \left(\frac{\mathrm{I}}{{\mathrm{I}}_0}\right)=-\sum {\mu }_i{t}_i$, where i represents water, lipid or protein. This equation was derived for a CT image and can be written in a matrix form with a negative sign μF = −U as the following:

$$\left(\begin{array}{ccc}\hfill {\mu }_W^L& \hfill {\mu }_L^L& \hfill {\mu }_P^L\\ \hfill {\mu }_W^H& \hfill {\mu }_L^H& \hfill {\mu }_P^H\\ \hfill 1& \hfill 1& \hfill 1\end{array}\right)\left(\begin{array}{c}{f}_W\\ f_L\\ f_P\end{array}\right)=\left(\begin{array}{c}-U^L\\ -U^H\\ 1\end{array}\right),$$ (17)

where ${\mu }_W^L$, ${\mu }_L^L,$ and ${\mu }_P^L$ are the linear attenuation coefficients of water, lipid, and protein, respectively. It describes the fraction of an x-ray or gamma ray beam that is absorbed or scattered per unit thickness of the absorber (water, lipid or protein). f_W, f_L, and f_P represent the volume fractions of water, lipid, and protein, respectively. U^L and U^H are the measured attenuations of the images, obtained by setting a general threshold on ln(I/I₀) to select the tissue area and then summing ln(I/I₀) in each pixel for each slice image in low and high energy bins, respectively. Equation 17 was solved using least-squares fitting. Each material fraction was represented as follows:

$$f_i=a_0+a_1{U}^L+a_2{U}^H.$$ (18)

In the calibration process, the image attenuation measurement at the low and high energies (U^L and U^H) and the fraction values (f_W, f_L, and f_P) were known. Then, the linear system of equations was solved to determine the system matrix calibration coefficients of a₀, a₁, and a₂. In the decomposition process, the image attenuation measurements from the tissue samples with unknown compositions were inputted into the system to determine the image-based measurements (water, lipid, and protein contents).¹⁴

Chemical analysis

To validate the results from the image-based measurements, a chemical analysis was performed to measure the water, lipid, and protein in the sample based on a standardized procedure devised by the United States Department of Agriculture.^{51, 52} Samples were weighed before and after placing them in a 95° oven for at least 48 h to get the mass of pure water. Next, the sample was grounded into slurry and mixed with petroleum ether, and then filtered using a Buchner funnel to extract the mass of protein. Finally, the petroleum ether was evaporated using heat and vacuum distillation to isolate the lipid content and determine the lipid mass. The mass of mineral ash was assumed to be negligible.

RESULTS

Image spatial resolution was compared using reconstructed images of a high-resolution phantom (Al wire insert) by TFIR and FBP at various number of projections. Figure 3 shows the reconstructed image of Al wire insert in the first energy bin 22–42 keV by TFIR and FBP at 204 projections [(a) and (b), respectively] and 614 projections [(c) and (d), respectively]. Two line ROIs were drawn across the center of an Al wire [crossed lines in (d) of Fig. 3] and the average line profile was then calculated to reduce the uncertainty caused by the artifacts. The average line profiles for the 4 Al wires were extracted from the images reconstructed by TFIR with 204 projections and by FBP with 614 projections, and then were fitted by a Gaussian function to get the FWHM, shown in (e)–(h) of Fig. 3 for Al wires with diameter of 1630, 1290, 1020, and 813 μm, respectively. The FWHM for TFIR with 204 projections using 4 Al wires is smaller than that of FBP with 614 projections, which indicates that compared to FBP, TFIR can reconstruct an image with threefold fewer projections without a loss in spatial resolution. Due to the fact that the thinnest Al wire with a diameter of 0.643 mm is smaller than the detector pixel size, its reconstructed image is blurred in both TFIR with 204 projections and FBP with 614 projections. Therefore, this Al wire is not useful for FWHM calculations.

Figure 3.

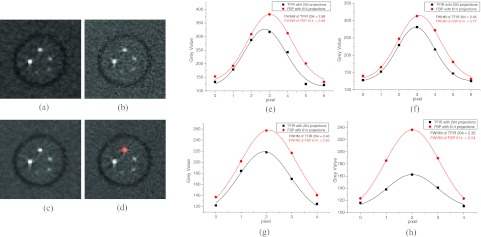
Images of a high-resolution phantom (Al wires insert) reconstructed using TFIR and FBP with 204 projections, (a) and (b), respectively, and with 614 projections, (c) and (d), respectively. The images were adjusted to the same window and level. Crossed lines in (d) indicate the regions for the line profiles. The line profiles for TFIR with 204 projections and FBP with 614 projections for 4 Al wires with diameters of 1630, 1290, 1020, and 813 μm are shown in (e), (f), (g), and (h), respectively.

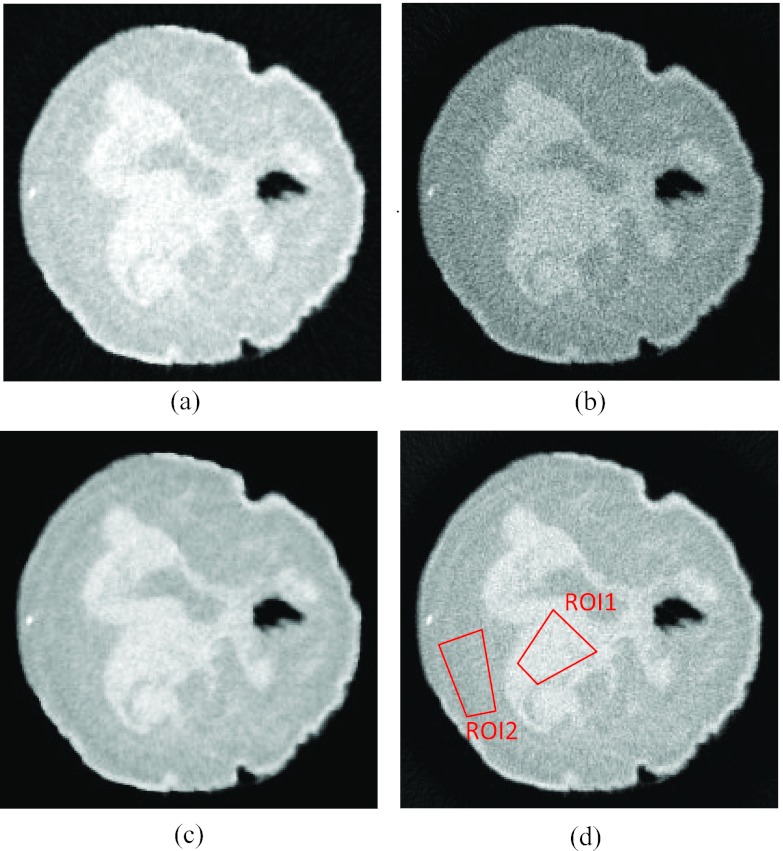
CNR comparison was made using reconstructed images of a postmortem breast sample. Figure 4 shows a CT slice of a postmortem breast sample in the first energy bin 22–42 keV reconstructed by TFIR and FBP at 204 projections [(a) and (b), respectively] and 614 projections [(c) and (d), respectively]. Two ROIs [red polygons in Fig. 4d] were drawn in pure glandular and adipose tissue regions to calculate CNR. The CNR value is 3.36 for TFIR with 204 projections and 3.04 for FBP with 614 projections. The results indicate that TFIR can produce comparable CNR with one third number of projections as compared to FBP. Similar results were obtained for CNR calculated from other postmortem breast samples. The spatial resolution and CNR were also studied for the high energy bin images and similar results were obtained.

Figure 4.

A CT slice of a postmortem breast reconstructed using (a) TFIR with 204 projections, (b) FBP with 204 projections, (c) TFIR with 614 projections and (d) FBP with 614 projections. The images were adjusted to the same window and level. The two polygons indicate the ROIs selected from glandular (ROI1) and adipose (ROI2) tissues to calculate CNR.

Furthermore, the breast tissue was decomposed into water, lipid, and protein contents using CT images reconstructed by TFIR with 204 projections and FBP with 614 projections. Figure 5 illustrates volumetric fractions of water, lipid, and protein for 5 postmortem samples, derived from image-based measurement (FBP with 614 projections and TFIR with 204 projections) and chemical analysis. Figure 6 shows the Bland-Altman analysis of volumetric fractions derived from image-based measurement, FBP with 614 projections (V_FBP) and TFIR with 204 projections (V_TFIR), for (a) water, (b) lipid, and (c) protein. The comparison indicates that TFIR can be applied to breast tissue decomposition by acquiring threefold fewer projections compared to the FBP technique and achieve similar breast tissue compositions as compared to the reference standard chemical analysis.

Figure 5.

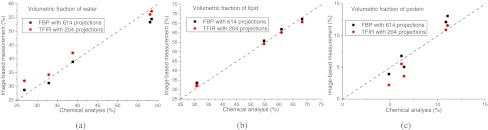
Volumetric fractions of breast composition of 5 postmortem breasts derived from image-based measurement (FBP with 614 projections and TFIR with 204 projections) and the chemical analysis, for (a) water, (b) lipid and (c) protein. The dashed line is the line of identity.

Figure 6.

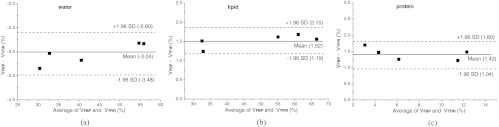
Bland-Altman analysis of volumetric fractions of breast composition of 5 postmortem breasts from image-based measurement using FBP with 614 projections (V_FBP) and TFIR with 204 projections (V_TFIR), for (a) water, (b) lipid and (c) protein.

DISCUSSIONS

In this study, some geometric approximations of the breast CT system were made in the TFIR technique. For example, the CZT detector in this breast CT system has 4 crystals with 16 pixels for each crystal and a pixel size of 0.8 mm. A gap of 0.57 mm exists between crystals. In the TFIR technique, this gap was assumed to be 0.8 mm to simplify the algorithm. As a result, in order to reconstruct the images without any loss in spatial resolution, 204 projections were required by TFIR.

The TFIR algorithm in this study was simplified, carefully implemented, and optimized for our spectral CT system. Furthermore, the system matrix is relatively small, which resulted in a reconstruction time of approximately 10 s for each CT slice. However, with the fast development of computer technology and graphics processing unit (GPU) assisted processing technique, it is possible to include more accurate geometric information for the TFIR reconstruction, which can potentially further reduce the required number of projections without any loss in spatial resolution. We have previously reported on a dual-dictionary learning based IR CT reconstruction technique.⁴⁵ However, the dual-dictionary learning technique requires previously built dictionaries with a reconstruction time of approximately 30 min for each CT slice. The TFIR technique is capable of reconstructing a sequence of related images that are more compressible than one image. The sequence of related images can be volume fractions of water, lipid, and protein, which require fewer projections without sacrificing accuracy. This approach can potentially be used for material decomposition in future studies. It should also be pointed out that the data fidelity term does not account for the statistics in CT systems and typically weighted least squares with diagonal weighting matrix is used. This will be investigated further in future studies.

The results of breast tissue decomposition from image-based measurements (TFIR with 204 projections and FBP with 614 projections) are in agreement with the chemical analysis. However, there are several sources of error in these measurements.¹⁴ The image-based breast tissue decomposition in this study is dependent on a reliable measurement of the energy-dependent attenuation coefficient. However, artifacts induced by pulse pile-up, field nonuniformity, and charge-sharing may lead to uncertainties in the measurement due to limitations of the CZT-based photon-counting detector. In the calibration process described in Sec. 2E, the use of polyoxymethylene plastic as a substitute for protein can introduce additional error in material decomposition studies. This is due to the fact that the calibration coefficients were extracted from polyoxymethylene plastic, whereas in tissue decomposition the same calibration coefficients were used to measure protein content. It should also be pointed out that due to the breast sample holder the diameter of the postmortem breast samples were approximately 9 cm, which is less than the average diameter of 14 cm for a breast in a clinical imaging situation. This technique will have to be applied to larger breast sizes in future studies.

In a multislit and multislice (MSMS) spiral CT system, the scanning time is determined by the detector frame time and the number of projections required for reconstruction. The frame time is limited by the counting capability of the detector, which is typically in the range of 1–50 ms.^{2, 43, 53} Therefore, further reduction of the frame time might result in incomplete collection of the charges generated by a single photon, leading to a poor energy resolution. The reduction in the number of projections needed to reconstruct a high quality image is deemed to be more efficient. The TFIR technique can reconstruct high quality images with one third number of projections as compared to the conventional FBP technique. Furthermore, the images can be used to accurately determine water, lipid, and protein contents in breast tissue. Therefore, for a MSMS breast CT system with a scanning time of approximately 10 s, the radiation dose could be reduced by a factor of two-third using photon-counting detectors with a scanning time that is comparable to the current breast CT systems that use flat-panel detectors.⁵⁴ It is also noted that the future MSMS breast CT systems should be designed to avoid smearing the object and locating it away from the center of rotation during image acquisition. In this study, for images reconstructed by TFIR with 204 projections, the number of projections were downsampled from the original dataset by extracting every sixth projection from the whole set of 1229 projections. This cannot be implemented in the future MSMS breast CT system because the main purpose of adopting the TFIR technique, dose reduction to patients, must be fulfilled. This can be addressed by using a high-power pulsed x-ray tube to acquire the projections at particular rotation angles. A similar technique has previously been implemented.⁵⁵

CONCLUSION

This study demonstrates that the TFIR technique can reduce the required number of projections by a factor of 3 as compared to the FBP technique without any reduction in image quality. The images reconstructed by the TFIR technique can also be used for accurate breast tissue decomposition. Therefore, the application of the TFIR technique can potentially reduce the radiation dose by a factor of two-third in a MSMS spiral CT system.