Optimization of ¹³C isotopic tracers for metabolic flux analysis in mammalian cells

Abstract

Mammalian cells consume and metabolize various substrates from their surroundings for energy generation and biomass synthesis. Glucose and glutamine, in particular, are the primary carbon sources for proliferating cancer cells. While this combination of substrates generates static labeling patterns for use in ¹³C metabolic flux analysis (MFA), the inability of single tracers to effectively label all pathways poses an obstacle for comprehensive flux determination within a given experiment. To address this issue we applied a genetic algorithm to optimize mixtures of ¹³C-labeled glucose and glutamine for use in MFA. We identified tracer combinations that minimized confidence intervals in an experimentally determined flux network describing central carbon metabolism in tumor cells. Additional simulations were used to determine the robustness of the [1,2-¹³C₂]glucose/[U-¹³C₅]glutamine tracer combination with respect to perturbations in the network. Finally, we experimentally validated the improved performance of this tracer set relative to glucose tracers alone in a cancer cell line. This versatile method allows researchers to determine the optimal tracer combination to use for a specific metabolic network, and our findings applied to cancer cells significantly enhance the ability of MFA experiments to precisely quantify fluxes in higher organisms.

1. Introduction

A key challenge facing systems biologists is the need to provide a rapid and robust characterization of cellular metabolism. Quantification of intracellular and extracellular fluxes enables researchers to measure the “pulse” of a given biological system, and these data aid in the design of metabolic engineering strategies and the elucidation of disease mechanisms (Antoniewicz et al., 2007b; Burgess et al., 2007; Crown et al., 2011; Metallo et al., 2011; Munger et al., 2008; Suthers et al., 2007; Zamboni, 2011). In particular, interest in the metabolic analysis of mammalian systems has increased of late, as metabolic defects have been implicated in cancer, mental disorders, diabetes, and related syndromes (Abou-Sleiman et al., 2006; Biddinger and Kahn, 2006; Christofk et al., 2008; Small et al., 2000).

¹³C metabolic flux analysis (MFA) and related methods enable researchers to quantify intracellular fluxes in vivo via the combined use of stable isotopic tracers, analytical methods such as NMR or mass spectrometry (MS), and computational tools (Hellerstein, 2004; Hiller et al., 2011; Sauer, 2006). While glucose tracers are effectively used to label single substrate microbial cultures and highly oxidative cells or tissues, many mammalian systems are highly compartmentalized and grow on complex media, metabolizing various substrates. For example, tumor cells divert most glucose carbon to lactate and use amino acids (such as glutamine) or fatty acids to contribute carbon to the tricarboxylic acid (TCA) cycle (Boros et al., 2005; DeBerardinis et al., 2007; Fantin et al., 2006) and hepatocytes undergoing gluconeogenesis utilize lactate, amino acids, and glycerol to produce glucose through various pathways (Previs et al., 1999; Yang et al., 2008). As a result, individual tracers are often only effective for characterizing specific pathways such as the TCA cycle or pentose phosphate pathway. Indeed, we recently quantified the dependence of tracer choice and labeling patterns on flux determination in tumor cells, demonstrating the specific utility of individual glucose and glutamine tracers throughout central carbon metabolism (Metallo et al., 2009).

To maximize the information obtained from a given experiment, an alternative approach is to apply multiple tracers simultaneously. This ability would be particularly advantageous in situations where sample number is limited, as in the testing of clinical materials (Boros et al., 2003; Hellerstein et al., 1991). However, the exact combination of tracers used must be chosen with care, as one tracer may mask information generated by another if they generate the same mass isotopomer distribution (MID). This optimization of tracer combinations cannot be accomplished experimentally given (1) the high cost of uniquely labeled tracers, (2) the time and care required for individual flux analysis experiments, and (3) both flux estimation and sensitivity analysis must be performed to ensure that the experimental significance of each flux is maintained.

Here we employed a genetic algorithm to generate mixtures of specifically ¹³C-labeled glucose and glutamine species. At each generation of the evolution we simulated MS measurements for each tracer mixture, re-estimated fluxes, and calculated confidence intervals using an elementary metabolite unit (EMU)-based metabolic flux analysis (MFA) algorithm. Tracer combinations were selected to advance via tournament selection. By coupling our tracer evaluation system to an evolutionary algorithm we identified optimal tracer mixtures that provide the most statistically significant flux values in a non-small cell lung carcinoma cell line. To gage the robustness of one tracer set ([1,2-¹³C₂]glucose+[U-¹³C₅]glutamine) we conducted simulated experiments in which the flux values were perturbed significantly from that of the original network. Finally, we validated the optimized tracer combination experimentally in tumor cells, demonstrating improvements over two other commonly used tracer sets.

2. Materials and methods

2.1. Genetic algorithm

We employed a genetic algorithm to search the space of possible tracer mixtures (Litvinenko et al., 2002; Whitley, 1994). In order to apply our evolutionary approach, we need to define (1) a phenotypic search space, (2) a method of encoding and decoding these phenotypes to and from chromosomes, and (3) a measure of each phenotype’s fitness.

We define phenotype as a vector of tracer composition fractions,

$$\mathit{c}=(f_{1,1},f_{1,2},\dots ,f_{1,N_1},\dots ,f_{i,1},f_{i,2},\dots ,f_{i,N_i},\dots ,f_{M,1},f_{M,2},\dots ,f_{M,N_M})$$ (1)

where c is the tracer composition vector and f_i,_j is the jth isotopologue fraction of substrate i. (Isotopologues are molecules that differ only in their isotopic composition.) There are M total substrates that can potentially be used as tracers and each substrate has N_i total isotopologues that can potentially be used as tracers. We define a chromosome as a translation of the vector of tracer composition fractions into a binary sequence. This sequence can be divided into sub-sequences of equal length whose relative magnitudes correspond to relative fractions. Phenotypes can be converted into chromosomes using the expression

$$h=\sum _k\lfloor 2^b·c_k\rfloor ·2^{b(k-1)}$$ (2)

where c_k are the elements of the tracer composition vector in Eq. (1) (i.e., f_1,1, f_1,2, etc.), b is the number of desired chromosome bits per tracer fraction, and h is in the decimal form of the chromo-some(to apply crossover and mutation events, h is converted to its binary representation to form a bit string). Chromosomes can be decoded back to tracer fractions as follows,

$$c_k=\frac{h\text{mod}{2}^{bk}-h\text{mod}{2}^{b(k-1)}}{2^{b(k-1)}}/\sum _{l\in S_k}\frac{h\text{mod}{2}^{bl}-h\text{mod}{2}^{b(l-1)}}{2^{b(l-1)}}$$ (3)

where S_k is the set of indices of all fractions in c representing the same substrate as c_k so that the denominator of Eq. (3) will renormalize isotopologue fractions in the event that their overall sum was altered during crossover and mutation. Fitness is expressed by a tracer mixture’s precision score, which is calculated from the parameter confidence intervals obtained from simulated MFA experiments (Metallo et al., 2009).

Briefly, the precision score relies on the robust and accurate nonlinear confidence intervals obtained via parameter continuation (Antoniewicz et al., 2006). The precision score for one particular flux is inversely related to the magnitude of that flux’s calculated confidence interval and is calculated as follows. A normalized range is first calculated for each flux using the formula

$$r_i=min\left(\frac{u_i}{\mid v_i\mid },\frac{v_i}{\mid v_i\mid }+\alpha \right)-max\left(\frac{l_i}{\mid v_i\mid },\frac{v_i}{\mid v_i\mid }-\alpha \right)$$ (4)

where v_i, l_i, u_i, and r_i are the estimated flux, lower bound, upper bound, and normalized range for the ith flux, and α is a cut-off parameter that prevents one excessively distant bound from overly influencing the scoring. The individual ranges are next converted into scores using a negative exponential function and summed into a final overall score via the expression

$$S=\sum _i{w}_i\text{exp}\left(-\frac{r_i}{\beta }\right)$$ (5)

where w_i is a weighting parameter for the ith flux, βis a range- scaling parameter, and S is the overall precision score. We empirically found that values of 1 and 3 for α and β result in a good dynamic range of scores. Each w_i is simply zero or one to enable inclusion of independent fluxes only. Thus, a perfectly identifiable flux with a confidence interval of zero results in a precision score of one while an unidentifiable flux returns a score of zero. The overall precision score is the summation of all individual precision scores for all independent fluxes under consideration.

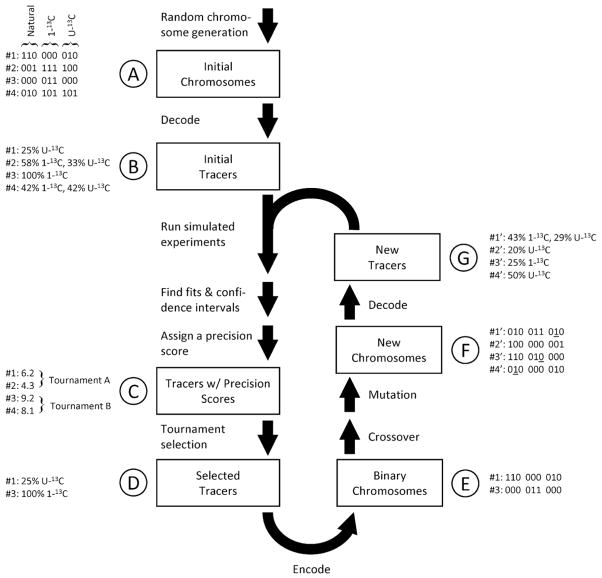
Fig. 1 describes the evolutionary process. First, a set of chromosomes are randomly generated. We designated 8 bits per isotopologue, allowing a resolution within less than 0.5% for each fraction. In creating the initial population, the on/off probability for each bit can be adjusted to control the average number of tracers participating in any given mixture. For all of the initial populations used in this study, an initial population of size 500 and an on/off probability of 10% was found to give realistic and practical results.

Fig. 1.

Tracer optimization by means of a genetic algorithm. The central flowchart illustrates the algorithm’s steps. A simple example is also provided where three isotopic forms of the tracer (naturally labeled, first-carbon labeled, and uniformly labeled) are considered. First, a random set of chromosomes is decoded to produce an initial population of tracer mixtures (A,B). Our selection criterion, the precision score, is generated for each mixture from confidence intervals calculated via simulated flux analysis experiments (D). Tracer mixtures are chosen for the next evolutionary round by tournament selection (D). The mixtures are encoded back to chromosomes (E), after which mutation and crossover events are applied to the selected to generate a new population (F). These new chromosomes are decoded into tracer mixtures and can participate in a new round of evolution if desired (G).

The initial chromosomes are next decoded by using Eq. (3) to give tracer composition vectors. Simulated flux analysis experiments are then conducted for each vector, producing parameter confidence intervals from which precision scores can be calculated. Tournament selection is then applied to choose successful phenotypes for recombination while still retaining some diversity (Goldberg, 1991). The surviving phenotypes are then encoded back to chromosomes and are modified by two-point crossover and point mutation events to form a new population (which can serve as a starting point for another iteration of the evolutionary process). For each of the evolutionary rounds in this study, a tournament size of four was used to select 25% of the current population for survival. The survivors were then mated using two-point crossover to create a completely new population equal in size to the previous population. The genetic algorithm can be set to stop after completing a pre-specified number of iterations or after no significant improvements have been made in precision score through a given number of iterations.

2.2. Cell culture and metabolite extraction

The A549 lung carcinoma cell line (ATCC) was maintained in high-glucose DMEM supplemented with 4 mM glutamine, 10% FBS, and 100 U ml⁻¹ penicillin/streptomycin (Invitrogen). Prior to labeling, cells were maintained in custom DMEM lacking amino acids, glucose, and pyruvate (Hyclone) supplemented with 25 mM glucose, 4 mM glutamine, 1X MEM essential amino acids (Invitrogen), 10% FBS, and antibiotics for at least 1 passage. For flux experiments semi-confluent cells were cultured with [1,2-¹³C₂] glucose+[U-¹³C₅]glutamine, a 1:1 mixture of [U-¹³C₆]glucose and [1-¹³C]glucose, or [U-¹³C₅]glutamine alone (Cambridge Isotope Laboratories) for 24 h to achieve isotopic steady state. Spent medium was collected and analyzed for glucose, lactate, glutamine, and glutamate on a YSI7100 analyzer. Extracellular fluxes were calculated from these measurements and cell counts on parallel plates. Metabolite extraction was conducted as previously described (Hiller et al., 2010). Briefly, cells were quenched with 400 μl −20 °C methanol, an equal volume of water was added, and cells were collected via scraping. Two volumes of chloroform were added, and the cells were vortexed at 4 °C for 30 min. Samples were centrifuged at 10,000 g for 10 min, and the aqueous phase was collected in a new tube for evaporation under airflow.

2.3. Derivatization and GC/MS analysis

Dried polar metabolites were dissolved in 50 μl of 2% methoxyamine hydrochloride in pyridine (Pierce) and held at 37 °C for 2 h. After reaction the solution was split equally to two tubes and 45 μl of either MBTSTFA+1% TBDMCS or MSTFA+1% TMCS (Pierce) was added. Samples were incubated for 60 min at 55 °C or 37 °C, respectively. Gas chromatography/mass spectrometry (GC/MS) analysis was performed using an Agilent 6890 GC equipped with a 30 m DB-35 MS capillary column connected to an Agilent 5975B MS operating under electron impact (EI) ionization at 70 eV. One μl of sample was injected in splitless mode at 270 °C, using helium as the carrier gas at a flow rate of 1 ml min⁻¹. The GC oven temperature was held at 100 °C for 3 min and increased to 300 °C at 3.5° min⁻¹ for a total run time of approximately 60 min. The MS source and quadrupole were held at 230 °C and 150 °C, respectively. The detector was operated in scanning mode for TBDMS derivatizations and in selected ion monitoring (SIM) mode for metabolites reacted with TMS. MIDs were obtained for each measured metabolite and incorporated with extracellular flux measurements for flux determination. The identity and values of these measured fragments and fluxes are listed in Table 1.

Table 1.

Intracellular mass isotopomer measurements for simulated metabolic flux analysis of the A549 carcinoma cell.

Metabolite	Carbons
3PG	123
AKG	12,345
Ala	23
Ala	123
Asp	12
Asp	12
Asp	234
Asp	1,234
Cit	123,456
Gln	12,345
GLP	123
Glu	2,345
Glu	12,345
Glu	12,345
Gly	2
Gly	12
Lac	23
Lac	123
Mal	1,234
P5P	12,345
Pyr	123
Ser	12
Ser	23
Ser	123
Suc	1,234

2.4. MFA calculations

Flux determination and confidence interval calculations were accomplished using a metabolic tracer analysis software package, Metran (Antoniewicz et al., 2006; Antoniewicz et al., 2007a; Young et al., 2008). A general description of calculations and assumptions as well as fitted fluxes and complete data sets are included as Supplementary Material.

3. Results and discussion

3.1. Tracer optimization

We applied our tracer optimization algorithm to the metabolism of the A549 lung carcinoma cell line, which was previously characterized using ¹³C MFA (Metallo et al., 2009). The major features of this flux network are a high glycolytic flux where glucose is almost completely excreted as lactate and a TCA cycle that is driven primarily by glutamine oxidation. See Table 2 for the metabolic network and atom transitions.

Table 2.

List of reactions and atom transitions for the A549 carcinoma model.

Metabolic reaction network and carbon atom transitions used for flux determination and modeling
Measured fluxes
Gluc.x (abcdef)→G6P (abcdef)
Lac (abc)→Lac.x (abc)
Gln.x (abcde)→Gln (abcde)
Glu (abcde)→Glu.x (abcde)
0.18 Asp+0.23 Glu+0.17 Ser+0.11 Gly+0.15 Ala+0.16 Gln→Biomass
Glycolysis
G6P (abcdef)↔F6P (abcdef)
F6P (abcdef)→DHAP (cba)+GAP (def)
DHAP (abc)↔GAP (abc)
GAP (abc)↔3PG (abc)
3PG (abc)→Pyr.c (abc)
Pyr.c (abc)↔Lac (abc)
Pyr.c (abc)↔Pyr.m (abc)
Glycerol synthesis
DHAP (abc)↔GLP (abc)
GLP (abc)→GLP.x (abc)
Pentose phosphate pathway
G6P (abcdef)→P5P (bcdef)+CO2 (a)
P5P (abcde)+P5P (fghij)↔S7P (abfghij)+GAP (cde)
S7P (abcdefg)+GAP (hij)↔F6P (abchij)+E4P (defg)
P5P (abcde)+E4P (fghi)↔F6P (abfghi)+GAP (cde)
Anaplerotic fluxes
Pyr.m (abc)+CO2 (d)→OAA (abcd)
Mal (abcd)↔Pyr.m (abc)+CO2 (d)
TCA Cycle
Pyr.m (abc)→AcCoA.m (bc)+CO2 (a)
AcCoA.m (ab)+OAA (cdef)→Cit (fedbac)
Cit (abcdef)↔AKG (abcde)+CO2 (f)
AKG (abcde)→Suc (bcde)+CO2 (a)
Suc (abcd)↔Fum (abcd)
Fum (abcd)↔Mal (abcd)
Mal (abcd)↔OAA (abcd)
Fatty acid synthesis
Cit (abcdef)→AcCoA.c (ed)+OAA (fcba)
AcCoA.c (ab)→FA (ab)
Amino acid biosynthesis
Pyr.m (abc)+Glu (defgh)→Ala (abc)+AKG (defgh)
OAA (abcd)+Glu (efghi)→Asp (abcd)+AKG (efghi)
3PG (abc)+Glu (defgh)→Ser (abc)+AKG (defgh)
Ser (abc)↔Gly (ab)+MEETHF (c)
Glutamine anaplerosis
Gln (abcde)→Glu (abcde)
Glu (abcde)↔AKG (abcde)
Biomass production
P5P (abcde)→NTP (abcde)
MEETHF (a)→MEETHF.x (a)
Dilution fluxes/compartmentalization
Gly.p (ab)→Gly (ab)
Ser.p (abc)→Ser (abc)
P5P.dil (abcde)→P5P.mnt (abcde)
0 P5P (abcde)→P5P.mnt (abcde)
GLP.dil (abc)→GLP.mnt (abc)
0 GLP (abc)→GLP.mnt (abc)
Suc.dil (abcd)→Suc.mnt (abcd)
0 Suc (abcd)→Suc.mnt (abcd)
0 Pyr.c (abc)→Pyr.mnt (abc)
0 Pyr.m (abc)→Pyr.mnt (abc)

Suffixes indicate localization to a specific compartment: .x, extracellular; .c, cytosolic; .m, mitochondrial; .p, protein; .d, dilution; .mnt, measurement. Dilution and measurement compartments do not partake in central metabolism. Metabolites lacking a suffix are assumed to be equilibrated between compartments.→indicates irreversible reactions while↔indicates reversible reactions.

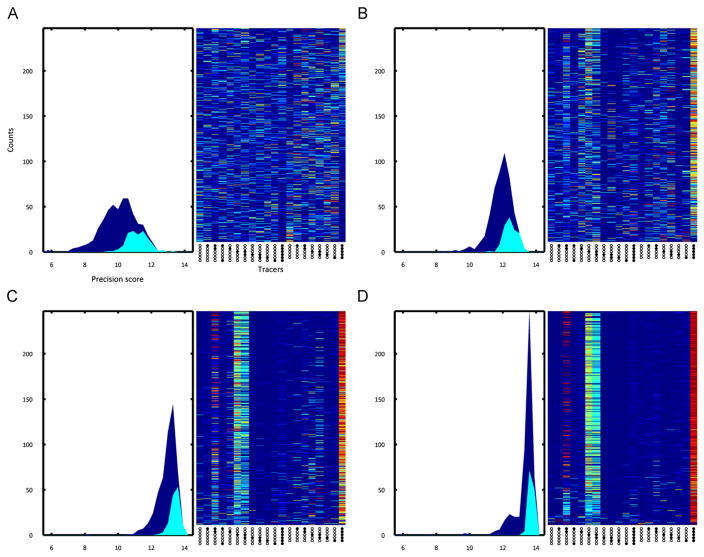
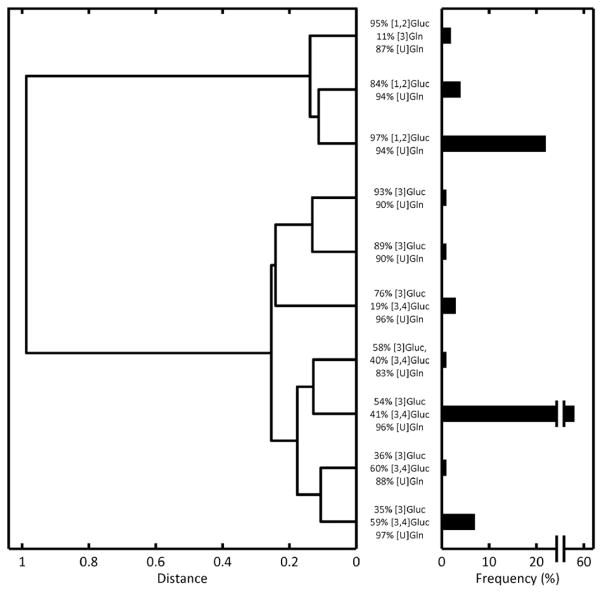
We considered 18 ¹³C-labeled substrates (11 glucose and 7 glutamine) along with naturally labeled glucose and glutamine as potential participants in the optimized tracer mixture (see Table 3 for the complete list of tracers and their accompanying abbreviations). A set of 500 randomized tracer mixtures was created as an initial population and subjected to ten rounds of evolution (Fig. 2). The mean precision score of the population progressed from 11.3 to 13.9 and the maximum score from 13.3 to 14.3. Hierarchical clustering revealed two primary motifs in the final selected population of tracer mixtures (Fig. 3). One group of mixtures chiefly used [1,2]Gluc as the glucose tracer, while the other group used a combination of [3] and [3,4]Gluc. All selected mixtures relied almost exclusively upon [U]Gln as the glutamine tracer.

Table 3.

Glucose and glutamine tracers chosen as potential tracer mixture components. Commercially available glucose and glutamine tracers were chosen for analysis.

Tracer	Abbreviation
[1-13C]glucose	[1]Gluc
[1,2-13C2]glucose	[1,2]Gluc
[1,6-13C2]glucose	[1,6]Gluc
[2-13C]glucose	[2]Gluc
[3-13C]glucose	[3]Gluc
[3,4-13C2]glucose	[3,4]Gluc
[4-13C]glucose	[4]Gluc
[4,5-13C2]glucose	[4,5]Gluc
[5-13C]glucose	[5]Gluc
[6-13C]glucose	[6]Gluc
[U-13C6]glucose	[U]Gluc
[1-13C]glutamine	[1]Gln
[1,2-13C2]glutamine	[1,2]Gln
[3-13C]glutamine	[3]Gln
[3,4-13C2]glutamine	[3,4]Gln
[4-13C]glutamine	[4]Gln
[5-13C]glutamine	[5]Gln
[U-13C5]glutamine	[U]Gln

Fig. 2.

Selected tracer mixtures after rounds 1,4,7, and 10 of tracer optimization are shown in subfigures (A)–(D), respectively. The left subplot of each subfigure shows the general (dark blue) and selected (cyan) tracer mixture populations distributed by precision score. The right subplot shows the tracer fractions of each mixture (sorted with highest scoring mixtures at the top), where columns correspond to tracer fractions and rows to tracer mixtures. A dark red slice corresponds to a tracer fraction of 100%, while dark blue corresponds to zero. By the final round of evolution, we see that the distribution of precision scores shift upwards by about two units and the initial randomly distributed set of tracer mixtures has been narrowed down to two different tracer mixtures: [1,2]Gluc/[U]Gln and [3]Gluc/[3,4]Gluc/[U]Gln.

Fig. 3.

Hierarchical cluster tree of high-scoring tracer mixtures. The 100 highest-scoring tracer mixtures (over all rounds of evolution) were taken and clustered by composition fraction. The length of each tree represents the distance (or dissimilarity) between the two tracer mixtures (or groups of tracer mixtures) being connected. The major tracers in each mixture are listed in the vertical direction. The bar lengths on the right axes represent the frequency of each cluster among the selected 100. The tree reveals that there are two general high-scoring mixtures: those using [1,2]Gluc and those using [3] and [3,4]Gluc. All mixtures predominantly utilize [U]Gln as a glutamine tracer.

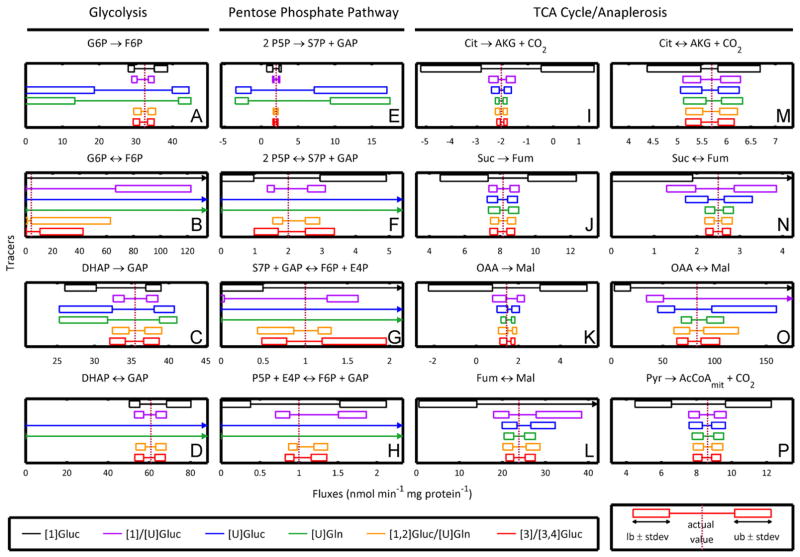
We simplified these two selected motifs into one mixture of 100% [1,2]Gluc and 100% [U]Gln and another of 50% [3]Gluc, 50% [3,4]Gluc, and 100% [U]Gln. With regards to precision score, these simplified versions perform comparably to the original selected tracers. To better characterize the performance of each tracer motif, we determined individual precision scores for each flux. We also calculated flux-by-flux precision scores for three traditional stand-alone isotopic tracers ([1]Gluc, [U]Gluc, and [U]Gln) as well as one traditional and simple tracer mixture (a 1:1 mixture of [1]Gluc and [U]Gluc). A heat map of precision-score ratios for each pairing of selected tracer mixture and traditional tracer for each flux is shown in Fig. 4. Confidence intervals for the tracer mixtures and traditional tracers are also shown for a selected set of fluxes in Fig. 5.

Fig. 4.

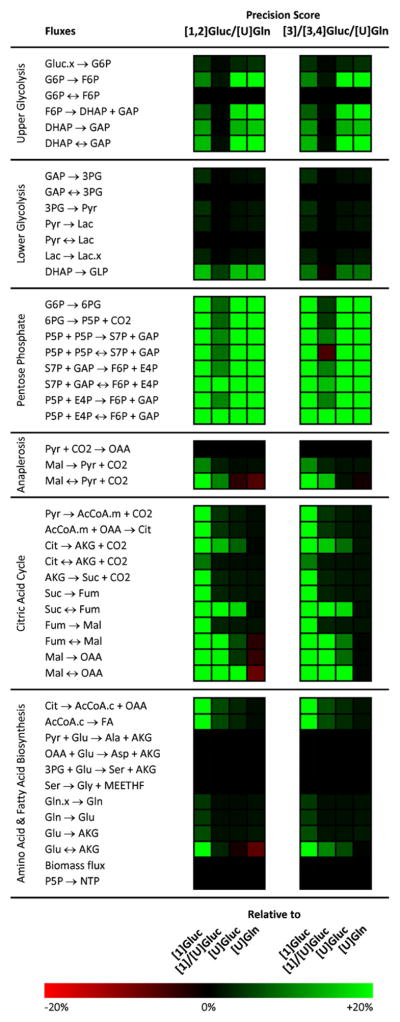
A heat map comparing flux-by-flux precision scores for traditional tracers ([1]Gluc, [1]/[U]Gluc, [U]Gluc, and [U]Gln) and evolved tracer mixtures ([1,2]Gluc/[U]Gln and [3]/[3,4]Gluc/[U]Gln). Green indicates a superior precision score for the evolved tracer and red indicates a superior score for the traditional tracer. As a point of reference, for a confidence interval distributed symmetrically around an estimated flux, a +/−20% change in precision score corresponds to a ±60% change in the confidence interval width.

Fig. 5.

Simulated confidence intervals for selected fluxes when using common ¹³C tracers compared to the high-scoring [1,2]Gluc/[U]Gln and [3]/[3,4]Gluc/[U]Gln tracer mixtures. Whereas glucose- and glutamine-only tracers perform poorly in different portions of the network, the tracer mixture performs consistently well across all of central carbon metabolism, including glycolysis (A)–(D), the pentose phosphate pathway (E)–(H), and the TCA cycle (I)–(P). In reactions→indicates net flux: (υ_F − υ_R); ↔indicates exchange flux: min(υ_F, υ_R).

3.2. Analysis of tracer behavior

The evolved tracer mixtures matched or outperformed all of the standard tracers with respect to precision scoring in reactions throughout central carbon metabolism. The precision score heat map (Fig. 4) quickly highlights the pentose phosphate pathway as the major area of improvement. The optimized tracers also strongly outperformed the [1]Gluc/[U]Gluc and [1]Gluc tracers in the TCA cycle and the [U]Gluc and [U]Gln tracers in glycolysis. To investigate our results further we can return to actual confidence intervals and compare fluxes tracer-by-tracer in Fig. 5.

For most glycolytic fluxes, the evolved mixtures demonstrated more precise confidence intervals than all standard tracers (Fig. 5A, C, D). In a few instances, the evolved mixtures led to confidence intervals comparable to those of [1]/[U]Gluc but still better than the rest (Fig. 5B). For almost all fluxes of the pentose phosphate pathway, the evolved mixtures again had more precise confidence intervals (Fig. 5E, G, H). In a few cases, [1]/[U]Gluc performed similarly well (Fig. 5F). For the majority of TCA cycle fluxes, the two evolved mixtures together with the [U]Gln tracer produce the narrowest confidence intervals (Fig. 5I, K, L, N, O). For some fluxes (Suc→Fum, Cit↔AKG+CO₂, and Pyr→AcCoA_mit + CO₂), the evolved mixtures outperform all standard tracers (Fig. 5J, M, P).

The high precision score of our selected [1,2]Gluc/[U]Gln mixture is to be expected, since [1,2]Gluc performed well in glycolysis and the PPP and [U]Gln performed well in the TCA cycle. Importantly, these tracers are demonstrated to be compatible given their lack of overlap with respect to metabolite labeling patterns, which might otherwise increase confidence intervals for determined fluxes. The appearance of the [3]Gluc/[3,4]Gluc/[U]Gln mixture as an optimal tracer is more surprising, and highlights the power of our evolutionary approach to find good tracers that could not easily have been chosen by intuition. To shed light on the reasons behind this mixture’s efficacy, we can compare the precision of this optimal tracer with three of its close relatives: [3]Gluc, [3,4]Gluc/[U]Gln, and [4]Gluc/[U]Gln. A flux-by-flux precision score heat map of the selected tracer mixture versus these three similar mixtures is shown in Fig. 6.

Fig. 6.

A heat map comparing flux-by-flux precision scores for the optimized [3]Gluc/[3,4]Gluc/[U]Gln tracer mixture to scores for the simpler [3]Gluc/[U]Gln, [3,4]Gluc/[U]Gln, and [4]Gluc/[U]Gln tracer mixtures. Green indicates a superior precision score for the evolved tracer and red indicates a superior score for the traditional tracer mixture. TCA cycle fluxes are not shown since precision scores there were very similar due to the common [U]Gln tracer. As a point of reference, for a confidence interval distributed symmetrically around an estimated flux, a ± 20% change in precision score corresponds to a ±60% change in the confidence interval width.

We first notice that [4]Gluc/[U]Gln scores lowest in the group, because of poor precision primarily in the pentose phosphate pathway and secondarily in upper glycolysis. As previously discussed (Metallo et al., 2009), the fourth atom of glucose is trapped in a cycle and fails to spread to other positions, regardless of the flux distribution. When glucose is labeled both at the third and fourth positions, we see that pentose phosphate precision improves; the third labeled carbon, not limited to a futile cycle, is able to spread through the PPP atoms and as a result exhibits more sensitivity to fluxes there. The solitary [3]Gluc tracer represents an additional improvement as the cycle of atoms that was previously fully labeled (and hence insensitive) is now able to show gradations in labeling as the third glucose atom spreads through the network.

Moving from [3]Gluc to our optimized glucose tracer of [3]Gluc/[3,4]Gluc represents the final step in the progression. The difference in precision is simple, as the precision score of the S7P+GAP↔E4P+F6P exchange reaction increases greatly when we partially label the fourth glucose carbon atom. This increase is most likely due to the atom transition E4P₂↔F6P₄ within this reaction, which brings label out of the pentose phosphate pathway into glycolysis which then directly leads to the GLP measurement.

3.3. Precision score sensitivity

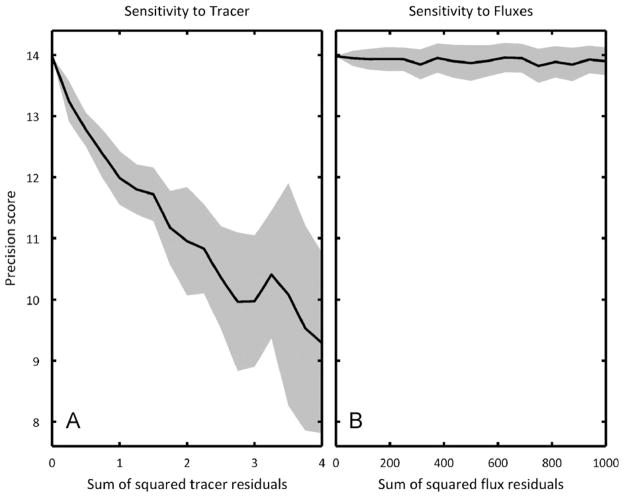
Here we have simulated precision scores for a single distribution of fluxes; however, fluxes in different experimental systems may vary significantly. To probe the sensitivity of our precision scoring to flux distribution, we simulated precision scores for [1,2]Gluc/[U]Gln for a large number of flux distributions varied randomly around the original to see how the precision score would change (Fig. 7B). As a control, we also varied the tracer composition in a separate set of simulations to determine the sensitivity of the precision score with respect to tracer composition (Fig. 7A). The precision score sensitivity to the flux distribution is much less than the sensitivity to tracer composition, so we can have confidence in our selected tracer mixtures even if we are not absolutely certain of the actual metabolic flux distribution upon which the optimization was based.

Fig. 7.

The sensitivity of precision score with respect to (A) tracer composition and (B) flux distribution. Solid lines indicate the average precision score for a particular sum of squared residuals while shading indicates one standard deviation above and below the average. In both subfigures, the initial tracer is a mixture of 100% [1,2]Gluc and 100% [U]Gln and the initial flux distribution is the carcinoma distribution used in the tracer optimization. In (A), the flux distribution is held constant and the tracer composition is varied from a sum of squared residuals of 0 (original tracer) up to 4 (completely different tracers). In (B), the tracer composition is held constant and the flux distribution is varied from a sum of squared residuals of 0 (original tracer) up to 1000 (a simultaneous 15% change for all independent fluxes). On these scales, the precision score is much more sensitive to tracer, meaning that a high-scoring tracer will serve well even if the actual flux distribution does match the hypothetical distribution used in the genetic algorithm.

3.4. Experimental validation

To validate the simulated results of our genetic algorithm, we conducted independent MFA experiments on the original A549 cell line with one of our optimized tracer mixtures ([1,2]Gluc/[U]Gln), one average tracer mixture ([1]Gluc/[U]Gluc), and one poor tracer ([U]Gln). We compared the resulting experimental precision scores to the previously simulated precision scores for each of the same tracers (Fig. 8).

Fig. 8.

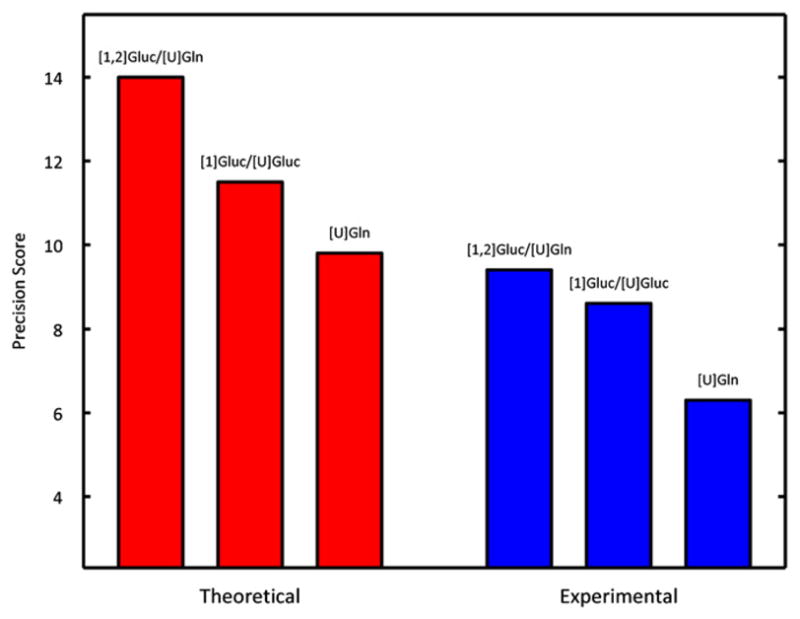
Simulated and experimental precision scores for experiments on A549 carcinoma metabolism utilizing three different tracers: [1,2]Gluc/[U]Gln, [1]Gluc/[U]Gluc, and [U]Gln. Experimental precision scores follow the same trend predicted in theory, validating the method.

These results experimentally confirm our findings, as the general trend in improved performance holds steady. In both simulation and experiment, [1,2]Gluc/[U]Gln scores best, followed by [1]Gluc/[U]Gluc, with [U]Gln scoring worst, validating our tracer optimization study. There were three minor differences in the score sets. First, the experimental scores overall were lower than those obtained from our simulations. To obtain acceptable fits we increased the minimum standard error of measurements for MIDs to 0.5%. Thus, the standard errors for experimental fits were higher than those used in the simulations, leading to increased confidence intervals and decreased precision scores. This adjustment was uniformly applied to all measurements and therefore did not bias the results of our validation. Second, the improvement in precision of the [1,2]Gluc/[U]Gln mixture over the [1]Gluc/[U]Gluc mixture was decreased when moving from simulation to experiment. This issue arose from assumptions that we originally made regarding the P5P measurement. This particular measurement turned out to be less reliable than expected and as a result was assigned a higher-than-average standard error. Since much of the optimized mixture’s advantage arises from gains made in pentose phosphate precision and many of the confidence intervals in this pathway depend heavily on the P5P measurement, the optimized tracer’s overall precision score suffered somewhat relative to the other scores. Finally, the actual fluxes determined for the different tracer combinations were slightly different, presumably due to changes in the cell culture upon passaging between experiments. Since atom transitions and tracers are the primary determinants which influence precision scoring such changes are unlikely to significantly affect scores (Fig. 7). Despite these discrepancies, the promiscuous, non-redundant labeling of metabolites by this tracer mixture allows significant improvements over established MFA methods.

4. Conclusion

We have created a genetic algorithm that can search through a large space of tracer combinations to find prominently performing mixtures for high-precision metabolic flux analysis. We applied this algorithm to tumor metabolism and discovered two optimal tracer mixtures, [1,2]Gluc/[U]Gln and [3]Gluc/[3,4]Gluc/[U]Gln. These tracers lead to flux estimates of superior quality in both glycolysis and the TCA cycle, where most typical, single-substrate glucose and glutamine tracers only target the former or the latter, respectively. These evolved mixtures also offer significant improvement for analysis of the pentose phosphate pathway. We have confirmed our theoretical results by experimenting with selected tracer mixtures and demonstrating that they do indeed generate more precise flux confidence intervals.

As a first step, we demonstrate that EMU-based algorithms can efficiently and reliably estimate fluxes and confidence intervals using multiple substrate compounds as tracers (as opposed to single tracers or mixtures of glucose tracers) (Antoniewicz et al., 2006; Young et al., 2008). These methods greatly strengthen experimental design capabilities for metabolic flux analysis. For example, biomass hydrolysates contain carbohydrates, amino acids, and other nutrients, and complex tracer mixtures would therefore be ideal in characterizing metabolic pathways in organisms engineered to produce biofuels from such source materials (Huo et al., 2011). In addition, we can customize tracers for both system-wide and more targeted flux studies with this method of selection. Although much of current MFA research is directed at measuring metabolism on large scales, some of the most powerful and meaningful applications occur in studies focusing on specific pathways or reactions (Boros et al., 2003; Burgess et al., 2007). Our genetic algorithm for tracer optimization is a powerful tool in designing experiments for such studies, which would otherwise be cost-prohibitive due to the expense of many tracers. Recently, Chang et al. developed a complementary application, OptMeas, which identifies the optimal measurement set (rather than optimal tracer) required to elucidate a unique flux distribution for a given metabolic network (Chang et al., 2008).

Our evolutionary selection proved its usefulness when it highlighted a tracer containing [3]Gluc and [3,4]Gluc as an important tracer in cancer metabolism. Even though we had extensive experience with this particular network and flux distribution, this optimal tracer mixture was unexpected and nonintuitive. In the future, as knowledge of metabolic reaction networks and measurement capabilities improve, this method may be applied to genome-scale networks (Suthers et al., 2007). Such applications might be significantly enhanced experimentally through the use of preselected tracer mixtures. Without a systematic search algorithm such as this, optimal tracer mixtures would most likely remain undiscovered. Furthermore, by studying these newly discovered tracers we can gain a deeper understanding of the complex network of atom transitions in metabolism that will aid us in further experimental design.

Abbreviations

AcCoA

Acetyl coenzyme A

AKG

α-ketoglutarate

Ala

alanine

Asp

aspartate

Cit

citrate

Fum

fumarate

Gln

glutamine

Glu

glutamate

Gly

glycine

Mal

malate

OAA

oxaloacetate

Lac

lactate

Pyr

pyruvate

Suc

succinate

Ser

serine

Gluc

glucose

G6P

glucose-6-phosphate

F6P

fructose-6-phosphate

DHAP

dihydroxyacetone phosphate

GAP

glyceraldehyde phosphate

GLP

glycerol-3-phosphate

3PG

3-phosphoglycerate

P5P

pentose-5-phosphate

E4P

erythrose-4-phosphate

S7P

sedoheptulose-7-phosphate

Appendix A. Supplementary materials

Supplementary materials associated with this article can be found in the online version at doi:10.1016/j.ymben.2011.12.004.