Accuracy and Precision of Radioactivity Quantification in Nuclear Medicine Images

Abstract

The ability to reliably quantify activity in nuclear medicine has a number of increasingly important applications. Dosimetry for targeted therapy treatment planning or for approval of new imaging agents requires accurate estimation of the activity in organs, tumors, or voxels at several imaging time points. Another important application is the use of quantitative metrics derived from images, such as the standard uptake value commonly used in positron emission tomography (PET), to diagnose and follow treatment of tumors. These measures require quantification of organ or tumor activities in nuclear medicine images. However, there are a number of physical, patient, and technical factors that limit the quantitative reliability of nuclear medicine images. There have been a large number of improvements in instrumentation, including the development of hybrid single-photon emission computed tomography/computed tomography and PET/computed tomography systems, and reconstruction methods, including the use of statistical iterative reconstruction methods, which have substantially improved the ability to obtain reliable quantitative information from planar, single-photon emission computed tomography, and PET images.

In vivo activity quantification is an important task in nuclear medicine. However, major imaging modalities (planar, single-photon emission computed tomography [SPECT], and positron emission tomography [PET] imaging) have factors that must be addressed to achieve reliable results. Understanding these factors and resulting limitations is important because they have implications about the suitability of a particular modality for a given task. Interpretation of results without appreciating the magnitude of the errors, in terms of accuracy and precision, may result in patient care errors.

Reliability of Quantitative Images

The goal of activity quantification is to enable diagnostic or therapeutic decisions based on estimates of activity in objects or regions in the body. Two criteria characterize the reliability of such estimates: accuracy and precision. Accuracy describes the deviation of an estimate of some quantity from the true value, whereas precision describes the variability of an estimate about its mean. Accuracy is often expressed in terms of the bias or relative error, whereas precision is described by the standard deviation or coefficient of variation.

High accuracy is desirable, but for many applications a consistent bias or deviation from the true value is acceptable, and variations in measurement reproducibility are not. For example, consider quantitative imaging for radioimmunotherapy treatment planning. For a typical radioimmunotherapy agent, a dose escalation study is first performed using imaging to determine the maximum tolerated dose (MTD) for critical organs. If an inaccurate yet reproducible error exists, then the estimated MTD would be inaccurate but of high precision. In this case, differences in the MTD would reflect biological variability in the patient cohort. Thus, the safety margin in setting the MTD would be based on biological variability. In contrast, if the estimated doses were accurate, but of very low precision, then the inability to isolate the relevant biological variability from the imprecision in physical measurements would significantly diminish the value of patient-specific dosimetry and require a larger safety margin for the MTD. As a result of the aforementioned considerations, we will discuss factors affecting both the accuracy and precision of the measurements.

Another important concept is the reliability of measures over a population. To determine the MTD, we estimate organ doses for each patient only once, but perform the study over many patients. Because patients differ in anatomy and physiology, it is important to understand how variations in these factors over the population affect the quantitative measurements.

Factors Affecting Reliability of Image-Based Activity Estimates

The process of estimating activity often involves implicit or explicit modeling of the image formation process. The factors in imaging systems that result in the failure to satisfy this model are often referred to as image degrading factors. Degrading factors can be divided into the following 3 categories: effects resulting from the physics of the image formation, factors resulting from the choice of image protocol parameters, and factors resulting from biology and physiology of the patient.

Physical Factors Affecting Radioactivity Quantification

The important physical factors are photon interactions in the patient, loss of spatial accuracy due to limited system resolution, partial volume effects (PVEs), and noise resulting from the random nature of radioactive decay and absorption. In PET, random coincidences play an additional role.

Attenuation and Scatter

Emitted photons undergo scattering and photoelectric absorption in the patient, which reduce the number of detected photons. Because projections are obtained at multiple views, the attenuation for a point inside an object depends on its average depth and the tissue composition between the point and the surface. Without compensation, attenuation results in interior regions having a lower estimated activity compared with superficial ones. For large objects, attenuation is the single largest factor degrading quantitative accuracy.

Compton scattering of a photon produces a change in both its direction and energy. Due to limited energy resolution, a significant number of scattered photons will be detected, and the change in direction means that scattered photons carry degraded information about the photons’ point of emission. The scatter point response function (SPRF) describes the distribution of detected scattered photons resulting from a point source. The SPRF depends on the patient and source position. It typically has a similar full-width at half maximum (FWHM) resolution but wider full-width at tenth maximum resolution than the point response function of unscattered photons. Scatter results in a loss of image contrast and degraded quantitative information. Images reconstructed with attenuation compensation but without scatter compensation result in a spurious increase in image intensity, especially in the interior of the image.

The magnitude of scatter effects depends on photon energy, source depth, energy window setting, and the energy resolution of the system. Scatter effects are larger for lower energy photons and for radionuclides with multiple-photon emission.

Imaging System Resolution

Nuclear medicine images have limited spatial resolution. This results in PVEs that worsen the quantitative accuracy more for smaller object sizes. In single-photon imaging, the resolution is determined largely by the collimator-detector response (CDR). For photons passing through the holes, the blurring is characterized by the geometric response function (GRF) with a width depending on both the hole dimensions and the distance from the collimator face.

Some photons penetrate through the collimator septa without interactions, whereas other scatter from the septa. Together these contribute long tails to the response function, especially for medium- and high-energy photons.

The final component of the CDR is the intrinsic response of the detector that results from imprecision in estimating the position of the interaction point of the gamma ray in the detector crystal due to crystal scatter and statistical variations.

In planar imaging, projecting activity in the patient to a single plane results in a mixture of resolutions for objects comprising the image. In SPECT, spatial variance of the CDR results in a spatially varying and asymmetric reconstructed point response function where the asymmetry depends on the collimator as well as the camera orbit. For a circular orbit, the resolution is the same on all radial lines. It is worst at the center, constant in the radial direction, and improves in the tangential direction with increasing distance from the center. For noncircular orbits there is even greater spatial variation in the resolution. Typical FWHM resolutions in SPECT range between 7 and 20 mm. The septal scatter and penetration components result in noise-like artifacts in the images and a contrast reduction.

In PET, the resolution is determined by crystal size, scatter in the crystals, positron range, and effects of annihilation photon acolinearity. Current whole-body scanners possess FWHM resolutions of between 5 and 7 mm at the center of the field-of-view (FOV); resolution degrades toward the edge of the FOV because of depth-of-interaction effects. For decays at the center of the detector ring, photons strike the detectors orthogonally. With increasing off-axis distances, the line of response of 2 such photons strikes the detectors at decreasing angles of incident, resulting in penetration into adjacent detector elements, and misregistration of the line of response. This parallax error decreases the image resolution with increasing distance from the scanner axis and becomes worse as the ring diameter decreases and as the cross sectional area of the detector is reduced.

Partial Volume Effects

PVEs are a combination of 2 factors. The first is image sampling, that is, each SPECT or PET voxel has a definite size, and the activity is assumed to be uniformly distributed inside the voxel. This is sometimes known as the partial voxel effect (thus a phantom in the shape of a true pyramid appears in the image like a stepped pyramid). The second factor is a consequence of the resolution properties of the detected photon events. For both PET and SPECT, these factors, described previously, blur the images, resulting in activity from multiple objects or organs contributing the intensity of a given image voxel. When imaging features in the body, PVEs can manifest as the spill-out of activity into surrounding objects from a hot object (typical of tumor imaging) and spill-over (or spill-in) of activity into a cold VOI (more typical in cardiac imaging). Partial volume corrections are especially important when quantifying the activity within objects of sizes less than twice the FWHM spatial resolution of the imaging system.

Image Noise

Because radioactive decay and photon interactions are independent random processes, the numbers of photons passing through an object and absorbed in a detector system are random variables governed by Poisson statistics. This produces statistical noise in the resulting images and imprecision in activity estimates.

Image reconstruction in SPECT and PET tends to correlate and amplify the high-frequency components of this noise, resulting in large voxel-to-voxel variations. Low-pass filtering can reduce the high-frequency noise, but at the expense of spatial resolution. Resolution recovery methods tend to correlate the midfrequency noise, resulting in a blobby noise texture.

Patient Factors

Images can be degraded by involuntary (heart beating and respiration) or voluntary motions. If motions are periodic with a period short compared with the acquisition time, these manifest themselves as a loss of spatial resolution. Activity within a given structure will be attributed to a larger volume corresponding to the motion path of the object being imaged. For example, a tumor in the base of the lung that moves 8 mm due to diaphragmatic motion will result in an image in which the activity is smeared over this additional 8 mm, resulting in a significant underestimation of the relative specific activity. Nonperiodic motion produces more complicated artifacts in reconstructed SPECT or PET images depending on type of motion and the acquisition geometry.

Interacquisition motion is important to consider when images are taken at multiple time points to measure a timeactivity curve. For short-lived radionuclides, it may be possible to minimize motion by retaining the patient on the couch and using restraints. For long-lived tracers, careful repositioning is necessary. Inconsistent repositioning and reshaping of organ VOIs lead to inaccuracies and imprecision. For voxel-based dosimetry, accurate registration at the voxel level of activity or dose-rate images is needed.

Anatomy

The size, shape, and geometrical relationships between organs and tissues affect the attenuation and photon scattering in the body. Larger patients attenuate more, producing more noise for the same administered activity, and a larger fraction of detected scattered photons. Organs that are smaller or elongated will have greater PVEs. The size and shape of patients also determines the minimum radius of rotation and the orbit when using body contouring; these affect the resolution and spatial variation of the resolution and thus impact the PVEs. All these factors contribute to variations in accuracy that manifest as imprecision over a patient population.

Physiology and Function

Different imaging agents possess different pharmacokinetics and the macro- and microdistribution within tumors and organs, and these factors will have profound effects on the PVEs. Patient diet can also affect the uptake of a radiopharmaceutical. For example, the amount of iodine in the diet can significantly affect the percent radioiodine uptake in the thyroid when planning for therapy and food eaten before an fluorodeoxyglucose (FDG) PET scan can significantly reduce the standard uptake value (SUV). For PET scans, the time after injection can also have an effect on the magnitude of the SUV.

Technical Factors

The collimator largely determines the sensitivity and resolution of a single-photon system. It also determines the magnitude and spatial variation of septal penetration and scatter effects that can introduce artifacts within images and biases into the quantitative estimates. Imaging smaller objects or objects in close proximity to a high-uptake organ requires a high-resolution collimator; isolated large organs with low uptake may benefit from using a higher sensitivity collimator to improve precision. To maximize spatial resolution, the minimum possible radius of rotation (or detector height) should be used. Noncircular orbits can exacerbate the nonuniform spatial resolution in SPECT but generally improve the overall image resolution and reduce PVEs. Generally, the number of projections over 360 degrees should be at least equal to the matrix size, although theoretically the value should be slightly more than 3 times the matrix size for a 360-degree acquisition to avoid angular aliasing. The matrix size should be chosen to avoid limiting image resolution, which means the voxel size should be one-half to one-third of the FWHM collimator resolution at a typical radius of rotation.

The use of wide energy windows increases both the number of scattered and unscattered photons that are counted. Energy window selection in both SPECT and PET has been shown to be less critical because the increased count statistics associated with the contribution from small angle scatter has been shown to improve the image quality.

The radiopharmaceutical is an important determinant of the reliability of quantitative estimates because it affects quantitative accuracy primarily through the biodistribution and kinetics. These have an important impact on PVEs as well as the number of counts in, and thus the precision of activity estimates for, objects of interest.

For single-photon imaging, the energy of the photons emitted can have an important impact on accuracy and precision. Intrinsic sensitivity of the scintillation camera is lower for high-energy photons than for medium-energy photons. In addition, high-energy collimators typically have poorer resolution and sensitivity characteristics than corresponding low-energy collimators. Isotopes with multiple photopeaks, including low-abundance high-energy photons, can also suffer from the effects of downscatter into the imaging energy windows. The choice of PET isotope can affect resolution through the differing positron range, and, for some isotopes (e.g., ¹²⁴I, ⁸⁶Y), the presence of prompt gamma-ray emission within the positron decay scheme can lead to an increase of coincidence events that do not provide spatial information about the site of radionuclide decay.

The reconstruction algorithm can have important effects on image noise properties. Generally, statistical image reconstruction algorithms will provide better results. The maximum likelihood-expectation maximization (ML-EM) algorithm and, to some extent, the closely related ordered subsets-expectation maximization (OS-EM) algorithm have the theoretical potential to produce unbiased estimates for objects larger than the image resolution when a sufficient number of iterations are used and all effects are modeled in the reconstruction. However, the resulting images will not be suitable for visual interpretation. Use of regularization, including postreconstruction filtering, will increase PVEs while improving precision. When regions of interest can be defined based on anatomical images, the overall reliability of activity estimates in large regions will likely be improved if unregularized images are used due to reduced PVEs.

Finally, image analysis, including registration of images in a time series and the method used to define the VOI, can result in bias and imprecision in activity estimates. Therefore, care should be taken to ensure the best possible registration between serial images, preferably using associated computed tomography (CT) scans from hybrid scanners if available.

Quantitative Planar Imaging

Imaging with a scintillation camera is measurement of 2D projections of a 3D activity distribution. Consequently, the source depth and extent in the direction parallel to the projection is not resolved. This complicates activity quantification because more than one organ can contribute to a particular pixel value in the projection image.

Attenuation Compensation

A common approximation in planar imaging assumes that the activity is at a depth d along a parallel to the projection direction. This information can be used to derive formulas to perform attenuation compensation. These methods are typically referred to as geometric-mean attenuation compensation methods. In these methods, 2 projection views (usually anterior and posterior views) are acquired. The measured count rates depend on the attenuation. If one assumes the activity to be concentrated at a single depth, the dependence on source depth can be eliminated by computing the geometric mean¹ of the 2 projections:

$$\begin{array}{cc}\hfill \sqrt{P_{\text{ant}}\cdot P_{\text{post}}}=& \sqrt{P_{\text{air}}{e}^{-\mu d}\cdot P_{\text{air}}{e}^{-\mu (T-d)}}\hfill \\ \hfill & =\sqrt{P_{\text{air}}^2\cdot e^{-\mu T}}=P_{\text{air}}\cdot e^{-\mu T∕2}\hfill \end{array}$$ (1)

where P_ant, P_post, and P_air are the detector counts from the anterior and posterior projections and in air (with no attenuation), μ is the linear attenuation coefficient, d is the distance from the source to the surface along the projection line toward the anterior detector, and T is the total distance within the patient (ie, the thickness) along the same projection line. This reduces the problem to a measurement of the total distance T through the patient for a particular projection bin. It is not necessary to determine both T and μ to correct for attenuation. Instead, one can measure the transmission through the patient by an external radiation source, for example, a ⁵⁷Co flood source. The exponential in Equation 1 is then obtained from the ratio of a measurement with the patient in site, P_Pat, and a reference measurement, P_Ref, without the patient on a pixel-by-pixel basis. Conversion from count rate to activity requires division by the detector sensitivity, defined in terms of counts per unit activity per unit time.

Recent SPECT/CT systems allow for fast transmission measurement using x-ray scout images.² The resolution with this technique is superior, and scaling to radionuclide energies is straightforward because of the high image quality and low image noise. Figure 1 shows transmission images obtained from a ⁵⁷Co source and from an x-ray measurement.

Figure 1.

A comparison between transmission images obtain from a ⁵⁷Co flood source (left) and a scout x-ray measurement (right). Note the difference in noise and spatial resolution. The studies were obtained from two different patients.

Note that Equation 1 assumes point-like sources and uniform attenuation. Fleming¹ developed a method that accounts for the source thickness and related self-attenuation by a correction term, but the method is not applicable when there is overlap in the projections of more than one organ or with background activity.

Scatter Compensation

Scatter can be estimated from measurements in additional energy windows. The triple energy window (TEW) method uses 2 narrow auxiliary energy windows, one just above and the other just below the photopeak window. The scatter in the photopeak window is then estimated according to

$$P{(x,y)}_{\text{scatter}}=\left[\frac{P{(x,y)}_{\text{lower}}}{W_{\text{lower}}}+\frac{P{(x,y)}_{\text{upper}}}{W_{\text{upper}}}\right]\cdot \frac{W_{\text{photopeak}}}{2}$$ (2)

where W is the energy window width. One advantage is that this method does not require use of an empirically determined scaling factor. However, the noise in the scatter estimate resulting from the use of the narrow energy windows may require low-pass filtering. Using wider scatter windows reduces image noise but results in a poorer accuracy of the trapezoidal approximation implicit in the formula. Another problem is potential negative pixel values after subtraction. Setting these negative values to zero may result in bias in organ quantification.

Scatter can also be compensated for using inverse-filtering methods. This requires an estimate of the SPRF, which can be obtained by experimental measurements or Monte Carlo simulations. This is especially appropriate when data from addition energy windows are not available.

Contribution of Events From Nontarget Tissue Activity

In planar imaging, pixel values may include contributions from additional organs or regions other than the target region that degrade the accuracy of organ activity estimates. Correction for organ overlap and background activity is therefore essential.

Background Subtraction

A background usually refers to contribution to the image of the object being studied from activity from unspecified overor underlying tissues. This contribution can be estimated from a representative region of interest (ROI) adjacent to the object of interest. When selecting the location of this ROI, it is important to avoid locations over an organ with significant activity uptake to reduce the spill-over due to the limited spatial resolution. By contrast, the ROI should be placed in a region that is representative of the background for the organ of interest. Both the activity distribution and object thickness should be representative of that for the organ.

Correction for Overlapping Organ Activities

Contribution from overlapping activity can be significant and depends on the time since injection. Overlapping activity compensation can be performed if parts of the overlapping organ can be separated from the target organ. By calculating the overlapping area and using the activity per area from the nonoverlapping area, a correction can be applied if the thickness of the overlapping part can be estimated. Such methods also involve estimation of the source thickness so that the correct scaling of the counts can be performed. Prior CT or MR images of the patient can be of assistance when determining overlapping organ thicknesses.

Quantitative SPECT

There have been several published reviews on quantitative SPECT. Tsui et al³ and the Society of Nuclear Medicine Computer and Instrumentation Council⁴ provide a taxonomy of the image degrading effects, as well as a description of compensation methods, and include some profiles that demonstrate the quantitative accuracy achievable with SPECT. Due to the theoretical advantages of statistical iterative reconstruction (IR) algorithms, in the following we confine our discussion to IR-based compensation methods.

IR methods can, in principle, compensate for any image degrading effect that can be incorporated into a computer model of the imaging system. Compensation is obtained by exactly modeling them in the process of computing the projections; the algorithm that performs this computation is often referred to as a projector. Furthermore, IR algorithms can be designed to take into account the noise properties of the projection data: the ML-EM algorithm maximizes the statistical likelihood of the estimated activity distribution given the projection data and a Poisson noise model.⁵ The maximum likelihood (ML) estimate has a number of important properties in estimation theory. If an unbiased estimator of a particular parameter exists, the ML estimator will be unbiased and thus have perfect accuracy.

Fast algorithms, such as the OS-EM algorithm,⁶ now reduce the computation time compared with ML-EM by factors of 8-30 by reducing the number of iterations to obtain the same image quality, and, although they are not as theoretically appealing as ML-EM, have become of great practical importance.

Attenuation Compensation

IR-based attenuation compensation requires a high quality map of the attenuation coefficients for each voxel in the image volume at the relevant photon energy. These maps should have a resolution on the order of the image resolution⁷ and be well-registered to the SPECT image.⁸ The attenuation of photons in SPECT is from each voxel toward each projection bin. As a result, the attenuation factor is different for each voxel contributing to a projection bin. This tends to average out the effects of noise in the attenuation map and means that noise propagation from attenuation maps into compensated SPECT images is less than in PET.⁹

Modern SPECT/CT systems generally provide well-registered attenuation maps. Because the x-rays are polychromatic with lower energies than typical photon energies, care must be taken in transforming the CT images to appropriate attenuation maps.¹⁰ This issue has largely been solved by manufacturers, with the possible exception of patients with metal objects or contrast material present. The noise level and resolution in CT-derived images is such that they are more than adequate as attenuation maps. One limitation is that motions can have different effects on the CT images than on the SPECT images. For SPECT/CT systems with slow rotation speeds, respiratory motion can result in artifacts in the attenuation maps. By contrast, high-speed CT scanners tend to capture the attenuation at a particular respiratory phase and do not exactly represent the average attenuation seen over the respiratory cycle by the SPECT projections. Poor registration can result from misalignment, patient motion, or bending of the imaging table; therefore, regular quality control and verification of registration for patient images are essential.

With well-registered CT-based attenuation maps, attenuation compensation is effective and produces accurate images. However, attenuation compensation will not account for increased noise introduced by the attenuation of photons. Therefore, although the accuracy of attenuation compensation for large patients should be as good as that for small patients, the images from large patients tend to be noisier.

Scatter Compensation

Most SPECT scatter compensation methods account for scatter by using energy- or spatial-based estimates. Energy-based scatter estimates use projections measured in a set of auxiliary energy windows to estimate the scatter in the photopeak energy window. The methods and considerations are similar to those discussed for planar imaging.

Spatial domain scatter estimation models scatter in the projection data based on an estimate of the activity distribution. In IR, the scatter model is applied to the current estimate of the activity distribution as part of the forward projection process. Both analytical and Monte Carlo–based scatter modeling have been used. Analytical scatter models can be broken down into exact^11,12 and approximate methods.^13-15 The exact methods tend to be computationally intensive, especially for modeling several scatter orders. The approximate methods are fast and generally provide good accuracy for photopeak energy windows but are less accurate for cases with large angle and multiple scatter. Monte Carlo scatter modeling provides the best accuracy but is computationally intensive.^16,17

In scatter compensation, the estimate is often subtracted from the measured projection data just as for planar imaging. Because of noise in the projections or the estimate, subtraction can result in negative values that can cause problems for some reconstruction algorithms such as OS-EM. Truncating the negatives can result in bias and artifacts in the reconstructed images. As a result, it is better to include the scatter estimate in the reconstruction algorithm as an additive term to the forward projection of the current estimate.

CDR Compensation

Compensation for the CDR is accomplished by modeling the CDR in the forward and backward projection steps of an IR algorithm.¹⁸Often only the geometrical component is modeled because analytical formulas for the geometrical CDR are available.¹⁹ For medium- and high-energy photons, it may be desirable to model the full CDR, which includes penetration and collimator scatter. Compensating for the CDR reduces PVEs and is important for quantitative applications where PVEs are large.

Partial Volume Effects

Partial volume compensation based on calibration involve the use of recovery coefficients (RCs).^20-22 The RC is the fraction of the true activity in an object that is recovered in the estimate. The RC depends on the size and shape of the object, the activity concentration in surrounding objects, and the resolution of the image.²³ Because the resolution is spatially varying, the RC also varies in space and depends on the collimator, radius of rotation, and reconstruction and image processing used. Ideally, a database of RCs obtained by measuring a set of RCs via phantom experiments using objects of various diameters would be created and used to compensate for PVEs by dividing the estimated activity by the appropriate RC. Because the RCs depend on several factors, including object and background activity and the shape of the object, it is impossible to create a complete database. Therefore, these empiric methods have been shown to be generally insufficient.²⁰

Postreconstruction-based methods more accurately estimate RCs for the specific object by modeling the effects of resolution on the estimated activities. This can be done for objects as a whole with the assumption that the activity concentrations in a set of VOIs in the object are uniform,^24,25 or on a pixel-by-pixel basis.^26-28

Motion

Compensating for motion requires detecting the motion and measuring its size and direction.^29-31 Motion detection can be done with physiological triggers, radioactive fiducial markers on the patient, and optical motion tracking, or derived from the projection images themselves. For all these monitors, correlating the signal with the internal organ position is difficult. Gating can be used to segment the acquisition into a series of images corresponding to approximately equal patient positions. For involuntary motions, dividing the imaging into segments is required and can be done either at the level of projection views or using list-mode acquisitions.

Calibration

Typically voxel values in SPECT images, even those reconstructed with attenuation compensation via IR, are not in units of Bq/cc (μCi/cc). It is thus necessary to determine a calibration factor to convert the reconstructed SPECT voxel values into activity per voxel. This can be done in 2 ways. The first, and perhaps the most reliable, is to acquire an image of a uniform phantom with a known activity concentration.³² The factor needed to convert the SPECT image to this known concentration is then equal to the requisite calibration factor and can be used for other SPECT studies acquired using the same protocol and reconstructed using the same reconstruction method. Note that the degree to which the SPECT images of this phantom are uniform is an indirect measure of the efficacy of compensation for the image degrading effects. Further, phantom-based calibration factors are not a substitute for scatter and attenuation compensation; without these, the calibration factor will depend on the patient size and will be spatially varying.

Because it is somewhat tedious to perform the aforementioned calibration experiment and because the calibration factor can change over time, an alternative method is to use the in-air camera sensitivity (cps/Bq or cps/μCi) to convert the SPECT voxel values to activity concentration.³³ The use of phantom calibration with more frequent sensitivity measurements is likely the optimal approach.

Accuracy and Precision Achievable With Quantitative SPECT

For ¹¹¹In imaging, with the inclusion of reconstruction-based compensation for attenuation, scatter, and CDR, accuracies of better than 5% were obtained for large organs in both physical phantoms and for a population of simulated phantoms.^33-35 A phantom study using TEW scatter compensation, attenuation compensation, and no CDR compensation resulted in errors of 6% in the liver and larger errors for other organs.³⁶ Dewaraja et al³⁷ performed a simulation study of ¹³¹I SPECT using attenuation, TEW scatter, and CDR compensation. The accuracy for compartments larger than 16 mL was better than 12% for a high-energy collimator, and better than 6% for an ultrahigh-energy collimator due to less septal penetration and improved resolution.

He et al evaluated the loss of precision due to noise and variations in anatomic and activity biodistribution.^34,35,38 For typical acquisition times, the precision due to noise in the projection data was the smaller effect; for a 30-minute acquisition with an administered activity of 185 MBq (5 mCi), the estimated precisions for all the organs studied were better than 1.5%, whereas over 49 different phantoms, the variation in accuracy was several times higher than this and on the order of the magnitude of the average accuracy.

Quantitative PET

PET is construed as a highly quantitative imaging modality due to the ability to calibrate PET scanners to provide image readout data directly in units of Bq/cc (μCi/cc). Calibration is performed by acquiring images on the PET scanner of a known ¹⁸F activity after uniform mixing in a cylindrical phantom of known volume. This known activity concentration in the phantom is used as the basis to convert the count density information into an activity concentration in the reconstructed, attenuation and scatter-corrected PET images, so that ROIs on the emission scans provide a read-out in Bq/cc or standardized uptake values (SUV).

Effect of Reconstruction on Quantification Accuracy

Filtered back projection is no longer the standard clinical reconstruction methodology and has been completely replaced by IR methods. The activity concentration within a lesion can be quoted as an average for the whole lesion (SUV_av) or the maximum voxel value (SUV_max). For a larger lesion, the SUV_av provides a more representative value for the whole tumor but is highly subjective and dependent on the drawn ROI. Thus, algorithms to automatically segment PET volumes are important to strive to eliminate this subjectivity. Therefore, the SUV_max is commonly used because it is totally independent of the accuracy of ROI, provided it contains the voxel having the maximum value. However, SUV_max is extremely dependent on image noise and thus depends on the reconstruction parameters as well as any applied postreconstruction filter.

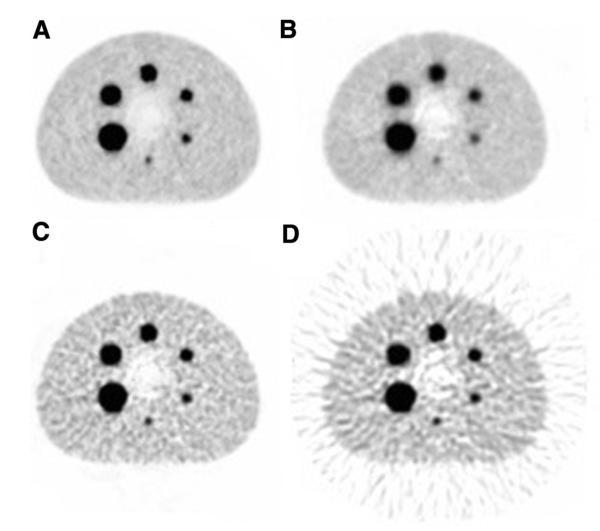
Figure 2 gives an example from a study by Mawlawi (unpublished) in which they measured the SUV_max for the 6 hot spheres in the IEC image quality phantom loaded with the same activity concentration of ¹⁸F, scanned in 2D and 3D, and reconstructed with different reconstruction parameters.³⁹ It shows that the selection of the reconstruction parameters can produce significant differences in the SUV_max.

Figure 2.

PET acquisition of an IEC quality phantom with all spheres filled with ¹⁸F. The same 3D acquisition data were reconstructed by OS-EM with (A) 2 iterations, 20 subsets; (B) 2 iterations, 5 subsets and with Fourier rebinning; (C) 5 iterations, 28 subsets, with Fourier rebinning; and (D) by filtered back-projection. The SUVmax varies between reconstructions for the largest sphere by: (A) 10.8, (B) 8.6, (C) 10.3 and (D) 10.4, and for the smallest sphere by: (A) 3.8, (B) 2.8, (C) 4.7 and (D) 4.8 respectively. Figure and data courtesy of Dr. Osama Mawlawi, MD Anderson Cancer Center, Houston, TX.

Attenuation Correction

When PET scanners were introduced, attenuation correction was performed using a ⁶⁸Ge or ¹³⁷Cs rod source, incorporated within the PET gantry. The equivalent photon energies used to obtain the attenuation map with the emission data resulted in accurate attenuation correction. With the introduction of PET/CT devices, the CT provided anatomical images for coregistration with the emission data and served as a rapid method to obtain the attenuation map. The appearance of PET/CT scanners introduced 2 additional sources of error into PET quantification: the difference in the photon energy used to acquire the attenuation map, and image registration mismatch due to PET/CT gantry misalignment and patient motion, voluntary or involuntary—especially respiratory motion.

CT Versus Rod Sources

The x-ray beam energy depends on the kilovoltage (kV_p) setting, which corresponds to the peak x-ray energy; the beam consists of a continuum of energies ranging up to the tube voltage, ie, 80-140 kV_p—the mean energy is approximately one-third of the peak. At 511 keV, photons interact with tissue almost exclusively by Compton scattering. However, over the x-ray energy range, photoelectric interactions are not negligible. For a body elemental composition, algorithms successfully map the Hounsfield coefficients to 511- keV attenuation coefficients required to compensate the PET emission data.⁴⁰ This has been verified in clinical studies^41,42 with ⁶⁸Ge rod source and CT attenuation correction to examine the effect on lesion SUV and reported insignificant differences. When high-Z materials are present in the form of surgical clips, prostheses, pacemakers, and CT contrast agents, the implemented mapping algorithms work less effectively and result in the selective mispositioning of radioactivity into regions of high-Z.³⁹

CT Contrast Agents

The use of intravenous contrast media in PET/CT can result in an overestimation of PET attenuation factors and a resulting incorrect interpretation. Mawlawi et al⁴³ studied the effect on FDG quantification of CT scans with and without contrast in the same patient. Results showed the highest increase on vascular structures, for example, an SUV_max change of 27% in the subclavian vein and 16.7% in the heart, but very small changes for liver, spleen, and site of malignancy.

Intravenous contrast-enhanced CT does lead to errors in quantitative values, but these are small relative to those that can be incurred following barium oral contrast agents, which can result in significant image artifacts. An example is shown in Figure 3 (left—CT showing barium in the bowel; middle—PET with attenuation correction; right—PET without attenuation correction and no false hot-spot artifact).

Figure 3.

Coronal whole-body projection images of a patient who had received an oral barium contrast agent before the PET scan. (A) CT image showing the accumulation of barium contrast agent in the bowel, (B) PET scan after CT attenuation correction showing hot spot of FDG activity just above the bladder at the location of the bowel, and (C) PET scan without CT attenuation correction no longer demonstrating a hot spot above the bladder.

Truncation Artifacts

Truncation artifacts manifest themselves as a rim of high activity concentration at the edge of the truncated CT image with an adjacent low-concentration region peripherally. These occur for obese patients when part of the patient’s body is beyond the field of view of the reconstruction volume. The magnitude of the effect of truncation artifacts on the quantification of lesions within the patient periphery has been studied by Mawlawi et al.⁴⁴

PET-CT Misregistration

The cause of misregistration between the PET and CT scanners can be mechanical misalignment, but such errors are readily checked and corrected by applying QA tests. Misregistration can also be the result of patient motion between the CT and the PET component of the scan. This can occur in patients who experience claustrophobia, back pain, or restlessness. Ensuring patient comfort with simple patient restraints can greatly minimize motion.

Respiratory Motion

The introduction of the CT resulted in the additional error associated with the mismatch between the CT image (acquired over seconds and often only a brief segment of the respiratory cycle) and the PET emission image (acquired over multiple respiratory cycles). The combined errors in SUVs in the lung resulting from respiratory motion can be as great as 34%.⁴⁵ Pevsner et al⁴⁶ evaluated the effect on PET tracer quantification from data for an IEC phantom at rest and in motion acquired with a standard clinical protocol. They showed that the activity concentration in the spheres was underestimated by as much as 75%, depending on the sphere diameter.

Nakamoto et al⁴⁷ studied 12 patients using ⁶⁸Ge transmission and CT attenuation correction methods to determine the effects of bowel gas movement on SUV measurements in the colon. Multiple mismatched areas were identified, resulting in overestimated and underestimated areas of local attenuation correction and consequently errors in tracer uptake. Such artifacts are more difficult to correct than those arising from cardiac or respiratory motion, which can be resolved by gating techniques.

Non-¹⁸Fluorine Radionuclides

Most clinical PET today uses the radionuclide ¹⁸F, and therefore the vast majority of the PET quantification focus has been on ¹⁸F radiotracers, especially FDG. Many other radionuclides are used for PET imaging, such as ¹¹C,¹³N, ¹⁵O, ⁶⁸Ga, and ⁸²Rb, which possess similar decay characteristics to ¹⁸F, and therefore the accuracy of quantification is assumed comparable. Some PET isotopes, especially ones relevant for targeted therapy applications, for example, ¹²⁴I, ⁸⁶Y, etc., have prompt gamma-ray emission that can either directly fall within the 511-keV energy window or downscatter and result in signal detection within this window. Due to their longer half-lives, these isotopes are becoming of increasing interest because of their potential application in radioimmuno-PET, where the contrast of the imaging agent is not reached within a few hours postadministration. The consequence of prompt gamma-rays is that they provide an aberrant source of “true coincidences” when 1 of the 2 colinear 511-keV photons is absorbed or otherwise not detected. However, these coincidences contain no information about the origin of the source decay. A study by Pentlow et al⁴⁸ of ¹²⁴I concluded that the resolution and quantification in 2D were only slightly degraded relative to ¹⁸F. Sphere detectability was only slightly worse if imaging time was increased to compensate for the lower positron abundance. However, in 3D, the quantitative accuracy was substantially reduced, which is important because PET scanners have increasingly become 3D-only (septaless) units.

Measurements of ⁸⁶Y in a phantom containing heterogeneity inserts of bone- and air-equivalent materials showed apparent activity up to 30% of the surrounding true activity in a bone-equivalent material. Even higher activities were observed if scatter correction was omitted.⁴⁹ Methods to remove spurious events resulting from prompt gamma-emissions have been published.^50,51

PET Imaging as a Quantitative Method for Dosimetry

The first use of ¹²⁴I to estimate the radiation doses was by Daghighian et al,⁵² who performed serial PET images of a patient with neuroblastoma who had been injected with ¹²⁴I-3F8 antibodies. Other researchers^53-56 have used PET image data from ¹²⁴I administered to patients with thyroid cancer to perform more accurate dosimetry. Kolbert et al⁵⁷ extended this to use serial ¹²⁴I PET data to determine normal organ dosimetry using patient-specific dosimetry. The use of PET for radionuclide dosimetry is in its infancy and will likely increase in importance in the near future.

Further Remarks

The need for accurate quantification of nuclear medicine scans has always been essential for the accurate estimation of organ doses resulting from radionuclide treatments and for the evaluation of new radiopharmaceuticals. However, there is a growing interest in the use of nuclear medicine methodologies to determine treatment response. These new response measures rely on the quantitative robustness of the nuclear medicine technique being used, whether the SUV commonly used in PET or another metric.

As described earlier in the text, there have been significant advances in the quantitative ability of planar, SPECT, and PET imaging during the past 10 to 15 years. These are a result of the significant advances in reconstruction techniques, which include methods of scatter and attenuation compensation, as well as gating and list-mode rebinning approaches to overcome motion blurring. Because of these developments, the accuracy of quantifying the concentration of a radionuclide in regions within the body can be <5% with SPECT or PET imaging, and provided there are no overlapping structures containing radioactivity, similar accuracy can also be obtained with planar gamma camera imaging. However, in all cases, careful attention to compensation for image degrading factors, selection of appropriate techniques, and recognition of the limitations of each modality are essential to achieve these levels of accuracy.