Multidimensional MAS NMR Spectroscopy for Site-Resolved Measurement of Proton Chemical Shift Anisotropy in Biological Solids

Abstract

The proton chemical shift (CS) tensor is a sensitive probe of structure and hydrogen bonding. Highly accurate quantum-chemical protocols exist for computation of ¹H magnetic shieldings in the various contexts, making proton chemical shifts potentially a powerful predictor of structural and electronic properties. However, ¹H CS tensors are not yet widely used in protein structure calculation due to scarcity of experimental data. While isotropic proton shifts can be readily measured in proteins even in the solid state, determination of the ¹H chemical shift anisotropy (CSA) tensors remains challenging, particularly in molecules containing multiple proton sites. We present a method for site-resolved measurement of amide proton CSAs in fully protonated solids under magic angle spinning. The approach consists of three concomitant 3D experiments yielding spectra determined by either mainly ¹H CSA, mainly ¹H-¹⁵N dipolar, or combined ¹H CSA and ¹H-¹⁵N dipolar interactions. The anisotropic interactions are recoupled using RN-sequences of appropriate symmetry, such as , and ¹⁵N/¹³C isotropic CS dimensions are introduced via a short selective ¹H-¹⁵N cross-polarization step. Accurate ¹H chemical shift tensor parameters are extracted by simultaneous fit of the lineshapes recorded in the three spectra. An application of this method is presented for an 89-residue protein, U-¹³C,¹⁵N-CAP-Gly domain of dynactin. The CSA parameters determined from the triple fits correlate with the hydrogen-bonding distances, and the trends are in excellent agreement with the prior solution NMR results. This approach is generally suited for recording proton CSA parameters in various biological and organic systems, including protein assemblies and nucleic acids.

INTRODUCTION

Hydrogen bonding is a main interaction stabilizing the secondary and tertiary structure elements in proteins. Chemical $R{12}_1^4$ shielding interactions being exquisitely sensitive to the local environment have long been used as an NMR probe of structure and hydrogen bonding interactions.^1–4 In particular, the chemical shift (CS) of protons forming hydrogen bonds has long been a subject of interest in solid-state NMR,^5–13 and the CS of participating heteronuclei has been investigated as well.^14,15 More recently, the relationship between proton CS tensor components and hydrogen bond formation has become a subject of study in solution NMR, as well.^16–20 In the case of protons, not only has the downfield shift of the proton isotropic shift due to a shortening of the H-bond donor-acceptor distance OH···O or NH···O been well documented,^{3,5–9,12,13} but evidence has also been reported of the simultaneous increase of the chemical shift anisotropy (CSA).^5,16–18,20 These findings suggest that a relationship must naturally exist between the CS tensor components and the isotropic shift, a conclusion that has indeed been verified in several experimental studies.^5,17,19,20 Two other common observations are that the principal axis of the least-shielded component is close to being perpendicular to the peptide plane and that the most-shielded-component axis makes a small angle with the NH bond direction, mostly less than 15° and never larger than 35.^18–22 The anisotropy of the chemical shift tensor could actually be a more sensitive measure of hydrogen-bond strength than the isotropic shift^9,12 and it is expected that the amide proton CS tensor in peptides and proteins can be a highly informative probe in protein structure determination.^10,13

Highly accurate quantum chemical protocols have been developed for computation of ¹H magnetic shielding tensors in peptides and proteins in the various structural contexts.^23,24 In particular, ab initio calculations of amide proton chemical shift tensors have confirmed the experimentally observed relationships between the hydrogen bond structure and the components and orientation of the proton CS tensor.^11,20,25,26 Ab initio calculations also suggest that the correlation of amide proton CSA tensor components with hydrogen-bond lengths may be more complex than what has been suggested in earlier reports on CSA of hydrogen bonds. For instance, Sharma et al. found that tensor components in addition to depending very strongly on the hydrogen bond length also exhibit a weaker dependence on the hydrogen bond angle.¹¹ Parker et al. concluded from DFT calculations that while the hydrogen bond geometry is the most important CSA determinant, longer-range cooperative effects of extended hydrogen networks make significant contributions.²⁵ Furthermore, Suzuki et al. recently observed, based on their calculations, that the origin of isotropic CS differences among protein amide protons is predominantly the magnetic anisotropy effect from the C=O acceptor.²⁶ A more complete understanding of the effects of molecular structure on the anisotropy of the proton chemical shift will undoubtedly be served by a broad database of experimental results, the current scarcity of which has often been held responsible for stagnant progress in this area.^11,18,19,26

Indeed, to date only a rather limited number of experimental amide proton CSA measurements have been reported. In solid systems, only three proton CSA measurements of peptide bonds have been presented in the literature. These were all performed on non-spinning low-molecular-weight peptide samples, using MREV8 multiple-pulse NMR,²⁷ single-crystal deuterium NMR,²¹ or 3D SLF/LG NMR.²² More recently, two methods were developed for extracting amide proton CSA data from proteins in solution. One of these employs cross-correlated relaxation of ¹⁵N-¹H spin pairs,^16,17,19,28 and the other measures the residual chemical-shift anisotropy of the protons in liquid-crystal dissolved proteins.¹⁸ A combination of these two methods produced a highly accurate set of CSA tensor parameters in a protein.²⁰

The lack of known attempts of such measurements in solid proteins is presumably due to the strong homonuclear interactions and the difficulties of extracting accurate proton CSA tensors in a site-resolved fashion under magic angle spinning (MAS) with the currently available experimental protocols. As to measurements of proton CSAs of other chemical moieties under MAS conditions, two 2D approaches have been reported where the CSA interaction is recoupled in the indirect dimension. Brouwer and Ripmeester achieved the recoupling by application of the R-symmetry-based pulse sequence $R{18}_2^5$,¹³ while Duma et al. employed rotary-resonance spin locking.²⁹ In both approaches the proton signal was detected in the direct dimension, either under free evolution^13,29 or under resolution enhancement by PMLG.¹³ In these experiments different proton sites could be measured individually thanks to the fact that the samples had relatively sparse proton spectra. However, since direct proton detection at MAS frequencies lower than 40 kHz does not produce the required resolution in protein spectra, any pulse sequence to be employed for ¹H CSA measurements requires an additional resolution-enhancement step.

The objective of the present work is to develop an MAS method for measuring amide proton CSAs in peptides and proteins. For this purpose we employ the RN-sequences of appropriate symmetry which, when applied to the protons, recouple their CSA interaction and their heteronuclear dipolar interactions, while they decouple to first order the isotropic shift and the homonuclear proton dipolar interaction.^13,30–32 For this study, we chose the $R{12}_1^4$ symmetry sequence as it is well suited for our experimental conditions: the range of available MAS frequencies (10–20 kHz) and the radio frequency (rf) power. The CSA is measured by detecting the evolution of the ¹H spin state under $R{12}_1^4$ irradiation, resulting in what we will call RN-¹H spectra. In order to distinguish between individual proton signals we resorted to detection through selective signal transfer to the adjacent ¹⁵N by short-contact-time cross-polarization. The presence of this nearby ¹⁵N introduces the recoupled ¹H-¹⁵N dipolar interaction and allows for two options. Either it is decoupled by irradiation of the ¹⁵N spins or it is left intact so that it can provide additional information that turns out to be highly beneficial for the determination of the proton CSA parameters, as demonstrated below. Thus we distinguish between undecoupled RN-¹H spectra, to be called RN-¹H(¹⁵N_und), and ¹⁵N-decoupled RN-¹H spectra, to be called RN-¹H(¹⁵N_dec). A concomitant measurement of ¹⁵N evolution under $R{12}_1^4$ irradiation applied on ¹H spins, resulting in what we will call RN-¹⁵N spectra, can be further included in the experimental repertoire for the sake of refining the reliability of the measured interaction parameters. It is identical to earlier ${RN}_n^{\nu }$ experiments for obtaining dipolar spectra of ¹H-¹⁵N or ¹H-¹³C spin pairs.^31,33–37 The method thus culminates in the curve fitting of up to three $R{12}_1^4$ spectra: RN-¹H(¹⁵N_und), RN-¹H(¹⁵N_dec), and RN-¹⁵N.

Following a theoretical description of the average-Hamiltonian approach for simulating the three kinds of spectra and a brief discussion of theoretical and experimental circumstances that may affect the accuracy of the method, we turn our attention to the experimental $R{12}_1^4$ results for an 89-residue protein, U-¹³C,¹⁵N-CAP-Gly domain of mammalian dynactin. The biological significance of CAP-Gly protein was discussed in our previous work,³⁸ and over the past several years we have pursued structural and dynamics characterization of CAP-Gly to understand its interactions with microtubules at atomic level and the mechanism of the disease-associated point mutations.^{39 1}H CSA tensors are very sensitive to hydrogen bonding environments and to secondary structure, as well as to motions occurring on timescales of submilliseconds and faster, and therefore, their knowledge is expected to provide important insights on the biological functions of CAP-Gly.

At 19.9 T, ¹H CSA lineshapes measured for forty-two residues in CAP-Gly in three sets of three-dimensional experiments, RN-¹H(¹⁵N_und), RN-¹H(¹⁵N_dec), and RN-¹⁵N, are well-resolved and the resulting ¹H CSA tensors have the general properties that are in accord with those that have been observed in prior solution NMR work on amide protons in ubiquitin¹⁹ and in GB3.²⁰ We present the analysis of the ¹H CSA tensor components in the context of the hydrogen bonding environments determined from the MAS NMR structure solved in our laboratory (PDB deposition code 2m02). Our work demonstrates that accurate amide proton CSA tensors can be recorded in a site-specific fashion in fully protonated systems, making our approach suitable for measurements of ¹H CSA parameters in heteronuclear spin pairs, such as ¹H¹³C, ¹H¹⁵N, or ¹H³¹P in proteins, protein assemblies, and other macromolecular and organic systems in the solid state.

EXPERIMENTS AND MATERIALS

Materials

U-¹³C,¹⁵N-CAP-Gly domain of mammalian dynactin was prepared from E. coli; the solid-state sample was generated by controlled precipitation polyethylene glycol by slow addition of solution of 32% PEG-3350 to the solution of 24.0 mg CAP-Gly (40 mg/ml), dissolved in 10 mM MES buffer (10mM MgCl₂, pH 6.0), as described previously.³⁸ 24.4 mg of precipitated protein were transferred into a 3.2 mm Bruker rotor and sealed using standard Bruker rotor tools.

Solid-State NMR Spectroscopy

The experiments on U-¹³C,¹⁵N-CAP-Gly domain of mammalian dynactin were conducted on a 19.9 T narrow bore Bruker AVIII spectrometer, operating at a Larmor frequency of 850.4 MHz for ¹H, 213.8 MHz for ¹³C, and 86.2 MHz for ¹⁵N. A 3.2 mm Bruker EFree MAS triple-resonance HCN probe was used. The experiments were acquired at an MAS frequency of 14 kHz, controlled to within ± 0.010 kHz using the Bruker MAS controller. The actual sample temperature was maintained at 4°C ± 0.2°C throughout the experiments.

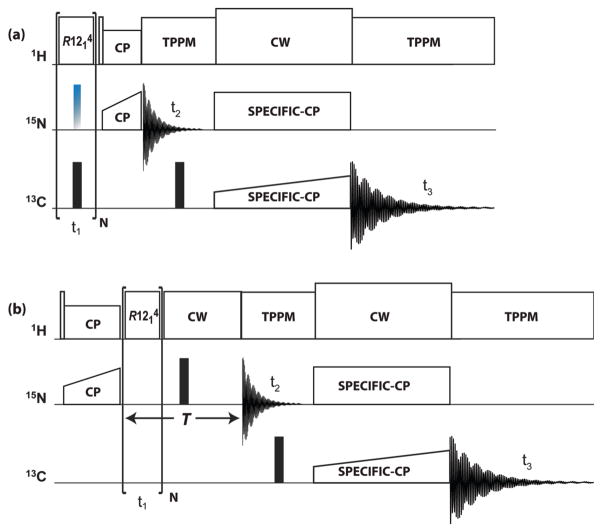
The pulse sequences applied in this work are schematically shown in Figure 1. To describe the spin dynamics associated with them we assign the symbols I and S to the ¹H and ¹⁵N spins, respectively. The RN-¹H spectra are obtained with the sequence shown in Figure 1(a). In these experiments the beginning spin state is I_z, and the time dependence of I_z coherence is monitored, either with or without decoupling of the I-S interaction. The RN-¹⁵N spectrum is measured with the sequence shown in Figure 1(b), which is similar to earlier $R{18}_n^{\nu }$ experiments used to obtain heteronuclear dipolar spectra.^{31–34,36,40} In this pulse sequence the spin state is prepared in the S_x state, and the evolution of the S_x coherence is monitored.

Figure 1.

Pulse sequences for (a) RN-¹H(¹⁵N_und) and RN-¹H(¹⁵N_dec), and (b) RN-¹⁵N 3D experiments. Rotor synchronized $R{12}_1^4$ symmetry rf pulses are applied during t₁ evolution time to reintroduce ¹H CSA or ¹H-¹⁵N dipolar interactions under MAS conditions. Empty and solid rectangles denote π/2 and π pulses, respectively. In (a) the time dependence of ¹H z-magnetization is monitored, either with application of the ¹⁵N decoupling π pulses (RN-¹H(¹⁵N_dec)) or without (RN-¹H(¹⁵N_und)). This optional decoupling pulse is colored in blue-grey. Site selective ¹H detection is accomplished by short-contact-time CP to ¹⁵N. In (b) the time evolution of ¹⁵N x-magnetization is monitored with refocusing of the chemical shift over a constant evolution period T. ¹⁵N-¹³C SPECIFIC-CP magnetization transfer is introduced following the t₂ evolution period, with the subsequent detection of the ¹³C signal during the t₃.

In the $R{12}_1^4$ -symmetry-based sequence the basic R element is a π pulse with its radio frequency (rf) field strength and phases determined by the symmetry properties of the pulse sequence.^{30–32,36,41–43} An $R{12}_1^4$ cycle consists of one rotor periods and contains 12 proton π pulses having rf amplitude 6 times the MAS frequency and phases alternating between 60° and −60°. In the RN-¹H(¹⁵N_dec) experiment a π pulse was applied on the ¹⁵N channel at the center of each RN cycle to decouple the ¹H-¹⁵N heteronuclear dipolar interactions. For the RN-¹H(¹⁵N_und) experiment, the ¹⁵N π decoupling pulse was omitted. For both RN-¹H(¹⁵N_dec) and RN-¹H(¹⁵N_und) experiments of the U-¹³C,¹⁵N-CAP-Gly, a decoupling π pulse with rf field strength of 78–80 kHz was applied on the ¹³C channel at the center of each R cycle. The dwell time in the $R{12}_1^4$ dimension was set equal to either one (RN-¹H(¹⁵N_und) and RN-¹⁵N) or two (RN-¹H(¹⁵N_dec)) rotor periods. 16 points were acquired in the $R{12}_1^4$ dimension, and 48 points were collected in the ¹⁵N evolution dimension. 128 and 72 scans were used for the RN-¹H(¹⁵N_dec) and RN-¹H(¹⁵N_und) experiments, respectively. The pulse delay was set to 2.5 s for all experiments.

The ¹H-¹⁵N CP contact time for the RN-¹H(¹⁵N_und) and RN-¹H(¹⁵N_dec) lineshape measurement was set equal to two rotor periods (142.86 μs); and for the RN-¹⁵N experiment- to 1700 μs. ¹H-¹⁵N cross polarization was performed by applying a linearly ramped rf field with the center of the ramp set at 59 kHz on ¹H nuclei (80–100% ramp), and a constant-amplitude rf field at 45 kHz on ¹⁵N. The band-selective magnetization transfer from ¹⁵N to ¹³C_α was realized by using 4.6 ms SPECIFIC-CP with tangent amplitude ramp on the ¹³C channel (center at 21 kHz). The ¹⁵N and ¹³C rf field strength for the SPECIFIC-CP were set to 2.5 times and 1.5 times the MAS frequency, respectively. ¹H CW decoupling was applied during the SPECIFIC-CP period with rf field strength of 90 kHz. SPINAL-64 decoupling⁴⁴ with rf field strength of 80–83 kHz was used during the acquisition period (t₃) and during the indirect ¹⁵N evolution time (t₂). A ¹³C π pulse with rf field strength of 78–80 kHz was applied at the center of t₂ to decouple the ¹⁵N-¹³C J-couplings.

Spectral Processing and Simulations

The $R{N}_n^{\nu }$ spectrum of a particular NH group is evaluated as the real-FT of the corresponding indirect-dimension time-domain signal, which was zero filled to 256 points prior to FT. Narrow center peaks were regularly observed in our experimental RN-¹H spectra as expected from ‘non-ideal’ conditions. In the time-domain these are detected as slowly decaying constant signal contributions, which have the uncomfortable effect of introducing sinc oscillations in the Fourier transform when the evolution time is curtailed in the experiment and zero-filling is applied prior to FT. To avoid having to deal with these artificial lineshape distortions, particularly in the context of curve fitting, we chose to suppress the wiggles by subtracting the average of the last point of the time-domain spectrum from the entire spectrum prior to zero-filling. While this subtraction of the tail signal also removes narrow center-peak components, broad center features do remain, particularly in the RN-¹⁵N spectra.

Numerical simulations were executed in Fortran-95. The programs were written with the intention of facilitating operations like implementation of average Hamiltonians, simultaneous least-squares curve fitting of more than one spectrum by the simplex method, Monte Carlo analysis, etc. In simulations based on time-dependent Hamiltonians time increments were kept below 1μs. For summation over crystallite orientations in powder-sample simulations we used the REPULSION polar-angle distributions.⁴⁵

THEORY

CSA notation

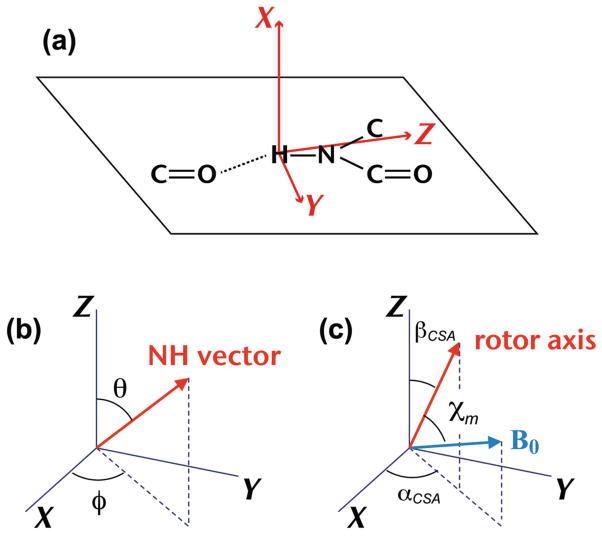
When reporting results of amide-proton CSA-tensor determinations it is useful to do so in a notation system that facilitates comparison between different amide groups. In particular, the nomenclature of the principal axes should be standardized with respect to their orientations in the molecular structure. For this purpose we will use a tensor-notation system,¹⁹ schematically depicted in Figure 2(a), where the Z-axis direction is the one that is roughly parallel to the NH bond and the X axis is approximately normal to the peptide plane. It is based on the general observations mentioned above that the principal axes of the most- and least-shielded tensor components are pointing in those approximate directions.^{11,18–22,25,26} Consequently, we expect the principal CS tensor values to relate to each other as δ_ZZ < δ_YY < δ_XX.

Figure 2.

(a) Orientation of the CSA principal axes XYZ in the molecular frame of a hydrogen-bonded amide group. (b) Relative orientations of the NH bond vector and the CSA axes XYZ. (c) Relative orientations of the magnetic field B₀, the rotor axis, and the CSA principal axes XYZ of a single crystal, depicted at the moment in the rotor cycle at which the rotation angle is zero (see text); χ_m is the magic angle.

The goal of the ${RN}_n^{\nu }$ experiments is to determine the three principal components of the CSA tensor and the polar angles (θ, φ) of the NH bond with respect to the principal axis system (PAS), as depicted in Figure 2(b). Figure 2(c) illustrates the polar angles β_CSA and α_CSA of the rotor-axis direction with respect to the PAS. The figure depicts the relative orientations of the tensor Z-axis, the rotor axis, and the magnetic field B₀ at the moment when they are coplanar and the angle between B₀ and Z equals β_CSA plus the magic angle χ_m. It is the rotor orientation for which we define the rotation angle to be zero. The CSA parameters used in spin-interaction equations presented below follow the notation δ_iso = (δ_XX+ δ_YY + δ_ZZ)/3, δ = δ_ZZ − δ_iso, and η = (δ_YY − δ_XX)/δ. Since there are many cases of amide groups in proteins where |δ_ZZ − δ_iso| is not larger than |δ_XX − δ_iso|,^19,20 η is not necessarily restricted between 0 and 1. We note that this notation is a modified Haeberlen notation adopted by us for convenient spectral simulations.

Average Hamiltonian

$R{12}_1^4$ is one of the symmetry-based $R{N}_n^{\nu }$ pulse sequences^30,41 designed for recoupling of CSA and heteronuclear dipolar interactions with suppression of isotropic shift and homonuclear dipolar interactions.^13,31 Various other sequences, such as $R{18}_2^5$ as $R{18}_1^7$, are suitable as well, and the choice of the sequence depends on the accessible MAS frequencies and rf power limits for each particular probe, as well as the scaling factors for the recoupling and the number of second-order terms that are retained in the Hamiltonian. The spectra can be simulated by stepwise integration of the Liouville-von Neumann equation under the time-dependent Hamiltonian that includes the RF irradiation and the CSA and dipolar interactions. As will be shown below, under the current conditions these calculations can be greatly simplified by application of average Hamiltonians that predict the stroboscopic signal detection at the end of each $R{N}_n^{\nu }$ cycle. The first-order average Hamiltonian for a CSA interaction of a single spin I with principal CS tensor components δ_XX, δ_YY, δ_ZZ is given by

$$H_{av}^{\mathit{CSA}}=-\lambda {\omega }_0\delta [\{3{sin}^2{\beta }_{\mathit{CSA}}-\eta ({cos}^2{\beta }_{\mathit{CSA}}+1)cos2{\alpha }_{\mathit{CSA}}\}(I_{x}cos2{\gamma }_{\mathit{CSA}}+I_{y}sin2{\gamma }_{\mathit{CSA}})+2\eta cos{\beta }_{\mathit{CSA}}sin2{\alpha }_{\mathit{CSA}}(I_{x}sin2{\gamma }_{\mathit{CSA}}-I_{y}cos2{\gamma }_{\mathit{CSA}})]$$ (1)

where ω₀ is the Larmor frequency, δ, η, α_CSA, β_CSA are as defined above, and γ_CSA is the rotation angle of the CSA tensor at time t = 0, whereby the zero rotation angle is defined as that of the crystal orientation where B₀, the rotor axis, and the δ_ZZ axis are coplanar, and the angle between the B₀ direction and the δ_ZZ axis is β_CSA + χ_m, as depicted in Fig. 2(b). For the special case of η = 0 the expression in Equation (1) is in full agreement with the Hamiltonian originally formulated by Zhao et al.³¹ Not having encountered the η-dependent terms of the average Hamiltonian in the literature, we verified Equation (1) by numerical simulations. The prefactor λ differs for different $R{N}_n^{\nu }$ sequences having this symmetry. It is 0.0515 for $R{12}_1^4$ and 0.0507 and 0.0525 for the closely related sequences $R{18}_2^5$ and $R{18}_1^7$, respectively.

The average dipolar Hamiltonian of a heteronuclear I, S spin pair under $R{12}_1^4$ irradiation of spin I is

$$H_{av}^D=-6\lambda b_{IS}{sin}^2{\beta }_D(I_x{S}_{z}cos2{\gamma }_D+I_y{S}_{z}sin2{\gamma }_D),$$ (2)

where λ is the same as in Equation (1), b_IS/2π = D is the dipolar coupling constant (DCC), β_D is the angle between the internuclear vector and the rotor axis, and γ_D is the rotation angle at t = 0, where in this case the rotation angle is defined to be zero for the rotor orientation at which the angle of the internuclear vector with B₀ equals β_D + χ_m. Equation (2) also agrees with Zhao et al.’s Hamiltonian expression.³¹ In the absence of molecular motions the dipolar interaction strength is given by

$$b_{IS}=-\frac{{\mu }_0{\gamma }_I{\gamma }_S\hslash }{4\pi r^3},$$ (3)

where r is the internuclear distance. We note that if the NH groups were undergoing rapid molecular motions, the dipolar interaction would be reduced and in most circumstances the tensor would lose its axial symmetry. Terms like those involving η in Equation (1) would then have to be included in $H_{av}^D$. Since in the samples under investigation molecular motions are not extensive, we omitted these terms. For detailed discussions of the information that can be extracted from reduced dipolar interactions we point the reader to relevant literature.^34,46

RN-¹⁵N and RN-¹H spectra detect the time dependence of the coefficients of S_x and I_z terms in the density matrix operator, respectively. The spectra are γ-encoded, i.e., they are independent of the γ angles in Equations (1) and (2).

In addition, the RN-¹H spectra are affected by the short-contact-time cross-polarization (CP) to ¹⁵N following the $R{12}_1^4$ sequence (see Figure 1(a)). A 90°_y pulse flips the I_z term emerging from the $R{12}_1^4$ evolution to I_x coherence, which is then transferred to S_x coherence by first-sideband Hartmann-Hahn-matched rf irradiation. Provided the contact time is an integer number of rotor periods, the average CP Hamiltonian is

$$H_{av}^{CP}={\omega }_{CP}\left\{(I_z{S}_z+I_y{S}_y)cos{\gamma }_D+(I_z{S}_y-I_y{S}_z)sin{\gamma }_D\right\}$$ (4)

with ω_CP given by

$${\omega }_{CP}=\frac{1}{4}\sqrt{2}{b}_{IS}sin2{\beta }_D$$ (5)

Here β_D is the angle of the NH bond with the rotor axis and γ_D is the rotation angle at the beginning of the contact period, whereby the zero angle is defined as in the context of Equation (2). If at t = 0 the expectation value of I_x is <I_x(0)>, then the expectation value <S_x> of S_x evolves according to

$$\langle S_x(t)\rangle =\langle I_x(0)\rangle {sin}^2({\omega }_{CP}t/2).$$ (6)

While the rate of this transfer is the same for any γ_D angle, the strong dependence on β_D causes a distortion of the spectrum.

Powder spectra are thus dependent on the strength D of the dipolar interaction, the size δ and asymmetry η of the CSA, and the polar angles θ and φ of the NH vector with respect to the PAS of the CSA tensor (see Figure 1(b)). Due to the symmetry properties of $R{12}_1^4$ the spectra are insensitive to δ_iso of the protons. The calculated spectra are independent of the signs of δ, η, and D. Furthermore, θ can be replaced by −θ or π − θ without altering the spectra and so can φ be replaced by −φ or π − φ. Hence, relevant values of the polar angles are confined to the range 0–90°. We note that if the dipolar tensor were not axially symmetric, the relevant range of either θ or φ would have been 0–180°. Spin relaxation during the $R{12}_1^4$ irradiation is represented in the form of Lorentzian line broadening of the calculated spectra. To account for it we introduce a Lorentzian line broadening parameter LB for each of the three spectra.

Examples of Spectra

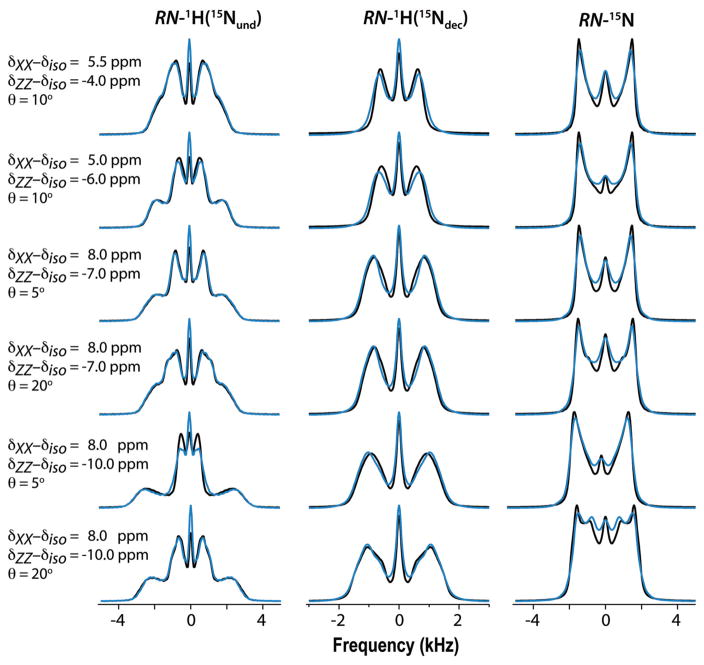
Figure 3 shows a collection of simulated $R{12}_1^4$ spectra for a variety of spin-interaction combinations. They serve as an indication of how strongly the lineshapes depend on those parameters. They are simulated by the two methods discussed above, i.e., by applying the average Hamiltonians and by stepwise integration of the Liouville-von Neumann equation under the full time-dependent Hamiltonian. Average-Hamiltonian simulations of decoupled spectra were performed by simply setting D = 0. The full Hamiltonian included, in addition to the spin operators of the ¹H¹⁵N spin pair, the CSAs and dipolar interactions of three additional protons located at characteristic positions in the vicinity of the amide group (see Supporting Information for details). The spectra calculated by the two methods are superposed in the figure, thereby demonstrating that the average Hamiltonian model is reasonable in representing the spin dynamics of the ¹H¹⁵N spin pair. The figure shows that interactions with other protons during the $R{12}_1^4$ irradiation are sufficiently suppressed and that the short-contact-time CP selectively transfers the amide proton spin coherence to the detected ¹⁵N. Only the RN-¹H(¹⁵N_dec) spectra show a rather substantial deviation between average- and full-Hamiltonian spectra. It is not due to the interaction with the neighboring protons because a full-Hamiltonian simulation in the absence of those neighbors (not shown) is nearly identical to the spectrum including the neighbors. The slight shortcoming of the average Hamiltonian to produce a more perfect spectrum is presumably due to the simplistic way it deals with the decoupling. In the Supporting Information we present Table S2 with CSA and dipolar-interaction parameters determined by simultaneous curve fitting of average-Hamiltonian simulations to the three full-Hamiltonian ¹H₄¹⁵N spectra, as well as fitting results of full-Hamiltonian ¹H¹⁵N spectra. The Table shows that, in general, the errors introduced by application of the average Hamiltonian are not larger than those associated with application of the full ¹H¹⁵N Hamiltonian. Nor do they exceed the uncertainties inherent in the analysis of experimental spectra (vide infra). Other simulations have demonstrated that the application of Eqs. (3) and (4) for evaluating the CP evolution produces spectra that are indistinguishable from those calculated by stepwise integration according to the ramped CP irradiation applied in our experiments. In a forthcoming publication we will address the features of single crystallite spectra that underlie the powder spectra, the origins of enhanced zero-frequency peaks encountered in experimental spectra, the effects of RF homogeneity, and other factors that may influence the lineshapes.

Figure 3.

Simulated $R{12}_1^4$ spectra evaluated with D = 10 kHz and indicated principal components δ_XX – δ_iso and δ_ZZ – δ_iso of the ¹H CSA tensor (δ_YY – δ_iso is not indicated as it is equal to minus the sum of the other two components) and polar angles θ of the NH vector. The azimuthal angle φ is constant at 45°. Black: Calculated with average Hamiltonians. Blue: Calculated with full $R{12}_1^4$ Hamiltonian including three nearby protons. Other parameters: ¹H Larmor frequency 850 MHz, MAS frequency 14 kHz, 64 $R{12}_1^4$ time-domain increments of 1/14 ms for RN-¹H(¹⁵N_und) and RN-¹⁵N spectra and 2/14 ms for RN-¹H(¹⁵N_dec) spectra, 2/14 ms CP contact time, and 200 Hz Lorentzian line broadening. Number of crystallite orientations and γ angles are 320 and 4, respectively.

RESULTS

Experimental Spectra

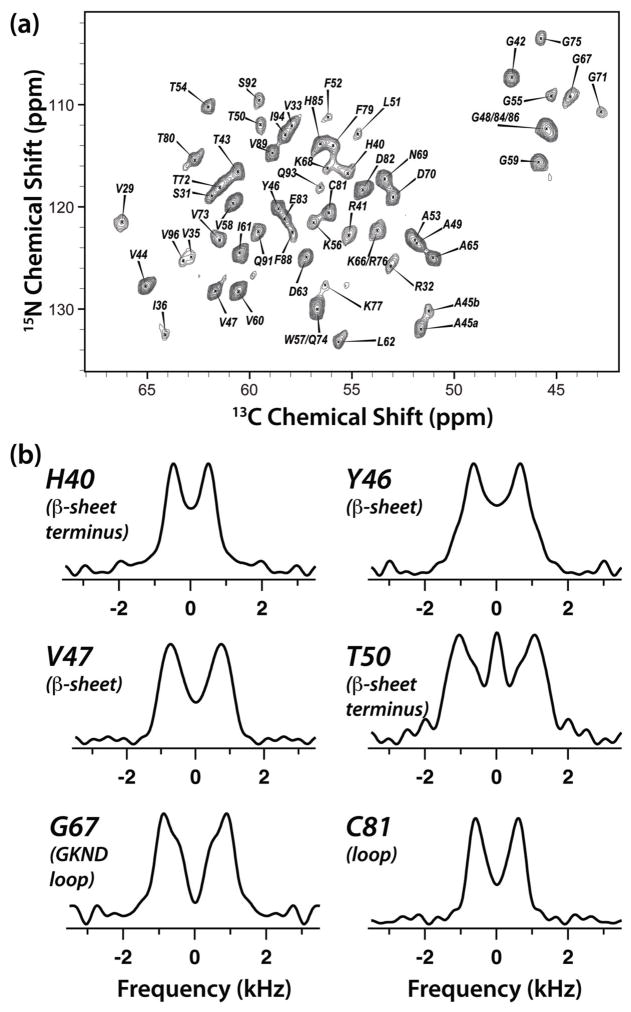
In Figure 4, the 2D NCA plane extracted from the 3D R12₁^4-1H(¹⁵N_dec) spectrum (Figure 1c) is illustrated together with six representative lineshapes of CAP-Gly residues H40, Y46, V47, T50, G67, and C81. These residues were judiciously chosen to represent β-sheet (Y46 and V47), termini of β-sheet (H40), and loop (T50, H40, G67, and C81) secondary structure regions of the protein (CAP-Gly contains essentially no α-helices). As anticipated, at 19.9 T both the resolution and the sensitivity are remarkably high permitting to extract excellent-quality lineshapes for forty-two residues of CAP-Gly from the three sets of 3D spectra.

Figure 4.

(a) The 2D NCA plane (at t₁ = 0) of the 3D R12₁^4-1H(¹⁵N_dec) spectrum of U-¹³C,¹⁵N-CAP-Gly domain of mammalian dynactin. The experiment was conducted at 19.9 T. Acquisition and processing parameters are presented in the Experiment section. (b) Experimental RN-¹H(¹⁵N_dec) lineshapes extracted from the 3D RN-¹H(¹⁵N_dec) spectrum for judiciously chosen CAP-Gly residues: H40 (terminus of β-sheet), Y46 (β-sheet), V47 (β-sheet), T50 (loop), T54 (loop), and C81 (loop).

In Figure 5, the experimental RN-¹H(¹⁵N_und), RN-¹H(¹⁵N_dec), and RN-¹⁵N lineshapes are depicted for the representative CAP-Gly residues spanning the various regions of the primary sequence and secondary structure, together with the best-fit calculated full-Hamiltonian spectra. The best-fit parameters and their uncertainty ranges are listed in Table 1. To extract the individual elements of the ¹H CSA tensors and the ¹H-¹⁵N dipolar coupling constant (DCC) as well as the polar angles defining the relative orientation of the NH bond and the CSA tensor of the amide proton, we have performed simultaneous fitting of each set of three $R{12}_1^4$ spectra. Also listed are the isotropic ¹H chemical shifts of U-¹³C,¹⁵N-CAP-Gly that were extracted from solution ¹H-¹⁵N HSQC spectra and reported by us previously.³⁸ Although we do not have evidence that the isotropic shifts in the liquid and solid state are identical, we utilized the solution shifts to evaluate the actual values of the principal components of the CSA tensors, δ_ii, from the δ_ii – δ_iso data resulting from our $R{12}_1^4$ analysis and it is these actual CSA components that are listed in Table 1. We next turn our attention to the curve fitting procedures permitting optimized accuracy of the values of the experimental observables to be derived.

Figure 5.

Experimental (black) and best-fit simulated with full Hamiltonian (blue) $R{12}_1^4$ -symmetry based RN-¹H(¹⁵N_und), RN-¹H(¹⁵N_dec), and RN-¹⁵N lineshapes of select residues of U-¹³C,¹⁵N-CAP-Gly domain of mammalian dynactin.

Table 1.

Spin-interaction parameters and their uncertainty limits obtained by triple curve fitting of average-Hamiltonian spectra to the experimental $R{12}_1^4$ spectra of amide protons of U-¹³C,¹⁵N CAP-Gly.

Residue (2° structure)	N…O Å	H…O Å	δiso ppm	δXX ppm	δYY ppm	δZZ ppm	Span ppm	DCC kHz	θ deg
V29 (loop)	N/A	N/A	8.58	16.5 ± 1.3	8.1 ± 1.3	1.2 ± 1.4	15.3 ± 1.3	9.7 ± 0.4	7 ± 9
G30 (loop)	2.94	2.05	8.93	15.5 ± 0.9	10.3 ± 1.0	−0.1 ± 0.6	15.6 ± 1.1	9.4 ± 0.2	11 ± 4
R32 (sheet)	N/A	N/A	8.92	16.3 ± 1.3	9.0 ± 1.2	1.5 ± 0.3	14.8 ± 1.4	9.5 ± 0.2	8 ± 3
V35 (sheet)	3.01	2.19	8.66	17.0 ± 1.2	8.6 ± 1.2	0.4 ± 1.3	16.5 ± 1.2	10.0 ± 0.4	14 ± 9
I36 (loop)	3.09	2.22	8.3	12.6 ± 2.0	10.9 ± 2.0	1.4 ± 2.1	11.1 ± 1.9	9.7 ± 0.7	19 ± 13
G39 (loop)	N/A	N/A	8.2	12.1 ± 3.5	10.9 ± 3.3	1.7 ± 3.5	10.4 ± 3.0	9.0 ± 1.1	12 ± 21
H40 (sheet)	N/A	N/A	6.22	10.9 ± 1.0	3.7 ± 2.0	4.0 ± 1.3	6.9 ± 1.2	8.9 ± 0.5	2 ± 32
R41 (sheet)	N/A	N/A	8.86	15.9 ± 0.8	9.3 ± 0.9	1.4 ± 0.9	14.6 ± 0.9	9.6 ± 0.3	0 ± 7
G42 (sheet)	3.07	2.18	8.91	17.5 ± 0.2	7.8 ± 0.3	1.4 ± 0.3	16.1 ± 0.4	10.3 ± 0.1	9 ± 4
T43 (sheet)	2.91	2.01	8.48	15.7 ± 0.5	9.0 ± 0.6	0.7 ± 0.6	15.0 ± 0.6	10.4 ± 0.2	13 ± 5
V44 (sheet)	3.21	2.28	9.32	17.5 ± 0.2	8.8 ± 0.2	1.7 ± 0.3	15.8 ± 0.5	10.3 ± 0.1	9 ± 4
Y46 (sheet)	3.27	2.31	7.63	13.3 ± 0.3	7.3 ± 0.4	2.3 ± 0.4	11.0 ± 0.5	10.0 ± 0.1	26 ± 4
V47 (sheet)	N/A	N/A	8.15	14.8 ± 0.2	9.3 ± 0.3	0.3 ± 0.3	14.4 ± 0.4	10.3 ± 0.1	9 ± 4
T50 (loop)	N/A	N/A	10.13	18.3 ± 1.1	12.5 ± 1.1	−0.4 ± 1.1	18.7 ± 1.1	9.9 ± 0.4	8 ± 8
L51 (loop)	N/A	N/A	7.74	14.7 ± 2.1	8.2 ± 2.5	0.4 ± 0.8	14.3 ± 1.9	10.8 ± 0.6	0 ± 14
F52 (loop)	N/A	N/A	6.46	11.8 ± 1.6	2.9 ± 1.6	4.7 ± 1.8	7.1 ± 3.1	10.1 ± 0.5	1 ± 46
T54 (loop)	N/A	N/A	8.42	15.0 ± 1.0	9.3 ± 1.0	1.0 ± 1.0	14.0 ± 1.0	9.2 ± 0.3	16 ± 8
G55 (loop)	N/A	N/A	8.81	15.6 ± 1.1	11.0 ± 1.1	−0.1 ± 1.2	15.7 ± 1.1	9.5 ± 0.4	11 ± 8
K56 (sheet)	N/A	N/A	8.51	14.3 ± 0.9	11.0 ± 1.0	0.2 ± 1.0	14.1 ± 1.0	9.3 ± 0.3	11 ± 8
V58 (sheet)	3.03	2.20	9.49	17.2 ± 0.2	9.7 ± 0.2	1.5 ± 0.2	15.7 ± 0.4	10.4 ± 0.1	11 ± 4
G59 (sheet)	2.62	1.70	10.02	18.4 ± 0.6	12.1 ± 0.7	−0.5 ± 0.4	18.9 ± 0.8	9.9 ± 0.3	10 ± 3
V60 (sheet)	3.08	2.12	9.07	16.8 ± 0.0	9.0 ± 0.2	1.4 ± 0.1	15.4 ± 0.3	10.2 ± 0.1	12 ± 3
I61 (sheet)	2.79	1.82	8.63	16.4 ± 0.2	8.6 ± 0.4	0.9 ± 0.3	15.4 ± 0.4	10.2 ± 0.1	12 ± 4
D63 (loop)	3.05	2.11	9.00	14.0 ± 0.6	10.5 ± 0.6	2.5 ± 0.6	11.4 ± 0.7	10.2 ± 0.2	17 ± 6
A65 (loop)	N/A	N/A	8.48	15.5 ± 0.2	9.5 ± 0.5	0.4 ± 0.4	15.1 ± 0.4	9.8 ± 0.1	11 ± 4
G67 (loop)	3.89	N/A	8.56	16.2 ± 0.8	7.2 ± 0.9	2.2 ± 0.9	14.1 ± 0.9	10.2 ± 0.3	12 ± 7
G67 (loop)	3.89	N/A	8.56	13.5 ± 0.8	11.4 ± 0.9	0.8 ± 0.9	12.7 ± 0.9	9.7 ± 0.3	29 ± 7
K68 (loop)	N/A	N/A	8.31	14.1 ± 0.9	9.4 ± 1.0	1.4 ± 1.0	12.7 ± 1.0	9.6 ± 0.3	16 ± 8
N69 (loop)	N/A	N/A	8.46	15.4 ± 0.2	8.3 ± 0.3	1.8 ± 0.3	13.6 ± 0.4	9.9 ± 0.1	9 ± 4
D70 (loop)	N/A	N/A	8.14	14.3 ± 0.4	8.2 ± 1.1	2.0 ± 0.8	12.2 ± 0.6	10.0 ± 0.2	26 ± 7
G71 (loop)	3.80	N/A	8.75	14.6 ± 2.0	10.8 ± 1.9	0.8 ± 2.0	13.8 ± 1.8	10.3 ± 0.6	18 ± 13
V73 (loop)	2.98	2.03	8.45	15.0 ± 0.2	7.8 ± 0.3	2.6 ± 0.4	12.5 ± 0.5	10.1 ± 0.1	7 ± 11
G75 (loop)	N/A	N/A	8.57	15.5 ± 1.7	10.3 ± 1.7	−0.1 ± 1.8	15.6 ± 1.6	9.9 ± 0.6	15 ± 11
F79 (loop)	N/A	N/A	7.95	14.8 ± 0.6	6.2 ± 0.6	2.9 ± 0.6	11.9 ± 0.7	9.9 ± 0.2	12 ± 6
T80 (loop)	N/A	N/A	8.65	15.0 ± 0.8	9.8 ± 0.9	1.1 ± 0.9	13.9 ± 0.9	9.9 ± 0.3	11 ± 7
C81 (loop)	3.40	2.43	7.92	13.3 ± 0.1	7.3 ± 0.3	3.2 ± 0.3	10.1 ± 0.4	10.0 ± 0.1	3 ± 7
D82 (loop)	N/A	N/A	8.23	15.2 ± 0.3	8.5 ± 0.0	0.8 ± 0.4	14.4 ± 0.4	9.8 ± 0.1	12
H85 (loop)	3.21	2.48	8.18	14.4 ± 0.4	7.1 ± 0.5	3.0 ± 0.4	11.3 ± 0.5	10.5 ± 0.2	1 ± 5
F88 (sheet)	N/A	N/A	8.90	16.2 ± 1.3	9.3 ± 1.6	1.2 ± 0.5	15.0 ± 0.9	9.7 ± 0.3	11 ± 7
V89 (sheet)	3.08	2.18	9.59	17.2 ± 0.3	10.5 ± 0.5	1.1 ± 0.4	16.0 ± 0.5	10.4 ± 0.2	11 ± 5
Q91 (loop)	N/A	N/A	9.39	17.7 ± 0.7	11.0 ± 0.8	−0.5 ± 0.8	18.3 ± 0.9	10.1 ± 0.3	8 ± 7
S92 (loop)	N/A	N/A	7.63	13.3 ± 1.3	6.4 ± 1.4	3.2 ± 1.4	10.1 ± 1.3	9.8 ± 0.5	0 ± 10
Q93 (loop)	3.13	N/A	7.87	13.6 ± 1.5	9.7 ± 1.5	0.3 ± 1.6	13.4 ± 1.5	9.7 ± 0.5	16 ± 11

Curve Fitting and Accuracy of ¹H CSA Parameters

The parameters to be adjusted by curve fitting of theoretical $R{12}_1^4$ lineshapes to experimental spectra are the five quantities δ, η, D, θ, φ defining the spin interactions and, in addition, the individual line-broadening parameters for each of the spectra. For the broadening we assumed a Lorentzian profile. When simultaneous fittings were performed on any combination of two of the RN-¹H and RN-¹⁵N spectra, the resulting parameters were consistently less accurate than the results of simultaneous triple fittings.

The least-squares simplex method was applied for finding the parameters that minimize χ², which is the sum of squares of the differences between the data points in the experimental and calculated spectra. The χ² evaluation was done after optimization of baseline correction and vertical scaling of the simulated spectra. As a rule, the χ² evaluations excluded the central regions bounded by ±0.5 kHz in RN-¹H(¹⁵N_und) spectra, ±0.5 or ±0.3 kHz in RN-¹H(¹⁵N_dec) spectra, and ±0.5 kHz in RN-¹⁵N spectra. Since the exclusion of the central region is practically impossible to define in the originating time-domain signal, it was necessary for the fits to be performed on the Fourier transformed spectra. In the fitting procedure no limits were placed on the data range of η. The δ_ii components evaluated from the best-fit δ and η were assigned to the X, Y, and Z axes following our convention described above.

Uncertainty limits of the least-squares parameters were estimated by Monte Carlo method as follows. We found a strong correlation between the uncertainty ranges and the heights of the cross peaks shown in the 2D NCA plane. When doing the fits, one also has to be aware of possible local χ² minima. An example of persisting ambiguity is G67 for which we listed two possible sets of parameters. Noticeable is the wide diversity of sometimes very large uncertainties of the polar angle θ. Although it appears from comparison between the lineshapes in Figure 3 that there is strong dependence on θ, the uncertainties can still be extensive due to a strong covariance between the polar angles and the CSA principal components. One particular example is H40, which is nearly axially symmetric about X and for which φ comes out to be close to 90°. It means that with the NH direction parallel to the YZ plane the angle θ is undetermined. Furthermore, as a consequence of small θ angles, the azimuthal angle φ is ill-defined in almost all other cases. Therefore, its value is not listed in Table 1. The table also lists the CSA span, which is the difference δ_XX – δ_ZZ. The reason for its inclusion is that its uncertainty is smaller than what one would derive from the uncertainties of δ_XX and δ_ZZ. Since the analysis procedure involves the performance of multiple simplex runs, we executed the initial stages of the fitting process by average-Hamiltonian simulations, which are quick on the computer, and completed the final steps by application of the full Hamiltonian.

One important example of the need for simultaneous fitting of all three RN spectra is the evaluation of the DCC. Although it is to be expected that the RN-¹⁵N spectrum is almost exclusively determined by the DCC value, the ¹H CSA interaction does have noticeable effect on the lineshape, especially at high magnetic fields. (This effect was assumed to be negligible in the prior literature, where most of the measurements were performed a lower magnetic field strength of 14.1 T.^34,47) Therefore, pre-knowledge of the actual values of δ and η is essential for evaluating the DCC if one wishes to perform single curve fitting of the RN-¹⁵N spectrum. For instance, a single fit of the RN-¹⁵N spectrum of residue G30 gives a DCC value ranging from 9.51 to 10.08 kHz when δ is kept at fixed values between 6.67 and −9.01 ppm, respectively. For comparison, the triple fit of the RN-¹H(¹⁵N_und), RN-¹H(¹⁵N_dec), and RN-¹⁵N spectra yields the DCC value of 9.4 kHz. We find similar differences between the single- and triple fit DCC values for other CAP-Gly residues, the magnitude of which depends on the actual values of δ and η.

DISCUSSION

Residue-Specific ¹H CSA Tensors of CAP-Gly Domain of Dynactin: Comparison with Earlier Solution NMR Studies

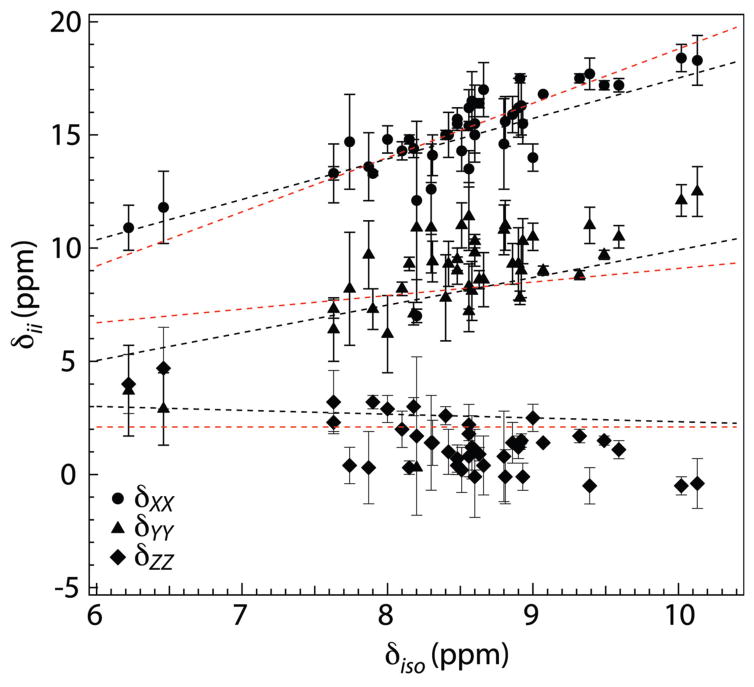
To assess the practical value of the CSA parameters of amide protons measured by our method, it is of interest to compare our experimental results with the generally consistent picture of the earlier CS-tensor studies of protons in peptide bonds. One commonly encountered property of the CSA components is their close adherence to a universal linear relationship with each other and with the isotropic shift.^17,19,20 To check how well our data agree with this behavior, we examined the relation of the CSA components of the CAP-Gly residues to their ¹H isotropic chemical shift and compared that relationship with its counterparts determined by two of the most advanced measurements of proton CSA in protein amide groups. In Figure 6 we plot the three components vs. δ_iso of forty-two CAP-Gly residues together with the straight lines that were fitted through the data points in the similar plot of ubiquitin results by Loth et al.¹⁹ and GB3 results by Yao et al.²⁰ The figure shows that the amide CSAs of our study closely follow the linear-relation trend of those earlier studies. The three best fit lines through our experimental data are: δ_XX = 2.0δ_iso − 1.7 ppm; δ_YY = 2.0δ_iso − 8.3 ppm; δ_ZZ = −1.04δ_iso + 10.2 ppm. As in those earlier studies, strong correlation was observed for δ_XX and δ_YY (with the Pearson coefficients R_P and statistical significance p being 0.85/4.3×10⁻¹³ and 0.78/7.5×10⁻¹⁰ for δ_XX and δ_YY, respectively), while for δ_YY, the correlation with the isotropic chemical shift is somewhat weaker (R_P = −0.65 and p = 2.3×10⁻⁶).

Figure 6.

Principal components of ¹H CSA tensors observed for 42 residues of U-¹³C,¹⁵N-CAP-Gly domain of mammalian dynactin, plotted as a function of the isotropic ¹H chemical shifts: δ_XX (circles), δ_YY (traingles), and δ_ZZ (diamonds). The straight lines represent the linear regression through similar CS plots of ubiquitin by Loth et al.¹⁹ (red: δ_XX = 2.4δ_iso − 5.2 ppm; δ_YY = 0.6δ_iso + 3.1 ppm; δ_ZZ = 2.1 ppm) and of GB3 by Yao et al.²⁰ (black: δ_XX = 1.79δ_iso − 0.38 ppm; δ_YY = 1.22δ_iso − 2.28 ppm; δ_ZZ = −0.17δ_iso + 4.03 ppm). The three best fit lines through our experimental data are (not shown): δ_XX = 2.0δ_iso − 1.7 ppm (R_P = 0.85, p = 4.3×10⁻¹³); δ_YY = 2.0δ_iso − 8.3 ppm (R_P = 0.78, p = 7.5×10⁻¹⁰); δ_ZZ = −1.04δ_iso + 10.2 ppm (R_P = −0.65, p = 3.3×10⁻⁶).

The numerical results of the peptide samples also comply with two other general properties of the amide proton CSA tensor, one being that, except for the residues with the smallest isotropic shift, δ_YY does not differ much from the average of δ_XX and δ_ZZ (η ~ 1) and the other that the angle θ is very often smaller than 15° and never larger than 35° (see Table 1). Unfortunately, we cannot verify compliance with the general observation that the tensor X axis is perpendicular to the peptide plane, because no interactions with backbone atoms other than the DCC with ¹⁵N are revealed by our method.

Based on these satisfying comparisons we conclude that $R{12}_1^4$ spectra are a promising route for providing proton CSA parameters that are useful for the further development of the study of amide hydrogen bonds in peptides and proteins.

Residue-Specific ¹H CSA Parameters of CAP-Gly: Relationships with Hydrogen Bonding Length

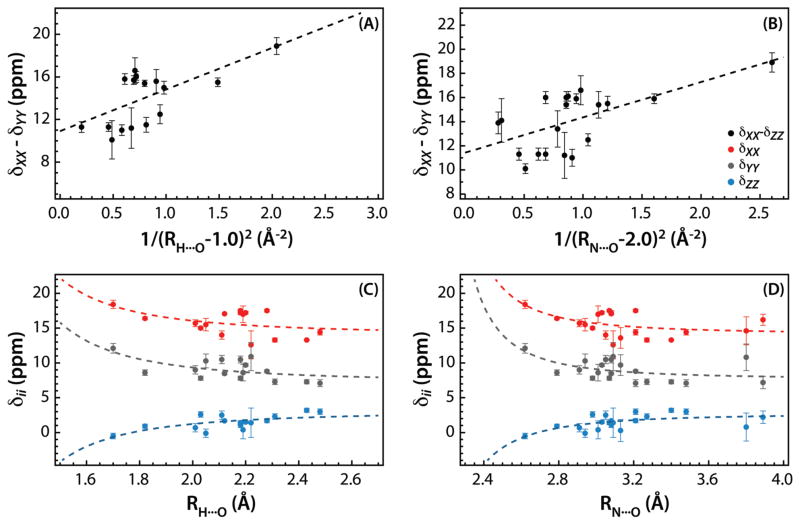
Another test of the practical validity of our results is an examination of the relation of the principal CS tensor components with the hydrogen bond length, which has repeatedly been shown in the literature to be a strong correlation. For this purpose we use the NH^⋯O and H^⋯O hydrogen bonding distances listed in Table 1 that were generated from the CAP-Gly structure solved by us using MAS NMR spectroscopy (PDB code 2m02), which will be reported in a forthcoming publication. The CAP-Gly samples for structure determination were prepared under conditions identical to those used for sample preparation in this work.

In Figure 7, we plot the principal components of the ¹H CSA tensor, δ_XX, δ_YY, and δ_ZZ, and the span, δ_XX-δ_YY, for a subset of residues forming hydrogen bonds, as the function of the NH^⋯O and H^⋯O hydrogen bond distances. As discussed previously by Tjandra and Bax, due to the electrostatic nature of the hydrogen bond, the electric field at the nucleus of the amide hydrogen participating in the hydrogen bond decreases as the square of the distance between the proton and the position of the negative charge on the oxygen atom, and hence the span of the ¹H CSA tensor is expected to roughly obey the following equation:¹⁷

Figure 7.

Correlation between principal components of ¹H CSA tensors and hydrogen bond length in U-¹³C,¹⁵N-CAP-Gly domain of mammalian dynactin. (A) and (B) show the correlation between the span, δ_XX-δ_ZZ (black) and the H^⋯O and N^⋯O distance, respectively. In (C) and (D), correlations of the principal components δ_XX (red), δ_YY (grey), and δ_ZZ (blue) are shown with the H^⋯O and N^⋯O distance, respectively. The H^⋯O and N^⋯O distances are extracted from the MAS NMR structure of CAP-Gly (PDB code 2m02). The dashed lines in (A)–(D) correspond to equation (7). In (A), B = 10.9 ppm, C = 3.9 ppm Ų, and D = 1.0 Ų. The Pearson correlation coefficient R = 0.63, and the statistical significance p = 0.007. In (B), B = 11.5 ppm, C = 2.6 ppm Ų, and D = 2.0 Ų. The Pearson correlation coefficient R = 0.61, and the statistical significance p = 0.0046. The dotted lines in (C) and (D) represent the fits of the principal components of the CSA tensors to equation (7) with the fixed values of coefficient D (1.0 Ų and 2.0 Ų for H^⋯O and N^⋯O distances, respectively). In (C), the Pearson coefficient R and the statistical significance p are 0.48/0.05, 0.60/0.01, and −0.69/0.002 for δ_XX, δ_YY, and δ_ZZ, respectively. In (D), the corresponding parameters are 0.48/0.03, 0.51/0.02, and −0.60/0.005.

$${\delta }_{XX}-{\delta }_{YY}=B+\frac{C}{{(r_{H-O}-D)}^2}$$ (7)

The best fit is obtained when B = 10.9 ppm, C = 3.9 ppm Ų, and D = 1.0 Å. The plot of the span vs. 1/(r_H^⋯O −1.0)² is shown in Figure 7(A), and the statistical analysis of the data reveals statistically significant correlation with R_P = 0.63 and p = 0.007. In Figure 7(C), we plotted δ_XX, δ_YY, and δ_ZZ, vs. the H^⋯O hydrogen bond distance. The dashed lines represent their fits to equation (7), where the coefficient D was fixed at 1.0 Å, determined from the fit of the span (see above). These fits again reveal statistically significant correlations for the individual principal components of the CSA tensors, with the Pearson coefficient R_P and the statistical significance p being 0.48/0.05, 0.60/0.01, and −0.69/0.002 for δ_XX, δ_YY, and δ_ZZ, respectively.

Since H^⋯O distances may have large associated uncertainties as the MAS NMR structure of CAP-Gly was determined on the basis of C-C distances, and proton positions were inferred computationally, we decided to also examine the relationship between the ¹H CSA tensors and the NH^⋯O hydrogen bond distances. The corresponding results are shown in Figures 7(B) and (D). The best fit of the span, δ_XX-δ_YY, to equation (7) is obtained when B = 11.5 ppm, C = 2.6 ppm Ų, and D = 2.0 Å. The plot of the span vs. 1/(r_H^⋯O −2.0)² is presented in Figure 7(B), and the statistical analysis of the data yields the Pearson correlation coefficient R_P = 0.61, and the statistical significance p = 0.0046. Similarly, the fits of the individual principal components of the CSA tensor shown as dashed lines in Figure 7(D) to equation (7) where D is fixed to 2.0 Å show statistically significant correlations with Pearson coefficient R_P and the statistical significance p being 0.48/0.03, 0.51/0.02, and −0.60/0.005 for δ_XX, δ_YY, and δ_ZZ, respectively.

Considerable scatter is present in all of the above data, as may be expected based on the conclusions of ab initio calculations that hydrogen bond distance is likely not the sole determinant of the ¹H CSA tensor.^11,20,25,26 To gain deeper understanding on the relationship of the ¹H CSA to hydrogen bond parameters much more experimental information is needed that will include a broad range of proteins and in particular a detailed survey of the CSA of various secondary structure kinds.

As discussed above, this study also underscores the importance of recording a set of three spectra, RN-¹H(¹⁵N_und), RN-¹H(¹⁵N_dec), and RN-¹⁵N, and performing their simultaneous triple fit, in order to obtain accurate values not only for the ¹H CSA but also for the ¹H-¹⁵N dipolar parameters.

Future Outlook

The results presented in this work speak to the excellent potential of the RN-based experiments for obtaining accurate and precise ¹H CSA tensors in a variety of systems. While work presented in this report was performed on a fully protonated protein sample, these experiments are expected to work well on perdeuterated samples; however, reduced sensitivity may be an issue and longer experiment times may be needed for extracting accurate ¹H CSA parameters. We point out that our approach is not limited to the measurement of amide proton CSA. It can be applied to recording ¹H CSA in any system as long as there is a heteronucleus (¹³C, ³¹P, ¹⁵N, etc.) nearby permitting cross polarization or scalar-based transfer from the proton of interest. Finally, the measurements are not limited to the $R{12}_1^4$ sequence employed in this study, and many other RN sequences with symmetries appropriate for recoupling chemical shift anisotropy will be applicable (see Table S3 with several examples), as we have shown in our recent work on recoupling heteronuclear CSA interactions.⁴⁸

CONCLUSIONS

In conclusion, we have demonstrated that proton CSA tensors can reliably be measured in 3D experiments, where in the indirect dimension $R{12}_1^4$ -or any other suitable symmetry-based recoupling allows ¹H CSA and ¹H-¹⁵N dipolar interactions to be represented in three combinations of relative magnitudes and where in the direct dimension ¹⁵N or ¹³C chemical shifts allow for site-selective detection. Simultaneous fitting of the three experimental spectra permits extracting accurate ¹H CSA tensor parameters as well as the ¹H-¹⁵N dipolar coupling constant together with the angles defining the relative orientations of the CSA tensor and the NH bond vector. Our results indicate that reliable estimates of the CSA and dipolar tensor parameters can be obtained under the average Hamiltonian model, and application of computationally expensive full-Hamiltonian calculations does not yield any noticeable improvements in the quality of the fits. As demonstrated in CAP-Gly domain of dynactin, our approach permits measurements of proton CSA tensors in systems with multiple proton sites, and is therefore anticipated to be particularly well suited for experiments on proteins, protein assemblies, and other macromolecular systems.