Bridging the gap between qualitative and quantitative colocalization results in fluorescence microscopy studies

Abstract

Quantitative colocalization studies suffer from the lack of unified approach to interpret obtained results. We developed a tool to characterize the results of colocalization experiments in a way so that they are understandable and comparable both qualitatively and quantitatively. Employing a fuzzy system model and computer simulation, we produced a set of just five linguistic variables tied to the values of popular colocalization coefficients: “Very Weak”, “Weak”, “Moderate”, “Strong”, and “Very Strong”. The use of the variables ensures that the results of colocalization studies are properly reported, easily shared, and universally understood by all researchers working in the field. When new coefficients are introduced, their values can be readily fitted into the set.

Fluorescence-based techniques revolutionized cell and molecular biological research by becoming its most indispensable tools¹. Applicability of fluorescence methodology made a leap forward with introduction of quantitative approaches. With the help of quantification, it became possible to interpret fluorescent observations objectively and analyze them statistically². Quantification of fluorescence ensured meaningful comparisons of the results between different labs and enabled development of informative mathematical simulations of studied processes³,⁴. Quantification is particularly important in colocalization observations when fluorophores of different colours, employed to label respective molecules in specific cellular locations, overlap and produce new colours as a mixture of the used⁵,⁶. The degree of this overlap is crucial to detect precise locations of the molecules of interest as well as envision the possibility of their interaction⁷,⁸.

One major limitation of quantitative colocalization studies is the lack of unified approach for interpretation of results. This is important because even after obtaining numerical values of colocalization coefficients, researchers need to describe the degree of colocalization using natural language with subjective qualifiers, such as “Weak”, “Moderate”, “Strong”, etc. This is understandable not only because natural language is the most expressive way to convey the information, but also because scientific results are usually presented in comparative terms. However, it can be also dangerously misleading, since it disconnects qualitative and quantitative aspects of observations: “Strong” colocalization in the case of overlap coefficient (standard values are from 0 to 1.0) may mean 0.99 to one researcher and 0.51 to another. This discrepancy can cause significant confusions and create errors. In addition, some researchers tend to describe colocalization using their own custom terminology, such as “Relatively Low”, “Slightly High”, etc., which is understandable to them, but may not be so to others. Thus, a solution that properly relates the numerical values of colocalization coefficients to their qualitative estimations, while maintaining the objectiveness of quantification, can be highly beneficial.

To address this issue, we report our findings on the use of the model of a fuzzy linguistic system⁹,¹⁰ to interpret the results of quantitative colocalization studies. A fuzzy system connects numeric crisp values of colocalization coefficients to fuzzy propositions that use fuzzy values such as "Weak" and "Strong", which are more descriptive and understandable to human users. A crisp value is related to fuzzy propositions by the membership functions, which assigns degrees of truth (between 0 and 1) of fuzzy propositions for the given crisp value. The final fuzzy proposition output is selected among all possible ones by essentially maximizing the degree of truth. Our aim was to provide a simple, consistent, and objective set of variables, tied to the ranges of values of respective coefficients used to estimate colocalization, which is very easy to understand and use.

Results

Selection of primary values

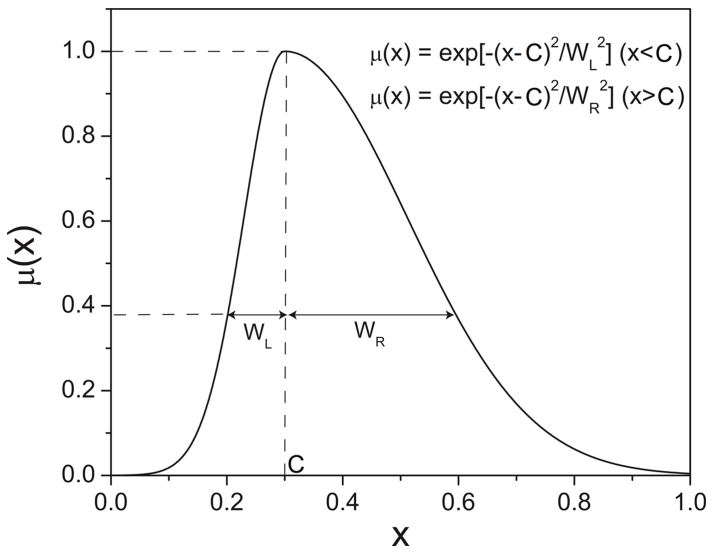
We started with primary values such as “Weak”, “Moderate”, and “Strong”, each assuming a Gaussian membership function (Fig. 1). The system ought to produce a "reasonable" description, meaning that the fuzzy predicates it generates should have sounded right to cell and molecular biologists. For example, if the actual value of colocalization is 0.8, then the predicate was presented as "The degree of colocalization is Strong", which indeed sounded right. Table 1 shows fuzzy predicates for the actual values of colocalization ranging from 0 to 0.9 (according to 0 to 1.0 scale). Initially, “Very” and “More or Less” modifiers were used in addition to the primary values to add more flexibility.

Figure 1. Gaussian membership function μ(x) centered at C with unequal left and right width W_L and W_R, respectively.

Table 1. Fuzzy predicates produced by the fuzzy system for the actual values of colocalization. The modifiers “Very” and “Less than” (or “More than”) use the square and the square root of the original membership functions, respectively. If the membership function of “Weak” is μ(x), the membership function of “Very Weak” is μ²(x).

Actual Colocalization Value (x)	0.1	0.2	0.3	0.4	0.5	0.6	0.7	0.8	0.9
Degree of colocalization/fuzzy linguistic variable	Very Weak	Weak	More than Weak	Less than Moderate	Moderate	More than Moderate	Less than Strong	Strong	Very Strong

Generation of computer simulated images and quantification of colocalization on them

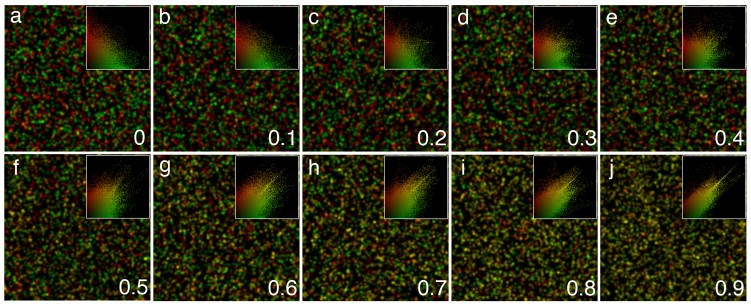
Since we could not know the actual values of colocalization in any given image in advance, we generated synthetic images with values of colocalization exactly known as a source of reference and quantified popular coefficients on them. Images were created with the help of the original software when virtual “molecules” were placed in a synthetic image with number of colocalized molecules precisely controlled (see Methods). The degree of colocalization in the images ranged from 0 to 0.9 (according to 0 to 1.0 scale) (Figure 2). The coefficients included Protein Proximity Index (PPI), Pearson's correlation coefficient (Rr), overlap coefficient (R), overlap coefficients k₁(k₂), and colocalization coefficients m₁(m₂) (Table 2). Calculations of coefficients showed gradual increases of their values strictly within the ranges of standard numbers, thus indicating excellent suitability of our synthetic images.

Figure 2. Computer-simulated images with predefined values of colocalization demonstrating its gradual increase (from 0 to 0.9 according to the 0 to 1.0 scale) as indicated by respective scatter grams at the upper right corner showing pixels concentrating along their diagonals as the degree of colocalization rises (a–j).

Images were generated by merging pairs of single-channel red and single-channel green computer-simulated images for the respective pair of channels. Then, they were used to adjust the widths of Gaussian membership functions (see Tables 1 and 2). Images were created using BioSim simulation software (see Methods for details).

Table 2. PPI and Rr, R, k₁(k₂), m₁(m₂) coefficients calculated on the set of computer-simulated synthetic images shown on Fig. 2.

Actual Colocalization Value (X) Value of coefficients	0	0.1	0.2	0.3	0.4	0.5	0.6	0.7	0.8	0.9
PPI	0.0	0.08	0.20	0.28	0.39	0.47	0.59	0.68	0.76	0.89
Rr	−0.42	−0.30	−0.14	−0.015	0.15	0.29	0.49	0.62	0.75	0.88
R	0.40	0.49	0.57	0.65	0.73	0.80	0.87	0.92	0.96	0.99
k1(k2)	0.40	0.49	0.57	0.65	0.73	0.80	0.87	0.92	0.96	0.99
m1(m2)	0.45	0.54	0.63	0.71	0.79	0.87	0.94	0.98	1.0	1.0

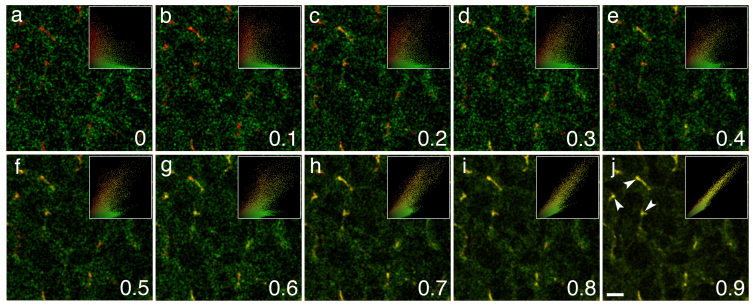
To demonstrate the applicability of our approach on biological imagery, we also created computer-simulated images modeled on a real biological image (see Methods). Figure 3 shows a panel of computer-simulated images with predefined values of colocalization modeled after a real biological image. Colocalization gradually increased in them, as indicated by respective scatter grams, eventually revealing structures with colocalization.

Figure 3. Computer-simulated images with predefined values of colocalization demonstrating its gradual increase (from 0 to 0.9 according to the 0 to 1.0 scale) as indicated by respective scatter grams at the upper right corner showing pixels concentrating along their diagonals as the degree of colocalization rises (a–j).

Images are modeled after a real biological image of liver stained for multidrug resistance protein 2 (Mrp2) (red fluorescence) and bile salt export pump (Bsep) (green fluorescence). Overlap of colours depicts colocalization at the bile canaliculi (arrowheads). Images were created using BioSim simulation software (see Methods for details). Scale bar, 2 μm.

Construction of fuzzy systems

After performing calculations of coefficients on the images, we constructed corresponding fuzzy systems for every coefficient to make them relevant (Table 3). To do so, we adjusted the width of Gaussian member functions to ensure that for each given image the fuzzy system produces the same fuzzy predicates for each coefficient as it does for actual colocalization values (Tables 1 and 2). For example, for an image with an actual value of colocalization 0.8, the fuzzy system for this value was presented as "The degree of colocalization is Strong". By adjusting the width of Gaussian membership functions, we ensured that the same predicate ought to be produced for all coefficients (Table 3). Given the nature of our simulation (virtual “molecules” had the same intensity regardless of the channel), R and k₁(k₂) coefficients yielded equal values.

Table 3. Parameters of Gaussian membership functions (center C, left width WL and right width WR) for PPI and Rr, R, k₁(k₂), m₁(m₂) coefficients generating the same fuzzy predicates as for the actual values shown on Table 1.

Parameter Value of coefficients	WL,WEAK	CWEAK	WR,WEAK	WL,MODERATE	CMODERATE	WR,MODERATE	WL,STRONG	CSTRONG	WR,STRONG
PPI	∞	0.0	0.32	0.09	0.5	0.09	0.32	1.0	∞
Rr	∞	−0.42	0.4	0.15	0.29	0.15	0.4	1.0	∞
R	∞	0.40	0.25	0.075	0.8	0.05	0.075	1.0	∞
k1(k2)	∞	0.40	0.25	0.075	0.8	0.05	0.075	1.0	∞
m1(m2)	∞	0.45	0.25	0.075	0.87	0.06	0.05	1.0	∞

Discussion

Results of our study show that degrees of colocalization, presented as linguistic variables, can be tied to the ranges of the respective coefficients values (Table 4). Our approach is advantageous to the recently reported attempt to systematize descriptions of quantitative colocalization observations based on terminology found in cell biological literature¹¹. Authors of the report provided non-matching and inconsistent variables for different coefficients, thus making them very hard to use in practice, as well as did not use any controls. Simplicity of our approach is based on the use of three primary values, such as “Weak”, “Moderate”, and “Strong”. Among the two initially employed modifiers, “Very” and “More or Less”, we used only “Very” as the most preferable one. Its use ensured consistency and flexibility of the set and brought the total number of variables to just five: “Very Weak”, “Weak”, “Moderate”, “Strong”, and “Very Strong”. To ensure that these variables are used correctly, they were applied to the ranges of values of coefficients obtained using computer-simulated images with exactly known degrees of colocalization. Thus, these variables are useable with precise understanding of what they represent.

Table 4. Degrees of colocalization as fuzzy linguistic variables and the respective ranges of values of popular coefficients used to estimate colocalization, such as PPI, Rr, R, k₁(k₂), and m₁(m₂). Set includes just five different variables: “Very Weak”, “Weak”, “Moderate”, “Strong”, and “Very Strong”, which can be used by cell and molecular biologists as a community-wide standard for describing the results of quantitative colocalization studies. PPI was calculated using PPA software. Other coefficients were calculated using CoLocalizer Pro software (see Methods). See Fig. 1 for description of a Gaussian membership function and Tables 1,2,3 for details about steps leading to creation of this Table.

Degree of colocalization/fuzzy linguistic variable Value of coefficients	Very Weak	Weak	Moderate	Strong	Very Strong
PPI	0 ~ 0.12	0.13 ~ 0.39	0.40 ~ 0.60	0.61 ~ 0.87	0.88 ~ 1.0
Rr	−1.0 ~ −0.27	−0.26 ~ 0.09	0.1 ~ 0.48	0.49 ~ 0.84	0.85 ~ 1.0
R	0 ~ 0.49	0.50 ~ 0.70	0.71 ~ 0.88	0.89 ~ 0.97	0.98 ~ 1.0
k1(k2)	0 ~ 0.49	0.50 ~ 0.70	0.71 ~ 0.88	0.89 ~ 0.97	0.98 ~ 1.0
m1(m2)	0 ~ 0.54	0.55 ~ 0.77	0.78 ~ 0.94	0.96 ~ 0.98	0.99 ~ 1.0

Importance of the described approach is not only in providing a framework for correct description of the results of colocalization studies in qualitative and quantitative terms for the currently used coefficients, but also in serving as a tool that allows accommodation of new ones. Since new and improved algorithms to quantify colocalization continue to be developed¹², computer-simulated images with known degrees of colocalization generated by us and shown in this study can be employed to obtain values of new coefficients, which can then be easily fitted into the set and Table 4 can be extended further. The images are available for download as Supplementary Information to this article. In the emerging era of bioimage informatics¹³, with increasing importance on standardization of collected image data⁵,¹⁴, the use of the variables will ensure that the results of quantitative colocalization studies are properly reported, easily shared, and universally understood by all researchers working in the field. Importantly, the use of our approach also represents a paradigm shift in colocalization studies since the results of quantifications now become presentable in familiar qualitative terms while still maintaining the objectiveness of calculations.

To conclude, our approach helps to bridge the gap between qualitative and quantitative aspects of colocalization detection. Given simplicity and consistency, as well as the fact that linguistic variables maintain the objectiveness of quantification, they can serve cell and molecular biologists as a community-wide standard for describing results of quantitative colocalization studies.

Methods

Design of a fuzzy system

The design of a fuzzy system started from a crisp system, such as a variable called "colocalization value" that can take any precise values on (0, 1). Then, we introduced fuzzy values, such as "Weak", "Moderate" and "Strong". A crisp proposition like "colocalization value is x" is either true (truth value 1) or false (truth value 0), whereas a fuzzy proposition like "colocalization value is Strong" has a truth value between 0 and 1, which was calculated by a membership function μ_STRONG(x). The fuzzy proposition with the largest truth value was then used as the output of the fuzzy system. Fuzzy values were modified using an adverb “Very”. The value “Very Strong” differs from “Strong” in that its membership function is μ_STRONG²(x).

Generation of synthetic computer-simulated images

Images with predefined values of colocalization were generated by merging pairs of green and red computer-simulated images for the red/green pair of channels. With the help of BioSim simulation computer software (MATLAB source code is available at www.anes.ucla.edu/~wuyong/biosim.zip), virtual “molecules” were placed in a synthetic image⁷. The number of colocalized molecules was precisely controlled via the software. The images were free of background noise. The degree of colocalization in the images ranged from 0 to 0.9 (according to 0 to 1.0 scale) (Figure 3). The images can be downloaded and used to obtain the ranges of values of newly-introduced colocalization coefficients, which can then be fitted into the set of linguistic variables shown on Table 4.

Generation of computer-simulated images modeled after a real biological image

Original images were acquired as described in the fluorescence microscopy section below. Prior to be used for modeling, they were processed for background correction using “Average Contrast and Fluorescence” settings with the help of CoLocalizer Pro software. Protein clusters, treated as point sources, were randomly positioned in a representative image according to biological structures. Each of the clusters generated an intensity distribution according to a Gaussian point spread function (PSF). The degree of colocalization was precisely controlled by knowing the exact number of clusters generated by BioSim software. Specifically labeled clusters were distinguishable from nonspecifically labeled ones by being significantly brighter. The degree of colocalization in the images ranged from 0 to 0.9 (according to the 0 to 1.0 scale).

Fluorescence microscopy

Images of fluorescence of liver bile canaliculi stained for multidrug resistance protein 2 (Mrp2) (red fluorescence) and bile salt export pump (Bsep) (green fluorescence), known to be colocalized¹⁵ were acquired using a confocal microscope LSM 410 (Carl Zeiss). Primary anti-Mrp2 and anti-Bsep antibodies were obtained commercially. Alexa 488 and Alexa 594 secondary antibodies (Invitrogen) were used for labeling Bsep and Mrp2, respectively. Dual-stained images were obtained using an immersion-oil Plan-Neofluar 40/0.75 objective and acquired by sequential laser scanning to minimize bleedthrough. Images were saved in lossless TIFF format to ensure reliability of quantification with a dimension of 512 × 512 pixels.

Quantification of colocalization

Colocalization was quantified using protein proximity index (PPI) and various coefficients. Protein proximity analysis (PPA) software (www.anes.ucla.edu/~wuyong/) was used to estimate PPI⁷. Coefficients included Pearson's correlation coefficient (Rr), overlap coefficient (R), overlap coefficients k₁(k₂), and colocalization coefficients m₁(m₂) and were calculated using CoLocalizer Pro 2.7.1 software (CoLocalization Research Software, www.colocalizer.com)⁸.

Author Contributions

V.Z. conceived and organized the study, designed and conducted experiments and wrote the paper. Y.W. designed fuzzy systems, created synthetic images, and contributed to writing. O.G.-Z. helped with study design, performed colocalization calculations, and contributed to writing.

Supplementary Material

Supplementary Information

Supplementary Information