Skip to main content
PMC home page
Scientific Reports logoLink to Scientific Reports
. 2013 Mar 4;3:1366. doi: 10.1038/srep01366

Two novel nonlinear optical carbonates in the deep-ultraviolet region: KBeCO3F and RbAlCO3F2

Lei Kang 1,3, Zheshuai Lin 1,a, Jingui Qin 2, Chuangtian Chen 1
PMCID: PMC3586702  PMID: 23455618

Abstract

With the rapid developments of the all-solid-state deep-ultraviolet (deep-UV) lasers, the good nonlinear optical (NLO) crystal applied in this spectral region is currently lacking. Here, we design two novel NLO carbonates KBeCO3F and RbAlCO3F2 from the first-principles theory implemented in the molecular engineering expert system especially for NLO crystals. Both structurally stable crystals possess very large energy band gaps and optical anisotropy, so they would become the very promising deep-UV NLO crystals alternative to KBBF. Recent experimental results on MNCO3F (M = K, Rb, Cs; N = Ca, Sr, Ba) not only confirm our calculations, but also suggest that the synthesis of the KBeCO3F and RbAlCO3F2 crystals is feasible.

Deep-ultraviolet (deep-UV, λ < 200 nm) nonlinear optical (NLO) crystals, as a key component of all-solid-state deep-UV lasers, have played important roles in many advanced scientific and technical areas1,2,3. Numerous attempts have been performed on the explorations of new deep-UV NLO materials with good performances4,5,6,7,8, and the dominant research field has been focused on the borates9,10,11. In particular, Potassium beryllium fluoroborate (KBe2BO3F2, KBBF) exhibits excellent NLO performance in the deep-UV region; till now KBBF is the sole NLO crystal that can practically generate the deep-UV lasers by direct SHG process1. However, the applications of KBBF are heavily hindered by the layering tendency in the single crystal growth processes12. Therefore, it is urgently demanded the emergence of new types deep-UV NLO materials.

To be a good deep-UV NLO material, the following four criterions are commonly considered13,14: (i) a wide UV transparency range down to the deep-UV region, corresponding to the large energy band gap and high damage threshold; (ii) a relatively large efficient second harmonic generation (SHG) coefficient (dij ≥ 0.39 pm/V, d36 of KH2PO4); (iii) a relative large birefringence (Δn ≥ 0.08) to achieve the phase matching condition in the deep-UV region; and (iv) good chemical stability and mechanical properties. According to the anionic group theory15,16, the planar [BO3]3− microscopic anionic groups have the dominant contribution to the macroscopic optical anisotropies in crystal, as in the KBBF case. Analogously, [CO3]2− and [NO3]− anionic groups are expected to be the good NLO micro-structural units as well since they have the similar planar triangle structure with the π-conjugated molecular orbitals which can produce the large birefringence and second-order susceptibility. The nitrates, however, are not considered as the NLO candidates for their hydrolysis. Thus, it is greatly desirable to explore the deep-UV NLO materials in carbonates.

The rapid developments of scientific computational resources make it possible to predict the new advanced materials directly from the first-principles theory17,18,19, although search for the best candidate for a special property is still a major task20. In this work, aiming at the additional NLO candidates in the deep-UV region, we design two structurally stable carbonates KBeCO3F and RbAlCO3F2. The energy band gaps and the linear and nonlinear optical properties of both crystals are determined by ab initio calculations with high precision, which clearly demonstrate their promising applications as good optoelectronic functional materials in the deep-UV region.

Results

In order to search for the suitable deep-UV carbonates, we employed the anionic group theory combined with first-principles calculations which are implemented in the molecular engineering expert system especially for NLO crystals originated from our group9,15. After numerous efforts, we have theoretically discovered two carbonates, KBeCO3F and RbAlCO3F2, according to the following materials design considerations: (i) the candidates are the fluoride carbonates since they can possess the larger energy band gaps compared with other carbonates21; (ii) the A-site cations are the metal cations without unclosed d or f electrons because the d-d or f-f electronic transitions have negative influences to the energy band gap. Especially the alkaline cations and the lightweight metal cations in the Group IIA and IIIA in the Periodic Table are taking into account; (iii) all [CO3]2− anionic groups are parallel (flat-lying) with respect to the overall structural layering. This structural feature has strong optical anisotropic responses to the incident light and exhibit large optical birefringence; and (iv) the orientation of all [CO3]2− groups is parallel to each other. This arrangement is favorable to the additive superposition of the microscopic second susceptibilities in the anionic groups, so produce large macroscopic SHG effects in crystal.

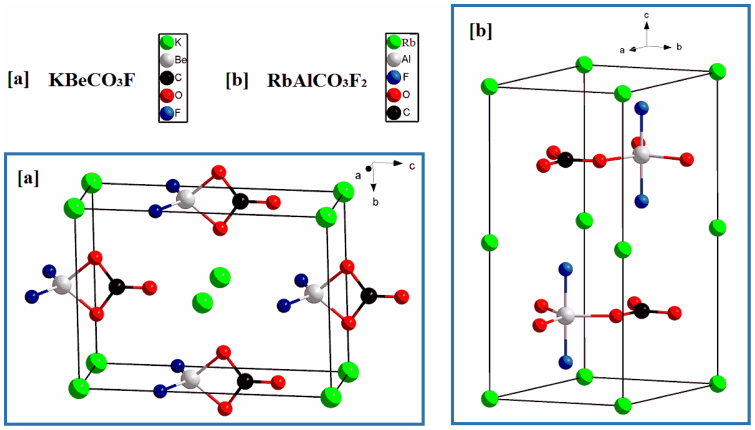
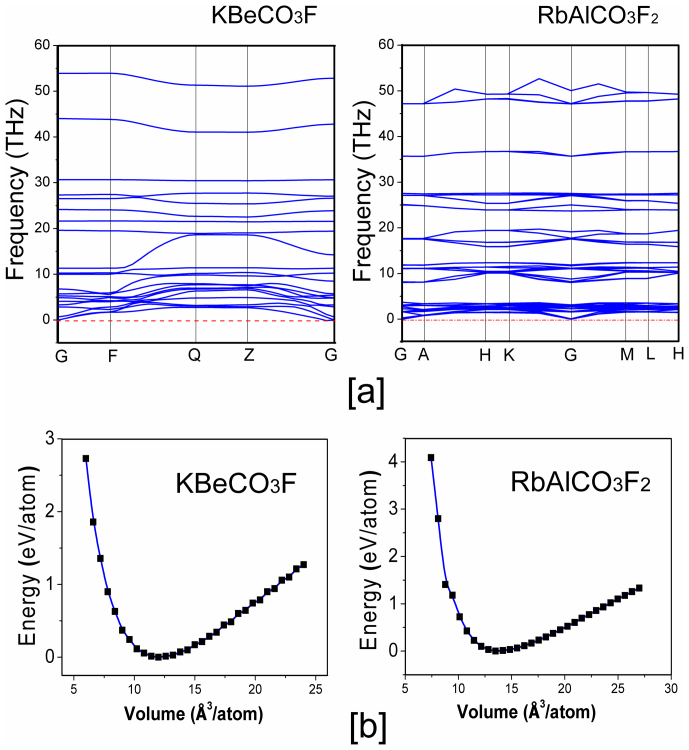
The structures of KBeCO3F and RbAlCO3F2 are plotted in Fig. 1 (their crystallographic data see Table S1 in the Supplementary Information). In KBeCO3F, the [BeO2F2] tetrahedra are connected with the [CO3] triangles by sharing their edges, forming the zero-dimensional [BeCO3F2] microscopic structures isolated by the K+ cations. In RbAlCO3F2, the [AlO3F2] trigonal bipyramids and [CO3] triangles are alternately arranged in a trigonal pattern and connected via common O corners, generating a two-dimensional infinite [AlCO3F2] layer parallel to the a–b plane. The Rb+ cations are located between these layers to balance charge and also hold the layers together through the coordination with O and F anions. Both structures clearly exhibit the parallel flat-lying arrangement of the [CO3]2− groups in crystals, so they are expected to have large SHG coefficients and birefringences. More importantly, the structural stabilities of both crystals are carefully verified by the first-principles methods18,19. Figure 2 displays the phonon spectra and the total energy as a function of volume per atom in KBeCO3F and RbAlCO3F2. In the phonon spectra (Figure 2(a)) none of the imaginary phonon modes is observed, and in the curves of the total energy as a function of volume per atom (Figure 2(b)) there has a single minimum in the wide range of volume modification. Both evidences clearly demonstrate that the titled crystals are kinetically stable.

Figure 1. Unit cell of KBeCO3F (a) and RbAlCO3F2 (b).

Figure 1

Open in a new tab

Figure 2. Evidences of the structural stabilities in KBeCO3F and RbAlCO3F2 from the first-principles studies.

Figure 2

Open in a new tab

(a) The phonon spectra. (b) The total energy as a function of volume per atom. The energy minimum is set as the zero point.

The calculated linear and nonlinear optical properties for KBeCO3F and RbAlCO3F2 are listed in Table 1, and the experimental results for KBBF are also shown as a comparison. It is clear that both KBeCO3F and RbAlCO3F2 possess very large energy band gaps, 7.61 eV (~164 nm) and 8.21eV (~152 nm), respectively. Meanwhile, the birefringences and SHG coefficients in both KBeCO3F and RbAlCO3F2 crystals are larger than those in KBBF. The large birefringences (Δn = 0.1297 in KBeCO3F and Δn = 0.0998 in RbAlCO3F2) guarantee the achievement of the SHG phase-matching condition in both crystals down to their UV absorption edge, thus their shortest phase-matching wavelengths very approach (or even exceed) the corresponding wavelength in KBBF (~161 nm)12. It should be emphasized that RbAlCO3F2 is optically uniaxial, which would be beneficial to its practical applications. The excellent optical properties in KBeCO3F and RbAlCO3F2 demonstrate that both crystals are comparable to KBBF for the deep-UV SHG capabilities. Upon being obtained, these crystals would have wide applications as the optoelectronic functional materials in the deep-UV spectral region.

Table 1. Comparison of the linear and nonlinear optical properties in KBeCO3F, RbAlCO3F2 and KBBF. Eg is the energy band gap, n is the refractive index at the wavelength ~ 400 nm, Δn is the birefringence, λPM is the shortest phase-matching wavelength, and dij is the SHG coefficient. For a uniaxial crystal, nx = ny = no and nz = ne.

Crystal Eg (eV) nx ny nz Δn λPM (nm) dij (pm/V)
KBeCO3F 7.61 1.5458 1.5149 1.4161 0.1297 164 d21 = −0.94; d22 = 0.70; d11 = 0.26; d12 = 0.15
RbAlCO3F2 8.21 1.4982 1.4982 1.3984 0.0998 152 d16 = −d22 = −0.69
KBBFa 8.26 1.4915 1.4915 1.4035 0.0880 161 d11 = 0.47
Open in a new tab

aRef. 12.

Discussion

To verify the reliability of our ab initio calculations on the optical properties in carbonates, we also applied our calculated methods on a family of recently synthesized NLO fluoride carbonates, MNCO3F (M = K, Rb, Cs; N = Ca, Sr, Ba)22. The preliminary optical measures revealed that these compounds possess wide energy band gap (UV absorption edge < 200 nm) and qualitatively exhibit good capabilities for the UV harmonic generation22. However, due to the very small size of the samples the obtained experimental data are not enough to determine their application prospects in the deep-UV region. Our calculated energy band gaps and SHG coefficients match the available experimental results very well (see Table S2 and S3 in the Supplementary Information), which strongly prove the validity and high precision of the first-principles studies on the UV NLO carbonate crystals. Since the MNCO3F series possess strong NLO effect and large birefringence, we predict that they are suitable to be good NLO crystals and excellent birefringent materials in the UV region. Nevertheless, these carbonates cannot be applied in the deep-UV region due to their relatively small energy band gaps (Eg ~ 6.3 eV).

The detailed electronic structure analysis show that the small energy gaps in MNCO3F are mainly due to the O 2p non-bonding states exclusively occupied at the valence band maximum, which have negligible small overlap with other electronic states and directly determine the energy band gap23 (see Figure S1 in the Supplementary Information). The energy spanning of these non-bonding states is as large as about 2.5 eV, and their complete elimination can significantly increase the energy band gap of crystals to more than 8.3 eV (UV absorption edge < 150 nm). Compared MNCO3F with our proposed crystals, the substitution of Ca, Sr or Ba atoms with the lightweight metal cations in the Group IIA or IIIA, Be or Al, can effectively remove the non-bonding orbitals in carbonates, analogous to the borate cases such as beryllium in KBBF24,25 and aluminum in BaAlBO3F (BABF)26,27,28. Indeed, Figure 3 clearly shows that the energy spanning of the non-bonding regions in KBeCO3F and RbAlCO3F2 reduces about 1.1 eV and 2.3 eV, respectively, compared with that in MNCO3F, exemplified by KSrCO3F. Therefore, the UV absorption edge of both KBeCO3F and RbAlCO3F2 are significantly blue-shifted. In addition, the similarity of the micro-structural features in the MNCO3F series and our proposed crystals suggests that it is feasible to synthesize KBeCO3F and RbAlCO3F2 in experiments.

Figure 3.

Figure 3

Open in a new tab

(a) (left) Partial density of states (PDOS) projected on the constituent atoms in MNCO3F, exemplified by the KSrCO3F crystal, (right) the PDOS zoomed-in to show the non-bonding states on oxygen atoms.(b) PDOS projected on the constituent atoms in KBeCO3F (left) and RbAlCO3F2 (right). The blue and red curves represent the s and p orbitals, respectively, and the shadow areas represent the region occupied by non-bonding states on oxygen atoms.

We surveyed throughout Inorganic Crystal Structure Database (ICSD)29, and found that only 14 fluoride carbonates whose energy band gaps may be large enough to transmit the UV radiation have been discovered and synthesized in experiments (see Table S4 in the Supplementary Information), in which seven are noncentrosymmetric and satisfy the SHG requirement. The very few report on UV NLO carbonates actually implies that the researches on this type of optoelectronic functional materials have been long-termly neglected and the broad developing space is available. We believe that our work would have great implications on the search and design of new NLO crystals in the deep-UV spectral region with the great help of advanced synthesis and single-crystal growth approaches.

Methods

First-principles computational methods and geometry optimizations

The first-principles calculations are performed by the plane-wave pseudopotential method30 implemented in the CASTEP package31 based on the density functional theory (DFT)32. The ion-electron interactions are modeled by the optimized normal-conserving pseudopotentials for all elements33,34,35. The kinetic energy cutoffs of 900 eV and Monkhorst-Pack k-point meshes36 with the spanning of less than 0.03/Å3 in the Brillouin zone are chosen. The supercell volume and the atomic positions for KBeCO3F and RbAlCO3F2 are fully optimized using the quasi-Newton method37. The convergence thresholds between optimization cycles for energy change, maximum force, maximum stress, and maximum displacement are set as 10−5 eV/atom, 0.03 eV/Å, 0.05 GPa, and 0.001 Å, respectively. The above computational set ups are sufficiently accurate for present purposes38.

Calculated methods for structural stability

To verify the structural stability, phonon spectra calculations on KBeCO3F and RbAlCO3F2 are performed. The positive eigenvalues for all phonon modes is the most important evidence for the structural stability in crystal. The structural stability can also be demonstrated by the total energy as a function of volume per atom. If there has only a single minimum in the wide range of volume modification, the studied geometrical structure would be stable. The studied methods on structural stability were also adopted by Yao18 and Sheng19.

Calculated methods for optical properties

When determining the linear optical properties the imaginary part of the dielectric function ε2 is calculated39, and then its real part is determined by Kramers-Kronig transform, from which the refractive indices (and the birefringence) are obtained. Moreover, the second-order susceptibility χ(2), i.e., the SHG coefficient dij, is calculated by the following formula developed by our group40:

graphic file with name srep01366-m1.jpg

where χαβγ(VE), χαβγ(VH) and χαβγ(two bands) denote the contributions from virtual-electron processes, virtual-hole processes and two-band processes, respectively. The formulae for calculating χαβγ(VE), χαβγ(VH) and χαβγ(two bands) are given as follows40:

graphic file with name srep01366-m2.jpg
graphic file with name srep01366-m3.jpg
graphic file with name srep01366-m4.jpg

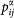Here, α, β and γ are Cartesian components, v and v′ denote valence bands, and c and c′ denote conduction bands. P(αβγ) denotes full permutation and explicitly shows the Kleinman symmetry of the SHG coefficients. The band energy difference and momentum matrix elements are denotes as Inline graphic and Inline graphic, respectively, and they are all implicitly k dependent.

It is well acknowledged that the DFT calculations with the exchange-correlation (XC) functional of generalized gradient approximation (GGA)41 always underestimate the energy band gap of crystals. For calculating the optical coefficients, a scissors operator42,43 is usually introduced to shift up all the conduction bands to agree with the measured band gap, which is not “purely” ab initio. Recently, we have examined several XC functionals beyond GGA on the determination of energy band gaps and optical properties in UV NLO crystals44. It was found that the hybrid functionals such PBE045, P3LYP46 and sX-LDA47 can predict the UV absorption edge very well, but the calculated electronic band structures and optical properties are not well reproduced compared to the scissors-corrected GGA method44. Indeed our calculations show that in the MNCO3F crystals the GGA energy band gaps are in large discrepancy to the experimental results (absolute error excesses 2.4 eV), while the PBE0 values are in good consistency with the measurements (see Table S2 in the Supplementary Information). Therefore, in this work the difference between PBE0 and GGA energy band gaps is set as the scissors operator, which is then used to determine the optical properties by GGA. The further tests have also revealed that the χ(2) values is insensitive to the modification (e.g. ~ ±0.5 eV) of the scissors operator because of the very large band gap (>6 eV) in the studied carbonates. Therefore, this computational procedure ensures that our first-principles studies are self-consistent without adjusting any parameter from experiments.

Author Contributions

L.K. performed the first-principles studies and prepared the data. Z.S.L. supervised the studies and wrote the manuscript. J.G.Q. and C.T.C. discussed results.

Supplementary Material

Supplementary Information

Supplementary Information for Two novel nonlinear optical carbonates in the deep-ultraviolet region: KBeCO3F and RbAlCO3F2

srep01366-s1.pdf (134.7KB, pdf)

Acknowledgments

The authors acknowledge the useful discussions with Zhuohong Yin. This work was supported by the National Natural Science Foundation of China under Grant Nos 11174297 and 91022036, and the National Basic Research Project of China (Nos 2010CB630701 and 2011CB922204).

References

  1. Cyranoski D. China's crystal cache. Nature 457, 953–955 (2009). [DOI] [PubMed] [Google Scholar]
  2. Xu Y. M. et al. Observation of a ubiquitous three-dimensional superconducting gap function in optimally doped Ba0.6K0.4Fe2As2. Nature Physics 7, 198–202 (2011). [Google Scholar]
  3. Mu R. et al. Visualizing Chemical Reactions Confined under Graphene. Angew. Chem. Int. Ed. 51, 4856–4859 (2012). [DOI] [PubMed] [Google Scholar]
  4. Wang S., Ye N., Li W. & Zhao D. Alkaline Beryllium Borate NaBeB3O6 and ABe2B3O7 (A = K, Rb) as UV Nonlinear Optical Crystals. J. Am. Chem. Soc. 132, 8779–8786 (2010). [DOI] [PubMed] [Google Scholar]
  5. Wang S. & Ye N. Na2CsBe6B5O15: An Alkaline Beryllium Borate as a Deep-UV Nonlinear Optical Crystal. J. Am. Chem. Soc. 133, 11458–11461 (2011). [DOI] [PubMed] [Google Scholar]
  6. Huang H. et al. NaSr3Be3B3O9F4: A Promising Deep-Ultraviolet Nonlinear Optical Material Resulting from the Cooperative Alignment of the Be3B3O12F10− Anionic Group. Angew. Chem. Int. Ed. 50, 9141–9144 (2011). [DOI] [PubMed] [Google Scholar]
  7. Yang Y. et al. A New Lithium Rubidium Borate Li6Rb5B11O22 with Isolated B11O22 Building Blocks. Cryst. Growth Des. 11, 3912–3916 (2011). [Google Scholar]
  8. McMillen C. D., Stritzinger J. T. & Kolis J. W. Two Novel Acentric Borate Fluorides: M3B6O11F2 (M = Sr, Ba). Inorg. Chem. 51, 3953–3955 (2012). [DOI] [PubMed] [Google Scholar]
  9. Becker P. Borate materials in nonlinear optics. Adv. Mater. 10, 979–992 (1998). [Google Scholar]
  10. Keszler D. A. Synthesis, crystal chemistry, and optical properties of metal berates. Curr. Opin. Solid State Mater. Sci. 4, 155–162 (1999). [Google Scholar]
  11. Ghotbi M. et al. Efficient third harmonic generation of microjoule picosecond pulses at 355 nm in BiB3O6. Appl. Phys. Lett. 89, 173124 (2006). [Google Scholar]
  12. Chen C. T., Wang G. L., Wang X. Y. & Xu Z. Y. Deep-UV nonlinear optical crystal KBe2BO3F2---discovery, growth, optical properties and applications. Appl. Phys. B 97, 9–25 (2009). [Google Scholar]
  13. Chen C. T. et al. Computer-assisted search for nonlinear optical crystals. Adv. Mater. 11, 1071–1078 (1999). [Google Scholar]
  14. Xia Y. N., Chen C. T., Tang D. Y. & Wu B. C. New nonlinear-optical crystals for UV and VUV harmonic-generation. Adv. Mater. 7, 79–81 (1995). [Google Scholar]
  15. Chen C. T. et al. Nonlinear optical borate crystals. (Wiley-VCH, Germany, 2012). [Google Scholar]
  16. Chen C. T., Lin Z. S. & Wang Z. Z. The development of new borate-based UV nonlinear optical crystals. Appl. Phys. B 80, 1–25 (2005). [Google Scholar]
  17. Zhang H. et al. Topological insulators in Bi2Se3, Bi2Te3 and Sb2Te3 with a single Dirac cone on the surface. Nature Physics 5, 438–442 (2009). [Google Scholar]
  18. Yao Y. et al. Comment on "New Metallic Carbon Crystal". Phys. Rev. Lett. 102, 229601 (2009). [DOI] [PubMed] [Google Scholar]
  19. Sheng X.-L., Yan Q.-B., Ye F., Zheng Q.-R. & Su G. T-carbon: a novel carbon allotrope. Phys. Rev. Lett. 106, 155703 (2011). [DOI] [PubMed] [Google Scholar]
  20. Katritzky A. R. et al. Quantitative Correlation of Physical and Chemical Properties with Chemical Structure: Utility for Prediction. Chem. Rev. 110, 5714–5789 (2010). [DOI] [PubMed] [Google Scholar]
  21. Grice J. D., Maisonneuve V. & Leblanc M. Natural and synthetic fluoride carbonates. Chem. Rev. 107, 114–132 (2007). [DOI] [PubMed] [Google Scholar]
  22. Zou G. H., Ye N., Huang L. & Lin X. S. Alkaline-Alkaline Earth Fluoride Carbonate Crystals ABCO3F (A = K, Rb, Cs; B = Ca, Sr, Ba) as Nonlinear Optical Materials. J. Am. Chem. Soc. 133, 20001–20007 (2011). [DOI] [PubMed] [Google Scholar]
  23. He R., Lin Z. S., Zheng T., Huang H. & Chen C. T. Energy band gap engineering in borate ultraviolet nonlinear optical crystals: ab initio studies. J. Phys: Condens. Matter 24, 145503 (2012). [DOI] [PubMed] [Google Scholar]
  24. Lin Z. H., Wang Z. Z., Chen C. T., Chen S. K. & Lee M. H. Mechanism for linear and nonlinear optical effects in KBe2BO3F2 (KBBF) crystal. Chem. Phys. Lett. 367, 523–527 (2003). [Google Scholar]
  25. Kang L. et al. Ab initio studies on the optical effects in the deep ultraviolet nonlinear optical crystals of the KBe2BO3F2 family. J. Phys: Condens. Matter 24, 335503 (2012). [DOI] [PubMed] [Google Scholar]
  26. Hu Z. G., Yoshimura M., Mori Y. & Sasaki T. Growth of a new nonlinear optical crystal-BaAlBO3F2. J. Cryst. Growth 260, 287–290 (2004). [Google Scholar]
  27. Yue Y. C. et al. Growth and nonlinear optical properties of BaAlBO3F2 crystal. J. Opt. Soc. Am. B 28, 861–866 (2011). [Google Scholar]
  28. Huang H., Lin Z. S., Bai L., Hu Z. G. & Chen C. T. Ab initio calculations on the borate nonlinear optical crystal BaAlBO3F2. J. Appl. Phys. 106, 103107 (2009). [Google Scholar]
  29. ICSD, 2012-1, Version 1.8.2, by Fachinformatiionszentrum Karlsruhe, Germany.
  30. Payne M. C., Teter M. P., Allan D. C., Arias T. A. & Joannopoulos J. D. Iterative minimization techniques for abinitio total-energy calculations - molecular-dynamics and conjugate gradients. Rev. Mod. Phys. 64, 1045–1097 (1992). [Google Scholar]
  31. Clark S. J. et al. First principles methods using CASTEP. Z. Kristall. 220, 567–570 (2005). [Google Scholar]
  32. Kohn W. & Sham L. J. Self-consistent equations including exchange and correlation effects. Phys. Rev. 140, 1133 (1965). [Google Scholar]
  33. Rappe A. M., Rabe K. M., Kaxiras E. & Joannopoulos J. D. Optimized pseudopotentials. Phys. Rev. B 41, 1227–1230 (1990). [DOI] [PubMed] [Google Scholar]
  34. Lin J. S., Qteish A., Payne M. C. & Heine V. Optimized and transferable nonlocal separable ab initio pseudopotentials. Phys. Rev. B 47, 4174–4180 (1993). [DOI] [PubMed] [Google Scholar]
  35. Kleinman L. & Bylander D. M. Efficacious form for model pseudopotentials. Phys. Rev. Lett. 48, 1425–1428 (1982). [Google Scholar]
  36. Monkhorst H. J. & Pack J. D. Special points for brillouin-zone integrations. Phys. Rev. B 13, 5188–5192 (1976). [Google Scholar]
  37. Pfrommer B. G., Cote M., Louie S. G. & Cohen M. L. Relaxation of crystals with the quasi-Newton method. J. Comput. Phys. 131, 233–240 (1997). [Google Scholar]
  38. Plckard Chris J. & Needs R. J. Ab initio random structure searching. J. Phys.: Condens. Matter 23, 053201 (2011). [DOI] [PubMed] [Google Scholar]
  39. Palik E. D. Handbook of Optical Constants of Solids. Orlando: Academic Press: New York (1985).
  40. Lin J., Lee M. H., Liu Z. P., Chen C. T. & Pickard C. J. Mechanism for linear and nonlinear optical effects in beta-BaB2O4 crystals. Phys. Rev. B 60, 13380–13389 (1999). [Google Scholar]
  41. Perdew J. P. & Wang Y. Accurate and simple analytic representation of the electron-gas correlation-energy. Phys. Rev. B 45, 13244–13249 (1992). [DOI] [PubMed] [Google Scholar]
  42. Godby R. W., Schluter M. & Sham L. J. Self-energy operators and exchange-correlation potentials in semiconductors. Phys. Rev. B 37, 10159–10175 (1988). [DOI] [PubMed] [Google Scholar]
  43. Wang C. S. & Klein B. M. 1st-principles electronic-structure of Si, Ge, GaP, GaAs, ZnS, and ZnSe.2. Optical-properites. Phys. Rev. B 24, 3417–3429 (1981). [Google Scholar]
  44. Lin Z. S. et al. Strategy for the optical property studies in ultraviolet nonlinear optical crystals from density functional theory. Comput. Mater. Sci. 60, 99–104 (2012). [Google Scholar]
  45. Adamo C. & Barone V. Toward reliable density functional methods without adjustable parameters: The PBE0 model. J. Chem. Phys. 110, 6158–6170 (1999). [Google Scholar]
  46. Becke A. D. Density-functional thermochemistry.3. The role of exact exchange. J. Chem. Phys. 98, 5648–5652 (1993). [Google Scholar]
  47. Seidl A., Gorling A., Vogl P., Majewski J. A. & Levy M. Generalized Kohn-Sham schemes and the band-gap problem. Phys. Rev. B 53, 3764–3774 (1996). [DOI] [PubMed] [Google Scholar]

Associated Data

This section collects any data citations, data availability statements, or supplementary materials included in this article.

Supplementary Materials

Supplementary Information

Supplementary Information for Two novel nonlinear optical carbonates in the deep-ultraviolet region: KBeCO3F and RbAlCO3F2

srep01366-s1.pdf (134.7KB, pdf)

Articles from Scientific Reports are provided here courtesy of Nature Publishing Group

RESOURCES