Statistical Analysis of Longitudinal Neuroimage Data with Linear Mixed Effects Models

Abstract

Longitudinal neuroimaging (LNI) studies are rapidly becoming more prevalent and growing in size. Today, no standardized computational tools exist for the analysis of LNI data and widely used methods are sub-optimal for the types of data encountered in real-life studies. Linear Mixed Effects (LME) modeling, a mature approach well known in the statistics community, offers a powerful and versatile framework for analyzing real-life LNI data. This article presents the theory behind LME models, contrasts it with other popular approaches in the context of LNI, and is accompanied with an array of computational tools that will be made freely available through FreeSurfer – a popular Magnetic Resonance Image (MRI) analysis software package.

Our core contribution is to provide a quantitative empirical evaluation of the performance of LME and competing alternatives popularly used in prior longitudinal structural MRI studies, namely repeated measures ANOVA and the analysis of annualized longitudinal change measures (e.g. atrophy rate). In our experiments, we analyzed MRI-derived longitudinal hippocampal volume and entorhinal cortex thickness measurements from a public dataset consisting of Alzheimer’s patients, subjects with mild cognitive impairment and healthy controls. Our results suggest that the LME approach offers superior statistical power in detecting longitudinal group differences.

1 INTRODUCTION

Longitudinal neuroimaging (LNI) studies have become increasingly widespread over the last decade, e.g. (Asami et al., 2011; Blockx et al., 2011; Chetelat et al., 2005; Davatzikos and Resnick, 2002; Desikan et al., 2011; Driscoll et al., 2011; Fjell et al., 2009; Fotenos et al., 2005; Fouquet et al., 2009; Frings et al., 2011; Giedd et al., 1999; Hedman et al., 2011; Ho et al., 2003; Holland et al., 2009; Holland et al., 2011; Hua et al., 2010; Hua et al., 2009; Jack Jr et al., 2009; Jack Jr et al., 2008; Josephs et al., 2008; Kaladjian et al., 2009; Kalkers et al., 2002; Ment et al., 2009; Pantelis et al., 2003; Paviour et al., 2006; Resnick et al., 2010; Sabuncu et al., 2011; Schumann et al., 2010; Sidtis et al., 2010; Sluimer et al., 2008; Sluimer et al., 2009; Sullivan et al., 2011; Thambisetty et al., 2011; Thambisetty et al., 2010; Tosun et al., 2010; Whitwell et al., 2011; Whitwell et al., 2007). Compared to the cross-sectional approach, the longitudinal design can provide increased statistical power by reducing the confounding effect of between-subject variability (Thompson et al., 2011). Moreover, a serial assessment can be the only way to unambiguously characterize the effect of interest in a randomized experiment, such as a drug trial (Davis et al., 2005; Dickerson and Sperling, 2005; Ge et al., 2000). Finally, longitudinal studies provide unique insights into the temporal dynamics of the underlying biological process (Jack Jr et al., 2012; Sabuncu et al., 2011).

LNI studies have yielded novel discoveries, yet a careful scrutiny of the literature reveals that the statistical methods commonly lack maturity and sophistication. We believe that the underutilization of appropriate methodology in LNI studies is mainly due to two related reasons. Firstly, the relevant statistical tools are not readily available in user-friendly neuroimage analysis software environments (such as SPM (Friston, 2007; SPM), FSL (Smith et al., 2004), or FreeSurfer (Fischl, 2012)). Secondly, the technical intricacies of modeling longitudinal data are not well understood and/or appreciated.

In this article, we advocate the use of Linear Mixed Effects (LME) modeling, which provides a flexible and powerful statistical framework for the analysis of longitudinal data (Fitzmaurice et al., 2011; Verbeke and Molenberghs, 2000). We discuss the theoretical underpinnings of the LME framework and contrast it with other methods popular in LNI.

There are two alternative approaches most commonly applied to the analysis of prior LNI data. These are (1) repeated measures analysis of variance (or within-subject ANOVA) (Girden, 1992), e.g., (Asami et al., 2011; Blockx et al., 2011; Bonne et al., 2001; Fouquet et al., 2009; Giedd et al., 1999; Ho et al., 2003; Kaladjian et al., 2009; Mathalon et al., 2001; Pantelis et al., 2003; Resnick et al., 2010; Sidtis et al., 2010; Sluimer et al., 2009),; and (2) cross-sectional (General Linear Model –GLM- based) analysis of summary measurements, such as percent annualized difference, e.g., (Desikan et al., 2011; Fjell et al., 2009; Fotenos et al., 2005; Fouquet et al., 2009; Frings et al., 2011; Hedman et al., 2011; Holland et al., 2009; Hua et al., 2010; Hua et al., 2009; Jack Jr et al., 2009; Josephs et al., 2008; Kalkers et al., 2002; Kasai et al., 2003; Paviour et al., 2006; Sabuncu et al., 2011; Sluimer et al., 2008; Whitwell et al., 2007). However, these methods are known to be sub-optimal for general real-life longitudinal data since they do not model the covariance structure of serial measurements appropriately and cannot handle imperfect timing and/or subject dropout (i.e., unbalanced data), in particular those cases with only a single time-point (Fitzmaurice et al., 2011).

Another related approach is the two-stage strategy for solving the hierarchical models adopted in functional neuroimaging (Friston, 2007). Yet these tools typically rely on assumptions that are unrealistic for the LNI design we consider here¹. For example, in LNI studies one usually has only a handful of scans per subject and not hundreds of time-points. Furthermore, a pre-whitening step is unlikely to be suitable since LNI data are not sampled at uniform time intervals and do not obey a stationary autoregressive structure.

The contributions of this article are multi-fold. First, we present a thorough overview of the LME approach in the context of longitudinal studies. Computational tools implementing this approach will accompany this article as a part of FreeSurfer, a MRI processing software, (Dale et al., 1999; Fischl et al., 2002; Fischl et al., 1999a; Fischl et al., 1999b). We use a widely studied longitudinal structural MRI dataset (from the Alzheimer’s Disease Neuroimaging Initiative, or ADNI) to illustrate how these tools can be used for exploratory data visualization, model specification, model selection, parameter estimation, hypothesis testing, and statistical power analysis including sample size estimation. We further perform a systematic empirical validation of the specificity, sensitivity and repeatability of the LME method and alternative approaches. Our results provide an objective quantification of the improvement in statistical detection afforded by the LME approach compared with competing methods. Finally, we assess the impact of including subjects with a single time point in the LME method.

The paper is organized as follows. Section 2.1 provides a discussion of the general characteristics of longitudinal data. Section 2.2 presents the LME method for the analysis of longitudinal data. Section 2.3 includes a brief description of alternative methods used in prior LNI studies. Section 2.4 offers a description of the data used in the experiments. In Section 3, we present experimental results that illustrate the proposed approach and compare it to benchmark methods. Finally, Section 4 provides a discussion of the main experimental findings and Section 5 closes with concluding remarks.

2 MATERIAL AND METHODS

2.1 The Characteristics of Longitudinal Data

In a longitudinal study, outcome variables are measured repeatedly on the same cohort of individuals at multiple time-points. The aim is to characterize changes in the individuals’ measurements over time and their association with clinical, experimental or biological factors. Unlike cross-sectional studies, where the measurement is obtained at a single occasion, longitudinal studies allow direct assessment of within-subject changes across different time points, free of any between-subject variability. Changes in the mean measurement over time can then be estimated with greater precision and without confounding cohort effects (Fitzmaurice et al., 2011). Furthermore, more accurate predictions about an individual’s measurement trajectory might be possible by pooling data across the population. This can be useful, for instance, to assess the effect of a drug in a specific individual in a pharmacological study.

In general, longitudinal data exhibit several distinctive characteristics. (1) Longitudinal measurements are ordered in time, reflecting the temporal trajectory of an underlying non-stationary continuous process. This is the major difference between vectors of repeated measures obtained in longitudinal studies and vectors of multivariate measurements from cross-sectional studies, where single measurements of multiple but distinct variables are taken simultaneously. (2) Typically, serial measurements obtained for a single subject are positively correlated. This correlation is due to the smooth trajectory of the underlying biological process. In general, we expect pairs of repeated measures that are close in time to be more highly correlated than pairs of repeated measures further separated in time. (3) Between-subject variance is not usually constant over the duration of the study; instead, it might for example increase as a function of time due to the diverging trajectories of individuals and/or groups. (4) Finally, missing data and non-uniform timing is extremely common, particularly for longitudinal studies of larger duration.

2.2 Linear Mixed Effects Modeling for Longitudinal Data

There are two aspects of longitudinal data that require careful modeling: the mean measurement trajectory over time and the correlation structure among serial measurements. The models for the mean and covariance are interdependent because the vector of residuals (i.e., the observed minus fitted measurements) depends on the specification of the model for the mean.

LME models use the linear regression paradigm (Montgomery et al., 2007) to parsimoniously describe the average measurement and its temporal trajectory. In this approach, the mean measurement is expressed as a linear combination of a set of independent variables. The temporal trajectory is then determined by the contribution of time and/or time-varying variables. A major advantage of this approach is that the subjects in the study are not required to have a common set of measurement times (i.e., the data can be unbalanced).

Like any other statistical method, the selection of independent variables that models the mean measurement has to be made based on subject-matter grounds. On the other hand, without any additional knowledge, a useful strategy to model the mean trajectory is to simply assume it is linear in time. This is the default implementation in our toolkit. A justification for this strategy is due to the limited duration of studies, which typically can expose local and simple trends. More complex trajectories can be captured via piecewise linear models or higher order (e.g. quadratic or cubic) polynomials. These models can be chosen by the user based on a graphical exploratory analysis of the data, such as by inspecting an illustration of smoothed measurements, e.g., a “lowess” plot (Cleveland, 1979). Then, as it is common in the linear regression paradigm, complex models can be compared to reduced models to determine whether they fit the data significantly better. For example, a quadratic model for the mean response over time can be compared to a linear model by testing the null hypothesis that the quadratic coefficient is zero.

There are generally three potential sources of variability influencing the correlation structure in longitudinal data: (1) between-subject variation, (2) inherent within-subject biological change, and (3) measurement error (Fitzmaurice et al., 2011). The first source of variability reflects natural variation in the individual’s measurement trajectory. Some individuals’ measurements are consistently higher than the population average, while others’ are consistently lower. The inherent within-individual biological variation is a consequence of some subject-specific biological process that progresses gradually over time. Hence, random departures from an individual’s modeled measurement trajectory are likely to be more similar when measurements are obtained close together in time. Finally, measurement error variance has a direct influence on the amount of correlation between serial measurements.

The LME method imposes structure on the covariance through the introduction of random effects. This approach provides both flexible and parsimonious models for the covariance and is particularly well suited to handling longitudinal data that are irregularly timed. A unique feature of these models is that they explicitly distinguish and allow the analysis of the between-subject and within-subject sources of variability. The following section provides the theoretical details of the LME framework.

2.2.1 Linear Mixed Effects Models: The Theory

Let us formally introduce the LME model for longitudinal data:

$$Y_i=X_i\beta +Z_i{b}_i+e_i,$$ (2.1)

where Y_i is the n_i × 1 vector of serial measurements for subject i (e.g. longitudinal MRI-derived thickness or volume measurements), n_i is the subject-specific number of serial measurements, X_i is the n_i × p subject design matrix for the fixed effects (including variables such as gender, education, clinical group, genotype and scan time), (β = β₁,β₂,…,β_p)^T is a p × 1 vector of unknown fixed effects regression coefficients, Z_i is the n_i × q,q ≤ p design matrix for the random effects (e.g. scan time), b_i =(b_i1,b_i2,…,b_iq)^T is a q × 1 vector of random effects and e_i = (e_i1, e_i2,…, e_ini)^T is a n_i × 1 vector of measurement errors. Here Z_i links the vector of random effects b_i to Y_i and its columns are a subset of the columns of X_i. That is, any component of β can be allowed to vary randomly by simply including the corresponding column of X_i in Z_i. For example, in a model with only a randomly varying intercept Z_i is a n_i × 1 vector composed of 1’s. Note that all random effects other than the intercept need to be time varying, so that Z_i is not singular (In fact the measurement time itself is usually a random effect). The following common distributional assumptions are made:

$$\begin{array}{c}{b}_i~N(0,\text{D}),\\ e_i~N\left(0,{\sigma }^2{I}_{n_i}\right),\end{array}$$

where N (0, Σ) denotes a zero mean multivariate Gaussian with covariance matrix Σ, I_ni denotes the n_i × n_i identity matrix, and b₁,…,b_m,e₁,…,e_m are independent with m being the number of subjects in the study. The components of b_i reflect how the subset of regression parameters for the i^th subject deviate from those of the population. The components of e_i represent random sampling or measurement errors.

The LME model provides an important distinction between the conditional and marginal means of Y_i. The conditional or subject-specific mean of Y_i, given b_i, is

$$E(Y_i\mid b_i)=X_i\beta +Z_i{b}_i,$$

while the marginal or population-averaged mean of Y_i is

$$E(Y_i)=X_i\beta .$$

Thus, in the LME model, the vector of regression parameters β (the fixed effects), is assumed to be the same for all individuals and have population-averaged interpretations, for example in terms of population mean trajectory. In contrast, the vector b_i (when summed with the corresponding fixed effects) makes up subject-specific regression coefficients, which describe the mean trajectory of the i^th individual.

We can also distinguish between the conditional covariance

$$\mathit{Cov}(Y_i\mid b_i)=\mathit{Cov}(e_i)={\sigma }^2{I}_{n_i},$$

and the marginal covariance of Y_i,

$$\mathit{Cov}(Y_i)=\mathit{Cov}(Z_i{b}_i)+\mathit{Cov}(e_i)=Z_i{DZ}_i^T+{\sigma }^2{I}_{n_i},$$

which is not a diagonal matrix.

Thus by introducing random effects, correlations among the components of Y_i can be modeled. One can see that the model allows for the explicit analysis of between-subject (D) and within-subject (σ²) sources of variation. Importantly, the marginal covariance of Y_i is expressed as a function of the time-varying random effects, which commonly includes measurement time itself.

Consider the following simple LME model, which has a randomly varying intercept and slope:

$$Y_{ij}=({\beta }_1+b_{11})+({\beta }_2+b_{21})t_{ij}+e_{ij},$$ (2.2)

where Y_ij is the j^th measurement from subject i, t_ij is the time of measurement, and j = 1, …, n_i. The model of (2.2) allows each individual’s measurements to have his or her own unique linear mean trajectory.

2.2.2 Parameter Estimation

In this section we consider the problem of estimating the unknown coefficients β and model parameters σ and D. Given the distributional assumptions that have been made, the vector of measurements are distributed as

$$Y_i~N({\text{X}}_{\text{i}}\beta ,{\text{Z}}_{\text{i}}{DZ}_i^T+{\sigma }^2{I}_{n_i}).$$ (2.3)

For given estimates D̂ and σ̂, we have a closed-form solution for the maximum likelihood (ML) estimate of β:

$$\widehat{\beta }={\left(\sum _{i=1}^m{X}_i^T{\widehat{\mathrm{\sum }}}_i^{-1}{X}_i\right)}^{-1}\sum _{i=1}^m{X}_i^T{\widehat{\mathrm{\sum }}}_i^{-1}{y}_i,$$ (2.4)

where ${\widehat{\mathrm{\sum }}}_i=Z_i\widehat{D}{Z}_i^T+{\widehat{\sigma }}^2{I}_{n_i}$ and y_i is the realization of the random vector Y_i.

An unbiased estimate for D̂ and σ̂ can be obtained via maximizing the following restricted likelihood function (ReML procedure) (Verbeke and Molenberghs, 2000):

$$l_{\mathit{ReML}}=\frac{1}{2}\sum _{i=1}^{m}log\left|{\mathrm{\sum }}_i^{-1}\right|-\frac{1}{2}\sum _{i=1}^m{\left(y_i-X_i\widehat{\beta }\right)}^T{\mathrm{\sum }}_i^{-1}\left(y_i-X_i\widehat{\beta }\right)-\frac{1}{2}log\left|\sum _{i=1}^m{X}_i^T{\mathrm{\sum }}_i^{-1}{X}_i\right|,$$ (2.5)

where ${\mathrm{\sum }}_i=Z_i{DZ}_i^T+{\sigma }^2{I}_{n_i}$.

There is no closed-form solution to the optimization of (2.5) and numerical iterative solvers need to be used. We have implemented three widely used optimization methods: The Expectation Maximization (EM) algorithm (Laird et al., 1987) and two Newton-Raphson based procedures using either the Hessian or the expected information matrix of the restricted log-likelihood. The forms for the first and second partial derivatives of l_ReML can be found in (Lindstrom and Bates, 1988). When the expected information matrix is used in the optimization procedure the algorithm is commonly referred to as the Fisher’s scoring scheme. Formulas for the expected information matrix can be found in (Kenward and Roger, 1997). Finally, we note that we do not impose any structure on D, other than it needs to be positive definite. To achieve this constraint, we parameterize it via its Cholesky decomposition.

2.2.3 Selection of Random Effects

In the LME approach, given a model for the mean, the covariance structure is determined by the choice of random effects. One good strategy to identify the appropriate set of random effects is via the likelihood ratio test, where the likelihood of nested models can be compared.

Here, one can start with a “basic model”, which would only include the bias as a random effect. Once the model parameters and coefficients are estimated for the basic model, the corresponding restricted maximum likelihood value can be computed. One would then proceed to add random effects to the basic model. For example, time-varying variables can be added to the basic model as additional random effects one by one in a greedy fashion, where the variable that produces the highest increase in the restricted likelihood function will be added, only if this increase is statistically significant. The significance of a likelihood increase in nested models can be assessed based on a chi-square mixture statistic (Fitzmaurice et al., 2011).

2.2.4 Hypothesis Testing

In conducting hypothesis tests, we will use β̂ and its estimated asymptotic covariance matrix

$$C\widehat{o}{v}_{\mathit{asymptotic}}(\widehat{\beta })={\left(\sum _{i=1}^m{X}_i^T{\widehat{\mathrm{\sum }}}_i^{-1}{X}_i\right)}^{-1},$$

where Σ̂_i is the ReML estimator of Σ_i.

In general, for a given contrast matrix L, the two competing hypotheses are H₀ : Lβ = 0 and H_A : Lβ ≠ 0.

Under the null hypothesis, it can be shown that the following F-distribution holds:

$$F=\frac{{\left(L\widehat{\beta }\right)}^T{\left({LC\widehat{o}v}_{\mathit{asymptotic}}\left(\widehat{\beta }\right)L^T\right)}^{-1}L\widehat{\beta }}{\mathit{rank}(L)}.$$ (2.6)

However, determining the degrees of freedom associated with the above F-test is challenging and several approximations have been proposed, e.g. (Satterthwaite, 1946). In particular, we have implemented a Satterthwaite-based approximation for the following scaled F-statistic:

$$F=\kappa \frac{{\left(L\widehat{\beta }\right)}^T{\left({LC\widehat{o}v}_{KR}\left(\widehat{\beta }\right)L^T\right)}^{-1}L\widehat{\beta }}{\mathit{rank}(L)},$$ (2.7)

where Côv_KR (β̂) is a small-sample bias corrected estimate of the covariance matrix of β̂. This procedure allows the covariance among the ReML covariance parameter estimates to be taken into account when estimating the effective degrees of freedom of the F-test and thus different contrasts will exhibit different degrees of freedom. Details on the computation of κ, Côv_KR (β̂) and the effective degrees of freedom can be found in (Kenward and Roger, 1997).

2.2.5 Sample Size Estimation and Statistical Power Analysis

Sample size and power calculations are more complex for longitudinal designs than for the simpler cross-sectional setting. The major challenge is missing data, which has a direct effect on power. In our toolbox, we have implemented two approximate methods for performing power calculations. The first method is intended for the planning phase, i.e., before data are collected, and can be used to obtain approximate estimates of the required sample size or the power to detect a particular effect size for a given sample size. The second method has a different purpose: namely, to provide an estimate of the power of a realized study, i.e., after the data have been collected.

The first method is based on a simple extension of the sample size and power formulae for a cross-sectional study with a univariate measurement (Fitzmaurice et al., 2011). In a two-group study, the approximate sample size N per group is:

$$N=\frac{{\left(z_{(1-\alpha /2)}+z_{(1-\gamma )}\right)}^{2}2{\varphi }^2}{{\delta }^2},$$ (2.8)

where 1 − γ is the power of the test, α is the significance level, z_(1−α/2), z_(1−γ) denote the (1 − α/2)×100% and (1 − γ)×100% percentiles of a standard normal distribution, δ is the effect of interest, which for example can be any element of the vector β considered as a mixed effect (e.g., intercept or slope) and ϕ² is the corresponding diagonal element of the following covariance matrix

$$C={\sigma }^2{\left(Z_c^T{Z}_c\right)}^{-1}+D,$$

with Z_c denoting the subject-level common random effects design matrix for the subjects in the study (i.e., assuming a balanced study).

Equation (2.8) can be re-arranged to determine the power of the planned study given a sample size:

$$z_{(1-\gamma )}=\sqrt{N\frac{{\delta }^2}{2{\varphi }^2}}-z_{(1-\alpha /2)}.$$ (2.9)

Finally, a conservative approach for adjusting for possible missing data is to inflate the required sample size N in each group to account for the expected proportion of subjects who will drop out before the completion of the study. E.g. if the rate of attrition is expected to be 10% in each group, the sample size in each group should be N/0.9.

The second method for power calculations allows a more precise approximation of the power of a realized (retrospective) experiment (given the actual unbalanced data over time with the missing data pattern). It is based on a non-central F-approximation to the distribution of the F-statistic in equation (2.6) under the alternative hypothesis (Helms, 1992). The degrees of freedom of the non-central F-distribution are c = rank(L) and $v_e={\displaystyle \sum _{i=1}^m}{n}_i-\mathit{rank}([XZ])$, with $X={[X_1^T{X}_2^T\dots X_m^T]}^T$ and Z = Diag ([Z₁, Z₂, …, Z_m]) being the full fixed and random effects design matrices of the study. The non-centrality parameter is given by nc = (Lβ̂)^T(LCôv_asymptotic(β̂)L^T)⁻¹Lβ̂.

This non-central F-distribution can be used to perform power computations for tests of fixed effect hypotheses. The approximate power is

$$1-\gamma =1-F(cv;c,v_e,nc),$$ (2.10)

where F(cv; c, v_e, nc) is the cumulative distribution function of the non-central F-distribution evaluated at the critical value cv = F⁻¹ (1 − α; c, v_e), which is the inverse of the cumulative distribution function of the central F-distribution with c,v_e degrees of freedom evaluated at 1 − α.

2.3 Alternative Methods for Analyzing Longitudinal Neuroimaging Data

Barring notable exceptions that use appropriate LME models, e.g. (Davatzikos and Resnick, 2002; Driscoll et al., 2011; Lau et al., 2008; Lerch et al., 2005; Shaw et al., 2008; Thambisetty et al., 2010; Tosun et al., 2010; Whitwell et al., 2011), there are two alternative methods that have been widely used to analyze LNI data in a large number of prior studies. The first approach is repeated measures (or within-subject) ANOVA, e.g. (Asami et al., 2011; Blockx et al., 2011; Bonne et al., 2001; Giedd et al., 1999; Ho et al., 2003; Kaladjian et al., 2009; Mathalon et al., 2001; Pantelis et al., 2003; Resnick et al., 2010; Sidtis et al., 2010; Sluimer et al., 2009), which can be shown to be equivalent to a linear model with at most a single random effect. Here, measurement occasions are treated as levels of a within-subject factor and time is not modeled as a continuous variable. Hence the method is only well suited for balanced longitudinal data with a small number of serial measurements. Furthermore, the correlation among repeated measurements, if modeled, is supposed to arise from the additive contribution of an individual-specific random effect, namely a random intercept. This imposes a particular covariance structure known as compound symmetry:

$$\begin{array}{c}\mathit{Var}\left(Y_{ij}\right)={\sigma }_b^2+{\sigma }_e^2\\ \mathit{Corr}\left(Y_{ij},Y_{ik}\right)=\frac{{\sigma }_b^2}{{\sigma }_b^2+{\sigma }_e^2}(i=1,\dots ,N);(j,k=1,\dots ,n),j\ne k\end{array}$$

where ${\sigma }_b^2$ and ${\sigma }_e^2$ are the variance of the random effect and the measurement error respectively. This structure for the covariance has some justification in certain designs. For example, in an fMRI experiment where the within-subject factor is randomly allocated to subjects, compound symmetry can hold. However, the constraint on the correlation among repeated measurements is not appropriate for longitudinal data, where the correlations are expected to decay with increasing separation in time. Also, the assumption of constant variance across time is often unrealistic.

Another common approach to the analysis of LNI data reduces the sequence of repeated measures for each individual to summary values (e.g. the annualized difference between two measures, the slope of a regression line, or deformation tensors), e.g. (Desikan et al., 2011; Fotenos et al., 2005; Fouquet et al., 2009; Frings et al., 2011; Hedman et al., 2011; Holland et al., 2009; Hua et al., 2010; Hua et al., 2009; Jack Jr et al., 2009; Josephs et al., 2008; Kalkers et al., 2002; Kasai et al., 2003; Paviour et al., 2006; Sabuncu et al., 2011; Sluimer et al., 2008; Whitwell et al., 2007). These summary measures are then submitted to standard parametric or non-parametric statistical methods for cross-sectional analysis. Such an approach is not appropriate when the data are unbalanced over time, since summary measures will not be drawn from the same distribution (e.g. will have different variance), violating a fundamental assumption made by standard statistical methods. In addition, as our experiments demonstrate there can be a significant loss in statistical power due to ignoring the correlation among the repeated measures and omitting subjects with a single time-point.

2.4 Longitudinal ADNI Data

In our experiments presented in the following section, we analyzed longitudinal brain MRI data (T1-weighted, 1.5 Tesla) from the Alzheimer Disease Neuroimaging Initiative (ADNI). The data were processed with FreeSurfer (version 5.1.0, http://surfer.nmr.mgh.harvard.edu) and its new longitudinal processing pipeline (http://surfer.nmr.mgh.harvard.edu/fswiki/LongitudinalProcessing) (Reuter and Fischl, 2011; Reuter et al., 2010; Reuter et al., 2012). The FreeSurfer processing pipeline is fully automatic and includes steps to compute a representation of the cortical surface between white and gray matter, a representation of the pial surface, a segmentation of white matter from the rest of the brain; to perform skull stripping, bias field correction, nonlinear registration of the cortical surface of an individual with a stereotaxic atlas, labeling of regions of the cortical surface, and labeling of sub-cortical brain structures. Furthermore, for each MRI scan, FreeSurfer automatically computes subject-specific thickness measurements across the entire cortical mantle and within anatomically defined cortical regions of interest (ROIs) such as the entorhinal cortex, volume estimates of a wide range of sub-cortical structures such as the hippocampus, and estimates of the intra-cranial volume (ICV). In all subsequent analyses, we summed the volumes of the two hippocampi to obtain the total hippocampal volume and averaged thickness measurements from the bilateral entorhinal cortex ROIs to compute the mean thickness within the entorhinal cortex.

The longitudinal stream in FreeSurfer (Reuter et al., 2012) utilizes an unbiased subject-specific template (Reuter and Fischl, 2011), which is created by co-registering scans from each time-point using a robust and inverse consistent registration algorithm (Reuter et al., 2010). Several steps in the processing of the serial MRI scans (e.g., skull stripping, atlas registration, etc.) are then initialized with common information from the subject-specific template. This strategy has been shown to lead to increased statistical power and better separation of groups based on atrophy rates (Reuter et al., 2012). Note that the publicly distributed version of FreeSurfer’s longitudinal stream does not handle subjects with a single MRI scan (i.e., single visit), which traditionally have been processed using cross-sectional tools. Since the cross-sectional image processing steps are different from the longitudinal stream, inclusion of single time point measurements in subsequent statistical analysis can introduce a bias, as demonstrated in our supplementary analysis. See also (Reuter et al., 2012) where a similar bias was quantified by processing the first time point cross-sectionally and the second longitudinally (initializing it with results from the first) in a test-retest study with no expected structural change. To address this issue we modified FreeSurfer’s longitudinal framework to process subjects with a single time point in the following manner: we created a pose normalized (upright) version of the input images by symmetrically registering it with its left-right reversed image into a mid-space (Reuter et al., 2010), we then processed it as the subject-specific template and used it for the initialization of subsequent image processing steps, such as skull stripping. This ensures the input image from a subject with a single scan undergoes the same processing and interpolation steps as serial images in the longitudinal stream and thus makes results comparable (see Supplementary Material).

Tables 1 and 2 provide descriptive statistics of the analyzed sample. We subdivided the subjects into five clinical groups. (1) Stable healthy control (HC): those who were clinically healthy throughout the follow-up period. (2) Converter HC (cHC): those who were clinically healthy at baseline but converted to Mild Cognitive Impairment (MCI, a transitional phase between healthy and dementia) (Gauthier et al., 2006) or dementia stage of Alzheimer’s disease (AD) within the follow-up period. (3): Stable MCI (sMCI): those who were categorized MCI at baseline and remained so throughout the study. (4) Converter MCI (cMCI): those who were MCI at baseline and progressed to the dementia phase of AD during follow-up. (5) AD patients: those who were diagnosed with dementia of the Alzheimer type at baseline.

Table 1.

Longitudinal ADNI sample characteristics

Variable	Stable HC	Converter HC	Stable MCI	Converter MCI	AD	p-value
Number of subjects	210	17	227	166	188
Baseline age	75.9 ± 5 [60–90]	76.7 ± 5.1 [63–84]	74.8 ± 7.7 [55–90]	74.7± 7.1 [55–89]	75.2 ± 7.5 [55–91]	0.3464
Female %	48.1	47.1	33.48	38.6	47.3	<0.01a
APOE-ε4 Carriers %	25.7	41.2	43.2	67.5	66	<0.0001a
Education	16.1 ± 2.8 [6–20]	16.1 ± 2.8 [12–20]	15.6 ± 3.1 [4–20]	15.7 ± 2.9 [6–20]	14.7 ± 3.2 [4–20]	<0.001

Baseline age (in years) and education values are in mean ± standard deviation; Ranges are listed in square brackets; p-values indicate effects across the groups

Key: Converter MCI, mild cognitive impairment subjects who convert to Alzheimer’s disease; Converter HC, healthy controls who convert to either MCI or Alzheimer’s disease.

^aUsing Fisher’s exact test; ANOVA-derived p-values were used in the other cases.

Table 2.

Number and timing of scans per time point by clinical group (Stable HC, N=210; Converter HC, N=17; Stable MCI, N=227; Converter MCI, N=166; AD, N=188).

Time point	Stable HC	Converter HC	Stable MCI	Converter MCI	AD	Time from baseline
baseline	210	17	227	166	188	0
year 0.5 (month 6)	197	17	194	161	166	0.58 ± 0.07 [0.21–0.94]
year 1	183	17	177	153	150	1.08 ± 0.07 [0.68–1.38]
year 1.5	0	0	153	136	0	1.59± 0.08 [1.26–1.92]
year 2	129	14	108	106	96	2.09 ± 0.10 [1.58–2.88]
year 3	115	6	68	70	0	3.09 ± 0.09 [2.52–3.45]
year 4	11	0	3	10	0	4.12 ± 0.09 [3.98–4.38]
Total	845	71	930	802	600

Time from baseline (in years) is in mean ± standard deviation; Ranges are listed in square brackets.

In our experiments, we only focused on two biomarkers, namely mean thickness within the entorhinal cortex (averaged across hemispheres; ECT) and total hippocampal volume (HV), since these are two classical MRI-derived markers that are known to be strongly associated with early AD (Dickerson et al., 2001; Jack Jr et al., 1997). These measurements were automatically computed using FreeSurfer.

ADNI is a multi-site study, where the MRI data were collected using a range of scanner types. Although a significant amount of effort was put into matching the imaging protocol and quality across sites (via phantom and subject scans), there is still a chance that the coil type has an effect on the analysis. We conducted a supplementary analysis to assess this effect. Our results indicate that there were two coil types that had a significant influence on the measurement of hippocampal volume (see Supplementary Table S3), but our general conclusions about longitudinal changes were not altered. Since there was a significant number of subjects for which coil type information were not provided (and therefore these subjects were omitted from the supplementary analysis), we decided to drop coil type information from all our subsequent analyses in order to boost sample size.

Unless specified otherwise, all analyses included the following independent variables as fixed effects: time from baseline, clinical group membership (HC was the reference group and there were indicator variables for all remaining groups. E.g., for the sMCI indicator, the value was one if the subject was clinically categorized as sMCI and zero otherwise), the interaction between clinical group indicators and time from baseline, baseline age, sex, APOE genotype status (one if e4 carrier and zero if not), the interaction between APOE genotype status and time (of scan) from baseline (note that this variable was included based on the evidence that e4 accelerates atrophy during the prodromal phases of AD (Jack Jr et al., 2008)), and education (in years). Furthermore an estimate of intra-cranial volume (ICV) (Buckner et al., 2004) was included as a fixed effect for the analysis of HV, but not ECT since there was no significant association with the latter. Random effects were determined via a likelihood ratio test as explained above. In all analyses both intercept and time were included in the final model as random effects. This suggests that compound symmetry did not hold for HV and ECT in the longitudinal ADNI.

In general, longitudinal studies are conducted to assess group differences between the trajectories of variables of interest. Therefore, we constrained our analysis to the association between the group-time interaction (i.e., group-specific atrophy rate) for the two biomarkers: HV and ECT.

3 RESULTS

3.1 Comparing rates of atrophy across four clinical groups

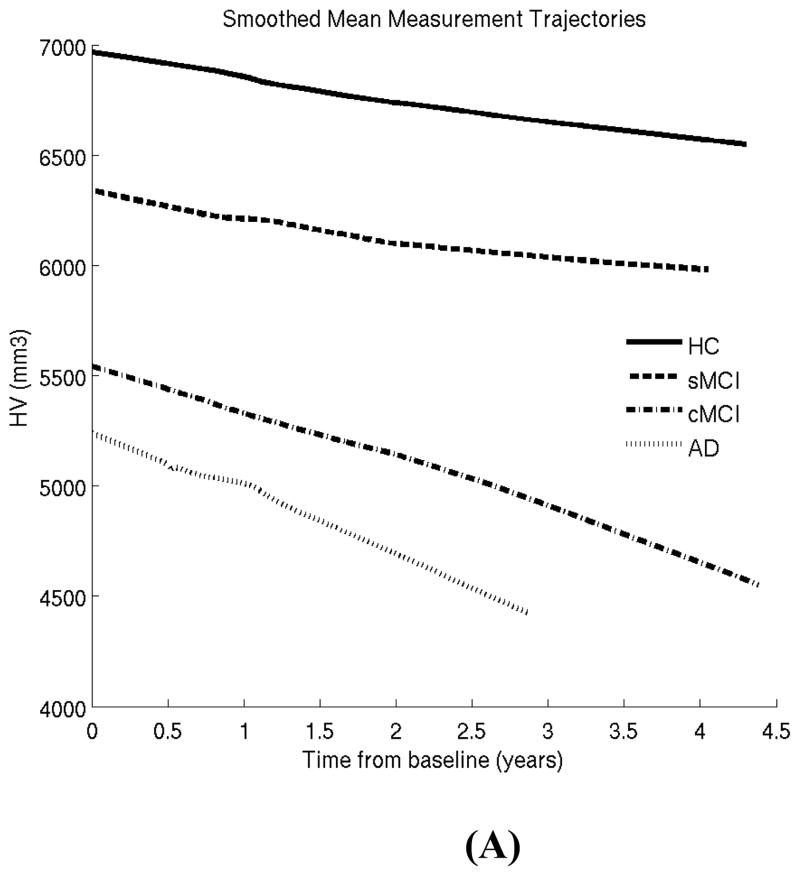
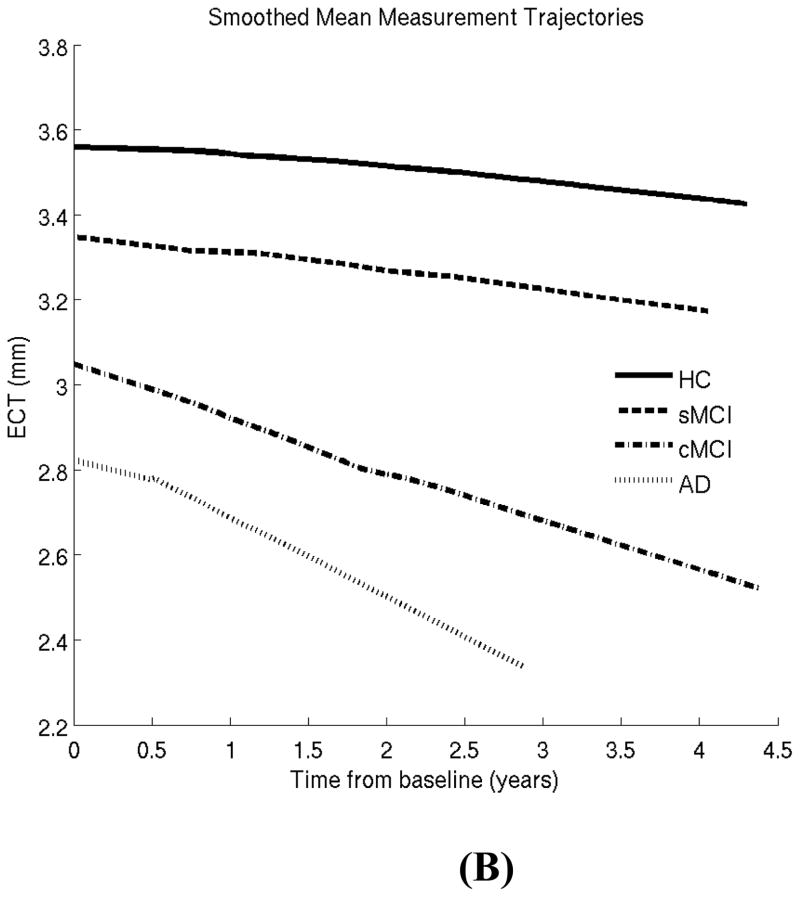
In our first experiment, we excluded converter HC subjects, since this is the smallest group (N=17) and little has been reported on this group in prior work. Our goal here is to illustrate the LME methodology for characterizing well-known differences between four well-studied clinical groups: HC, stable MCI, converter MCI and AD patients (see Tables 1 and 2 and previous section). Figure 1 shows the lowess plots for the two biomarkers (HV and ECT) in these four clinical groups. These plots reveal that a linear model is likely to be sufficient to capture follow-up trends and there is no need for including higher order terms for time.

Figure 1.

Locally weighted smoothed mean measurement trajectory (lowess plot) for each of the four clinical groups. This method produces a smooth curve by centering a window of fixed size at each time-point and fitting a straight line to the data within that window. The lowess estimate of the mean at a time-point is simply the predicted values at that time-point from the fitted regression line. In this plot, the fraction of the total number of data points included in the sliding window was set to 0.7. HC: healthy control; sMCI: stable MCI; cMCI: converter MCI; AD: Alzheimer patients. (A) Hippocampal volume (HV). (B) Entorhinal cortex thickness (ECT).

The hypotheses we tested and the inference results (F-value, degrees of freedom –DF-, and uncorrected p-value) are as follows. Note that somewhat unusually, the DF depends on the contrast, because of the Satterthwaite-based approximation we use (see Equation 2.7). We include exact expressions for these hypotheses in the Supplementary Material.

• H1)Is there any difference in the rate of change among the four groups (HC, sMCI, cMCI, and AD)?

  HV: F value = 43.7, DF = [3 645.3], p = 0

  ECT: F value = 40.4, DF = [3 632.9], p = 0

• H2)Is there any difference in the rate of change between HC and sMCI?

  HV: F value = 13.8, DF = [1 552.9], p = 2.3e-4

  ECT: F value = 14.6, DF = [1 526.7], p = 1.5e-4

• H3)Is there any difference in the rate of change between sMCI and cMCI?

  HV: F value = 28.3, DF = [1 578.3], p = 1.5e-7

  ECT: F value = 30.3, DF = [1 554.3], p = 5.5e-8

• H4)Is there any difference in the rate of change between cMCI and AD?

  HV: F value = 5.1, DF = [1 798.8], p = 0.02

  ECT: F value = 1.4, DF = [1 830.6], p = 0.22

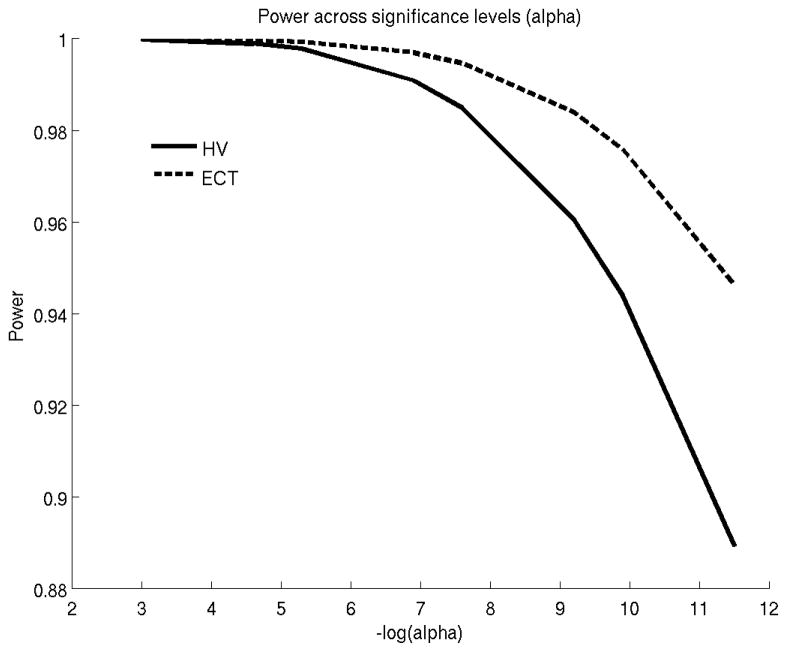
Figure 2 shows the retrospective power (Equation 2.8) for comparing the rates of atrophy between sMCI and cMCI using the ADNI data. ECT provides slightly more power than HV in detecting longitudinal group differences. Table 3 provides sample size estimates (based on Equation 2.9) for prospective studies that compare atrophy rates between sMCI versus cMCI and AD versus HC. Effect sizes and dropout rates were computed based on the ADNI sample.

Figure 2.

Statistical power versus alpha (false positive rate) to discriminate the atrophy rates of stable and converter MCIs. HV: hippocampal volume. ECT: entorhinal cortex thickness.

Table 3.

Conservative estimates of total sample size (2N, where N is the number of subjects in each group) for two prospective longitudinal studies (two-year studies with 5 serial scans obtained every six months from baseline) comparing Alzheimer patients (AD) vs healthy controls (HC) and stable MCI (sMCI) vs converter MCI (cMCI) groups, respectively. The power is set to 80% and the effect size (rate of change per year) is set to the slope regression coefficient estimated by the analysis of the ADNI data. Sample size estimates were inflated by a factor of 1.84 based on the drop out rate observed in the ADNI data (45.5% of subjects dropped out at the end of 2 years).

Prospective longitudinal studies	Effect size (per year)	Total sample size
AD vs HC/HV	−131.94 mm3	30
AD vs HC/ECT	−0.1 mm	32
cMCI vs sMCI/HV	−62.99 mm3	162
cMCI vs sMCI/ECT	−0.05 mm	146

Key: HV, total hippocampal volume; ECT, average entorhinal cortical thickness

3.2 Comparing rates of atrophy between HC and converter HC

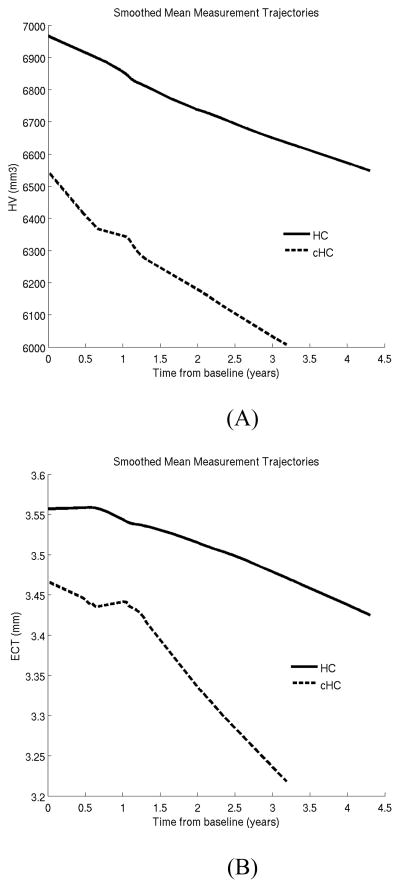
Our second experiment focused on the converter HC (cHC) subjects (N=17), who were clinically healthy at baseline yet progressed to MCI or AD over the course of the study. Mean time for conversion was 2.6 years from baseline (with a standard deviation of 1.1 years). We compared HV and ECT atrophy rates between cHC and HC subjects. Figure 3 shows the corresponding lowess plots. For entorhinal cortex, the lowess plot suggests that cHC subjects exhibit a nonlinear trajectory, which can be captured with the following piecewise linear model:

$${\beta }_1+{\beta }_{2}t+{\beta }_3{(t-1.2)}_{+},$$ (3.1)

where t is time (in years) from baseline, and (x) is only nonzero and equal to x if x is positive and zero otherwise. We note that the term 1.2 in Equation (3.1) comes from the visual inspection of Figure 3b that reveals a breakpoint in the trajectory of ECT around 1.2 years. For the hippocampus, we adopted a simple linear model as we did in the previous experiment.

Figure 3.

Locally weighted smoothed mean measurement trajectory (lowess plot) for two groups. This method produces a smooth curve by centering a window of fixed size at each time-point and fitting a straight line to the data within that window. The lowess estimate of the mean at a time-point is simply the predicted values at that time-point from the fitted regression line. In this plot, the fraction of the total number of data points included in the sliding window was set to 0.7. HC: healthy controls who remained so throughout the study; and cHC: converter HCs, who were healthy at baseline but progressed to MCI or AD during follow-up. Mean time to progression was 2.6 years from baseline. (A) Hippocampal volume (HV). (B) Entorhinal cortex thickness (ECT).

The hypotheses we tested and the inference results are as follows.

• H5)Is there any difference between the trajectories of cHC and HC?

  HV: F value = 8.8, DF = [1 218.0], p = 0.0034

  ECT²: F value = 4.3, DF = [2 392.7], p = 1.5e-4

• H6)Is there any difference between the first and second slopes of the piecewise linear model in cHC subjects?

  ECT: F value = 4.5, DF = [1 622.3], p = 0.034

• H7)Is there any difference in the first slopes of HC and sHC subjects?

  ECT: F value = 0.0, DF = [1 685.4], p = 0.97

• H8)Is there any difference in the second slopes of HC and sHC subjects?

  ECT: F value = 7.6, DF = [1 514.2], p = 0.006

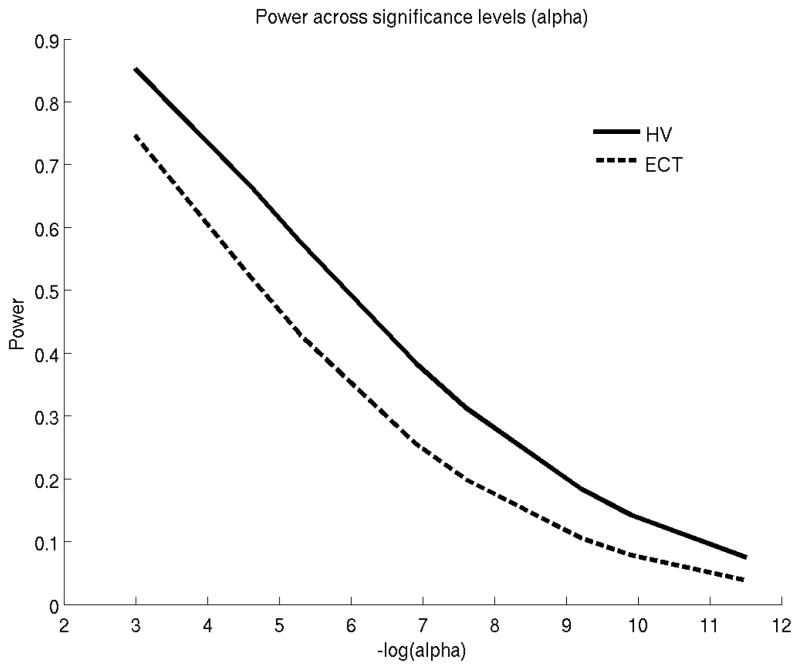
Figure 4 shows the retrospective power (Equation 2.10) for comparing the rates of atrophy between HC and cHC using the ADNI data. Here, HV provides slightly more power than ECT in detecting longitudinal group differences.

Figure 4.

Statistical power versus alpha (false positive rate) to discriminate the atrophy rates of stable and converter healthy controls (HC). HV: hippocampal volume. ECT: entorhinal cortex thickness.

3.3 Comparison of LME to alternative methods

In the third experiment, our goal was to provide an objective comparison of the LME approach with the two widely-used alternative methods, namely repeated measures ANOVA (rm-ANOVA) and cross-sectional analysis of the slope (x-slope), i.e. annualized rate of atrophy estimated for each individual. We implemented rm-ANOVA via a LME model with a single random effect for the intercept. As we discuss above, this imposes a compound symmetry structure on the covariance between repeated measures – a model that is unlikely to be appropriate for typical LNI data. For the second benchmark, we estimated each subject’s slope using the best-fit line (in the least square sense) to its longitudinal measurements. Then we conducted a standard least-square regression (GLM) with the same independent variables as the other two methods.

We were interested in assessing the specificity, sensitivity and reliability of the three methods in a realistic longitudinal design. To achieve this, we conducted two-group comparison analyses on the rates of HV loss in HC subjects and AD patients, using an empirical strategy inspired by (Thirion et al., 2007). There were two main reasons for our particular choice of biomarker and groups. Firstly, from prior work we were confident that there is a significant difference between the HV atrophy rates of HC and AD groups (Jack Jr et al., 2010). Secondly, our sample size estimates (see Table 3) indicated that with a relatively small number of subjects, we had a good chance of detecting the difference in atrophy rates. Hence, we could draw a relatively large number of pseudo-independent subsamples (with say N = 10–30 subjects from each group) from the entire ADNI sample to conduct our analyses.

For each sample size value (e.g. N = 15 per group), we randomly selected two sets of independent AD+HC samples, (i.e., two independent samples of 2N) from the eligible portion of the ADNI sample (all ADNI HC and AD subjects). There was no overlap between the two independent samples and each sample contained the same number of AD and HC subjects. We repeated this procedure 200 times to obtain 200 random pairs of independent AD+HC samples of a certain size (that is, 400 random AD+HC samples in total).

For each sample, we used the three methods (LME, rm-ANOVA and x-slope) to compute parametric p-values for the difference between the rates of atrophy of the two clinical groups (AD vs. HC). Next, we conducted a permutation test (Good, 2000; Nichols and Holmes, 2002) for each sample by shuffling the clinical group memberships and repeating the inference (2000 permutations). A non-parametric p-value was computed for each sample and each method based on the ranking (with respect to the 2000 permutations) of the corresponding parametric p-values. The permutation approach relies on assumptions that are weaker than those required for the parametric p-values and is known to yield an accurate assessment of the probability of false positive (type 1 error, p-value, or equivalently specificity) when the number of permutations is large (Nichols and Holmes, 2002).

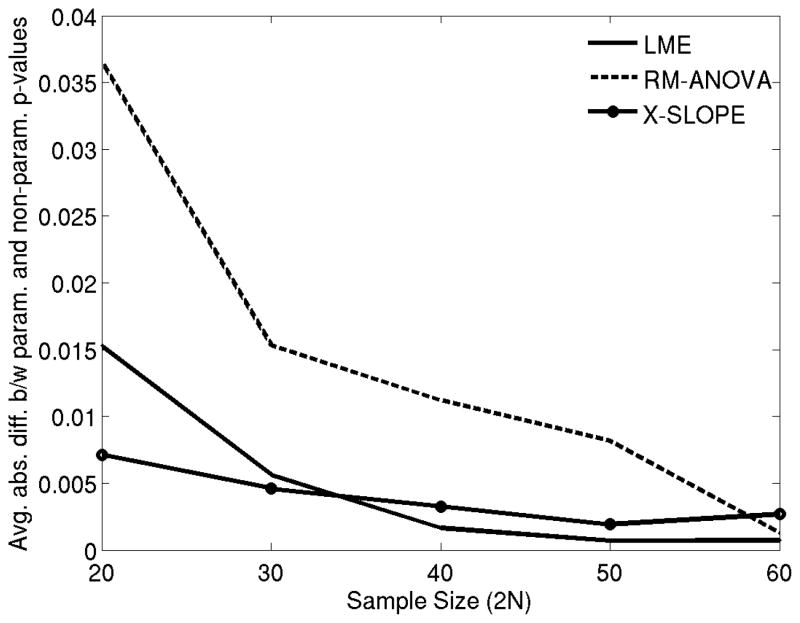
Thus, we considered the agreement between the parametric and non-parametric p-values as a measurement of the accuracy of the parametric p-values, or the specificity of the parametric model. Figure 5 shows the mean (averaged across the 400 random AD+HC samples) absolute difference between the parametric and non-parametric p-values for different sample sizes and different methods. These results revealed that both LME and x-slope provided significantly higher specificity than rm-ANOVA for modest sample sizes (2N less than 50).

Figure 5.

The mean absolute difference between non-parametric and parametric p-values for three statistical methods in comparing hippocampal volume loss rates between healthy controls (HC) and Alzheimer patients (AD) (Experiment 3) as a function of total sample size. LME: Linear Mixed Effects model with random intercept and slope. Rm-ANOVA: random effects ANOVA. X-Slope: GLM-based cross-sectional analysis of annualized rate of atrophy (slope).

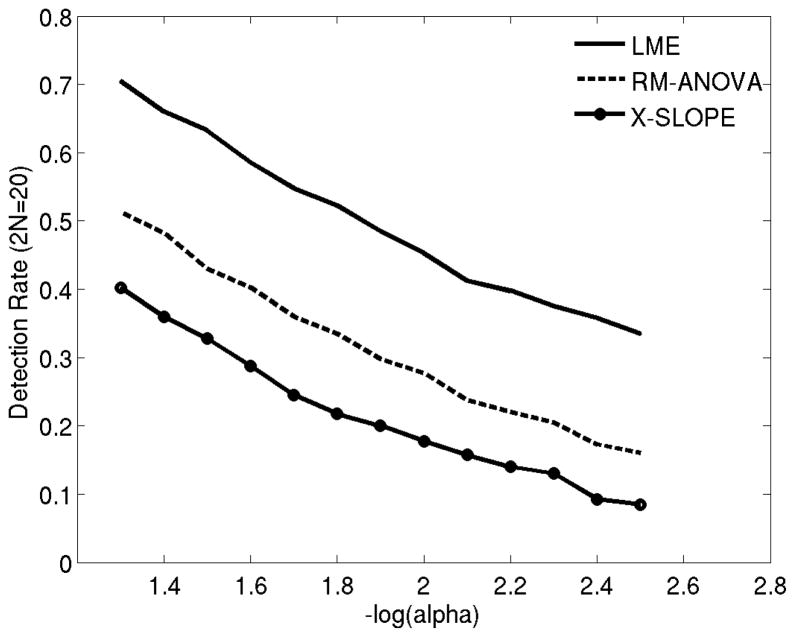
To assess sensitivity, we computed the detection (true positive) rate across the 400 samples (200 pairs) for a range of p-value (alpha) thresholds and 2N=20 (see Figure 6). Here we assumed that the underlying ground truth was that there is a difference between hippocampal atrophy rates of HC versus AD subjects. Instances where the p-value was less than an alpha threshold were considered a “detection” and remaining cases were treated as a false negative. The true positive rate (or sensitivity) was quantified as the fraction of detections. Our results indicate that LME yields significantly higher sensitivity than the two alternative approaches. Note that, these results indicate we have about 70% power with the threshold (alpha) set to 0.05 and 2N = 20. This is in agreement with the approximate sample size estimate computed for 80% power (Table 3).

Figure 6.

Detection rate (the frequency of true positives) in differentiating hippocampal volume loss rates between healthy controls and AD patients (Experiment 3), as a function of alpha (p-value threshold) with 2N=20 subjects. LME: Linear Mixed Effects model with random intercept and slope. Rm-ANOVA: random effects ANOVA. X-Slope: GLM-based cross-sectional analysis of annualized rate of atrophy (slope).

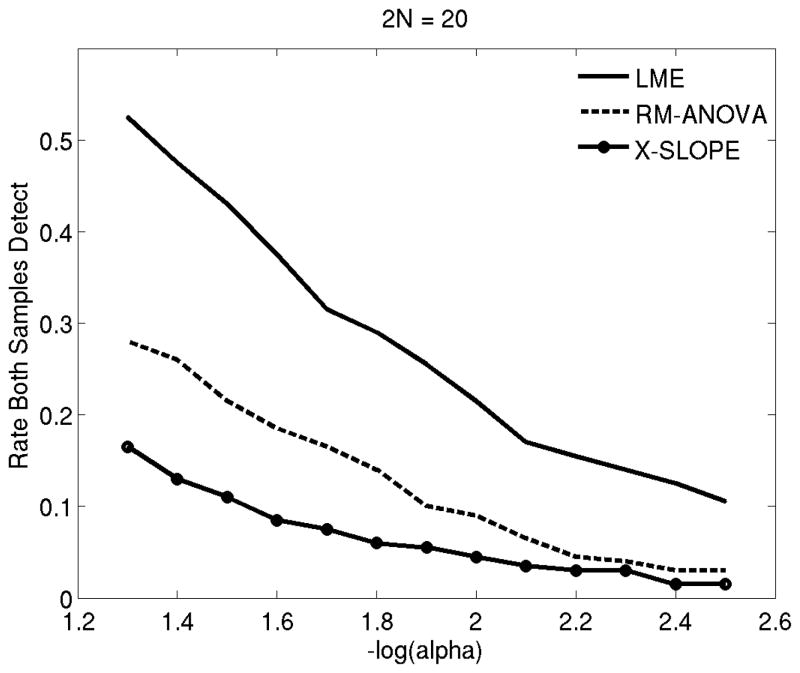
Finally, we were interested in quantifying repeatability, by comparing results between the two independent samples obtained at each random draw (200 pairs). Figure 7 shows the rate at which each method was able to detect the difference in both samples for a range of p-value thresholds (alpha values). These results suggest that LME yields longitudinal findings that are more likely to be repeatable in an independent sample.

Figure 7.

Repeatability (the frequency at which a method differentiates hippocampal volume loss rates between healthy controls and AD patients in two independent samples of 2N= 20) versus alpha (p-value threshold) (Experiment 3). LME: Linear Mixed Effects model with random intercept and slope. Rm-ANOVA: random effects ANOVA. X-Slope: GLM-based cross-sectional analysis of annualized rate of atrophy (slope).

3.4 Assessing the effect of including subjects with a single time point

In this final experiment, our goal was to quantify the effect of including subjects with a single time-point into the LME-based analysis of longitudinal data. The theoretical expectation is that data from subjects with a single visit may contain valuable information about between-subject variability, which can in turn improve our inference on the remaining longitudinal measurements. In practice, most studies choose to exclude these subjects in their analyses, because their methods cannot handle these cases and/or they are cautious of introducing a bias into the analysis, since there might be inter-group differences in dropout rates. However, the LME approach recommends to include all scans from all time-points into the analysis (Fitzmaurice et al., 2011).

As an objective assessment, we conducted the following experiment. We first established a sample of 50HC+50AD subjects from the ADNI data, in which each subject has four repeated measurements (MRI-derived hippocampal volume). We call this the “full sample.” We then performed 1000 simulations. In each simulation we randomly selected 20 subjects from the AD group (20% of the full sample) to remove their last three repeated measures from the data (therefore leaving only their baseline HV measurements). Thus, for each simulation we had a “reduced sample,” which consisted of a group of 50HC+30AD completers (i.e., they had all four repeated measures) and 20 AD subjects with a single measurement (“dropouts”). We then fit two LME models with the same independent variables as above: one model was based on the reduced sample excluding the dropouts (i.e., only 50HC+30AD completers). The second model was computed based on the entire reduced sample, which included the 20 AD dropouts. We then compared these model fits with that obtained on the full sample. Figure 8 shows the difference between the fixed effect coefficient estimates obtained on the reduced sample (with and without the dropouts) and full sample. These results suggest that including subjects with a single time-point (dropouts) increases the accuracy of the model fit, and would thus lead to improved inference.

Figure 8.

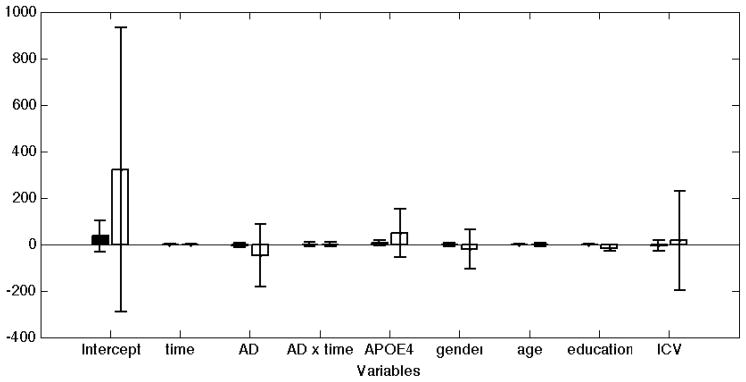
The influence of including subjects with a single time-point on LME-based inference results. MRI-derived total hippocampal volume was the dependent variable. The full sample contained 50 HC and 50 AD subjects, all with 4 visits (scans). We had 1000 random simulations, in which a reduced dataset was generated, by treating 20 random AD subjects as dropouts and discarding their last three scans. The y-axis shows the average difference between the coefficient estimates obtained on the reduced sample by including (black bars) or discarding (white bars) the 20 dropout AD patients, and the coefficients from the full sample. The error bars show the standard deviations across 1000 random simulations. These results suggest that including the subjects with a single time-point increases the accuracy of the model fit and introduces minimal bias.

4 DISCUSSION

Linear Mixed Effects (LME) models offer a more powerful and versatile framework for the analysis of longitudinal data than many other popular methods (Fitzmaurice et al., 2011). The LME approach elegantly handles unbalanced data (with variable missing rates across time-points and imperfect timing), makes use of subjects with a single time-point to characterize inter-subject variation, and provides a parsimonious way to represent the group mean trajectory and covariance structure between serial measurements. Yet, its use in neuroimaging seems to be limited to a small number of studies, which represent a minority in the rapidly growing LNI literature. We found that many prior LNI studies used sub-optimal approaches that at best offer reduced power to detect effects and at worst can lead to incorrect inferences. Our goal in this work was to advocate the use of LME models for LNI data analysis by providing the theoretical background and the implementation of an array of computational tools that build on the LME framework. We intended to illustrate the proper use of these tools using a well studied, real-life longitudinal dataset. Finally and most importantly, we provided a validation of our tools and an objective comparison with two popular alternative methods via analyses on these data.

In the first experiment, we applied the LME model to a well-known pair of AD biomarkers (hippocampal volume –HV- and entorhinal cortex thickness –ECT-) and obtained results that were in agreement with prior work. The lowess plots revealed that a linear model was suitable to characterize the longitudinal trajectories in the follow-up period. Our inferences indicated that there was a significant difference between the HV and ECT atrophy rates across HC, sMCI, and cMCI subjects. This difference diminished (and became statistically insignificant for ECT) when comparing cMCI subjects and AD patients.

In the second experiment, we compared atrophy rates between HC subjects and converter HC subjects, who were clinically healthy at baseline but progressed to MCI or clinical AD at follow-up. The lowess plots revealed an intriguing, nonlinear trajectory of entorhinal cortex thickness in the cHC group, which could be captured via a piece-wise linear model with a knot at 1.2 years. Our LME-based inference further confirmed that this was an appropriate model, since the two slopes of the piece-wise linear model were statistically significantly different. Intriguingly, the knot (or elbow) of the piece-wise linear model (at around 1.2 years) was on average about 1.4 years prior to the event of clinical conversion, suggesting that atrophy rates accelerate prior to the beginning of clinical symptoms. Furthermore, our inferences confirmed that in the cHC group both HV and ECT exhibited an overall longitudinal trajectory that was statistically significantly different from the controls. For ECT this difference was driven by the apparently sudden acceleration of atrophy in the cHC subjects at around the end of the first year of the study. For HV, there was no such nonlinearity that was discernible in the group trajectories.

In the third experiment, our goal was to provide an objective assessment of the three competing methods widely used to analyze longitudinal data. We focused on HV, a well-established marker of AD, which also has a relatively large effect size. This enabled us to interrogate a large number of random sub-samples of relatively small size, where the effect of interest was detectable and average across these random experiments. The ADNI data, with its variable missing data pattern, imperfect follow-up timing, and multi-site nature, provided a perfect example of a realistic LNI study, in which we can objectively quantify the performance of the different methods. Our results supplied evidence supporting our theoretical expectations: the LME approach provides more sensitivity in a realistic LNI setting than repeated measures ANOVA or the analysis of summary metrics such as annualized atrophy rates, with good control on specificity. Furthermore, the resulting findings are more likely to be replicated in an independent study.

Finally, in a fourth experiment, we aimed to quantify the improvement in model fit afforded by the LME method by including subjects with a single time-point. To achieve this, we first established a full dataset with 50 AD and 50 HC subjects, all of which had four scans. Then we simulated 1000 random subsets of this sample, where 20 AD patients dropped out after the first visit. Our results, once again, were in line with the theoretical expectations: including subjects with a single time point can dramatically improve the accuracy of the model fit in the LME approach.

The present study focused on the univariate analysis, where the correction for “multiple comparisons” is not an issue. In future work, we intend to extend the LME framework and our computational tools to the mass-univariate setting, where one interrogates effects across a large number of pixels/voxels. This will be the topic of an upcoming follow-up paper.

5 CONCLUSIONS

The Linear Mixed Effects (LME) approach provides a powerful and flexible framework for the analysis of LNI data. We have implemented and validated these computational tools, which will be made freely available within FreeSurfer to complement its longitudinal image-processing pipeline.

HIGHLIGHTS.

• We discuss Linear Mixed Effects (LME) models in the context of longitudinal imaging

• We contrast LME with widely used methods in longitudinal imaging

• We illustrate, validate and benchmark LME-based computational tools

• These tools will be freely available in FreeSurfer