The structural, connectomic and network covariance of the human brain

Abstract

Though it is widely appreciated that complex structural, functional and morphological relationships exist between distinct areas of the human cerebral cortex, the extent to which such relationships coincide remains insufficiently appreciated. Here we determine the extent to which correlations between brain regions are modulated by either structural, connectomic or network-theoretic properties using a structural neuroimaging data set of magnetic resonance imaging (MRI) and diffusion tensor imaging (DTI) volumes acquired from N = 110 healthy human adults. To identify the linear relationships between all available pairs of regions, we use canonical correlation analysis to test whether a statistically significant correlation exists between each pair of cortical parcels as quantified via structural, connectomic or network-theoretic measures. In addition to this, we investigate (1) how each group of canonical variables (whether structural, connectomic or network-theoretic) contributes to the overall correlation and, additionally, (2) whether each individual variable makes a significant contribution to the test of the omnibus null hypothesis according to which no correlation between regions exists across subjects. We find that, although region-to-region correlations are extensively modulated by structural and connectomic measures, there are appreciable differences in how these two groups of measures drive inter-regional correlation patterns. Additionally, our results indicate that the network-theoretic properties of the cortex are strong modulators of region-to-region covariance. Our findings are useful for understanding the structural and connectomic relationship between various parts of the brain, and can inform theoretical and computational models of cortical information processing.

Introduction

It is widely appreciated that complex structural, functional and morphological relationships exist between distinct areas of the human cerebral cortex. Among the most telling of these relationships is that of structural connectivity, where distinct gyral and sulcal gray matter (GM) structures are physically connected by white matter (WM) tracts. Structural connectivity patterns aid one in understanding how different areas of the brain process inputs, exchange information, and respond to either exogenous or endogenous stimuli. For this reason, the study of connectivity patterns in the brain is an active topic of scientific investigation (Eguiluz, Chialvo et al. 2005; Achard, Salvador et al. 2006; Bassett and Bullmore 2006; De Luca, Beckmann et al. 2006; Honey, Kotter et al. 2007; Greicius, Supekar et al. 2009; Hagmann, Cammoun et al. 2010). In addition to structural connectivity, however, various areas of the brain can also share intricate relationships as a consequence of genetic, developmental and environmental factors which can alter the structural and functional relationships between brain regions (Lerch, Worsley et al. 2006; He, Chen et al. 2007; Chen, He et al. 2008). At the macroscopic scale, the most obvious structural delineation scheme for the cortex involves dividing the cerebral surface into gyri and sulci, given that the morphometric, areal and volumetric properties of these structures can be resolved using currently available neuroimaging methodologies. Thus, to understand how different parts of the brain can interact with each other, it is very helpful to elucidate the extent to which the structural properties of gyri and sulci (such as their cortical thickness, area, curvature, etc.) co-vary across subjects (He, Chen et al. 2007).

In addition to the structure of covariance between the anatomic and connectivity properties of different brain regions, it is also useful and enlightening to investigate the individual place of each brain region within the full ensemble of brain connections (Gong, He et al. 2009). In the context of network theory, brain regions and WM fibers can be conceptualized as nodes and edges, respectively, and local network topology can be explored by quantifying the relative prominence of various nodes at the local or at the global level (Chen, He et al. 2008). By studying the covariance patterns of network properties between different nodes across subjects, one can identify the roles of various brain regions within their overarching networks, as quantified using graph-theoretic measures such as degree, betweenness centrality, local efficiency, etc.

In this article, we seek to determine the extent to which the patterns of correlation between brain regions are modulated by structural, connectomic and/or network-theoretic properties. Starting from a structural neuroimaging data set of magnetic resonance imaging (MRI) and diffusion tensor imaging (DTI) volumes acquired from N = 110 healthy human adults, we use automated image processing methods to segment and parcel the brain of each subject into 165 regions and to compute the structural, connectomic and network-theoretic properties of each region. To identify the co-linear relationships between all available pairs of regions, we use canonical correlation analysis to test whether a statistically significant correlation exists between each pair of cortical parcels as quantified via structural, connectomic or network-theoretic measures. In addition to this, we investigate (1) how each group of canonical variables (whether structural, connectomic or network-theoretic) contributes to the overall correlation and, additionally, (2) whether each individual variable makes a unique contribution to the test of the omnibus null hypothesis according to which no correlation between regions exists across subjects. Our findings are useful for understanding the structural and connectomic relationship between various parts of the brain, provide an overarching picture of brain connectedness, and can inform theoretical and computational models of cortical information processing.

Methods

Subjects

T₁-weighted MRI volumes from N = 110 healthy, right-handed human subjects aged 25 to 36 were obtained from the Integrated Data Archive (IDA; http://ida.loni.ucla.edu) of the Laboratory of Neuro Imaging (LONI) at the University of California, Los Angeles. Data were obtained from a variety of projects in which subjects provided their informed written consent as required by the Declaration of Helsinki, U.S. 45 CFR 46, and with the approval of local ethics committees at their respective research institutions. All subjects were healthy normal controls with no neurological pathology or history of psychiatric illnesses. Data sets deposited in the LONI IDA are fully anonymized for the purposes of sharing, re-use, and re-purposing, and linked coding or keys to subject identity are not maintained. Consequently, in accordance with the U.S. Health Insurance Portability and Accountability Act (HIPAA; http://www.hhs.gov/ocr/privacy), our study does not involve human subjects’ materials.

Image processing

The LONI Pipeline environment (http://pipeline.loni.ucla.edu) was used for all major image processing operations, including bias field correction, skull stripping, image alignment, etc. This program is a graphical environment for the construction, execution and validation of neuroimaging data analysis and facilitates automated data format conversion while providing a large library of computational tools (MacKenzie-Graham, Payan et al. 2008; Dinov, Van Horn et al. 2009; Dinov, Lozev et al. 2010). DTI data were analyzed in native subject space using second-order Runge-Kutta tractography in the Diffusion Toolkit component of the TrackVis (http://trackvis.org) software package for white matter fiber tract reconstruction. The 3D Slicer (http://slicer.org) program, an openly available software platform from the National Alliance for Medical Image Computing (NA-MIC; http://www.na-mic.org) for visualization. Segmentation and regional parcellation were performed using FreeSurfer (Dale, Fischl et al. 1999; Fischl, Sereno et al. 1999; Fischl, Salat et al. 2002) following methodology described in (Destrieux, Fischl et al. 2010). For each hemisphere, 74 cortical structures were identified in addition to 7 subcortical structures and to the cerebellum. One midline structure (the brain stem) was also included, for a total of 165 parcels for the entire brain. The cortex was divided into 7 lobes, with the number of parcels in each being equal to 21 (frontal, Fro), 8 (insula, Ins), 8 (limbic, Lim), 11 (temporal, Tem), 11 (parietal, Par), 15 (occipital, Occ). Cortical surface area, GM volume, mean curvature and mean thickness were extracted for each parcellated region.

Connectivity calculation and representation

To compute connectivity between regions for each subject, the location of each fiber tract end-point extremity within the brain was identified, while the GM volume associated with every parcel was also delineated. For those fibers which both originated as well as terminated within any two distinct parcels of the 165 available, each fiber extremity was associated with the appropriate parcel. For each such fiber, the corresponding entry in the connectivity matrix of the subject’s brain was appropriately updated to reflect an increment in fiber count (Hagmann, Cammoun et al. 2008; Hagmann, Cammoun et al. 2010). To compute relative connectivity density, each subject’s connectivity matrix was normalized over the total number of fibers within that subject. The average length of the fibers connecting every pair of regions was also recorded, as was the average fractional anisotropy (FA) of each fiber line as reconstructed via second-order Runge-Kutta tractography (Basser, Pajevic et al. 2000). Processing workflows to compute inter-regional connectivity matrices were constructed using purpose-built software.

Connectogram design

Connectivity was represented circularly using a framework based on Circos software (Krzywinski, Schein et al. 2009). Parcellated regions were displayed as a circle of radially aligned elements (a ‘connectogram’) representing the left and right hemispheres positioned symmetrically on the corresponding side of the vertical axis. Parcellated regions were assigned unique RGB colors as shown in Figure 3, and all RGB codes are provided in (Irimia 2012). Arrangement of parcellations within each lobe of the connectogram was performed in the order of their locations along the antero-posterior axis of the cortical surface associated with the published FS normal population atlas (Destrieux, Fischl et al. 2010). Cortical lobes were assigned unique color schemes: black to red to yellow (Fro), charlotte to turquoise to forest green (Ins), primrose to lavender rose (Lim), etc. Subcortical structures were colored light gray to black. An unambiguous abbreviation scheme was created to label each parcellation. Within the outermost circle which represents cortical parcellations, five circular heat maps were created to encode one of the five structural measures associated with the corresponding parcellation. Proceeding towards the center of the circle, these measures are total GM volume, total area of the surface associated with parcellation, mean cortical thickness, mean curvature and connectivity per unit volume. This latter measure was calculated as the density of fibers with endings within that parcellation divided by the parcellation’s total GM volume. The value of each structural measure was encoded as a color using a color scheme mapping that ranged from the minimum to the maximum of the data set. Specifically, the cortical thickness t with values in the interval [t_min, t_max] was normalized as t₁ = (t − t_min)/(t_max − t_min). The value of t₁ was associated with a unique color; for example, nuances at the extremities of the color map correspond to t_min and t_max, as required. For the brain stem, cerebellum and subcortical structures, values for area, thickness and curvature were unavailable from FS and their appropriate heat map entries were drawn in white. The methodology for generating connectograms is described is described in detail elsewhere (Irimia 2012).

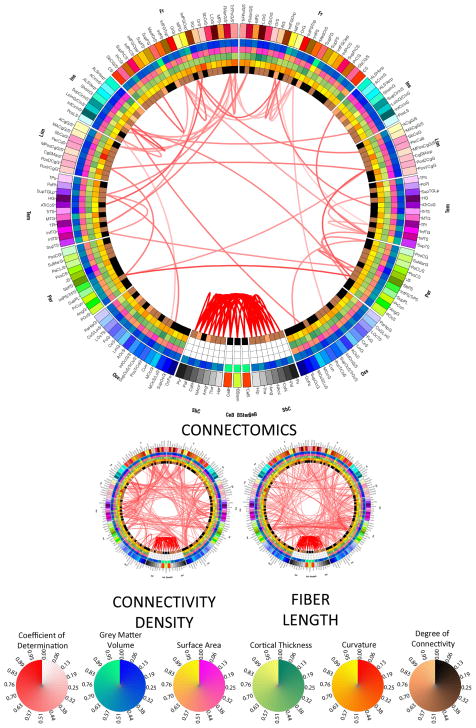
Figure 3.

As in Figure 2, for the two connectomic measures.

Network metrics

Nodes here are denoted by parcellated regions and edges are represented by fiber tracts. Network metrics were computed for each subject and included measures of global and local influence and segregation. As metrics of influence, the degree, betweenness centrality and participation coefficient of each node were computed. The node degree is the number of edges connected to a node and its calculation has fundamental impact upon many network measures; moreover, node degree distributions are highly informative of network architecture (Rubinov and Sporns 2010). The betweenness centrality of a node, on the other hand, is the fraction of all shortest paths in the network that pass through the node (Freeman 1978). Finally, the participation coefficient is a measure that assesses the diversity of connections between network partitions; for example, nodes of high degree that have a variety of connections with different network partitions have a high participation coefficient (Guimera and Amaral 2005). As measures of segregation, the clustering coefficient, local efficiency and eccentricity of each node were calculated. The first of these measures the density of connections between a node’s neighbors (Watts and Strogatz 1998), whereas the local efficiency of a node is the average of the inverse entries in the connectivity matrix computed on the neighborhood of the node (Latora and Marchiori 2001). The eccentricity of a node is the length of the shortest path between that node and the most distant node in the network.

Statistical analysis

We sought to identify the linear relationships between all available pairs of network nodes (i.e. cortical parcels) in the context of a canonical correlation model (Rencher 2002). For each subject s = 1, …, N, let C(s) represent the connectivity density matrix of subject s as determined using the methods previously described, and let c_ij(s) represent the entry in C(s) that is indexed by i and j, i.e. the connectivity density of the connection between vertices v_i and v_j. Similarly, let L(s) represent the average fiber length matrix and l_ij be the average length of WM fibers linking v_i to v_j. For each pair of vertices, the variables included in the canonical correlation analysis were either structural, connectomic or network-theoretic. The structural variables included were cortical area, curvature and thickness. The connectomic variables included were (1) the sum of connectivity densities for the connections linking each node to all its neighbors, i.e. Σ_k c_ik for node v_i and Σ_k c_jk for node v_j, as well as (2) the sum of physical lengths associated with these connections, i.e. Σ_k l_ik for node v_i and Σ_k l_jk for node v_j. Finally, the network-theoretic variables included for each node were the measures of influence (degree, betweenness centrality, participation coefficient), integration (characteristic path length), and segregation (clustering coefficient, local efficiency, eccentricity) previously described, for a total of p = 12 variables included in the analysis (three structural, two connectomic, and seven network-theoretic variables). Subsequently, for each pair of nodes v_i and v_j, two matrices X(v_i) and Y(v_i) were created, where X contains the values of canonical variables associated with node v_i, and Y contains the values of variables associated with node v_i (hence forward, the dependence of X and Y upon v_i and v_j shall be assumed and consequently no longer stated explicitly). X is of dimensions q × N and Y is of dimensions p × N, where p = q = 12 for the omnibus analysis and N = 110 in our case. Indices along the first dimension in each of X and Y indicate entries associated with each of the p = q = 12 canonical variables, whereas indices along the second dimension indicate the values assumed by each of these variables in subject s, where s = 1, …, 110. Thus,

$$\mathit{X}=\left(\begin{array}{c}{\mathit{x}}_1\\ ⋮\\ {\mathit{x}}_q\end{array}\right)=\left(\begin{array}{ccc}{x}_{1,1}& \dots & x_{N,1}\\ ⋮& \ddots & ⋮\\ x_{q,1}& \dots & x_{q,N}\end{array}\right)$$

and

$${\mathit{x}}_i=(\begin{array}{ccc}{x}_{i,1}& \dots & x_{N,1}\end{array}),\text{where}i=1,\dots ,q$$

and similarly for Y. For each pair of nodes v_i and v_j, these matrices were used to perform a canonical correlation analysis, i.e. to test the sequence of 12 null hypotheses $H_0^{(1)},\dots ,H_0^{(12)}$ that the 1^st through 12^th correlations are all zero against the corresponding alternative hypotheses. Explicitly, let x₁, …, x_q and y₁, …, y_p be the two sets of canonical variables whose correlative relationships are being investigated. The overall sample covariance matrix can be written as

$$\mathit{S}=\left(\begin{array}{cc}{\mathit{S}}_{yy}& {\mathit{S}}_{yx}\\ {\mathit{S}}_{xy}& {\mathit{S}}_{xx}\end{array}\right),$$

where S_yy, S_xx, S_yx and S_xy are blocks denoting the covariance matrices for the groups of variables indicated by the corresponding subscripts, e.g. S_xy is the covariance matrix of x₁, …, x_q and y₁, …, y_p. One can define an R²-like measure of association between the two sets of canonical variables as

$$R_M^2=\mid {\mathit{S}}_{yy}^{-1}{\mathit{S}}_{yx}{\mathit{S}}_{xx}^{-1}{\mathit{S}}_{xy}\mid ={\prod }_{i=1}^{min(p,q)}{r}_i^2,$$

where the variables $r_i^2$ are the eigenvalues of ${\mathit{S}}_{yy}^{-1}{\mathit{S}}_{yx}{\mathit{S}}_{xx}^{-1}{\mathit{S}}_{xy}$ (see also Chapter 11 in (Rencher 2002)); these eigenvalues are also canonical correlations which provide meaningful measures of association between the underlying variables (p. 362 in (Rencher 2002)). Under the null hypothesis H₀, there is no linear relationship between the x_i’s and the y_i’s, and H₀ is equivalent to the statement that all canonical correlations $r_i^2$ are non-significant. This hypothesis can be tested by means of Wilks’ Λ (likelihood ratio) statistic

$$\mathrm{\Lambda }=\frac{\mid \mathit{s}\mid }{\mid {\mathit{s}}_{yy}\mid \mid {\mathit{s}}_{xx}\mid }={\prod }_{i=1}^{min(p,q)}(1-r_i^2),$$

which is distributed as Λ_{p,q,n−q−1}. The null hypothesis is rejected if Λ ≤ Λ_{α,p,q,n−q−1}. In the case of the canonical correlation analysis for the omnibus model, p = q = 12 and Wilks’ Λ can be transformed to an approximate F-statistic, which can allow the null hypothesis to be tested against the theoretical F-distribution (cf. pp. 162–164 in (Rencher 2002) for details) having appropriate degrees-of-freedom. Specifically, with v_H = q and v_E = n − q − 1, one can define

$$\begin{array}{c}{\text{df}}_1={pv}_H\\ {\text{df}}_2=wt-\frac{1}{2}({pv}_H-2)\\ w=v_E+v_H-\frac{1}{2}(p+v_H+1)\\ t=\sqrt{\frac{p^2{v}_H^2-4}{p^2+v_H^2-5}}\end{array}$$

and the null hypothesis can be tested based on the value of the approximate F statistic given by

$$F=\frac{1-{\mathrm{\Lambda }}^{1/t}}{{\mathrm{\Lambda }}^{1/t}}\frac{{\text{df}}_1}{{\text{df}}_2}$$

with df₁ and df₂ degrees of freedom. In this study, the omnibus null hypothesis was rejected at a significance level of α = 10⁻¹⁵ subject to the Bonferroni correction for multiple comparisons.

By means of the multivariate approach described above, the null hypothesis was tested as to whether a statistically significant correlation existed between each pair of cortical parcels, as quantified by means of a multivariate feature vector which included structural, connectomic and network-theoretic measures.

In addition to assessing the omnibus hypothesis between each region pair, another set of interesting questions refer to how each individual canonical variable contributes to the overall correlation or, more precisely, whether each individual variable makes a significant contribution to the test of the null hypothesis. To investigate this, a lower-order-design (LOD, also known as ‘leave-one-out’) canonical correlation analysis (pp. 231–232 in (Rencher 2002)) was implemented. In this approach, exactly one of the 12 variables was removed at a time from the full canonical correlation model, and null hypotheses were tested on the 12 reduced models using the same approach as in the case of the omnibus hypothesis. This was done to determine whether the canonical variable being removed made a significant contribution to the test of the null hypothesis H₀ above and beyond the 11 variables already available. To test this hypothesis and thereby compare each reduced model to the full model, partial Λ and F statistics were calculated (p. 232 in (Rencher 2002)), and the test of the significance of each variable in the presence of the other 11 variables was performed. Specifically, the partial Λ statistic is given by

$${\mathrm{\Lambda }}_{\mathit{LOD}}=\frac{{\mathrm{\Lambda }}_f}{{\mathrm{\Lambda }}_r}$$

where Λ_f is the lambda statistic associated with the full model with N_f = 12 variables, and Λ_r is the lambda statistic associated with the reduced model of N_r = 11 variables. Λ_LOD is distributed as Λ_1,vH,vE−Nr, where the number of error degrees of freedom, v_E − N_r, has been adjusted for the N_r = 11 variables in the reduced model (p. 232 in (Rencher 2002)). Λ_LOD has an exact F-transformation of the form

$$F=\frac{1-{\mathrm{\Lambda }}_{\mathit{LOD}}}{{\mathrm{\Lambda }}_{\mathit{LOD}}}\frac{v_E-N_r}{v_H}$$

which is distributed as F_vH,vE−Nr and allows one to determine whether the canonical variable being removed makes a significant contribution to the test of the null hypothesis H₀ above and beyond the 11 variables already available. From among those pairs of regions that are significantly correlated according to the full canonical correlation analysis, we thus identified—by means of this LOD approach—those subsets of cortical region pairs whose structural, connectomic or network-theoretic correlations are significantly modulated by each individual canonical variable. For each of these subsets of connections as well as for the omnibus analysis, connectograms were generated to evaluate and compare the patterns of correlation between all cortical regions.

Results

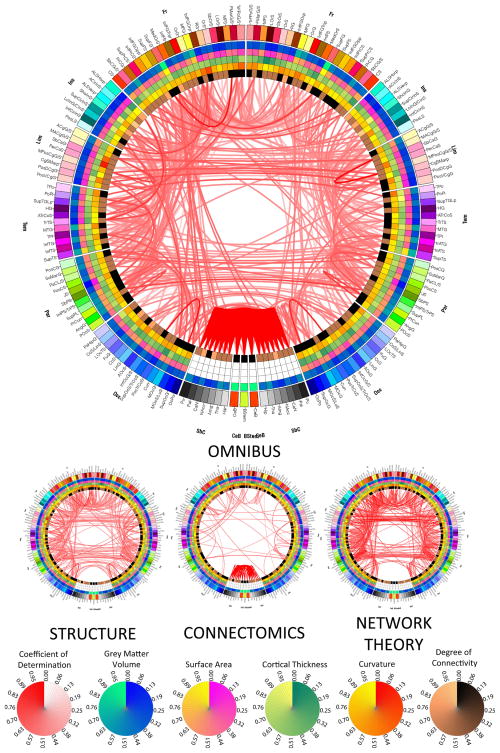
Figure 1 displays the results of the omnibus canonical correlation performed on all 12 descriptive variables (3 structural, 2 connectomic, and 7 network-theoretic measures). In addition, the connectograms for the three reduced canonical correlation models are also displayed for comparison. In each of these three models, exactly one of the three groups of descriptive variables is omitted; for example, the structure connectogram illustrates the effect caused by removing all three structural descriptive variables from the canonical correlation model. It should be noted that, in Figures 1–4, the thresholds being used to display connections are α_th = 10⁻¹⁰ and α_th = 10⁻⁵ for larger and smaller connectograms, respectively. The LOD canonical model was calculated only for those pairs of parcels for which α had been found to be lower than α_th = 10⁻¹⁰ in the omnibus model. For this reason, if a links is present in each small connectogram, a link must also exist in the large connectogram. This was found to be optimal for allowing the reader to discern patterns of covariance without displaying too many connections at the same time.

Figure 1.

Results of canonical correlation analysis. The presence of a link indicates that significant canonical correlation exists between the two regions connected by that link, as quantified via a multivariate feature vector (see text for details). For the large connectogram, the canonical correlation was performed on all 11 descriptive variables (3 structural, 2 connectomic, and 6 network-theoretic measures), whereas a reduced canonical correlation model was used to obtain the results displayed in each of the three small connectograms. In each of these three models, exactly one of the three groups of descriptive variables is omitted; thus, the structure connectogram illustrates the effect caused by removing all three structural descriptive variables (area, cortical thickness and curvature) from the full canonical correlation model. The threshold being used to display connections is α = 10⁻¹⁰ and α = 10⁻⁵ for the large and small connectograms, respectively. Each color map is linear, with a range from the minimum value being displayed (v_min, corresponding to zero on the circular map) to the maximum value (v_max, corresponding to unity). For example, the color associated with the value of 0.45 on any of the color maps corresponds to v_min + 0.45 (v_max − v_min).

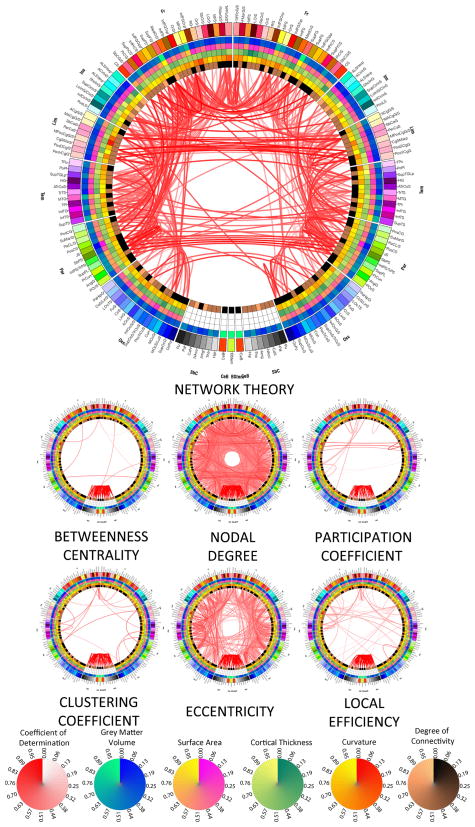
Figure 4.

As in Figure 2, for the six network-theoretic measures.

As explained in the previous section, wedges on the outermost ring of the connectogram depict the colors of each cortical parcel, using anatomically-defined color and abbreviation schemes described in detail elsewhere (Irimia 2012). Within the outermost circle which represents cortical parcellations, each of the five circular heat maps encodes one of the five structural measures associated with the corresponding parcellation. Proceeding towards the center of the circle, these measures are total GM volume, total area of the surface associated with parcellation, mean cortical thickness, mean curvature and connectivity per unit volume. A link is drawn between two parcels if and only if the coefficient of determination R² for the two regions is significant, and the opacity of the link is directly proportional to the value of R². For example, a link which is almost transparent reflects a low value of the coefficient of determination, whereas a link which is completely opaque reflects a high value of R².

The omnibus analysis connectogram reveals the presence of appreciable correlation between brain regions as quantified via structural, connectomic and network-theoretic properties, both inter- and intra-hemispherically. Notably, although many cortico-cortical correlations are found to be appreciable, the strongest values of the canonical correlation of determination R² are found between non-neocortical regions. In addition to the latter, however, R² is also appreciable for certain pairs of neocortical regions, both inter-hemispherically (left to right superior frontal gyrus, precentral gyrus, central sulcus), intra-hemispherically (superior occipital gyrus to superior occipital sulcus, bilaterally), and within a single hemisphere (left middle frontal sulcus to left superior frontal sulcus, and right middle anterior cingulate cortex to right middle posterior cingulate cortex). An additional insight offered by Figure 1 is the fact that structural and network-theoretic descriptive variables modulate region-to-region correlations to a greater extent than connectomic measures do, which clearly contradicts the view that cortical correlations of structural properties can be treated as surrogates of connectomic correlations.

In contrast to Figure 1 (which summarizes the results of the omnibus canonical correlation analysis), Figures 2–4 display the results of the 12 LOD canonical correlation analyses, whereby the extent to which each canonical variable contributes to the overall correlation is quantified. This is summarized in three separate figures, with the effects of removing each structural, connectomic and network-theoretic variable from the full model being illustrated in Figures 2, 3 and 4, respectively. In each of these figures, the larger connectogram being displayed shows the effect of removing the entire group of descriptive variables being investigated; thus, the larger connectograms in Figures 2–4 are identical to the smaller connectograms in Figure 1. By contrast, the smaller connectograms in each of Figures 2–4 illustrate the effect of removing exactly one variable from the full canonical correlation model.

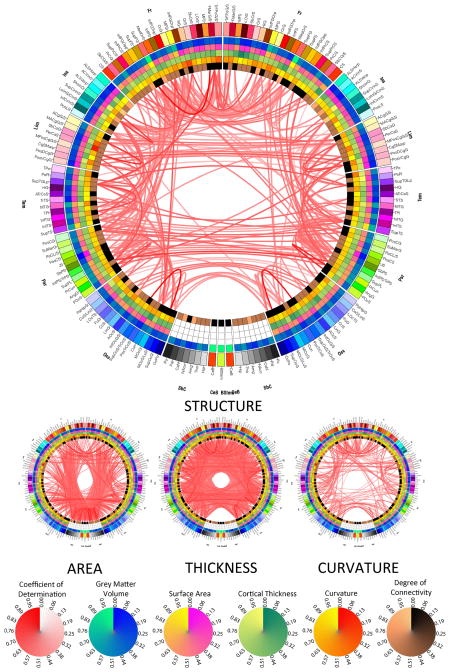
Figure 2.

Results of LOD canonical correlation analyses investigating the effect of removing structural measures from the omnibus model in Figure 1. The large connectogram displays the effect of removing all three structural measures, while small connectograms show the effect of removing exactly one of these three canonical variables from the full model, as indicated. Also shown are circular color bars for each measure, with ranges from the minimum to the maximum value of the measure being encoded. Similarly, link transparency encodes the value of the coefficient of determination R² (see text for details), with colors being mapped from the minimum to the maximum value of the coefficient within the connectogram.

The small connectogram on the left hand side (LHS) in Figure 2 shows that regional area modulates an abundance of correlative relationships between frontal lobe and non-neocortical structures, especially bilateral ones in cases such as the precentral gyrus, middle frontal gyrus, superior frontal gyrus, and superior circular insular sulcus. Additionally, the left and right precunei are two structures whose strong correlative relationship is significantly modulated by their cortical areas. Compared to area, however, cortical thickness appears to be a much more important factor in determining the covariational structure of the brain. Thus, from the standpoint of thickness, the brain appears to be very correlated both intra- and inter-hemispherically, notable examples of this being the bilateral correlations between the superior occipital gyrus and sulcus, which are appreciably modulated by the cortical thickness of these structures. By contrast, most structures whose correlation is significantly dictated by curvature are inter-hemispheric and bilaterally symmetric, such as between the left and right superior frontal gyri, precentral gyri, anterior cingulate cortices, supramarginal gyri as well as other structures.

Figure 3 summarizes the dependence of structural correlations upon one of two connectomic measures, namely connectivity density and fiber length, respectively. As expected from the normal human brain, correlation patterns modulated by connectivity density are bilaterally symmetric (i.e. symmetric with respect to the longitudinal fissure) both inter- and intra-hemispherically. Inter-hemispheric correlations that are modulated significantly by density are those between the left and right recti gyri, superior temporal gyri, as well as between insular sulci. Left-hemisphere correlations include (1) frontomarginal cortex to temporal lobe structures, (2) the anterior longitudinal sulcus to the transverse temporal sulcus, and (3) the superior occipital gyrus to the superior occipital sulcus. Other correlations modulated by connectivity density are between occipital and temporal structures (bilaterally), insular and temporal structures (also bilaterally), and between non-neocortical structures. On the other hand, correlations modulated by fiber length are mostly inter-hemispheric, between frontal structures (left to right precentral gyrus, left to right subcentral gyrus/sulcus), limbic structures (left to right cingulate structures, such as the anterior cingulate gyrus/sulcus, the marginal part of the cingulate sulcus, and the posterior dorsal cingulate gyrus). Other inter-hemispheric correlations are between parietal structures (such as between submarginal gyri, superior parietal lobules, and angular gyri), whereas intra-hemispheric correlations modulated by fiber length are between (1) limbic and parietal structures, and between (2) frontal and parietal parcels (bilaterally in both cases).

Figure 4 illustrates the fact that two network-theoretic properties of the brain (eccentricity and nodal degree) are important modulators of the correlative relationships between various cortical and subcortical structures. By contrast, betweenness centrality, local efficiency as well as the clustering and participation coefficients were not found to contribute to correlation patterns appreciably (see also Supplementary Material). For the most part, community structure was found to modulate intra-hemispheric correlations in a bilaterally symmetric way (between all combinations of lobes), with the notable exceptions of some inter-hemispheric correlations (between limbic lobe structures, and parieto-limbic correlations). Similarly, eccentricity significantly influences the correlation patterns that exist within each hemisphere, especially with regard to parieto-limbic and temporo-insular relationships. Finally, nodal degree affects a wide variety of correlations between all cortical lobes, both intra- and inter-hemispherically.

Discussion

An important relationship between brain function and structure is the fact that functional specialization can lead to anatomic change (Lerch, Worsley et al. 2006), e.g. in the case of trained musicians who feature enlarged sensorimotor, premotor and parietal areas (Schlaug 2001). Because functional changes such as these can prompt or modulate structural changes in the brain, one can expect that the manner in which the anatomic features of certain brain areas are correlated across individuals may partly reflect functional interactions between these areas. Conversely, because genotypic factors modulate, to a large extent, whether and how different parts of the brain develop across individuals, it can be hypothesized that correlations in cortical area, thickness or in other properties as induced by genetic factors can influence the degree and extent of proficiency achieved by the individual in areas such as analytic processing speed, spatial acuity, artistic talent, etc. Consequently, to determine the extent to which brain structure constrains function and vice versa, it is essential to investigate how anatomic features are correlated across brain regions, as well as whether the existence of such correlations is partly due to WM connectivity between regions or to the type of network connections between them. To do so for the healthy adult population is necessary in order to establish a reference space of correlative relationships which apply to the human brain, and to identify the characteristics of a population which can be used as a normative sample in comparative statistical studies of neurological and psychiatric disease. Importantly, a useful feature of our approach which can make it particularly appealing to other researchers is the fact that the methodologies we employed here (3D Slicer, from www.slicer.org; the LONI pipeline, from http://pipeline.loni.ucla.edu; and Circos, from http://circos.ca) are freely available and systematically well documented in our previous publications (MacKenzie-Graham, Payan et al. 2008; Dinov, Van Horn et al. 2009; Dinov, Lozev et al. 2010; Irimia 2012).

The fact that correlative relationships exist between various regions of the brain has been recognized for some time (Lerch, Worsley et al. 2006; He, Chen et al. 2007). Lerch and colleagues (2006), for example, found that association cortex (Brodmann Area 44) is structurally correlated with other brain areas in a manner which is very similar to that in which this former region is connected to other brain areas via WM tracts. Because cortical thickness reflects the size, number and spatial distribution of cells in the nervous system, it is a particularly attractive measure for investigating the network properties of the cortex, as demonstrated by Evans et al. (2008). Correlative relationships between brain regions have been alternatively attributed to mutually trophic effects mediated by axonal connections (Ferrer, Blanco et al. 1995), tissue type similarities (Cohen, Lombardo et al. 2008), heredity (Schmitt, Lenroot et al. 2008), and/or environment-related plasticity (Mechelli, Friston et al. 2005). In particular, the study by Mechelli et al. attempted to identify topographical principles governing structural variability across individuals, and hypothesized that different regions’ GM density (i.e. regional GM volume normalized with respect to the entire brain) co-vary symmetrically with respect to the longitudinal fissure. These authors found that, for a few selected regions, GM density in one hemisphere is generally a good predictor of GM density in the homotopic regions of the contralateral hemisphere. Recently, He et al. (2007) parcellated the human cortex into 54 regions and investigated which pairs of cortical regions showed statistically significant associations in cortical thickness. They found that the 15 pairs with the highest correlations in thickness were associated with WM fiber tracts that had been mapped by neuroanatomists. Although these authors initially speculated that morphometry-based cortico-cortical correlates provide approximate reflection of the true anatomical connections among neuronal elements, a subsequent study by the same group (Gong, He et al. 2012) found that cortical thickness correlations reflect underlying WM connectivity only to a moderate extent, namely that only 35–40% of cortical thickness correlations are associated with underlying WM connections between the correlated regions in question.

In this study, we applied a connectomic approach to identify not only whether correlative relationships between any pair of brain regions exist, but also whether such relationships are related to anatomic, connectomic or network-theoretic factors. For this reason, our study is significant because it is the first one to determine and quantify systematically if and how structural features are shared by brain regions due to WM connectivity or due to the nature of network connections between them (as quantified using graph theory metrics). In addition, for each correlative relationship which is due to structure, connectomics or network properties, we determined whether the correlation is due to area, thickness or curvature (for correlations modulated by structure), by connectivity density or fiber length (for correlations modulated by connectomics), or by one of seven graph-theoretic measures (for correlations modulated by network properties). Thus, an important reason for which our study is useful is because it reveals and quantifies, for the first time, the interplay between these former three sets of factors in determining how brain regions share common features. Another reason for its importance is the fact that we hereby establish a reference space of brain feature correlations which is based on a normative sample of healthy adults. This reference space can be used to study how brain correlations are altered in disease, and its use may lead to improved understanding of how brain structure, function and circuitry are affected by various pathologies, including dementia, psychiatric diseases, and in conditions of neurological concern such as traumatic brain injury.

Our investigation is motivated primarily by the fact that studies of cortical thickness correlations have provided insight into a variety of clinical conditions. For instance, He et al. (2008) found that Alzheimer’s Disease (AD) patients exhibit decreased thickness correlations bilaterally between parietal regions, as well as increased inter-correlations between temporal and parietal cortices. Lerch et al. (2008) used a leave-one-out multivariate discriminant analysis to confirm that cortical thickness could be used to accurately predict AD diagnosis and proposed their framework as a valuable method for improving diagnostic accuracy. In another study, van Haren et al. (2011) found that the brain of schizophrenics exhibits appreciable thinning in frontal and temporal areas and that such thinning is correlated with outcome and with the pharmacological therapeutic regimen of patients. In temporal lobe epilepsy (Bernhardt, Worsley et al. 2008; Bernhardt, Rozen et al. 2009; Bernhardt, Chen et al. 2011), graph-theoretic analysis of cortical thickness correlation networks has revealed disrupted small-world organization including features such as altered connectivity between hubs, increased path length and clustering, as well as higher vulnerability to targeted attacks. In autism, structural differences from controls have been observed in cortical areas involved in social cognition, communication, and repetitive behaviors (Hyde, Samson et al. 2010). Consequently, it can be expected that network properties are, in some senses, specific to various clinical populations, and that such differences may even have prognostic clinical value.

The presence of a significant canonical correlation between any pair of cortical regions, as represented in Figures 1–4, denotes the existence of a statistically significant modulatory relationship between these regions. Furthermore, the presence of a link in a connectogram implies that a significant value of R² is associated with the canonical correlation between the connectomic variables for the two cortical regions involved. For example, the presence of a link in the curvature connectogram of Figure 2 implies that curvature is a critical feature in determining the significance of the canonical correlation, and that its removal from the feature vectors of the two regions (as done via the LOD model) causes the canonical correlation to become statistically insignificant. The implication is that the two regions whose feature vectors are being compared share curvature as a significantly correlated feature, and that one region’s change in curvature from one subject to the next is associated with a corresponding significant change in the curvature of the other region. The same argument applies to any of the other 11 canonical variables whenever a link is present in that variable’s connectogram for some pair of regions; this implies that our study systematically reveals and quantifies a variety of relationships between brain regions in the healthy adult brain, and that the features shared by cortical areas include not only structural properties, but also connectomic and network-theoretical properties. In particular, the existence of significant correlations based on the latter two types of features implies that cortical regions can share not only structural properties, but also WM connectivity patterns and graph-theoretical properties, which may bear relevance to future studies of structural and functional connectivity.

In some respects, studies of brain network properties inferred via DTI tractography have been compared favorably to analyses of cortical thickness correlation (Gong, He et al. 2009), and have revealed prominent network features such as small worldness and ‘rich club’ structure (He, Wang et al. 2009). Furthermore, it has been found that many topological properties of structural brain networks can be extracted from network analysis of structural correlation matrices using a variety of measures (He and Evans 2010). Our present study confirms the previous conclusion of Gong et al. according to which thickness correlations do reflect the underlying fiber connection to some extent, although the former should not simply be taken as a proxy measure of the latter. Additionally, we find that this is the case not only for cortical thickness correlations, but also for the other structural, connectomic and network-theoretic measures considered in our study. Specifically, whereas correlation between regions—as computed based on our 12 computed properties—may occasionally be strong, the large differences we find between the correlational patterns associated with each of these 12 properties indicate that WM connectivity is not the (sole) reason for the existence of correlative relationships between brain regions. For this reason, we propose that the term ‘connectivity’ should be reserved for denoting physical connectivity as mediated by WM fibers, and not to correlative relationships. An important consequence of this conceptual distinction is that, since statistical correlations between regions do not generally imply physical connectivity between them, it may not be entirely valid to use network metrics computed from correlation-based adjacency matrices in order to infer the information-theoretic properties of the brain. In (Gong, He et al. 2012), for example, significant differences were found in the locations of hub regions in correlative vs. connectivity networks, though some consistent agreement was also found in this respect; similarly, the local efficiencies of nodes in the two network types (correlative vs. connectivity-derived) were found by Gong et al. to be weakly and insignificantly correlated (r = −0.11, p = 0.32). Similarly, in (Chen, He et al. 2008), the authors investigate the intrinsic modular structure of human brain networks derived from thickness measurements and speculate that interregional correlations in thickness might arise from interactions between underlying neuronal substrates through their anatomical connections. Chen et al. also compute the vertex properties of nodes associated with primary motor cortex and the edge properties of connections between this structure, on the one hand, and parietal, temporal and frontal association cortices, on the other hand. They conclude that the high betweenness centrality of these nodes is possibly due to their importance in managing information flow across the network. Nevertheless, since networks derived from thickness correlations differ markedly from those derived from WM connectivity, it is not expectable that the inferred properties of these two network types can be assumed to be identical or even similar. Specifically, since correlation network properties do not reflect the presence of physical connections that carry information between regions, it may not be entirely valid to claim that the high betweenness centrality of a node as computed from a correlation network is due to increased information flow management by that node. The primary reason for this is because, whereas WM connections can physically transmit information between regions, correlation networks are statistical constructs which reflect connectivity information only to a very limited extent.

One disadvantage of our study is the fact that current DTI tractography algorithms are not entirely satisfactory from the standpoint of their ability to map WM connections accurately and precisely throughout the brain. For example, crossing and kissing fibers are poorly resolved by many tractography algorithms, including the one used here. Furthermore, the presence of phenomena such as scanner noise and subject motion implies that existing WM connections can be missed while other (nonexistent) connections may be inadvertently created. Furthermore, as in the study of Gong et al. (Gong, He et al. 2012), cortical thickness cannot be defined for non-cerebral structures, which implies that the role played by the latter in modulating the thickness of cortical regions cannot be assessed using our current method. It is also useful to note that the topic of structural covariance in the human cortex can and has been investigated using related statistical techniques, such as partial correlation by Joshi et al. (2010). In these authors’ study, however, only partial correlations of GM volumes were considered in the analysis, whereas in our case the measures included were not only volumetric, but also morphometric, connectomic and network-theoretic. Additionally, our study includes an analysis of 165 parcels compared to the 33 parcels of Joshi et al.

Finally, it is important to note that, as Wu et al. (2012) noted previously, the network properties of the cortex change as a function of age, particularly with respect to measures such as the connector ratio between modules as well as the topological distribution of inter-modular connections. This finding has been confirmed for both structural and thickness correlation networks, and age-dependent changes in brain network topology have been quantified in both (Chen, He et al. 2011). Consequently, two limitations of our study are that (1) temporal dynamics of brain networks are not captured here, and additionally that (2) our results quantify brain structure over a population sample with an age range of 25–36 years. Thus, since some age-dependent variability in brain structure is bound to exist within our population, the approach implemented here cannot be used to tease out brain structure at some given age value within the interval from 25 to 36 years due to the fact that brain structure variability due to age is confounded here with variability due to other factors (e.g. genetic differences). Nevertheless, our study does offer a representative view of how inter-regional correlations in the adult brain are modulated by brain structure and network properties even though the influence of age upon structure is not resolved here.

Conclusion

We have found that cortical structure and connectivity patterns modulate inter-regional brain correlations differently, and that network-theoretic cortex properties strongly modulate region-to-region covariance. Nevertheless, the inter-regional covariance patterns associated with each of these three types of measures was found to differ appreciably, which appears to contradict the hypothesis that structural correlations are surrogates of connectomic correlations. Consequently, more research into teasing out the properties of structural correlation patterns from those of connectivity networks is required in order to fully clarify the extent to which inter-regional relationships as computed based on correlative brain network translate into analogous relationships driven by physical WM connectivity.

Research Highlights.

• structure and connectivity modulate inter-regional brain correlations differently

• network-theoretic cortex properties strongly modulate region-to-region covariance

• findings can inform computational models of cortical information processing

Abbreviations

DTI

diffusion tensor imaging

FA

fractional anisotropy

Fro

frontal

GM

gray matter

HIPAA

Health Insurance Portability and Accountability Act

IDA

integrated data archive

Ins

insula

Lim

limbic

LOD

lower order design

LONI

Laboratory of Neuro Imaging

MRI

magnetic resonance imaging

Par

parietal

Tem

temporal

Occ

occipital

WM

white matter