Effects of olivo-ponto-cerebellar atrophy (OPCA) on finger interaction and coordination

Abstract

Objectives

We investigated changes in finger interaction and coordination in patients with olivo-ponto-cerebellar atrophy (OPCA) using the recently developed approach to motor synergies based on the principle of motor abundance.

Methods

OPCA patients and control subjects performed sets of maximal and submaximal force production tasks by the fingers of each of the hands. Indices of multi-finger synergies were quantified within the framework of the uncontrolled manifold hypothesis.

Results

The patients showed lower maximal forces, higher indices of finger interdependence (enslaving), and lower indices of multi-finger synergies stabilizing total force in four-finger tasks. In addition, the patients showed an impaired ability to adjust synergies in preparation to a quick action (small and delayed anticipatory synergy adjustments). The synergy indices showed significant correlations with the clinical scores (both UPDRS total motor scores and ataxia related sub-scores). The observed changes in the indices of finger interaction and coordination were qualitatively similar to those reported earlier for patients with Parkinson’s disease; however, the magnitude of the changes was much higher in the OPCA group.

Conclusions

These findings fit the hypotheses on the role of the cerebellum in assembling motor synergies and in the feed-forward control of action. They suggest that the synergy index measured in artificial, constrained laboratory tasks may be predictive of more general changes in motor behavior.

Significance

The results suggest that studies of multi-digit synergies may be particularly sensitive to subcortical disorders and may provide a much-needed tool for quantitative assessment of impaired coordination in such patients.

Introduction

Since the classical studies of Babinski (1899), the cerebellum has been implicated in the organization of motor synergies (Thach et al., 1993; Houk et al., 1996; Brandauer et al., 2012). In particular, the notion of distributed processing modules (DPMs) has been introduced by the group of James Houk (Beiser and Houk, 1998; Houk, 2005) to describe neurophysiological circuits involving the basal ganglia (movement initiation) and the cerebellum (specification of parameters of actions). The idea of DPMs is similar to the idea of “brain operators” proposed by Bernstein (1935). Both DPMs and brain operators are assumed to link groups of neurophysiological variables thus facilitating synergy formation. Other research suggests that the cerebellum is also involved in predictive, feed-forward control (Miall, 1998; Nowak et al., 2002; Diedrichsen et al., 2005; Brandauer et al., 2010). These conclusions have been based to a large degree on studies of patients with cerebellar disorders including those with olivo-ponto-cerebellar atrophy (OPCA). OPCA is a variant of multisystem atrophy that describes a group of heterogeneous disorders characterized by a combination of progressive parkinsonism and cerebellar ataxia. It is characterized pathologically by neuronal loss in the ventral pons, inferior olives, and cerebellar cortex (Berciano, 1992).

Recent progress in the understanding of multi-element synergies (reviewed in Latash et al., 2007; Latash, 2010) allows the performance of quantitative assessment of synergies and their feed-forward adjustments in anticipation of a quick action. Synergies have been defined as neural organizations of redundant sets of elements (for example, digits, joints, muscles etc.) that stabilize their combined action (for example, total force and/or total moment of force) by covaried outputs of the individual elements. Analysis of synergies has been performed within the framework of the uncontrolled manifold (UCM) hypothesis (Scholz and Schöner, 1999; reviewed in Latash et al., 2007). According to this hypothesis, variance across repetitive trials within a redundant set of elemental variables (e.g., individual finger forces during multi-finger pressing tasks) may be considered as a combination of “good variance” (V_GOOD) in the space of elemental variables, which does not affect an important performance variable (e.g., total finger force), and “bad variance” (V_BAD), which does. The total variance is the sum of V_GOOD and V_BAD (V_TOTAL = V_GOOD + V_BAD). A synergy is defined as: V_GOOD > V_BAD (each variance is quantified per degree of freedom in the corresponding sub-space). In previous studies, a synergy index has been used to reflect the relative amount of “good variance”: ΔV = (V_GOOD − V_BAD)/V_TOTAL (reviewed in Latash 2010). Recently, consistent changes in the synergy index have been documented in healthy aging, fatigue, and Parkinson’s disease (Shinohara et al., 2004; Olafsdottir et al., 2007; Singh et al., 2010; Park et al., 2011, 2012).

Finger coordination is vitally important in everyday actions and shows early and significant impairment across a variety of neurological conditions, including cerebellar disorders (Gilman, 2000; Fellows et al., 2001). It is important to note that human fingers are non-independent. For example, when a person is asked to press with one finger, other fingers of the hand also produce forces. This phenomenon, addressed as a lack of individuation or enslaving (Zatsiorsky et al., 2000; Lang and Schieber, 2004), gets contributions from various factors including the mechanical coupling among fingers, multi-digit extrinsic hand muscles, and overlapping cortical finger representations (reviewed in Schieber and Santello, 2004; van Duinen and Gandevia, 2011). Recent studies have documented increased enslaving (lower individuation) in patients with Parkinson’s disease (Park et al., 2012) and those with cerebellar disorders (Brandauer et al., 2012), suggesting that subcortical structures also can contribute to the observed patterns of enslaving.

Hypotheses on the role of the cerebellum in feed-forward control of movements primarily have been based on observations of changed anticipatory postural adjustments (APAs, Traub et al., 1980; Cerri et al., 2005) and grip-load force coupling in patients with cerebellar disorders (Bastian, 2006; Nowak et al., 2007; Wolpert et al., 1998). Analysis of synergies allows the quantification of another aspect of feed-forward control. When a person prepares to perform a quick action from a steady state, synergies that stabilized the performance during the steady-state phase show attenuation 150–200 ms prior to the action initiation. This phenomenon, called anticipatory synergy adjustments (ASAs), has been documented for both multi-finger and whole-body actions (Olafsdottir et al., 2005; Shim et al., 2005; Klous et al., 2011). Deficits in ASAs have been documented in healthy elderly and patients with Parkinson’s disease (Olafsdottir et al., 2007; Park et al., 2012). Note that APAs and ASAs are two different types of feed-forward adjustments in preparation to an expected perturbation (Klous et al., 2011; Krishnan et al., 2011). ASAs are associated with changes in co-variation of elemental variables resulting in zero net mechanical effect, while APAs are associated with changes in average across repetitive trials patterns resulting in net force production. Therefore, APAs and ASAs emphasize changes in trend of performance variables and their stability properties, respectively, while both represent features of feed-forward movement control. We would like to emphasize that while ASAs are feed-forward adjustment of synergy parameters, synergies themselves may be based on both feed-forward and feedback mechanisms (Todorov and Jordan, 2002; Latash et al. 2005; Goodman and Latash, 2006).

The purpose of this study was to quantify changes in multi-finger synergies and feed-forward synergy adjustments (ASAs) to action preparation in OPCA patients. Based on the hypothesized role of the cerebellum in motor synergies and feed-forward control, we tested the following hypotheses: (1) Patients with OPCA will show lower indices of multi-finger synergies during constant force production tasks; and (2) These patients will show delayed and reduced ASAs. We also explored possible changes in enslaving and their relation to maximal voluntary force production (cf. Shinohara et al., 2003; Braundauer et al., 2012).

Methods

Subjects

Seven patients with olivo-ponto-cerebellar atrophy (OPCA; age 68.57 ± 7.46 years; 3 females) and nine age-matched control subjects (CS; age 64.11 ± 6.85 years; 4 females) were recruited. As detailed in Table 1, all OPCA diagnoses were based on prominent clinical signs of cerebellar ataxia (difficulty with finger-to-nose and tandem walking), parkinsonian signs/symptoms, and MRI documented pontine and cerebellar atrophy (see Figure 1 for a typical MRI findings, subject # 4, Table 1). No patient was actively taking drugs that could cause either parkinsonian or cerebellar dysfunctions, except one subject (subject #2, who was using vaproic acid) at the time of the evaluation. All participants except one OPCA subject (OPCA #6 in Table 1) were right-hand dominant as determined by the Edinburgh Handedness Inventory. United Parkinson’s Rating Scales (UPDRS)-motor scores were obtained for all OPCA subjects, and the scores were decomposed into ataxia related sub-scores and more parkinsonian-specific sub-scores (Table 2).

Table 1.

Description of the participants

OPCA group
Patient	Gender, M/F	Age, yr	Handedness, R/L	Time since ataxia, yr	UPDRS Motor Score	Other clinical symptoms	Potential confounders	Brain MRI cerebellar pontine atrophy
1	F	66	R	6	29	Hand and chin tremors	History of bipolar disorder	Present per our review
2	F	60	R	12	33	Tremor, bladder & breathing dysfunctions.		Present per our review on Depokate
3	F	64	R	6	26	Bladder, orthostatic hypotension & speech swallow difficulty		Present per medical records
4	M	62	R	5	15	Bladder, speech, sexual disorders and RBD		Prominent per our review
5	M	62	R	7	16	Speech problem and bladder problem		Prominent per our review
6	M	76	L	5–10	9	---		Moderate to severe per our review
7	M	73	L	6	39	Swallow difficulty		Prominent per our review

CS group
Control	Gender, M/F	Age, yr	Handedness, R/L
1	F	67	R
2	F	56	R
3	F	66	R
4	F	70	R
5	M	54	R
6	M	60	R
7	M	61	R
8	M	68	R
9	M	75	R

Figure 1.

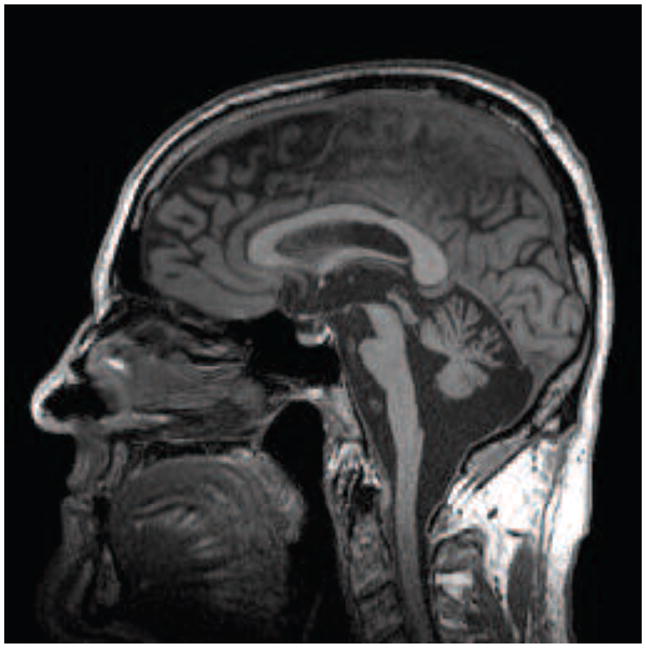
The MRI sagittal image of the brain of patient 4 in Table 1. Note the neuronal loss in the ventral pons and cerebellar cortex

Table 2.

Patient comparisons between the studies of OPCA and Parkinson’s disease

n	PD group (Park et al., 2012)	OPCA group
	10	7
	UPDRS - Total score (mean ± SD)	11.6 ± 4.4	23.9 ± 10.8
UPDRS - Ataxia score (mean ± SD)	7.6 ± 2.8	18.1 ± 6.8
UPDRS - No ataxia score (mean ± SD)	4.0 ± 3.7	5.9 ± 4.9

Means and standard deviations (SD) of the United Parkinson’s Rating Scales (UPDRS)-motor score (total score) and its ataxia-related score (ataxia score) and parkinsonian-specific score (no-ataxia score) in the OPCA group and the Parkinson’s disease (PD) group in the previous study (Park et al., 2012).

Apparatus

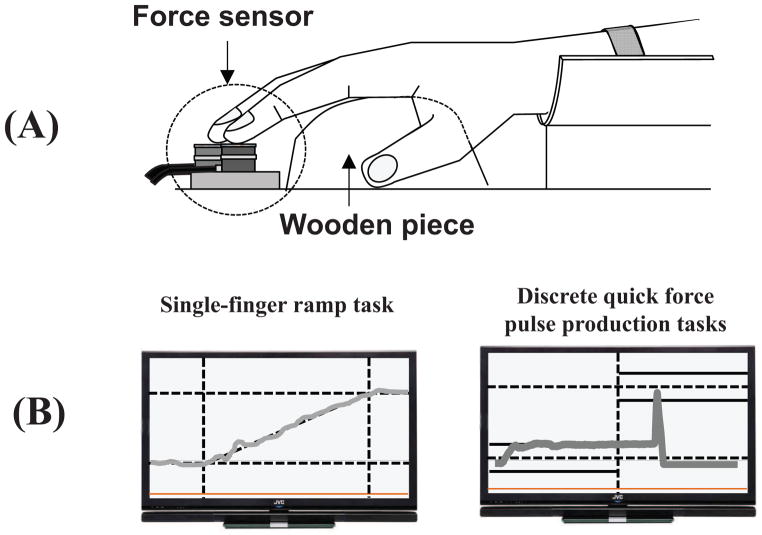
Four force sensors (Model 208A03, PCB Piezotronics Inc., Depew, NY, USA) were used to measure fingertip pressing forces in the vertical direction (Fig. 2A). The contact surface of each sensor was covered with sandpaper (300-grit) to increase friction and the sensors were affixed to a wooden panel (for details of the apparatus see Olafsdottir et al., 2007; Park et al., 2012). Their positions were adjusted in the medio-lateral and anterior-posterior directions to match individual hand and finger anatomy. A wooden piece was placed underneath the subject’s palm in order to maintain a constant hand and finger configuration during the tests. A customized LabView program was written to digitize force signals from the sensors. The sampling frequency was set at 200 Hz with a 16-bit resolution.

Figure 2.

A: The experimental setup. The subjects placed their palm on a wooden piece. The force sensors (gray cylinders) were attached to a wooden frame. B: The feedback during single-finger ramp tasks (left) and discrete quick force pulse production tasks (right).

Experimental procedures

Subjects sat in a chair facing a 19-inch computer screen (Fig. 2B) positioned at eye level. The monitor showed real-time finger force feedback. Both hands were tested in a random order. The forearm of the tested side was strapped into the wrist-forearm brace to avoid forearm and wrist movement during trials. Prior to each trial, all sensor signals were set at zero when subjects placed their fingertips on the sensor centers and relaxed their hand. As a result, only active downward forces were measured by the sensors. The experiment consisted of three blocks including (1) maximal voluntary contraction (MVC) tasks, (2) single-finger ramp tasks, and (3) quick force pulse production tasks. An experimenter demonstrated the experimental procedures to subjects, and subjects were given ample practice (2–5 min) prior to each block.

Maximal voluntary contraction (MVC) tasks

The MVC force of the four fingers (MVC_TOT) was measured for both hands. Subjects were instructed to press on the sensors with the four fingers and produce maximal total force within 8 s. The subjects were instructed to relax immediately after reaching a maximal force and not to maintain the maximal force for more than one second. Two attempts were performed by each hand, and the trial with the higher MVC level was selected to set further tasks.

Single-finger ramp tasks

During single-finger ramp tasks, the computer screen showed a force template and subjects were asked to match it with force produced by an instructed finger. The 20-s template consisted of a horizontal segment at zero force for the first 4 s, followed by a slanted line from 0% to 40% of the peak force of the task finger in the MVC task over the next 12 s, followed by another horizontal segment for the last 4 s. Subjects were asked to pay attention to the force production of the task finger only, while keeping all other fingers (non-task fingers) on the sensors at all times.

Discrete quick force pulse production tasks

The computer screen showed two horizontal lines corresponding to 5% of MVC_TOT and 25% of MVC_TOT with ±5% MVC error margins. Subjects were instructed to press on the sensors with all four fingers and match their total force, F_TOT, with the initial force level as accurately as possible. After 5 s (shown by a vertical line on the screen), the task was to produce in a self-paced manner a very quick force pulse to the target. The target force levels (e.g., 5% of MVC_TOT and 25% of MVC_TOT) were visible at all times on the computer screen. Each subject performed at least 25 trials with each hand. Additional trials were given if the subject made a major mistake (for example, pressing before the cursor reached the vertical line, pressing several times within one trial, or changing the baseline force slowly in preparation to pressing).

Data analysis

The force data were digitally low-pass filtered with a zero-lag, 4^th-order Butterworth filter at 10 Hz. The data processing was done with a customized Matlab code.

Enslaving matrix (E)

The enslaving matrix (E) reflects the unintentional force production by non-task fingers when an instructed finger produces force. For each single-finger ramp trial, linear regressions of the forces produced by each finger against F_TOT over a 10-s time interval were computed. The first and last 1-s intervals were excluded to avoid edge effects. The regression coefficients in F_i,j = f_i⁰ + k_i,j · F_TOT,j were used to construct:

$$\mathbf{E}=\left[\begin{array}{llll}\hfill k_{I,I}\hfill & \hfill k_{I,M}\hfill & \hfill k_{I,R}\hfill & \hfill k_{I,L}\hfill \\ \hfill k_{M,I}\hfill & \hfill k_{M,M}\hfill & \hfill k_{M,R}\hfill & \hfill k_{M,L}\hfill \\ \hfill k_{R,I}\hfill & \hfill k_{R,M}\hfill & \hfill k_{R,R}\hfill & \hfill k_{R,L}\hfill \\ \hfill k_{L,I}\hfill & \hfill k_{L,M}\hfill & \hfill k_{L,R}\hfill & \hfill k_{L,L}\hfill \end{array}\right],$$

where i = {I, M, R, L} and j = {I, M, R, L}; j represents a task finger. F_i,j and F_TOT,j indicate the individual i-finger force and F_TOT, respectively, when j-finger was the task-finger. An overall index of enslaving, EN_j, was computed for each finger as the average k_i,j across the non-task fingers when j-finger was the task-finger: EN_j = Σ_i k_i,j/3, (i ≠j), where i, j = {I, M, R, L}.

Discrete quick pulse force production tasks

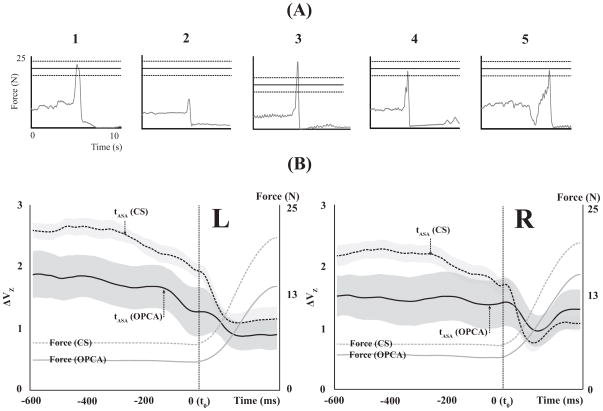
The trials with the following errors were excluded from further analysis: The peak force (F_PEAK) was outside the ± 5% error margins of the target force, the time to peak force was over 1 s, the baseline force was not stabilized prior to pressing, and/or the force pulse showed multiple peaks (Fig. 3A). The following variables were computed only for the accepted trials.

Figure 3.

A: Typical examples of an accepted trial (left plot) and rejected trials because of low F_PEAK, high F_PEAK, multiple force peaks, and drift in the baseline force prior to the force pulse. B: The total force (gray lines) and synergy index (black line, z-transformed ΔV, ΔV_Z) of the left (L) and right hands (R) for the OPCA subjects (OPCA, solid line) and control subjects (CS, dashed line) during the discrete quick force production tasks. Averages and standard errors across the OPCA and CS groups are presented for the synergy index (ΔV_Z), and the averages across each group are presented for the total force.

The time (t₀) of initiation of F_TOT change was defined as the time when the first derivative of force (dF/dt) reached 5% of its peak value in that particular trial. The time to reach F_PEAK (t_PEAK) was defined as the time of F_PEAK with respect to t₀.

An index of multi-finger force stabilizing synergy was computed within the framework of the uncontrolled manifold (UCM) hypothesis (Scholz and Schöner, 1999; for computational details see Latash et al., 2001; Park et al., 2012). First, all the accepted trials for each hand and each subject were aligned with respect to t₀. Second, finger forces were transformed into finger modes (m) with the help of the E matrix. The variance in the m space across trials was quantified separately in two sub-spaces for each time sample. The first sub-space (UCM) corresponded to no changes in F_TOT. The second sub-space was the orthogonal complement (ORT) to the UCM; variance within ORT changed F_TOT. The two variance components (V_UCM and V_ORT) were further combined into a single metric, a synergy index, ΔV, which was computed for each time sample and formed a time function: $\mathrm{\Delta }V(t)=\frac{V_{\mathit{UCM}}(t)/3-V_{\mathit{ORT}}(t)/1}{V_{\mathit{TOT}}(t)/4}$, where each variance index is normalized by the number of degrees- of-freedom in the corresponding spaces; V_TOT stands for total variance.

Note that ΔV > 0 indicates a F_TOT-stabilizing synergy; a higher ΔV implies a stronger synergy. For further statistical analysis, ΔV was log-transformed (ΔV_Z) using the Fischer transformation applied for the computational boundaries, from −4 to 1.333. The average value and standard deviation (SD) of ΔV_Z were computed for the steady-state interval, {−600; −400 ms} prior to t₀. The time of initiation of changes in ΔV_Z (time of anticipatory synergy adjustment, t_ASA) was defined as the time when ΔV_Z dropped below its average steady-state value by more than two SDs. Negative values of t_ASA mean that ΔV_Z started to drop before the initiation of F_TOT changes (t₀).

Statistics

Standard descriptive statistics and mixed-design ANOVAs with repeated measures were used to explore how the main outcome variables (e.g., MVC, EN, Δ V_Z, t_PEAK, F_PEAK, and t_ASA) were affected by Group (two levels: OPCA and CS) and Hand (two levels: left and right). Variables with computational boundaries were subjected to Fisher’s z-transformation. To explore the relationship between clinical test scores and the synergy index (Δ V_Z), linear regression analysis was performed. Mann-Whitney tests were performed to explore significant effects with Bonferroni p-values adjusted for multiple comparisons (e.g., p < 0.0083 instead of the nominal p < 0.05).

Results

Maximal voluntary contraction (MVC) force and enslaving

The peak force during the four-finger maximal voluntary contraction (MVC) in OPCA subjects was smaller than that in the CS group for both hands (by 26.53% for the right hand and by 39.21% for left hand). These data are presented in Table 3. A two-way repeated measures ANOVA on MVC_TOT with factors Group and Hand showed a main effect of Group [F_[1,14] = 4.87, p < 0.05] without other effects.

Table 3.

Performance characteristics

		MVC (N)		EN (normalized)								Timing Variables (s)
		Left	Right	Left				Right				Left		Right
				ENI	ENM	ENR	ENL	ENI	ENM	ENR	ENL	tASA	tPEAK	tASA	tPEAK
OPCA group	Mean	54.3	47.1	0.071	0.089	0.139	0.133	0.083	0.081	0.126	0.074	−0.128	0.259	−0.048	0.317
	SE	8.0	8.9	0.022	0.019	0.011	0.016	0.032	0.021	0.023	0.013	0.030	0.035	0.031	0.036
Control (CS) group	Mean	73.9	77.5	0.038	0.051	0.123	0.074	0.031	0.040	0.107	0.076	−0.283	0.143	−0.272	0.152
	SE	7.5	8.2	0.004	0.012	0.014	0.013	0.013	0.007	0.022	0.015	0.029	0.011	0.030	0.012

Means and standard errors (SE) of maximal voluntary contraction (MVC) forces, enslaving (EN), the time to reach F_PEAK (t_PEAK), and the time of anticipatory synergy adjustment (t_ASA) are presented. I - index, M - middle, R - ring, L - little fingers, IMRL - all four fingers.

Both groups showed substantial force production by the non-task fingers (enslaving) during single-finger ramp force production tasks. The enslaving index (EN) in the OPCA group was larger than in the CS group for both hands (by 50.49% and by 43.79% for the left and right hand respectively, Table 3). These findings were supported by a three-way repeated measures ANOVA on EN with factors Group, Hand, and Finger, which showed significant main effects for Group [F_[1,14] = 4.61, p < 0.05] and Finger [F_[3,42] = 14.83, p < 0.001] without other effects. Post-hoc comparisons confirmed that EN_I, EN_M < EN_L < EN_R (p < 0.05).

Quick force pulse characteristics

One OPCA subject (OPCA #2 in Table 1) was able to perform this task with the right hand only. On average, the percentage of rejected trials for the OPCA group (mean: 42.0 %; max: 67.9%; min: 16.0%) was larger than that for the CS group (mean: 25.3 %; max: 40.0%; min: 4.6%). The rather strict screening procedure was used to make sure that erratic trials (for examples see Fig. 3A) did not sway the outcome of the analyses.

Compared to the control group, the OPCA group showed significantly longer time to peak force, t_PEAK (by 80.4%) and SD of t_PEAK (by 104.4%). The difference in t_PEAK between the groups was about 120 ms for the left hand and 160 ms for the right hand (OPCA > CS, Table 3). Also, average t_PEAK for the left hand was smaller than that for the right hand. These findings were supported by two-way ANOVA on the average and SD of t_PEAK with factors Group [main effects, F_[1,13] = 18.84, p < 0.01 for average t_PEAK; F_[1,13] = 13.58, p < 0.01 for SD of t_PEAK] and Hand [main effects, F_[1,13] = 5.43, p < 0.05 for average t_PEAK]. For the peak force magnitude (F_PEAK), there was no difference between the two groups in average F_PEAK, whereas the OPCA group showed a higher SD of F_PEAK across trials (p < 0.05).

Multi-digit synergies and ASAs

Both OPCA and CS groups showed positive ΔV indices during steady-state force production. The magnitude of ΔV_Z (z-transformed ΔV) at steady-state in the OPCA group was smaller than in the CS group for both hands (by ~35%). In addition, ΔV_Z in the left hand was larger than in the right hand for both groups (Fig. 3B). ANOVA showed significant main effects of Group [F_[1,13] = 6.75, p < 0.05] and Hand [F_[1,13] = 5.94, p < 0.05] without a Group × Hand interaction. <Figure 3 about here>

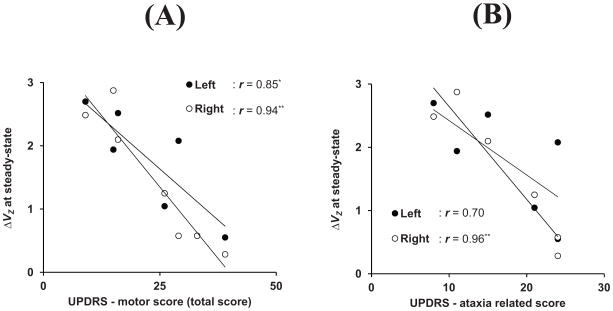
There were significant correlations between ΔV_Z at steady-state and the clinical UPDRS total score as well as with the ataxia-related sub-score within the OPCA group (Figures 4A and 4B, respectively).

Figure 4.

Relationships between the synergy index (ΔV_Z) during steady-state force production and UPDRS total score (panel A) and ataxia-related score (panel B) within the OPCA group. Open and closed circles represent individual OPCA subject data computed for the right (n = 7) and left hands (n = 6), respectively. The coefficients of correlation (r) are shown (* - p < 0.05; ** - p < 0.01).

The CS group showed an earlier drop in ΔV_Z in preparation to the force pulse as compared to the OPCA group (on average by 180 ms, Fig. 3B and Table 3). The magnitude of the drop, Δ V_t0-ss was larger in the CS group (by about of 68.5%). These findings were supported by two-way repeated-measures ANOVAs on t_ASA and Δ V_t0-ss, which showed a significant main effect of Group [F_[1,13] = 38.32, p < 0.001 for t_ASA; F_[1,13] = 6.25, p < 0.05 for Δ V_t0-ss] without other effects.

Discussion

The results of our study support the two hypotheses formulated in the Introduction. In particular, patients with OPCA showed lower indices of multi-finger synergies during constant force production tasks as compared to the CS group. In addition, the patients showed anticipatory synergy adjustments (ASAs) that both were delayed and reduced in magnitude. The relative differences between the OPCA group and the CS group were larger than those reported earlier in a study of patients with Parkinson’s disease (Park et al., 2012). In addition, the OPCA patients showed significantly reduced maximal voluntary contraction (MVC) forces and significantly increased indices of unintended force production by non-instructed fingers (enslaving, cf. Brandauer et al., 2012). In the following sections, we discuss the implications of these results and the role of subcortical structures, particularly the cerebellum, in motor synergies and aspects of feed-forward control.

The term “synergy” has been used for over 100 years to describe coordinated motor actions by sets of elements such as joints, muscles, digits, etc. (Babinski 1899; Rispal-Padel et al., 1981; Thach et al., 1993). Most commonly, this term has been used to describe parallel changes in muscle activation levels over time and/or across repetitive trials (Ting and Macpherson, 2005; Tresch and Jarc, 2009; Roh et al., 2011). Only recently an explicit, operational definition has been introduced that allows identifying and quantifying synergies in relation to stability properties of motor actions (Latash et al., 2007). Within this framework (the principle of abundance, Gelfand and Latash, 1998; Latash, 2012), synergies are task-specific neural organizations that ensure both stable and flexible motor performance with respect to functionally important variables. To our knowledge, this study is the first to quantify the differences in synergies between OPCA patients and healthy controls using this definition.

Impaired multi-digit synergies may be expected to lead to functional consequences such as deficient grasping (cf. Rost et al., 2005; Brandauer et al., 2008) that may interfere with stability of everyday actions relying on the hand function. The finding of such impaired synergies also may be indicative of a more general problem with organizing motor synergies not limited to multi-digit coordination. In the previous study of patients with Parkinson’s disease (Park et al., 2012), we did not detect significant correlation between UPDRS scores and synergy indices. This could be at least partially related to the selection of early-stage patients and the narrow range of UPDRS scores in that study. UPDRS scores (especially the ataxia related measurements) of OPCA subjects in the current study were much larger on average and wider in range as compared to the scores in Park et al. (2012). The finding of the significant correlations between the indices of the force stabilizing synergies and UPDRS total motor scores and ataxia-related sub-scores within the OPCA group suggests that, indeed, the synergy index measured in our artificial, constrained laboratory tasks may be predictive of more general changes in motor behavior. Our current data lend further support to the role of the cerebellum in synergy formation. Additional studies are warranted to further refine the role of the basal ganglia and cerebellar circuits in synergic mechanisms.

Another factor that may compromise flexible patterns of digit involvement is the increased enslaving (low finger individuation). Note that in the current study, the increased enslaving in the OPCA group was associated with a drop in the MVC force. Earlier studies documented parallel changes in the MVC and enslaving indices in healthy individuals: Both indices are lower in older persons as compared to younger persons and in females as compared to males (Shinohara et al., 2003). Our findings suggest that subcortical disorders associated with OPCA lead to violation of this general rule.

Cerebellar disorders have been linked to deficits in feed-forward control of muscle activations (Bastian, 2006; Cerri et al., 2005; Nowak et al., 2002, 2007; Wolpert et al., 1998). We provide evidence for a deficit in another component of feed-forward control, namely anticipatory synergy adjustments (ASAs, Olafsdottir et al., 2005). The purpose of ASAs is to attenuate stabilization of a performance variable by a synergy in preparation to a quick change in that variable. Otherwise, the actor would be forced to fight his/her own synergy, which resists changes in the variable. This may be a reason for slower actions by persons with reduced ASAs. In our study, we observed significantly slower force pulses associated with reduced ASAs in the OPCA group (see also Konczak et al., 2010; Park et al., 2012). The differences between the two groups were similar to those reported in comparisons of older vs. younger persons (Olafsdottir et al., 2007) and patients with Parkinson’s disease vs. healthy controls (Park et al., 2012). The consistency of these results across several studies suggests that ASAs are a major component of the motor function.

We would like to emphasize the qualitative difference in the studies of synergies of patients with cortical and subcortical disorders. Reisman and Scholz (2003) reported no major changes in synergy indices during reaching movements by the ipsi-and contra-lesional hands of stroke survivors, whereas the overall performance of the contra-lesional hand was severely impaired. In the current study, as well as in an earlier study of patients with Parkinson’s disease (Park et al., 2012), we observed relatively mild differences in performance accompanied by significant deficits in the associated synergies. These results suggest that studies of synergies may be particularly sensitive to subcortical disorders, provide a much-needed tool for quantitative assessment of impaired coordination in such patients, and understand the differential yet synergistic role of basal ganglia and cerebellum.

Highlights.

1. Patients with olivo-ponto-cerebellar atrophy (OPCA) show lower maximal voluntary force and higher indices of enslaving (lower finger individuation).

2. Patients with OPCA show lower indices of multi-finger synergies in force production tasks and impaired ability to adjust synergies in a feed-forward fashion.

3. Indices of motor synergies are highly sensitive to subcortical disorders.