Accurate Calculations of Binding, Folding, and Transfer Free Energies by a Scaled Generalized Born Method

Abstract

The Poisson-Boltzmann (PB) equation is widely used for modeling solvation effects. The computational cost of PB has restricted its applications largely to single-conformation calculations. The generalized Born (GB) model provides an approximation at substantially reduced cost. Currently the best GB methods reproduce PB results for electrostatic solvation energies with errors at ~5 kcal/mol. When two proteins form a complex, the net electrostatic contributions to the binding free energy are typically of the order of 5 to 10 kcal/mol. Similarly, the net contributions of individual residues to protein folding free energy are < 5 kcal/mol. Clearly in these applications the accuracy of current GB methods is insufficient. Here we present a simple scaling scheme that allows our GB method, GBr⁶, to reproduce PB results for binding, folding, and transfer free energies with high accuracy. From an ensemble of conformations sampled from molecular dynamics simulations, five were judiciously selected for PB calculations. These PB results were used for scaling GBr⁶. Tests on the binding free energies of the barnase-barstar, GTPase-WASp, and U1A-U1hpII complexes and on the folding free energy of FKBP show that the effects of point mutations calculated by scaled GBr⁶ are accurate to within 0.3 kcal/mol of PB results. Similar accuracy was also achieved for the free energies of transfer for ribonuclease Sa and insulin from the crystalline phase to the solution phase at various pH’s. This method makes it possible to thoroughly sample the transient-complex ensemble in predicting protein binding rate constants and to incorporate conformational sampling in electrostatic modeling (such as done in the MM-GBSA approach) without loss of accuracy.

I. Introduction

Electrostatic interactions make important contributions to fundamental properties such as protein binding free energy, protein folding stability, and protein solubility. Point mutations and variations of salt concentration and pH are often used to probe such contributions. Computational methods that reliably predict those energetic effects are highly desirable, both for elucidating the underlying physical principles and for protein design. Developing such methods is a formidable task, since the free energy of binding, for example, is a small difference between two large quantities, namely the free energy due to interactions within the complex in the solvent environment and the solvation energy of the subunits in the unbound state. The effects of point mutations on the free energy of binding or folding are even smaller. The Poisson-Boltzmann (PB) equation^1–8 has found great success in modeling electrostatic contributions to mutational effects on protein binding free energy^9–12 and protein folding stability^13–15. We have also been able to use the PB equation model the effects of salt and pH on protein solubility.^{16, 17} However, the computational cost of solving the PB equation presents a major stumbling block.

There has been some efforts devoted to the development of fast PB methods.^{4, 6} An alternative that holds great promise is the generalized Born (GB) model,¹⁸ which approximates the PB equation at substantially reduced computational cost. Considerable efforts have been invested on developing GB methods that would hold down the computational cost but have great accuracy in reproducing the PB results.^19–26

The reduced computational cost of the GB model opens new avenues for more realistic modeling of electrostatic effects, such as the inclusion of protein conformational sampling.²⁷ However, the small magnitudes of electrostatic contributions to binding and folding free energies pose a challenging demand on the accuracy of calculations. Up to date, the errors of the best GB methods in reproducing PB solvation energies are about 0.5% in relative terms, or roughly several kcal/mol in absolute terms.^{26, 28} The scatter of these errors among different proteins also appears to be random.

The electrostatic contributions to protein-protein binding free energies typically have an order of magnitude of 10 kcal/mol.^{9, 10} Therefore even the current most accurate GB methods (when benchmarked against PB results) may be inadequate for predicting binding free energy. One idea for improving accuracy is to reparameterize GB methods against PB results. One such attempt was made in calculating protein-ligand binding free energy²⁹, using PB results for a subset of ligands as training data, but the error (as measured against PB results) in that work was still relatively large, about 5 kcal/mol. In fact, our recently developed GB method²⁶, GBr⁶, has even smaller errors on protein-protein binding free energies (~1 kcal/mol for protein complexes studied here) without any reparameterization.

Here we take a different approach to GB reparameterization. The aim of the reparameterization is to allow for conformational sampling in electrostatic modeling. For each protein or protein complex, we generate an ensemble of conformations from molecular dynamics simulations. The raw GB result for the solvation energy of each conformation in the ensemble is calculated, and five conformations are selected to be representative of the variations in solvation energy of the ensemble. PB results for the solvation energies of the five representative conformations are then calculated and used for scaling the corresponding raw GB results. The scaling factor is finally applied to the rest of the conformation ensemble. Accuracy of the scaling method is assessed by comparing the scaled GB results and PB results for the whole ensemble. While the scaling method is applicable to any GB method, we report here results for GBr⁶. We refer to the reincarnation scaled GBr⁶, or sGBr⁶ in short.

We test scaled GBr⁶ on a number of applications. Mutational and salt effects on the binding free energies are calculated for four protein-protein and protein-RNA complexes. To assess the accuracy of scaled GBr⁶ for calculating mutational effects on folding free energy, 26 mutants of the FK506-binding protein (FKBP) are studied. In addition, scaled GBr⁶ is used to calculate the pH dependence of solubility of two proteins, ribonuclease Sa and insulin.

As another important application, we use scaled GBr⁶ to calculate the electrostatic interaction energy of the transient complex along the protein-protein association pathway, which predicts the electrostatic enhancement of the protein binding rate.^30–33 The transient complex consists of an ensemble of configurations, each of which presents a slightly different relative separation and relative orientation between the two subunits in a complex. Four pairs of binding proteins are studied.

In all these applications, we show that the relevant small differences in electrostatic solvation energy obtained by scaled GBr⁶ are accurate to within 0.3 kcal/mol of the corresponding PB results. These diverse applications illustrate the wide utility of our GB scaling approach.

II. Theory

In previous studies, we have described the theoretical models for calculating electrostatic contributions to free energies of protein binding^{9, 10} and folding,^{13, 14} for calculating the electrostatic rate enhancement of protein binding,^30–33 and for calculating the pH dependence of protein solubility.¹⁷ Here we give brief outlines of these models.

2.1 Binding free energy

When two proteins, A and B, bind to form a complex C, the electrostatic contribution to the binding free energy is calculated as

$$\mathrm{\Delta }{G}_{\mathrm{b}}=G_{\text{el}}(\mathrm{C})-G_{\text{el}}(\mathrm{A})-G_{\text{el}}(\mathrm{B}),$$ (1)

where G_el(X), X = A, B, or C, is the electrostatic free energy of molecule X. G_el(X) can be decomposed into a Coulomb term and a solvation term:

$$G_{\text{el}}(\mathrm{X})=G_{\text{Coul}}(\mathrm{X})+G_{\text{solv}}(\mathrm{X}).$$ (2)

By this decomposition, ΔG_b has a Coulombic component and a solvation component. These will be denoted as ΔG_{b; Coul} and ΔG_{b; solv}, respectively. When a point mutation is introduced, ΔG_b can be calculated for the wild-type (wt) pair of proteins and for the mutant (mt) pair. The change in ΔG_b by the mutation is

$$\mathrm{\Delta }\mathrm{\Delta }{G}_{\mathrm{b}}=\mathrm{\Delta }{G}_{\mathrm{b}}(\text{mt})-\mathrm{\Delta }{G}_{\mathrm{b}}(\text{wt}).$$ (3)

2.2 Folding free energy

For protein folding, we are interested in mutational effects on the electrostatic contribution to the folding free energy. It is assumed that, in the unfolded state, individual residues do not interact and hence the contributions of residues other than the one under mutation are the same in the wild-type protein and the mutant. (Residual charge-charge interctions in the unfolded state have been modeled previously.³⁴) Neglecting the electrostatic free energy of the “other” residues in the unfoled state (which does not affect the change in folding free energy by the mutation), the electrostatic contribution to the folding free energy is

$$\mathrm{\Delta }{G}_{\mathrm{f}}=G_{\text{el}}(\text{protein})-G_{\text{el}}(\text{residue}),$$ (4)

where the two terms on the right-hand side represent the electrostatic free energies of the protein in the folded state and the residue under mutation, respectively. The solvation component of ΔG_f will be denoted as ΔG_{f; solv}. The mutational effect on ΔG_f is given by

$$\mathrm{\Delta }\mathrm{\Delta }{G}_{\mathrm{f}}=\mathrm{\Delta }{G}_{\mathrm{f}}(\text{mt})-\mathrm{\Delta }{G}_{\mathrm{f}}(\text{wt}).$$ (5)

Notice that even ΔG_f(wt) is mutant-specific; we will come back to this point in Subsection 3.4.

2.3. pH dependence of solubility

The effect of pH on protein solubility can be calculated from the pH dependence of the transfer free energy of a protein from the condensed phase to the solution phase. Both the solution phase and the condensed phase are modeled as continuum dielectrics, with the dielectric constants taking a value appropriate for water (equal to 78.5 at room temperature) for the former and a value (~55) intermediate between those for water and for the solute protein. The electrostatic component of the transfer free energy, which is what is relevant for determining the pH dependence of solubility, is

$$\mathrm{\Delta }{G}_{\mathrm{t}}=G_{\text{solv}}({\epsilon }_{\mathrm{s}}=78.5)-G_{\text{solv}}({\epsilon }_{\mathrm{s}}=55),$$ (6)

where G_solv(ε_s) is the electrostatic solvation energy of the solute protein in a continuum solvent with dielectric constant ε_s. This result uses the fact that the Coulomb term is the same in both phases. G_solv(ε_s) at each pH was calculated by averaging over conformations sampled from constant-pH molecular dynamics simulations.

2.4 Electrostatic rate enhancement

According to the transient-complex theory,^{30, 32, 33} the rate constant for the association of two proteins under diffusion control can be predicted as

$$k_{\mathrm{a}}=k_{\mathrm{a}0}{e}^{-\mathrm{\Delta }{G_{\text{el}}}^{*}/k_{\mathrm{B}}T},$$ (7)

where k_a0 is a basal rate constant and ΔG_el* is the electrostatic interaction energy of the proteins in the transient-complex ensemble. ΔG_el* is calculated as the average over configurations representing the transient complex. For each configuration, the electrostatic interaction energy is as defined by eq (1), except that C now represents the transient-complex configuration.

III. Computation Details

3.1 Generation of conformational ensembles

For calculating electrostatic contributions to protein binding and folding free energies by scaled GBr⁶, conformations were generated by explicit-solvent molecular dynamics (MD) simulations. Four protein-protein and protein-RNA complexes were studied: an enzyme-inhibitor complex formed by barnase and barstar; complexes formed the Wiskott-Aldrich Syndrome protein (WASp) with two homologous Rho GTPases, Cdc42 and TC10; and a protein-RNA complex formed by the U1A protein and stem/loop II of the U1 small nuclear RNA (U1SLII). The first and last complexes were previously studied by PB calculations.^{9, 11} The two GTPase-WASp complexes have been studied experimentally.³⁵ These and other systems studied here are shown in Figure 1.

Figure 1.

Systems studied in the present work. (a)–(c) Complexes of barnase and barstar, WASp and Cdc42, U1A and U1SLII. The first and second subunits are shown in blue and red, respectively. (d) FKBP. (e) Ribonuclease Sa. (f) Insulin hexamer. Mutated residues in (a)–(d) and titrated residues in (e) and (f) are labeled.

The simulation of the barnase-barstar complex was carried out as follows. Starting from the X-ray structure of the complex (Protein Data Bank entry 1brs³⁶), hydrogens, four Na⁺ ions as neutralizing counter ions, and 9,558 TIP3P water molecules were added by the LEAP program in the Amber pakage.³⁷ The side chains of arginine and lysine residues were positively charged, side chains of aspartate and glutamate residues were negatively charged, and side chains of histidine residues were neutral (appropriate for a nominal pH of 7). The force field was ff99SB.³⁸ The solvent (water molecules plus counter ions) was relaxed first by 200 steps of energy minimization and then by 100 ps of MD simulation at a constant pressure MD, all the while the protein complex was fixed. Next, the whole system was energy minimized with decreasing harmonic constraints applied to the protein complex, from 50 kcal/mol·A² to 0, for a total of 2500 steps. The cutoff for the non-bonded interactions was 9 Å, and the particle mesh Ewald method was used to treat long-range electrostatic interactions. The whole system was then heated for 40 ps at constant volume to a final temperature of 298 K. Finally the simulation was continued at constant pressure and temperature. Bond lengths involving hydrogen atoms were restrained by the SHAKE algorithm³⁹ throughout the simulation, allowing a time step of 2 fs. The first 2 ns of the constant pressure and temperature simulation was discarded; thereafter conformations were sampled at every 10 ps, and a total of 548 conformations were collected.

For the Cdc42-WASp complex, an NMR structure with 20 models was available (Protein Data Bank entry 1cee).⁴⁰ We randomly picked five (models 1, 5, 9, 13, and 17) of the 20 to generate conformational ensembles. No structure for the TC10-WASp complex was available. We modeled its structure by aligning the structure of unbound TC10 (Protein Data Bank entry 2atx³⁵) to Cdc42 in the five NMR models of the Cdc42-WASp complex. From these 10 starting structures (five for each complex), MD simulations were carried out following the protocol for the barnase-barstar complex. For each of the 10 simulations, 100 conformations were sampled at every 10 ps after discarding the first 1 ns of the constant pressure and temperature simulation.

The starting structure for the U1A-U1SLII complex was as prepared in our previous study.¹¹ 100 conformations were sampled at every 20 ps after discarding the first 2 ns of the constant pressure and temperature simulation.

FKBP was chosen as a model system for folding because it is a protein being studied experimentally in our laboratory.⁴¹ We have accumulated experimental data for the effects of a large number of charge mutations on the folding stability (J. Batra, HT, and HXZ, to be published). The same mutations are the targets of the present study. Starting from the X-ray structure (Protein Data Bank entry 1fkb⁴²), the MD simulation of FKBP followed the protocol for the barnase-barstar complex. 200 conformations were sampled at every 15 ps after discarding the first 1 ns of the constant pressure and temperature simulation.

Previously we have used PB calculations to predict the pH dependences of the solubility of two proteins, ribonuclease Sa and insulin.¹⁷ The transfer free energy from the condensed phase to the solution phase was calculated by averaging over conformations sampled from constant-pH MD simulations, which were based on the GB model.⁴³ For testing scaled GBr⁶, here we simply took the conformations generated in our previous work and used the PB results calculated there as the benchmark. We just point out that 100 conformations were collected at each of nine pH values (2.3, 2.9, 3.6, 4.0, 4.5, 4.8, 5.0, 5.2, and 5.4) for ribonuclease Sa and at each of eight pH values (4.0, 4.5, 5.0, 5.5, 5.75, 6.25, 6.75, and 7.0) for insulin.

We have obtained PB results for the electrostatic interaction energies of the transient complexes of four protein pairs, formed by barnase and barstar, interleukin-4 (IL4) and interleukin-4 binding protein (IL4BP), colicin E9 and immunity protein 9 (Im9), and acetylcholinesterase (AChE) and fasciculin (fas).^30–32 Each transient complex was represented by 100 configurations, generated by sampling in the six-dimensional space of relative translation and rotation (the conformations of the two subunits were held fixed). Here we used the same configurations and the PB results to test scaled GBr⁶.

3.2 Mutation protocol

In the present work mutational effects on binding free energy were calculated for the barnase-barstar complex, the two GTPase-WASp complexes and the U1A-U1SLII complex. Similarly mutational effects on folding free energy were calculated for FKBP. Mutations were modeled on each of the conformations collected from MD simulations of a “wild-type” protein or protein complex, and the protocol for mutation was the same as developed previously in single-conformation studies.^{9, 11, 13, 14} Briefly, for each single mutation, the LEAP program was used to replace the wild-type side chain with the mutant side chain. The new side chain was then energy minimized in vacuum (while holding the rest of protein or protein complex fixed) up to 50,000 steps. Multiple mutations were decomposed into a series of single mutations.

The 17 mutations on the barnase-barstar complex studied previously⁹ were also the target of the present work. Of these, 11 are single mutations (bnK27A, bnD54A, bnR59A, bnE60A, bnR83Q, bnR87A, bnH102A, bsD35A, bsD39A, bsE76A, and bsE80A; bn and bs refer to barnase and barstar, respectively). The remaining 6 are double mutations (bnK27A/bsD39A, bnR59A/bsD35A, bnR59A/bsE76A, bnR59A/bsE80A, bnR83Q/bsD39A, and bnR87A/bsD39A). Similarly, seven single mutations (R7Q, K20Q, K22Q, K23Q, K50A, K60Q, and R70Q) on the U1A in its complex with U1SLII, studied previously,¹¹ were the target of the present work.

For the Cdc42-WASp complex, the present study covered of a total of 10 mutations. Of these, 7 were single mutations (E49K on Cdc42, K230A, K230E, K231A, K231E, K232A, and K232E on WASp), 1 was a double mutation (E49K/E178K on Cdc42), and 2 were triple mutations (K230A/K231A/K232A and K230E/K231E/K232E on WASp). Two mutations were studied on the TC10-WASp complex: K63E and K63E/T192E; both are on TC10. For the purpose of making error assessment on scaled GBr⁶, we group together the 12 mutations on the two related GTPase-WASp complexes.

We studied 26 mutations on FKBP to find their effects on the folding free energy. These include 17 single, 5 double, 2 triple, 1 quadruple, and 1 quintuple mutation (listed on Figure 6 below).

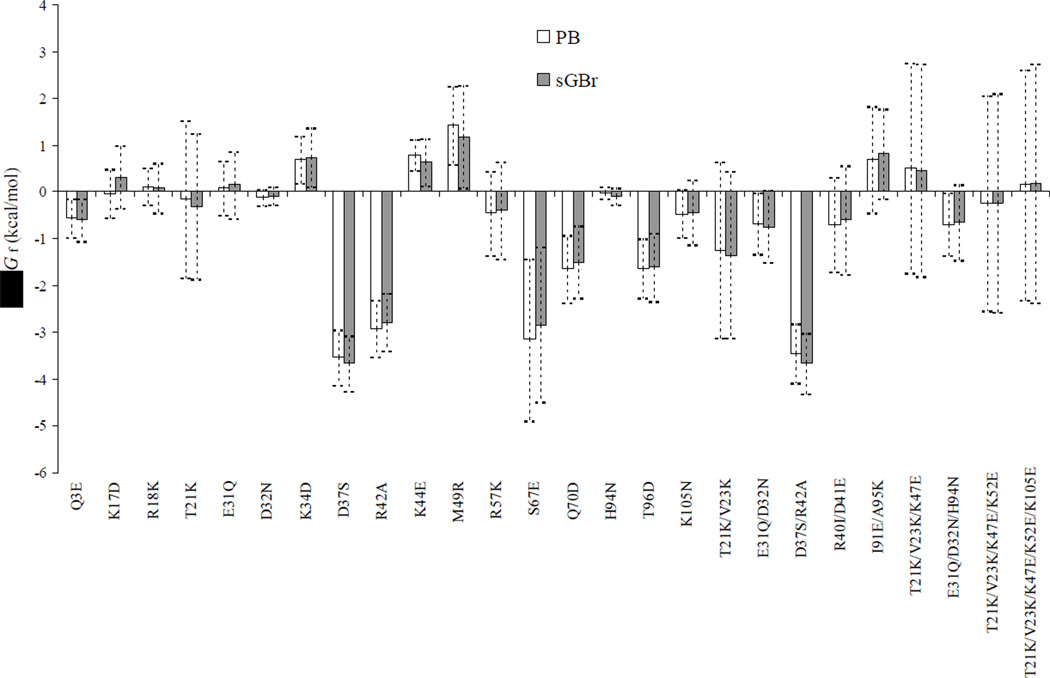
Figure 6.

Comparison of scaled GBr⁶ and PB results for ΔΔG_f of 26 mutations on FKBP. Error bars indicate standard deviations within the conformational ensemble.

3.3 PB and GB calculations

The PB results for benchmarking scaled GBr⁶ on pH dependence of protein solubility and on electrostatic interaction energy of transient complex were available from previous studies.^{17, 31} PB results for electrostatic contributions to binding and folding free energies were newly calculated here on the conformational ensembles described above. The calculations were done by the UHBD program² following a previously established protocol.^{9, 11, 13, 14} In particular, the dielectric boundary between the protein or RNA low dielectric and the solvent high dielectric was specified by the van der Waals surface instead of the more popularly used molecular surface. We have had most success with the former surface in comparing PB calculations with experimental results for mutational effects on protein folding and binding free energies^{9–11, 13, 14} and for electrostatic enhancement of protein binding rates.^{32, 33} The van der Waals surface is also what is modeled into our GB method, GBr⁶.²⁶

Mutational effects on the barnase-barstar binding free energy were calculated for an ionic strength of 25 mM. In addition, PB and GB calculations were also carried out for the wild-type complex at ionic strengths of 50, 125, 225, 325, 525, and 1000 mM to test scaled GBr⁶ on salt effects. The ionic strengths for PB and GB calculations were 100 mM for the GTPase-WASp complexes, 160 mM for the U1A-U1SLII complex, and 150 mM for FKBP. All calculations used the Amber94 atomic partial charges⁴⁴ and Bondi radii (H, 1.2 Å; O, 1.5 Å; N, 1.55 Å; C, 1.7 Å; S and P, 1.8 Å).⁴⁵ Except for the U1A-U1SLII complex, all PB results were obtained by solving the linearized PB equation. For the protein-RNA complex, the full PB equation was solved due to the high charges on the system. We have developed a version of GBr⁶ called GBr⁶NL,⁴⁶ which mimics the full nonlinear PB equation. However, since the nonlinear PB equation has not been modeled by other GB methods and our scaling-based reparameterization was intended for GB methods in general, even for the U1A-U1SLII complex we used raw GBr⁶ results for scaling. (We did use the nonlinear PB results for the U1A-U1SLII complex to test the scaling method on GBr⁶NL. As expected, the raw GBr⁶NL results had slightly less deviations from the PB targets than the raw GBr⁶ results, but the scaling method worked equally well for the two GB versions.)

3.4 GB scaling protocol

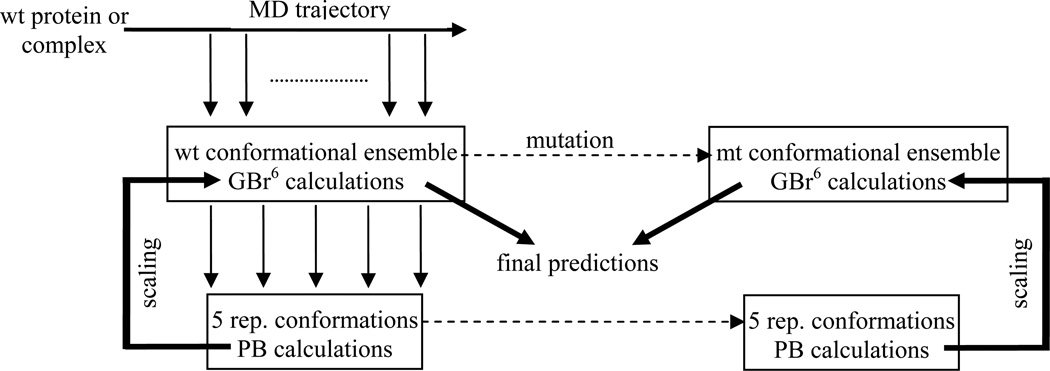
Rather than refine GBr⁶ internally, our strategy for reparameterization was to take raw GBr⁶ results and post-process them by scaling. The scaling was based on PB results for a small number (five) of conformations judiciously selected as representatives of the conformation ensemble. The selection varied somewhat from application to application, but followed the same overall design, as illustrated in Figure 2.

Figure 2.

Illustration of the scaling protocol.

Let us illustrate the scaling protocol using mutational effects on the binding free energy of a protein complex. First, for each conformation in the ensemble, the raw GBr⁶ result for ΔG_b(wt) was calculated. Then, five conformations were selected for scaling purpose, based on the mean (m) and standard deviation (σ) of the raw GBr⁶ results within the conformational ensemble. The representative conformations had raw GBr⁶ results closest to the following target values: m, m ± 0.5σ, m ∓ 0.75σ, m ± 1.0σ, and m ∓ 1.5σ. The first or second set of signs was chosen depending on whether the actual value of the first conformation was above or below m. Other target values were experimented, but the above values resulted in the best overall performance. We now refer to the raw GBr⁶ results for the solvation component of ΔG_b(wt) as ΔG_GB(i), i = 1 to 5, of the five conformations

The corresponding PB results, ΔG_PB(i), i = 1 to 5, for the five representative conformations were also obtained. The average of the five individual ratios, ΔG_PB(i)/ΔG_GB(i), was finally taken as the factor (λ) for scaling the raw GBr⁶ results of the whole conformational ensemble. The same five representative conformations were also used for calculating the scaling factors of all mutants of the same protein complex. For each mutant, calculating the scaling factor involved again obtaining PB results on the five representative conformations. The ratio ΔG_PB(i)/ΔG_GB(i) could spuriously deviate significantly from 1 when the magnitudes of ΔG_{b; solv} calculated by GBr⁶ or PB on the representative conformations were too small. To prevent the scaling factor from being biased by such spurious ratios, we filtered out ratios outside the range of 0.75 to 1.25. This filtering was triggered only rarely in the present study.

After the scaling factors were separately found for the wild-type complex and each mutant, the mutational effect on the electrostatic contribution to the binding free energy was calculated as

$$\mathrm{\Delta }\mathrm{\Delta }{G}_{\mathrm{b}}=[\lambda (\text{mt})\mathrm{\Delta }{G}_{\text{GB}}(\text{mt})+\mathrm{\Delta }{G}_{\mathrm{b};\text{Coul}}(\text{mt})]-[\lambda (\text{wt})\mathrm{\Delta }{G}_{\text{GB}}(\text{wt})+\mathrm{\Delta }{G}_{\mathrm{b};\text{Coul}}(\text{wt})].$$ (8)

This equation was applied to the individual conformations in the ensemble, all using the same scaling factors λ(mt) and λ(wt). The final, ensemble-averaged, prediction for the mutational effect was taken as average of the results for ΔΔG_b calculated on the individual conformations. The same procedure was also adopted for studying salt effects on the binding free energy. In that case ‘mt’ and ‘wt’ refer to the salt concentration of interest and a reference salt concentration, respectively.

The scaling protocol for mutational effects on the folding free energy was similar. In this case, ΔG_f, as defined in eq (4), was used for scaling. As noted in Subsection 2.2, even ΔG_f(wt) is mutant-specific; therefore, unlike in the case of binding free energy, it is not possible to have one set of five representative conformations that is applicable to all mutants. Instead, for each mutant, the five representative conformations were selected based on GBr⁶ results for ΔG_f(wt). The scaling factors for the wild-type protein and the mutant were then found by obtaining PB results for the solvation components of ΔG_f(wt) ΔG_f(mt) on these five conformations.

Extensions of the scaling protocol to studies of pH dependence of protein solubility and electrostatic rate enhancement were straightforward. For the former we just mention that ΔG_t, the electrostatic component of the transfer free energy, was used for scaling. For the latter study, we mention that the interaction energy ΔG_el* itself, as opposed to its changes by mutation or by salt, was of direct interest.

IV. Results and Discussion

4.1 Importance of conformational sampling

The premise of our method for GB reparameterization is that results calculated from an extensive conformational ensemble are much more reliable than those from a single conformation. It can be argued, from both fundamental and practical points of view, that a conformational ensemble is superior to a single conformation for predicting binding and folding free energies. In mimicking experimental measurements, an ensemble of conformations is obviously more realistic than a single conformation; experimental results are averages over a conformational ensemble under certain solvent conditions. In a statistical sense, the errors of calculation results decrease with increasing size of the conformational ensemble.

We use PB results for the effects of 17 mutations on the binding free energy of the barnase-barstar complex to illustrate the comparison between ensemble and single-conformation predictions. For each mutation, we take the mean value of the PB results for ΔΔG_b over the 548 sampled conformations as the ensemble prediction. For all the mutants, the ranges of variation of ΔΔG_b within the conformational ensemble were found to be comparable to the magnitudes of the mean ΔΔG_b values (Table 1). For example, for the barnase R59A mutation, PB results for ΔΔG_b among the 548 conformations varied from 3.1 to 6.5 kcal, spanning a range of 3.4 kcal/mol. In comparison, the mean ΔΔG_b is 4.8 kcal/mol and the standard deviation is 0.6 kcal/mol. The fact that, relative to the mean value, the range of variation of ΔΔG_b is large whereas the standard deviation is small provides direct evidence that the ensemble prediction is much more reliable than single-conformation predictions.

Table 1.

PB, sGBr⁶, and experimental results (in kcal/mol) for ΔΔG_b of 17 mutations on the barnase-barstar complex^a

Mutants	PB range	PB m ± sd	sGBr6 m ± sd	Expt
bnK27A	3.97 to 6.77	5.28 ± 0.50	5.34 ± 0.43	5.4
bnD54A	−2.93 to −1.36	−2.05 ± 0.26	−1.91 ± 0.17	−0.9
bnR59A	3.11 to 6.52	4.82 ± 0.57	4.89 ± 0.53	5.2
bnE60A	−1.40 to 0.65	−0.52 ± 0.35	−0.31 ± 0.36	−0.3
bnR83Q	4.08 to 8.82	6.72 ± 0.61	6.69 ± 0.57	5.4
bnR87A	3.89 to 6.20	4.91 ± 0.43	4.84 ± 0.39	5.5
bnH102A	0.28 to 2.39	1.50 ± 0.34	1.55 ± 0.36	6.1
bsD35A	2.17 to 6.13	3.82 ± 0.72	3.92 ± 0.61	4.5
bsD39A	5.56 to 10.32	7.97 ± 0.83	8.05 ± 0.79	7.7
bsE76A	1.92 to 4.83	3.35 ± 0.54	3.37 ± 0.52	1.4
bsE80A	−0.16 to 0.95	0.38 ± 0.18	0.39 ± 0.13	0.5
bnK27A/bsD39A	6.93 to 11.25	9.24 ± 0.83	9.25 ± 0.75	8.2
bnR59A/bsD35A	4.27 to 9.71	7.02 ± 0.89	7.03 ± 0.80	6.3
bnR59A/bsE76A	2.97 to 6.39	4.63 ± 0.58	4.68 ± 0.53	4.9
bnR59A/bsE80A	2.99 to 6.47	4.74 ± 0.60	4.88 ± 0.54	5.1
bnR83Q/bsD39A	6.93 to 11.68	9.36 ± 0.92	9.33 ± 0.91	6.4
bnR87A/bsD39A	5.88 to 10.52	8.17 ± 0.86	8.20 ± 0.80	7.1

^aPB and sGBr⁶ results were calculated on 548 conformations sampled from an MD simulation. Range, m, and sd refer to the range of variation, the mean, and the standard deviation, respectively, of ΔΔG_b among the conformations.

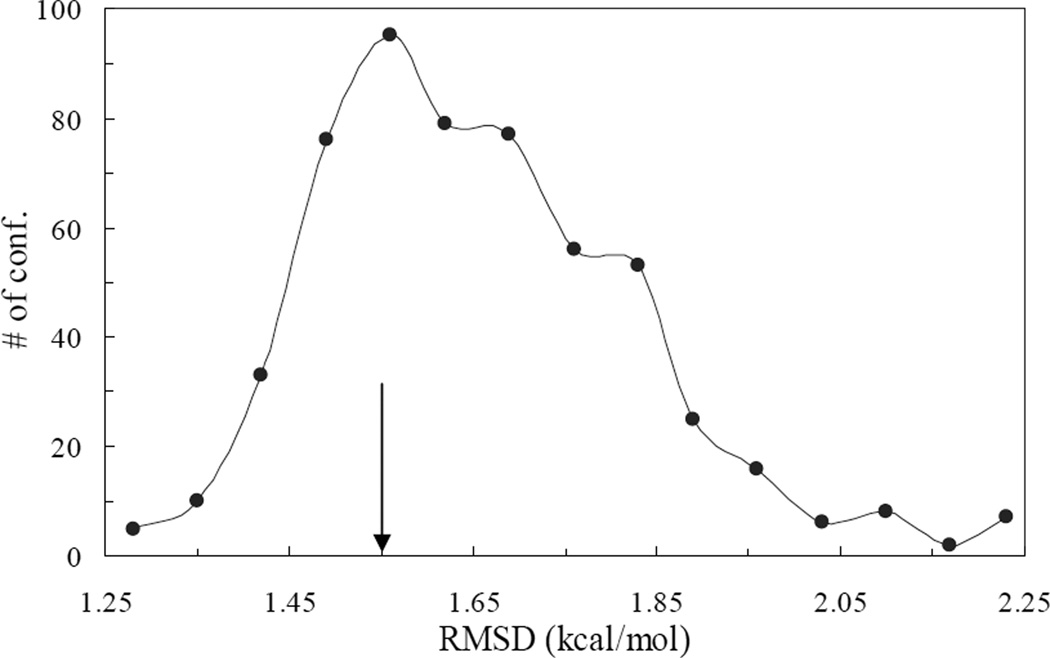
We further assess the ensemble and single-conformation predictions against experimental binding data for the 17 mutations (Table 1).^47–49 For each single conformation, we measure prediction error by the root-mean-square-deviation (RMSD) between PB results for ΔΔG_b and experimental data for the 17 mutations. The errors calculated over the 548 sampled conformations are presented in Figure 3 as a histogram. They range from 1.25 to 2.27 kcal/mol. In comparison, the ensemble prediction has an RMSD of 1.55 kcal/mol from experiment. The latter value places the ensemble prediction in the 31st percentile of the single-conformation predictions. In other words, the probability of a randomly chosen single conformation performing worse than the ensemble is 69%. We thus show that, relative to single-conformation predictions, the ensemble prediction is not only more precise (as measured by standard deviation of the ensemble) but also more accurate (as measured by RMSD from experiment).

Figure 3.

Distribution of PB-experiment difference among 548 conformations of the barnase-barstar complex. On each conformation, PB results for ΔΔG_b of 17 mutations were obtained and their RMSD from experiment was used as the measure of PB-experiment difference. A vertical arrow, at 1.55 kcal/mol, indicates the RMSD of the ensemble prediction.

4.2 Performance of raw GBr⁶

To establish a baseline for assessing the performance of scaled GBr⁶, we first benchmark the original GBr⁶ against PB. For each ΔΔG_b, ΔΔG_f, ΔG_t, or ΔG_el* value, we take the ensemble-averaged PB result as the target and measure error as the deviation of the ensemble-averaged GBr⁶ result from the PB target. When multiple mutants on the same protein or protein complex are studied (for ΔΔG_b and ΔΔG_f results), or when one protein is studied at different pH (for ΔG_t results), we report a single error value, which is given by the RMSD from the PB targets among all the mutants or all the pH values.

The errors of the original GBr⁶ for the various types of calculations are summarized in Table 2. For the barnase-barstar complex, ΔΔG_b errors calculated by GBr⁶ for the 17 individual mutations ranged from 0.1 to 1.9 kcal/mol, resulting in an overall RMSD of 0.85 kcal/mol. Similar ΔΔG_b errors are also seen for mutations on the GTPase-WASp and U1A-U1SLII complexes.

Table 2.

Errors of raw GBr⁶ and sGBr⁶ as measured by deviations from PB results (all in kcal/mol)

System	# of conf.	# of mt or pHa	PB results	GBr6 error	sGBr6 error
ΔΔGb
Bn-Bs	548	17	−2.1 to 9.4	0.85	0.09
GTPase-WASp #1	100	12	−1.2 to 7.9	1.12	0.14
GTPase-WASp #5	100	12	−1.9 to 7.2	1.28	0.19
GTPase-WASp #9	100	12	−1.8 to 8.6	0.95	0.20
GTPase-WASp #13	100	12	−1.5 to 8.3	1.30	0.32
GTPase-WASp #17	100	12	−3.1 to 6.7	1.30	0.32
U1A-U1SLII	100	12	0.1 to 3.1	0.69	0.05
ΔΔGf
FKBP	200	26	−3.5 to 1.4	1.11	0.14
ΔGt
RNase Sa	100	9	−13.8 to −12.5	0.46	0.07
Insulin	100	8	−63.2 to −60.9	6.83	0.34
ΔGel*
Bn-Bs	100		−3.30	2.85	0.07
IL4-IL4BP	100		−3.05	2.94	0.22
E9-Im9	100		−4.33	2.32	0.07
AChE-fas	100		−4.04	4.61	0.06

^aIn ΔΔG_b and ΔΔG_f calculations, multiple mutations on a given protein or protein complex were studied. Error was measured by RMSD among the mutations. In ΔG_t calculations, a given protein was studied at multiple pH values; again RMSD was used as the measure of error.

It is interesting to note that the ΔΔG_b errors seen on these complexes are suppressed by error cancellation between calculations on a complex and calculations on the separate subunits. For example, for the barnase R59A mutation, GBr⁶ overestimated the magnitude of the solvation energy of the complex by 2.22 kcal/mol, and at the same time overestimated the magnitudes of the solvation energies of the two subunits by 2.61 and 0.05 kcal/mol, respectively. Taken together, the net error on ΔG_b(mt) was only 0.44 kcal/mol. While this error cancellation was widely seen on the protein complexes studied here, there is no guarantee that it will always occur. It is possible that, for a given protein complex, GBr⁶ overestimates the solvation energy of the complex but at the same time underestimates the solvation energies of the subunits. In that situation, the errors accumulate rather than cancel. Errors from calculations on a mutant and those on the wild-type complex may also either cancel or accumulate. For the barnase R59A mutation, GBr⁶ errors on ΔG_b(mt) and ΔG_b(wt) occurred in opposite directions, resulting in an accumulative error of 0.64 kcal/mol on ΔΔG_b. On the other hand, for the U1A-U1SLII complex, GBr⁶ errors on ΔG_b(mt) and ΔG_b(wt) occurred in the same direction; otherwise the differences in ΔΔG_b between GBr⁶ and PB, which was from solving the nonlinear PB equation for this particular complex, would have been much greater.

The ΔΔG_f errors calculated by GBr⁶ for the 26 individual mutations on FKBP ranged reached 2.4 kcal/mol. Even though the overall RMSD of 1.1 kcal/mol of all the 26 mutations is only slightly more than what was found above for the mutational effects on the binding free energy of the barnase-barstar complex, the ΔΔG_f errors on FKBP are much more significant. According to PB calculations (see Figure 6 below), of the 26 mutations, 9 changed the folding free energy of FKBP by less than 0.5 kcal/mol, and another 8 by 0.5 to 1.0 kcal/mol; the largest effect of an individual mutation was 3.5 kcal/mol. In contrast, as shown in Table 1 under the “PB m ± sd” heading, only 2 of the 17 mutations on the barnase-barstar complex affected the binding free energy by less than 1.0 kcal/mol; the largest effect of an individual mutation was 9.4 kcal/mol.

The ΔG_t results calculated by GBr⁶ for ribonuclease Sa at nine pH values deviated from their PB targeted by 0.2 to 0.9 kcal/mol, resulting in an overall RMSD of 0.46 kcal/mol. Deviations of such magnitudes are significant because the PB results at the nine pH values differed at most by only 1.3 kcal/mol, and it is these small differences that predict the pH dependence of the solubility.¹⁷ For insulin, the deviations of GBr⁶ results for ΔG_t results at eight pH values were quite large, ranging from 2.5 to 9.3 kcal/mol (with an RMSD of 6.8 kcal/mol). The larger deviations most likely were due to the large size of the insulin hexamer (with a total of 306 residues); our GBr⁶ method was benchmarked on a set of proteins with up to 250 residues.²⁶

In our previous study,³¹ the PB results for ΔG_el* calculated on the transient-complex ensembles of the barnase-barstar, IL4-IL4BP, E9-Im9, and AChE-fas protein pairs were −3.3, −4.3, −3.1, and −4.0 kcal/mol, respectively. The corresponding GBr⁶ results obtained here were −0.45, −1.4, −0.73, and 0.57 kcal/mol, respectively. The raw GBr⁶ results thus had large errors.

While the ensemble-averaged values of ΔΔG_b, ΔΔG_f, ΔG_t, and ΔG_el* obtained by GBr⁶ had relatively large deviations from the PB targets, in each application the GBr⁶ and PB sets of values calculated on the individual conformations did show strong correlations. In Figure 4 we illustrate the correlations on the E49K/E178K mutation of Cdc42 for binding and on the T21K mutation of FKBP for folding. From linear regression analyses with the requirement of a zero intercept, the correlation R² values were ~0.99. The strong correlations between raw GBr⁶ results and their PB counterparts are the foundation of our scaling-based GB reparameterization. The errors of raw GBr⁶ are manifested by a non-unity slope of the GBr⁶-PB correlation, which, as will be seen shortly, is rectified by the scaling.

Figure 4.

Correlation of GBr⁶ and PB results for ΔG_{b; solv} (ΔG_{f; solv}), the solvation component of the electrostatic contribution to the binding (folding) free energy. Both sets of results were calculated on the same conformational ensemble. (a)–(b) ΔG_{b; solv} of wild-type Cdc42-WASp complex and the Cdc42 E49K/E178K mutant. (c)–(d) ΔG_{f; solv} of wild-type FKBP and the T21K mutant.

4.3 Performance of scaled GBr⁶

Upon applying scaling factors calculated on a small subset of five conformations, the errors of GBr⁶ on ΔΔG_b, ΔΔG_f, ΔG_t, and ΔG_el* all dropped to within 0.3 kcal/mol (Table 2). Just like in the previous subsection, errors refer to deviations from the PB targets. For the barnase-barstar complex, the errors of scaled GBr⁶ for 13 of the 17 mutations was less than 0.1 kcal/mol and the errors of the remaining 4 mutations were less than 0.2 kcal/mol; the overall RMSD was 0.09 kcal/mol. Notice that the latter value is much smaller than the fluctuations of the PB results for ΔΔG_b within the conformational ensemble (see Table 1). The final predictions of scaled GBr⁶ for ΔΔG_b are given in Table 1 for comparison against experimental and PB results. The RMSD of scaled GBr⁶ results from experiment was 1.53 kcal/mol, virtually the same as the 1.55-kcal/mol RMSD of PB results from experiment. We further tested scaled GBr⁶ for predicting salt effects on the binding free energy of the barnase-barstar complex. According to PB calculations, increasing ionic strength from 25 mM to 1 M reduces the magnitude of the binding free energy by 2.2 kcal/mol. As Figure 5 shows, scaled GBr⁶ remarkably well reproduces the salt dependence of the binding free energy obtained by PB.

Figure 5.

Comparison of scaled GBr⁶ and PB results for the salt dependence of the barnase-barstar binding free energy. Changes in ΔG_b from the respective results at an ionic strength of 25 mM are displayed.

Very good agreement between scaled GBr⁶ and PB were also observed for the GTPase-WASp complexes. As summarized in Table 2, the RMSDs of scaled GBr⁶ from PB, calculated over 12 mutations on the two related complexes, ranged from 0.14 to 0.32 kcal/mol among conformational ensembles sampled using five different NMR models as starting structures. The average RMSD over the five conformational ensembles was 0.23 kcal/mol.

The highly charged protein-RNA complex between U1A and U1SLII did not present an obstacle for the scaling method. The RMSD between scaled GBr⁶ and PB was just 0.05 kcal/mol among seven mutations. Note that for this system the PB results were obtained from solving the nonlinear PB equation, so the test on this system demonstrates that scaled GBr⁶ can work well even for highly charged systems such as protein-nucleic acid complexes, for which the nonlinear PB equation would otherwise be required. Solving the full nonlinear PB equation takes much longer CPU time than solving the linearized version. For highly charged systems, scaled GBr⁶ affords especially significant gain in computational speed and yet can still be highly accurate for calculating small electrostatic effects such as those caused by mutations on binding free energy.

The success of scaled GBr⁶ with predicting binding free energy was repeated on predicting folding free energy. For 26 mutations on FKBP, the RMSD from PB targets was just 0.14 kcal/mol. A comparison between ΔΔG_f results obtained by scaled GBr⁶ and PB for the 26 mutations is displayed in Figure 6. Note that scaled GBr⁶ performed equally well for single mutations and for multiple mutations. Once again the deviations of GBr⁶ from PB are much smaller than the fluctuations of the PB results for ΔΔG_f within the conformational ensemble.

Let us use a binding example and a folding example to illustrate how scaled GBr⁶ achieved its accuracy. The binding example is the E49K/E178K mutation of Cdc42 and the folding example is the T21K mutation of FKBP. The correlations between raw GBr⁶ and PB for these two examples have been shown in Figure 4. For binding, the slope of the linear repression between raw GBr⁶ and PB was 1.0306 for the wild-type complex and 1.0427 for the mutant. The optimal scaling would be to use these slopes as scaling factors. However, obtaining these slopes would require PB results for the whole conformational ensemble, which defeats the purpose of designing GB methods. By using PB results for a small subset of five conformations, we obtained scaling factors of 1.0306 for the wild-type complex and 1.0403 for the mutant. These scaling factors are very close to the slopes from linear regression, hence explaining why scaled GBr⁶ were so accurate. Similarly, for the folding examples, the slopes from linear regression were 1.0004 for wild-type FKBP and 0.9972 for the mutant. For the subset of five conformations, the scaling factors were found to be 1.0016 for the wild-type protein and 0.9982 for the mutant. The latter pairs of values again are very close to the respective slopes.

Raw GBr⁶ already did a good job in reproducing PB for ΔG_t of ribonuclease Sa. Scaling was able to further reduce the RMSD, from 0.46 to 0.07 kcal/mol, among nine pH values. For insulin, scaled GBr⁶ dramatically reduced the error on ΔG_t, from 6.8 kcal/mol to 0.34 kcal/mol. For ΔG_el* of the four protein pairs, scaling was able to totally eliminate the large errors of raw GBr⁶. Scaled GBr⁶ results differed from the PB targets by 0.2 kcal/mol or less for all the four protein pairs.

We carried out some experimentation with the number of representative conformations used for calculating scaling factors. Our conclusion is that five is the optimal compromise between accuracy (demanding more conformations) and computational cost (demanding less conformations). However, it seems that even with fewer numbers of conformations, the performance of scaled GBr⁶ will not deteriorate significantly. In our test on the barnase-barstar complex, using only three representative conformations (the first, second, and third, or the first, third, and last of the original five), the RMSD between scaled GBr⁶ and PB increased only minutely, from 0.09 to 0.14 kcal/mol. Our original GBr⁶ is already quite accurate. It is expected that, when the scaling scheme developed here is applied to less accurate GB methods, improvement in accuracy even more dramatic than presented here will be achieved.

4.4 Cross validations

It is interesting to know how well the scaling scheme works when scaling factors obtained on five conformations selected from one sub-ensemble are applied to another sub-ensemble. As an example, an early portion of a MD trajectory may be used to generate the conformations for producing the scaling factors, which may then be applied to conformations sampled from the continuation of the MD simulation. To address the question posed above, we designed two types of cross-validation tests, depending on how the conformations were divided into sub-ensembles. The barnase-barstar complex was chosen for this purpose simply because it happened to have the most conformations (548) saved and PB results calculated for benchmarking. In the first cross-validation test, the 548 conformations were divided into four equal sub-ensembles according to time sequence. In the second cross-validation test, every fourth conformation was collected into a sub-ensemble, and each of the fist four conformations of the whole ensemble started a different sub-ensemble.

We refer to the sub-ensemble from which the scaling factors were obtained as the training sub-ensemble, and examine whether the scaling factors when applied to a different sub-ensemble would lead to larger errors than when applied to the training sub-ensemble itself. As the results in Table 3 show, for both types of cross-validation tests, applying the scaling factors to the training or a different sub-ensemble produces very similar errors.

Table 3.

Cross validation of sGBr⁶ on ΔΔG_b results of 17 mutations on the barnase-barstar complex^a

Training	Type-1 test	Type-2 test
Sub-ensemble 1	0.15 (0.08)	0.06 (0.06)
Sub-ensemble 2	0.09 (0.09)	0.15 (0.15)
Sub-ensemble 3	0.14 (0.16)	0.14 (0.14)
Sub-ensemble 4	0.14 (0.12)	0.12 (0.12)
Average	0.13 (0.11)	0.12 (0.12)

^aUnder each type of test, error in kcal/mol, as measured by RMSD from PB targets, is given. The number in parentheses represents the error when the scaling factors were applied to the training sub-ensemble itself; the number outside represents the error obtained on the other three sub-ensembles.

A caveat about the cross-validation tests is that the different sub-ensembles must all be part of the conformational fluctuations within a single deep energy well. If the protein or protein complex undergoes a conformational transition and different sub-ensembles are collected before and after the transition, cross validation clearly will fail. It is important that, in designing scaling schemes, such conformational transitions are recognized and one set of scaling factors is used for each unique deep energy well.

V. Conclusion

We have demonstrated that a scaled GB method accurately reproduces PB results for binding and folding free energies, transfer energies between crystalline and solution phases, and electrostatic interaction energies in transient complexes. The scaled GB method thus opens the door to incorporate conformational sampling in robust and accurate modeling of small electrostatic effects, which fall within the error range of current GB methods.

The deviations of scaled GBr⁶ from PB are much smaller than the fluctuations of PB results within conformational ensembles. Our scaling scheme thus seems to have pushed GB methods to their accuracy limit. In our opinion, reparameterization without reference to any PB results will never be able to reach such a level of accuracy. Combining one of the most accurate raw GB method with a PB-guided scaling method, scaled GBr⁶ promises to be a prototype for a new generation of fast continuum solvation models for incorporating conformational sampling in binding and folding free energy and other related calculations.