Abstract
Complex morphologies in lipid membranes typically arise due to chemical heterogeneity, but in the tilted gel phase, complex shapes can form spontaneously even in a membrane containing only a single lipid component. We explore this phenomenon via experiments and coarse-grained simulations on giant unilamellar vesicles of 1,2-dipalmitoyl-sn-glycero-3-phosphocholine. When cooled from the untilted Lα liquid-crystalline phase into the  tilted gel phase, vesicles deform from smooth spheres to disordered, highly crumpled shapes. We propose that this shape evolution is driven by nucleation of complex membrane microstructure with topological defects in the tilt orientation that induce nonuniform membrane curvature. Coarse-grained simulations demonstrate this mechanism and show that kinetic competition between curvature change and defect motion can trap vesicles in deeply metastable, defect-rich structures.
tilted gel phase, vesicles deform from smooth spheres to disordered, highly crumpled shapes. We propose that this shape evolution is driven by nucleation of complex membrane microstructure with topological defects in the tilt orientation that induce nonuniform membrane curvature. Coarse-grained simulations demonstrate this mechanism and show that kinetic competition between curvature change and defect motion can trap vesicles in deeply metastable, defect-rich structures.
Complex morphologies in lipid membranes arise typically due to chemical heterogeneities. For example, clustering of different lipid species can result in membrane domains with different intrinsic curvatures (1) and transmembrane proteins can induce local curvature (2). Here we explore another mechanism that produces complex shapes in membranes of a single lipid component without chemical heterogeneity: the formation of topological defects in a membrane with in-plane orientational order and their trapping to produce highly disordered morphologies.
In this paper, we present coordinated experimental and computational studies of giant unilamellar vesicles (GUVs), i.e., single-bilayer shells, as they cool from the untilted liquid-crystalline phase (Lα) into the tilted gel phase  . In the gel phase, the local molecular tilt has orientational order; i.e., the molecules point in a particular direction within the 2D plane. Hence, the gel phase exhibits microstructural point defects, vortices in the tilt direction, which can be considered as positive or negative topological “charges” according to which way the tilt direction rotates about the defect core (3). A spherical vesicle must have defects with a total topological charge of +2, as shown by the Gauss–Bonnet theorem (just as one cannot comb the hair on a coconut without leaving at least two defects). In general, there is a fundamental geometric connection between 2D order and defects within a membrane and the 3D shape of the membrane: Curvature drives formation of topological defects, and conversely, defects can induce curvature (4–6). This interaction has been explored in liquid crystals (7, 8), faceted block copolymer vesicles (9), liquid-crystalline elastomers (10), colloidal crystals (11), and superfluids (12), and we investigate how it affects the shape of GUVs.
. In the gel phase, the local molecular tilt has orientational order; i.e., the molecules point in a particular direction within the 2D plane. Hence, the gel phase exhibits microstructural point defects, vortices in the tilt direction, which can be considered as positive or negative topological “charges” according to which way the tilt direction rotates about the defect core (3). A spherical vesicle must have defects with a total topological charge of +2, as shown by the Gauss–Bonnet theorem (just as one cannot comb the hair on a coconut without leaving at least two defects). In general, there is a fundamental geometric connection between 2D order and defects within a membrane and the 3D shape of the membrane: Curvature drives formation of topological defects, and conversely, defects can induce curvature (4–6). This interaction has been explored in liquid crystals (7, 8), faceted block copolymer vesicles (9), liquid-crystalline elastomers (10), colloidal crystals (11), and superfluids (12), and we investigate how it affects the shape of GUVs.
Results and Discussion
Previous theories have predicted that a lipid vesicle with in-plane tilt order will have a smooth and elongated ground state with a defect of charge +1 at each end (13, 14). To test this prediction experimentally, we prepare GUVs in water from the lipid 1,2-dipalmitoyl-sn-glycero-3-phosphocholine (DPPC) above the melting temperature Tm, using an electro-formation method. Resulting GUVs vary in size with an average radius of ∼15 μm. The sample is then cooled from the untilted Lα phase to the tilted  phase. Through this transition, the shape evolution and microstructure are observed using laser scanning confocal fluorescence microscopy and polarized fluorescence microscopy. Materials and Methods are described below.
phase. Through this transition, the shape evolution and microstructure are observed using laser scanning confocal fluorescence microscopy and polarized fluorescence microscopy. Materials and Methods are described below.
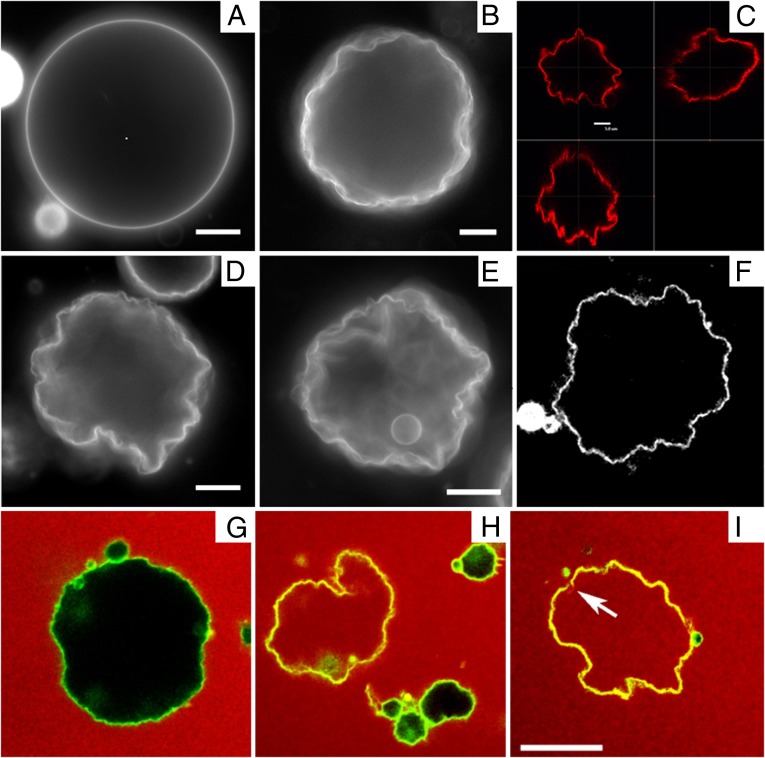
In the Lα phase, vesicles are smooth and approximately spherical as shown in Fig. 1A. When cooled into the 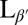 phase, vesicles become crumpled and disordered in appearance, as shown in Fig. 1 B–F, with shapes that are far more complex than expected (13, 14). The crumpled state is stable over long time periods. When reheated into the Lα phase, vesicles revert to their spherical shape. This observation raises questions: What drives formation of these morphologies? And what prevents vesicles from reaching the predicted ground state?
phase, vesicles become crumpled and disordered in appearance, as shown in Fig. 1 B–F, with shapes that are far more complex than expected (13, 14). The crumpled state is stable over long time periods. When reheated into the Lα phase, vesicles revert to their spherical shape. This observation raises questions: What drives formation of these morphologies? And what prevents vesicles from reaching the predicted ground state?
Fig. 1.
Fluorescence microscopy of DPPC vesicles labeled with 0.09 mol% NBD-PE. (A) Vesicle above Tm in the Lα phase. (B, D, and E) Vesicles cooled below Tm into the 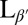 phase. (Scale bars, 10 μm.) (C and F) Confocal images showing slices through a crumpled vesicle. (Scale bar for C, 5 μm; image width for F, 117 μm.) (G–I) Confocal images of vesicles in the
phase. (Scale bars, 10 μm.) (C and F) Confocal images showing slices through a crumpled vesicle. (Scale bar for C, 5 μm; image width for F, 117 μm.) (G–I) Confocal images of vesicles in the 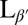 phase dispersed in a 12-μM fluorescent dextran solution before crumpling. Some vesicles remain intact and appear black in the interior (G and H), whereas others show leakage and appear red inside (H and I). Note that the vesicle in I has a clear break in the membrane, as indicated by the arrow. (Scale bar, 20 μm.)
phase dispersed in a 12-μM fluorescent dextran solution before crumpling. Some vesicles remain intact and appear black in the interior (G and H), whereas others show leakage and appear red inside (H and I). Note that the vesicle in I has a clear break in the membrane, as indicated by the arrow. (Scale bar, 20 μm.)
We hypothesize that vesicle shape evolution in the tilted phase is driven by nucleation and dynamics of many +/− topological defects in addition to the two + defects required by topology, analogous to the defect-rich microstructure formed in liquid-crystal thin films on cooling from the untilted smectic-A phase into the tilted smectic-C phase (15, 16). Each of these defects would generate a locally curved region of the vesicle.
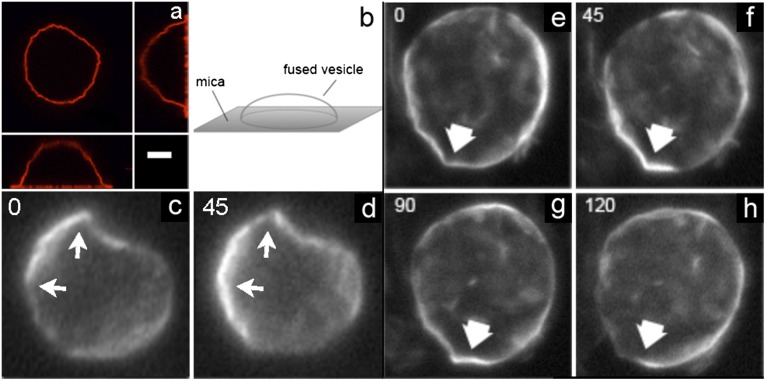
To test this hypothesis, we must examine tilt microstructure in gel phase GUVs. Recently Bernchou et al. showed that polarized fluorescence microscopy with the probe Laurdan can visualize tilt orientation around a single defect in a flat lipid gel phase bilayer domain absorbed onto a mica substrate (17). Probe molecules tilted in a direction parallel to the polarizer give a strong fluorescence signal (light state) compared with those tilted perpendicular to the polarizer (dark state). As the polarizer rotates, molecules with different tilt orientations align with the polarizer and their fluorescence intensity increases, providing a direct method for visualizing lipid tilt orientation. We use this method to image crumpled vesicles that are partially fused onto a mica surface, immobilizing them so that multiple images can be taken with different polarizer orientations, using a microscope focused on a plane slightly above the substrate (Fig. 2 A and B). Examples of two different gel-phase vesicles imaged with different polarizer orientations are shown in Fig. 2 C–H. These images reveal that lipid tilt orientation varies as a function of position around the vesicle, consistent with the hypothesis that the membrane’s tilt microstructure contains a population of point defects.
Fig. 2.
Polarized fluorescence microscopy images of a single vesicle labeled with 0.5 mol% Laurdan in the gel phase. (A and B) The vesicles are immobilized by partial fusion onto a mica surface as shown in the unpolarized confocal image (A) and diagram (B). (Scale bar, 10 μm.) (C–H) Images show two different vesicles with the focal plane slightly above the mica surface. The vesicles are illuminated by different angles of linearly polarized light (angle indicated in left corner, in degrees). The arrows indicate regions where tilt defects can be observed by rotating the polarizer.
We note that images in Fig. 2 are less convoluted than those in Fig. 1 simply as a matter of selection. Because the polarized imaging system has a greater depth of field than confocal imaging, vesicles with the least convoluted contours are chosen to give the clearest polarization images of the vesicle walls.
To confirm that the crumpled shapes are driven by topological defects in membrane tilt, we compare our results for DPPC vesicles with those for vesicles prepared from the lipid sphingomyelin, which exhibits a gel phase that lacks molecular tilt (18). On cooling into the untilted gel phase, sphingomyelin vesicles remain relatively smooth. Some examples are observed of slightly faceted vesicles, as would be expected for a transition to the more rigid gel phase, but no highly crumpled vesicles are seen. The effects of surface tension across the transition can also be largely ruled out as a mechanism for this effect, using this comparison. Scattering experiments (19) have also shown that for unstressed membranes surface tension does not significantly change across the transition.
The vesicle shapes we present here are somewhat similar to results from other experiments on lipid vesicles, but their physical origin is different: (a) A “wrinkling transition” was recently reported in polymerized and partially polymerized vesicles, analogous to a glass transition into a quenched state (20, 21). This phenomenon differs from our experiment because our vesicles are not polymerized. (b) Highly scalloped surface topographies have been seen in vesicles formed from quaternary lipid mixtures (22). These shape changes derive from membrane phase separation into phases with different intrinsic curvatures, whereas our vesicles have only a single component. (c) Other experiments have demonstrated the formation of small faceted vesicles when membranes are vitrified in the gel phase for cryo-transmission electron microscopy (23). These results are observed only in very small vesicles, 50 nm in size, much smaller than the GUVs investigated here. (d) A recent paper has reported dramatic shape changes in vesicles under high ionic conditions, resulting from extensive pore formation in the membrane at the gel phase transition (24). To test whether vesicles remain intact through the phase transition, we perform a dye leakage assay, shown in Fig. 1 G–I. Although some vesicles break and allow dye into their interior (Fig. 1 H and I), we observe many examples where the vesicle remains intact (Fig. 1 G and H), indicating that the crumpled surface maintains a continuous bilayer barrier to the exterior solution. Hence, pore formation is not necessary for the crumpling behavior observed. We note that vesicles with the most highly crumpled shapes are typically those that leak (e.g., Fig. 1I). Leakage is usually due to a single localized gap rather than widespread pore formation (Fig. 1I, arrow).
Once a population of defects is nucleated in the membrane, we hypothesize that subsequent coevolution of microstructure and membrane shape is driven by two competing mechanisms. First, defects of opposite sign attract, so nearby +/− pairs should diffuse and pair annihilate as observed in freestanding smectic-C thin films (15, 16). Second, the presence of +/− defects induces the membrane to deform with higher/lower Gaussian curvature, respectively. The resulting higher Gaussian curvature near a positive defect repels negative defects, an effect that inhibits pair annihilation. This latter mechanism can thus trap defects in deeply metastable states, producing a disordered morphology with nonuniform Gaussian curvature.
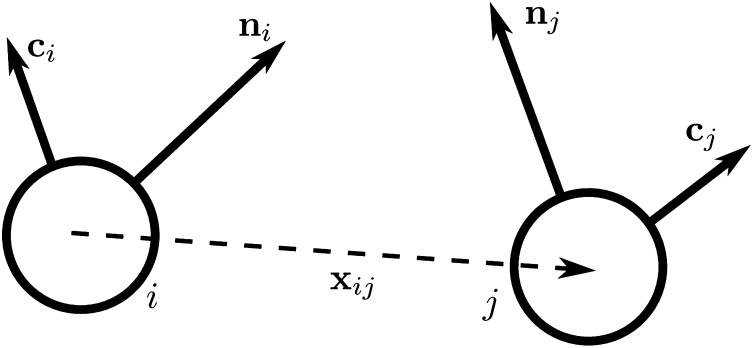
To gain insight into these competing mechanisms and their role in morphology selection, we perform coarse-grained simulations of vesicles in an orientationally ordered membrane containing topological defects. For this purpose we superimpose a tilt orientation degree of freedom onto a highly coarse-grained membrane model recently introduced by Li and coworkers (25–27), where the lipid bilayer is represented by a single layer of point particles, each representing a patch of membrane of order 20 nm2, and solvent is implicit. To generalize this model to describe tilted lipid membranes, we assign each particle two vector degrees of freedom: a vector 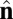 representing the outward layer normal direction, as in Li’s original model, and an additional vector
representing the outward layer normal direction, as in Li’s original model, and an additional vector 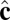 representing the local tilt direction, projected in the plane of the membrane (Fig. 3). We add terms to the coarse-grained particle interaction potential favoring orientational order of the tilt vectors and coupling tilt with membrane curvature. Details of the simulation model and procedure are presented in Materials and Methods, and results are shown in Movie S1. Although this model is too coarse-grained to capture details of lipid structural changes at the molecular scale during a phase transition, it is useful to study the geometric interaction between tilt order and membrane curvature.
representing the local tilt direction, projected in the plane of the membrane (Fig. 3). We add terms to the coarse-grained particle interaction potential favoring orientational order of the tilt vectors and coupling tilt with membrane curvature. Details of the simulation model and procedure are presented in Materials and Methods, and results are shown in Movie S1. Although this model is too coarse-grained to capture details of lipid structural changes at the molecular scale during a phase transition, it is useful to study the geometric interaction between tilt order and membrane curvature.
Fig. 3.
Schematic illustration of our two-vector model for interacting coarse-grained particles. Each particle has a vector 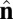 , which aligns along the local membrane normal, and a vector
, which aligns along the local membrane normal, and a vector 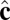 , which represents the long-range tilt order within the local tangent plane.
, which represents the long-range tilt order within the local tangent plane.
We note that this model assumes the membrane is in a fluid phase, without hexatic bond-orientational order. In the experiment we search for indications of hexatic order, such as star-like point defects with sharp direction orientation boundaries, but do not observe such features. If any hexatic order is present, it must have a very short range, and hence the membrane acts as a tilted fluid on the long length scales relevant to defect interaction.
The simulation begins with a spherical vesicle composed of coarse-grained particles with local tilt vector 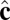 randomly oriented in the membrane plane. Using coarse-grained particle dynamics with a Langevin thermostat, we quench from a high-temperature state without tilt order into the low-temperature phase with tilt order. The simulated vesicle shows spontaneous formation of a population of point defects that then coarsen via pair annihilation while, simultaneously, the overall vesicle shape evolves. Regions near an isolated positive defect bulge outward with higher Gaussian curvature, whereas regions near an isolated negative defect flatten or form a locally saddle-like shape with lower Gaussian curvature.
randomly oriented in the membrane plane. Using coarse-grained particle dynamics with a Langevin thermostat, we quench from a high-temperature state without tilt order into the low-temperature phase with tilt order. The simulated vesicle shows spontaneous formation of a population of point defects that then coarsen via pair annihilation while, simultaneously, the overall vesicle shape evolves. Regions near an isolated positive defect bulge outward with higher Gaussian curvature, whereas regions near an isolated negative defect flatten or form a locally saddle-like shape with lower Gaussian curvature.
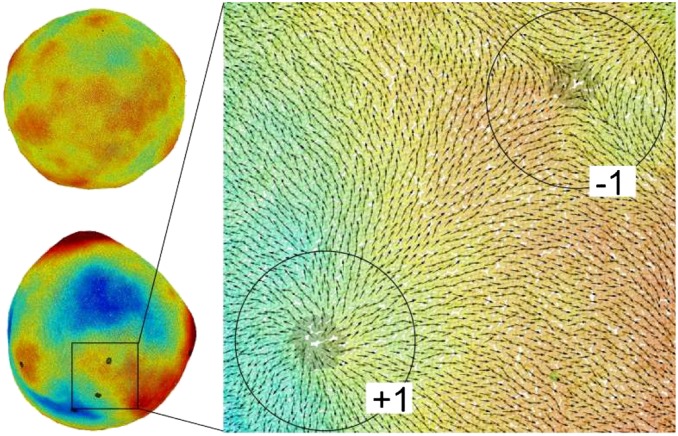
For a system containing 100,000 coarse-grained particles, representing a vesicle of approximate diameter 0.8 μm, the simulated vesicle never reaches the prolate ground state. Instead, defect pair annihilation slows and eventually reaches a final state containing 10 defects (6 positive, 4 negative) with nonuniform Gaussian curvature as shown in Fig. 4 and Movie S1. The enlarged view shows local defect structure. The microstructure in the final state appears to be deeply metastable and no further defect pair annihilation is observed even after long simulation times.
Fig. 4.
Coarse-grained simulation of a lipid vesicle. (Upper Left) High-temperature Lα phase. (Lower Left and Right) Low-temperature 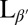 phase. Arrows represent the tilt direction
phase. Arrows represent the tilt direction 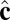 , black dots represent defects in the tilt direction, and colors represent distance from the center of mass of the vesicle.
, black dots represent defects in the tilt direction, and colors represent distance from the center of mass of the vesicle.
The final morphology depends on the relative viscosities for translational and rotational degrees of freedom. If translational viscosity is low and rotational viscosity is high, so that membrane deformation is fast and defect motion is slow, the simulation gives the disordered structure shown in Fig. 5 and the first simulation in Movie S1. By contrast, if the translational viscosity is high and rotational viscosity is low, so that membrane deformation is slow and defect motion is fast, the simulation gives the much smoother structure shown in Fig. 6 and the second simulation in Movie S1. The final morphology also depends on the system size. In simulation of vesicles with much smaller radius, defect diffusion is sufficiently fast to allow all extra pairs to annihilate, enabling the system to relax to the theoretically predicted prolate ground state.
Fig. 5.
Shape and defect configuration for a simulated vesicle with low translational viscosity and high rotational viscosity. The color images (Left) represent distance from the center of mass of the vesicle, and the grayscale images (Right) represent the tilt direction, showing the optical intensity that would be observed with polarized fluorescence microscopy. This vesicle has five +1 defects and three −1 defects. Note the similarity with the experimental images of Fig. 2, in particular at the points indicated by the arrows.
Fig. 6.
Shape and defect configuration for a simulated vesicle with high translational viscosity and low rotational viscosity. The color images (Left) represent distance from the center of mass of the vesicle, and the grayscale images (Right) represent the tilt direction, showing the optical intensity that would be observed with polarized fluorescence microscopy. This vesicle has only two defects of charge +1, which is the minimum required by topology. Note that it is much smoother than the simulated vesicle of Fig. 5.
From these observations we conclude that the final morphology is determined via kinetic competition between defect mobility and changing membrane curvature. If defect mobility is fast compared with membrane motion, or if the vesicle size is relatively small, then all extra defect pairs quickly annihilate before the overall membrane shape has changed significantly, and the vesicle reaches the prolate ground state with only two defects. However, if defect mobility is relatively slow compared with membrane translation, or if the vesicle size is larger, defects become trapped in deeply metastable states and the vesicle forms a crumpled morphology with nonuniform Gaussian curvature. We speculate that the kinetic trapping of topological defects in deeply metastable states may occur in other orientationally ordered lipid membranes and may be involved more generally in pattern formation processes that produce highly disordered shapes.
In conclusion, we have shown that DPPC vesicles become crumpled at the transition to the 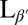 tilted gel phase and propose that this morphology is the result of coupling between membrane curvature and topological defects in the tilt direction. Kinetic trapping of defects arises when pair annihilation is arrested by formation of regions of high/low Gaussian curvature around defects of positive/negative topological charge, respectively. Coarse-grained simulations demonstrate this mechanism and reveal how kinetic competition between curvature changes and defect pair annihilation determines whether the vesicle reaches its ground state or becomes trapped in a disordered metastable morphology. These results reveal a fundamental pattern-formation mechanism for orientationally ordered thin films with potential applications in a variety of soft materials, including synthetic and biological membranes.
tilted gel phase and propose that this morphology is the result of coupling between membrane curvature and topological defects in the tilt direction. Kinetic trapping of defects arises when pair annihilation is arrested by formation of regions of high/low Gaussian curvature around defects of positive/negative topological charge, respectively. Coarse-grained simulations demonstrate this mechanism and reveal how kinetic competition between curvature changes and defect pair annihilation determines whether the vesicle reaches its ground state or becomes trapped in a disordered metastable morphology. These results reveal a fundamental pattern-formation mechanism for orientationally ordered thin films with potential applications in a variety of soft materials, including synthetic and biological membranes.
Materials and Methods
Experiment.
Lipids are amphiphilic molecules and therefore form bilayers in aqueous solution. The exact state of this bilayer is temperature dependent, and several thermotropic phases are known to exist for lipid assemblies. The familiar fluid lipid membrane consists of a single bilayer in the Lα phase, in which the molecules exhibit short-range in-plane packing. Individual lipid molecules can rotate and diffuse in the plane of the membrane; their tails are disordered with zero average tilt with respect to the bilayer plane. This phase is also known as the lipid bilayer liquid crystalline phase. At temperatures below this phase the membrane will exhibit the so-called “gel” phase 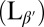 . In the gel phase, lipid molecules in the bilayer have a longer-range orthorhombic packing. They are able to rotate but diffusion is highly restricted. In this phase the lipid tails are also more extended than in the liquid crystalline phase, and they are tilted with respect to the membrane normal. The degree of chain tilt can vary greatly between lipid species. The tilt angle for DPPC has been measured to be ∼32° with respect to the bilayer normal (28), whereas other lipids, for example sphingomyelin, are observed to a have a very low tilt (∼4°).
. In the gel phase, lipid molecules in the bilayer have a longer-range orthorhombic packing. They are able to rotate but diffusion is highly restricted. In this phase the lipid tails are also more extended than in the liquid crystalline phase, and they are tilted with respect to the membrane normal. The degree of chain tilt can vary greatly between lipid species. The tilt angle for DPPC has been measured to be ∼32° with respect to the bilayer normal (28), whereas other lipids, for example sphingomyelin, are observed to a have a very low tilt (∼4°).
The lipid DPPC is used in this study as an example of a material with a high tilt angle and with a transition into the gel phase close to room temperature at 42 °C. Lipid bilayers stacked in a bulk lamellar phase can be considered analogous to smectic phases. The untilted Lα can be likened to the smectic-A phase and the tilted 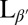 phase to a smectic-C with additional in-plane order as the tilted fatty acid chains organize in a tilted configuration.
phase to a smectic-C with additional in-plane order as the tilted fatty acid chains organize in a tilted configuration.
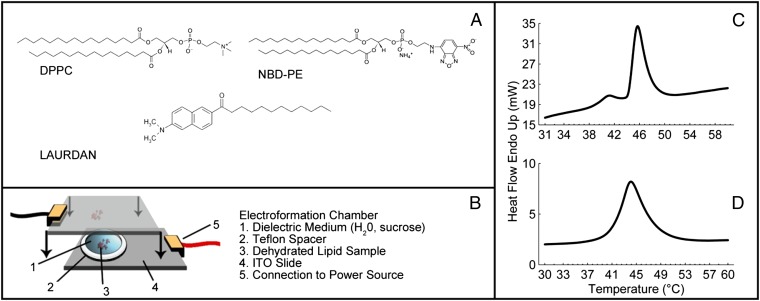
To investigate the interplay between topological defects and membrane curvature, we prepare GUVs from DPPC at a temperature above Tm, using an electro-formation method as illustrated in Fig. 7B. Lipid chloroform solutions are spotted onto conductive plates and dried under vacuum overnight. Dried lipid films are then rehydrated with an aqueous solution at 50 °C with an applied sinusoidal electric field of 1 millivolts peak to peak (mVpp)/μm at 5 Hz for 4–10 h. During this time GUVs form on the indium tin oxide (ITO) surfaces in the chamber and can be released into the solution by gentle shaking. Finally the GUV solution is removed from the chamber by pipette, maintaining the temperature at 8 °C above Tm, and stored at that temperature for a short time until microscopy is performed. The vesicles generated by this method vary in size with an average radius of ∼15 μm. Sphingomyelin vesicles are also prepared as a comparison. All lipids used in this study are supplied by Avanti Polar Lipids and used without modification. The DPPC is mixed in chloroform solution with 0.09 mol% of the fluorescent label NBD-PE [1,2-dipalmitoyl-sn-glycero-3-phosphoethanolamine-N-(7-nitro-2–1,3-benzoxadiazol-4-yl) (ammonium salt)] or 0.5 mol% of the fluorescent probe Laurdan (Sigma Aldrich) and vortexed for several seconds. Molecular structures are shown in Fig. 7A. Laurdan is an amphiphilic dye that partitions into the lipid bilayer. In a tilted bilayer with Laurdan included, incident light polarized in the same plane as the tilt angle will result in a strong fluorescence signal, whereas light incident at 90° to this plane will produce a minimal signal.
Fig. 7.
(A) Molecular structures for the materials used in this study, including the lipid DPPC and the fluorescent dyes. (B) Schematic of the electro-formation chamber used to prepare GUVs. (C and D) DSC traces of the lipid phase transition in DPPC (C) and sphingomyelin (D). ITO, indium tin oxide.
Fluorescence microscopy is carried out on a reflection Leica DM2500P microscope equipped with polarizing filters. Laser scanning confocal microscopy is performed on a Nikon microscope system. Differential scanning calorimetry is carried out using a Perkin-Elmer 8000 differential scanning calorimeter (DSC) on lipid/water samples in the bulk lamellar phase (Fig. 7 C and D). Samples for DSC measurements on pure lipid compounds are prepared in chloroform and dried in a nitrogen stream and by vacuum overnight to remove the chloroform. Lipids are then rehydrated with water to a concentration of >50 mg/mL and ∼5 mg filled into a sealed liquid aluminum DSC pan for measurement.
Simulation.
In our coarse-grained simulations of membranes with tilt order, we generalize an earlier coarse-grained model for membranes without tilt order (25–27). We have recently used a similar model for membranes with internal nematic order (29).
Each particle carries two vector degrees of freedom: a vector 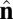 representing the outward layer normal direction and a vector
representing the outward layer normal direction and a vector 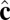 representing the local membrane tilt direction, projected into the plane of the membrane. They are constrained to be orthogonal unit vectors, as shown in Fig. 3. The particle–particle interactions are governed by the pair potential
representing the local membrane tilt direction, projected into the plane of the membrane. They are constrained to be orthogonal unit vectors, as shown in Fig. 3. The particle–particle interactions are governed by the pair potential
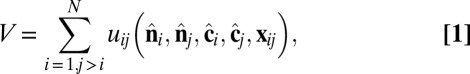 |
which combines isotropic short-range repulsion and anisotropic longer-range attraction,
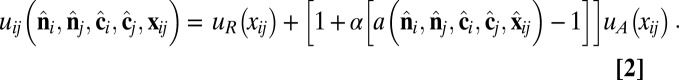 |
The repulsive and attractive components have the forms
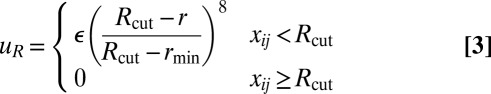 |
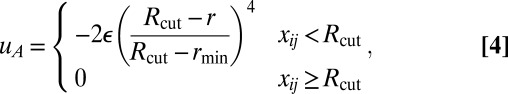 |
where rmin = 21/6d, Rcut = 2.55d, and d and ε are units of length and energy, respectively. In the attractive component, 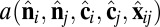 is an orientation-dependent function given by
is an orientation-dependent function given by
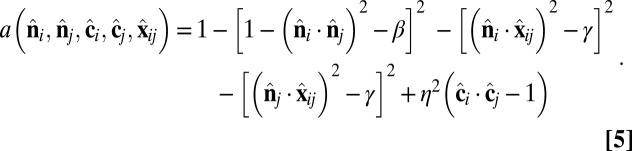 |
In the 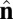 -dependent terms, the coefficients are defined as β = sin2(θ0) and γ = sin2(θ0/2). These terms favor an angle θ0 between the
-dependent terms, the coefficients are defined as β = sin2(θ0) and γ = sin2(θ0/2). These terms favor an angle θ0 between the 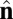 vectors of neighboring particles, and hence favor a spontaneous curvature of the membrane. The
vectors of neighboring particles, and hence favor a spontaneous curvature of the membrane. The 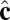 -dependent term favors alignment of the
-dependent term favors alignment of the 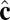 vectors of neighboring particles parallel to each other and hence favors tilt order within the membrane. The coefficient α controls the strength of the anisotropic orientational interaction.
vectors of neighboring particles parallel to each other and hence favors tilt order within the membrane. The coefficient α controls the strength of the anisotropic orientational interaction.
The system evolves via particle dynamics with forces and torques calculated from the potential. The Lagrangian for a single particle is
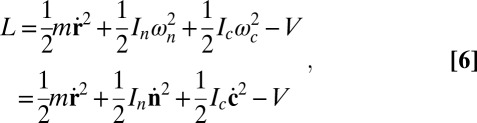 |
where V is summed over all of the neighbors interacting with that particle. With the constraints 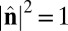 ,
, 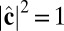 , and
, and 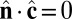 , the Lagrangian equations of motion are
, the Lagrangian equations of motion are
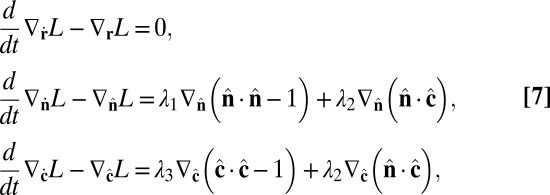 |
where the generalized gradient is defined as
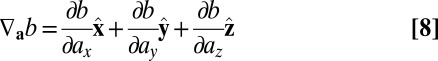 |
in Cartesian coordinates. The Lagrange multipliers are determined by the constraints,
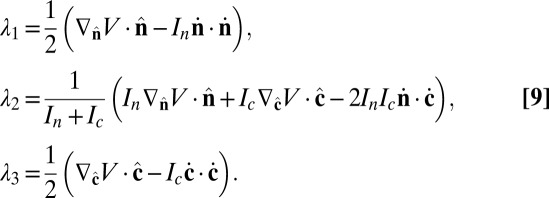 |
Combining Eqs. 7 and 9, the equations of motion become
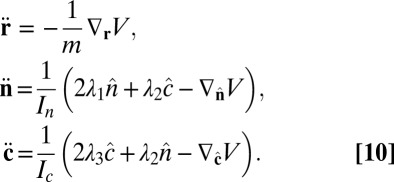 |
We perform coarse-grained molecular-dynamics simulation with a Langevin thermostat applied on both translational and rotational degrees of freedom. We impose periodic boundary conditions on all three directions of the simulation box. The system contains 114,891 coarse-grained particles, and each of them carries 6 df. The numerical time integration of the equations of motion (10) is performed by using an Adams–Moulton third-order method, which uses the same information as the popular Beeman algorithm but is even more accurate. To match the time steps for translational and rotational degrees of freedom, the moments of inertia of both 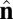 and
and 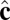 vectors are chosen to be In = Ic = md2. We use the parameters α = 3.1, η = 0.25, and θ0 = 0.015. We begin the simulation with an initial spherical vesicle constructed by depositing particles on a sphere via random sequential adsorption (30) and then maintain a high temperature kBT/ε ∼ 0.35 until it relaxes into equilibrium. We then quench the vesicle to low temperature kBT/ε ∼ 0.2 in several million time steps (∼ 105
md2/ε).
vectors are chosen to be In = Ic = md2. We use the parameters α = 3.1, η = 0.25, and θ0 = 0.015. We begin the simulation with an initial spherical vesicle constructed by depositing particles on a sphere via random sequential adsorption (30) and then maintain a high temperature kBT/ε ∼ 0.35 until it relaxes into equilibrium. We then quench the vesicle to low temperature kBT/ε ∼ 0.2 in several million time steps (∼ 105
md2/ε).
Supplementary Material
Acknowledgments
This work was supported by National Science Foundation Grants DMR-0605889, DMR-0852791, and DMR-1106014.
Footnotes
The authors declare no conflict of interest.
This article is a PNAS Direct Submission.
This article contains supporting information online at www.pnas.org/lookup/suppl/doi:10.1073/pnas.1213994110/-/DCSupplemental.
References
- 1.Simons K, Vaz WLC. Model systems, lipid rafts, and cell membranes. Annu Rev Biophys Biomol Struct. 2004;33:269–295. doi: 10.1146/annurev.biophys.32.110601.141803. [DOI] [PubMed] [Google Scholar]
- 2.Zimmerberg J, Kozlov MM. How proteins produce cellular membrane curvature. Nat Rev Mol Cell Biol. 2006;7(1):9–19. doi: 10.1038/nrm1784. [DOI] [PubMed] [Google Scholar]
- 3.Chaikin PM, Lubensky TC. Principles of Condensed Matter Physics. Cambridge, UK: Cambridge Univ Press; 1995. [Google Scholar]
- 4.Bowick MJ, Travesset A. The statistical mechanics of membranes. Phys Rep. 2001;344:255–308. [Google Scholar]
- 5.Nelson DR. Defects and Geometry in Condensed Matter Physics. Cambridge, UK: Cambridge Univ Press; 2002. [Google Scholar]
- 6.Selinger RLB, Konya A, Travesset A, Selinger JV. Monte Carlo studies of the XY model on two-dimensional curved surfaces. J Phys Chem B. 2011;115(48):13989–13993. doi: 10.1021/jp205128g. [DOI] [PubMed] [Google Scholar]
- 7.Nelson DR, Peliti L. Fluctuations in membranes with crystalline and hexatic order. J Phys (Paris) 1987;48:1085–1092. [Google Scholar]
- 8.Fernández-Nieves A, et al. Novel defect structures in nematic liquid crystal shells. Phys Rev Lett. 2007;99(15):157801. doi: 10.1103/PhysRevLett.99.157801. [DOI] [PubMed] [Google Scholar]
- 9.Xing X, et al. Morphology of nematic and smectic vesicles. Proc Natl Acad Sci USA. 2012;109(14):5202–5206. doi: 10.1073/pnas.1115684109. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 10.Modes CD, Warner M. Blueprinting nematic glass: Systematically constructing and combining active points of curvature for emergent morphology. Phys Rev E Stat Nonlin Soft Matter Phys. 2011;84(2 Pt 1):021711. doi: 10.1103/PhysRevE.84.021711. [DOI] [PubMed] [Google Scholar]
- 11.Bausch AR, et al. Grain boundary scars and spherical crystallography. Science. 2003;299(5613):1716–1718. doi: 10.1126/science.1081160. [DOI] [PubMed] [Google Scholar]
- 12.Turner AM, Vitelli V, Nelson DR. Vortices on curved surfaces. Rev Mod Phys. 2010;82:1301–1348. [Google Scholar]
- 13.Park J, Lubensky TC, MacKintosh FC. n-atic order and continuous shape changes of deformable surfaces of genus zero. Europhys Lett. 1992;20:279–284. [Google Scholar]
- 14.Jiang H, Huber G, Pelcovits RA, Powers TR. Vesicle shape, molecular tilt, and the suppression of necks. Phys Rev E Stat Nonlin Soft Matter Phys. 2007;76(3 Pt 1):031908. doi: 10.1103/PhysRevE.76.031908. [DOI] [PubMed] [Google Scholar]
- 15.Svenšek D, Zumer S. Hydrodynamics of pair-annihilating disclinations in SmC films. Phys Rev Lett. 2003;90(15):155501. doi: 10.1103/PhysRevLett.90.155501. [DOI] [PubMed] [Google Scholar]
- 16.Link DR, Chattham N, Maclennan JE, Clark NA. Effect of high spontaneous polarization on defect structures and orientational dynamics of tilted chiral smectic freely suspended films. Phys Rev E Stat Nonlin Soft Matter Phys. 2005;71(2 Pt 1):021704. doi: 10.1103/PhysRevE.71.021704. [DOI] [PubMed] [Google Scholar]
- 17.Bernchou U, et al. Texture of lipid bilayer domains. J Am Chem Soc. 2009;131(40):14130–14131. doi: 10.1021/ja903375m. [DOI] [PubMed] [Google Scholar]
- 18.Maulik PR, Shipley GG. Interactions of N-stearoyl sphingomyelin with cholesterol and dipalmitoylphosphatidylcholine in bilayer membranes. Biophys J. 1996;70(5):2256–2265. doi: 10.1016/S0006-3495(96)79791-6. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 19.Daillant J, et al. Structure and fluctuations of a single floating lipid bilayer. Proc Natl Acad Sci USA. 2005;102(33):11639–11644. doi: 10.1073/pnas.0504588102. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 20.Mutz M, Bensimon D, Brienne MJ. Wrinkling transition in partially polymerized vesicles. Phys Rev Lett. 1991;67(7):923–926. doi: 10.1103/PhysRevLett.67.923. [DOI] [PubMed] [Google Scholar]
- 21.Chaieb S, Natrajan VK, El-rahman AA. Glassy conformations in wrinkled membranes. Phys Rev Lett. 2006;96(7):078101. doi: 10.1103/PhysRevLett.96.078101. [DOI] [PubMed] [Google Scholar]
- 22.Konyakhina TM, et al. Control of a nanoscopic-to-macroscopic transition: Modulated phases in four-component DSPC/DOPC/POPC/Chol giant unilamellar vesicles. Biophys J. 2011;101(2):L8–L10. doi: 10.1016/j.bpj.2011.06.019. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 23.Hammarstroem L, Velikian I, Karlsson G, Edwards K. Cryo-TEM evidence: Sonication of dihexadecyl phosphate does not produce closed bilayers with smooth curvature. Langmuir. 1995;11:408–410. [Google Scholar]
- 24.Riske KA, Amaral LQ, Lamy MT. Extensive bilayer perforation coupled with the phase transition region of an anionic phospholipid. Langmuir. 2009;25(17):10083–10091. doi: 10.1021/la9012137. [DOI] [PubMed] [Google Scholar]
- 25.Liu P, Li J, Zhang Y-W. Pressure-temperature phase diagram for shapes of vesicles: A coarse-grained molecular dynamics study. Appl Phys Lett. 2009;95:143104. [Google Scholar]
- 26.Zheng C, Liu P, Li J, Zhang Y-W. Phase diagrams for multi-component membrane vesicles: A coarse-grained modeling study. Langmuir. 2010;26(15):12659–12666. doi: 10.1021/la1020143. [DOI] [PubMed] [Google Scholar]
- 27.Yuan H, Huang C, Li J, Lykotrafitis G, Zhang S. One-particle-thick, solvent-free, coarse-grained model for biological and biomimetic fluid membranes. Phys Rev E Stat Nonlin Soft Matter Phys. 2010;82(1 Pt 1):011905. doi: 10.1103/PhysRevE.82.011905. [DOI] [PubMed] [Google Scholar]
- 28.Tristram-Nagle S, et al. Measurement of chain tilt angle in fully hydrated bilayers of gel phase lecithins. Biophys J. 1993;64(4):1097–1109. doi: 10.1016/S0006-3495(93)81475-9. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 29.Geng J, Selinger JV, Selinger RLB. 2011. Coarse-grained modeling of a deformable self-assembled nematic vesicle. Available at http://arxiv.org/abs/1112.4513. Accessed December 19, 2011.
- 30.Feder J. Random sequential adsorption. J Theor Biol. 1980;87:237–254. [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.