Neuronal long-range temporal correlations and avalanche dynamics are correlated with behavioral scaling laws

Abstract

Scale-free fluctuations are ubiquitous in behavioral performance and neuronal activity. In time scales from seconds to hundreds of seconds, psychophysical dynamics and the amplitude fluctuations of neuronal oscillations are governed by power-law-form long-range temporal correlations (LRTCs). In millisecond time scales, neuronal activity comprises cascade-like neuronal avalanches that exhibit power-law size and lifetime distributions. However, it remains unknown whether these neuronal scaling laws are correlated with those characterizing behavioral performance or whether neuronal LRTCs and avalanches are related. Here, we show that the neuronal scaling laws are strongly correlated both with each other and with behavioral scaling laws. We used source reconstructed magneto- and electroencephalographic recordings to characterize the dynamics of ongoing cortical activity. We found robust power-law scaling in neuronal LRTCs and avalanches in resting-state data and during the performance of audiovisual threshold stimulus detection tasks. The LRTC scaling exponents of the behavioral performance fluctuations were correlated with those of concurrent neuronal avalanches and LRTCs in anatomically identified brain systems. The behavioral exponents also were correlated with neuronal scaling laws derived from a resting-state condition and with a similar anatomical topography. Finally, despite the difference in time scales, the scaling exponents of neuronal LRTCs and avalanches were strongly correlated during both rest and task performance. Thus, long and short time-scale neuronal dynamics are related and functionally significant at the behavioral level. These data suggest that the temporal structures of human cognitive fluctuations and behavioral variability stem from the scaling laws of individual and intrinsic brain dynamics.

Human cognitive and behavioral performance is highly variable and exhibits slow fluctuations that are salient in continuous performance tasks (CPTs) (1). Psychophysical time series have been known since the early 1950s to be nonrandomly clustered (2), and later studies have shown that hit-rate and/or reaction-time fluctuations in CPT data are fractal and power-law autocorrelated across hundreds of seconds (3–9). The biological origins and relevance of these dynamic, however, remain unclear (10, 11).

Similar to those in behavioral performance, the fluctuations of collective neuronal activity at many levels of the nervous system are scale-free and governed by power-law scaling laws. On long time scales (10⁰−10³ s), scale-free fluctuations and long-range temporal correlations (LRTCs) are salient in the amplitude envelopes of spontaneous neuronal oscillations in data recorded with magneto- and electroencephalography (M/EEG) (12). It appears that these oscillation amplitude fluctuations reflect the underlying dynamic architecture of spontaneous brain activity discovered with functional MRI (fMRI) and defined by correlated slow fluctuations in blood oxygenation level–dependent (BOLD) signals among well-delineated functional brain systems (13–15). The oscillation amplitudes are directly correlated with these BOLD fluctuations (16–20) and exhibit interareal correlations that closely match those of BOLD signals (17, 21–23). Moreover, BOLD signals also exhibit scale-free temporal (24–26) and spatiotemporal correlations (27–29). The scaling laws of LRTCs thus are a unifying fundamental characteristic of spontaneous brain activity (1, 30, 31).

On short time scales (10⁻³−10⁻¹ s), negative deflections in local field potentials form spatiotemporal cascades of activity, “neuronal avalanches” (32–34), the size and lifetime distributions of which are power laws akin to those of a critical branching process (33). Neuronal avalanches characterize spontaneous neuronal network activity in organotypic cultures (32), brain slices in vitro (35), and monkey (34) and human cortex (36) in vivo. In monkey cortex, the avalanches are delimited by cycles of ongoing neuronal oscillations (34) showing that in addition to LRTCs (12), neuronal avalanches also coexist with neuronal oscillations.

The power-law scaling behavior and fractal properties of neuronal LRTCs and avalanches strongly suggest that the brain operates near a critical state (12, 30, 32, 33, 37). Computational modeling predicts that LRTCs and neuronal avalanches are coupled (38) and suggests that they coemerge from neuronal interactions in a critical regime (30). So far, however, neither the relationship between LRTCs and avalanche dynamics nor their significance at the behavioral level has been elucidated. We hypothesize here that the scaling laws of LRTCs and neuronal avalanches are related and are correlated with the interindividual variability in behavioral scaling laws. We test the hypothesis with source reconstructed task- and resting-state M/EEG recordings and show that behavioral scaling laws, LTRCs, and neuronal avalanches are strongly correlated.

Results

Paradigm for Mapping Individual Behavioral and Neuronal Scaling Laws.

As an experimental task that yields psychometric data for probing the scaling laws of cognitive dynamics (7), we used a factorial audiovisual threshold-stimulus detection task (TSDT) in which the subjects were presented independent and continuous auditory and/or visual stimulus streams. The subjects attended either the visual or the auditory stream, or both streams concurrently, and reported each perceived stimulus in the attended modality. In TSDTs, the stimulus intensity is adjusted before the experiment so that approximately half the stimuli are perceived and then kept constant (Fig. 1A and Fig. S1A) (7, 39). Auditory, visual, and audiovisual tasks revealed complex temporal structures in individual behavioral time series with intermittent sequences of detected (Hits) and undetected stimuli (Misses) (Fig. 1B). We used detrended fluctuation analysis (DFA) to evaluate the underlying scaling laws and found that the Hit–Miss series were characterized by robust LRTCs (Fig. 1C and Fig. S2A; r² = 0.978 ± 0.003, mean ± SD for 56 datasets). At the group level, the behavioral scaling exponents were significantly modulated by both the stimulus modality (auditory/visual) and the task (uni-/bimodal) (Fig. S2A). Nevertheless, although the task effects accounted for 11% of total variance in behavioral scaling exponents, as much as 44% of total variance was attributable to interindividual variability.

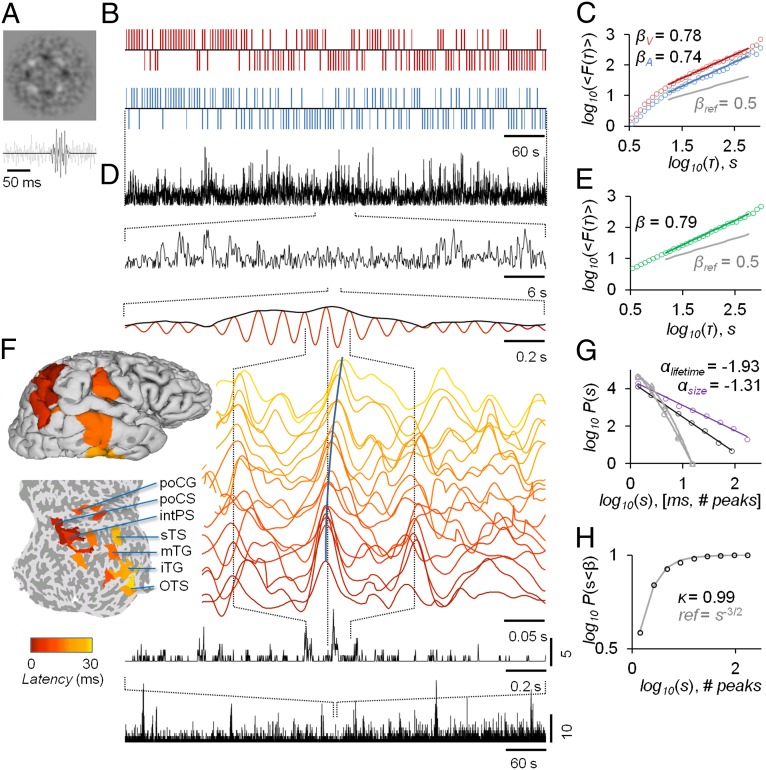
Fig. 1.

Paradigm for mapping individual behavioral and neuronal scaling laws with TSDTs and source-reconstructed M/EEG recordings. (A) Examples of noise-embedded visual and auditory stimuli whose SNRs are tuned before the experiment to yield an ∼50% hit rate and then kept constant (Fig. S1). (B) Behavioral performance time series of detected (upward ticks) and undetected (downward ticks) display rich dynamics in a bimodal audiovisual TSDT (visual, red; auditory, blue; time series are for the first 10 min of a 30-min session of a representative subject). (C) Visual and auditory detection time series exhibit LRTCs that may be characterized for each subject by DFA exponents, β_V and β_A. (D) Amplitude fluctuations of neuronal oscillations in local cortical patches (here, 10 Hz in the inferior parietal gyrus) are fractally self-similar and (E) show robust LRTC. (F) Avalanche dynamics are salient in source-reconstructed broad-band data. The time series of cortical patches in the example avalanche (see also Fig. S3A) are color coded by the peak latency. These colors correspond to those displayed on pial and flattened cortical surfaces and show the progression of this activity cascade from posterior parietal to temporal and postcentral loci. (Bottom) The avalanche time series (black lines) show the number of cortical patches in which a peak was found, with zeros indicating interavalanche periods. (G) The sizes and lifetimes of cortical avalanches are approximately power-law distributed with exponents, α, close to those of a critical branching process (−1.5 and −2, respectively). (H) In line with this notion, the kappa index, κ, for the size distribution is close to 1. All data in this figure are from the same 30-min session of a subject representative in having β closest to population mean.

To test whether the scaling laws of neuronal activity underlie the interindividual variability in the behavioral scaling laws, we used M/EEG for noninvasive measurements of ongoing brain activity and source reconstruction methods for transforming filtered M/EEG data into time series of 400 patches fully covering the cortical surface (Materials and Methods). We extracted amplitude fluctuations of ongoing cortical oscillations with narrow- (Fig. 1D) and broad-band filters. The scaling exponents of LRTCs in neuronal amplitude fluctuations then were estimated with DFA (Fig. 1E). These source-level data revealed fractal amplitude fluctuations (Fig. 1D) and hence corroborate earlier M/EEG sensor-level (12) and electrocorticographic (40) investigations in revealing highly robust LRTCs in all studied frequency bands (r² = 0.993 ± 0.0006; Fig. S2B). The mean LRTC scaling exponents of 10-Hz amplitudes were significantly different among the three task conditions (Fig. S2B).

To obtain a complementary view of the scaling laws of human brain dynamics, we searched for neuronal avalanches—uninterrupted cascades of large-magnitude events across the cortical surface—by using broad-band filtered data and peak detection (34). These events were salient in source-reconstructed M/EEG data (Fig. 1F and Fig. S3A) and were characterized by power-law size and lifetime distributions with exponents close to those of a critical branching process (−1.5 and −2, respectively (33) (Fig. 1 G and H). To confirm the power-law nature of these distributions, we reproduced all analyses with surrogate data. Although the size and lifetime distributions of surrogate data were fit by exponentials better than by power laws (P < 10⁻⁴, T test), the original data were much better represented by a power-law than by an exponential (P < 10⁻¹⁰, T test; for further corroboration, see Fig. S3 B–D). Like those of LRTCs, the scaling exponents of neuronal avalanches were modulated by the tasks (Fig. S3 B and C). To confirm that the LRTCs and neuronal avalanches in these data were not attributable to artificial sources, we reproduced these analyses on inverse-modeled empty-room magnetoencephalography (MEG) data as well as on forward- and inverse-modeled simulated uncorrelated brain activity. These control experiments rule out the possibility that environmental or instrument noise, the mixing of neuronal signals at the scalp level, or the source reconstruction methods might contribute to the power-law scaling behavior of LRTCs and avalanches found here to characterize brain activity (Fig. S4).

Neuronal and Behavioral Scaling Laws Are Correlated.

To test our hypothesis of a relation between power-law scaling of brain activity and behavior, we first averaged the DFA exponents across brain regions and task conditions. Individual variation in the DFA exponents of the behavioral time series exhibited a remarkable dependence on the LRTCs of 10-Hz oscillations, whether estimated from task data or from separate resting-state data (Fig. 2A). A similar relationship was found throughout frequency bands from 5 to 30 Hz, for broad-band amplitudes, and for the DFA exponents of the avalanche time series (Fig. 2B). Interestingly, the short–time scale avalanche dynamics, as quantified by the power-law exponents of size or lifetime distributions, also were correlated with the behavioral scaling exponents in both task- and resting-state data (Fig. 2C and Fig. S5 A and B). Hence, a large fraction of interindividual variability in behavioral scaling laws is explained linearly by corresponding variability in the neuronal scaling laws.

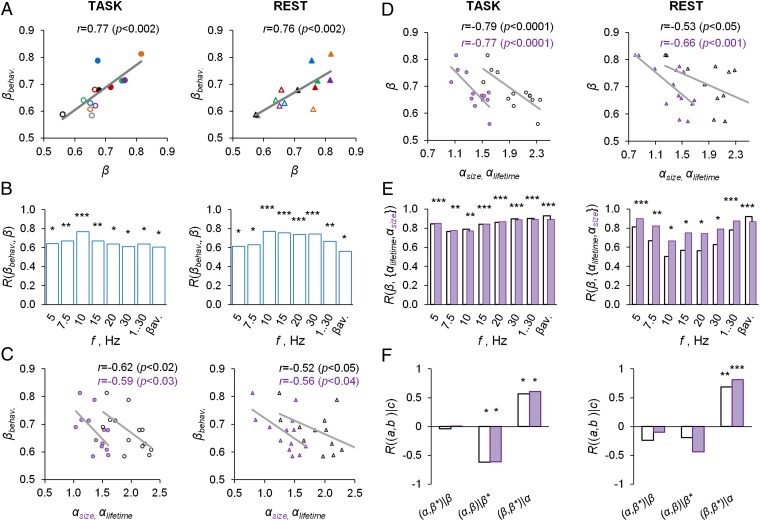
Fig. 2.

Scale-free neuronal dynamics are correlated with interindividual variability in behavioral scaling laws. (A) Mean local LRTCs in the 10-Hz band (β) both during the TSDT task performance and in a separate resting-state session are correlated with the mean behavioral scaling exponents (β_behav.). (B) This correlation was significant in frequency bands from 5 to 30 Hz, in broad-band data, and for the avalanche DFA (*P < 0.05, **P < 0.01; ***P < 0.005). (C) Scaling exponents of the size (purple) and lifetime (black) distributions of neuronal avalanches in task- and resting-state data are correlated with the behavioral scaling exponents. (D) The LRTC scaling exponents of neuronal amplitude fluctuations in the 10-Hz and (E) all other studied frequency bands are strongly correlated with the scaling exponents of neuronal avalanches. (F) Partial correlation analysis shows that neuronal LRTCs also are correlated with behavioral LRTC when the contribution of neuronal avalanches is factored out and that the correlation between avalanches (α) and behavioral LRTC (β*) is mediated through the correlation between neuronal LRTCs (β) and avalanches (see also D and E).

To test whether arousal fluctuations driven by the autonomic nervous system played a role in this correlation, we characterized the scaling behavior of heart-rate fluctuations and evaluated the correlation of these scaling exponents with those of behavioral and neuronal (10-Hz) LRTCs during task performance (Fig. S6 A–D). The scaling exponents of heart-rate variability indeed were correlated with both neuronal and behavioral exponents, but a partial correlation analysis revealed that the correlation with behavior was indirect and that the neuronal LRTCs were a mediating variable (Fig. S6E). The same result was found when comparing heart-rate and neuronal LRTCs measured during rest with task-state behavioral LRTCs (Fig. S6 F–H).

We then tested our second hypothesis about whether the LRTC and avalanche dynamics were related. The LRTCs of 10-Hz oscillations were strongly correlated with the scaling exponents of neuronal avalanches (Fig. 2D and Fig. S5B). Surprisingly, the correlation between LRTCs and avalanches was even more pronounced in the other frequency bands (Fig. 2E). These data thus indicate that short (10⁻³−10⁻¹ s) and long (10⁰−10³ s) time-scale neuronal dynamics are related and correlated with behavioral scaling laws. The correlation between neuronal LRTCs and avalanches raises the question of whether they both are directly correlated with the behavioral scaling laws. We addressed this question with a partial correlation analysis and found that, in fact, the correlation of neuronal avalanches with behavior was fully explained by their correlation with neuronal LRTCs, although factoring out the contribution of neuronal avalanches did not alter the correlation between neuronal and behavioral LRTCs (Fig. 2F).

Specific Cortical Regions Underlie the Correlation Between Neuronal and Behavioral Scaling Laws.

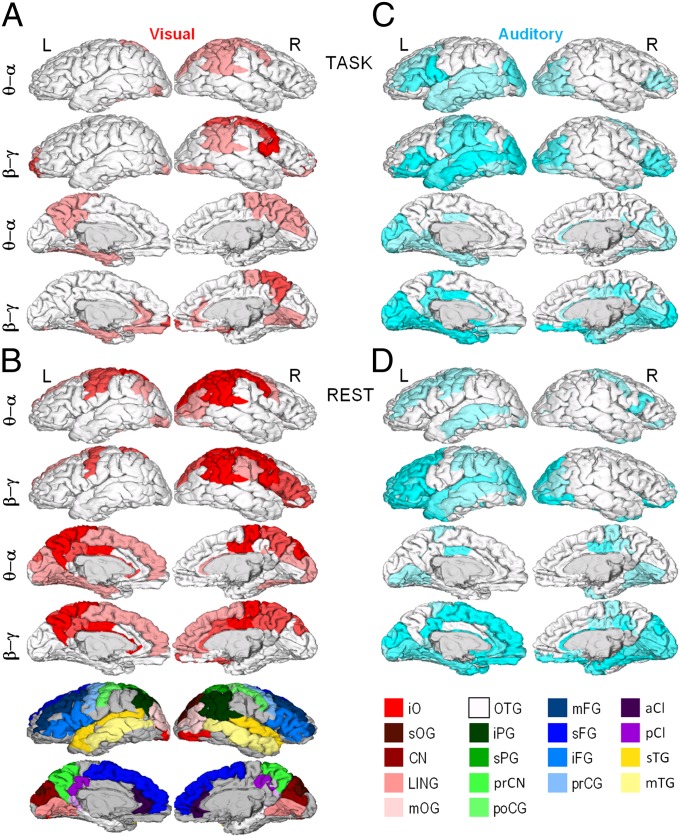
The cortical structures underlying brain–behavior correlations were identified by correlating the DFA exponents of each cortical patch with the exponents of the behavioral scaling laws. For clarity, we collapsed the data into θ/α (5, 7.5, and 10 Hz) and β/γ (15, 20, and 30 Hz) frequency bands. In both θ/α and β/γ bands, visual behavioral LRTCs were correlated with neuronal LRTCs during task performance in the posterior parietal cortex and, in the β/γ band, also in the cuneus and inferotemporal visual regions. These cortical regions are task relevant in supporting visual attentional and representational functions, respectively. In addition, however, neuronal and behavioral LRTCs in the visual task were correlated in assumingly task-irrelevant sensorimotor regions and in those belonging to the default mode system, such as the posterior cingulate, precuneus, medial prefrontal cortex, and inferior parietal cortex (Fig. 3A). These observations are well in line with the notion that the detection-probability fluctuations in TSDT experiments may be determined largely by antagonistic (41) fluctuations of modality-specific attentional and default-mode systems (1, 19). When comparing the visual behavioral LRTCs with neuronal LRTCs in the resting state, we found a similar, albeit more widespread, anatomical pattern of correlations (Fig. 3B). This suggests that individual endogenous brain dynamics largely are preserved during the tasks. The resting-state data also show that the brain–behavior correlation of LRTCs in the sensorimotor system cannot be explained simply by motor response–related amplitude transients during task performance. Additional analyses of sensorimotor amplitude time series and motor responses showed that even during task performance, the motor responses do not bias the correlation between sensorimotor and behavioral LRTC exponents or introduce artificial correlations (Fig. S7). Similar to the visual modality, the comparison of neuronal and behavioral scaling laws in the auditory task revealed significant correlations in both task-relevant and -irrelevant regions, although the neuronal correlates of the behavioral scaling laws in visual and auditory tasks clearly involved distinct cortical regions (compare Fig. 3 A and B with C and D). Task-relevant structures included predominantly the inferior frontal and superior temporal gyri that support auditory attentional and sensory processing, respectively, as well as the anterior cingulate and insula (Fig. 3C). Neuronal LRTCs in the conceivably task-irrelevant visual cortical areas in the occipital and inferotemporal cortices, however, also were strongly correlated with behavioral LRTCs in the auditory task. Importantly, these regions together closely match those found to be correlated with auditory TSDT performance in fMRI (42). A similar anatomical pattern also was observed in the resting state (Fig. 3D), corroborating the notion that endogenous neuronal dynamics are preserved during task performance.

Fig. 3.

Neuronal correlates of behavioral scaling laws. Pearson correlation coefficients were computed between β_behav. and β in the six narrow-frequency bands for each cortical patch (Fig. 2B), and significant (P < 0.05, FDR corrected) correlations were displayed on cortical surfaces collapsed into θ/α (5, 7.5, and 10 Hz) and β/γ (15, 20, and 30 Hz) frequency ranges. For each cortical patch of the Destrieux parcellation, the color intensity indicates the fraction of significant correlations across the three bands (pale, 1/3; medium, 2/3; full, 3/3). (A) Correlation of visual behavioral scaling exponents, β_V, with the β of neuronal LRTCs during visual task performance. (B) Correlation of β_V with β in separate resting-state data. (C) Correlation of auditory behavioral scaling exponents, β_A, with the β of neuronal LRTCs during auditory task performance. (D) Correlation of β_A with β in separate resting-state data. a, Anterior; C, central; CI, cingulate; CN, cuneus; F, frontal; G, gyrus; i, inferior; LIN, lingual; m, middle; O, occipital; P, parietal; p, posterior; pr, pre; s, superior; T, temporal. Colors: red, occipital; green, parietal; blue, frontal; yellow, temporal; purple, cingulate. iPG shows the angular part.

Discussion

In the present study, we found that the strength of autocorrelations in neuronal oscillations during task performance, as indexed by individual LRTC scaling exponents, was correlated with the LRTCs in behavioral time series. Importantly, these behavioral scaling exponents were correlated with neuronal exponents also measured during the performance of another task or during rest, indicating that the relationship is not specific to the concurrent task (Fig. S8) and suggests that this neuronal dynamics arises endogenously. The neuronal sources showing correlations between brain and behavior were localized to task-positive systems, including the visual and auditory cortices, as well as to regions controlling attention. Interestingly, neuronal LRTCs in a subset of the default-mode network (DMN) also were correlated with behavioral LRTCs. These observations are in line with fMRI studies suggesting that out-of-phase slow fluctuations (41) in such task-relevant and task-irrelevant structures, e.g., in somatosensory (43) and auditory (42) TSDTs, predict trial-by-trial variation in behavioral performance. Furthermore, a recent study shows that DMN activity might underlie focused attentional states during continuous performance tasks (44). These BOLD signals and the oscillation amplitude fluctuations, such as those measured in this study, covary in intrinsic connectivity networks (16, 18, 19, 21, 22).

Importantly, because similar albeit more widespread correlations between neuronal and behavioral LRTCs also were observed during rest (Fig. 3), the individual phenotypic variability in neuronal scaling laws may be a determinant of the dynamic nature of variability in task performance. Supporting this idea, LRTCs in oscillations are heritable (45), test–retest reliable (46), and correlated with brain pathologies (40, 47–50). Considering that the exponents of autonomic nervous system fluctuations were correlated only indirectly with behavior (Fig. S6), the intrinsic organization of neuronal networks as reflected in scaling laws of neuronal fluctuations is a likely physiological substrate of the scaling laws governing the variability in psychophysical performance (1, 12).

The notion of phenotypic and individual neuronal scaling laws is in line with computational modeling showing that emergent fluctuations in resting-state neuronal activity with realistic structural connectivity exhibit spatiotemporal power-law scaling (51). The individual variability in the scaling laws of neuronal avalanches, LRTCs, and behavior thus might arise mechanistically from the dynamics of neuronal activity in the individual brain architecture of structural connectivity (30, 38, 52, 53) together with individual variability in the expression of cellular level mechanisms (54–56) that regulate, for instance, the excitation–inhibition balance (38). Neuronal avalanches appear phenomenologically distinct from LRTCs in that they involve a spatial dimension and time scales much shorter than those typically associated with LRTCs (10⁻³−10⁻¹ vs. 10⁰−10³ s, respectively). Nevertheless, as predicted theoretically (38), we found that the power-law exponents of avalanche size and lifetime distributions were strongly correlated with those of LRTCs in a range of frequency bands. Although the avalanche exponents also were correlated with behavioral LRTCs, this relationship was indirect and mediated by neuronal LRTCs. We suggest that neuronal avalanches and oscillations exhibiting LRTCs coemerge in near–critical-state brain dynamics and reflect propagating neuronal activity at widespread spatial and temporal scales.

Criticality has gained widespread interest in neuroscience as a framework for understanding the character and functional implications of variability in brain activity (12, 30, 32). The metastability of critical systems maximizes their dynamic range (57), storage capacity (58), and computational power. Fractal self-similarity, power-law scaling behavior, and “1/f noise” at the phenomenological level are typical for systems exhibiting “avalanche dynamics” and operating in a critical (37) or self-organized critical state (59). Nevertheless, the fact that numerous complex systems exhibit similar dynamics raises the question of whether fractal neuronal dynamics are an epiphenomenon without functional relevance. Our results contribute to this context in two respects. First, the discovery that neuronal scaling only in well-delineated and task-specific brain systems is correlated with human behavioral scaling suggests that neuronal criticality is not epiphenomenal. Second, the observations of LRTCs and neuronal avalanches with power-law size and lifetime distributions add to the growing body of data suggesting that the human brain operates near a critical regime (12, 30, 32, 33), which may fundamentally determine the dynamics of human perceptual, cognitive, and behavioral processes.

Materials and Methods

Subjects and Stimuli.

Fourteen healthy subjects (seven females) participated in the experiment, which comprised three continuous 30-min M/EEG task-state recordings followed by a 10-min resting-state recording. In each of three 30-min task-state experiments, continuous, concurrent, and uncorrelated series of constant-intensity noise-embedded threshold-level auditory and visual stimuli were presented. The interstimulus interval ranged from 1.5 to 6 s, with a mean of 3.75 s, yielding a total of 480 auditory and visual stimuli per experiment. Before each experiment, the subject was instructed to indicate the perception of each stimulus in the attended sensory modality by pressing a button with the index finger (left/right hand pseudo-randomly counterbalanced across subjects). In the three randomly ordered task-state recordings, the tasks were to attend the auditory (A), the visual (V), or both (B) stimuli. Before the onset of the experiment, the intensities of auditory and visual stimuli with respect to the continuous background, as indexed by a signal-to-noise ratio (SNR), were calibrated separately to yield an initial detection probability (hit rate, HR) of ∼50%. After calibration, these SNR values were kept constant throughout the experiment.

M/EEG Recordings and Source Reconstruction.

We recorded 366-channel M/EEG data with 204 planar gradiometers, 102 magnetometers, and 60 EEG electrodes (Elekta Neuromag Ltd.) at a 600-Hz sampling rate. The MaxFilter software was used to suppress extracranial noise and to colocalize the signal space data from different recording sessions and subjects. For cortical surface reconstructions, we recorded T1-weighted (magnetization-prepared rapid gradient echo) anatomical magnetic resonance images at a ≤ 1 × 1 × 1-mm resolution with a 1.5-T MRI scanner (Siemens). This study was approved by the Ethical Committee of Helsinki University Central Hospital and was performed according to the Declaration of Helsinki. Written informed consent was obtained from each subject before the experiment. FreeSurfer software was used for automatic volumetric segmentation of the MRI data, surface reconstruction, flattening, cortical parcellation, and labeling with the Destrieux atlas; the MNE software was used to create three-layer boundary element conductivity and cortically constrained source models, to colocalize M/EEG–MRI data, and to prepare the forward and inverse operators (SI Materials and Methods). M/EEG time series were filtered into seven frequency bands, f. A bank of Morlet wavelets (f = 5, 7.5, 10, 15, 20, and 30 Hz) yielded narrow-band data and a finite impulse-response filter was used for broad-band filtering from 0.1 to 45 Hz (pass-band from 1 to 30 Hz). After filtering, M/EEG sensor data were inverse transformed and then collapsed into time series of 400 cortical patches with individual fidelity-optimized parcellations (FOPs; SI Materials and Methods). Statistics and visualization were performed in the 148-patch Destrieux parcellation. The scaling exponent of each Destrieux parcellation patch was calculated by averaging the exponents of corresponding subpatches in the FOPs.

Estimation of Neuronal and Behavioral Scaling Laws.

The monofractal scaling exponents of neuronal and behavioral LRTCs were estimated with DFA (12) of band-amplitude envelopes and Hit–Miss time series (SI Materials and Methods). A single neuronal avalanche was defined as a set of continuous samples in which one or more peaks in broad-band filtered data were observed. The number of peaks in the avalanche was taken as its size and the time spanned by the samples as its lifetime. The scaling exponents of the size and lifetime distributions then were estimated as in ref. 34 and the κ indices as in ref. 58 (for details, see SI Materials and Methods).

Statistical Analysis.

The correlations among neuronal and behavioral LRTC scaling exponents and those of avalanche dynamics were assessed with Pearson correlation coefficients. In Fig. 2, the behavioral scaling exponents were averaged across conditions (β_behav.; Fig. 2A), the neuronal scaling exponents were averaged across patches and task conditions for each frequency band (Fig. 2B), and the significance of the correlation coefficient was assessed with t-statistics: 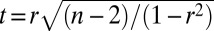, where r is the correlation coefficient and n is the sample size (number of subjects). To measure the degree of association between β_behav., β, and α_{lifetime/size}, we used a partial correlation analysis by computing Pearson correlation coefficients between each pair of sets, regressing out the effect of the third set (Fig. 2F and Fig. S6).

In Fig. 3, the correlation between behavioral scaling exponents and the patchwise neuronal scaling exponents was estimated with the Pearson correlation coefficient as above. To identify the most central cortical regions underlying behavioral scaling laws separately for the auditory and visual modalities, the fraction of significant coefficients (P < 0.05, corrected for multiple comparisons) was assessed in the unimodal tasks (Fig. 3). False discovery rate (FDR) control was applied to correct the statistical significance for multiple comparisons collectively across all cortical regions and the six frequency bands.

To estimate the task and modality effects on the behavioral scaling exponents, two-way ANOVA was applied with task (auditory/visual) and modality (uni-/bimodal) as the independent variables and the scaling exponents were computed for each subject and condition as the dependent variables. The task effect for the neuronal and avalanche scaling exponents was estimated using one-way ANOVA with condition (either auditory/visual/audiovisual or task/rest) as the independent variables and scaling exponents of each subject and condition as the dependent variable.