Abstract
Biphasic contact analysis is essential to obtain a complete understanding of soft tissue biomechanics, and the importance of physiological structure on the joint biomechanics has long been recognized; however, up to date, there is no successful developments of biphasic finite element contact analysis for 3D geometries of physiological joints. The aim of this study is to develop a finite element formulation for biphasic contact of 3D physiological joints. The augmented Lagrangian method was used to enforce the continuity of contact traction and fluid pressure across the contact interface. The biphasic contact method was implemented in the commercial software COMSOL multiphysics. The accuracy of the implementation was verified using 3D biphasic contact problems, including indentation with a flat-ended indenter and contact of glenohumeral cartilage layers. The ability of the method to model multibody biphasic contact of physiological joints was proved by a 3D knee model. The 3D biphasic finite element contact method developed in this study can be used to study the biphasic behaviors of the physiological joints.
Keywords: biphasic contact, augmented Lagrangian method, finite element method, articular cartilage, knee joint
1 Introduction
Osteoarthritis is a degenerative disease that affects cartilage and subchondral bone of articulating joints. Mechanical behavior of the articular cartilage has long been associated with the initiation of this disease. Clinical and animal studies have been used to test these hypotheses; however, not all of the mechanical components can be measured, and not all of the observed failures are at the surface of the tissues (Freeman, 1975). Because of this fundamental limitation of experimental measures, a numerical solution of articular cartilage is essential to obtain a more complete understanding of the diarthrodial joint biomechanics.
Biphasic theory (Mow et al., 1980) has been widely used to model biomechanical behavior of hydrated soft tissues, such as articular cartilage and meniscus. It considers hydrated soft tissues as mixture of a porous-permeable solid phase and an interstitial fluid phase. Analytical solutions for the biphasic contact mechanics in axisymmetric joints have been developed (Ateshian et al., 1994; Ateshian and Wang, 1995; Wu et al., 1997; Wu et al., 1998a), but these solutions apply to fairly idealized problems. In order to investigate the biomechanical behavior of human diarthrodial joints which are tremendously complex, it is necessary to use numerical methods, such as the finite element method. Donzelli and Spilker (Donzelli and Spilker, 1998; Donzelli et al., 1999) implemented a Lagrange multiplier finite element method to investigate the contact mechanics of biphasic cartilage layers in 2D under small deformations, and they found that the surface curvature of articular cartilage significantly changed the stress and strain in the tissue. Yang and Spilker (Yang and Spilker, 2007) extended the Lagrange multiplier finite element method to 3D contact problems. Chen et al. (Chen et al., 2005) investigated contact mechanics of biphasic cartilage layers in 2D under large deformations and sliding, also using a Lagrange multiplier method, whereas Ateshian et al. (Ateshian et al., 2010) used an augmented Lagrangian method to investigate biphasic contact mechanics in 3D. Beside self-developed biphasic contact programs, the commercial finite element software ABAQUS is a program widely used to study soft tissue contact (Federico et al., 2004; Pawaskar et al., 2010; Pawaskar et al., 2011; Warner et al., 2001; Wu et al., 1998b). However, the ‘drainage-only-flow’ boundary condition implemented in ABAQUS (i.e. the fluid only flows from the interior to the exterior of the cartilage layer) is inconsistent with the equation of conservation of mass across the contact interface (Hou et al., 1989). Recently, Guo and Spilker developed an augmented Lagrangian method for 2D and 2D axisymmetric contact problems of cartilage layers, and implemented it in COMSOL Multiphysics (Guo et al., 2012a; Guo et al., 2012b; Guo and Spilker, 2011a; Guo and Spilker, 2011b).
In sum, though the importance of physiological structure and fluid flow on the joint biomechanics has long been recognized (Fithian et al., 1990), to date, there have been no successful developments of biphasic finite element contact analysis for 3D geometries of physiological joints. The aim of this paper is to extend the augmented Lagrangian method developed in our previous study (Guo et al., 2012b; Guo and Spilker, 2011b) to 3D contact problems. Several example problems are provided to verify the accuracy of the method. The ability of the method to simulate multibody biphasic contact of physiological joint is proved via a 3D knee model with physiological geometries.
2 Methods
The velocity-pressure (v-p) formulation of infinitesimal deformation linear biphasic theory (Almeida and Spilker, 1997) was adopted in this study based on its robustness with tetrahedral elements. A standard continuum mechanics nomenclature was adopted, and the indicial notation was used. The governing equations are
| (1) |
| (2) |
where superscripts s and f refer to the solid and fluid phases, respectively; is the solid phase velocity, which is the time derivative of the solid phase displacements ; κ is the permeability of the fluid phase; p is the fluid pressure; (),i denotes the partial derivative; and are the solid and fluid phase stress tensors; is the solid phase strain tensor (the superscript s is omitted); is the material property tensor of the solid phase; and δij is the Kronecker delta. The solid phase and fluid phase stress tensors are defined as:
| (3) |
| (4) |
where φs and φf are the solid and fluid volume fractions, respectively, for the saturated (φs + φf = 1) mixture.
The initial and boundary conditions on the non-contacting boundaries are
| (5) |
| (6) |
| (7) |
| (8) |
| (9) |
where an over-bar signifies a prescribed value of the quality; the subscript ()0 denotes an initial value; total stress is defined as the sum of the fluid and solid stress, ; and the relative fluid flow is defined as or Q =−κp,ini. The boundaries Γβ, β=u, v, p, t, and Q, correspond to portions on which displacement, velocity, pressure, total traction, and relative flow, respectively, are prescribed.
Biphasic contact boundary conditions were taken from the theoretical work of Hou et al. (Hou et al., 1989), and they were defined as
| (10) |
| (11) |
| (12) |
| (13) |
where superscripts A and B refers to two deformable bodies. These equations correspond to kinematic conditions on the continuity of location of points in contact, Eq. (10); continuity of the relative flow across the contact boundary, Eq. (11); kinetic continuity conditions on the fluid pressure, Eq. (12); and the normal component of solid phase elastic stress, Eq. (13), on the contact boundary. The continuity equation of the relative flow across the contact boundary, Eq. (11), is under the assumption that the permeability is isotropic and constant.
To enforce the contact constraint, the augmented Lagrangian framework for single-phase contact problem (Simo and Laursen, 1992) was adapted to the current biphasic contact framework (Table 1). An augmentation component was introduced for the contact pressure, and an additional iteration level was added where the usual displacement and fluid pressure variables were solved separately from the contact pressure. The algorithm repeated this procedure until it fulfilled a convergence criterion.
Table 1.
Augmented Lagrangian algorithm for biphasic contact of soft tissue

|
where tn is the normal component of the contact pressure; ηn is the normal penalty factor with units of force per volume; g is the gap distance between the destination boundary and source boundary; GTOL is the tolerance for gap distance
The biphasic contact equations were implemented in commercial finite element software (COMSOL Multiphysics 4.2®, COMSOL, Inc., Burlington, MA). As with earlier biphasic implementations in COMSOL (Guo and Spilker, 2011b; Spilker et al., 2009), solid mechanics from the Structural Mechanics Module and Darcy’s Law from the Earth Science Module were combined and coupled to obtain the biphasic equations. A contact pair was used to enforce contact constraint for the solid phase, and an identity pair was used to enforce fluid continuity constraint for the fluid phase (for details see Appendix A).
3 Example Problems
3.1 Indentation test
Indentation experiments are frequently used to study the biomechanical properties of articular cartilage. A mathematical solution was developed by Mak et al. (Mak et al., 1987). Spilker et al. (Spilker et al., 1992) presented a finite element solution, but the porous indenter was modeled as a free draining boundary and the contact between the indenter and the cartilage was not modeled. In 2007, Yang and Spilker (Yang and Spilker, 2007) modeled the 3D indentation test, and they used Lagrange multiplier method to model the biphasic contact. In this study, biphasic indentation test with flat-ended indenter was used to verify that the contact algorithm functioned as expected.
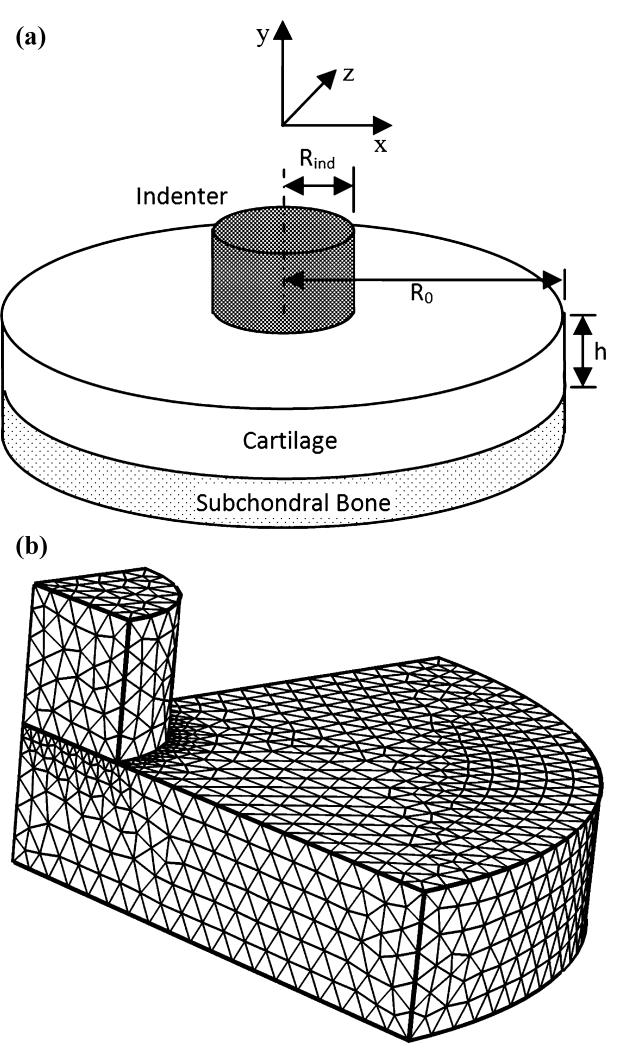
The indentation with a flat-ended indenter was modeled (Figure 1). A layer of soft tissue of uniform thickness, h=0.75 mm, was attached to subchondral bone at its lower surface, and indented normal to the tissue surface by a flat-ended cylindrical indenter of radius and height, Rind =0.75mm. The radius of soft tissue was R0=4Rind mm since a previous study has demonstrated that the tissue response is negligible for R0<4Rind (Spilker et al., 1992). The subchondral bone was modeled as an impermeable, fixed surface. The top surface of the indenter was subjected to a displacement of −0.075mm in a ramp time of 500s and then held. A free-draining boundary condition was applied on the top surface of the indenter and on the cartilage surface outside of the contact area. Material properties of the cartilage were Young’s modulus E = 0.5417 MPa, Poisson’s ratio ν = 0.0833, permeability κ = 4.0 × 10−15m4N−1S−1, and solid content φs = 0.2. Material properties of the indenter were E = 541.7MPa ,ν = 0.125, κ = 4.0 × 10−12m4N−1s−1, and φs = 0.95. The model was discretized with a total of 22998 tetrahedral elements. The bottom surface of the indenter was set as source boundary, and the top surface of the cartilage was set as destination boundary. To get a better computational solution, the destination boundary had finer mesh than the source boundary.
Figure 1.
A schematic diagram of the biphasic indentation test with a flat-ended cylindrical indenter (a) and meshed quadrant of the model (b).
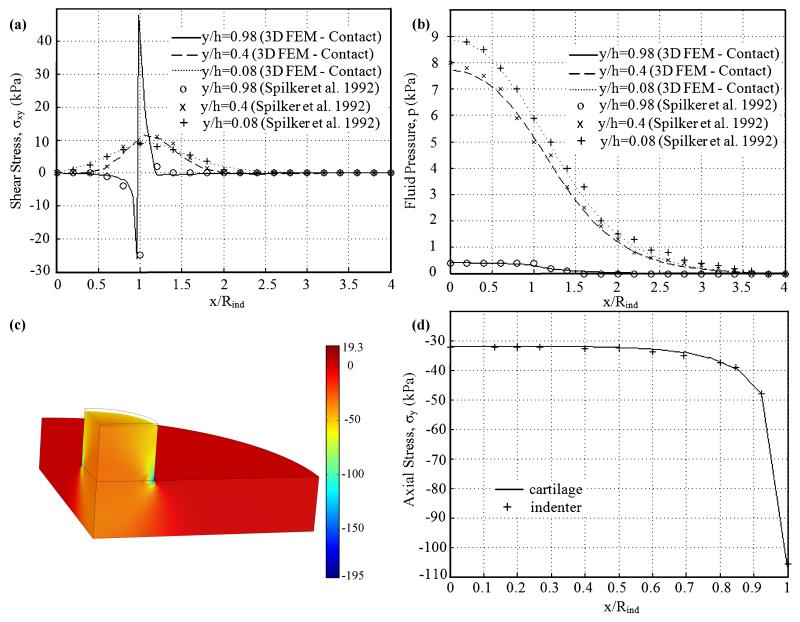
Results on shear stress σxy, and fluid pressure p, at several depths were in good agreement with a previous study (Figure 2). For shear stress at the top level of the cartilage (Figure 2a), smooth distribution was found under the loaded surface; minimum values were found at the inside edge of the indenter; shear stress increased rapidly to a maximum value at the outer edge of the indenter and then decreased rapidly to zero for r>Rind. Shear stress at the middle and bottom level of the tissue varied smoothly with no boundary layers. The fluid pressure (Figure 2b) increased with increasing depth, and varied smoothly.
Figure 2.
Comparison of the shear stress σxy (a), and fluid pressure p (b) at several depths at t=500s predicted by the 3D biphasic contact finite element model and the 2D noncontact model of Spilker et al. (Spilker et al., 1992). Distribution of axial stress (c, in kPa) at t=250s on the deformed geometry. Continuity of axial stress (d) between the two bodies along the contact boundary at t=250s.
Distribution of axial stress (Figure 2c) was in excellent agreement with results of a 3D finite element solution of this indentation problem based on a Lagrange multiplier method (Yang and Spilker, 2007). Large fluid pressure was found at mid-thickness and bottom surface of the tissue under the loaded area, and fluid pressure was negligible at the indenter and the tissue where r>2Rind. Very large negative axial stress was found at the edge of the indenter. Negligible axial stress was found in the tissue for r>Rind. To examine the contact continuity conditions along the contact surface, axial stress between the two bodies along the contact boundary at t=250s were shown (Figure 2d). The continuity conditions were accurately satisfied for both derived quality (axial stress) and primary parameters (displacement and fluid pressure, data not shown). In sum, a biphasic indentation test was modeled in a 3D model. Results at several depths were in good agreement with the published axisymmetric solutions. Distribution of results was consistent with the previous solutions. The satisfaction of continuity conditions was observed. All these results demonstrated the accuracy of the augmented Lagrangian method developed in this study.
3.2 Glenohumeral Joint Contact
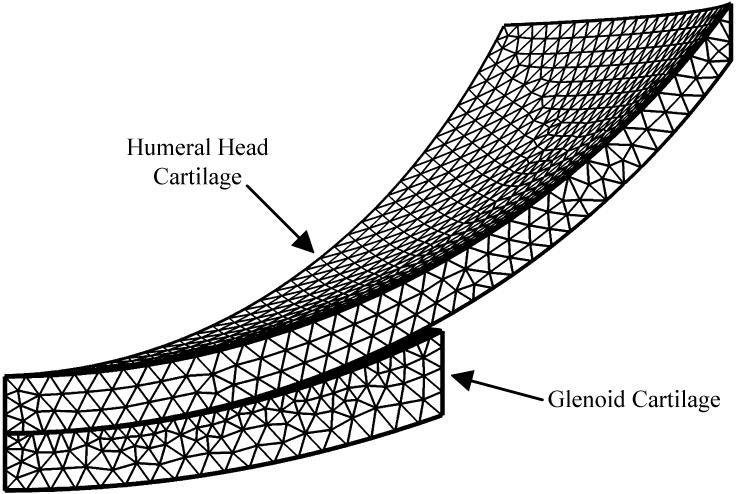
Unlike the indentation test with flat-ended indenter, the glenohumeral joint contact involves evolving contact boundary. Yang and Spilker (Yang and Spilker, 2007) modeled the 3D human glenohumeral joint using a Lagrange multiplier method. The same 3D model of the human glenohumeral joint was developed to compare against the published solution. The geometry of the model (Figure 3) was based on average values of stereophotogrammetric data (Soslowsky et al., 1990). The contact-side radiuses of the glenoid cartilage and the humeral head cartilage were 26mm and 23.5mm, respectively. The bone-side radius of the glenoid cartilage was 34.5mm, and 23.5mm for the humeral head cartilage. The thicknesses at the center were 1.5mm for both cartilages. The width of the glenoid cartilage was 11.5mm, and 19.1mm for the humeral head cartilage. Subchondral bones were assumed to be rigid and impermeable, and were not explicitly modeled. Bone-cartilage interfaces were modeled as impermeable surfaces. A compressive vertical displacement of 0.2mm was applied to the humerus-bone surface in a ramp time of 10s and then held. The glenoid-bone surface was held fixed. The bottom surface of the humeral head cartilage layer was set as source boundary, and the top surface of the glenoid cartilage layer was set as destination boundary. The model was discretized with 18627 tetrahedral elements. To get a better computational solution, the destination boundary had finer mesh than the source boundary. The material properties of the glenoid cartilage (Yang and Spilker, 2007) were Young’s modulus E = 0.559MPa, Poisson’s ratio ν = 0.02, permeability κ = 1.16 × 10−15m4N−1S−1, and solid content φs = 0.2. The material properties of the humeral head cartilage (Yang and Spilker, 2007) were Young’s modulus E = 0.5565MPa, Poisson’s ratio, ν = 0.05, permeability κ = 1.7 × 10−15m4N−1s−1, and solid content φs = 0.2.
Figure 3.
Meshed one-eighth geometry for glenoid and humeral head cartilage layers. Subchondral bones were assumed to be rigid and impermeable, and were not explicitly modeled.
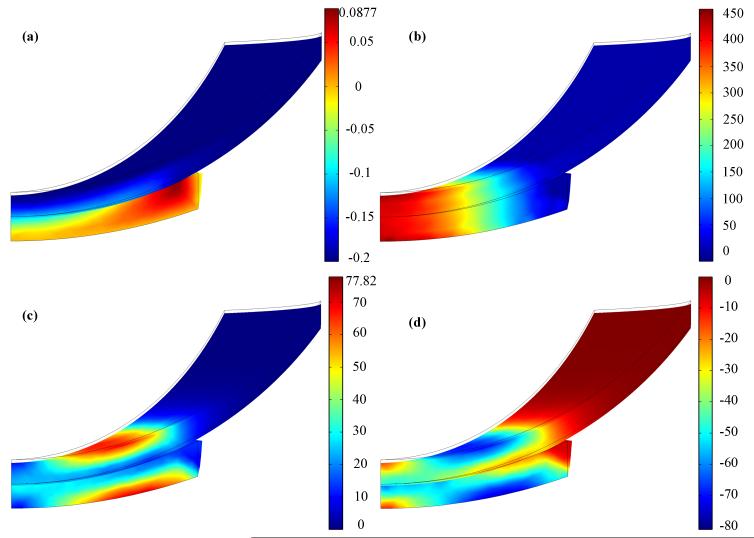
Results of axial displacement (Figure 4a) and fluid pressure (Figure 4b) showed good agreement with the 3D finite element solution based on the Lagrange multiplier method (Yang and Spilker, 2007). Continuity conditions for fluid pressure and displacement across contact interface were accurately satisfied. Tensile deformation was observed at the outer portion of the contact surface. Maximum fluid pressure was found at the center of the glenohumeral cartilage layers and decreased toward the edge of the contact. Maximum and minimum principal elastic stresses for the solid phase are shown in figures 4c and 4d. The solid phase experienced relatively low stress since a large portion of the load was carried by the fluid phase. Peak values of both principal elastic stress occurred at the cartilage-bone interface, away from the center. The circular bands of these peak values were smaller than the contact radius. These findings agreed with Yang and Spilker’s solutions (Yang and Spilker, 2007). All these results demonstrated the accuracy of the present biphasic contact method.
Figure 4.
Distributions of axial displacement (a, in mm), fluid pressure (b, in kPa), maximum principal elastic stress (c, kPa), and minimum principal elastic stress (d, kPa) of the shoulder cartilage on the deformed geometry at 10 s. Boundary lines are initial position.
3.3 Knee Joint Contact
Up to now, most of the finite element models of the knee joint consider cartilage and meniscus as solid. Several biphasic models of the knee joint (Donzelli, 1995; Guo et al., 2012a; Wilson et al., 2003; Zhang, 2000) have been developed to study the interaction between the fluid and solid matrix of the soft tissues during loading. Donzelli (Donzelli, 1995) presented a biphasic solution of the 2D axisymmetric knee using the Lagrange multiplier method, but the ability of the implementation to solve the 3D physiological knee model has not yet been demonstrated. Zhang et al. developed a magnetic resonance image based 3D biphasic finite element model of the human knee joint (Zhang, 2000). But physiological contact problems were not solved because fluid flow was assumed not to take place between contact surfaces, which is inconsistent with the equation of conservation of mass across the contact interface (Hou et al., 1989). Wilson et al. (Wilson et al., 2003) developed a 2D axisymmetric biphasic model of human knee to study the initiation of the osteoarthritis. However, they assumed that no fluid flow takes place between contact surfaces. Furthermore, their model included a thin flexible membrane with a low stiffness that was inserted between the articular cartilage layers and the meniscus - the membrane could absorb most of the applied load, which is not physiologically meaningful. Guo and Spilker (Guo et al., 2012a) recently presented a theoretically consistent 2D axisymmetric solution of the knee joint. In sum, up to now, there is no theoretically consistent 3D biphasic physiological knee model.
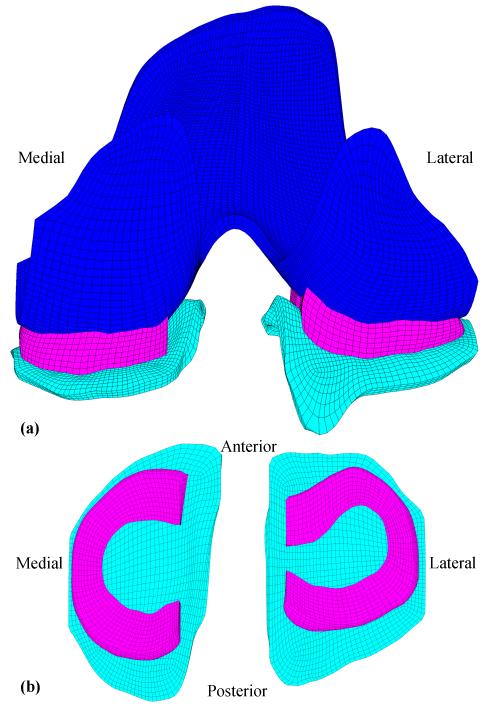
Biphasic contact of a 3D physiological knee joint was modeled in this study, and this 3D knee model was used to verify the ability of the biphasic contact method to model contact of physiological structures. The geometries of the model were from the Open Knee model (Erdemir and Sibole, 2010), which is an open source 3D finite element representation of the knee joint: the knee specimen (female, 70 years) was imaged using a 1.0 Tesla extremity MRI scanner; geometries of tissue structures were provided in IGES format; the model was meshed using TrueGrid. Because this study focused on the biphasic contact of the 3D knee joint, only soft tissues were included in this study (Figure 5). The model consisted of 35313 hexahedral elements.
Figure 5.
(a) Posterior view of the finite element model of the human knee soft tissues, including femoral cartilages, menisci, and tibial cartilages. (b) Top view of the menisci and tibial cartilages.
Three contact pairs were defined in the medial and lateral sides of the knee joint, respectively, to detect contact between the femoral cartilage and tibial cartilage (1), tibial cartilage and meniscus (2), and meniscus and femoral cartilage (3). The bottom surfaces of the tibial cartilages were held fixed, and the top surface of the femoral cartilage was subjected to a compressive axial displacement of 0.8 mm applied in a ramp time of 100s and then held. Fluid continuity condition was applied to the contact area of the cartilages and menisci. Free draining boundary conditions were applied on the peripheral surfaces and surfaces outside of the contact area of the cartilages and menisci. Linear isotropic biphasic material properties were used for femoral and tibial cartilages: Young’s modulus E = 0.69MPa, Poisson’s ratio ν = 0.018, permeability κ = 3 × 10−15m4N−1s−1, and solid content φs = 0.25 (Cohen et al., 1993); while transverse isotropic biphasic material properties (Chern et al., 1990; Proctor et al., 1989; Whipple et al., 1985) were used for meniscus: the transverse moduli Er = Es = 0.075MPa, the circumferential modulus Eθ = 100MPa, Poisson’s ratios νrθ = 0.0015, νθz = 2, and νrz = 0.5, permeability κ = 1.26 × 10−15m4N−1s−1, and solid content φs = 0.25. Two cylindrical coordinate systems were defined as material coordinate systems for the menisci: the medial meniscus has a fairly C shape, and the middle point between anterior and posterior horn was set as the origin the cylindrical coordinate system; the lateral meniscus has a fairly circular shape, so the middle point of the lateral meniscus was set as the origin. The four meniscal attachments were modeled as springs with stiffness of 2000 N/mm (Haut Donahue et al., 2002), respectively.
In the initial position, the femoral cartilage was in contact with the menisci and not in contact with the tibial cartilages. As the femoral cartilage pressed down, the menisci had a very large deformation because of its low transverse moduli. Because of the meniscal attachments, the meniscal horn only deformed in the vertical direction, and the deformation in the horizontal direction was neglectable. At the end of the ramp displacement, femoral cartilage was in contact with both menisci and tibial cartilages. During the compression process, the contact algorithm detected correctly the contact in the model.
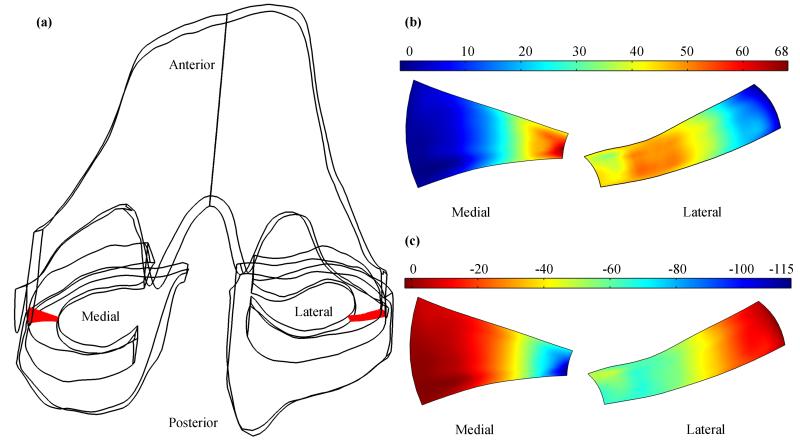
Peak values of fluid pressure were found in the inner one-third part of the medial meniscus and inner two-thirds part of the lateral meniscus (Figure 6b). This observation is consistent with the model settings. The fluid was not allowed to move in or out from the inner surface of the meniscus and was allowed to move in or out from the other three surfaces. Fluid flow meet great resistance at the top and bottom menical surfaces because these two surfaces were in contact with hydrated cartilages, and fluid flow faced no resistance at the peripheral meniscal surafce because of the free draining boundary condition applied; therefore, most of the fluid was moving from the inner part of the meniscus to the periphery, high fluid pressure was created in the inner part of the meniscus, and low fluid pressure in the periphery of the meniscus. Total normal stress (Figure 6c) had similar distributions as the fluid pressure. Distributions of fluid pressure and total normal stress are in good agreement with the 2D axisymmetric solutions (Donzelli, 1995; Guo et al., 2012a). The distributions of total normal stress indicate that the inner part of the meniscus carried most of the compression load. The difference of the medial and lateral distributions of fluid pressure and total normal stress is probably caused by the difference of structures: the medial meniscus is fairly C shape, yet the lateral meniscus is more like a circle. It is of interest in the future study to investigate the effect of the shapes of the menisci on the fluid pressurization and load distribution.
Figure 6.
(a) location of two random meniscal slices (shown as red) in the 3D knee model. Distributions of fluid pressure (b, in kPa) and total normal stress (c, in kPa) at 100s on the selected meniscal slices.
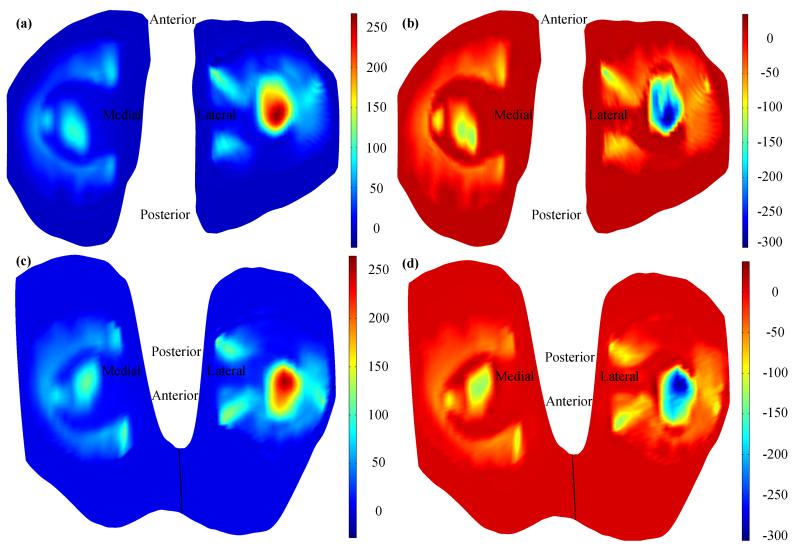
Distributions of fluid pressure on the tibial cartilages (Figure 7a) matched with that on the femoral cartilages (Figure 7c). The match was also observed for the total normal stress (Figure 7b and d). Since the femoral surface of the meniscus and tibial surface of the meniscus had same distributions of fluid pressure and total normal stress (Figure 6b and c), the matches of fluid pressure and total normal stress observed on the tibial cartilages and femoral cartilages indicate that the load applied on the femoral cartilage was transmitted through the fluid phase and solid phase of the menisci; and that the continuity conditions for fluid pressure and total normal stress were accurately satisfied, respectively. Peak values of fluid pressure and total normal stress on the tibial and femoral cartilages were both observed on the lateral side (Figure 7). The peak value of the fluid pressure on the lateral side is approximately 150 kPa larger than that on the medial side, and the peak value of the total normal stress on the lateral side is approximately 160 kPa larger than that on the medial side. The difference of results on the lateral and medial sides is probably caused by the difference of meniscal structures. In the future study, the effect of structure on the distributions of fluid pressure and stress can be investigated using the present 3D knee model.
Figure 7.
Distributions of fluid pressure (a, in kPa) and total normal stress (b, in kPa) on the tibial cartilages, and distributions of fluid pressure (c, in kPa) and total normal stress (d, in kPa) on the femoral cartilages.
In sum, a 3D biphasic model of a physiological knee joint was developed. A normal compression displacement was applied linearly, and the contact algorithm detected correctly the contact in the model during the loading process. The results of fluid pressure were consistent with the model settings. The continuity conditions were accurately satisfied for both fluid pressure and total normal stress. All these results demonstrated the ability of the present augmented Lagrangian method to model 3D biphasic contact of physiological joints.
4 Concluding Remarks
The aim of this study is to develop a 3D biphasic contact method for physiological joints. An augmented Lagrangian finite element method was developed. The finite element formulation was implemented in COMSOL Multiphysics. The accuracy of the 3D implementation was verified using indentation with a flat-ended indenter and contact of idealized glenohumeral cartilage layers. The method’s ability to model multibody biphasic contact was verified by a 3D knee model with physiological geometrics. The method was proven to be robust and able to model 3D biphasic contact of physiological joints. The present biphasic contact method can be used to investigate the fluid pressurization of physiological joints in daily activity and the effect of the physiological structure on the biphasic behaviors of the joints, thus to provide more complete understandings of hydrated soft tissues. One limitation of the 3D augmented Lagrangian method developed in this study is that it only applies to problems with small deformation because of the linear elastic biphasic theory adopted in this study. For problems with finite deformation, hyperelastic biphasic theory (Holmes and Mow, 1990) should be used to replace the linear elastic biphasic theory.
Acknowledgements
This study was supported by a grant from the National Institute of Arthritis and Musculoskeletal and Skin Diseases of U.S. National Institutes of Health (R01 AR057343-01A2).
Appendix A. Implementation of 3D Biphasic Contact Modeling in COMSOL Multiphysics
To obtain the infinitesimal deformation linear biphasic equations, solid mechanics from the Structural Mechanics Module and Darcy’s Law from the Earth Science Module were coupled. The governing equation for the solid mechanics mode is
| (A1) |
and the governing equation for Darcy’s Law mode is
| (A2) |
where ρ is fluid density, g is the magnitude of gravitational acceleration, D is the elevation, and Qm is a mass source term.
The COMSOL user interface is built around the equations and coefficients in the modules, and thus the COMSOL equations and the biphasic equations appeared to be slightly different. To insure that the biphasic equations were exactly represented, the following settings were used:
| (A3) |
| (A4) |
the fluid density, ρ, and porosity, φf, were assumed to be constant, therefore, we have (ρφf),t = 0; finally, the gravity effects were turned off, which set the elevation D to zero. The initial and boundary conditions found in the user interface of COMSOL Multiphysics corresponded to the initial and boundary conditions on the non-contacting boundaries, Eqs. (5-9).
Beside kinematic continuity conditions for displacement and contact traction that a single-phase contact problem consists of (Eqs. 10 and 13), biphasic contact problem has two additional continuity conditions on relative fluid flow and fluid pressure (Eqs. 11 and 12). COMSOL Multiphysics solves single-phase contact problems using an augmented Lagrangian method, and the normal component of the contact pressure is given by
| (A5) |
where g is the gap distance from the destination boundary to the source boundary in the direction normal to the destination surface, and ηn is the normal penalty factor with units of force per volume. The augmented Lagrangian method ensures that the contact boundaries overlap by an acceptably negligible amount g as the penalty factor goes to infinity.
The augmented Lagrangian framework for single-phase contact problem was extended to biphasic contact framework: the contact pair was used to enforce continuity conditions of the solid phase (Eqs. 10 and 13), and the identity pair was used to enforce continuity conditions of the fluid phase (Eqs. 11 and 12). To enforce free-draining boundary condition on the top surface of the soft tissue outside of the contact area, “Atmosphere/Gage” was used as the boundary condition of the identity pair.
References
- Almeida ES, Spilker RL. Mixed and penalty finite element models for the nonlinear behavior of biphasic soft tissues in finite deformation: Part I--alternate formulations. Comput Methods Biomech Biomed Engin. 1997;1(1):25–46. doi: 10.1080/01495739708936693. [DOI] [PubMed] [Google Scholar]
- Ateshian GA, Lai WM, Zhu WB, Mow VC. An asymptotic solution for the contact of two biphasic cartilage layers. J Biomech. 1994;27(11):1347–1360. doi: 10.1016/0021-9290(94)90044-2. [DOI] [PubMed] [Google Scholar]
- Ateshian GA, Maas S, Weiss JA. Finite element algorithm for frictionless contact of porous permeable media under finite deformation and sliding. ASME J Biomech Eng. 2010;132(6):061006. doi: 10.1115/1.4001034. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ateshian GA, Wang H. A theoretical solution for the frictionless rolling contact of cylindrical biphasic articular cartilage layers. J Biomech. 1995;28(11):1341–1355. doi: 10.1016/0021-9290(95)00008-6. [DOI] [PubMed] [Google Scholar]
- Chen X, Chen Y, Hisada T. Development of a finite element procedure of contact analysis for articular cartilage with large deformation based on the biphasic theory. JSME Int J Ser C. 2005;48(4):537–546. [Google Scholar]
- Chern KY, Zhu WB, Kelly MA, Mow VC. Anisotropic shear properties of bovine meniscus; Paper presented at: the 36th Annual Meeting of the Orthopaedic Research Society; New Orleans, LA, USA. 1990. [Google Scholar]
- Cohen B, Gardner TR, Ateshian GA. The influence of transverse isotropy on cartilage indentation behavior-A study of the human humeral head; Paper presented at: the 39th Annual Meeting of the Orthopaedic Research Society; Chicago, IL, USA. 1993. [Google Scholar]
- Donzelli PS. A mixed-penalty contact finite element formulation for biphasic soft tissue [PhD Thesis] Rensselaer Polytechnic Institute; Troy, NY, USA: 1995. [Google Scholar]
- Donzelli PS, Spilker RL. A contact finite element formulation for biological soft hydrated tissues. Comput Methods Appl Mech Eng. 1998;153(1-2):63–79. [Google Scholar]
- Donzelli PS, Spilker RL, Ateshian GA, Mow VC. Contact analysis of biphasic transversely isotropic cartilage layers and correlations with tissue failure. J Biomech. 1999;32(10):1037–1047. doi: 10.1016/s0021-9290(99)00106-2. [DOI] [PubMed] [Google Scholar]
- Erdemir A, Sibole S. Open knee: a three-dimensional finite element representation of the knee joint, user’s guide. version 1.0.0. 2010 [Google Scholar]
- Federico S, Rosa GL, Herzog W, Wu JZ. Effect of fluid boundary conditions on joint contact mechanics and applications to the modeling of osteoarthritic joints. ASME J Biomech Eng. 2004;126(2):220–225. doi: 10.1115/1.1691445. Erratum in: 2005, ASME J Biomech Eng 2127, 2205-2209. [DOI] [PubMed] [Google Scholar]
- Fithian DC, Kelly MA, Mow VC. Material properties and structure-function relationships in the menisci. Clin Orthop Relat Res. 1990;252(1):19–31. [PubMed] [Google Scholar]
- Freeman MA. Pathogenesis of osteoarthrosis, a hypothesis. Ann Rheum Dis, Supplement. 1975;34(1):120–121. [PubMed] [Google Scholar]
- Guo H, Maher SA, Spilker RL. Biphasic finite element analysis of the human knee joint; Paper presented at: the 58th Annual Meeting of the Orthopaedic Research Society; San Fransico, CA, USA. 2012a. [Google Scholar]
- Guo H, Nickel JC, Iwasaki LR, Spilker RL. An augmented Lagrangian method for sliding contact of soft tissue. ASME J Biomech Eng. 2012b;134(8):084503. doi: 10.1115/1.4007177. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Guo H, Spilker RL. An augmented Lagrange finite element implementation for 2D axisymmetric contact of biphasic tissues; Paper presented at: the 37th Annual Northeast Bioengineering Conference; Rensselaer Polytechnic Institute, Troy, NY, USA. 2011a. [Google Scholar]
- Guo H, Spilker RL. Biphasic finite element modeling of hydrated soft tissue contact using an augmented Lagrangian Method. ASME J Biomech Eng. 2011b;133(11):111001. doi: 10.1115/1.4005378. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Haut Donahue TL, Hull ML, Rashid MM, Jacobs CR. A finite element model of the human knee joint for the study of tibio-femoral contact mechanics. ASME J Biomech Eng. 2002;124(3):273–280. doi: 10.1115/1.1470171. [DOI] [PubMed] [Google Scholar]
- Holmes MH, Mow VC. The non-linear characteristics of soft gels and hydrated connective tissues in ultrafiltration. J Biomech. 1990;23(11):1145–1156. doi: 10.1016/0021-9290(90)90007-p. [DOI] [PubMed] [Google Scholar]
- Hou JS, Holmes MH, Lai WM, Mow VC. Boundary conditions at the cartilage-synovial fluid interface for joint lubrication and theoretical verifications. ASME J Biomech Eng. 1989;111(1):78–87. doi: 10.1115/1.3168343. [DOI] [PubMed] [Google Scholar]
- Mak AF, Lai WM, Mow VC. Biphasic indentation of articular cartilage-I, Theoretical analysis. J Biomech. 1987;20(7):703–714. doi: 10.1016/0021-9290(87)90036-4. [DOI] [PubMed] [Google Scholar]
- Mow VC, Kuei SC, Lai WM, Armstrong CG. Biphasic creep and stress relaxation of articular cartilage in compression, theory and experiments. ASME J Biomech Eng. 1980;102(1):73–84. doi: 10.1115/1.3138202. [DOI] [PubMed] [Google Scholar]
- Pawaskar SS, Fisher J, Jin Z. Robust and general method for determining surface fluid flow boundary conditions in articular cartilage contact mechanics modeling. ASME J Biomech Eng. 2010;132(3):031001. doi: 10.1115/1.4000869. [DOI] [PubMed] [Google Scholar]
- Pawaskar SS, Ingham E, Fisher J, Jin Z. Fluid load support and contact mechanics of hemiarthroplasty in the natural hip joint. Med Eng Phys. 2011;33(1):96–105. doi: 10.1016/j.medengphy.2010.09.009. [DOI] [PubMed] [Google Scholar]
- Proctor C, Schmidt MB, Whipple RR, Kelly MA, Mow VC. Material properties of the normal medial bovine meniscus. J Orthop Res. 1989;7(6):771–782. doi: 10.1002/jor.1100070602. [DOI] [PubMed] [Google Scholar]
- Simo JC, Laursen TA. An augmented Lagrangian treatment of contact problems involving friction. Comput Struct. 1992;42(1):97–116. [Google Scholar]
- Soslowsky IJ, Ateshian GA, Mow VC. Stereophotogrammetric determination of joint anatomy and contact areas. In: Mow VC, Ratcliffe TA, Woo SL, editors. Biomechanics of Diarthrodial Joints. Springer-Verlag; Berlin: 1990. pp. 243–268. [Google Scholar]
- Spilker RL, Nickel JC, Iwasaki LR. A biphasic finite element model of in vitro plowing tests of the temporomandibular joint disc. Ann Biomed Eng. 2009;37(6):1152–1164. doi: 10.1007/s10439-009-9685-2. [DOI] [PubMed] [Google Scholar]
- Spilker RL, Suh JK, Mow VC. A finite element analysis of the indentation stress-relaxation response of linear biphasic articular cartilage. ASME J Biomech Eng. 1992;114(2):191–201. doi: 10.1115/1.2891371. [DOI] [PubMed] [Google Scholar]
- Warner MD, Taylor WR, Clift SE. Finite element biphasic indentation of cartilage: a comparison of experimental indenter and physiological contact geometries. Proc Inst Mech Eng Pt H J Eng Med. 2001;215(5):487–496. doi: 10.1243/0954411011536082. [DOI] [PubMed] [Google Scholar]
- Whipple RR, Wirth CR, Mow VC. Anisotropic and zonal variations in the tensile properties of the meniscus; Paper presented at: the 10th Annual Meeting of the Orthopaedic Research Society; 1985. [Google Scholar]
- Wilson W, van Rietbergen B, van Donkelaar CC, Huiskes R. Pathways of load-induced cartilage damage causing cartilage degeneration in the knee after meniscectomy. J Biomech. 2003;36(6):845–851. doi: 10.1016/s0021-9290(03)00004-6. [DOI] [PubMed] [Google Scholar]
- Wu JZ, Herzog W, Epstein M. An improved solution for the contact of two biphasic cartilage layers. J Biomech. 1997;30(4):371–375. doi: 10.1016/s0021-9290(96)00148-0. [DOI] [PubMed] [Google Scholar]
- Wu JZ, Herzog W, Epstein M. Articular joint mechanics with biphasic cartilage layers under dynamic loading. ASME J Biomech Eng. 1998a;120(1):77–84. doi: 10.1115/1.2834310. [DOI] [PubMed] [Google Scholar]
- Wu JZ, Herzog W, Epstein M. Evaluation of the finite element software ABAQUS for biomechanical modelling of biphasic tissues. J Biomech. 1998b;31(2):165–169. doi: 10.1016/s0021-9290(97)00117-6. [DOI] [PubMed] [Google Scholar]
- Yang T, Spilker RL. A lagrange multiplier mixed finite element formulation for three-dimensional contact of biphasic tissues. ASME J Biomech Eng. 2007;129(3):457–471. doi: 10.1115/1.2737056. [DOI] [PubMed] [Google Scholar]
- Zhang H. Geometric and finite element modeling of the tibio-menisco-femoral contact under passive knee motion [PhD Thesis] University of Rochester; Rochester, NY, USA: 2000. [Google Scholar]