Six just-noticeable differences in retinal image quality in 1 line of visual acuity: Toward quantification of happy versus unhappy patients with 20/20 acuity

Abstract

Purpose

To determine the number of JND's of wavefront blur necessary to induce a one line loss of best corrected visual acuity (VA).

Setting

Visual Optics Institute, College of Optometry, University of Houston, Houston, Texas, USA.

Methods

The 3mm wavefront error of a well corrected average eye was scaled to yield 9 small steps of blur quantified in units of log Visual Strehl (log VS). For each level of log VS, 10 unique three line acuity charts were convolved with the resulting point spread functions. Using a temporal forced choice paradigm, subjects compared each test chart to a reference test chart indicating which chart was blurrier. The difference between 80% and 50% on the psychometric functions defined a JND. VA was measured for 6 log VS values. The number of JND's necessary to lose one line of acuity was defined as the change in log VS necessary to lose one line of acuity divided by the 1 JND in log VS.

Results

Linear regression revealed log VS = −2.98 * (logMAR acuity) - 0.31; R² = 0.961. The average JND in log VS is 0.049 ±0.012 resulting in an average of 6.1 JND's per line of log MAR acuity.

Conclusions

The RIQ metric, log VS, is highly correlated with logMAR acuity. The 6 JND's in log VS before 1 line of acuity is lost may provide an objective explanation for the distinction between “20/20 happy” and “20/20 unhappy” and other aberration related clinical complaints when acuity is near normal.

Introduction

Visual performance can be measured in a variety of ways depending on the question of interest (e.g., dark adaptation, color vision, stereo acuity, visual acuity, etc.). Of all the methods to measure visual performance high contrast photopic visual acuity is the most common and universal metric of visual performance in clinical practice.

Change in retinal image quality (RIQ) when large enough will induce a change in visual acuity^1–7. On the other hand, if the change in RIQ is relatively small, there may be a noticeable change in RIQ that is not reflected by a change in acuity³.

To illustrate consider the simulations of the RIQ of the 3 logMAR charts displayed in Figure 1. Panel A of Figure 1 illustrates the retinal image of a diffraction limited (6mm pupil) logMAR chart and represents the best RIQ with which the chart can be imaged on the retina. Similarly, Panel B is designed to illustrate the combined effects of diffraction (6mm pupil) and a small amount of simple defocus blur (0.08 D) designed to produce a noticeable loss in RIQ letter quality but not enough to change acuity. Finally, panel C is designed to illustrate the combined effects of diffraction (6mm pupil) and an amount of simple defocus blur (0.15 D) that alters acuity.

Figure 1.

Panel A – Retinal image simulation of a diffraction limited (6mm pupil) logMAR chart. Panel B – Retinal image simulation of the combined effects of diffraction (6mm pupil) and a small amount of simple defocus blur designed to produce a noticeable loss in RIQ letter and no loss of acuity. Panel C – Retinal image simulation of the combined effects of diffraction (6mm pupil) and an amount of simple defocus blur that alters measured acuity. Single line in all three panels corresponds to 0.0 logMAR acuity.

Although simple defocus was used to generate the illustrations of Figure 1, the same effects can be and are generated by combinations of higher order aberrations in the absence of or in presence of minimal defocus or astigmatic errors.

Our long term goal is to develop an understanding of the number of Just Noticeable Differences (JND) in RIQ prior to a significant acuity loss and use this understanding to objectively define the difference between “20/20 happy and 20/20 unhappy” patient in refractive surgery and other therapies designed to optically correct the eye. To this end, the purpose of the current study had two short term goals. First, the short term goal was to define a just noticeable difference (JND) in 0.0 logMAR (20/20 Snellen) blur using the RIQ metric called the visual Strehl (VS). The VS is designed to capture diffraction effects, wavefront error effects (high and low order aberrations) and neural effects⁸. The VS has been demonstrated to objectively predict a patient's selection of best focus⁹, subjective refraction⁸ and have a predictive linear relationship with logMAR acuity^8,10. Our second short term goal was to capitalize on the linear relationship between log VS and logMAR acuity to calculate the number of JND's necessary to lose 1-line of visual acuity near the acuity of 0.0 logMAR (20/20 Snellen).

Methods

Overview

Two experiments were performed. Experiment 1 determined the change in log VS necessary to produce a just noticeable difference (JND) in acuity. Experiment 2 determined the change in photopic high contrast acuity for each 0.3 change in log VS from 0.00 to −1.50 log VS. The results of Experiment 1 and 2 were used to calculate the number of JND's necessary to lose 1 line of logMAR acuity near the normal acuity threshold.

Protection of Human Subjects

Prior to subject enrollment the research protocol was approved by the University of Houston Institutional Review Board (IRB) and at enrollment each subject signed an IRB approved informed consent.

Subjects

Three healthy normal volunteers with best corrected visual acuity of 20/20 or better in at least one eye served as subjects (see Table 1 for the refractive corrections and the best corrected visual acuities for each subject). The mean age of the subjects was 25 years with a range of 24 to 27 years.

Table 1.

The best sphero-cylindrical correction visual acuity of study eye for the three normal subjects.

Subject Identifier	Best Correction	Visual acuity (logMAR)
Subject 1	Plano	−0.12
Subject 2	−2.75 D	−0.14
Subject 3	−0.25 DS −1.00 Dc × 160	−0.04

Experimental set-up

The eye with the better best corrected visual acuity of each subject was dilated with 1% tropicamide to minimize accommodation and to ensure that the eye's pupil was larger than the 3-mm artificial pupil. The fellow eye was occluded. The test eye of each subject was trial-frame refracted to best visual acuity through a 3 mm artificial pupil and viewed the 300 cd/m² test targets at 10 feet. To fix the testing distance, the subject placed their head in a chin and forehead rest (Headspot, University of Houston College of Optometry).

The WFE of interest

RIQ as measured by log VS was varied by scaling the WFE of a typical normal young adult eye up and down. To select the WFE of interest, we capitalized on the best-corrected 100 eye WFE data set¹¹. We first calculated the log VS for each of the 100 eyes from the best corrected WFE and determined the mean log VS for the population. We then selected the eye having a log VS closest to the population mean to be the normal eye of interest. Figure 2 displays the sign and magnitude of each Zernike coefficient for the best corrected (sphere, cylinder and axis) WFE of the eye of interest through the 5^th radial order over a 3mm pupil per the ANSI standard¹².

Figure 2.

RMS error (micrometers) of normal WFE of interest for Zernike modes through the fifth radial order over a 3 mm pupil.

Calculation of Visual Strehl (VS)

VS was calculated using the optical transfer function (OTF) method⁸. In overview the VS is designed to capture both optical and neural components of visual processing, where the OTF is weighted by the neural contrast sensitivity function (CSF_N) as measured by Campbell and Green¹³ relative to a perfect diffraction-limited system. Log VS is calculated as follows:

$$\log VS=\log \frac{{\int }_{-\infty }^{\infty }{\int }_{-\infty }^{\infty }CS{F}_N(f_x,f_y)\cdot OTF(f_x,f_y)d{f}_{x}d{f}_y}{{\int }_{-\infty }^{\infty }{\int }_{-\infty }^{\infty }CS{F}_N(f_x,f_y)\cdot OT{F}_{DL}(f_x,f_y)d{f}_{x}d{f}_y}$$

Where:

• log VS is the log of the visual Strehl

• CSF_N is the neural contrast sensitivity function

• OTF is the measured optical transfer function

• OTF_DL is the diffraction limited optical transfer function

JND in log VS (Experiment 1)

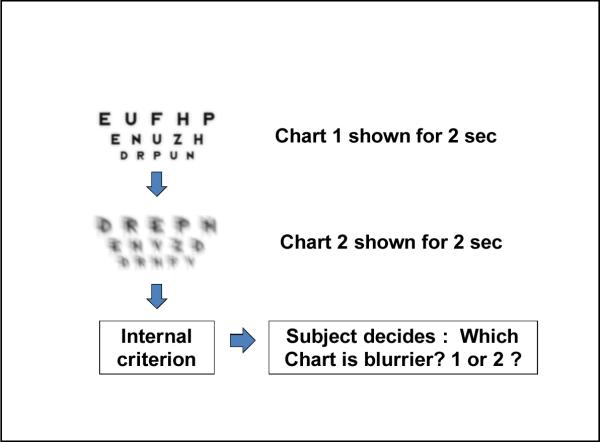
The JND for the log VS discrimination threshold was measured using a two alternative temporal forced choice paradigm. On each trial, the subject viewed two different 3-line (−0.1, 0.0 and 0.1 logMAR) logMAR test charts through a 3 mm pupil with best subjective refraction. Each chart is shown for a period of 2 seconds following which the subject's task was to compare the two charts and indicate which one of the two charts was blurrier (See Figure 3). In each presentation one of the two charts was a reference chart constructed using the WFE displayed in Figure 2.

Figure 3.

Diagrammatic representation of the JND experiment procedure for each trial.

To determine the range of interest for estimating a JND in log VS, a preliminary experiment was conducted using the method of adjustment to define the smallest log VS change necessary for subjects to detect both an increase and decrease in RIQ 100% of the time. The resulting range of log VS was then divided to yield 9 smaller log VS values ranging from 0.00 to −0.40 in 0.05 log unit steps with log VS of −0.20 as the middle reference value.

To create the WFE for each test chart, the coefficient of each Zernike mode of the average subject (Figure 2) was scaled up and or down to achieve the desired log VS for each 0.05 log VS step. In turn, each test chart was created by convolving the PSFs of the scaled WFE with a perfectly constructed test chart. In total there were 180 unique charts (90 test charts and 90 reference charts) making 90 two-alternative forced choice pairs for a given experimental run. Each subject repeated the experiment 3 times.

Generation of the logMAR acuity charts

Visual Optics Laboratory Professional (VOL Pro version 6.89, Sarver and Associates, Inc, Carbondale IL) software was used to generate unaberrated and aberrated logMAR acuity charts scaled for a 10 foot test distance using each scaled wavefront error. VOL Pro utilizes an equally identifiable (Bailey Lovie) letter set to generate the letters contained in each line of the logMAR chart randomly with the caveat that no letter can be repeated on any given line. Once generated, the charts were printed using a poster printer at a resolution of 300 dots/inch on high quality paper.

Data analysis

For each experimental run, each subject's percent “blurrier” responses as a function of log VS were fit with a psychometric function using a probit curve fitting analysis to define the threshold value and associated standard deviation. The JND was defined as log VS between 50% and 80% discrimination probability on the fitted function (Figure 4).

Figure 4.

Typical psychometric function for one experimental run of one subject. Percent “blurrier” responses as a function of log VS was fit with a psychometric function and used to define the JND as distance between the 50% and 80% response thresholds in units of log VS.

Acuity as a function of log VS (Experiment 2)

As in the JND experiment, the coefficient of each Zernike mode of our average normal WFE was scaled up and down to yield different levels of blur scaled using log VS. The range of log VS values was larger than in the JND experiment, ranging from 0.00 to −1.50 log VS in steps of 0.3 log VS. For each of the 6 test conditions, three unique 11-line logMAR charts (0.7 logMAR to −0.3 logMAR) of 100% contrast were convolved with the PSFs of the scaled WFE. For each chart, each subject's acuity was recorded as the total number of letters read correctly up to fifth letter missed. As in previous experiments^1,5,14, logMAR acuity for each chart was calculated as follows:

• logMAR acuity = x - (LC*0.02), Where:

  • x = logMAR acuity for the largest test line given the test distance
  • LC = total number of letters read correctly.

Data analysis (Experiment 2)

For each subject, acuity for each of the 6 levels of log VS was defined as the mean of three measurements. In order to determine the change in log VS necessary to induce a 1-line change in acuity, the log VS was plotted as a function of the mean log MAR acuity for all three subjects and the resulting data were fit using a least squares linear regression.

Number of JND's in one line of acuity

The number of JND's necessary to lose one line of acuity was defined as the change in log VS necessary to lose one line of acuity divided by the 1 JND in VS.

Results

A typical psychometric function from a single experimental run of the JND experiment is shown in Figure 4.

Table 2 displays the JND for each subject for each run, the average JND for each subject and the associated standard deviation for each subject and the mean JND with its associated standard deviation.

Table 2.

JND's in log VS for each subject for each run along with means and standard deviations for each subject and mean of means and standard deviation of means for all subjects.

	Run #	JND	Mean	SD
	1	0.053
Subject 1	2	0.062	0.058	0.005
	3	0.058
	1	0.026
Subject 2	2	0.050	0.041	0.013
	3	0.046
	1	0.037
Subject 3	2	0.036	0.047	0.018
	3	0.067
All Subjects			0.049	0.012

For experiment two, average results for all three subject are graphically displayed in Figure 5 by plotting log VS as a function of average logMAR visual acuity for each subject. Since logMAR acuity and metric values are both dependent variables, the priniciple element, log VS has been used for the regression analysis. The regression analysis reveal that across subjects log VS is well correlated with acuity (R² = 0.96) and that a change of 1 line of acuity is associated with a −0.298 change in log VS.

Figure 5.

Log VS as a function of mean of mean logMAR acuity. Error bars represent 1 SD for each subject.

From Experiment 1 and 2, to calculate the number of JND's necessary to lose 1 line of logMAR acuity, the log VS necessary to induce 1 line of BCVA (0.298) was divided by the average JND (0.049 ± 0.012) yielding 6.1 JND's per line near the normal acuity threshold.

Discussion

When log VS is regressed against mean logMAR acuity, log MAR acuity accounts for 96% of the variance in log VS (R² = 0.96). The best fitting linear regression analysis reveals that a change of 0.298 in log VS induced a loss or gain of one line of logMAR acuity near the normal acuity threshold of −0.15 (~20/15 Snellen)¹⁵. Given the average JND for log VS is 0.049 log VS, there are approximately 6 JND's in log VS for 1 line of acuity loss. Given there are 5 letters in each line of a logMAR acuity chart and on average 6 JND's in blur before a line of acuity is lost, there was slightly more than one JND in log VS per one letter of lost acuity supporting the common observation that patients can detect blur before any acuity is lost. These finding suggest there is a way to objectively verify the statement of some refractive surgery patients “I can see 20/20 but it is not as good as it used to be” as well as objectively to differentiate between the “20/20 happy” and “20/20 unhappy” patient. That is, one could measure the habitual log VS prior to surgery and the habitual log VS after surgery and determine the degree to which RIQ defines the difference between the “20/20 happy” and “20/20 unhappy” patient.

These finding suggest that the RIQ metric log VS can be used to model therapy (e.g., various corneal refractive surgeries, intraocular lens designs to increase the depth of focus, contact lenses for the highly aberrated eye, etc.) and objectively evaluate the probability they will produce blur noticeable to the patient with or without an acuity loss. Further, since VS includes diffraction effects, aberration effects, and neural effects the metric does not suffer from limitations imposed by geometric approaches where the effects of diffraction and high order aberrations are ignored (e.g., equivalent blur circle size^3,16. Nor does the RIQ metric VS suffer from the equivalent diopters¹¹ assumption that all aberrations are equal^5,14 or the complex interaction between aberrations that increase or decrease visual acuity depending upon the modes interacting^1,6–7.

On the other hand, while encouraging, our findings are limited in that only one underlying WFE for one pupil size was scaled up and down. Studies currently being conducted focus on whether the findings reported here can be generalized to other underlying WFEs and whether the findings hold across pupil diameters.

Comparison to other studies

To compare the study reported here to other studies that used dioptric blur as the metric of RIQ, the blur discrimination threshold expressed in log VS (0.049 ± 0.012) was converted into equivalent diopters¹¹ yielding a JND of 0.038D ± 0.007 (Table 3).

Table 3.

Average JND, in units of diopters necessary to detect blur, the criterion used, and the visual task for 6 different studies.

	Target used	Blur criterion	Average JND (D)
Our study	Log MAR	80%	0.038
Legras et al 2004	Log MAR E	75%	0.035
Jacobs et al 1989	Landolt C	50%	0.05 to 0.07
Burton and Haig, 1984	Vehicle	75%	0.23
Wang et al 2005a	Small square wave harmonic	100%	0.45
Wang et al 2005b	Small square wave harmonic	100%	0.48

Not surprisingly, JND is target specific. For studies that used small letter targets^3,16–17 and our study, the discrimination thresholds are in good agreement with the variation attributed to the different experimental methods and criterions. For larger targets such as a vehicle¹⁸ or a complex square wave harmonic target^19–20, discrimination thresholds are larger than those reported for small letters.

Conclusion

The retinal image quality metric log VS calculated from the WFE of the eye is highly correlated with logMAR acuity. The JND for log VS near normal acuity levels using a two alternative temporal forced choice paradigm to detect blur is 0.049 log VS. On average there are 6 JND's in log VS before 1 line of acuity is lost indicating that blur is detected before 1 letter of acuity is lost. The change in log VS induced by any given clinical intervention designed to improve visual performance should help to objectively evaluate the effectiveness of the intervention providing an objective criteria for evaluating the difference between “20/20 happy” and “20/20 unhappy”.