Dimensionality effects in the electronic structure of organic semiconductors consisting of polar repeat units

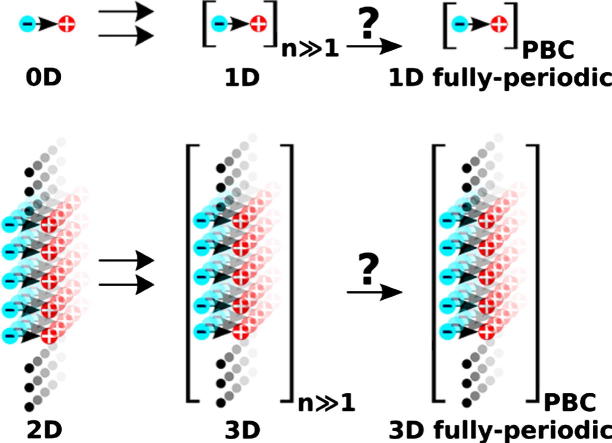
Graphical abstract

Highlights

► We describe monolayers consisting of molecules with polar repeat units. ► The global energy gap in such layers can vanish. ► In such films the dipole moment per molecule saturates beyond a certain length. ► These effects result from electrostatic dimensionality effects. ► This represents an “organic electronics” analogue to inorganic “polar surfaces”.

Abstract

In conjugated organic molecules, excitation gaps typically decrease reciprocally with increasing the number of repeat units, n. This usually holds for individual molecules as well as for the corresponding bulk materials. Here, we show using density-functional theory calculations that a qualitatively different evolution is found for layers built from molecules consisting of polar repeat units. Whereas a 1/n-dependence is still observed in the case of isolated polar molecules, the global gap decreases essentially linearly with n in the corresponding 2D-periodic systems and vanishes beyond a certain molecular length, with the frontier states being localized at opposite ends of the layer. The latter is accompanied by a saturation of the dipole moment per molecule, an effect not observed in the isolated polar molecules. Interestingly, in both cases the limit of the gap for long (but finite) molecules differs qualitatively from that of infinite length obtained in 1D-periodic and 3D-periodic calculations, the latter serving as models for polymers and the bulk. We rationalize these dimensionality effects as a consequence of the potential gradient within the finite-length layers. They arise from the collective action of intra-molecular dipoles in the 2D periodic layers and can be traced back to surface effects.

1. Introduction

Among the most important properties of materials are their excitation gaps, where depending on the application one either primarily cares about the fundamental gap (sometimes also referred to as the transport gap), defined as the difference between the first ionization energy and the electron affinity, and the excitation gap given by the energy difference between the first excited state and the ground state [1,2]. The excitation gap is related to the optical gap which determines the usefulness of a given material for applications like photovoltaic cells (see below), while the transport gap determines charge carrier injection and the electrical characteristics of electronic devices such as transistors. “Gap-engineering” is thus of considerable relevance and one of the best-known handles enabling such tuning in conjugated organic molecules is changing their length. Usually, the gap decreases reciprocally with an increasing number of repeat units n for moderate n, followed by a more shallow decrease for larger n and convergence to a finite gap in the polymer limit [3]. The gaps are also modified by inter-molecular interactions in the condensed phase, resulting in polarization and orbitals overlapping (e.g. causing the formation of (weakly) dispersing bands). These effects decrease the ionization energy, increase the electron affinity and reduce the excitation gap [4]. The latter is also affected by excitonic couplings described, e.g. [3] as H-aggregate formation.

Additional effects are encountered in polar systems as we discuss below for the instructive example of conjugated molecules consisting of polar repeat units: There the 1/n dependence of the gap is still observed in isolated molecules. It breaks down, however, when assembling these molecules into self-assembled monolayers (SAMs), where beyond a certain limit the gap even vanishes. This behavior is reminiscent of what is observed for inorganic polar surfaces, as we briefly discuss at the end of this article. It directly results from the long-range electrostatic interactions of the dipoles and is intimately related to dimensionality effects, i.e. it can neither be recovered when studying isolated chains nor in 3D fully-periodic calculations. The latter is a consequence of ‘surface-effects’ which are intrinsically not considered when employing 3D periodic boundary conditions (PBC).

To illustrate that, we study oligopyrimidinethiols (see below for a detailed description of the system) of different lengths as prototypical model systems characterized by dipole moments distributed along the backbone. They are chosen because (i) monolayers of pyrimidine-derivatives have been realized experimentally [5–8], (ii) the electronic structure of the corresponding self-assembled monolayers (SAMs) is relatively well understood from quantum-mechanical calculations [9,10] and (iii) both experiment and calculation have found interesting electronic properties of such layers: The experimental electrical characterization has shown that SAMs of molecules containing pyrimidines act as rectifiers [8], and some of us have recently reported on collective effects in terpyrimidine layers [10]. These cause the frontier orbitals to localize on opposite ends of the rod-like molecules accompanied by a drastic decrease of the gap in the SAM compared to the isolated molecules, a situation reminiscent of the quantum-confined Stark-effect in semiconductor quantum wells [11,12] present here without applying an external electric field.

To obtain a comprehensive understanding of the evolution of the energy gap of such SAMs with n, we systematically compare them to the corresponding isolated molecules as sketched in Fig. 1 (top vs. bottom row). For molecules, this corresponds to the transition from a single repeat unit to rod-like 1D-extended systems of up to 30 repeat units. This will further on be denoted as transition from 0D to 1D. In case of layers where the molecular dipoles are arranged in parallel, the equivalent transition from SAMs of monopyrimidinethiols (several Å thick) to such of up to 30 rings (more than 10 nm thick) is denoted as the 2D → 3D transition. In addition, we also calculate the 1D fully-periodic and 3D fully-periodic situations employing periodic boundary conditions either in the direction of the chain axis (1D fully-periodic) or in all directions (3D fully-periodic) [13]. These are compared to the respective systems of long but finite length (denoted as 1D and 3D in Fig. 1).

Fig. 1.

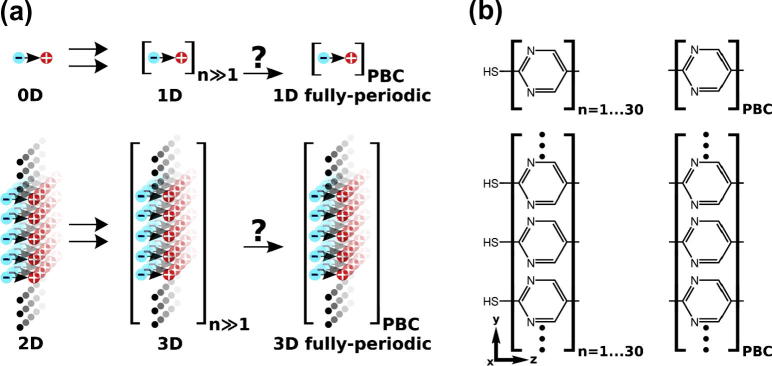
(a) Upper graph: conceptual sketch of the transition from 0D (single repeat unit) to 1D (many repeat units) to the 1D fully-periodic case, for the latter applying periodic boundary conditions (PBC) in the chain direction. Lower graph: analogous transition from a 2D system (consisting of a single 2D-periodic sheet of dipoles) to a 3D situation (many neighboring periodic sheets) to the 3D fully-periodic case. (b) Realization of those transitions using the example of oligopyrimidinethiol molecules. The coordinate system is indicated; for a top view of the unit cell used in the periodic calculations, see Ref. [10].

2. The system

2.1. Chosen molecules and considerations regarding the stability of the formed layers

Oligopyrimidinethiols consist of a thiol group and multiple copies of the polar repeat unit pyrimidine (Fig. 1b). The latter allows for a systematic change of the molecular dipole moment via the number of connected monomers. The purpose of the thiol group is to facilitate binding to a metallic substrate and in this way energetically stabilize layers with parallel molecular dipoles, i.e. it prevents an anti-parallel arrangement of the chains. For (substituted) monopyrimidinethiols it has been shown that well-ordered SAMs indeed adsorb on Au(1 1 1) [5–7] and in addition it was found that SAMs also form from molecules including more than one repeat unit [8]. Up to what chain-length the gain in energy due to binding to the substrate compensates for the energetic cost of the parallel arrangement of the dipoles depends on several factors including the chosen metal–organic binding chemistry and the lateral distance of the dipoles. Indeed it has been shown by Gershevitz and co-workers that order in SAMs can be reduced when the molecular dipole moments are very large [14]. Considering, however, that pyrimidines in the present conceptual study are chosen just as a prototypical test-case, one could also imagine building the SAMs in a layer by layer fashion (in some sense reminiscent of self-assembled nano-dielectrics) (SANDs) [15,16]) with chemical stabilization of the order within a given layer, e.g. by cross-linking before proceeding with the fabrication of the next one. It also should be mentioned that simple electrostatic considerations show that achieving a certain net-dipole per molecule by distributing that dipole moment over the individual rings is clearly favorable over “concentrating” the dipole in a single substituent [17]. In passing we note that the stability of stacked dipole layers is heavily investigated also in a completely different context, namely the field of polar (oxide) surfaces (see brief discussion at the end of the article). Moreover, assemblies of polar molecules stacked so that their dipole moments add up, causing huge voltage drops, have also been observed for certain organic multilayer structures [18,19].

2.2. Chosen unit cells

Individual molecules are studied using open boundary conditions (i.e. as isolated molecules), while for the 1D fully-periodic case periodic boundary conditions in the z-direction are applied. As discussed elsewhere [10], when investigating oligopyrimidine monolayers we use a (5.11 × 8.86) Ų unit cell with upright standing molecules, which would be consistent with a (√3 × 3) surface unit-cell if the SAM were bonded, e.g. to a Au(1 1 1) surface. Consequently, in all monolayer calculations (denoted as 2D and 3D in Fig. 1a) periodic boundary conditions are applied, but only within the plane of the SAMs (i.e. in the x- and y-directions). Systems with up to 30 pyrimidine units per chain are calculated explicitly for the 0D → 1D and 2D → 3D transitions (i.e. with open boundary conditions in the z-direction). Periodic boundary conditions are, however, used also in z-direction to model the limit of fully periodic systems (as indicated in the rightmost sketches of Fig. 1a). In these calculations, the thiol group is removed and a cell height of 4.42 Å is used.

3. Methods

All calculations were done with the Perdew–Burke–Ernzerhof exchange correlation (xc) functional [20] using the PARSEC real-space code [21,22] (that allows a combination of open and periodic boundary conditions [23,24]) and norm-conserving pseudo potentials [25]. To analyze the electronic structure of organic semiconductors consisting of polar repeat units, we will calculate various quantities like dipole moments, potential distributions, densities of states, charge rearrangements and orbital energies with a particular emphasis on determining the evolution of ‘the gap’. As already mentioned in the introduction, this is not a uniquely defined quantity as for most materials fundamental and excitation gap do not coincide [1,2]. Although neither of them is described by the orbital (i.e. Kohn–Sham) gap obtained with standard-functionals, our calculations can be most easily interpreted as trends in the fundamental gap, where the discussed electrostatic effects are directly relevant. The situation is more complex for the excitation gap, where excitonic effects need to be considered as well, although also in that case most of the observed trends can be expected to prevail. Moreover, as in the 3D case for large n the frontier orbitals get increasingly localized on opposing ends of the layer (vide infra), the oscillator strength for a transition to the lowest excited π−π^* state of the entire SAM can be expected to decrease significantly. This implies that then the optical gap (defined as excitation energy to the first optically allowed state) should no longer be associated with that global gap, but rather with the local π−π^* gap described in the results section.

Regarding the choice of the functional it should be mentioned that PBE does not correctly describe all the details of the electronic structure of oligopyrimidines. In particular, it can get the ordering of the low binding-energy σ- and π-orbitals wrong [10], an error that can be explained in terms of an orbital-dependent self-interaction error [26]. In principle, this problem can be mitigated with hybrid functionals [10]. Together with periodic boundary conditions their use is, however, computationally extraordinarily demanding. This makes their use too expensive for the longer chains, where several subsequent calculations were needed to obtain convergence (see below). Nevertheless, for shorter chains we performed comparative studies using the popular B3LYP hybrid functional and the Hartree–Fock method with Gaussian 03 [27]. The results are given in Appendix B. While the molecular dipoles agree quite well, not unexpectedly the polarizability is overestimated and gaps are underestimated in the PBE calculations, which are two well-known phenomena [2]. Nevertheless, all trends reported below for gaps, molecular dipoles and polarizabilities are confirmed. As elaborated in the discussion below, they are caused by electrostatic effects and the primary consequence of the Kohn–Sham gap underestimating the fundamental gap will, in fact, be that gap closure and dipole saturation in real systems will occur at a somewhat larger number of repeat units than calculated with PBE. We thus conclude that PBE is sufficient for our conceptual study in which we focus on trends. We further note that both the PBE and the B3LYP calculations do not account for the renormalization of the gap due to polarization in neighboring molecules, which narrows the gap in molecular arrays compared to isolated molecules. The reason is that no long-range correlation is included in these functionals [28–30]. Thus, the fact that in our calculations in spite of the neglect of long-range correlation we see a sharp gap reduction in 2D and 3D systems, compared to their 0D and 1D counterparts, further supports our interpretation that all observed phenomena are exclusively rooted in the electrostatic field of the pyrimidine dipoles.

When periodic boundary conditions were applied, a Monkhorst–Pack [31] k-point grid was used. In the 2D-periodic calculations, an 8 × 5 k-points grid was chosen for the x,y-plane together with open boundary conditions in z-direction (see coordinate system in Fig. 1b). 20 k_z-points were used in the 1D- and 3D-periodic calculations, where the thiol group was removed. A Fermi temperature of 100 K (less than 0.01 eV) was chosen. Much higher electronic temperatures were needed to reach convergence for the 2D-periodic assemblies of longer chains. In these cases, results for 100 K were obtained by several subsequent calculations with a gradually reduced temperature. The reason is that a finite electronic temperature “thermally” broadens electronic states in energy, which allows for partial occupancies. In cases where the energy gap is small (see below), partial occupancies are essential for achieving convergence in the self-consistent field procedure (see, for instance, Ref. [32]). The impact of the choice of the Fermi temperature on our results is discussed in detail in Appendix A.

In all calculations, the (band) gap was determined as the difference between the highest occupied and the lowest unoccupied eigenvalues. Projections of the density of states (DOS) onto atoms were generated using ionic radii of 1.5 bohr and the corresponding plots were broadened by convolutions with Gaussian functions (σ = 0.05 eV). 3D representations of the systems and potential energy plots were produced with XCrysDen [33].

All used geometries were based on the geometry-optimized terpyrimidinethiol calculated using the PBE functional and the aug-cc-pVTZ basis set in Gaussian 03, as used in Ref. [10]. Different to oligophenyls and due to lack of steric hindrance, this is a planar geometry. Additional pyrimidine rings were added/removed without reoptimization. This is a reasonable procedure, as for the above-mentioned terpyrimidinethiol the difference in bond length between the two inter-ring bonds is <0.005 Å.

4. Results and discussion

The evolution of the PBE calculated HOMO–LUMO energy gap with chain length is shown in Fig. 2 for the isolated oligopyrimidinethiol molecule for up to 30 rings (orange (light gray in b/w) stars). As expected [3], the gap first decreases linearly with the inverse number of monomers n and then approaches a finite value (≈1.6 eV) in the 1D limit (long but finite molecules); a 1/n plot is shown in Appendix B. The band gaps of the corresponding self-assembled monolayers are shown as green (dark gray in b/w) rectangles. In sharp contrast to the situation for the isolated molecules, they decrease much faster with n, and beyond 8 repeat units the gap vanishes completely [34]. It remains zero in the 3D limit (SAMs of long but finite molecules, cf. Fig. 1a).

Fig. 2.

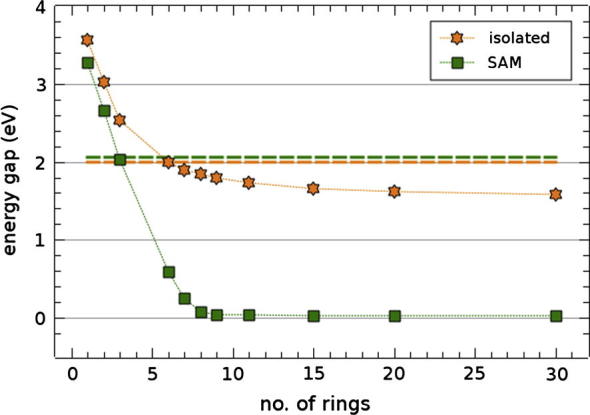
Evolution of the PBE Kohn–Sham energy gaps of oligopyrimidinethiol molecules (orange (light gray in b/w) stars) and SAMs (green (dark gray in b/w) rectangles) with the number of pyrimidine units. The dashed horizontal lines show the values for infinite length (i.e. a 1D-periodic chain) in orange (light gray in b/w) and the 3D-periodic bulk in green (dark gray in b/w)). (For interpretation of the references to color in this figure legend, the reader is referred to the web version of this article.)

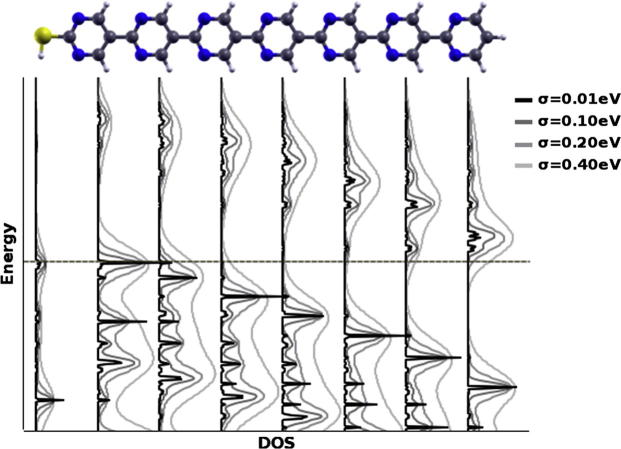
To understand this evolution of the electronic structure of such SAMs, it is useful to take a look at the DOS projected onto each of the pyrimidine layers separately. This quantity reveals at which energies electronic states can be found on the individual rings. The result for a SAM consisting of heptamers is shown in Fig. 3, where the horizontal gray line indicates the energy of the highest occupied state. Viewed from left to right, the highest occupied DOS peaks on each of the rings are successively shifted down in energy. They correspond to states that are largely localized on only one ring, and weights on neighboring pyrimidines are hardly visible (owing to the σ-character of these states, cf. Ref. [10]). The situation is less clear for the lowest unoccupied peaks. The respective states contribute significantly to the DOS on several neighboring rings, which makes the gradient in energy somewhat less well resolved than for the occupied states. Although the gap between the highest occupied and lowest unoccupied DOS peaks on each ring (the “local gap”) is quite sizeable, the gradient leads to a strong reduction of the global gap of the SAM (defined as the difference between the highest occupied and lowest unoccupied states in the entire SAM). To emphasize this, the rightmost curve in Fig. 3 shows the total DOS, where the nearly-closed global gap is visible. It is easy to extrapolate from the heptamer case to situations with fewer or more repeat units. A consequence of the observed behavior is that locally the layer is semiconducting irrespective of its thickness, and at the same time the band gap is closed globally between the opposing surfaces for slabs of sufficient thickness (with PBE for 8 or more rings). In other words, any method probing the electronic states only over a finite length (limited number of rings) would obtain a non-zero gap. It would also find the Fermi-energy shifted away from mid-gap towards either the conduction- or the valence-band edges (depending on the surface), thus, mimicking the band-structure of an n-type or p-type doped semiconductor. A method probing the whole system, in contrast, would show a zero-gap situation. In addition to the closure of the global gap, the above-mentioned gradient causes the highest occupied states to be localized on the high-energy side of the SAM and the lowest unoccupied states on the opposite surface of the slab, as shown by the real-space representations of the respective peaks in the total DOS in Fig. 3. The actual nature of the highest occupied states (σ vs. π) is impacted by the chosen functional as described in the Methods section and in more detail in Ref. [10]. In the latter we show explicitly for terpyrimidine, the corresponding thiol and the thiolate that energy and localization of both the σ- and π-states are affected by the potential gradient.

Fig. 3.

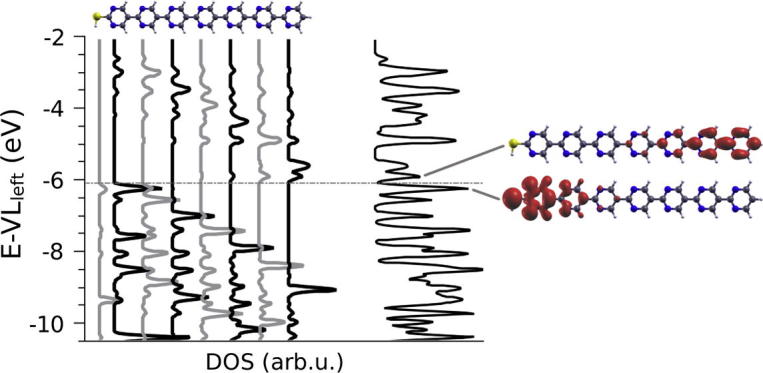
Density of states projected onto the thiol group and the individual pyrimidine rings for a monolayer consisting of molecules with 7 repeat units plotted alternatingly in black and grey to improve visibility; the molecular structure at the top of the plot serves as guide to the eye and the left vacuum energy VL_left (cf. Fig. 4) is set to zero. The dash-dotted horizontal gray line indicates the energy of the highest occupied state. In addition, the rightmost curve shows the total DOS. Real-space representations of the lowest unoccupied and highest occupied peaks are depicted. The latter includes two crossing bands (as evidenced also by the higher associated DOS), one being derived from a σ- and the other from a π-orbital. This also results in the mixed σ- and π-character in the real-space representation. Note that this near-degeneracy might be a consequence of an orbital-dependent self-interaction error mentioned in the ‘Methods’ section [10].

This can be understood best by considering the electrostatics across the SAM. The (x,y-plane averaged) electron potential energy across SAMs with 3, 6, and 15 repeat units is depicted in Fig. 4a. The potential is constant outside the SAM and, importantly, it takes different values left and right of the SAM. For SAMs below 8 repeat units, the energy step ΔE_vac between the left and right vacuum energies [35] (cf., Fig. 4a) is found to increase linearly with the SAM thickness (not shown). Consequently, the slope in the potentials is the same (highlighted by the shorter light gray line in Fig. 4a). It is this decrease in electrostatic energy across the SAM which is reflected in the electronic eigenvalues and thus causes the gradient in the local electronic structure described in Fig. 3. If that potential gradient remained the same for longer chains, this would eventually result in unoccupied states at the “right” end of the SAM lying below the occupied ones at the “left” end. As a consequence, to maintain thermodynamic equilibrium, either charge must be transferred between the two ends of the SAM or the molecular backbone must get polarized (vide infra). In other words, the occupied states at the left end of the SAM become pinned at the unoccupied ones at the right and, thus, ΔE_vac cannot exceed a certain maximum value. Therefore, beyond n = 8 the gradient in the potential and DOS gradually decreases (see the potential for n = 15 in Fig. 4a).

Fig. 4.

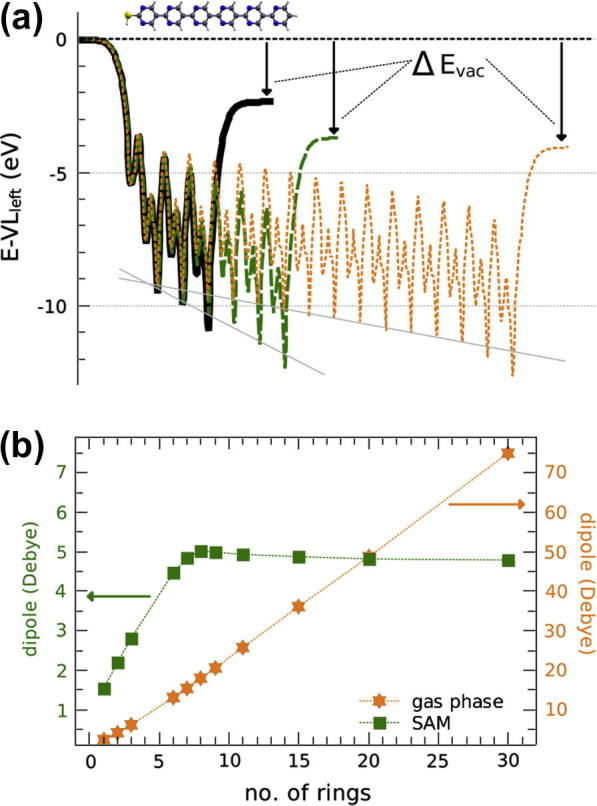
(a) (x,y)-averaged electrostatic energy of an electron across monolayers for 3, 6, and 15 repeat units aligned at the “left” vacuum energy, VL_left. The step in energy across the layer, ΔE_vac, is indicated by vertical black arrows. The light gray inclined lines serve as a guide to the eye to illustrate the net potential gradients across the respective SAMs (note that when “drawing” those lines the potential in the region of the terminal ring has not been considered as that ring is subject to a qualitatively different bonding environment). (b) Evolution of the molecular dipole moment of oligopyrimidinethiol molecules (orange (light gray in b/w) stars) and SAMs (green (dark gray in b/w) rectangles) with increasing number of pyrimidine units; note that the scales differ by a factor of 10. (For interpretation of the references to color in this figure legend, the reader is referred to the web version of this article.)

These gradients are intimately related to the molecular dipole moments, as described by the Helmholtz solution to the Poisson equation [36–38]. It reads:

$$\mathrm{\Delta }{E}_{\mathit{vac}}=\frac{(-e){\mu }_{\perp }}{{\epsilon }_{0}A}$$ (1)

with e being the positive elementary charge, ε₀ the vacuum permittivity and A the area per molecule. μ_⊥ denotes the dipole moment per molecule along the z-direction. ΔE_vac, the difference in vacuum energy between “left” and “right” side of the monolayer is then simply proportional to μ_⊥ [39]. This is also the reason why the above-described gradients in potential energy and DOS are absent in oligomeric systems consisting of a-polar repeat units (see Ref. [10] and Appendix C, where the analogue to Fig. 2 is shown for essentially a-polar oligophenylthiols).

The situation is relatively simple for the isolated molecules. The molecular dipole increases essentially linearly with n (as shown in panel b as orange (light gray) stars) [40]. It does so without limit, and yet the gap remains finite at all lengths (cf. Fig. 2). This is possible because in the spirit of Eq. (1) the isolated molecule corresponds to A → ∞, which results in ΔE_vac = 0; i.e. the dipoles in an isolated molecule do not introduce an overall shift in the vacuum energy. In particular, dipoles far away from a certain repeat unit do not influence its energy electrostatically, which explains why the gap converges to a finite, non-zero value with increasing chain length like it does for apolar molecules.

In contrast, in a SAM A and ΔE_vac assume finite, non-zero values. As a consequence of the above-described saturation of ΔE_vac, also the dipole per molecule increases only until the gap vanishes (green (dark gray) rectangles in Fig. 4b). At which chain-length this happens is determined by A (the packing density), the gap of the monomer-SAM and the speed at which the latter is reduced by oligomerization. For the PBE functional and the packing density described in the section “The System” this occurs for eight repeat units. Note that also μ_⊥ itself is a function of the packing density, because the molecular dipoles depolarize each other as they get closer, an effect extensively discussed in the literature [14,41–51]. This is reflected in Fig. 4b, where also for small n the dipole moment per molecule increases much more gradually in the SAM than for the isolated molecule (note that for the sake of clarity the scale on the y-axis is reduced by a factor of 10 in the SAM case compared to the isolated molecules).

The saturation of the dipole per molecule in the SAM above n = 8 is possible only if each additionally added pyrimidine dipole is fully compensated by some other dipole of equal magnitude but opposite sign. These counter-dipoles need to be extended as the electric field they cause is the reason for the decreased potential gradient across the whole SAM shown in Fig. 4a. In general, one can think of two different microscopic mechanisms to establish this compensating field: The counterdipoles are induced either (i) via polarization of each of the rings, i.e. a series of small dipoles resulting from a short-range redistribution of electronic charge, or (ii) via long-range charge transfer between the opposing surfaces of the slab [52]. As occupied and unoccupied states very close in energy exist and are located on opposing ends of the SAM, the latter process appears more plausible. However, possibility (i) cannot be excluded in the light of previous studies, where polarization was found to be the primary mechanism establishing thermodynamic equilibrium in comparable energetic situations [53,54]. To decide between the two scenarios, a detailed and somewhat lengthy analysis of charge rearrangements is required (see Appendix A). In short, our analysis hints towards the dominant role of long-range charge transfer between the two ends of the molecules. This long-range charge transfer then reduces the effective dipole-moment per pyrimidine ring, which in turn also decreases the depolarization of neighboring chains (vide supra). In other words, the local charge rearrangements within the rings, in fact, counteract the field originating from the long-range transfer. These two effects balance to establish thermodynamic equilibrium.

All phenomena discussed above result from the intra- and intermolecular interaction of the pyrimidine dipoles. Dipoles, however, are uniquely defined only as long as the number of repeat units is finite (and, of course, as long as the system remains charge-neutral) [55]. This naturally leads to the question of what happens in the limiting case of “infinite length”, i.e. the 1D and 3D fully-periodic cases (see Fig. 1a). One might expect that the result is given already by the 1D and 3D limits discussed above for long but finite molecules, where we found a gap of 1.6 eV for isolated molecules and 0 eV in the SAM. This is, however, not the case. The band gaps obtained when applying the corresponding periodic boundary conditions are depicted in Fig. 2 as dashed horizontal lines. Interestingly, 1D-periodic and 3D-periodic gaps are practically identical [56] and both do not coincide with the respective 1D and 3D limits for long but finite molecules. The reason is actually quite simple: the potential gradient which causes the reduction of the gap (Fig. 4a) is absent in a periodic calculation, as there the potential is forced to be equal on opposite sides of the unit cell. This raises two questions: How can the conflicting results for very long and infinitely extended chains be reconciled, and which physical situation is described by which calculation?

The easiest way to approach this issue is to first compare the 3D and 3D fully-periodic cases (cf. Fig. 1), where the key to understanding lies in the above-discussed reduction of the potential gradient with increasing SAM thickness (beyond 8 rings, see Fig. 4a). The global gap in all 3D calculations considering finite-size pyrimidinethiols remains zero for arbitrarily large n > 8. The larger n, the less relevant this quantity, however, becomes as the spatial separation between the respective frontier states which determine the global gap increases (vide supra). With increasing n the potential approaches ring-periodicity, causing the local gap to converge to the gap of the fully-periodic calculation. This is illustrated in Fig. 5, where the DOS projected on the individual rings is compared for n = 30 and for the periodic calculation. Locally (illustrated here for the center of the 30-ring SAM) the DOS’s essentially coincide, while the global gap is determined by the states on the “left” and “right” surfaces. Thus, the very need to distinguish between a local and a global gap is a consequence of including such “surfaces” of the SAM in the calculation. It is not captured when using periodic boundary conditions also in the z-direction (i.e. the 3D fully-periodic case), which rather – by definition – describe an infinitely extended, surface-free, situation [57,58].

Fig. 5.

Density of states projected onto the thiol group and the individual pyrimidine rings for a monolayer consisting of molecules with 30 repeat units (crossed black areas) and for the 3D-periodic case (gray areas). DOS curves are scaled and energy axes shifted such that the correspondence of local gap and bulk gap is visible in the center of the SAM. The shown molecular structure serves as a guide to the eye. The dotted horizontal gray line indicates the energy of the highest occupied state.

This reasoning does not directly apply to a 1D calculation, where ΔE_vac = 0 also for finite systems. Still, the scenarios are related as also across finite-length molecules the local electrostatic environment of each pyrimidine generated by all other rings is different for different positions within the chain. This effect leads to localization of the frontier states on opposite ends of the molecule also in gas phase and, by definition, vanishes in the fully periodic case which leads to an increase of the gap (see Fig. 2).

To better illustrate the various situations, the electrostatic potentials across finite-length molecules (1D) and SAMs (3D) are compared to the corresponding fully-periodic cases in Fig. 6. With isolines drawn every 0.5 eV, they show the electrostatic potential in a plane close to the molecules. For the 1D case (upper left panel), the fact that each repeat unit is shifted by a different potential is visible from the increasing radii of the innermost circular isolines as well as from the overall asymmetry of the outer ones; all isolines are closed because ΔE_vac = 0. This is different in the 3D case shown in the lower panel, where most isolines are open. The energy significantly decreases across the SAM, by roughly 0.5 eV per repeat unit with the total drop ΔE_vac amounting to about 4 eV. This comparison between 1D and 3D case directly illustrates the collective interaction of dipoles which is only present in the latter situation. No such gradients are present in the respective periodic calculations (illustrated in the right panels of Fig. 6).

Fig. 6.

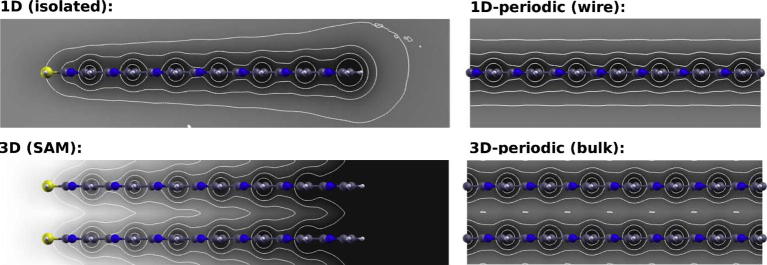
Contour plots of the calculated electrostatic energy of an electron in a plane near the oligopyrimidines (approx. 1.6 Å away from the hydrogen atoms to avoid oscillations near the nuclei). Isolines are drawn every 0.5 eV in an energy interval of 4 eV (black being the lowest energy). Shown are the situation in gas phase (1D), in a SAM (3D), in the bulk (3D-periodic) and the polymer (1D-periodic), anticlockwise from top left panel.

Because the gradient vanishes, the neighboring infinitely long molecules in the 3D-periodic calculation hardly interact with each other, resulting in the 3D-periodic gap being essentially identical to the 1D-periodic one [56]. A possible explanation for the apparent similarity of 3D periodic and 1D periodic systems is the fact that the potential of periodic dipoles decays rapidly, as a Bessel function, away from the wire, as was already shown by Lennard–Jones and Dent [59]. Importantly, the opposite is true for oligopyrimidines of finite length: With a potential gradient across the SAM, neighboring molecules strongly affect each other (see lower left panel), and for the gap for terpyrimidine molecules we have found a decrease by no less than 0.8 eV in the transition from isolated molecule to densely packed SAM (corresponding to the 1D → 2D transition) [10].

Finally, we note that the topics discussed in this work are reminiscent of those encountered in the study of polar (oxide) surfaces [60–63]. There, the so-called Tasker Type III surface is formed by cuts through an ionic crystal along a direction oriented such that each unit cell contributes with a dipole moment perpendicular to the surface [64]. Realizing such surfaces experimentally is difficult. Still, for thin films, unreconstructed flat layers could be grown layer by layer [65–67]. More common, however, is the observation of atomic rearrangements at the surface and adsorption/desorption processes that compensate for the dipole across the slab or crystal [68,69]. Another scenario discussed in the literature [61] is compensation through relaxation of electronic charge, which is strongly reminiscent of the situation discussed here (note that, for methodological reasons, it is also the only possible outcome of our calculations as we neither consider the presence of adsorbates nor allow for rearrangements in the structure of the molecular layers [70]; see section “The system” for a discussion of the stability of the layers discussed in the present paper). Traditionally, inorganic polar surfaces have been studied for macroscopic crystals. Only relatively recently, finite-size effects have been predicted for very thin slabs, namely thickness-depended electronic properties similar to what we have discussed above for SAMs [71].

It should also be noted that for all our conclusions we have assumed thermodynamic equilibrium. That thermodynamic equilibrium is not necessarily always established when stacking dipolar layers in the spirit of the 2D–3D transition described above has been observed for films of polar molecules, where voltage drops of up to 28 V across these films have been reported [18,19]. This implies the presence of unoccupied states below the Fermi energy of the substrate. In this case the above-described saturation of the dipole moment is obviously not observed and one is dealing with the unusual situation of a “negative global gap” within the thin film. This situation appears quite counterintuitive and is observed only under dark conditions; it is found to decay upon illumination with light (i.e. when thermodynamic equilibrium is established).

5. Conclusion

Using the example of oligopyrimidinethiols, we have demonstrated that in SAMs of polar molecules the evolution of the band gap with the molecular length differs qualitatively from what is known for organic semiconductor molecules. Namely, it rapidly decreases to zero and the frontier states localize on opposite ends of the SAM. This is accompanied by a saturation of the dipole moment per molecule at the same number of repeat units at which the gap closes. We show that these observations are due to dimensionality effects in the dipole–dipole interaction between the molecules. For finite-size systems (i.e. when considering the effect of surfaces), our observations imply that it is useful to distinguish between a global gap (the one that closes) and a local one on each ring that remains finite independent of the molecular length. The local gap is the only relevant quantity that remains when studying the fully periodic situation by imposing periodic boundary conditions. The described strategies for tuning the band gap and orbital localization can potentially be of use for designing new materials for optoelectronic devices that, e.g. facilitate the dissociation of excitons in solar cells.

Appendix A. Reduction of the electric field across the SAM: charge transfer compared with polarization

At the very beginning of this section, a word of caution is needed. The reader should be aware of the fact that standard xc-functionals are known to overestimate long-range charge transfer [72]. Thus, the results presented in the following have to be treated with certain care, especially regarding any quantitative conclusions.

In SAMs with vanishing band gap, counterdipoles must exist which generate a compensating electric field that prevents the situation of a ‘negative band gap’ (see main text). They reduce the slope of the electrostatic potential, shown in Fig. 4a. If it were possible to compare, for a given molecular length, the charge density in the absence of counterdipoles (finite gap) and the density with the compensation mechanism being ‘switched on’ (zero gap), one could make a statement about its microscopic origin. This is indeed possible by changing the Fermi temperature in the calculation. The approach is indicated in Fig. A1, which shows the ring-projected DOS for the SAM with seven repeat units. Like in the main text, a broadening of σ = 0.00862 eV (corresponding to 100 K) was used in the calculation and the energy of the highest occupied state is indicated by the dashed gray horizontal line. After the calculation, the curves were broadened additionally using Gaussians of σ = 0.01 eV, σ = 0.10 eV, σ = 0.20 eV, and σ = 0.40 eV. For σ = 0.01 eV, the global gap is positive and no compensating field has to be induced. Already for σ = 0.10 eV (and all higher effective temperatures), unoccupied states at the rightmost rings are found below the highest occupied states at the leftmost rings. When high temperatures are used in the self-consistent calculation, counterdipoles must be induced also for seven repeat units, and by comparing the charge density of such a calculation with the original one (σ = 0.00862 eV), the microscopic details of the compensation mechanism can be observed.

Fig. A1.

Ring-projected DOS for the SAM of 7 repeat units (like in Fig. 3 of the main text), with the energy of the highest occupied state being indicated by the dashed gray horizontal line. After the calculations, the curves were broadened by Gaussians of σ = 0.01 eV, σ = 0.10 eV, σ = 0.20 eV, and σ = 0.40 eV to illustrate the effect of the Fermi temperature on the band gap.

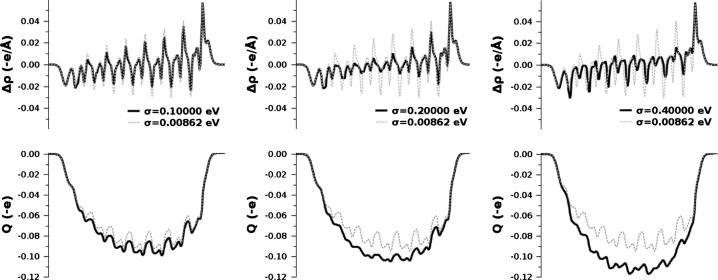
For σ = 0.1 eV, σ = 0.2 eV, and σ = 0.4 eV, we compare the plane-integrated charge density, ${\rho }_{\sigma }(z)={\int }_0^a{\int }_0^b{\rho }_{\sigma }(x\text{,}y\text{,}z)\mathit{dx}\mathit{dy}$ (a and b being lattice vectors), with ${\rho }_{\sigma =0.00862}(z)$, the density of the original calculation (yielding a finite gap). The curves $\mathrm{\Delta }{\rho }_{\sigma }(z)={\rho }_{\sigma }(z)-{\rho }_{\sigma =0.00862}(z)$ are shown in the upper panel of Fig. A2.

Fig. A2.

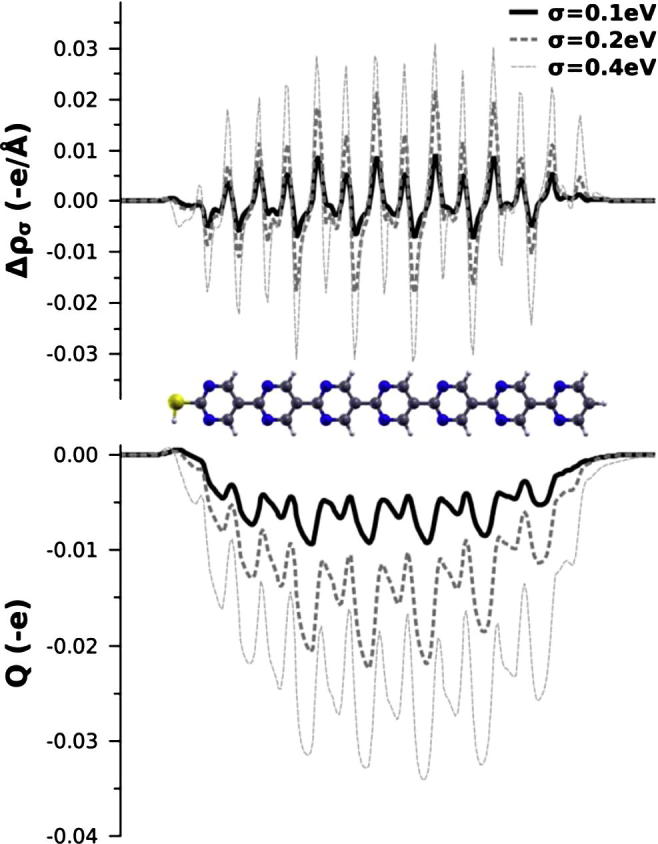
Top: plane-integrated charge density differences $\mathrm{\Delta }{\rho }_{\sigma }(z)={\rho }_{\sigma }(z)-{\rho }_{\sigma =0.00862}(z)$ for the SAM of 7 repeat units and used Fermi temperatures of σ = 0.1 eV, σ = 0.2 eV, and σ = 0.4 eV. Bottom: corresponding cumulative charge rearrangements, Q.

These curves show that (i) the whole molecular backbone is involved in the charge rearrangements and that (ii) the features get more pronounced with increasing Fermi temperature (when the counterdipole has to increase). To discriminate between polarization (short-range charge transfer) and long-range charge transfer, it is useful to integrate $\mathrm{\Delta }{\rho }_{\sigma }$ along the z-axis and obtain the cumulative charge rearrangements, $Q(z)={\int }_0^z\mathrm{\Delta }{\rho }_{\sigma }(z^{\prime }){\mathit{dz}}^{\prime }$, shown in the lower panel of Fig. A2.

These curves can be interpreted as the sum of smooth curves (indicative of long-range transfer) and oscillations from polarization, showing that the compensating electric field results from a mixture of charge-transfer between the molecular ‘ends’, and polarization of the backbone. Both contributions get more pronounced with increasing Fermi temperature (i.e. with increasing the ‘negative’ initial gap in Fig. A1). One cannot, however, conclude from these calculations whether the effect of charge transfer is enhanced or reduced by the polarizations.

It is, thus, interesting to look at the situation also from a slightly different perspective. Instead of comparing the situation in the SAM with active and inactive compensating field, one can compare for each case the plane-integrated charge density of a molecule in the SAM with the plane-integrated charge density of the same molecule in vacuum: $\mathrm{\Delta }\rho (z)={\rho }_{\text{SAM}}(z)-{\rho }_{\text{molecule}}(z)$ and Q(z) being defined as $Q(z)={\int }_o^z\mathrm{\Delta }{\rho }_{\sigma }(z^{\prime }){\mathit{dz}}^{\prime }$, in analogy to above. Physically, the $\mathrm{\Delta }\rho (z)$ defined this way represents the sum of two effects: (i) the depolarization of the molecular dipoles when the molecules are assembled as a SAM (for references, see main text) and (ii) the charge rearrangements which prevent the situation of a ‘negative gap’. This is shown for σ = 0.1 eV, σ = 0.2 eV, and σ = 0.4 eV in Fig. A3.

Fig. A3.

Top: plane-integrated charge density differences $\mathrm{\Delta }\rho (z)={\rho }_{\text{SAM}}(z)-{\rho }_{\text{molecule}}(z)$ describing the depolarization of the molecular dipoles upon SAM-formation, for 7 repeat units and σ = 0.1 eV, σ = 0.2 eV, and σ = 0.4 eV. Δρ for the reference system with σ = 0.00862 eV is shown as dashed gray curve in each panel. Bottom: corresponding cumulative charge rearrangements.

In addition, each plot shows the corresponding curves also for the original calculation (σ = 0.00862 eV), where the gap is >0 and no compensation mechanism is active (dashed gray curves). Therefore, the latter plots show depolarization only. The shape of the Q-plots is reminiscent of Fig. A2, i.e. the molecules are depolarized through a combination of long-range charge transfer and polarization of the backbone. Regarding the black curves, it is interesting to observe that an increased temperature causes the rearrangements along the molecular backbone to decrease (best seen in the Δρ-plots). Close to the molecular ‘ends’, they remain unchanged. The net counterdipole, however, must increase with σ and this is possible by increased charge-transfer along the molecular axis. Hardly visible in the charge rearrangements, this is nicely shown in the Q-plots, where area below the black curves successively increases with increasing σ.

To sum up: when the molecules depolarize upon SAM-formation, this is done via (i) end-to-end charge transfer and (ii) polarization of the backbone. When the band gap of the resulting SAM vanishes (at increased σ), polarization effects decrease in magnitude and at the same time the amount of long-range charge transfer increases.

This allows re-interpreting Fig. A2. It can be viewed as showing the difference between each two curves of the respective panels of Fig. A3, i.e. the data shown in Fig. A2 is equivalent to the difference in the molecule-to-SAM depolarization for two values of σ. From this perspective, a reasonable explanation of Fig. A2 is that the polarization component in Q corresponds to a reduction of the depolarization the molecules underwent during SAM-formation, i.e. an effect that counteracts the consequences of the end-to-end charge transfer.

Appendix B. Methodological tests

See (Figs. B1–B3).

Fig. B1.

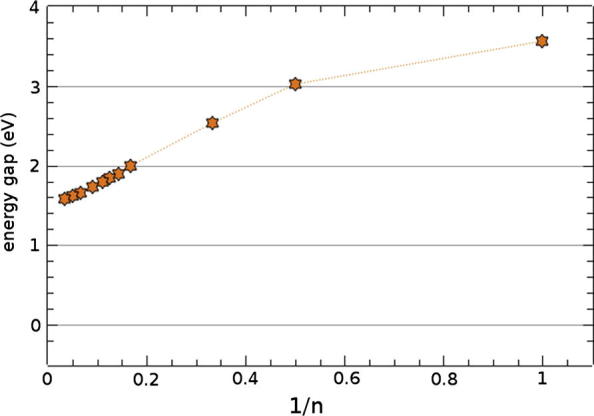
Evolution of the energy gap of isolated oligopyrimidinethiol molecules (see Fig. 2 in the main text) as a function of the inverse number of pyrimidine units.

Fig. B2.

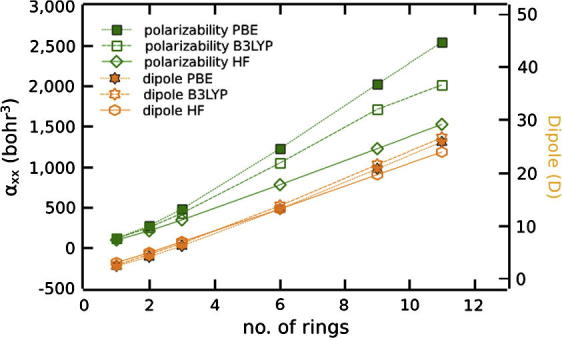
Polarizability and dipole moment of isolated oligopyrimidinethiol molecules as a function of the backbone length calculated with different methods. All three methods predict very similar dipole moments and the same trend for the polarizability. Calculated with Gaussian 03 [27] and the 6-311G^** basis set.

Fig. B3.

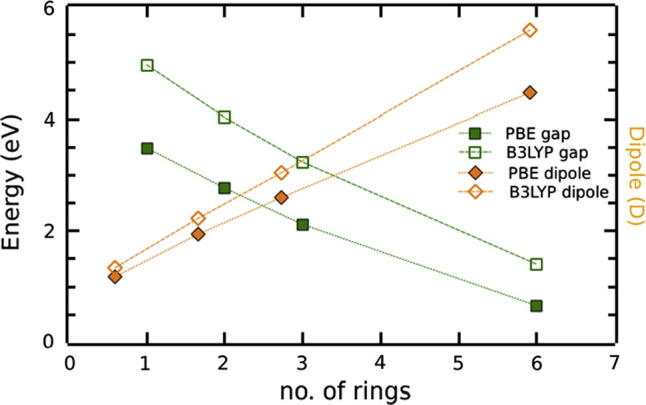
Band gap and dipole moment of SAMs formed by oligopyrimidinethiols as the number of rings increases, calculated with B3LYP and PBE. Both methods agree qualitatively. Results were obtained with Gaussian 03, using the 6-31G^* basis set together with 2D periodic boundary conditions and the option NKPoint = 6.

Appendix C. Analogue of Fig. 2 for oligophenyls

See Fig. C1.

Fig. C1.

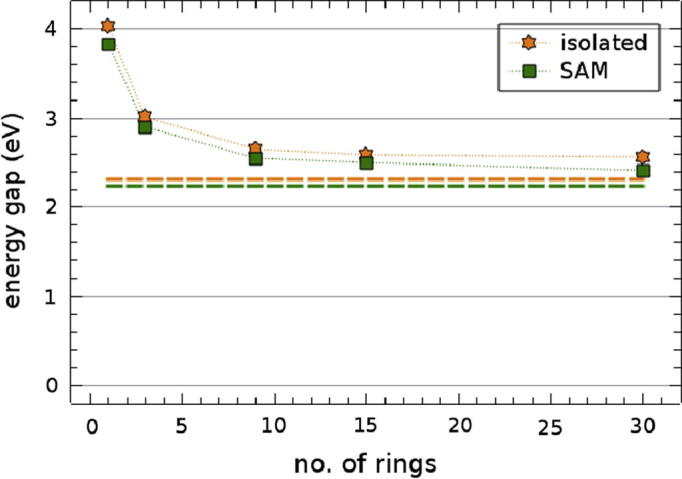
Evolution of the PBE Kohn–Sham energy gaps of oligophenylthiol molecules (orange (light gray in b/w) stars) and SAMs (green (dark gray in b/w) rectangles) with the number of phenyl units (cf. Fig. 2 in the main text). The dashed horizontal lines show the values for infinite length (i.e. a 1D-periodic chain) in orange (light gray in b/w) and the 3D-periodic bulk in green (dark gray in b/w)). (For interpretation of the references to color in this figure legend, the reader is referred to the web version of this article.)