An adaptive large neighborhood search heuristic for Two-Echelon Vehicle Routing Problems arising in city logistics

Abstract

In this paper, we propose an adaptive large neighborhood search heuristic for the Two-Echelon Vehicle Routing Problem (2E-VRP) and the Location Routing Problem (LRP). The 2E-VRP arises in two-level transportation systems such as those encountered in the context of city logistics. In such systems, freight arrives at a major terminal and is shipped through intermediate satellite facilities to the final customers. The LRP can be seen as a special case of the 2E-VRP in which vehicle routing is performed only at the second level. We have developed new neighborhood search operators by exploiting the structure of the two problem classes considered and have also adapted existing operators from the literature. The operators are used in a hierarchical scheme reflecting the multi-level nature of the problem. Computational experiments conducted on several sets of instances from the literature show that our algorithm outperforms existing solution methods for the 2E-VRP and achieves excellent results on the LRP.

1. Introduction

We consider multi-level distribution systems in which freight arrives at a central depot and is transported further to so-called satellite facilities. From there, it is brought to the final customers by smaller vehicles. An important problem arising in the operation of such systems is how to efficiently route vehicles operating at both levels to service customers. This problem is known in the literature as the Two-Echelon Vehicle Routing Problem (2E-VRP).

As its name implies, the 2E-VRP considers two levels. The first level is the delivery from the central depot to the satellite facilities and the second level is the delivery from the satellites to the customers. A limit on the number of vehicles is imposed at each level. The objective is to minimize the total routing cost of the system. We assume that the location of the satellite facilities is known, but that customers are not assigned to a specific satellite facility in advance. Clearly, the 2E-VRP is a generalization of the classical Vehicle Routing Problem (VRP) and is thus NP-hard.

One application of the 2E-VRP is the concept of city logistics. In most cities space is limited, especially in the city center, and has to be shared between private and public passenger transport as well as parking facilities. Moreover, freight transportation produces congestion, polluting emissions and noise, and the presence of large, heavy vehicles is an uncomforting factor to the citizens. Frequently, large vehicles have low average loads and a high number of empty trips. Therefore, officials want to reduce the number of vehicles, especially freight vehicles, in the city center and they want to switch from large to smaller vehicles. The key idea is to develop an integrated logistics system encompassing all components by consolidating freight that comes from different shippers and coordinating the freight transportation in the city. These activities are included in so-called city logistics systems.

Consolidation and coordination activities arising in city logistics can be performed in a multi-level system. Multi-level systems are also common in multimodal freight transportation systems, where the different transportation modes induce a natural decomposition. To change from one level to another, intermodal cross-docking facilities are often used. These systems also arise in several other applications and they are needed whenever there is no direct shipping. Perboli et al. [22] mention more examples such as express delivery services, grocery and hypermarket-product distribution, spare-parts distribution in the automotive market, e-commerce and home delivery services, and newspaper and press distribution.

To our knowledge, the only existing heuristic for the 2E-VRP is a multi-start procedure by Crainic et al. [11]. Therefore, our objective is to propose a more general framework for problems with location and routing decisions. To this end, we have developed an adaptive large neighborhood search (ALNS) heuristic. ALNS is an efficient metaheuristic paradigm that has yielded excellent results for several different routing problems (see, e.g. [24]). We have designed several new operators that take advantage of the structure of the problem and we have also adapted existing operators for the vehicle routing problem.

The proposed methodology is also used to address the Location Routing Problem (LRP), in which the number and locations of a set of facilities have to be determined simultaneously with the routes of vehicles servicing customers out of the selected facilities. The 2E-VRP is used to model the LRP, and the proposed ALNS heuristic is equally successful for both the 2E-VRP and the LRP using the same operators and parameter values.

The contributions of this paper are the following. First, we propose a new solution method for the 2E-VRP that outperforms existing algorithms. Second, we show that the single-level LRP can be modeled as a special case of the 2E-VRP and that our algorithm performs well on instances from the literature. Finally, we propose a new set of larger instances for the 2E-VRP containing up to 200 customers and 10 satellite facilities.

The remainder of the paper is organized as follows. The problem is first described in Section 2 and an overview of the literature is given in Section 3. The solution method is then presented in detail in Section 4. Section 5 explains the adaptations necessary to solve the LRP and the minor algorithmic modifications. Finally, Section 6 presents computational results and Section 7 contains the conclusion.

2. Problem description

The 2E-VRP can be defined on a directed graph $G=(V,A)$, where V is the set of nodes and A is the set of arcs. The set V comprises three subsets of nodes: the depot node v₀, the subset V_s containing m satellites and the subset V_c of n customers. The traveling cost between node i and node j is given by c_ij. Each customer i has a demand d_i, which cannot be split. The demand cannot be delivered by direct shipping from the depot, but must be consolidated in a satellite. The deliveries to the satellite facilities on the first level can be split. The vehicles have a capacity limit that has to be respected. This capacity is the same for all vehicles belonging to the same level, but can differ for each level. The capacities of the first and second-level vehicles are denoted by K₁ and K₂, respectively. The number of vehicles available is given by b₁ for the first level and by b₂ for the second level.

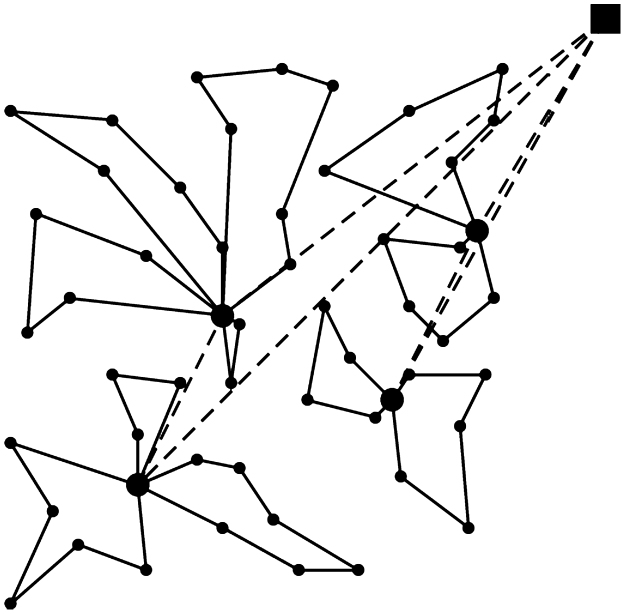
Fig. 1 illustrates a 2E-VRP solution. The square represents the depot, the large dots are the satellite facilities and the small dots are the customers. The routes that serve the satellite facilities from the depot are called the first-level routes and they are represented by dashed lines. The second-level routes are those that start from a satellite facility and visit the customers.

Fig. 1.

A solution to the 2E-VRP.

The demand of a satellite facility is the sum of the customer demands that are assigned to it. Therefore, any change to the customer assignment affects the first-level routing, and a previously optimal solution to the first-level VRP can become a very poor or infeasible solution.

The LRP can also be modeled as a 2E-VRP. In the LRP, there is a set V_s of m possible depots, where each depot j is associated with a capacity limit W_j and an opening cost O_j, and a set V_c of n customers with given demands. The goal is to open a subset of depots and design routes from each depot such that customer demand is fulfilled, the capacity of the vehicles and depots is respected, and the opening cost of the depots as well as the routing cost is minimized. Costs for using a vehicle can also be added on the outgoing arcs of the satellites.

To model the LRP as a 2E-VRP, we introduce a dummy node for the first-level depot v₀. The set of possible depots then corresponds to the satellite facilities. The important difference is that the first level now consists only of single customer routes and the cost of going from v₀ to a satellite is the opening cost of the corresponding potential depot.

3. Literature review

We first review the literature on Two-Echelon Routing Problems and then on Location Routing Problems.

3.1. Two-Echelon Routing Problems

One of the first applications of routing in a two-echelon system was introduced by Jacobsen and Madsen [17]. They considered the problem of distributing newspapers via transfer points. Three decisions have to be made in this problem: choosing the number and locations of the transfer points, designing tours from the printing office to the transfer points, and designing tours from the transfer points to the retailers. They developed a heuristic algorithm in which customers are assigned to their nearest satellite and the first- and second-level routes are constructed by three fast procedures. Unlike in the 2E-VRP, split deliveries on the first level were not considered.

Crainic et al. [13] introduced and analyzed a possible organizational and technological framework for integrated urban freight management. They also proposed a location-allocation formulation for the problem of locating satellite facilities in a multi-echelon system. Customers were grouped into customer zones, and the cost of servicing a demand was measured by the cost of a path to the respective customer zone. Data from the city of Rome were used.

The 2E-VRP is a rather new problem, and it has been the object of a small number of studies. A flow-based formulation was introduced by Perboli et al. [22], who discussed several variants of the 2E-VRP. Three sets of instances were introduced, based on the instances for the VRP. These instances have up to 50 customers and 4 satellites. The authors presented two families of inequalities, which were used within a branch-and-cut framework. They were able to solve instances with 21 customers to optimality. Moreover, they also developed two mathematical programming-based heuristics. These heuristics use the proposed model and focus on the assignment variables that specify the customers serviced by each satellite facility.

A formulation for the time-dependent version with fleet synchronization and customer time windows was proposed by Crainic et al. [14]. The authors reviewed the current state of the art, proposed a formulation for the time-dependent case and discussed promising algorithmic directions.

Perboli and Tadei [20] proposed several new classes of valid inequalities. These are based on the Traveling Salesman Problem and the VRP, the network flow formulation, and the connectivity of the transportation-system graph. Their approach is able to solve seven new instances to optimality and reduce the optimality gap on several other instances.

A family of multi-start heuristics for the 2E-VRP was proposed by Crainic et al. [11]. Their method is based on separating the first-level and the second-level routing. More precisely, they assign customers to satellites and solve the resulting $m+1$ VRPs, where m is the number of satellite facilities, by an exact algorithm. The solution is then perturbed and a local search is applied until a maximum number of iterations is reached. The perturbation phase consists of randomized changes to the customer-to-satellite assignment. A clustering based heuristic is used as local search, where the neighborhood consists of assigning customers to new satellites. More precisely, the customers are sorted in increasing order according to the difference between the current and the next best satellite assignment. Then, one after another, all the customers for which this new assignment is feasible are inserted into the new positions.

Crainic et al. [12] provided an analysis of the impact of parameters on total cost in a 2E-VRP. They studied different locations of the depot, the satellites, the distribution of the customers and the number of satellites using the algorithm of Crainic et al. [11]. They analyzed up to which point opening satellites can reduce the total cost. They concluded that the 2E-VRP performs better compared to the classical VRP when the depot is located externally with respect to the customer area.

In our computational study we compare our algorithm to the best solutions found by Crainic et al. [11], Perboli et al. [22] and Perboli and Tadei [20].

3.2. The Location Routing Problem

A seminal introduction to location routing was provided by Laporte [18]. His paper reviews the state of the art on heuristic and exact methods for this problem class. It also illustrates the different versions of problems that combine location and routing and describes in which applications they arise. Moreover, different formulations are provided.

Early heuristics for the LRP were developed by Tuzun and Burke [32], Barreto [3], and Prins et al. [30,29]. We refer to Nagy and Salhi [19] for a literature review.

More recently, Prins et al. [27] proposed a Lagrangean relaxation-granular tabu search (LRGTS) algorithm. They decompose the problem into a depot-location phase and a routing phase and alternate between the two. For the depot-location phase they aggregate customers into supercustomers and solve a facility location problem by a Lagrangean relaxation approach. For the routing phase they developed a granular tabu search completed by a local search based on move, swap and extended 2-opt moves. The move operator shifts one customer to another position, while swap exchanges two customers. The 2-opt operator was introduced by Croes [15]. Two edges of a tour are deleted and reconnected in such a way that the sequence between those edges has to be inverted. If the solution has not improved, they perform restarts using edge frequency information.

A greedy randomized adaptive search procedure (GRASP) calling an evolutionary local search (ELS) was developed by Duhamel et al. [16]. They alternate between solutions encoded as giant tours, where the splitting procedure is used for evaluation, and complete LRP solutions. Moreover, they use a tabu list for opening depots and apply a local search based on move, swap and extended 2-opt operators.

In Pirkwieser and Raidl [23], a variable neighborhood search was combined with three different ILP-based very large neighborhood searches (VLNS). Two of these operate on routes and one on customer sequences. The authors presented several combinations of the VLSN with VNS. They also showed results for the LRP as well as for the periodic LRP.

Yu et al. [33] proposed a simulated annealing (SA) algorithm. A solution is represented as a giant tour. Move, swap and 2-opt are used as neighborhoods and they operate on the giant tour. Therefore, a neighborhood move can change a customer position, open or close depots or reassign customers to satellites.

Several exact algorithms have been proposed recently. Belenguer et al. [5] introduced a two-index integer programming formulation and families of valid inequalities. They were able to solve instances with up to 50 customers. Contardo et al. [10] proposed a branch-and-cut algorithm and were able to solve larger instances with 88 customers and 8 depots. Akca et al. [1] presented a set partitioning formulation for the LRP and developed a branch-and-price algorithm that was able to solve instances of up to 40 customers to optimality. Baldacci et al. [2] also proposed a branch-and-price algorithm that can solve instances with up to 199 customers and 14 facilities. Finally, Contardo et al. [9] developed a branch-and-cut-and-price algorithm that yields improved bounds and could solve some of the open instances from the literature.

In the Two-Echelon Location Routing Problem (2E-LRP), the number and location of two types of capacitated facilities have to be determined. Furthermore, the size of the two different vehicle fleets and the routes on each level have to be optimized. Boccia et al. [7] proposed three mixed-integer programming models for the 2E-LRP and tested them on instances they generated. A heuristic for the same problem was proposed by Boccia et al. [6]. The authors developed a tabu search that is based on a decomposition of the problem into two location-routing sub-problems and a further decomposition of these sub-problems into a capacitated facility location problem and a multi-depot vehicle routing problem. They perform simple moves on every level and refer to their method as a multi-phase iterative-nested approach.

For the LRP, among the heuristic algorithms that were cited above, that of Prins et al. [27] performs very well and also has a very low runtime. Pirkwieser and Raidl [23] have only tested one instance set from the literature and the average solution quality of their algorithm is slightly worse, but it is faster than the algorithm of Prins et al. [27]. Duhamel et al. [16] achieved good results, but they only report the best solution found over five runs. Yu et al. [33] achieved good results too. Yu et al. [33] and Prins et al. [27] only report one run of their respective algorithms, which use randomization. These four algorithms and the exact solution procedures mentioned have found the best known solutions to which we compare in Section 6.

4. Solution method

The key ideas of the ALNS algorithm that we propose are the following. At every iteration, a number q of customers are removed by a destroy operator, put in a customer pool and then re-inserted by a repair operator. Some of the operators that we use explicitly open or close satellites, while others apply to a more restricted area of the search space, i.e., they remove a smaller number of customers and keep the current satellite configuration unchanged. The operators are selected by a roulette wheel mechanism based on their past success. Every operator is associated with a score. Operators that have successfully found new improving solutions have a higher score and therefore a higher probability of being chosen again.

ALNS was first developed by Ropke and Pisinger [31] for the pickup and delivery problem and these authors later solved several variants of the vehicle routing problem with a general algorithm based on the same methodology [24]. Compared to the latter method, we have a simplified mechanism to update the score and the acceptance criterion has no parameter. In addition, we apply a local search step after some of the operators.

Our algorithm works as follows (see Algorithm 1). Starting from an initial solution, a destroy operator is first chosen to remove q customers and a repair operator is then used to insert them back into the current solution. Since we are dealing with a two-level problem, we use a hierarchical structure for the destroy operators. There are two types of destroy operators: some that change the given configuration of satellites by opening or closing satellites and others that only affect a smaller part of the solution. In the following, D_L represents the set of destroy operators that have a large impact, D_S the set of operators that have a small impact, and R is the set of repair operators. The destroy operators in set D_L, i.e., Satellite Removal, Satellite Opening and Satellite Swap, are executed whenever $\omega$ iterations have been performed without improvement. The new solution yielded by any of these operators is passed through a local search phase. Moreover, it is accepted as a new incumbent even if it is not improving, i.e., it gets a free pass through the acceptance decision. Solutions yielded by the operators in set D_S are only passed through local search if they are within $\theta$ percent of the best found solution s^⁎. Moreover, they are only accepted as a new incumbent solution if they have a better objective value than the current incumbent.

We differentiate between the small- and the large-impact destroy operators for the following reasons. The operators in set D_L change the solutions substantially, especially on the first level. The repair operators are designed to insert a limited number of requests in a partial solution. Therefore, the large impact operators overburden the capabilities of the repair operators. The solution can be further improved in the local-search phase. Furthermore, the free pass as a new incumbent helps to explore the search space more thoroughly with the operators in set D_S, while keeping the satellite configuration fixed.

Algorithm 1

Basic steps of ALNS.

$s\leftarrow \mathit{InitialSolution}$, $\mathit{InitializeScores}(\mathit{\pi }),i\leftarrow 0$

repeat

if i=$\omega$then

$N^{-}\leftarrow \mathit{ChooseDestroyOperator}(D_L,\mathit{\pi })$

else

$N^{-}\leftarrow \mathit{ChooseDestroyOperator}(D_S,\mathit{\pi })$

end if

$N^{+}\leftarrow \mathit{ChooseRepairOperator}(R,\mathit{\pi })$

$s\prime \leftarrow \mathit{DestroyAndRepair}(s,N^{-},N^{+})$

if i=$\omega$then

$s\prime \leftarrow \mathit{LocalSearch}(s\prime )$

$s\leftarrow s\prime$ // free pass

$i\leftarrow 0$

else if$f(s\prime )<(1+\theta )f(s^{⁎})$then

$s\prime \leftarrow \mathit{LocalSearch}(s\prime )$

end if

if$f(s\prime )<f(s)$then

$s\leftarrow s\prime$

$i\leftarrow 0$

else

$i\leftarrow i+1$

end if

if$f(s)<f(s^{⁎})$then

$s^{⁎}\leftarrow s$

end if

Update scores $(\mathit{\pi })$

until the stopping condition is met

return s⁎

4.1. Search space

To rely on simple procedures to construct an initial solution and modify this solution, the search is not restricted to feasible solutions. Instead, we allow violations of the constraints on vehicle capacity, number of vehicles available, and the capacity limits at the satellites (for the LRP), and we use a weighted penalty function to take these violations into account. More precisely, we consider the objective function $f(s)=c(s)+\alpha d(s)+\beta e(s)+\gamma g(s)$, where c(s) is the operating cost of the system (i.e., routing cost and eventual opening cost of depots), d(s), e(s) and g(s) represent violations of the vehicle capacity, number of vehicles, and satellite capacity constraints, respectively, and $\alpha$, $\beta$ and $\gamma$ are the corresponding weights.

The weights $\alpha$, $\beta$ and $\gamma$ are adjusted dynamically during the search within the interval $[\iota ;\kappa ]$, which has been determined experimentally. The lower endpoint guarantees that when a violation occurs, the algorithm starts off with a reasonable value, and the upper endpoint prevents the weights from going to infinity. Whenever the vehicle capacity constraint, the number of available vehicles, or the capacity limit at the satellites is exceeded, the respective weight is multiplied by the factor $\delta >1$; when the solution is feasible, the respective weight is divided by $\delta$.

4.2. Initial solution

To construct an initial solution, every customer is first assigned to a satellite facility by a roulette wheel selection mechanism based on the distance to the customer. Then, the VRPs for the second level are solved by means of the Clarke and Wright [8] savings algorithm for every satellite. Finally, with the given demand at each satellite, the first-level routes are constructed using again the savings algorithm.

4.3. Destroy operators

In the following, we describe the destroy operators used in the algorithm. Some of them are new, while others have been proposed by Ropke and Pisinger [31] and have been adapted to the 2E-VRP. Whenever applicable, the number of customers to remove, q, is randomly chosen in the range $[\rho ,\tau ]$.

4.3.1. Satellite Removal

Among all the open satellites, we choose one randomly and close it. All customers that are currently assigned to this satellite are removed and put in the customer pool. Therefore, all the routes starting at that satellite are removed as well. Moreover, we select among the other satellites a random one and open it, in case it is not already open. This prevents situations in which all satellites would be closed because the only open one has been closed by the operator. This mechanism is also important for diversification.

4.3.2. Satellite Opening

Here, we choose a satellite randomly among those that are closed and open it. Then, the q customers that are closest to this satellite are removed from their current route and inserted into the customer pool.

4.3.3. Satellite Swap

First, we apply the Satellite Removal operator. Next, a new satellite is chosen at random by a roulette wheel selection and is opened. The probability that a satellite is chosen is inversely proportional to the distance with respect to the satellite that has been removed. We want to favor the swaps of satellites that are close to each other so that the solution is not changed too drastically.

4.3.4. Random Removal

This operator was proposed by Ropke and Pisinger [31]. It simply chooses q customers at random and puts them into the customer pool.

4.3.5. Worst Removal

The Worst Removal is also based on a similar operator used by Ropke and Pisinger [31]. This operator removes the q customers with the highest removal gain. More precisely, the gain is defined as the difference between the cost when the customer is in the solution and the cost when it is removed. The gain is normalized by dividing it by the average cost of the ingoing arcs of the corresponding node. The purpose of this normalization is to avoid repeatedly choosing customers that are located far away from the remaining ones. The cost is also perturbed by a factor $d\in [0.8,1.2]$ in order to randomize the search.

4.3.6. Related Removal

A seed customer is chosen randomly and the $q-1$ customers that are located closest to the seed customer are identified. All of these customers are then removed from their current routes and put into the customer pool. Related Removal is similar to the one used by Pisinger and Ropke [24], but while they choose a chain of customers that are most related to each other based on the distance, we simple move the $q-1$ that are the closest to the seed customer.

4.3.7. Route Removal

The Route Removal operator removes a random route and puts the corresponding customers into the customer pool. The opening of a new route at the corresponding satellite by an insertion operator is then forbidden to avoid cycling. Like Satellite Removal, this operator has a mechanism that can open a previously closed satellite because, in rare cases, all customers could be served by a single route originating from the only open satellite.

4.3.8. Route Redistribution

For each open satellite, we choose a random number k, $1\le k\le 3$, of routes to be removed. The selection of the k routes works in the following way. One after another, we remove the routes containing the customer with the minimum distance between the satellite it is currently assigned to and any other open satellite. To introduce some randomization, distances are perturbed by a factor $d\in [0.8,1.2]$. This operator is based on the idea that the customers that are close to several satellites may benefit more from reassignment than those for which the best assignment is more obvious. For example, the reassignment of a customer that is at the edge of a town, close to a satellite, but farther from the other ones, is not likely to reduce the cost.

4.4. Repair operators

The repair operators can only insert customers into routes originating from open satellites, i.e., satellites that currently have customers assigned to them or those that were opened by a destroy operator in the same iteration.

4.4.1. Greedy Insertion

For Greedy Insertion, the customers are inserted in a random order one after the other into the position that minimizes the insertion cost over all the open satellites and routes. We also check the possibility of opening a new route unless this is forbidden because the Route Removal operator was applied to the considered satellite. For the first level, we check whether the first-level routes would still be feasible after the increase in demand at this satellite facility. If not, we look for the cheapest insertion position of this satellite in the first-level routes. Afterwards, one-customer moves and swaps are performed for the first level to improve the routes. Note that Ropke and Pisinger [31] insert the customers according to the insertion cost and therefore they also recompute the insertion cost after each insertion. We chose the insertion by random order because we wanted to have a simple and fast insertion operator. Regret Insertion uses a more sophisticated mechanism with recalculations.

4.4.2. Greedy Insertion Perturbation

This operator works like Greedy Insertion. The difference is that when we compute the insertion cost of a customer at each position, the cost is perturbed by a factor $d\in [0.8,1.2]$ to introduce randomization. This operator was inspired by the algorithm of Ropke and Pisinger [31], which also added noise to their insertion heuristics.

4.4.3. Greedy Insertion Forbidden

This operator works like Greedy Insertion but it is not allowed to serve a customer from the same satellite from which it was removed. We introduce this operator mostly for diversification purposes.

4.4.4. Regret Insertion

In the regret heuristic, customers are treated in the order of their regret value. The regret value is the cost difference between the best insertion position and the second best. Thus, customers with a high regret value should be inserted first. More precisely, a regret-k heuristic chooses to insert customer i among the set $U$ of untreated customers according to $i≔\arg {\max }_{i\in U}({\sum }_{h=2}^k\mathrm{\Delta }{f}_i^h-\mathrm{\Delta }{f}_i^1)$, where $\mathrm{\Delta }{f}_i^h$ is the cost of inserting customer i at the hth cheapest position. This heuristic uses look-ahead information and can prevent situations where we have to insert a customer in a poor position because the better positions are no longer available. Unlike Ropke and Pisinger [31], we compute the regret value based on different positions that can also be in the same route, whereas they only look at insertion positions in different routes. Once a customer has been inserted, the insertion positions of the remaining unplaced customers have to be recomputed by considering the change caused by inserting this customer at a position. In this operator we do not compute the first-level cost change, but we focus on the second-level insertion cost only. Computing the first-level cost change would be too demanding, because after every insertion we should solve the first-level VRP for every customer and every satellite facility.

4.4.5. First level local search

At each iteration, we also check if we can improve the first-level VRP. First, we perform a procedure where we generate a giant tour that contains all the satellites that serve at least one customer. We create this giant tour with a simple procedure that first inserts the customer that is farthest away from the depot into an empty tour. We then insert the remaining satellites at their respective cheapest position. Afterwards, we split the giant tour in a greedy way by going back to the depot whenever the capacity is exceeded even if this implies splitting customer demands. We finally improve the tour by performing moves and swaps with a maximum sequence length of one node. We also check for a solution that only contains out-and-back tours, i.e., tours that only contain one satellite, in case the local search could not find these tours. In the end, the best of these solutions is accepted.

4.5. Local search

Local search is performed after the Satellite Removal, Satellite Swap or Satellite Opening operator is applied. It is also executed for every new promising solution, i.e., a solution that is within a certain threshold $\theta$ of the best solution found. Local search is performed for the VRPs of each satellite separately. Since it does not change the demand assigned to each satellite, there is no impact on the first level.

The local search consists of the following operators, which are performed sequentially: split, move, swap, 2-opt and 2-opt^⁎. The split procedure was developed by Beasley [4] and it has been used in several genetic algorithms for routing problems (see for example [26]). In our implementation, we create a giant tour by linking the routes one after another. Afterwards, the depot node is deleted from every occurrence and reinserted with the split procedure.

The move operator relocates one customer to the best position in the same route or in a different route. Swap exchanges all possible segments of customers. For swap we consider sequences with a length of 1–4 customers. Both operators are performed inter-route and intra-route and all possible positions are examined, while 2-opt is performed intra-route.

Finally, we perform 2-opt^⁎ [25] for every pair of routes u and v and every node $i\in u$ and $j\in v$. More precisely, edges (i, $i+1$) and (j, $j+1$) can be replaced by edges (i, $j+1$) and (j, $i+1$) or by edges (i, j) and ($i+1$, $j+1$), thus reversing the direction of visit between j and the depot as well as between $i+1$ and the depot.

Moves are performed in a first-improvement manner as long as an improvement can be found.

4.6. Selection of destroy and repair operators

The selection is based on the success of each operator in the previous iterations. The destroy and repair operators are weighted and chosen independently. Every time operator j finds a new global best solution, $\sigma$ is added to the score ${\pi }_j$. The selection of the operators is based on a roulette wheel selection mechanism in which the probability of operator j being selected is ${\pi }_j/{\sum }_{k=1}^p{\pi }_k$ and p is the number of operators considered.

5. Location Routing Problem

The algorithm described in the previous section for the 2E-VRP is also able to solve the single level LRP with only minor modifications in the generation of the initial solution. The parameters and operators are the same for both problems.

The main difference between the settings of the 2E-VRP and the LRP is that in the latter problem there is no first-level depot and the satellites have both a capacity and a fixed cost. To account for this, we introduce a dummy node for the first-level depot and the cost of visiting a satellite corresponds to its opening cost. For satellite visits, only out-and-back tours are allowed and the capacity of each vehicle corresponds to the capacity of each depot. Therefore, for instances that have heterogenous depot capacities, the vehicles have different capacity limits which depend on the satellite visited.

For the LRP, the generation of the initial solution is done as follows. Among all the possible combinations of satellites to open, we chose the one that yields the lowest cost and whose capacity is large enough to accommodate the total demand. As for the 2E-VRP, customers are randomly assigned to a satellite with a bias towards the shortest distance.

6. Computational results

We have performed extensive computational experiments to set parameter values by sensitivity analyses and to compare the algorithm to state-of-the-art heuristics for both the 2E-VRP and the LRP. When we refer to the best known solutions, we include the best results that were found by the algorithms cited in Section 3.

Our algorithm was coded in C++, compiled with GCC version 4.5.1 and tested on an 2.2 GHz AMD Opteron 275 Processor.

6.1. Instance description

For the 2E-VRP, we have considered three instance sets from the literature. Sets numbered 2 and 3 were proposed by Perboli et al. [22] and they are based on the following instances by Christofides and Eilon: E-n13-k4, E-n22-k4, E-n33-k4 and E-n51-k5. These authors have also proposed a very small set of instances (set 1) with just 1 depot, 12 customers and 2 satellites, which we did not use.

Set 4 was proposed by Crainic et al. [12] and contains 54 instances. Each has 50 customers and the number of satellites is either 2, 3 or 5. They were generated using three different customer distributions and three satellite location patterns (see [12] for more details).

For the LRP, we have also considered three sets of instances. The first one was proposed by Prins et al. [28]. It contains 30 instances with capacitated vehicles and depots. The number of customers ranges from 20 to 200 and the number of depots from 5 to 10. This set is referred to as set “Prodhon” in the literature. The second set, which is denoted set “Tuzun” in the literature, contains instances with uncapacitated depots and was introduced by Tuzun and Burke [32]. It contains 36 instances with 100, 150 or 200 customers and 10 or 20 depots. The vehicles are capacitated. The third set, with 13 instances, was taken from Barreto [3]. These contain capacitated depots and vehicles and the set is referred to as set “Barreto”. These sets have a homogenous, unlimited fleet, but the sets Prodhon and Tuzun have a fixed cost for each vehicle used.

We also introduce a new set of larger instances for the 2E-VRP, which we call set 5. To create this set, the 17 instances containing more than 50 customers from the set Prodhon of the LRP instances were adapted to the 2E-VRP. The missing data is the depot location, and for the first-level fleet the capacity limit and the limit on the number of vehicles. Moreover, for those instance the number of available vehicles for the second level is unlimited and there is a fixed cost per vehicle used. To obtain a more homogenous set of instances for the 2E-VRP, we removed the fixed cost per vehicle and we limited the fleet for the second level experimentally. The number of vehicles used in the best solution from preliminary tests was multiplied by 1.2 and rounded up. Concerning the first-level fleet, the limit on the number of vehicles was set to 5, and the capacity restriction of the vehicles was set to $\lceil {\sum }_{i\in V_c}{d}_i/3\rceil$, so that at least 3 tours will be executed. Since we wanted to picture a setting where the depot is located on the outskirts of a city, we decided to place it in the northeast corner. Therefore, the depot coordinates were chosen to be $1.33x_{\max }$ and $1.33y_{\max }$, where $x_{\max }={\max }_{i\in V_c}{x}_i$ and $y_{\max }={\max }_{i\in V_c}{y}_i$.

A summary of the instance characteristics is given in Table 5 in the Appendix.

6.2. Parameter settings and sensitivity analyses

As mentioned above, the parameter settings are the same for both problems considered. We have chosen a representative subset of instances for the 2E-VRP and the LRP to tune the algorithm and find reasonable values for $\omega$ and $\tau$.

The 2E-VRP instances are insensitive to changes in $\omega$, which is the threshold for the number of iterations without improvement after which the satellite destroy operators are called. For the LRP instances, we noticed that values for $\omega$ in the range [100; 2000] yield the best solution quality. Therefore, we opted for setting $\omega$ to 100. The number of customers to remove is a random integer between $\rho$ and $\tau$. We set $\rho$ to 1. As suggested in Pisinger and Ropke [24], we set $\tau$ to min $\{60,0.4n\}$. We also performed sensitivity analyses for $\tau$ on the same subset of instances that we used for testing $\omega$. Again, the 2E-VRP instances are insensitive to changes. For the LRP instances, we noticed that when we increase $\tau$ beyond $0.5n$ the solution quality becomes worse.

For the weighted penalty function, $\delta$ was set to 1.1, $\iota$ to 5 and $\kappa$ to 10,000. These values were chosen according to preliminary tests. The value $\sigma$, added to the score ${\pi }_j$ every time a new best solution is found, is set to 1.

The stopping condition of the algorithm is the number of iterations performed. Preliminary tests showed that 500,000 iterations usually provide a good trade-off between run time and solution quality.

For the Regret Insertion, we used a regret-3 heuristic and the threshold $\theta$ that identifies a promising solution that will undergo local search is set to 2%. Both values are also based on preliminary tests.

Table 1 provides statistics on the different operators. The second column shows the average cost deviation of the solutions found with and without this operator for a subset of representative instances. We ran the algorithm excluding each of the respective operators while keeping the other ones. The Regret Insertion is the most useful operator, followed by Route Removal and Route Redistribution. The results suggest that we can leave out some of the operators, but when we remove more than one of these operators, the solution quality becomes worse. Greedy Insertion Perturbation, for example, seems not necessary for this subset of instances, but in some cases this operator helps escaping from a local optimum. In the third column of Table 1, we provide the average number of times a new best solution was found. These statistics are taken from five runs over all the instances of the 2E-VRP. The operators that change the satellite configuration hardly ever find a new best solution. This is because a change in the configuration affects the solution in a fundamental way and cannot be repaired in just one iteration. Among the destroy operators, Route Redistribution delivers a new best solution the least often. From the repair operators Regret Insertion is the most successful, followed by Greedy and Greedy Perturbation.

Table 1.

Statistics for the destroy and repair operators.

Operator	Solution degradation without this operator	Average number of new best solutions found by the operator
Related Removal	0.05	13.19
Random Removal	0.01	18.95
Worst Removal	0.00	9.04
Route Removal	0.11	17.80
Route Redistribution	0.11	1.38
Satellite Removal	−0.02	0.05
Satellite Opening	0.01	0.00
Satellite Swap	0.00	0.06
Greedy Insertion	0.02	4.11
Regret Insertion	0.32	12.99
Greedy Insertion Perturbation	−0.01	4.05
Greedy Insertion Forbidden	0.03	1.05

We have also evaluated the local search operators for the same subset of 2E-VRP instances. The operators move, swap, 2-opt and 2-opt^⁎ have already been used in local search heuristics for many VRP variants. However, to our knowledge, the split operator has never been used in a local search framework, but only as a splitting procedure inside evolutionary algorithms. Our tests for the same subset of 2E-VRP instances show that the solutions found without the split operator are on average 0.2% worse than with the operator. It is powerful, because it can not only minimize the number of vehicles used, but also reassign customers from the beginning and end of each tour to other tours in the way ejection chains work.

6.3. Computational results

We have compared our ALNS with other solution methods from the literature. In Table 2, we compare the ALNS to the best solutions found by the previous algorithms of Perboli and Tadei [20], Perboli et al. [22], Perboli and Tadei [21] and Crainic et al. [11]. We give the average and minimum solution value of five runs, and the percentage deviation to the best known solutions. All values are averaged over the instances of the sets. We report the runtime in seconds in column T, which shows the total time, and in column T^⁎, which shows the time at which the solution was found. Detailed results for all instances can be found in the Appendix in Tables 6–8. For set 4, we report the average and the minimum of five runs. For sets 2 and 3, these are equivalent as the instances are smaller and the ALNS yields the same results in each of the five runs.

Table 2.

Results for the three 2E-VRP sets compared to the best known solutions from the literature.

Set	BKS	ALNS avg.	% dev.	ALNS min	% dev.	T (s)	T⁎ (s)
2	565.71	565.55	−0.03	565.55	−0.03	93	1
3	634.14	632.45	−0.20	632.45	−0.20	93	5
4	1429.61	1401.39	−1.93	1400.96	−1.96	169	32

Sets 2 and 3 contain small instances with up to 50 customers and two or three satellites. The ALNS is either improving the upper bound or finds the optimal solution for the instances where it is known. More precisely, for the 21 instances of set 2, we found 19 ties, one improvement and one solution that is slightly worse (0.01%). For the 18 instances of set 3, we found 9 improvements and 9 ties. For set 2, we found 14 out of the 15 optimal solutions and for set 3, we found all 8 solutions for which optimality was proven. For all instances but five from instance set 4, the average solution quality of the ALNS is better than the quality of the best solutions found in the literature and for those five instances the gap to the best known solutions is very small (below 0.5%).

Table 3 shows results for the new larger instances that we created for the 2E-VRP. The table shows solution values of the ALNS with a stopping condition of 500 K iterations and of 5000 K iterations. Runtimes are given in minutes. The BKS were found with longer runtimes. When we compare the ALNS with a stopping condition of 500 K iterations, the average deviation to the BKS is still quite large. Apparently for these difficult instances a longer runtime is needed.

Table 3.

Results for the new set of larger 2E-VRP instances.

Instance name	BKS	ALNS 500 K	% dev. to BKS	ALNS 5000 K	% dev. to BKS	T⁎ (min) 500 K	T (min) 500 K
100-10-1	1130.23	1137	0.6	1133.17	0.26	1.94	5.89
100-10-1b	916.48	928.01	1.26	917.05	0.06	0.75	6.62
100-10-2	990.58	1009.49	1.91	997.42	0.69	1.95	6.77
100-10-2b	768.61	773.58	0.65	770.7	0.27	2.83	5.67
100-10-3	1043.25	1055.28	1.15	1047.05	0.36	1.33	5.87
100-10-3b	850.92	861.88	1.29	862.11	1.32	2.11	6.52
100-5-1	1565.45	1588.73	1.49	1578.4	0.83	2.26	7.15
100-5-1b	1111.34	1126.93	1.4	1118.95	0.68	4.37	7.94
100-5-2	1016.32	1022.29	0.59	1016.32	0	3.87	5.94
100-5-2b	782.25	789.05	0.87	784.06	0.23	2.61	7.2
100-5-3	1045.29	1046.67	0.13	1046.05	0.07	3.48	6.92
100-5-3b	828.99	828.99	0	828.99	0	0.48	6.96
200-10-1	1574.12	1626.83	3.35	1597.19	1.47	3.45	14.8
200-10-1b	1201.75	1239.79	3.17	1225.9	2.01	6.23	11.54
200-10-2	1374.74	1416.87	3.06	1385.9	0.81	8.27	17.87
200-10-2b	1003.75	1018.57	1.48	1016.14	1.23	3.68	17.63
200-10-3	1787.73	1808.24	1.15	1799.85	0.68	5.09	15.27
200-10-3b	1200.74	1208.38	0.64	1203.05	0.19	7.96	20.28
Avg.	1121.81	1138.14	1.34	1129.35	0.62	3.48	9.82

We have also tested our algorithm on the three sets of instances for the LRP. Table 4 shows a summary of the best and most recent heuristic algorithms from the literature, the percentage deviation to the best known solutions, which have been found by all algorithms published so far, and the runtime in seconds. More precisely, we show the results for the TS of Tuzun and Burke [32], the GRASP of Prins et al. [30], the $\mathrm{MA}|\mathrm{PM}$ of Prins et al. [29], the LRGTS of Prins et al. [27], the GRASP $\times$ ELS of Duhamel et al. [16], the VLNS of Pirkwieser and Raidl [23] and the SA of Yu et al. [33].

Table 4.

Average % deviation to the BKS and CPU times in seconds over all the instances of the three instance sets for the LRP.

Algorithm/set	% dev. to BKS			CPU time in seconds
	Prodhon	Tuzun	Barreto	Prodhon	Tuzun	Barreto
TS	−	3.97	−	−	12	−
GRASP, 1 run	3.60	3.15	1.59	97	160	20
$\mathrm{MA}|\mathrm{PM}$, 1 run	1.38	1.53	2.02	77	203	36
LRGTS, 1 run	0.73	1.50	1.62	18	21	18
GRASP $\times$ ELS, min of 5 runs	1.07	0.96	0.04	258	607	14
VLNS, avg. of 30 runs	0.86	−	−	7	−	−
SA, 1 run	0.41	1.15	0.28	422	826	154
ALNS – 500 K, 5 runs
Avg., T	0.69	0.56	0.21	451	830	177
Min, T⁎	0.40	0.10	0.12	173	391	58
ALNS – 5000 K, 5 runs
Avg., T	0.41	0.17	0.08	4221	8103	1772
Min, T⁎	0.30	−0.04	0.02	1714	3703	564

Duhamel et al. [16] performed five runs and they only report the best solution found over the runs and the CPU time required to reach it within the corresponding run. Therefore, we cannot compare to the average solution quality of their algorithm. Yu et al. [33] and Prins et al. [29,30,27] only report one run of their respective algorithms, so it is difficult to assess the solution quality.

Pirkwieser and Raidl [23] report the average over 30 runs. We report both the average and the best solution of the ALNS found over five runs and also the time in CPU seconds, required to find the solutions (T^⁎) as well as the total running time of the algorithm (T). We show the results for 500 K iterations as well as for 5000 K.

The following computing environments were used. Duhamel et al. [16] implemented their algorithm using the Borland C++ 6.0 package and used a Quad Core 2.83 GHz computer under Windows XP with 8 GB of memory. The algorithms of Prins et al. [27,29,30] were implemented in C++ and the experiments were carried out using a Dell PC Optiplex GX260 with a 2.4 GHz Pentium and 512 MB of RAM under Windows XP. Pirkwieser and Raidl [23] coded their algorithm in C++, compiled with GCC 4.3 and executed it on a single core of a 2.83 GHz Intel Core2 Quad Q9550 with 8 GB RAM. For the VLNS they used CPLEX version 12.1. The tabu search of Tuzun and Burke [32] was coded in C++ and run on a Gateway 2000 PC Model G6-266M with a 266 MHz Pentium II processor and the SA of Yu et al. [33] was implemented in C and run on a PC with an Intel Core2 Quad CPU with 2.6 GHz and 2 GB memory.

Among the existing heuristic solution methods the LRGTS of Prins et al. [27], the VLNS of Pirkwieser and Raidl [23], the GRASP×ELS of Duhamel et al. [16] and the SA by Yu et al. [33] have obtained the best results so far.

For the set Prodhon, the VLNS obtains slightly worse results than the LRGTS, but it also needs less time. However, because the algorithms were run on different machines and different compilers were used, it is hard to make a direct comparison of run times. In terms of solution quality, the ALNS has comparable results to the LRGTS for the set Prodhon, while the SA obtains better results.

For the set Tuzun, the ALNS outperforms all the existing solution methods. The ALNS performs better on the set Tuzun because there is no capacity limit on the satellites in this set.

For the set Barreto, the SA yields similar results to ALNS, while the GRASP×ELS yields the best results.

In terms of runtime, our method is slower than the existing methods, except for the SA which has a comparable runtime. It is also worth mentioning that we compare runtimes from different machines and our computer seems to have a worse performance with a clock speed of 2.2 GHz compared to the machines used for the other algorithms. Moreover, since we are solving two problem classes, the data structures were not tailored for the LRP, but for the more complex 2E-VRP and there is a small computing overhead to solve both problem classes with the same code.

Detailed results for the LRP can be found in the Appendix (Tables 9–11). For set Prodhon, the solution quality of the ALNS is comparable to previous solution methods. On some instances the performance of the ALNS is not so good and this is mainly due to tight capacities on the depots. For set Tuzun, with uncapacitated depots, the ALNS can find several new best solutions. For three instances the average solution quality is even better than the best known solutions. For 12 instances the minimum of five runs can already improve the best solutions. Note that these results are achieved for the larger instances with 150 or 200 customers and 10 or 20 depots. For set Barreto, the ALNS finds the optimal or best known solutions in all but four instances.

Table 12 in the Appendix shows the best solutions found for the LRP instances. For the set Prodhon our algorithm yields 16 ties and one new best known solutions, while for the remaining 13 instances we did not find nor improve the best found solution. For the set Tuzun, we find 19 new best solutions, 11 ties and 6 worse solutions. For the set Barreto, we find 11 ties and two slightly worse solutions.

Table 13 in the Appendix lists the best solutions for the 2E-VRP. The ALNS yields 59 new best found solutions for the 93 instances that were tested.

7. Conclusion

We have presented an ALNS heuristic for the 2E-VRP that also yields excellent results on the LRP. We have shown an easy modeling approach to transform LRP instances into 2E-VRP instances so as to address both problems with the same operators and parameter values. Our method uses existing operators and new operators designed specifically for the problem classes considered. It is simple and relies on a small number of parameters.

We have tested three instance sets from the literature for the 2E-VRP and three other sets for the LRP. For the 2E-VRP, our solution method outperforms existing algorithms from the literature. For the LRP, we achieve competitive results and outperform existing solutions methods on one instance set. Moreover, we have found several new best known solutions for standard benchmark instances. For the 2E-VRP we found 59 new best solutions out of 93 instances and for the LRP we improved 20 best found solutions out of 79 instances.

Finally, we have also proposed a new data set for the 2E-VRP that contains larger instances with 100 or 200 customers and 5 or 10 satellites.

Future research will focus on extending this approach to solve rich vehicle problems that occur in city logistics or other multi-tiered systems. An important issue is time dependency and the synchronization of visits from the first and second-level vehicles at the satellites.

Appendix

Table 5

Table 5.

Characteristics of the 2E-VRP and LRP instances.

Set	Instances	m	n	m1	m2	K1	K2
2	6	2	21	3	4	15,000	6000
2	6	2	32	3	4	20,000	8000
2	6	2	50	3	5	400	160
2	3	4	50	4	5	400	160
3	6	2	21	3	4	15,000	6000
3	6	2	32	3	4	20,000	8000
3	6	2	50	3	5	400	160
4	18	2	50	3	6	12,500	5000
4	18	3	50	3	6	12,500	5000
4	18	5	50	3	6	12,500	5000
5	6	5	100	5	$m_2\in [\mathrm{15,32}]$	$K_1\in [\mathrm{520,528}]$	$K_2\in \{\mathrm{70,150}\}$
5	6	10	100	5	$m_2\in [\mathrm{17,35}]$	$K_1\in [\mathrm{512,537}]$	$K_2\in \{\mathrm{70,150}\}$
5	6	10	200	5	$m_2\in [\mathrm{30,63}]$	$K_1\in [\mathrm{1026,1034}]$	$K_2\in \{\mathrm{70,150}\}$
Prodhon	4	5	20	–	100	–	$K_2\in \{\mathrm{70,150}\}$
Prodhon	8	5	50	–	100	–	$K_2\in \{\mathrm{70,150}\}$
Prodhon	6	5	100	–	100	–	$K_2\in \{\mathrm{70,150}\}$
Prodhon	6	10	100	–	100	–	$K_2\in \{\mathrm{70,150}\}$
Prodhon	6	10	200	–	100	–	$K_2\in \{\mathrm{70,150}\}$
Tuzun	6	10	100	–	100	–	150
Tuzun	6	20	100	–	100	–	150
Tuzun	6	10	150	–	100	–	150
Tuzun	6	20	150	–	100	–	150
Tuzun	6	10	200	–	100	–	150
Tuzun	6	20	200	–	100	–	150
Barreto	13	$m\in \{\mathrm{5,8},10\}$	$n\in [\mathrm{21,150}]$		100		$K_2\in [\mathrm{160,9000000}]$

lists the characteristics of the 2E-VRP and LRP instances. For sets 2, 3, 4 and 5 of the 2E-VRP and sets Prodhon, Tuzun and Barreto of the LRP, the table lists the number of instances that have the same characteristics with respect to m, the number of depots, n, the number of customers, m₁ and m₂, the number of the first- and second-level vehicles, and K₁ and K₂, the capacity level for the first and the second level, respectively. Tables 6–8

Table 6.

Results and runtimes in seconds for set 2 for the 2E-VRP.

Instance	BKS	ALNS avg.	% dev	T (s)	T⁎ (s)
E-n22-k4-s6-17	417.07⁎	417.07	0.00	37	0
E-n22-k4-s8-14	384.96⁎	384.96	0.00	34	0
E-n22-k4-s9-19	470.60⁎	470.60	0.00	35	0
E-n22-k4-s10-14	371.50⁎	371.50	0.00	37	0
E-n22-k4-s11-12	427.22⁎	427.22	0.00	31	0
E-n22-k4-s12-16	392.78⁎	392.78	0.00	36	0
E-n33-k4-s1-9	730.16⁎	730.16	0.00	74	0
E-n33-k4-s2-13	714.63⁎	714.63	0.00	64	0
E-n33-k4-s3-17	707.41⁎	707.48	0.01	58	0
E-n33-k4-s4-5	778.73⁎	778.74	0.00	77	3
E-n33-k4-s7-25	756.84⁎	756.85	0.00	53	0
E-n33-k4-s14-22	779.05⁎	779.05	0.00	85	0
E-n51-k5-s2-17	597.49	597.49	0.00	100	7
E-n51-k5-s4-46	530.76⁎	530.76	0.00	173	0
E-n51-k5-s6-12	554.8	554.81	0.00	149	2
E-n51-k5-s11-19	581.64	581.64	0.00	182	6
E-n51-k5-s27-47	538.22⁎	538.22	0.00	136	1
E-n51-k5-s32-37	552.28⁎	552.28	0.00	141	1
E-n51-k5-s2-4-17-46	530.76	530.76	0.00	154	1
E-n51-k5-s6-12-32-37	531.92	531.92	0.00	150	0
E-n51-k5-s11-19-27-47	531.12	527.63	−0.66	147	1
Avg.	565.71	565.55	−0.03	93	1

Table 7.

Results and runtimes in seconds for set 3 for the 2E-VRP.

Instance	BKS	ALNS avg.	% dev	T (s)	T⁎ (s)
E-n22-k4-s13-14	526.15⁎	526.15	0.00	43	0
E-n22-k4-s13-16	521.09	521.09	0.00	44	0
E-n22-k4-s13-17	496.38⁎	496.38	0.00	49	0
E-n22-k4-s14-19	498.80⁎	498.80	0.00	43	0
E-n22-k4-s17-19	512.80⁎	512.81	0.00	26	0
E-n22-k4-s19-21	520.42⁎	520.42	0.00	34	0
E-n33-k4-s16-22	672.17	672.17	0.00	76	3
E-n33-k4-s16-24	666.02	666.02	0.00	77	0
E-n33-k4-s19-26	680.36⁎	680.37	0.00	84	0
E-n33-k4-s22-26	680.89	680.37	−0.08	77	0
E-n33-k4-s24-28	670.86⁎	670.43	−0.06	88	0
E-n33-k4-s25-28	650.95⁎	650.58	−0.06	63	0
E-n51-k5-s12-18	692.37	690.59	−0.26	147	4
E-n51-k5-s12-41	691.37	683.05	−1.20	133	38
E-n51-k5-s12-43	712.48	710.41	−0.29	217	1
E-n51-k5-s39-41	729.94	728.54	−0.19	155	18
E-n51-k5-s40-41	729.94	723.75	−0.85	154	17
E-n51-k5-s40-43	757.30	752.15	−0.68	158	15
Avg.	634.14	632.45	−0.20	93	5

Table 8.

Results and runtimes in seconds for set 4 for the 2E-VRP.

Instance	BKS	Source	ALNS avg.	% dev	ALNS min	% dev	T (s)	T⁎ (s)
Instance50-s2-01.dat	1590	DIVING	1569.42	−1.29	1569.42	−1.29	235	6
Instance50-s2-02.dat	1442	DIVING	1441.02	−0.07	1438.33	−0.25	155	43
Instance50-s2-03.dat	1603	DIVING	1570.43	−2.03	1570.43	−2.03	183	3
Instance50-s2-04.dat	1440.77	MultiStart	1424.04	−1.16	1424.04	−1.16	130	11
Instance50-s2-05.dat	2188.15	MultiStart	2194.11	0.27	2194.11	0.27	614	63
Instance50-s2-06.dat	1310.8	MultiStart	1279.87	−2.36	1279.87	−2.36	99	2
Instance50-s2-07.dat	1486	DIVING, SEMI	1458.63	−1.84	1458.63	−1.84	169	6
Instance50-s2-08.dat	1369.78	MultiStart	1360.32	−0.69	1360.32	−0.69	205	5
Instance50-s2-09.dat	1489	SEMI	1450.27	−2.6	1450.27	−2.6	204	46
Instance50-s2-10.dat	1410.42	CI, MultiStart	1360.56	−3.54	1360.56	−3.54	174	1
Instance50-s2-11.dat	2070	SEMI	2059.88	−0.49	2059.88	−0.49	648	101
Instance50-s2-12.dat	1266.21	MultiStart	1209.42	−4.49	1209.42	−4.49	205	44
Instance50-s2-13.dat	1553.71	MultiStart	1481.83	−4.63	1481.83	−4.63	220	25
Instance50-s2-14.dat	1399	DIVING	1393.61	−0.39	1393.61	−0.39	189	6
Instance50-s2-15.dat	1554	DIVING	1489.94	−4.12	1489.94	−4.12	173	9
Instance50-s2-16.dat	1410.42	MultiStart	1387.83	−1.6	1387.83	−1.6	147	6
Instance50-s2-17.dat	2106.72	CI,MultiStart	2088.49	−0.87	2088.49	−0.87	625	165
Instance50-s2-18.dat	1226	DIVING	1227.61	0.13	1227.61	0.13	94	3
Instance50-s3-19.dat	1576.82	FC, CI, MultiStart	1546.28	−1.94	1546.28	−1.94	171	25
Instance50-s3-20.dat	1296.00	SEMI	1272.97	−1.78	1272.97	−1.78	99	12
Instance50-s3-21.dat	1591	DIVING	1577.82	−0.83	1577.82	−0.83	155	61
Instance50-s3-22.dat	1316.99	MultiStart	1281.83	−2.67	1281.83	−2.67	127	2
Instance50-s3-23.dat	1681.29	MultiStart	1652.98	−1.68	1652.98	−1.68	175	5
Instance50-s3-24.dat	1330.09	MultiStart	1282.68	−3.56	1282.68	−3.56	110	2
Instance50-s3-25.dat	1580	SEMI	1440.84	−8.81	1440.68	−8.82	154	53
Instance50-s3-26.dat	1161.86	MultiStart	1167.46	0.48	1167.46	0.48	96	0
Instance50-s3-27.dat	1505.94	FC, CI, MultiStart	1447.79	−3.86	1444.5	−4.08	163	12
Instance50-s3-28.dat	1211.44	MultiStart	1210.44	−0.08	1210.44	−0.08	143	7
Instance50-s3-29.dat	1688.89	MultiStart	1561.81	−7.52	1559.82	−7.64	178	102
Instance50-s3-30.dat	1239.07	MultiStart	1211.59	−2.22	1211.59	−2.22	132	5
Instance50-s3-31.dat	1533.98	FC, CI, MultiStart	1440.86	−6.07	1440.86	−6.07	144	37
Instance50-s3-32.dat	1196	MultiStart	1199	0.25	1199	0.25	102	11
Instance50-s3-33.dat	1574.32	FC, CI, MultiStart	1478.86	−6.06	1478.86	−6.06	159	16
Instance50-s3-34.dat	1234	MultiStart	1233.92	−0.01	1233.92	−0.01	93	4
Instance50-s3-35.dat	1598.66	MultiStart	1570.8	−1.74	1570.72	−1.75	182	116
Instance50-s3-36.dat	1229	MultiStart	1228.89	−0.01	1228.89	−0.01	123	6
Instance50-s5-37.dat	1528.73	Perboli et al.	1528.81	0.01	1528.73	0	143	55
Instance50-s5-38.dat	1185.58	Perboli et al.	1163.07	−1.9	1163.07	−1.9	88	15
Instance50-s5-39.dat	1525.24	Perboli et al.	1520.92	−0.28	1520.92	−0.28	158	33
Instance50-s5-40.dat	1179.64	Perboli et al.	1165.24	−1.22	1163.04	−1.41	84	20
Instance50-s5-41.dat	1681.04	Perboli et al.	1652.98	−1.67	1652.98	−1.67	150	12
Instance50-s5-42.dat	1223.09	Perboli et al.	1190.17	−2.69	1190.17	−2.69	95	31
Instance50-s5-43.dat	1422.29	Perboli et al.	1408.95	−0.94	1406.11	−1.14	151	60
Instance50-s5-44.dat	1039.39	Perboli et al.	1035.32	−0.39	1035.03	−0.42	109	30
Instance50-s5-45.dat	1444.82	Perboli et al.	1406.43	−2.66	1403.1	−2.89	144	104
Instance50-s5-46.dat	1068.5	Perboli et al.	1058.97	−0.89	1058.11	−0.97	74	17
Instance50-s5-47.dat	1581.57	Perboli et al.	1564.41	−1.09	1559.82	−1.38	185	103
Instance50-s5-48.dat	1092.32	Perboli et al.	1074.5	−1.63	1074.5	−1.63	83	2
Instance50-s5-49.dat	1441.64	Perboli et al.	1435.28	−0.44	1434.88	−0.47	140	81
Instance50-s5-50.dat	1089.67	Perboli et al.	1065.25	−2.24	1065.25	−2.24	92	16
Instance50-s5-51.dat	1436.3	Perboli et al.	1387.72	−3.38	1387.51	−3.4	138	46
Instance50-s5-52.dat	1109.52	Perboli et al.	1103.76	−0.52	1103.42	−0.55	102	47
Instance50-s5-53.dat	1552.75	Perboli et al.	1545.73	−0.45	1545.73	−0.45	148	37
Instance50-s5-54.dat	1135.39	Perboli et al.	1113.62	−1.92	1113.62	−1.92	90	2
Avg.	1428.65		1401.39	−1.85	1400.96	−1.88	169	32

show detailed results for the three instance sets of the 2E-VRP. An asterisk indicates that the solution was proven to be optimal. Tables 9–11

Table 9.

Results for the set Prodhon for the LRP.

Instance	BKS	ALNS avg.	% dev.	ALNS min	% dev.	T (s)	T⁎ (s)
20-5-1a	54,793⁎	54,793.00	0.00	54,793.00	0.00	39	0
20-5-1b	39,104⁎	39,104.00	0.00	39,104.00	0.00	54	0
20-5-2a	48,908⁎	48,908.00	0.00	48,908.00	0.00	38	0
20-5-2b	37,542⁎	37,542.00	0.00	37,542.00	0.00	67	0
50-5-1	90,111⁎	90,111.00	0.00	90,111.00	0.00	101	4
50-5-1b	63,242⁎	63,242.00	0.00	63,242.00	0.00	65	6
50-5-2	88,298⁎	88,576.80	0.32	88,443.00	0.16	99	42
50-5-2b	67,308⁎	67,448.20	0.21	67,340.00	0.05	200	73
50-5-2bis	84,055⁎	84,119.00	0.08	84,055.00	0.00	107	67
50-5-2bbis	51,822⁎	51,840.00	0.03	51,822.00	0.00	98	32
50-5-3	86,203⁎	86,261.60	0.07	86,203.00	0.00	101	44
50-5-3b	61,830⁎	61,830.00	0.00	61,830.00	0.00	137	16
100-5-1	274,814⁎	276,364.00	0.56	275,636.00	0.30	520	204
100-5-1b	213,615.00	215,059.00	0.68	214,735.00	0.52	1190	545
100-5-2	193,671⁎	193,903.00	0.12	193,752.00	0.04	463	188
100-5-2b	157,095⁎	157,156.60	0.04	157,095.00	0.00	859	608
100-5-3	200,079⁎	200,495.60	0.21	200,305.00	0.11	454	102
100-5-3b	152,441⁎	152,899.80	0.30	152,441.00	0.00	684	137
100-10-1	287,983.00	299,982.40	4.17	296,877.00	3.09	210	49
100-10-1b	231,763.00	240,289.20	3.68	235,849.00	1.76	188	83
100-10-2	243,590⁎	245,548.20	0.80	244,740.00	0.47	136	63
100-10-2b	203,988⁎	204,494.60	0.25	204,016.00	0.01	261	135
100-10-3	250,882.00	254,882.00	1.59	253,801.00	1.16	202	62
100-10-3b	204,317.00	206,175.20	0.91	205,609.00	0.63	224	130
200-10-1	477,248.00	483,204.80	1.25	480,883.00	0.76	752	348
200-10-1b	378,351.00	380,538.80	0.58	378,961.00	0.16	1346	275
200-10-2	449,571.00	451,750.60	0.48	450,451.00	0.20	1201	375
200-10-2b	374,330.00	376,111.80	0.48	374,751.00	0.11	1349	579
200-10-3	469,433.00	479,366.60	2.12	475,373.00	1.27	1251	371
200-10-3b	362,817.00	369,614.00	1.87	366,902.00	1.13	1137	651
Avg.	196,640.13	198,720.39	0.69	197,852.33	0.40	451	173

Table 10.

Results for the set Tuzun for the LRP.

Instance	n	m	BKS	ALNS avg.	% dev.	ALNS min	% dev.	T (s)	T⁎ (s)
111112	100	10	1467.68⁎	1475.67	0.54	1467.68	0.00	275	153
111122	100	20	1449.2	1464.72	1.07	1452.14	0.20	321	148
111212	100	10	1394.8⁎	1400.49	0.41	1394.93	0.01	244	110
111222	100	20	1432.29	1441.21	0.62	1433.42	0.08	376	144
112112	100	10	1167.16⁎	1173.04	0.50	1167.53	0.03	489	274
112122	100	20	1102.24	1102.34	0.01	1102.24	0.00	373	178
112212	100	10	791.66⁎	791.83	0.02	791.66	0.00	739	215
112222	100	20	728.3	728.32	0.00	728.3	0.00	384	96
113112	100	10	1238.24	1240.31	0.17	1238.7	0.04	357	157
113122	100	20	1245.31	1248.17	0.23	1246.52	0.10	445	237
113212	100	10	902.26⁎	902.27	0.00	902.26	0.00	321	59
113222	100	20	1018.29	1018.56	0.03	1018.29	0.00	386	150
131112	150	10	1866.75	1939.52	3.90	1922.7	3.00	504	360
131122	150	20	1833.95	1857.29	1.27	1847.93	0.76	635	146
131212	150	10	1965.12	2009.44	2.26	1975.83	0.55	664	331
131222	150	20	1801.39	1838.51	2.06	1806.31	0.27	485	155
132112	150	10	1443.33⁎	1449.15	0.40	1447.43	0.28	1049	628
132122	150	20	1441.98	1446.91	0.34	1445.32	0.23	805	352
132212	150	10	1205.09	1205.83	0.06	1204.98	−0.01	2197	780
132222	150	20	930.99	933.14	0.23	931.49	0.05	982	431
133112	150	10	1699.92	1700.39	0.03	1694.64	−0.31	1046	612
133122	150	20	1400.01	1403.5	0.25	1400.5	0.03	925	457
133212	150	10	1199.51	1199.27	−0.02	1198.67	−0.07	1375	624
133222	150	20	1152.18	1154.36	0.19	1152.01	−0.01	911	450
121112	200	10	2259.87	2278.272	0.81	2265.15	0.23	944	309
121122	200	20	2185.41	2192.61	0.33	2183.05	−0.11	847	369
121212	200	10	2234.78	2247.75	0.58	2233.55	−0.06	907	533
121222	200	20	2241.04	2263.196	0.99	2230.94	−0.45	860	257
122112	200	10	2089.77	2093.78	0.19	2082.6	−0.34	1606	908
122122	200	20	1709.56	1732	1.31	1710.67	0.06	941	515
122212	200	10	1466.62	1462.15	−0.30	1458.55	−0.55	1861	617
122222	200	20	1084.78	1086.08	0.12	1085.29	0.05	812	541
123112	200	10	1970.44	1971.01	0.03	1964.75	−0.29	968	529
123122	200	20	1918.93	1952.31	1.74	1926.64	0.40	740	363
123212	200	10	1771.06	1764.16	−0.39	1762.09	−0.51	2055	1283
123222	200	20	1393.16	1395.38	0.16	1393.06	−0.01	1038	620
Avg.			1505.64	1515.64	0.56	1507.44	0.10	830	391

Table 11.

Results for the set Barreto for the LRP.

Instance	BKS	ALNS avg.	% dev.	ALNS min	% dev.	T (s)	T⁎ (s)
Christofides69-50×5	565.60⁎	565.60	0.00	565.60	0.00	73	5
Christofides69-75×10	848.85⁎	854.88	0.71	853.47	0.54	207	54
Christofides69-100×10	833.40⁎	835.39	0.24	833.43	0.00	403	92
Daskin95-88×8	355.78⁎	355.78	0.00	355.78	0.00	250	69
Daskin95-150×10	43,919.90	44,497.24	1.31	44,309.20	0.89	613	283
Gaskell67-21×5	424.90⁎	424.90	0.00	424.90	0.00	25	0
Gaskell67-22×5	585.11⁎	585.11	0.00	585.11	0.00	21	0
Gaskell67-29×5	512.10⁎	512.10	0.00	512.10	0.00	40	0
Gaskell67-32×5	562.22⁎	562.22	0.00	562.22	0.00	58	0
Gaskell67-32×5	504.33⁎	504.33	0.00	504.33	0.00	55	0
Gaskell67-36×5	460.37⁎	460.37	0.00	460.37	0.00	61	0
Min92-27×5	3062.00⁎	3062.02	0.00	3062.02	0.00	38	0
Min92-134×8	5709.00	5732.62	0.41	5712.99	0.07	460	253
Avg.	4487.96	4534.81	0.21	4518.58	0.12	177	58

show detailed results for the three instances sets of the LRP.

Tables 12 and 13

Table 12.

Best found solutions for the LRP.

Instance	BKS	ALNS BKS	% dev.	Instance	BKS	ALNS BKS	% dev.
Pr20-5-1a	54,793⁎	54,793	0	Tu113212	902.26⁎	902.26	0
Pr20-5-1b	39,104⁎	39,104	0	Tu113222	1018.29	1018.29	0
Pr20-5-2a	48,908⁎	48,908	0	Tu131112	1866.75	1914.41	2.55
Pr20-5-2b	37,542⁎	37,542	0	Tu131122	1833.95	1823.53	−0.57
Pr50-5-1	90,111⁎	90,111	0	Tu131212	1965.12	1975.83	0.55
Pr50-5-1b	63,242⁎	63,242	0	Tu131222	1801.39	1796.45	−0.27
Pr50-5-2	88,298⁎	88,298	0	Tu132112	1443.33⁎	1444.73	0.1
Pr50-5-2b	67,308⁎	67,308	0	Tu132122	1441.98	1434.63	−0.51
Pr50-5-2bis	84,055⁎	84,055	0	Tu132212	1205.09	1204.42	−0.06
Pr50-5-2bbis	51,822⁎	51,822	0	Tu132222	930.99	931.28	0.03
Pr50-5-3	86,203⁎	86,203	0	Tu133112	1699.92	1694.18	−0.34
Pr50-5-3b	61,830⁎	61,830	0	Tu133122	1400.01	1392.01	−0.57
Pr100-5-1	274,814⁎	275,524	0.26	Tu133212	1199.51	1198.28	−0.1
Pr100-5-1b	213,615	213,704	0.04	Tu133222	1152.18	1151.8	−0.03
Pr100-5-2	193,671⁎	193,671	0	Tu121112	2259.87	2251.93	−0.35
Pr100-5-2b	157,095⁎	157,095	0	Tu121122	2185.41	2159.93	−1.17
Pr100-5-3	200,079⁎	200,246	0.08	Tu121212	2234.78	2220.01	−0.66
Pr100-5-3b	152,441⁎	152,441	0	Tu121222	2241.04	2230.94	−0.45
Pr100-10-1	287,983	292,868	1.7	Tu122112	2089.77	2073.73	−0.77
Pr100-10-1b	231,763	233,146	0.6	Tu122122	1709.56	1692.17	−1.02
Pr100-10-2	243,590⁎	243,829	0.1	Tu122212	1466.62	1453.18	−0.92
Pr100-10-2b	203,988⁎	203,988	0	Tu122222	1084.78	1082.74	−0.19
Pr100-10-3	250,882	253,722	1.13	Tu123112	1970.44	1960.3	−0.51
Pr100-10-3b	204,317	204,601	0.14	Tu123122	1918.93	1926.64	0.4
Pr200-10-1	477,248	478,951	0.36	Tu123212	1771.06	1762.03	−0.51
Pr200-10-1b	378,351	378,065	−0.08	Tu123222	1393.16	1391.68	−0.11
Pr200-10-2	449,571	450,377	0.18	Ba-Chris69-50×5	565.6⁎	565.6	0
Pr200-10-2b	374,330	374,751	0.11	Ba-Chris69-75×10	848.85⁎	848.91	0.01
Pr200-10-3	469,433⁎	474,087	0.99	Ba-Chris69-100×10	833.43⁎	833.43	0
Pr200-10-3b	362,817	366,416	0.99	Ba-Das95-88×8	355.78⁎	355.78	0
Tu111112.00	1467.68⁎	1467.68	0	Ba-Das95-150×10	43,919.9	44,004.9	0.19
Tu111122.00	1449.2	1449.2	0	Ba-Gas67-21×5	424.9⁎	424.9	0
Tu111212.00	1394.8⁎	1394.8	0	Ba-Gas67-22×5	585.11⁎	585.11	0
Tu111222.00	1432.29	1432.29	0	Ba-Gas67-29×5	512.1⁎	512.1	0
Tu112112.00	1167.16⁎	1167.16	0	Ba-Gas67-32×5	562.22⁎	562.22	0
Tu112122.00	1102.24	1102.24	0	Ba-Gas67-32×5	504.33⁎	504.33	0
Tu112212.00	791.66⁎	791.66	0	Ba-Gas67-36×5	460.37⁎	460.37	0
Tu112222.00	728.3	728.3	0	Ba-Min92-27×5	3062.02⁎	3062.02	0
Tu113112.00	1238.24	1238.49	0.02	Ba-Min92-134×8	5709	5709	0
Tu113122.00	1245.31	1245.31	0

Table 13.

Best found solutions for the 2E-VRP.

Instance	BKS	ALNS BKS	% dev.	Instance	BKS	ALNS BKS	% dev.
E-n22-k4-s6-17	417.07⁎	417.07	0.00	Instance50-s2-08.dat	1369.78	1360.32	−0.69
E-n22-k4-s8-14	384.96⁎	384.96	0.00	Instance50-s2-09.dat	1489.00	1450.27	−2.60
E-n22-k4-s9-19	470.60⁎	470.60	0.00	Instance50-s2-10.dat	1410.42	1360.56	−3.54
E-n22-k4-s10-14	371.50⁎	371.50	0.00	Instance50-s2-11.dat	2070.00	2051.19	−0.91
E-n22-k4-s11-12	427.22⁎	427.22	0.00	Instance50-s2-12.dat	1266.21	1209.42	−4.49
E-n22-k4-s12-16	392.78⁎	392.78	0.00	Instance50-s2-13.dat	1553.71	1481.83	−4.63
E-n33-k4-s1-9	730.16⁎	730.16	0.00	Instance50-s2-14.dat	1399.00	1393.61	−0.39
E-n33-k4-s2-13	714.63⁎	714.63	0.00	Instance50-s2-15.dat	1554.00	1489.94	−4.12
E-n33-k4-s3-17	707.41⁎	707.48	0.01	Instance50-s2-16.dat	1410.42	1387.83	−1.60
E-n33-k4-s4-5	778.73⁎	778.74	0.00	Instance50-s2-17.dat	2106.72	2088.49	−0.87
E-n33-k4-s7-25	756.84⁎	756.85	0.00	Instance50-s2-18.dat	1226.00	1227.61	0.13
E-n33-k4-s14-22	779.05⁎	779.05	0.00	Instance50-s3-19.dat	1576.82	1546.28	−1.94
E-n51-k5-s2-17	597.49	597.49	0.00	Instance50-s3-20.dat	1296.00	1272.97	−1.78
E-n51-k5-s4-46	530.76⁎	530.76	0.00	Instance50-s3-21.dat	1591.00	1577.82	−0.83
E-n51-k5-s6-12	554.80	554.81	0.00	Instance50-s3-22.dat	1316.99	1281.83	−2.67
E-n51-k5-s11-19	581.64	581.64	0.00	Instance50-s3-23.dat	1681.29	1652.98	−1.68
E-n51-k5-s27-47	538.22⁎	538.22	0.00	Instance50-s3-24.dat	1330.09	1282.68	−3.56
E-n51-k5-s32-37	552.28⁎	552.28	0.00	Instance50-s3-25.dat	1580.00	1440.68	−8.82
E-n51-k5-s2-4-17-46	530.76	530.76	0.00	Instance50-s3-26.dat	1161.86	1167.46	0.48
E-n51-k5-s6-12-32-37	531.92	531.92	0.00	Instance50-s3-27.dat	1505.94	1444.50	−4.08
E-n51-k5-s11-19-2 7-47	531.12	527.63	−0.66	Instance50-s3-28.dat	1211.44	1210.44	−0.08
E-n22-k4-s13-14	526.15⁎	526.15	0.00	Instance50-s3-29.dat	1688.89	1559.76	−7.65
E-n22-k4-s13-16	521.09	521.09	0.00	Instance50-s3-30.dat	1239.07	1211.59	−2.22
E-n22-k4-s13-17	496.38⁎	496.38	0.00	Instance50-s3-31.dat	1533.98	1440.86	−6.07
E-n22-k4-s14-19	498.80⁎	498.80	0.00	Instance50-s3-32.dat	1196	1199.00	0.25
E-n22-k4-s17-19	512.80⁎	512.81	0.00	Instance50-s3-33.dat	1574.32	1478.86	−6.06
E-n22-k4-s19-21	520.42⁎	520.42	0.00	Instance50-s3-34.dat	1234	1233.92	−0.01
E-n33-k4-s16-22	672.17	672.17	0.00	Instance50-s3-35.dat	1598.66	1570.72	−1.75
E-n33-k4-s16-24	666.02	666.02	0.00	Instance50-s3-36.dat	1229	1228.89	−0.01
E-n33-k4-s19-26	680.36⁎	680.37	0.00	Instance50-s5-37.dat	1528.73	1528.73	0.00
E-n33-k4-s22-26	680.89	680.37	−0.08	Instance50-s5-38.dat	1185.58	1163.07	−1.90
E-n33-k4-s24-28	670.86⁎	670.43	−0.06	Instance50-s5-39.dat	1525.24	1520.92	−0.28
E-n33-k4-s25-28	650.95⁎	650.58	−0.06	Instance50-s5-40.dat	1179.64	1163.04	−1.41
E-n51-k5-s12-18	692.37	690.59	−0.26	Instance50-s5-41.dat	1681.04	1652.98	−1.67
E-n51-k5-s12-41	691.37	683.05	−1.20	Instance50-s5-42.dat	1223.09	1190.17	−2.69
E-n51-k5-s12-43	712.48	710.41	−0.29	Instance50-s5-43.dat	1422.29	1406.11	−1.14
E-n51-k5-s39-41	729.94	728.54	−0.19	Instance50-s5-44.dat	1039.39	1035.03	−0.42
E-n51-k5-s40-41	729.94	723.75	−0.85	Instance50-s5-45.dat	1444.82	1402.41	−2.94
E-n51-k5-s40-43	761.54	752.15	−0.68	Instance50-s5-46.dat	1068.50	1058.11	−0.97
Instance50-s2-01.dat	1590.00	1569.42	−1.29	Instance50-s5-47.dat	1581.57	1559.76	−1.38
Instance50-s2-02.dat	1442.00	1438.33	−0.25	Instance50-s5-48.dat	1092.32	1074.50	−1.63
Instance50-s2-03.dat	1603.00	1570.43	−2.03	Instance50-s5-49.dat	1441.64	1434.88	−0.47
Instance50-s2-04.dat	1440.77	1424.04	−1.16	Instance50-s5-50.dat	1089.67	1065.25	−2.24
Instance50-s2-05.dat	2188.15	2194.11	0.27	Instance50-s5-51.dat	1436.30	1387.51	−3.40
Instance50-s2-06.dat	1310.80	1279.87	−2.36	Instance50-s5-52.dat	1109.52	1103.42	−0.55
Instance50-s2-07.dat	1486.00	1458.63	−1.84	Instance50-s5-53.dat	1552.75	1545.73	−0.45
				Instance50-s5-54.dat	1135.39	1113.62	−1.92

show the new best solutions for the 2E-VRP and LRP instances.