Evaluating long-term effects of a psychiatric treatment using instrumental variable and matching approaches

Abstract

Evaluating treatment effects in non-randomized studies is challenging due to the potential unmeasured confounding and complex form of observed confounding. Propensity score based approaches, such as matching or weighting, are commonly used to handle observed confounding variables. The instrumental variable (IV) method is known to guard against unmeasured confounding if a good instrument can be identified. We propose to combine both methods to estimate the long-term treatment effect in a longitudinal psychiatric study. The NIMH collaborative Multi-site Treatment study of children with Attention-deficit/hyperactivity disorder (ADHD) compared different treatment strategies for children diagnosed with ADHD (known as MTA study). The first 14 months is a randomized study and the participants are allowed to choose their desired treatment strategies afterwards. Follow-up measurements are taken at 24, 36 and 72 months. Randomization is often considered as a good instrument since it is not associated with any covariate, observed or unobserved. We first apply a randomization based IV method to estimate the self-selected medication effect on outcome at the end of 72 months. However this approach yields results with huge standard errors due to randomization’s weak relationship with later treatment selection. We then consider the self-selection right after the randomization as an instrument, because it is associated with later treatment selection and it is unlikely to affect the outcome directly given the five-year time lapse. To better control the confounding due to observed factors, propensity score matching is used to create a subpopulation with comparable covariate distributions across different self-selected treatments. Using MTA data, matching-enhanced IV estimation yields the most sensible result, while other estimation strategies tend to imply a spurious significant effect. Also, our simulation study shows that the matching-enhanced IV estimation outperforms non-matched methods in terms of relative bias.

1. Introduction

Causal inference is essential for understanding whether psychiatric treatments work and for whom. Generally, psychiatric disorders are chronic, so treatments must be studied using longitudinal data. Even when mental health interventions are studied in randomized trials, frequently encountered noncompliances such as treatment switching, and protocol violations necessitate the use of observational study methods to address various biases that inevitably complicate inference in these studies. Inappropriate causal inference can lead to dire consequences such as children taking ineffective medication with potential side effects over long periods of time or discontinuing effective medication due to excess concern about nonexistent side effects. This paper evaluates some observational study approaches for causal inference in estimating long-term effects in psychiatry research.

Much of health outcome research is concerned with the question of estimating the treatment effect with an observational dataset. Unlike randomized studies, patients receiving treatment may differ from the untreated patients in prognostic variables that affect outcomes. Hence, differences in patient outcomes are due to both treatment effects and differential prognostic factors of patients. Thus, it is crucial in observational studies to tease out the selection bias by some statistical adjustment. Such selection bias could come from both measured confounders (observed patient characteristics, such as age) and unmeasured confounders (unobserved patient characteristics, such as disease severity). For measured confounders, under a cross-sectional setup, proper covariance adjustment method or propensity score based analysis (matching, stratification or weighting) yield an unbiased estimator of the treatment effect (Rosenbaum and Rubin, 1983; Rosenbaum, 2002). In the longitudinal setup, inverse probability of treatment weighting or propensity score stratification can be applied to control potential time-varying confounding (Robins, et al. 2000; Marcus, et al. 2008).

When unmeasured confounders are present, the conventional adjustment methods are not appropriate since they all assume treatment ignorability in one way or another. Instrumental variable method is a well-established approach in econometrics to handle unmeasured confounding. An Instrumental variable is predictive of the treatment but not independently associated with the outcome. Assume a simple linear model of homogeneous treatment effect,

$$Y_i(A_i=a)=\alpha +\beta a+{\epsilon }_i$$

where Y is the outcome, A is the treatment indicator and E(ε_i) = 0, we can define an instrumental variable R if it satisfies the following two conditions:

1. R is independent of ε_i.

2. E(A_i | R_i = r) is a nonconstant function of r.

Consequently, the causal parameter β can be consistently estimated with the following systems of equations using the two-stage least squares method (2SLS):

$$\begin{array}{l}{Y}_i=\alpha +\beta A_i+{\epsilon }_i\\ A_i=\lambda +\gamma R_i+{\delta }_i.\end{array}$$

Confounding bias in the estimation of β is usually due to dependence between A_i and ε_i in the first model above. We can define instrumental variables analogously in a longitudinal framework and Hogan and Lancaster (2004) provide a thorough discussion.

In practical applications, it may be quite difficult to find an ideal instrumental variable meeting both of the conditions above. Sometimes, we may find a variable that is associated with the outcome only through the treatment received, but it is not very predictive of the treatment. This is referred as a weak instrument and may result in a very unstable treatment effect estimate. It presents an extremely wide confidence interval, which makes it of little use. On the other hand, we may find a variable that predicts the treatment well, but it is linked to the outcome through some pathway other than the treatment. This is referred as endogeneity and it may introduce bias in the treatment effect estimation. Researchers need to be cautious of both of these conditions, and emphasizing only one may lead to invalid results.

In this paper, we propose a novel way of combining IV estimation with propensity score matching to improve the IV estimator. Our goal is to estimate the medication effect for a later time period in a longitudinal study, rather than estimating a time-varying treatment effect over time. We compare our proposed method with several commonly used estimation strategies using a longitudinal dataset from a Multisite multimodal Treatment study of children with Attention-deficit/hyperactivity disorder (ADHD), abbreviated as MTA. To gain more insight into the performance of different estimation strategies, we also compare them in a simulated longitudinal dataset. The paper is organized as follows: section 2 provides a background on the MTA study and some preliminary results from the literature; section 3 sets up the framework for IV estimation, introduces our matching-enhanced IV method and several other alternative estimation strategies; section 4 presents the results of different estimation methods using the MTA data; section 5 presents the results using the simulated dataset; section 6 concludes the paper with some discussion.

2. MTA Study

Attention Deficit Hyperactive Disorder (ADHD) is the most commonly diagnosed behavioral disorder of childhood. Children with ADHD show a persistent pattern of inattention and/or hyperactivity-impulsivity that is more frequently displayed and is more severe than is typically observed in individuals at a comparable level of development. In the United States, approximately 7.8% of all school-aged children have been diagnosed with ADHD at some point in their lives (Brock et al., 2009). Current available treatments focus on reducing the symptoms of ADHD and improving functioning. Treatments include medication, behavioral therapy, education or training, or a combination of treatments.

The NIMH sponsored MTA study is the largest treatment study of ADHD. The study involved six different sites around the country and included 579 children ages 7 to 10 years when diagnosed as having DSM-IV ADHD. Approximately 20% of the participants were girls and about the same proportion was African American. For the first 14 months, children were randomly assigned to one of the four treatment groups: systematic medication management (MedMgt), multicomponent behavior therapy (Beh), their combination (Comb) or usual community care (CC). The children were followed up at 24, 36, 72, 96 and 120 months after the initial 14-month intervention period. More detailed descriptions on the study design are presented in Molina, et al. (2009).

One of the fundamental questions that the MTA study was designed to address is how long-term medication and behavioral treatments compare with one another. The primary outcome of interest is ADHD symptoms as rated by parents and teachers. Analyses on earlier released data showed that, at the end of the 14-month randomized treatment period, all groups showed improvement over baseline, but Comb and MedMgt children showed significantly greater improvements in ADHD than did Beh or CC children. However, approximately half of the initial advantage of Comb and MedMgt had disappeared by the first follow-up evaluation, 10 months after the termination of the treatment. By the next follow-up, 36 months after the enrollment, there were no significant treatment group differences in ADHD symptoms (The MTA Cooperative Group, 2004 a & b).

An important design feature of the MTA study is that it became observational after 14 months, when the study-delivered treatments ended. Any treatments received thereafter by the children were outside of the study context (i.e., naturally selected from community providers). Having observed no advantage of medication use at 36 months, a self-selection bias was speculated. Children with higher severity of psychopathology during the MTA follow-up phases would be more likely to have adverse outcomes, and the same individual also would be more likely to receive medication after the initial 14-month intervention period. Such association, in turn, could mask beneficial long-term effects of medication. To test this hypothesis, Swanson and colleagues (2007) conducted propensity score analyses with quintile stratification. They built a propensity score model for medication usage at 36 months with observed covariates presumed related to medication use and found no significant difference in the outcome with each stratum. They concluded that they failed to confirm the self-selection hypothesis.

In this paper, we extend the investigation of the self-selection bias in MTA study beyond just the observed confounders by adopting an IV approach. Marcus and Gibbons (2001) applied IV estimation to MTA data to investigate the noncompliance issue in the randomization phase of the study. We want to extend this work to the long-term observational phase, i.e., we are interested in estimating the self-selected medication effect on outcomes at the end of 72 months. One major practical difficulty with IV analysis is the selection of the instrumental variable, and a poor choice may lead to unstable estimation with big standard errors. In the following sections, we compare several possible candidates of the instrumental variable and propose a strategy to improve the estimation by combining IV analysis with propensity score matching.

3. Matching Enhanced IV Method

Though instrumental variables have many desirable theoretical properties in estimating the treatment effect in the presence of unmeasured confounders, it is usually hard to identify a good instrumental variable in practice. When the treatment assignment is based on some random mechanism, good instruments might be identified by taking advantage of such randomness to remove endogeneity. In a study of veteran status of Vietnam era on mortality, Angrist et al. (1996) used the lottery number that assigned priority for the draft as an instrument. The lottery number was generated randomly, so it had nothing to do with the death of the individual. On the other hand, since the lottery number determined the priority for conscription, individuals with a low lottery number should have served in the military and those with a high lottery number would not have served, if the compliance with the draft had been perfect. Therefore, the lottery number (low vs. high) had a very strong association with the received treatment (serving in the military) and it served as an ideal instrument. In general, the treatment assignment can be used as an instrument if the assignment is ignorable, but the compliance with the assignment is not perfect so that the receipt of treatment is nonignorable (Hirano, et al. 2000).

In MTA study, the initial treatment assignment was generated randomly. After 14 months, the study became observational so that the children could receive medication according to their preference. It is possible that some children assigned to medication might want to stay with the drug and some other children assigned with non-drug treatment might never try the medication. If the relationship between the random treatment assignment and later self-selected treatment is strong, the randomization is a very good instrument since it should not affect the outcome by nature. In order to estimate the treatment effect in a longer time frame with potential unmeasured confounding, a dataset with information up to the end of 72 months is used. The study period is broken into several parts, the initial 14 months, 15–24 months, 25–36 months, and 37–72 months. To keep the comparison focused, we only look at the medication vs. non-medication effect. In the first time period, children assigned to medication management (MedMgt) and combined (Comb) groups are classified into high medication use group and children assigned to behavioral (Beh) and community care (CC) groups are classified into low medication use group. For the next three time periods, a 50% rule is adopted to determine the medication status that is consistent with Swanson et al. (2007). Children are considered to be on high medication use if stimulant medication has been used for at least 50% of the days since the previous assessment and low medication use otherwise. Therefore, we have a longitudinal binary indicator of treatment for each child.

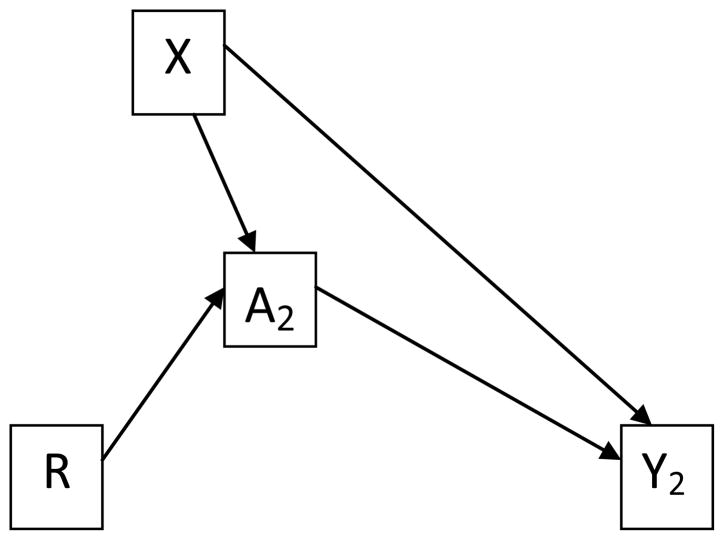
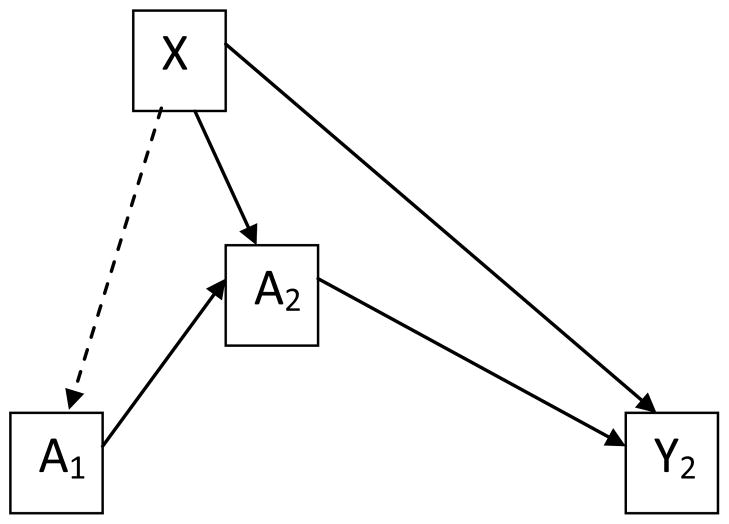
Several IV estimation strategies are considered to estimate the effect of medication during 37–72 months. The first one is using the baseline randomization as the instrumental variable (figure 1, R for randomization, X for covariates, A₂ for treatment indicator of 37–72 months, and Y₂ for the outcome at the end of 72 months). The second one is using the treatment selection during the 15–24 month (A₁) as the instrument. Because the children self-selected their medication use during both 15–24 and 37–72 month periods, we expect a strong association between the two treatment selections. However, a potential problem of using previous self-selection as the instrument is that it may introduce endogeneity since the self-selection might be determined by certain individual characteristics that may also affect the outcome, shown as the dotted line in figure 2. This is a general illustration that does not distinguish unmeasured confounding from measured confounding.

Figure 1.

Randomization as IV

Figure 2.

Self-selection as IV

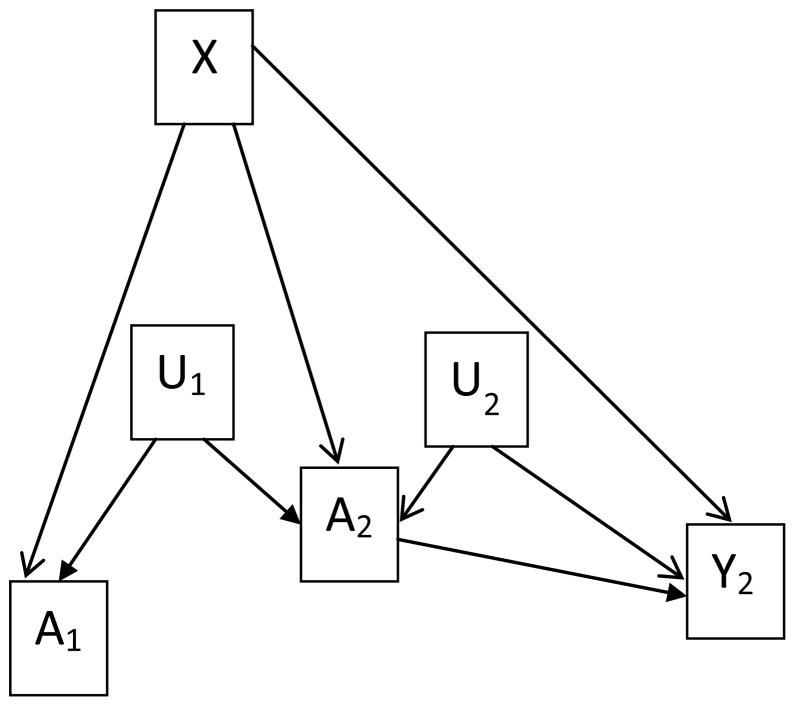
To explicitly specify the impact due to unmeasured confounding, we introduce two more variables in figure 3, U₁ and U₂. U₁ denotes the unobserved factor accounting for the high correlation between treatment self-selections, but is not related to the final outcome. U₂ denotes a potential unmeasured confounder which occurred during the later time period. Now, X only denotes observed covariates. We think this is a reasonable representation for the MTA study for following reasons. This is a well-designed study and a large number of relevant covariates have been collected in its early stages. So the chance of missing an important confounder is very small, at least in the early stage, i.e. for A₁. Moreover, for the unobserved confounder, U₂, in the last time period, it is unlikely to affect A₁ given that they are several years apart. Therefore, it is sensible to use A₁ as the instrument to remove unmeasured confounding bias due to U₂.

Figure 3.

Self-selection as IV with unmeasured covariates

As known in the literature, matching on observed covariates often leads to more robust confounding adjustment than the regular regression methods, since the latter may suffer from model misspecification and often depends on model extrapolation. Also, Small and Rosenbaum (2008), and Baiocchi et al (2010) show that matching can be used to build a stronger instrument and that a small study with a stronger instrument is likely to be more powerful than a large study with a weak instrument. So, we match on all characteristics observed prior to the first treatment selection via propensity scores. The propensity score is estimated as the conditional probability of receiving a high medication status given all the observed covariates up to 14 months. Then a one-to-one matching is conducted between the high medication use group and the low use group at 14 month and the IV estimation is subsequently performed on the matched subset. Ideally, if the matching balances the covariate distributions between the two groups, it removes the confounding effect due to all observed characteristics relating to the first treatment selection. Hence, it creates a randomization-like scheme and yields a stronger instrument.

4. MTA Example

We apply these IV estimation strategies to assess the treatment effect of taking medication during the fourth time period (37–72 months) in the MTA study. The outcome is severity of ADHD symptoms at the 72-month assessment as reported by the parents or the teachers. The overall severity of symptoms is defined as the average rating per item (0–3) of the 18 DSM-IV symptoms on the Swanson, Nolan and Pelham (SNAP) rating scale, obtained by averaging across domains (the nine inattention items and the nine hyperactivity-impulsivity items). The outcome could fall anywhere between 0 and 3, thus regarded as continuous. We also consider numerous covariates in the analysis, including 15 baseline covariates and 20 covariates measured at 14 months prior to the observational phase. Baseline covariates include gender, race, birth weight, family intactness, family income, grade, previous medication use, mother’s age, problems at birth (heart problem, born addicted, emotional problem, muscle problem), having learning problem, developmentally delayed, having emotional problem. Covariates at 14 months include patents observations (total problem behavior, total social skill, aggression problem, CDI, Conners rating score, hyperactive score, ODD score, inattention score, academic behavior score, ADHD score), teachers observations (total problem behavior, total social skill, hyperactive score, ODD score, inattention score, anxiety score, ADHD score), Wechsler individual achievement test score (reading, math, spelling). There are three treatment indicators: randomization (medication vs. no medication) for 0–14 months, medication use status (high vs. low) for 15–24 months, medication use status (high vs. low) for 37–72 months. Incomplete data is an issue for this dataset with missingness occurred in about 50% of the children. This is due to either 1) children not participating in the follow-up study; or 2) incomplete information in covariates, exposures or outcomes for some of the children who participated. To focus on comparing the performance of different IV estimation strategies, we assume missing completely at random and use the subset with complete information, which results in a working dataset of 269 children. This is also consistent with the practice in Molina et al. (2009) where nonparticipants are removed from the analysis. Three IV estimation strategies are applied and results are presented in Table 1 (results from regular regression analysis are also included for reference):

Table 1.

Treatment Effect under Different IV Strategies

Method	Treatment Effect	95% CI	P-value
Regular Regression	0.200	[0.06, 0.34]	0.004
Randomization as IV	0.833	[−8.09, 9.75]	0.855
Self-selection as IV	0.539	[0.12, 0.96]	0.012
Matching-enhanced IV	0.250	[−0.22, 0.72]	0.298

1. Use baseline randomization as the instrument

   We dichotomize the four randomized groups into two groups, medication or not. Standard two-stage least squares (2SLS) estimation is used with 15 baseline covariates. The ivreg function in R’s AER library is used to implement all IV estimations (Kleiber and Zeileis, 2008).

2. Use time-1 self-selection as the instrument

   The time-1 self-selection of medication is defined as the self-reported cumulative use of stimulants during 15–24 months. If the reported days of use are more than 50% of the days in the period, the child is considered to be a high medication user. Otherwise, the child is in the low medication use group. Standard two-stage least squares (2SLS) estimation is used with baseline covariates and other measurements available at 14 months, which include parents and teachers’ evaluation related to ADHD and the Wechsler individual achievement test. This is referred as direct use of time-1 self-selection as the instrument. To control for observed confounding, we include 35 covariates in the regression model.

3. Use time-1 self-selection as the instrument in the matched subset

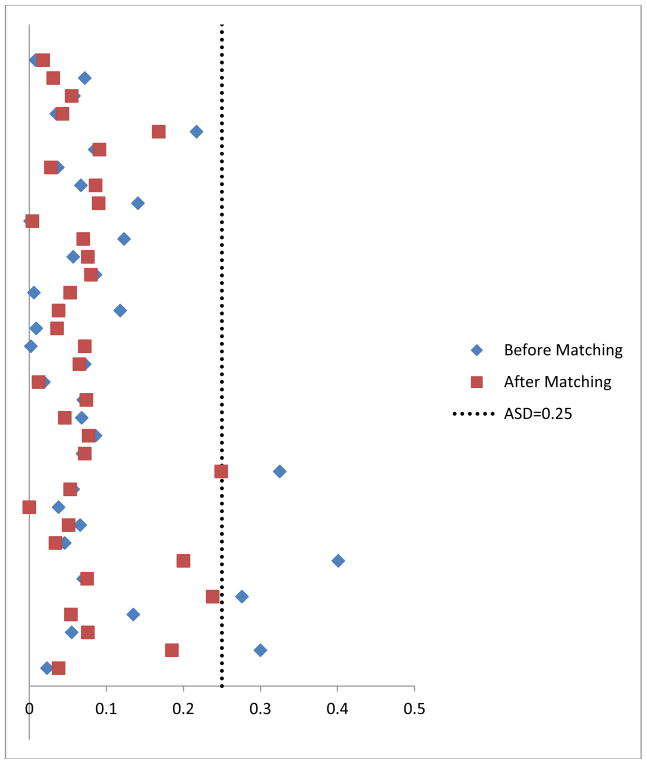
   Propensity score matching is performed prior to the IV estimation to reduce the impact of endogeneity due to observed covariates. The propensity score is calculated as the probability of selecting treatment during 15–24 month period conditional on all 35 covariates. A logistic regression model is used to estimate the propensity score. Optimal pair matching is conducted using nbpMatching library in R (Lu, et al. 2011). 113 high-low medication use pairs are created and the covariates’ balance before and after matching is presented in Figure 4 as a forest plot (Love, 2002). The absolute standardized mean differences are used as a measure for checking balance (Rosenbaum and Rubin, 1985). As a rule of thumb, the balance is regarded as good if the absolute standardized difference is less than 0.25 (Stuart and Rubin, 2008). As shown in the figure, as a group, the absolute standardized differences of covariates become much closer to zero after matching, and we are comfortable with the post-matching balance on all covariates since none of them is bigger than 0.25. Then, standard two-stage least squares (2SLS) estimation is applied to the matched subset.

Figure 4.

Covariates Balance before/after Matching

As shown in table 1, there are some interesting findings. Not considering unmeasured confounding, we first run a linear regression model using only the main effects of all 35 covariates, which is referred as “regular linear regression” hereafter. A significant harmful effect is identified. It implies that high medication use tends to increase the ADHD severity by 0.2 points, on average. Many studies have shown that the medication works quite effectively to enhance attention span and impulse control, hence to improve ADHD symptoms (Kidd, 2000). Therefore, it is unexpected that taking medication has a negative impact and it is possibly due to self-selection effect (Jensen, et al. 2007). To explore the potential impact of unmeasured confounding, IV estimation is employed. Using the baseline randomization as the instrument, which is not associated with both observed and unobserved confounders, we get a treatment effect of 0.833 points with a huge standard error (4.549). The confidence interval is so wide that it is practically useless. This is primarily due to the fact that randomization is a very weak instrument, in terms of its association with the self-selected medication behavior several years later. Weak instruments often lead to unstable estimates of the treatment effect (Hogan and Lancaster, 2004). Therefore, we consider early self-selection as the instrument to improve the stability of the estimation. The direct use of time-1 self-selection as instrument yields a significant harmful effect of 0.539 points. To better remove the impact of measured confounders, we match on all baseline covariates and covariates measured at 14 months to create a randomization-like scenario. The matching-enhanced IV estimation yields an insignificant treatment effect of 0.25 points with a 95% confidence interval [−0.22, 0.72].

The results from different IV analyses are not quite conclusive, which is consistent with Swanson’s finding based on 36-month data (Swanson et al. 2007). Using the ideal instrument, randomization, implies no treatment effect. But the evidence is too weak due to the huge variance. Early self-selection may be a good candidate of instrument for two reasons; 1) early self-selection is nontrivially related to later self-selection since they are the medication behavior from the same child; 2) early self-selection is unlikely to affect later outcomes independently (it may be related to later outcomes through later medication use or some other factors). Because the medication acts on the central nervous system with a dopamine-agonistic effect that stimulates nerve cells to enhance attention span and impulse control (Kidd, 2000), it is unlikely that taking drug at an early time still has an impact on the central nervous system several years later regardless of later medication taking behavior. Using self-selection as an instrument seems to reduce the estimate’s variance successfully, but shows a significant harmful effect, which is considered unlikely by psychiatrists. This is possibly due to model misspecification or observed covariate imbalance, given that there are a large number of covariates. Therefore, we further improve the IV estimation by applying matching, which is known as a more robust way for adjusting for measured confounding. The matching-enhanced IV estimation reveals no treatment effect with a small standard error. In the following section, we conduct a simulation study to gain more insight on the performance of the proposed method for various scenarios of unmeasured confounding.

5. A Simulation Study

The goal of this simulation study is to gain more insights into how different IV estimation strategies perform in a longitudinal setup with unmeasured covariates. To mimic the structure of the MTA dataset, we generate a sequence of repeated measures with three time points, t=0, 1, 2, and several variables as defined below:

• A_t: treatment indicators, t=0, 1, 2.

• X: an observed continuous covariate.

• U₁, U₂: unobserved binary covariates (independent).

• Y_t: outcome measurements, t=0, 1, 2.

For simplicity, both X and U’s are assumed to be constant over time. X is generated from a Normal distribution, N(14, 3²) and U₁ is generated from a Bernoulli distribution with p=0.3 and U₂ is generated from a Bernoulli distribution with p=0.5. A_t and Y_t are generated from the models specified below for each time point:

• Time 0

  A₀ is the randomization, generated from a Bernoulli distribution with p=0.5.

  $$Y_0=b_{00}+b_{01}{A}_0+b_{02}{(X-14)}^2+b_{03}{U}_2+e_0$$
• Time 1

  $$\begin{array}{l}\mathit{Logit}[P(A_1=1)]=a_{10}+a_{11}X+a_{12}{U}_1+a_{13}{A}_0+a_{14}{U}_2\\ Y_1=b_{10}+b_{11}{A}_1+b_{12}{(X-14)}^2+b_{13}{U}_2+e_1\end{array}$$
• Time 2

  $$\begin{array}{l}\mathit{Logit}[P(A_2=1)]=a_{20}+a_{21}X+a_{22}{U}_1+a_{23}{U}_2\\ Y_2=b_{20}+b_{21}{A}_2+b_{22}{(X-14)}^2+b_{23}{U}_2+e_2\end{array}$$

As implied by simulation models, A₁ is associated with A₀, which reflects the fact that randomization may be associated with kids’ first self-selection of treatment, as we observed in MTA study. With a common factor U₁, A₁ and A₂ are associated since both are self-selected. All outcome measurements are affected by treatment received and covariates, both observed X and unobserved U₂. We also introduce a quadratic term of X in the response model to avoid the trivial case where we can always specify the correct response model in analyses.

In terms of the parameter setup, at time 0, b₀₀ = 3, b₀₁ = 5, b₀₂ = 0.1, b₀₃ = 3; at time 1, b₁₀ = 4, b₁₁ = 4, b₁₂ = 0.3, b₁₃ = 2; at time 2, b₂₀ = 3, b₂₁ = 3, b₂₂ = 0.3, b₂₃ = 6, which implies a treatment effect of 3. All error terms are independent N (0, 1).

The key feature of the simulation is that we vary the association between U₂ and self-selected treatment, A₁ and A₂, to gauge the impact due to unmeasured covariates. For A₁ to be a valid instrument, we first set a₁₄ = 0. We vary a₂₃ to be 0, 0.5, 1, 3 to reflect different magnitudes of unmeasured confounding related to the outcome (table 2). The goal is to examine the performance of different IV strategies when the unmeasured confounding kicks in and gets stronger. To further explore the potential risk of using A₁ as the instrument, we also vary a₁₄ to be 0.25, 0.5, and 1 to reflect different degrees of deviation from being a valid instrument (table 3). We generate 1000 simulated runs for each scenario and report the point estimates, percentages of absolute relative bias ( $\left|\frac{\mathit{estimate}-\mathit{truth}}{\mathit{truth}}\right|\times 100\%$) and Monte Carlo standard errors. For each simulated dataset, the sample size is 1000.

Table 2.

Simulation results for as valid instrument (true effect=3)

		Method*	Estimate	Abs. Rel. Bias	Std. Error
U2 is not associated with A1 or A2.		R-IV	16.60	443%	727.30
		S-IV	4.68	56%	2.63
		M-IV	3.86	29%	2.44
		Regression	3.35	12%	0.40
U2 is only associated with A2.	Moderate Association	R-IV	−66.24	2308%	2115
		S-IV	4.31	44%	2.48
		M-IV	3.58	19%	2.26
		Regression	3.92	31%	0.36
	Strong association	R-IV	4.20	40%	284.10
		S-IV	4.71	57%	2.78
		M-IV	3.73	24%	2.47
		Regression	4.53	51%	0.38
	Very strong association	R-IV	42.23	1308%	940.69
		S-IV	4.81	60%	3.63
		M-IV	3.56	19%	3.77
		Regression	6.26	109%	0.35

^*: R-IV for using randomization as the instrument, S-IV for using self-selection as the instrument, M-IV for matching enhanced IV estimation, and Regression for using the conventional linear regression model.

Table 3.

Simulation results for A₁ associated with U₂ (true effect=3)

		Method	Estimate	Abs. Rel. Bias	Std. Error
U2 is associated with both A1 and A2.	Weak association	R-IV	−120.02	4100%	3671
		S-IV	7.18	139%	2.82
		M-IV	6.58	119%	2.65
		Regression	6.27	109%	0.34
	Moderate association	R-IV	−11.09	470%	350.3
		S-IV	8.64	188%	2.41
		M-IV	8.39	180%	2.25
		Regression	6.27	109%	0.36
	Strong association	R-IV	−2.71	190%	502.4
		S-IV	10.84	261%	2.12
		M-IV	10.30	243%	1.98
		Regression	6.27	109%	0.35

Table 2 presents the results when A₁ is a valid instrument. When there is no unmeasured confounding and IV estimation is not necessary, the regular regression model yields the best result. When unmeasured confounding (U₂ on A₂) is present, the matched enhanced IV method outperforms other methods in terms of the relative bias and the self-selection based IV method shows some moderate relative bias. As the unmeasured confounding gets stronger, the regular regression method introduces more bias. We also note that the regular regression method always has the smallest variance. Given the relatively high bias associated with this method, smaller variance often leads to a wrong conclusion (confidence intervals do not cover the true treatment effect) in practice. In all scenarios, the randomization based IV method is of no practical value because the estimates are so volatile.

Table 3 presents the results when A₁ is contaminated with unmeasured confounding. Since the unmeasured confounding on A₂ is fixed, the regular regression method provides quite consistent results with about 100% relative bias. When unmeasured confounding on A₁ is weak, the matching enhanced IV method yields similar bias results to the regression method. However, as the magnitude of unmeasured confounding grows, the biases with both self-selection based IV and matching enhanced IV methods increase dramatically. If this is the case, it is vital to identify other better instrument in order to obtain accurate estimates.

6. Discussion

The MTA study starts as a randomized trial for a short period of time, and then, follows the participants for a long time as observational. To estimate the treatment effect in the later phase of the study, instrumental variable estimation may be applied since it is quite likely that the treatment selection in the observational phase is affected by unmeasured confounders. Using the baseline randomization as the instrument is immune to all unmeasured confounders, but it produces highly unstable treatment effect estimates since the association between randomization and future self-selected treatment is very weak. Early self-selection may be a good candidate of the instrument for later self-selection because: 1) it usually carries a good correlation with later self-selection; 2) for drug studies, taking drug in the past is unlikely to affect the current outcome if no drug is taken recently, especially when they are several years apart; 3) for well designed studies like MTA, a large number of covariates has been collected at baseline, therefore, the chance of missing important confounding factors is slim, at least in the early stage of the study. As shown in the simulation study, when early self-selection is a valid instrument, it always yields least biased results. Also, even if there is unmeasured confounding related to early self-selection, matching enhanced IV estimation still offers results more sensible compared to other methods, as long as the magnitude of unmeasured confounding is low. In many practical circumstances, it is very hard to test the validity of certain instrument selection. Sensitivity analyses can be useful in determining how the magnitude of the departure from this assumption is associated with various levels of bias in the IV estimate. Interested readers may refer to the work by Small (2007), Small and Rosenbaum (2008), and Angrist and Lavy (1996) for further discussion.

When applied to MTA data, the matching-enhanced IV estimator shows an insignificant effect with a reasonable standard error. This is sensible both biologically and statistically. The regression method shows a harmful treatment effect of similar magnitude but highly significant, which is biologically implausible and it is probably due to the lack of control of the potential unmeasured confounding in later time period. On the other hand, the randomization based IV method also yields an insignificant effect. But it comes with too much variation and it is not that meaningful statistically. Therefore, we would be comfortable with matching-enhanced IV estimation results, which is also consistent with evidence from other psychiatric literature.

Matching is a well-known method for adjusting observed confounders. So, matching alone cannot remove any confounding due to unmeasured covariates. After a valid instrument is identified, matching may improve the estimation by balancing the covariates distribution, in the sense of recreating a randomization-like scheme. Particularly, matching enhanced IV estimation may excel in following scenarios: First, when the response model has a complex functional structure, i.e. not just simple linear combinations of the covariates, matching reduces the dependence on model specification since it improves covariates balance prior to the analysis (Hade and Lu, 2011). Second, in longitudinal studies like MTA, time-varying confounding is common and it may be partitioned into two components—confounding effect related to earlier self-selection and confounding effect unrelated to earlier self-selection. If the confounding related to earlier self-selection can be controlled by thoroughly collecting relevant covariate information, we can use early self-selection as instrument to handle unmeasured confounding in later time period. Usually, it is easier to collect complete data in early stage than in later stage due to compliance and attrition issues.

Another issue with the instrumental variable approach is the interpretation of the estimated effect. First, IV method has a long history in economics research in the context of regression models with constant treatment effects. It works well for a carefully identified group of people where homogeneous effect is plausible. However, it doesn’t apply to a population where treatment effects are heterogeneous. In MTA example, we have a well-defined children population with close ages, thus we think a constant average treatment effect is a meaningful measure of the medication effect. Second, as pointed out by Angrist, et al. (1996), the IV estimand carries the interpretation of the average causal effect of compliers. In many observational studies, it is not the same as the average causal effect of the study population because we do not know their potential compliance behavior. The MTA study is unique in the sense that the observational phase is an extension of a randomized trial. Since the children have first gone through a randomized study phase and the majority of them complied, the estimated effect should be close to the average population effect for this specific study population.

Our investigation has several limitations. First, it uses only about half of the participants enrolled. This is primarily due to the missingness in the covariates. The reduction in sample size certainly has some non-trivial impact on the significance of the finding. Therefore, our findings cannot be generalized to the entire MTA population without strong assumptions. The use of MTA data example is more for illustrating a real longitudinal study with both randomization and observational components. For clinical evaluation of ADHD treatment, readers should refer to publications on the subjective matter (The MTA Cooperative Group, 1999; Jensen, et al. 2007; Swanson, et al. 2007; Molina, et al. 2009). On the other hand, if we could carefully screen out covariates with high missing rates but low confounding effects, we may enhance our analyses with a much bigger sample size. Second, an important assumption for using earlier self-selection as the instrument is that the earlier selection has no direct impact on the later outcome. This is reasonable for evaluating drug effect since you need to take the drug on a regular basis to maintain the beneficial effect. However, this might not work well for some educational program, such as smoking cessation counseling. Since one episode of the education may have some permanent impact on people’s behavior, earlier participation in educational program may independently affect the health outcome regardless of the later participation status. Third, the two-stage least squares method assumes continuous outcome and exposure. We dichotomize the exposure to binary to apply the proposed matching enhanced strategy since we use a bipartite matching algorithm, which requires two distinct groups. A possible extension to maintain the continuous exposure structure is using a nonbipartite matching algorithm to match subjects close on covariates and far on exposure (Lu, et al. 2001; Baiocchi, et al. 2010).