Abstract
Magnetic resonance (MR) images of the tongue have been used in both clinical studies and scientific research to reveal tongue structure. In order to extract different features of the tongue and its relation to the vocal tract, it is beneficial to acquire three orthogonal image volumes—e.g., axial, sagittal, and coronal volumes. In order to maintain both low noise and high visual detail and minimize the blurred effect due to involuntary motion artifacts, each set of images is acquired with an in-plane resolution that is much better than the through-plane resolution. As a result, any one data set, by itself, is not ideal for automatic volumetric analyses such as segmentation, registration, and atlas building or even for visualization when oblique slices are required. This paper presents a method of super-resolution volume reconstruction of the tongue that generates an isotropic image volume using the three orthogonal image volumes. The method uses preprocessing steps that include registration and intensity matching and a data combination approach with the edge-preserving property carried out by Markov random field optimization. The performance of the proposed method was demonstrated on fifteen clinical datasets, preserving anatomical details and yielding superior results when compared with different reconstruction methods as visually and quantitatively assessed.
Keywords: Super-resolution volume reconstruction, human tongue, magnetic resonance imaging (MRI)
I. INTRODUCTION
The mortality rate of oral cancer including tongue cancer is not considered to be high, but its morbidity in terms of speech, mastication, and swallowing problems is significant and seriously affects the quality of life of these cancer patients. Characterizing the relationship between structure and function in the tongue is becoming a core requirement for both clinical diagnosis and scientific studies in the tongue/speech research community [1], [2]. In recent years, medical imaging, especially magnetic resonance imaging (MRI), has played an important role in this effort. MRI is a noninvasive technology that has been extensively used over last two decades to analyze tongue structure and function ranging from studies of the vocal tract [3]-[6] to studies on tongue muscle deformation [1],[7]-[9]. For instance, high-resolution MRI provides exquisite depiction of muscle anatomy while cine MRI offers temporal information about its surface motion. With the growth in the number of images that can be acquired, research studies now involve 3D high-resolution images taken from different individuals, time points, and MRI modalities. Therefore, the requirement for automated methods that carry out image analysis of the acquired tongue image data is expected to grow rapidly.
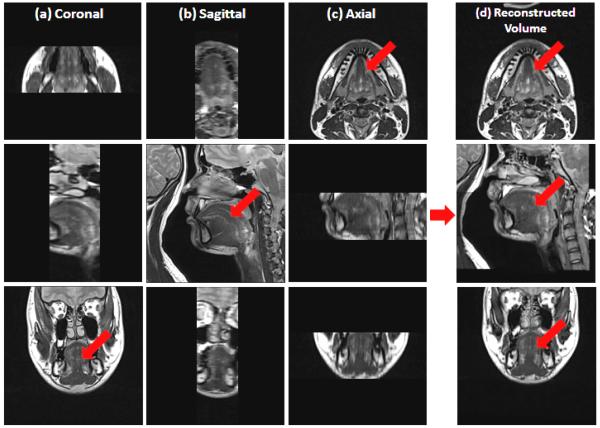
Time limitations of current MRI acquisition protocols make it difficult to acquire a single high-resolution 3D structural image of the tongue and vocal tract. It is almost certain that tongue motion—particularly the gross motion of swallowing—will spoil every attempt to acquire such data. The 3D acquisition takes at least 4–5 min and holding the tongue steady for more than 2–3 min will be likely to induce the involuntary motion. Therefore, in our current acquisition protocol, three orthogonal volumes with axial, sagittal, and coronal orientations are acquired one after the other. Motion may occur between these scans but the subject will return the tongue to a resting position for each scan. To speed up each acquisition, the fields of view (FOVs) of each acquired orientation are limited to encompass only the tongue itself, as shown in Figs. 1(a)–(c). Also, in order to rapidly acquire each stack of images with contiguous images (no gaps between the images), the through-plane resolution is worse than the in-plane resolution. In our case, the images have an in-plane resolution of 0.94 mm × 0.94 mm but are 3 mm thick.
Fig. 1.
Tongue images are acquired in three orthogonal volumes with field of view encompassing the tongue and surrounding structures. (a) Coronal, (b) sagittal, and (c) axial volumes are illustrated. The final super-resolution volume using the proposed method is shown in (d). The red arrows indicate the tongue region.
Because the slices are relatively thick and the regions of interest are tongue regions (e.g., tongue muscles) where certain muscle bundles are short and thin, none of the acquired image stacks are ideal for 3D volumetric analyses such as segmentation, registration, and atlas building or even for visualization when oblique views are required. In particular, since each volume has poorer resolution in the slice-selection direction than in the in-plane direction, it is difficult to observe tongue muscles clearly in any one of the volumes. Therefore, reconstruction of a single high-resolution volumetric tongue MR image from the available orthogonal image stacks will improve our ability to visualize and analyze the tongue in living subjects.
In this work, we develop a fully automated and accurate super-resolution volume reconstruction method from three orthogonal image stacks of the same subject by extending our preliminary approach [10]. We present a refined preprocessing and reconstruction algorithm design and provide validations on both tongue and brain data. This application is quite special in the sense that the function of the tongue involves a highly complex coordination of its different muscles to produce the precise movements necessary for proper speech, mastication, and deglutition. In addition, the tongue is a muscular hydrostat, with no bones or joints, thereby requiring an architecture of 3D orthogonal muscles to move and deform it when producing speech [11]. Because of the nonrigid motion (e.g., tongue motion or swallowing), different FOV, and different intensity distributions between scans, our problem posed unique challenges, requiring specialized preprocessing. The challenges motivate us to use a number of preprocessing steps including motion correction, intensity normalization, etc., followed by a region-based maximum a posteriori (MAP) Markov random field (MRF) approach. The region-based approach allows us to reconstruct the tongue at high resolution, because it resides in the intersection of the image fields of view, as well as other regions around the tongue which are also used in the analysis of speech production. In order to preserve important anatomical features such as the subtle boundaries of muscle, we use edge-preserving regularization. To our knowledge, this is the first attempt at super-resolution reconstruction applied to in vivo tongue high-resolution MR images for both normal and diseased subjects. The resulting super-resolution volume improves both the signal-to-noise ratio (SNR) and resolution over the source images, thereby approximating an original high-resolution volume whose acquisition would have taken too long for the subject to refrain from swallowing (or making other motions).
Improvements in visualizing the internal structure of the tongue may provide better ways to determine tongue cancer boundaries relative to the tongue muscles leading to better tumor staging and planning for cancer surgery. For example, the impact of surgery on speech can be better understood by visualizing the muscles that will be affected by surgery and knowing their role in speech production. For scientific study of the role of muscles, this approach provides an alternative to the visualization of tongue muscle topography in cadaveric anatomy. In a cadaveric specimen, the lack of a rigid framework and the muscle tone provided by the co-contraction of interdigitated extrinsic and intrinsic muscles lead to a loss of the in vivo topography. In summary, our reconstruction method yields a high resolution, volumetric image of the in vivo tongue that can be ideal for both clinical and scientific purposes.
The structure of this paper is as follows. Related work is reviewed in Section II. Section III shows the proposed method using a region-based MAP-MRF approach. Section IV explains the validation method, followed by the experimental results of the proposed method on numerical simulations and in vivo MR images of the tongue in Section V. Section VI provides a discussion, and finally, Section VII concludes the paper.
II. RELATED WORK
Super-resolution image reconstruction from multiple low-resolution images has been an area of active research since the seminal work by Tsai and Huang [12]. It is an important problem in a variety of fields such as video restoration, surveillance, remote sensing, and medical imaging [13]-[15]. A super-resolution reconstruction can overcome the limitations of the imaging system and enhance the performance of a variety of postprocessing tasks such as image segmentation, registration, atlas building, and motion analysis. If one knows the point spread function (PSF) of the imaging/camera system and also observes enough samples of shifted images, then resolution can be improved and noise reduced over the individual observations up to the limits posed by Shannon [16], [17]. It remains a difficult problem in practice, however, due to insufficient numbers of observed images, inexact registration, and inaccurate PSF and noise models.
Super-resolution methods can be categorized into nonuniform interpolation, frequency domain, and spatial domain approaches [13]-[15], [18]. The nonuniform interpolation approach is the most intuitive method consisting of successive steps including (i) registration, (ii) nonuniform interpolation, and (iii) deblurring process. The advantages of this approach are that it is computationally inexpensive and makes real-time application possible. The disadvantages of this approach are that degradation models are limited and the optimality of the whole reconstruction is not guaranteed [14].
The frequency domain approach utilizes aliasing in low-resolution images to reconstruct a high-resolution image [14]. Tsai and Huang [12] first formulated the multiframe super-resolution reconstruction approach in the frequency domain. This approach is based on fundamental principles including (i) the shifting property of the Fourier transform, (ii) the aliasing relationship between the continuous Fourier transform and the discrete Fourier transform (DFT), and (iii) the band-limited property of the original scene. Frequency domain approaches are generally intuitive and computationally efficient; however, they cannot easily incorporate spatial knowledge such as spatially-varying degradation and poor image registration [18], [19] and they are also very sensitive to modeling errors [20].
The spatial domain approach synthesizes high-resolution information by either learning from training sets (i.e., example-based approaches) to incorporate models involving spatially-varying physical phenomena, or by performing regularized reconstruction (i.e., model-based approaches). Example-based approaches capture the co-occurrence between low-resolution and high-resolution patches and synthesize high-resolution images by combining the highresolution patches [21]-[30]. Model-based approaches incorporate forward models that specify how the highresolution true image is transformed by the physics of the imaging system to generate low-resolution images including global or local motion, motion blur, varying PSF, compression artifacts, etc. This approach provides flexibility in modeling physical phenomenon whereas the computational complexity may be demanding [18]. Examples of the model-based approach include the projection onto convex sets (POCS) approach [14] and the maximum likelihood (ML)-POCS hybrid reconstruction approach [14]. The POCS approach simultaneously solves the restoration and interpolation problem to obtain the high-resolution image. The ML-POCS hybrid reconstruction approach finds high-resolution estimates by minimizing the ML cost functional with constraints. A super-resolution reconstruction is found by solving an inverse problem yielding a high-resolution image that is likely to be the source of the acquired images under the modeled imaging conditions [31]. The classical solution of a linear inverse problem is analytically obtained through the Moore-Penrose pseudo-inverse of the observation model [14]. In practice, however, the computation is demanding and therefore iterative solutions such as steepest descent [32] and expectation maximization [33] have been adopted to solve the problem [31]. In the present work, we adopt a model-based spatial domain approach because it allows us to incorporate a priori knowledge using constrained reconstruction algorithms to enhance the resolution through a variety of postprocessing techniques. A comprehensive survey on super-resolution reconstruction can be found in [14] and [15].
Several studies have succeeded in reconstructing a high-resolution volume from a set of multislice MR images [15], [34]-[40]. Important factors in any MRI experiment include how to balance interdependent variables such as image resolution, SNR, and acquisition time. Longer acquisition time provides higher spatial resolution and SNR compared with shorter acquisition time and vice versa [34]. Super-resolution reconstruction methods in MRI were first proposed by Peled et al. [39] and Greenspan et al. [40], adapting algorithms from computer vision community. A recent study has shown that super-resolution volume reconstruction provides better trade-offs between resolution, SNR, and acquisition time than direct high-resolution acquisition, which is especially useful when SNR and time constraints are taken into account [34]. In the present work, image acquisition is limited by the time constraints of speech and therefore the factors were balanced to optimize the super-resolution reconstruction.
In brain imaging it is common to take multiple scans of the same subject from different orientations, where the acquired images typically have better in-plane than through-plane resolution. In particular, model-based reconstruction approaches have been actively used. Bai et al. [41] proposed a MAP super-resolution method to reconstruct a high-resolution volume from two orthogonal scans of the same subject. This strategy is at the heart of the method we propose here. In addition, Gholipour et al. [35] investigated a MAP super-resolution method with image priors based on image gradients. Both of these methods used orthogonal stacks. Shilling et al. [37] proposed a superresolution reconstruction approach using rotated slice stacks based on POCS formalism for image-guided brain surgery. These methods did not address subject motion.
In addition, several researchers have developed methods for fetal brain imaging where due to uncontrolled motion it is common to acquire multiple orthogonal 2D multiplanar acquisitions with anisotropic voxel sizes [18], [42], [43]. To yield a single high-resolution registered volume image of the fetal brain from this kind of data, Rousseau [29] investigated so-called brain hallucination by incorporating a high-resolution brain image of a different subject (an atlas) in order to synthesize likely high-resolution texture patches from a low-resolution image of a subject. Although this method is promising, we maintain that it is better to reconstruct higher-resolution images from actual imaging data whenever possible rather than relying on examples that may or may not be representative of the object actually being imaged. This is especially true in the imaging of abnormal anatomy, such as the tongue cancer patients who are the primary target of our scientific studies on the tongue. Rousseau et al. [18] incorporated a registration method to correct motion and the final reconstruction process was based on a local neighborhood approach with a Gaussian kernel. Jiang et al. [43] proposed motion correction using registration and B-spline based scattered interpolation to reconstruct the final 3D fetal brain. The methods in [18], [43] addressed the subject motion but employed scatter data interpolation, which ignores the physics of imaging. Gholipour et al. [31] proposed maximum likelihood (M-estimation) error norm to reconstruct fetal MR images using a model of subject motion. This work addressed both inter-slice motion and anisotropic slice acquisition using slice-to-volume registration and M-estimation solution, respectively. Our work also incorporated a model of subject and tongue motion. In recent work, Rousseau [42] used an edge-preserving regularization method to reconstruct high-resolution images from the fetal MRI images and investigated the impact of the number of low-resolution images used. These approaches incorporate registration to align the observed data to a single anatomical model; this is a strategy we also use herein (although we use deformable registration due to the nature of the human tongue).
A super-resolution reconstruction technique was successfully adopted to reconstruct diffusion-weighted images (DWI) from multiple anisotropic orthogonal DWI scans [44]. The problem of patient motion was addressed by aligning the volumes both in space and q-space. This advanced the state-of-the-art super-resolution MRI application. In addition, a MAP formulation was used to tackle the reconstruction problem. In the present work, we propose similarly to investigate a super-resolution reconstruction approach for tongue MR images for the first time, aiming to advance the state-of-the-art super-resolution MRI application. Inspired by the DWI application and recent developments in brain MR imaging [41], [42], our approach uses an MR image acquisition model, region-based subject/tongue motion correction, intensity matching between scans, and a region-based MAP formulation with an edge-preserving regularization to preserve crisp muscle information.
III. METHOD
We view super-resolution volume reconstruction as an inverse problem that combines denoising, deblurring, and up-sampling in order to recover a high-quality volume from several low-resolution volumes. In contrast to other super-resolution frameworks, our application poses unique challenges in that multislice tongue MR data is affected by nonrigid motion (e.g., tongue motion or swallowing) between acquisitions and each volume is acquired with a different field-of-view (FOV). To efficiently tackle this problem, our proposed method comprises several steps: (1) preprocessing to address different orientation, size, and resolution, (2) registration to correct subject motion between acquisitions, (3) intensity normalization between volumes, and (4) a region-based MAP-MRF reconstruction. A flowchart of the proposed method is shown in Fig. 2.
Fig. 2.
A flowchart of the proposed method.
A. Imaging Model with Partial Overlap Region
In our problem, the imaging system involves a coordinate transformation, a non-uniform decimation, a PSF, noise, and a limited FOV, as illustrated in Fig. 3. Let the high-resolution volume be defined on the open and bounded domain Ω.
Fig. 3.

A model of the imaging system.
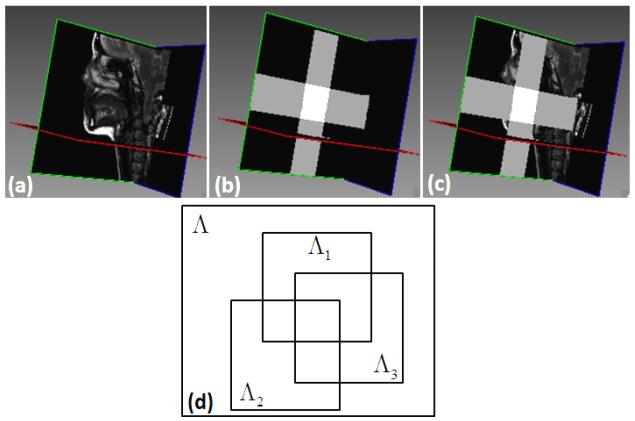
The FOVs of the low-resolution volumes are not identical because the acquisition protocols are designed to be “tight” around the tongue in each orientation (see Fig. 4). Let Λ1, Λ2, and Λ3 be the regions formed on the image domain by the axial, coronal, and sagittal volumes, respectively. In particular, Λk ⊂ Ω is a subset of pixels at which the value of each low-resolution volume is observed acquisitions.
Fig. 4.
One representative final super-resolution image is shown in (a); regions defined from each low-resolution volume are shown in (b); a volume with regions defined from from each low-resolution volume is illustrated in (c); and a schematic drawing of each region is shown in (d).
For example, as illustrated in Figs. 4 (b) and (c), the white region represents SΛ1∩Λ2∩Λ3, the horizontal gray regions represent SΛ1∩Λ3, and vertical gray regions represent SΛ1∩Λ3, where SΛ denotes the characteristic function of the domain of high-resolution volume, i.e.
| (1) |
The imaging model that incorporates the overlap regions (see Fig. 3) is then given by
| (2) |
where k denotes the k-th observation, gk is one of the observed image volumes, is a coordinate transformation, is a downsampling operator, is an impulse response function (i.e., PSF) that blurs f, and nk is a Gaussian noise with zero mean and variance . This model is combined as . As is conventionally, we model the PSF as a Gaussian function [45]. The goal of this work is to reconstruct a single high-resolution volume f from three orthogonal scans that approximates the original in-plane resolution in all three directions.
B. Preprocessing
The three volumes to be combined into one super-resolution volume have different slice positions, orientations, and volume sizes. Therefore, several preprocessing steps are applied prior to the reconstruction of the super-resolution volume: (i) generation of an isotropic volume, (ii) conversion of the orientation of each volume to the orientation of the target reference volume, (iii) padding of zero values to yield the same volume sizes, (iv) registration to correct subject motion between volumes, and (v) matching of intensities in the overlap region using spline regression. These steps are now summarized.
1) Isotropic Volume Generation
According to our imaging model, each low-resolution volume has its resolution degraded in only one dimension (slice-selection direction). In order to up-sample each volume in the slice-selection direction, a 5th-order B-spline interpolation is used.
2) Orientation Conversion and Zero-padding
The orientation of each volume is converted to that of the target reference volume. This step is required so that registration starts with the anatomy appearing in each volume roughly aligned. Without this step, the registration is likely to fail due to small overlap regions. In addition, although the previous steps produce an isotropic volume with the same orientation, the size of each volume is still different. For convenience in registration, each volume is padded with zero values in order to create digital volumes all having the same voxel dimensions. Without this step, the registration produces the same volume size as the target volume size (e.g., 256 × 256 × 20 in the case of axial stack). Masks indicating the region of valid data—i.e., Λ1, Λ2, and Λ3—are also created (see Fig. 4) for use in both registration and region-based reconstruction.
3) Registration
We use image registration to correct for subject motion between acquisitions. Accurate registration is of great importance in this application because small perturbations in alignment can lead to visible artifacts after applying the MAP-MRF reconstruction algorithm. This is because uncertainty in registration increases the variance of intensity values at each spatial location. To obtain accurate and robust registration results, we compute a global displacement estimate followed by a local deformation estimate. The global displacement estimate is characterized by an affine registration accounting for translation, rotation, and scaling (12 degrees of freedom in 3D). We use mutual information (MI) [46] as the similarity measure for this step because orientation of acquisition can cause intensity differences even when the same pulse sequence on the same scanner is used. The algorithm we use is different than a conventional MI registration algorithm because of the FOV differences in the volumes.
We denote the images and defined on the open and bounded domains Ω1 and Ω2 as the template and target images, respectively. Mutual information can be computed using joint entropy as
| (3) |
where i1 = I1(u1(x)), i2 = I2(x), and pI1(i1) and pI2(i2) are marginal distributions. Here, pu1(i1, i2) denotes joint distribution of I1(u1(x)) and I2(x) in the overlap region which can be computed the Parzen window given by
| (4) |
where φ is a Gaussian kernel whose width is controlled by ρ.
In this global registration step, we use the overlap regions of the two volumes to weight the evaluation of MI in order to emphasize influence on parameter estimation to regions that are known to be overlapping. Of note, two of the volumes were registered to the target reference volume. The optimal values for the twelve parameters that maximize the given energy functional are obtained by solving the associated Euler-Lagrange equations, and a gradient descent method [47] is performed. In addition, we use a coarse-to-fine multiresolution scheme for computational efficiency and robustness.
In order to achieve sub-voxel accuracy, we estimate a local deformation using a modification of the diffeomorphic demons method [48]. Since diffeomorphic demons is an intensity-based registration method, we perform histogram matching between the two images to ensure that corresponding points in different volumes have similar intensity values for the local deformation model. The only modification that we make to diffeomorphic demons is to incorporate the overlap region in order to restrict the domain of registration (similar in concept to the global displacement estimation step).
4) Intensity Matching
Now that the volumes are registered, a more careful analysis of the intensity differences that exist between the images can be carried out via a spline based intensity regression method that uses local intensity matching. We first revert to the original intensities (instead of the histogram-matched intensities) and recognize that if the registration is accurate then the overlap regions provide evidence of how the intensities of the different acquisitions correspond. In particular, we can observe intensity pairs at each voxel within the corresponding overlap regions and compute a regression that represents an estimate of the transformation required to make the intensities of one volume match those of another. In this step, intensity values of two volumes are matched to those of the target reference volume. We use 10–15 control points in a cubic spline fit to compute two such transformations that are then used to map the intensities of two volumes into the target volume.
C. MAP-MRF Reconstruction
Once we have three preprocessed, orthogonal volumes, regularized reconstruction is carried out. Classical methods including Tikhonov regularization [49], Gaussian and Gibbs regularizations [50], and Laplacian regularization [19] have been used to achieve various image reconstruction objectives. But these methods often create oversmoothing of edges [20] in direct opposition to our super-resolution goals. Edge-preserving regularization methods, including total variation (TV) [51], [52], bilateral TV [20], and half-quadratic regularization [53], have been developed to solve this problem.
In this work, we use the edge-preserving regularization method of Villain et al. [54] wherein MAP estimation with a half-quadratic approach is used to obtain a high-resolution volume f given three orthogonal low-resolution images, i.e.
| (5) |
where denotes the estimated solution. Applying Bayes rule, this can be written as
| (6) |
where P (g1, g2, g3|f) and P(f) represent likelihood and prior, respectively.
1) Likelihood Model
We assume that each observed image is corrupted by additive Gaussian noise, which is a good approximation since the MR images in the regions of interest (i.e., tongue region) have high SNR. Accordingly, the likelihood is determined by the image formation process of Eq. (2) with additive noise, yielding
| (7) |
where Q denotes a normalization factor and D(f) using the region-based approach (see Fig. 4 (d)) is given by
| (8) |
Here, because the precise positions of these acquired volumes relative to the anatomy might be slightly wrong even after motion correction and to reduce the effects of “seams” between different regions, we use blurred versions of the masks—termed “softmasks”—which are given by
| (9) |
where * denotes the convolution operator and Gσ is a unit-height Gaussian kernel with standard deviation σ. In this work, we set σ = 2 mm. The softmasks provide a probabilistic confidence about the intensity value of each scan, thereby allowing a soft transition between scans.
2) Prior Model
The MRF is defined over a graph G =< V, E > where V is the set of nodes representing the random variables s = {sv}v∈V, E is the set of edges connecting the nodes, and the clique c is defined by the neighborhood system. The clique of MRF is defined by the local neighborhoods around pixels. Our prior model can be defined as
| (10) |
Here, W is a normalization factor and , where δ denotes a scaling factor and Δxc and dc denote the difference of the values and the distance of the two voxels in clique c, respectively (we set δ=0.8 in our implementation).
Maximization of Eq. (6) is equivalent to minimizing the negative of the logarithm of the posterior probability, i.e.
| (11) |
which leads to the following form:
| (12) |
where is a balancing parameter, controlling the smoothness of the reconstructed image (we set λ=0.5 in our implementation).
3) Half-quadratic Approach
In order to efficiently minimize the objective function in Eq. (12), we adopt a half-quadratic regularization technique incorporating the region-based approach as in [54], [55].
The summary of the MAP-MRF reconstruction algorithm is shown below.
Algorithm 1 MAP-MRF Reconstruction
|
D. Implementation
The preprocessing steps including resampling, re-orientation, global displacement (affine registration), local deformation model (diffeomorphic demons registration), and intensity matching were implemented using C++ and ITK (Insight Segmentation and Registration Toolkit) [56] and took 18 × 2 min. The MAP-MRF reconstruction step was also implemented using C++ and took about 5 × 1 min. The proposed method was performed on an Intel i7 CPU with a clock speed of 1.74 GHz and 8 GByte memory. In addition, the ALGLIB library [57] was used to implement spline-based regression part. We used a multiresolution scheme for our global displacement model. The parameters are first estimated at the coarsest level, which are then used as the starting parameters for the subsequent level. Transformations at each level of the pyramid are accumulated and propagated. This scheme helps avoid local minima caused by partial overlap. In our implementation we use two levels. Parameters used in the experiments were determined empirically to produce the best visual results. Once the parameters were determined, the same parameters were used in all experiments including tongue and brain datasets.
IV. VALIDATION
A. Evaluation using tongue data
1) Tongue data
Fifteen high-resolution MR datasets were used in these experiments. They came from twelve normal speakers and three patients who had tongue cancer surgically resected (glossectomy). All MRI scanning was performed on a Siemens 3.0 T Tim Treo system using an 8-channel head and neck coil. In addition, T2-weighted Turbo Spin Echo sequence with echo train length of 12 and TE/TR of 62ms/2500ms was used. The field of view was 240 mm × 240 mm with resolution of 256 × 256. Each dataset contained a sagittal, coronal, and axial stack of images containing the tongue and surrounding structures. The image size for high-resolution MRI was 256 × 256 [notdef] z (z ranges from 10 to 24) with 0.94 mm × 0.94 mm in-plane resolution and 3 mm slice thickness. The datasets were acquired at rest position and the subjects were required to remain still from 1.5 to 3 minutes for each orientation.
2) Quantitative analysis
The proposed method was first evaluated using fifteen simulated datasets as described in IV-A. In order to quantitatively evaluate the performance of the proposed method in terms of accuracy of the reconstruction, the final super-resolution volume using the proposed method was considered as our ground truth data. The ground truth was constructed with 256 × 256 × 256 voxels with resolution of 0.94 mm × 0.94 mm × 0.94 mm. Three low-resolution volumes (i.e., axial, sagittal, and coronal volumes) were formed where the voxel dimensions was 0.94 mm × 0.94 mm in-plane and the slice thickness was 3.76 mm (subsampling by a factor 4). Prior to subsampling the volumes in slice-selection directions, Gaussian filtering with σ = 0.5 (in-plane) and σ = 2 (slice-selection direction) was applied in order to avoid an anti-aliasing effect.
In what follows, volume reconstruction was carried out in four ways. First, 5th-order B-spline interpolation was performed in each plane independently. Second, averaging of three up-sampled volumes was performed. Third, reconstruction from three up-sampled volumes using Tikhonov regularization [58] was performed. Finally, the proposed method using three up-sampled volumes was carried out. In this simulation study, preprocessing steps were not necessary except the up-sampling process using 5th-order B-spline interpolation as the volumes are already aligned and intensity values between volumes are identical. Tikhonov regularization is one of the most common approaches using quadratic functions, which takes the form
| (13) |
where represents the reconstructed volume, λ1 denotes the balancing parameter, and we set L = I in this experiment.
As a quantitative measure, the peak signal-to-noise ratio (PSNR), which is defined as
| (14) |
where MAXX denotes the maximum possible voxel value of the volume, ΩR denotes a reference image domain, X denotes a reference volume and represents a reconstructed volume.
3) Noise simulations
To test robustness, Gaussian noise with zero mean and standard deviations of 50 (2% of intensity level) and 75 (3% of intensity level), respectively were added to investigate the effect of noise on the reconstruction. The same quantitative analysis as described in Sec. IV-A2 was performed to evaluate the performance of the different reconstruction methods.
B. Evaluation using brain Data
1) Brain data
Three isotropic high-resolution brain MR datasets were used to objectively evaluate and compare the performance of different reconstruction methods. For each subject, two magnetization prepared rapid gradient echo (MP-RAGE) images were obtained using a 3.0T MR scanner (Intera, Phillips Medical Systems, Netherlands). The MP-RAGE was acquired with the following parameters: 132 slices, axial orientation, 0.8 mm slice thickness, 8° flip angle, TE = 3.9ms, TR = 8.43ms, 256 × 256 matrix, and 212 × 212 cm FOV. The image size for these datasets was 288 × 288 × 225 with isotropic resolution (i.e., 0.8 mm × 0.8 mm × 0.8 mm).
2) Quantitative analysis
A challenge in testing the proposed method is the lack of ground truth available in in vivo volumetric tongue MR data. In order to avoid potential bias in our experiments, we used two high resolution brain datasets with isotropic resolution to evaluate the performance of different reconstruction methods. Three low-resolution volumes (i.e., axial, sagittal, and coronal volumes) were formed where the voxel dimensions were 0.5 mm × 0.5 mm in-plane and the slice thickness was 2.0 mm (subsampling by a factor 4). Prior to subsampling the volumes in slice-selection directions, Gaussian filtering with σ = 0.5 (in-plane) and σ = 2 (slice-selection direction) was applied in order to avoid anti-aliasing effect. The same quantitative analysis as described in Sec. IV-A2 was performed to evaluate the performance of the different reconstruction methods.
V. RESULTS
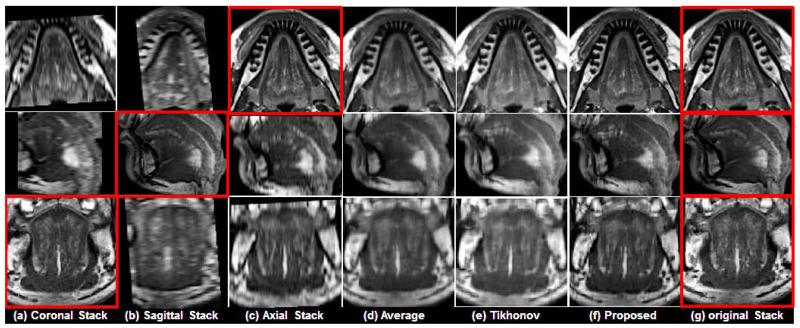
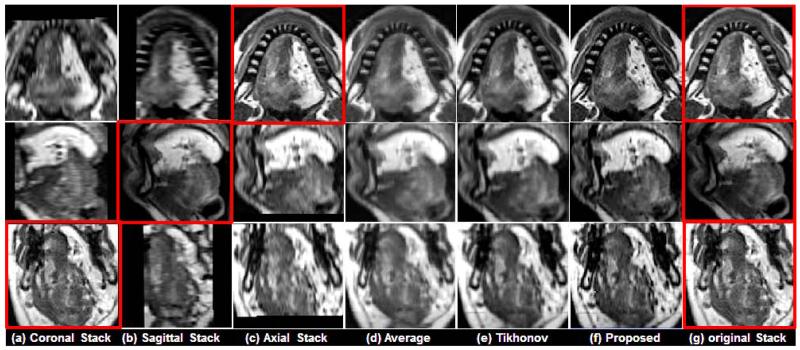
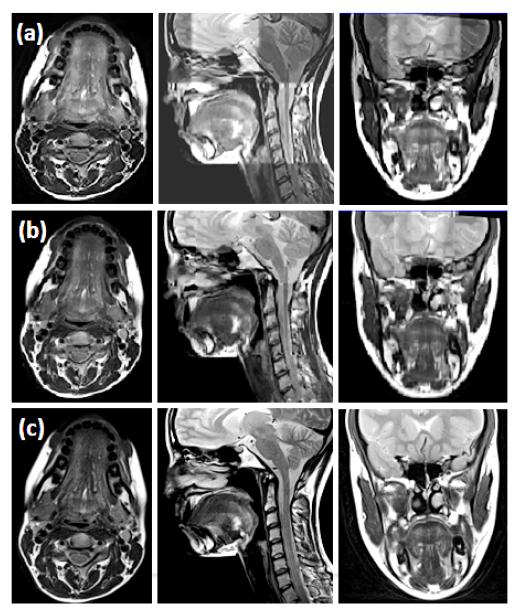
In Figs. 5 and 6, two representative results using a normal subject (Fig. 5) and a glossectomy patient (Fig. 6) with different reconstruction methods are demonstrated, respectively. The rows show slices of three orthogonal views including axial, sagittal, and coronal, respectively. The first three columns ((a)-(c)) show three original scans after isotropic resampling (i.e., 0.94 mm × 0.94 mm × 0.94 mm) in the coronal, sagittal, and axial planes, respectively. Panel (d) shows the reconstruction using averaging, (e) shows reconstruction using Tikhonov regularization, and (f) shows the reconstruction using the proposed method. Panel (g) shows the original three orthogonal volumes.
Fig. 5.
Comparison of different reconstruction methods on a normal subject. The original coronal, sagittal, and axial volumes are shown in (a), (b), and (c), respectively. B-spline interpolation was used to yield higher pixel resolutions equal to that of the highest resolution orientations, which are indicated by the red boxes. Three different reconstruction methods including simple averaging, Tikhonov regularization, and the proposed method are shown in (d), (e), and (f), respectively. For reference, the highest resolution images from each original volume are repeated in (g).
Fig. 6.
Comparison of different reconstruction methods using a glossectomy patient. The original coronal, sagittal, and axial volumes are shown in (a), (b), and (c), respectively. B-spline interpolation was used to yield higher pixel resolutions equal to that of the highest resolution orientations, which are indicated by the red boxes. Three different reconstruction methods include (d) simple averaging, (e) Tikhonov regularization, and (f) the proposed method, respectively. For reference, the highest resolution images from each original volume is repeated in (g)
As shown in Figs. 5 and 6, the proposed method provided better muscle and fine anatomical detail than the other methods. The target reference volume into which the other volumes were registered was the axial volume in both cases. In our experiments, preprocessing steps (e.g., registration) were not validated in a quantitative manner. Instead, the quality of the results were confirmed visually. Please notice that the reconstructed images and the original images shown in the figures may not be exactly the same except in the axial slice, because the data are aligned to the axial stack.
A. Quantitative analysis using tongue data
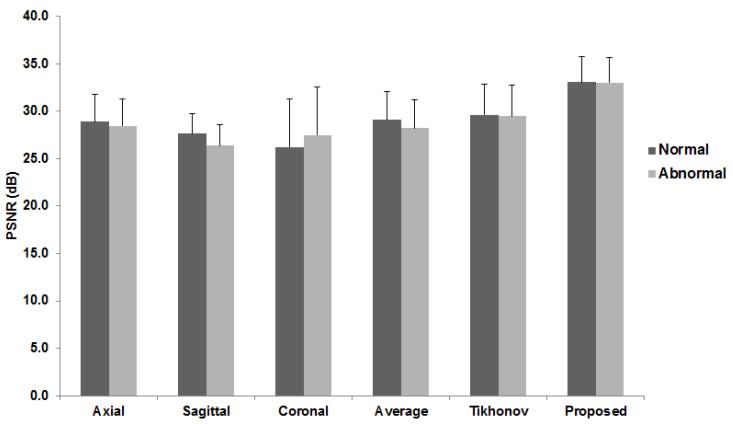
Fig. 7 illustrates results using the simulated data. Figs. 7 (a), (b), and (c) show the reconstructed results using the B-spline interpolation method [59] in which resolution was degraded in only one direction. Figs. 7 (d), (e), and (f) were reconstructed from three volumes (i.e., Figs. 7 (a), (b), and (c)) using averaging, Tikhonov regularization, and the proposed method, respectively, in which the proposed method provided a more visually detailed result than the other methods. Fig. 8 illustrates the PSNR results using the normal and patient datasets, respectively, in which the proposed method outperformed the other methods. Patients have more complex anatomy and scar tissue than controls due to forearm flap reconstruction. Therefore it is more challenging to reconstruct but the results show that the proposed method was able to produce equally good results.
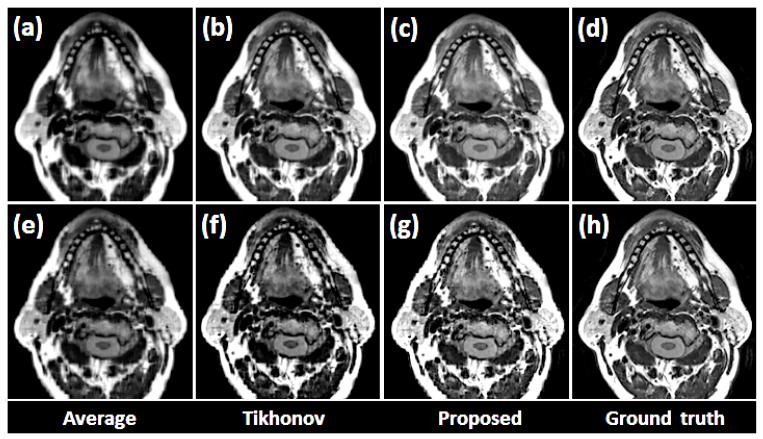
Fig. 7.
Comparison of different reconstruction methods using a simulation study. Reconstructed volume are shown in (a), (b), and (c), respectively. B-spline interpolation was used to yield higher pixel resolutions equal to that of the highest resolution orientations, which are indicated by the red boxes. Three different reconstruction methods including simple averaging, Tikhonov regularization, and the proposed method are depicted in (d), (e), and (f), respectively. Ground truth data is illustrated in (g). The proposed method provides more detailed anatomical information than averaging and Tikhonov regularization methods as visually assessed.
Fig. 8.
PSNR was measured using fifteen human datasets consisting of twelve normal and three abnormal subjects to compare the performance of the reconstruction methods quantitatively.
In addition, to compare the impact of anti-aliasing [60], volumes were reconstructed both with and without the use of Gaussian filtering. Results are shown in Fig. 9. It is observed that volumes reconstructed without using Gaussian filtering have step-like artifacts (see second row). The averaging result in Fig. 9 (e) without using Gaussian filtering had better PSNR as compared with the one using Gaussian filtering in Fig. 9 (a) as the averaging is similar to the low-pass filtering, removing the step-like artifacts. The reconstructed volume using Tikhonov regularization (Fig. 9 (b)) provided almost similar results. However, the reconstructed volumes using the proposed method use edge-preserving property and therefore the aliasing artifacts are more prominent in Fig. 9 (g) than in Fig. 9 (c). The reconstructed volume (Fig. 9 (c)) using Gaussian filtering provided the best result as assessed both visually
Fig. 9.
Comparison of effect of Gaussian filtering that removes anti-aliasing effect using a simulation study. The first row shows reconstructed volumes generated using Gaussian filtering that removes anti-aliasing effects including (a) averaging (PSNR = 24.36 dB), (b) Tikhonov regularization (PSNR = 27.74 dB), (c) the proposed method (PSNR = 28.74 dB), and (d) ground truth, respectively. The second row shows reconstructed volumes generated without using Gaussian filtering that removes anti-aliasing effects including (e) averaging (PSNR = 25.71 dB), (f) Tikhonov regularization (PSNR = 27.42 dB), (g) the proposed method (PSNR = 26.87 dB), and (h) ground truth, respectively. (d) and (h) are the same.
B. Noise simulations using tongue data
Gaussian noise images with two power levels were added as depicted in Fig. 10. Table I summarizes the quantitative results after the reconstruction, showing that the proposed method is better than the other reconstruction methods. However, increasing the noise in our simulation degraded the proposed method (lower PSNR) while both averaging and Tikhonov regularization remained largely unaffected. This can be explained by the edge-preserving property of our method, which has a tendency to also preserve noise when it is present, whereas both averaging and Tikhonov regularization tend to suppress noise.
Fig. 10.
To simulate the performance of the reconstruction in the presence of the noise, Gaussian noise images with two power levels were added to ground truth in (a): Gaussian noise with zero mean and standard deviations of (b) 50 and (c) 75, respectively
TABLE I.
PSNR (DB) FOR DIFFERENT RECONSTRUCTION METHODS ON SIMULATION DATA (MEAN±SD)
| Axial | Sagittal | Coronal | Averaging | Tikhonov regularization | Proposed method | |
|---|---|---|---|---|---|---|
| No noise | 28.8±3.3 | 27.4±3.2 | 26.5±4.4 | 28.9±3.6 | 29.3±3.6 | 33.1±3.1 |
| Gaussian Noise (m=0, σ=50) | 27.9±2.8 | 26.7±2.8 | 25.6±3.8 | 28.2±3.0 | 28.7±3.6 | 31.3±2.1 |
| Gaussian Noise (m=0, σ=75) | 26.8±2.6 | 26.1±2.7 | 25.1±3.4 | 26.9±2.6 | 28.5±3.2 | 29.7±3.7 |
C. Quantitative analysis using brain data
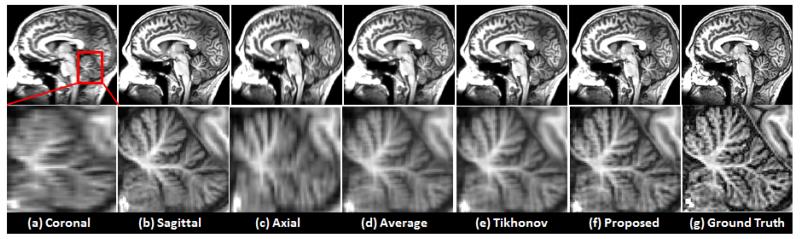
Fig. 11 illustrates reconstruction results using the brain data. Figs. 11 (a), (b), and (c) show the reconstructed results using the B-spline interpolation method in which resolution was degraded in only one direction. Figs. 11 (d), (e), and (f) were reconstructed from three volumes (i.e., Figs. 11 (a), (b), and (c)) using averaging, Tikhonov regularization, and the proposed method, respectively. Fig. 11 (g) shows the high-resolution ground truth data. Fig. 12 illustrates the quantitative measure (i.e. PSNR) of three datasets, where the proposed method provided better performance, confirming the proposed method is not biased with respect to the use of different datasets.
Fig. 11.
Brain datasets were used to gauge the performance of the different reconstruction methods. The images in the second row illustrate the enlarged region shown in red box in the first column.
Fig. 12.
PSNR (dB) for different reconstruction methods on brain data. Dotted lines represent the mean of the three datasets.
Fig. 13 shows the importance of using both registration and subsequent intensity matching steps. Figs. 13 (a) and (b) illustrate that misalignments and difference in intensity distributions between scans were significant, respectively. The proposed approach corrects this problem as shown in Fig. 13 (c). In addition, Fig. 14 illustrates that the reconstruction results with and without using a region-based reconstruction approach. Fig. 14 (a) has intensity mismatch compared to the Fig. 14 (b).
Fig. 13.
One example showing the super-resolution volume reconstruction (a) without using registration and intensity matching, (b) without using intensity matching after registration, and (c) the proposed method.
Fig. 14.
The results of super-resolution reconstruction with and without using the region-based approach. (a) MAP-MRF reconstruction without using the region-based approach, (b) the proposed method, and (c) original three volumes. Axial, sagittal, and coronal volumes are shown in the first, second, and third columns, respectively.
VI. DISCUSSION
In our application it was of great importance to preserve crisp muscle details and fine structures. Therefore we treated them as edges and adopted an edge-preserving regularization as in [54]. The half-quadratic approach was carried out to minimize the objective function in the tongue MR images. In addition, we compared the results with a regularization scheme which does not use the edge-preserving property. Other edge-preserving regularization methods [61]-[64] are likely to give similar results.
In our experimental results, patients have more complex anatomy than controls. They have considerable scar tissue, their muscles are deformed around the scar and missing in the area of the resection, and they are asymmetrical. Therefore, it was possible that their datasets would be more difficult to align. However, it is seen from our experimental results that all were reconstructed with equally good success.
Noise simulations were also carried out to confirm the robustness of the proposed algorithm. Since the proposed algorithm tends to preserve noise due to the use of edge-preserving regularization, we tested it with a large amount of noise using Gaussian noise with zero mean and standard deviations of 50 and 75, respectively, the performance of the proposed method was better than other methods in our experiments.
Evaluation of the proposed study was a challenging task. In fact, the notion of accuracy is ill-posed in this application as precise validation is typically impossible due to the lack of ground truth available other than simulation and visual assessment. We considered the final reconstruction volume as our ground truth and simulated the reconstruction step. Moreover, we used the brain data to further evaluate the algorithm and avoid bias in our evaluation. The brain data allowed us to more definitively determine the quality of the algorithm because of its isotropic resolution. This leads to more confidence in the interpretation of the tongue data and is very important because the tongue itself is highly anisotropic. The tip is quite thin and it gets thicker towards the back. This is best seen in the sagittal orientation. On the other hand, only the axial plane allows us to see the lateral shape of the tip. In this paper, the axial orientation was chosen as the target. However, in a study where tongue tip thickness is the critical feature, the sagittal orientation might be chosen as the target.
The intensity matching results, while good, were not optimal because the regression was performed only on overlapped regions and therefore the full range of the tongue intensity may not have been covered. In our future work, we will make use of all three datasets to perform high-dimensional regression and devise a weighting scheme to incorporate any difference in resolutions between the stacks. In addition, the performance of the reconstruction algorithm depends on the choice of the balancing parameter, which is a matter of modeling. In our future work, we will investigate the mechanism to find the best parameter in terms of the reconstruction performance.
The reconstruction quality heavily depends on the registration performance. In our work, we know the overlapped regions (i.e., tongue region) and explicitly used the region in our registration, which is an optimal way to deal with partial overlap. In addition, although affine registration may capture the differences of different stacks acquired at rest position, we further incorporated the diffeomorphic demons registration to accommodate subtle deformation in order to maximize the reconstruction quality. Diffeomorphic demons depends on accurate image intensities, however, these are only fully corrected after registration. Furthermore, intensities should only truly match if there were no differences in the direction of blurring between the images, which is obviously untrue.
In the clinical scenario, MRI has been used for structural imaging. The proposed super-resolution volume reconstruction provides the groundwork for the full 3D volumetric analyses such as image segmentation, registration, and atlas building. In addition, it overcomes the limitations of slice thickness problems. Therefore, this automated postprocessing technique can be potentially used in any body part to improve 3D resolution and decrease the noise in the images. In addition, because poorer through plane quality is acceptable, it could be used for patients that are unable to hold still for a long period of time, but require good image resolution for diagnoses and treatment.
To our knowledge, there have been no prior attempts to perform super-resolution volume reconstruction in tongue MR imaging domain. We successfully implemented and evaluated interpolation, averaging, and MAP-MRF reconstruction using the Tikhonov regularization and compared with the proposed method. The proposed method provided the best performance and groundwork for further analyses.
VII. CONCLUSION
In this work, a super-resolution reconstruction technique based on the region-based MAP-MRF with an edge-preserving regularization and half-quadratic approach was developed for volumetric tongue MR images acquired from three orthogonal acquisitions. Experimental results show that the proposed method has superior performance to the interpolation-based method, simple averaging, and Tikhonov regularization. It also better preserved the anatomical details as quantitatively confirmed. The proposed method allows full 3D high-resolution volumetric data, thereby potentially improving further image/motion and visual analyses.
ACKNOWLEDGMENT
This work was supported by NIH grants: R01CA133015 and R00DC009279. We would like to thank Sarah Ying, M.D., Johns Hopkins University, Department of Radiology, for sharing brain data in our simulation study. We would like to thank the reviewers for their helpful comments.
APPENDIX A
HALF-QUADRATIC APPROACH
The main idea in half-quadratic approach is to introduce and minimize a new objective function, which has the same minimum as the original non-quadratic objective function J(f). By introducing auxiliary variable l, the original objective function J(f) can be replaced by an augmented objective function K(f, l). We first define an auxiliary function ψ as follows:
| (15) |
This leads to the new prior model given by
| (16) |
The augmented objective function can then be given by
| (17) |
which is a quadratic function whose minimization with respect to f and l yields explicit and closed-form expressions, respectively. Minimizing K(f, l) with respect to f leads to the following form:
| (18) |
where its minimum value is achieved at ms [65]. Solving for ms yields an explicit expression of each condition in Eq. (8), i.e.
| (19) |
where σn denotes standard deviation of the final super-resolution volume and the sums extend to the neighborhood of the currently visited voxel s. In addition, to minimize K(f, l) with respect to l, we take the derivative, set it equal to zero and solve for l, yielding
| (20) |
We also use an over-relaxation scheme to speed-up convergence as follows:
| (21) |
where we set α=1.2 in our implementation. The overall minimization of K(f, l) is achieved by alternating between minimization with respect to f and then with respect to l using Eqs. (21) and (20), respectively.
Contributor Information
Jonghye Woo, University of Maryland and Johns Hopkins University, Baltimore, MD.
Emi Z. Murano, Johns Hopkins University, Baltimore, MD
Maureen Stone, University of Maryland, Baltimore, MD.
Jerry L. Prince, Johns Hopkins University, Baltimore, MD.
REFERENCES
- [1].Stone M, Davis E, Douglas A, Aiver M, Gullapalli R, Levine W, Lundberg A. Modeling tongue surface contours from cine-mri images. Journal of speech, language, and hearing research. 2001;44(5):1026–1040. doi: 10.1044/1092-4388(2001/081). [DOI] [PubMed] [Google Scholar]
- [2].Wilhelms-Tricarico R. Physiological modeling of speech production: Methods for modeling soft-tissue articulators. Journal of the Acoustical Society of America. 1995;97:3085–3098. doi: 10.1121/1.411871. [DOI] [PubMed] [Google Scholar]
- [3].Narayanan S, Byrd D, Kaun A. Geometry, kinematics, and acoustics of tamil liquid consonants. The Journal of the Acoustical Society of America. 1999;106:1993–2007. doi: 10.1121/1.427946. [DOI] [PubMed] [Google Scholar]
- [4].Narayanan S, Alwan A, Haker K. An articulatory study of fricative consonants using magnetic resonance imaging. Journal of the Acoustical Society of America. 1995;98(3):1325–1347. [Google Scholar]
- [5].Bresch E, Kim Y, Nayak K, Byrd D, Narayanan S. Seeing speech: Capturing vocal tract shaping using real-time magnetic resonance imaging. IEEE Signal Processing Magazine. 2008;25(3):123–132. [Google Scholar]
- [6].Lakshminarayanan A, Lee S, McCutcheon M. MR imaging of the vocal tract during vowel production. Journal of Magnetic Resonance Imaging. 1991;1(1):71–76. doi: 10.1002/jmri.1880010109. [DOI] [PubMed] [Google Scholar]
- [7].Stone M, Liu X, Chen H, Prince J. A preliminary application of principal components and cluster analysis to internal tongue deformation patterns. Computer methods in biomechanics and biomedical engineering. 2010;13(4):493–503. doi: 10.1080/10255842.2010.484809. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [8].Napadow V, Chen Q, Wedeen V, Gilbert R. Intramural mechanics of the human tongue in association with physiological deformations. Journal of biomechanics. 1999;32(1):1–12. doi: 10.1016/s0021-9290(98)00109-2. [DOI] [PubMed] [Google Scholar]
- [9].Takano S, Honda K. An MRI analysis of the extrinsic tongue muscles during vowel production. Speech communication. 2007;49(1):49–58. [Google Scholar]
- [10].Woo J, Bai Y, Roy S, Murano E, Stone M, Prince J. Super-resolution reconstruction for tongue MR images. SPIE Conference on Medical Imaging. 2012;8314:83140C. doi: 10.1117/12.911445. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [11].Reichard R, Stone M, Woo J, Murano E, Prince J. Motion of apical and laminal/s/in normal and post-glossectomy speakers. Acoustical Society of America. 2012:3346. [Google Scholar]
- [12].Tsai R, Huang T. Multiframe image restoration and registration. Advances in computer vision and image processing. 1984;1(2):317–339. [Google Scholar]
- [13].Borman S, Stevenson RL. Super-resolution from image sequences - a review; Proceedings of the 1998 Midwest Symposium on Systems and Circuits; Washington, DC, USA. 1998; IEEE Computer Society; p. 374. ser. MWSCAS ’98. [Online]. Available: http://dl.acm.org/citation.cfm?id=824469.825197. [Google Scholar]
- [14].Park S, Park M, Kang M. Super-resolution image reconstruction: a technical overview. IEEE Signal Processing Magazine. 2003;20(3):21–36. [Google Scholar]
- [15].Greenspan H. Super-resolution in medical imaging. The Computer Journal. 2009;52(1):43–63. [Google Scholar]
- [16].Unger M, Pock T, Werlberger M, Bischof H. A convex approach for variational super-resolution; Proceedings of the 32nd DAGM conference on Pattern recognition; Berlin, Heidelberg. 2010; Springer-Verlag; pp. 313–322. [Online]. Available: http://dl.acm.org/citation.cfm?id=1926258.1926296. [Google Scholar]
- [17].Shannon C. A mathematical theory of communication. ACM SIGMOBILE Mobile Computing and Communications Review. 2001;5(1):3–55. [Google Scholar]
- [18].Rousseau F, Glenn O, Iordanova B, Rodriguez-Carranza C, Vigneron D, Barkovich J, Studholme C. Registration-based approach for reconstruction of high-resolution in utero fetal MR brain images. Academic radiology. 2006;13(9):1072–1081. doi: 10.1016/j.acra.2006.05.003. [DOI] [PubMed] [Google Scholar]
- [19].Shen H, Zhang L, Huang B, Li P. A MAP approach for joint motion estimation, segmentation, and super resolution. IEEE Transactions on Image Processing. 2007;16(2):479–490. doi: 10.1109/tip.2006.888334. [DOI] [PubMed] [Google Scholar]
- [20].Farsiu S, Robinson M, Elad M, Milanfar P. Fast and robust multiframe super resolution. IEEE Transactions on Image Processing. 2004;13(10):1327–1344. doi: 10.1109/tip.2004.834669. [DOI] [PubMed] [Google Scholar]
- [21].Kim K, Kwon Y. Example-based learning for single-image super-resolution. Pattern Recognition. 2008:456–465. [Google Scholar]
- [22].Glasner D, Bagon S, Irani M. Super-resolution from a single image; Computer Vision, 2009 IEEE 12th International Conference on. Ieee.2009. pp. 349–356. [Google Scholar]
- [23].Yang J, Wright J, Huang T, Ma Y. Image super-resolution via sparse representation. IEEE Transactions on Image Processing. 2010;19(11):2861–2873. doi: 10.1109/TIP.2010.2050625. [DOI] [PubMed] [Google Scholar]
- [24].Baker S, Kanade T. Limits on super-resolution and how to break them. IEEE Transactions on Pattern Analysis and Machine Intelligence. 2002:1167–1183. [Google Scholar]
- [25].Chan T, Zhang J, Pu J, Huang H. Neighbor embedding based super-resolution algorithm through edge detection and feature selection. Pattern Recognition Letters. 2009;30(5):494–502. [Google Scholar]
- [26].Freeman W, Jones T, Pasztor E. Example-based super-resolution. Computer Graphics and Applications, IEEE. 2002;22(2):56–65. [Google Scholar]
- [27].Freeman W, Pasztor E, Carmichael O. Learning low-level vision. International Journal of Computer Vision. 2000;40(1):25–47. [Google Scholar]
- [28].Liu C, Shum H, Freeman W. Face hallucination: theory and practice. International Journal of Computer Vision. 2007;75(1):115–134. [Google Scholar]
- [29].Rousseau F. Brain hallucination. Computer Vision-ECCV 2008. 2008:497–508. [Google Scholar]
- [30].Sun J, ning Zheng N, Tao H, yeung Shum H. Image hallucination with primal sketch priors. IEEE Conference on Computer Vision and Pattern Recognition. 2003:729–736. [Google Scholar]
- [31].Gholipour A, Estroff J, Warfield S. Robust super-resolution volume reconstruction from slice acquisitions: application to fetal brain MRI. IEEE Transactions on Medical Imaging. 2010;29(10):1739–1758. doi: 10.1109/TMI.2010.2051680. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [32].Elad M, Hel-Or Y. A fast super-resolution reconstruction algorithm for pure translational motion and common space-invariant blur. IEEE Transactions on Image Processing. 2001;10(8):1187–1193. doi: 10.1109/83.935034. [DOI] [PubMed] [Google Scholar]
- [33].Woods N, Galatsanos N, Katsaggelos A. Stochastic methods for joint registration, restoration, and interpolation of multiple undersampled images. IEEE Transactions on Image Processing. 2006;15(1):201–213. doi: 10.1109/tip.2005.860355. [DOI] [PubMed] [Google Scholar]
- [34].Plenge E, Poot D, Bernsen M, Kotek G, Houston G, Wielopolski P, van der Weerd L, Niessen W, Meijering E. Super-resolution methods in MRI: Can they improve the trade-off between resolution, signal-to-noise ratio, and acquisition time? Magnetic Resonance in Medicine. 2012 doi: 10.1002/mrm.24187. [DOI] [PubMed] [Google Scholar]
- [35].Gholipour A, Estroff J, Sahin M, Prabhu S, Warfield S. Maximum a posteriori estimation of isotropic high-resolution volumetric MRI from orthogonal thick-slice scans. Medical Image Computing and Computer-Assisted Intervention–MICCAI 2010. 2010:109–116. doi: 10.1007/978-3-642-15745-5_14. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [36].Poot D, Van Meir V, Sijbers J. General and efficient super-resolution method for multi-slice MRI. Medical Image Computing and Computer-Assisted Intervention–MICCAI 2010. 2010:615–622. doi: 10.1007/978-3-642-15705-9_75. [DOI] [PubMed] [Google Scholar]
- [37].Shilling R, Robbie T, Bailloeul T, Mewes K, Mersereau R, Brummer M. A super-resolution framework for 3-d high-resolution and high-contrast imaging using 2-d multislice MRI. Medical Imaging, IEEE Transactions on. 2009;28(5):633–644. doi: 10.1109/TMI.2008.2007348. [DOI] [PubMed] [Google Scholar]
- [38].Scherrer B, Gholipour A, Warfield S. Super-resolution in diffusion-weighted imaging. Medical Image Computing and Computer-Assisted Intervention–MICCAI 2011. 2011:124–132. doi: 10.1007/978-3-642-23629-7_16. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [39].Peled S, Yeshurun Y. Superresolution in MRI: application to human white matter fiber tract visualization by diffusion tensor imaging. Magnetic resonance in medicine. 2001;45(1):29–35. doi: 10.1002/1522-2594(200101)45:1<29::aid-mrm1005>3.0.co;2-z. [DOI] [PubMed] [Google Scholar]
- [40].Greenspan H, Oz G, Kiryati N, Peled S. MRI inter-slice reconstruction using super-resolution. Magnetic Resonance Imaging. 2002;20(5):437–446. doi: 10.1016/s0730-725x(02)00511-8. [DOI] [PubMed] [Google Scholar]
- [41].Bai Y, Han X, Prince J. Super-resolution reconstruction of MR brain images; Proc. of 38th Annual Conference on Information Sciences and Systems (CISS04); 2004. [Google Scholar]
- [42].Rousseau F, Kim K, Studholme C, Koob M, Dietemann J. On super-resolution for fetal brain MRI. Medical Image Computing and Computer-Assisted Intervention–MICCAI 2010. 2010:355–362. doi: 10.1007/978-3-642-15745-5_44. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [43].Jiang S, Xue H, Glover A, Rutherford M, Rueckert D, Hajnal J. MRI of moving subjects using multislice snapshot images with volume reconstruction (svr): application to fetal, neonatal, and adult brain studies. IEEE Transactions on Medical Imaging. 2007;26(7):967–980. doi: 10.1109/TMI.2007.895456. [DOI] [PubMed] [Google Scholar]
- [44].Scherrer B, Gholipour A, Warfield S. Super-resolution reconstruction to increase the spatial resolution of diffusion weighted images from orthogonal anisotropic acquisitions. Medical Image Analysis. 2012 doi: 10.1016/j.media.2012.05.003. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [45].Carmi E, Liu S, Alon N, Fiat A, Fiat D. Resolution enhancement in MRI. Magnetic resonance imaging. 2006;24(2):133–154. doi: 10.1016/j.mri.2005.09.011. [DOI] [PubMed] [Google Scholar]
- [46].Viola P, Wells WM. Alignment by maximization of mutual information. International Journal of Computer Vision. 1997;24(2):137–154. [Google Scholar]
- [47].Hermosillo G, Chefd’Hotel C, Faugeras O. Variational methods for multimodal image matching. International Journal of Computer Vision. 2002;50(3):329–343. [Google Scholar]
- [48].Vercauteren T, Pennec X, Perchant A, Ayache N. Diffeomorphic demons: Efficient non-parametric image registration. NeuroImage. 2009;45(1):S61–S72. doi: 10.1016/j.neuroimage.2008.10.040. [DOI] [PubMed] [Google Scholar]
- [49].Nguyen N, Milanfar P, Golub G. A computationally efficient superresolution image reconstruction algorithm. IEEE Transactions on Image Processing. 2001;10(4):573–583. doi: 10.1109/83.913592. [DOI] [PubMed] [Google Scholar]
- [50].Hardie R, Barnard K, Armstrong E. Joint MAP registration and high-resolution image estimation using a sequence of undersampled images. IEEE Transactions on Image Processing. 1997;6(12):1621–1633. doi: 10.1109/83.650116. [DOI] [PubMed] [Google Scholar]
- [51].Ng M, Shen H, Lam E, Zhang L. A total variation regularization based super-resolution reconstruction algorithm for digital video. EURASIP Journal on Advances in Signal Processing. 2007;2007(74585) [Google Scholar]
- [52].Chan T, Ng M, Yau A, Yip A. Superresolution image reconstruction using fast inpainting algorithms. Applied and Computational Harmonic Analysis. 2007;23(1):3–24. [Google Scholar]
- [53].Chantas G, Galatsanos N, Woods N. Super-resolution based on fast registration and maximum a posteriori reconstruction. IEEE Transactions on Image Processing. 2007;16(7):1821–1830. doi: 10.1109/tip.2007.896664. [DOI] [PubMed] [Google Scholar]
- [54].Villain N, Goussard Y, Idier J, Allain M. Three-dimensional edge-preserving image enhancement for computed tomography. IEEE Transactions on Medical Imaging. 2003;22(10):1275–1287. doi: 10.1109/TMI.2003.817767. [DOI] [PubMed] [Google Scholar]
- [55].Charbonnier P, Blanc-Féraud L, Aubert G, Barlaud M. Deterministic edge-preserving regularization in computed imaging. IEEE Transactions on Image Processing. 1997;6(2):298–311. doi: 10.1109/83.551699. [DOI] [PubMed] [Google Scholar]
- [56].Ibanez L, Schroeder W, Ng L, Cates J. The ITK Software Guide: The Insight Segmentation and Registration Toolkit. Kitware; 2003. [Google Scholar]
- [57].Bochkanov S, Bystritsky V. ALGLIB ( www.alglib.net) 2008 www.alglib.net [Google Scholar]
- [58].Tikhonov A. Regularization of incorrectly posed problems. Soviet Math. Dokl. 1963;4(6):1624–1627. [Google Scholar]
- [59].Unser M. Splines: A perfect fit for signal and image processing. Signal Processing Magazine, IEEE. 1999;16(6):22–38. [Google Scholar]
- [60].Vandewalle P, Sbaiz L, Vandewalle J, Vetterli M. Super-resolution from unregistered and totally aliased signals using subspace methods. Signal Processing, IEEE Transactions on. 2007;55(7):3687–3703. [Google Scholar]
- [61].Charbonnier P, Blanc-Feraud L, Aubert G, Barlaud M. Two deterministic half-quadratic regularization algorithms for computed imaging; IEEE International Conference on Image Processing; 1994; pp. 168–172. IEEE. [Google Scholar]
- [62].Geman S, McClure DE. Bayesian image analysis: an application to single photon emission tomography. Statistical Computind Section Proceedings of American Statistical Association. 1985;21(2):12–18. [Google Scholar]
- [63].Green P. Bayesian reconstructions from emission tomography data using a modified EM algorithm. IEEE Transactions on Medical Imaging. 1990;9(1):84–93. doi: 10.1109/42.52985. [DOI] [PubMed] [Google Scholar]
- [64].Hebert T, Leahy R. A generalized EM algorithm for 3-d bayesian reconstruction from poisson data using gibbs priors. IEEE Transactions on Medical Imaging. 1989;8(2):194–202. doi: 10.1109/42.24868. [DOI] [PubMed] [Google Scholar]
- [65].Brette S, Idier J. Optimized single site update algorithms for image deblurring; International Conference on Image Processing; 1996. pp. 65–68. IEEE. [Google Scholar]