ATHENA: A TOOL FOR META-DIMENSIONAL ANALYSIS APPLIED TO GENOTYPES AND GENE EXPRESSION DATA TO PREDICT HDL CHOLESTEROL LEVELS

Abstract

Technology is driving the field of human genetics research with advances in techniques to generate high-throughput data that interrogate various levels of biological regulation. With this massive amount of data comes the important task of using powerful bioinformatics techniques to sift through the noise to find true signals that predict various human traits. A popular analytical method thus far has been the genome-wide association study (GWAS), which assesses the association of single nucleotide polymorphisms (SNPs) with the trait of interest. Unfortunately, GWAS has not been able to explain a substantial proportion of the estimated heritability for most complex traits. Due to the inherently complex nature of biology, this phenomenon could be a factor of the simplistic study design. A more powerful analysis may be a systems biology approach that integrates different types of data, or a meta-dimensional analysis. For this study we used the Analysis Tool for Heritable and Environmental Network Associations (ATHENA) to integrate high-throughput SNPs and gene expression variables (EVs) to predict high-density lipoprotein cholesterol (HDL-C) levels. We generated multivariable models that consisted of SNPs only, EVs only, and SNPs + EVs with testing r-squared values of 0.16, 0.11, and 0.18, respectively. Additionally, using just the SNPs and EVs from the best models, we generated a model with a testing r-squared of 0.32. A linear regression model with the same variables resulted in an adjusted r-squared of 0.23. With this systems biology approach, we were able to integrate different types of high-throughput data to generate meta-dimensional models that are predictive for the HDL-C in our data set. Additionally, our modeling method was able to capture more of the HDL-C variation than a linear regression model that included the same variables.

1. Introduction

1.1. A Case for Meta-dimensional Analysis

Over the past decade, high-throughput technology has become considerably more efficient and less expensive¹. The human genetics field has reaped the benefits of these advancements via extensive exploratory analyses largely in the form of GWAS. These studies have led to the discovery of thousands of SNPs that are significantly associated with hundreds of common, complex human traits². However, for many of these traits, a large proportion of the estimated heritability remains unexplained by these DNA variants³.

One of the leading hypotheses regarding this “missing heritability” is that GWAS may not be robust to the inherent complexity of biological processes, and, therefore, may be missing large chunks of the underlying etiology⁴. Two areas where this complexity might lie are in non-additive interactions (gene-gene or gene-environment) and within the different levels of biological regulation. First, because traditional GWAS specifically identify SNPs with large main effects, interactions without large main effects would be missed. Next, complex phenotypes could be under the influence of more than one level of biological regulation. Various types of –omic data (i.e. transcriptomic and methylomic) analyzed simultaneously could take into account trait variation that would be missed by SNP data alone⁵. In order to account for complex etiology, a more powerful meta-dimensional analysis would have to be performed. A meta-dimensional analysis is one that integrates different types of high-throughput data while allowing for non-linear interactions in order to identify multi-variable prediction models that include data from from different levels of biological regulation⁶. For example, analyzing microarray gene expression data and SNP genotypes data simultaneously to identify models that predict a complex human disease, such as breast cancer.

In order to successfully perform a meta-dimensional analysis, computational tools need to be able to perform the following tasks successfully: sift through the high level of noise inherent to high-throughput data in order to identify true signals, simultaneously analyze continuous and categorical predictor and outcome variables, and identify main and interaction effects in order to generate a final predictive model. Currently, no single analysis method performs all of these tasks at once. Some candidates that may come together to create a successful analysis pipeline include tree-based methods (i.e. Random Forests⁷), Bayesian networks, computational evolution methods, and various types of clustering and correlation techniques. For this paper, we propose a meta-dimensional analysis tool called ATHENA that combines a tree-based filtering method with a computational evolution modeling method in order to integrate SNP genotypes and gene expression variables to predict HDL-C levels.

1.2. The Genetics of HDL Cholesterol

HDL particles are small, dense lipoproteins that circulate throughout the body. Many anti-atherogenic properties have been ascribed to HDL, and low HDL-C levels are strongly and independently associated with increased risk for cardiovascular disease⁸. HDL-C has a relatively large genetic component with heritability estimates between 40–80%^8,9. Many common variants have been found to be significantly associated with HDL-C in humans, but collectively they only explain a small proportion of the estimated heritability. A recent study used significant GWAS SNPs to perform polygenic scoring and found that the best model only explained ~4.75% of the variation in the HDL-C trait¹⁰. Some groups have begun to examine a more complex genetic architecture to explain the missing heritability and several gene-gene interactions have been identified^11–13. In this study, we aim to go a step further by integrating SNPs and gene expression data to find complex models that predict HDL-C levels.

2. Methods

2.1. The Analysis Tool for Heritable and Environmental Network Associations (ATHENA)

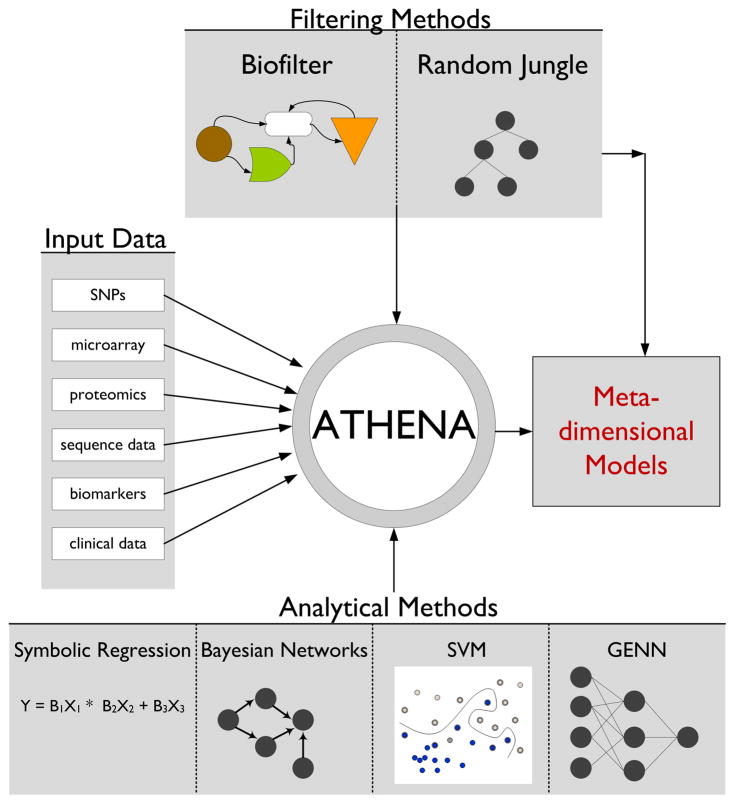
ATHENA is a multi-functional software package designed by our lab to analyze various types of high-throughput data in order to generate multi-variable models. ATHENA has been tested extensively on simulated data and applied to biological data sets in order to demonstrate its utility on “noisy” data^14–17. Figure 1 shows the full current and future functionality of ATHENA.

Fig 1.

Components of the ATHENA software package

The main components of ATHENA are a filtering step and a modeling step. The filtering step can be a statistical filter (Random Jungle¹⁸) or one that prioritizes variables based on their known biological functions (Biofilter¹⁹). Currently, ATHENA has two different computational evolution modeling techniques--Grammatical Evolution Symbolic Regression (GESR) and Grammatical Evolution Neural Networks (GENN). For this analysis, we used Random Jungle (RJ) as the statistical filter and Grammatical Evolution Neural Networks (GENN) as the modeling technique.

2.1.1. ATHENA filtering: Random Jungle

RJ is a faster, parallelized version of the tree-based variable selection method Random Forests (RF). Briefly, RF uses a bootstrap sample of the data to grow a “forest” of decision or regression trees with no pruning. The trees are then tested using the out-of-bag individuals not present in the bootstrap sample to determine which variables are most important for outcome prediction. Importantly, RF can identify main and interaction effects⁷. We chose RJ as the statistical filter because of its capability to analyze millions of quantitative and categorical variables in a relatively computationally efficient manner. Also, the output is a list of variables ranked by an importance score. For this analysis, importance is defined as the percent increase in mean squared error after permuting the variable values while taking into account correlation patterns between the variables²⁰. This output lends itself nicely to selecting a subset of variables for input into a modeling technique that is less robust to noise.

2.1.2. ATHENA modeling: Grammatical Evolution Neural Networks

GENN uses a variation of genetic programming (GP) called grammatical evolution (GE) to optimize artificial neural networks to identify a model that predicts a given outcome^21–23. GP is a computational technique that uses concepts of survival of the fittest in order to evolve a fit solution from an original population of random solutions²⁴. GE is a more efficient version of GP because the solutions are represented as binary strings, which can be translated into a functional solution, or computer program, via grammar rules²⁵. All of the evolutionary operations that are applied to the solutions are done so at the level of the binary string. Below is the algorithm that GENN uses to identify the “fittest” solution:

1. Divide the data into five equal parts for cross-validation (4/5 = training set; 1/5 = testing set).

2. Generate random sub-populations, or demes, of binary strings across multiple processors.

3. Calculate the fitness (i.e. balanced accuracy or mean squared error) of the solutions using the training set.

4. Select the solutions with the highest fitness, which undergo crossover, mutation, migration between demes, and reproduction to create the next generation of solutions.

5. Repeat Steps 3–4 for a user-defined number of generations.

6. Test the final best model using the testing set and save the model.

7. Repeat steps 2–6 for each the other four cross-validation data divisions.

8. Select the overall best model out of the five models using cross-validation consistency first and then testing set fitness to break ties.

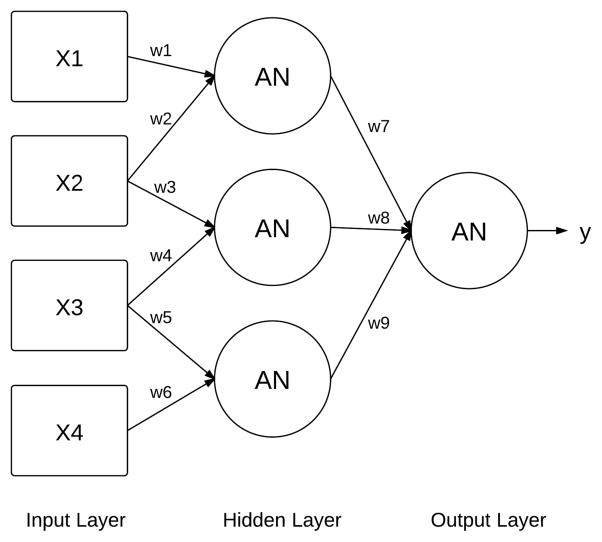
The solutions in GENN are artificial neural networks (ANNs). Briefly, ANNs are directed graphs with an input layer (independent variables), hidden layer(s) (processing elements), and an output layer that predicts the outcome of interest²⁶. Figure 2 illustrates an example of a two-layer ANN. ANNs are a good candidate for this type of analysis because they are able to model complex, non-linear relationships between variables. Traditionally, ANNs are optimized using a hill-climbing algorithm, such as back-propagation, which iteratively alters the weights (or constants) until prediction no longer improves²³. This optimization technique is not ideal for a genetic analysis where the correct variables and the network architecture are not known a priori. GENN addresses this issue by evolving the ANNs so that the data drives the optimization of all aspects of the network. GENN has been tested on simulated and biological data and was often found to outperform other prediction techniques^16,22,27.

Fig 2.

An example of a two-layer ANN. X=input variable; w=weight; AN=activation node; y=predicted output

2.1.3. ATHENA filtering-modeling pipeline

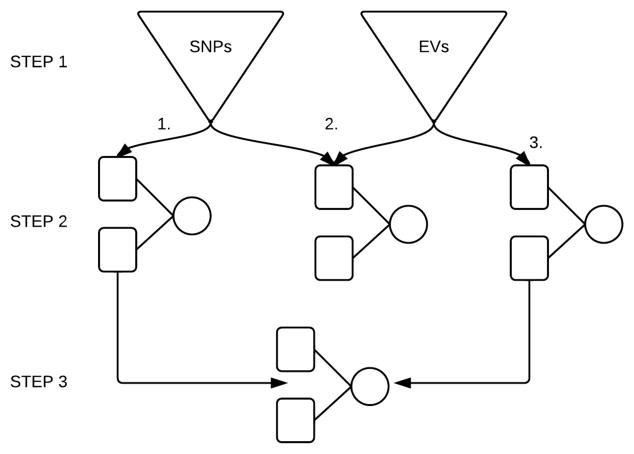
Figure 3 below summarizes the filtering-modeling pipeline that was used for this analysis.

Fig 3.

ATHENA filtering-modeling pipeline for this analysis. Step 1. RJ filtering of SNPs and EVs; Step 2. GENN analysis of filtered SNPs only (2.1), EVs only (2.3), and SNPs and EVs together (2.2); Step 3. GENN analysis of SNPs and EVs from the best GENN model from Steps 2.1 and 2.3.

In Step 1, we filtered the ~2.7 million SNPs and ~24,000 EVs separately in RJ. This was done because RJ has not been sufficiently tested to determine the effect of the overwhelmingly larger number of SNPs versus EVs that were present in this data set (~112x more SNPs). After filtering, we analyzed the filtered SNPs (Step 2.1), the filtered EVs (Step 2.3), and the filtered SNPs and EVs together (Step 2.2) in GENN. Because GENN has been shown to outperform other methods specifically at prediction modeling when the noise in the data is substantially reduced, we also assessed just the SNPs and EVs that were in the best ANN models from Steps 2.1 and 2.3 in a final GENN analysis (Step 3).

2.2. Cholesterol and Pharmacogenetics Dataset

The data for this study comes from the simvastatin clinical trial Cholesterol and Pharmacogenetics (CAP)²⁸. The characteristics of the 480 individuals in this analysis are shown in Table 1. The genomic data consists of ~2.7 million SNP genotype dosages and ~24,000 gene expression levels. SNPs were genotyped on Illumina HumanHap 300K BeadChip and Illumina HumanHap 610-Quad BeadChip and imputed to HapMap data using the IMPUTE2 software²⁹. Imputation probabilities were used to calculate genotype dosages. Gene expression levels were measured in patient-derived immortalized lymphoblastoid cell lines (LCLs) using the Illumina HumanRef8v3 BeadArray. The gene expression data was corrected for potential confounders by extracting the residuals from a linear regression model that included known covariates (day of assay, cell count, gender, and age) and the top nine principal components for unknown covariates. Our outcome of interest was the mean HDL-C level from the first and follow-up visit before any medication was administered. HDL-C was adjusted for gender, age, body mass index (BMI), and smoking status. All of the individuals in this subset of the cohort were European-American.

Table 1.

Data set characteristics

Clinical trait	Value
Age in years (mean [sd])	54.4 [12.7]
BMI (mean [sd])	27.6 [5.3]
HDL-C in mg/dl (mean [sd])	53.4 [16.3]
Smoker (% smoker)	13.2
Gender (% male)	54.1

3. Results

3.1. Random Jungle

Table 2 below lists the important parameter setting values that were used for RJ for each analysis. Table 2 also displays the computation times and the number of variables that remained after backward elimination. The values for bootstrap sample size and number of trees were previously tuned for each data set as suggested by the method developers¹⁸.

Table 2.

RJ filtering parameter settings

Parameter	EV analysis	SNP analysis
Bootstrap Sample Size	11250	684342
Number of Trees	4000	4032
Tree Type	Regression trees	Regression trees
Importance Score	Permutation-based	Permutation-based
Backward Elimination	Discard negative scores	Discard negative scores
Number of Processors	4 (500 trees/processor)	64 (63 trees/processor)
Compute Time (hours)	0.6	52
Remaining Variables	1447	209346

In order to have a comparable threshold for both data sets, we chose an importance score cut-off because it has the same statistical meaning for both the SNPs and EVs. The threshold of 10 was chosen because it generated similar distributions of scores in both data sets. This cut-off resulted in a filtered data set that consisted of 418 SNPs and 241 EVs.

3.2. GENN

The filtered EV and SNP variables were analyzed both separately and simultaneously by GENN. In addition, the SNPs and EVs from the best GENN models were analyzed together. Table 3 shows the GENN parameters that were used for these analyses. These parameters were selected based on a tuning analysis where we swept over various settings and selected based on prediction optimization. A detailed description of the parameters can be found in a previous ATHENA publication¹⁴. The fitness function used by GENN for analysis of quantitative outcomes is shown below:

$$r-\mathit{squared}=1-\left[\frac{{\displaystyle \sum _i}{(y_i-{\widehat{y}}_i)}^2}{{\displaystyle \sum _i}{(y_i-\overline{y})}^2}\right]$$ (1)

where y is the observed value, y-hat is the predicted value, and y-bar is the mean value for the quantitative outcome.

Table 3.

GENN parameter settings

Parameter	Steps 2.1, 2.3	Steps 2.2, 3
Number of demes (processors)	100	100
Population Size/Deme	3000	1000
Number of generations	1125	250
Number of migrations	45	10
Probability of Crossover	0.9	0.9
Probability of Mutation	0.01	0.01
Fitness	r-squared	r-squared
Analysis time (hours)	8	1

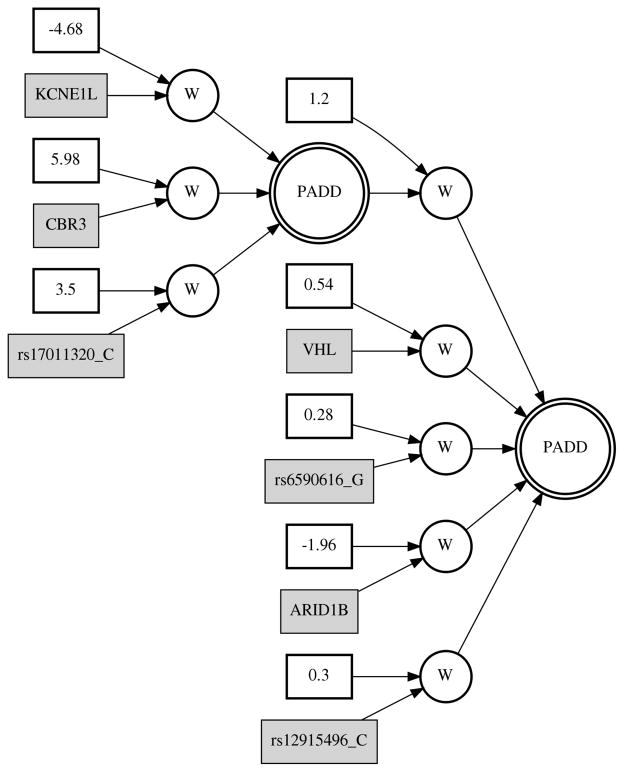
Figure 4 shows the resulting best ANN models from each of the following analyses: a. SNPs only (Step 2.1), b. EVs only (Step 2.3), and c. SNPs and EVs together (Step 2.2). The r-squared values from the testing cross-validation set for each of the models were 0.16, 0.11, and 0.18, respectively.

Fig 4.

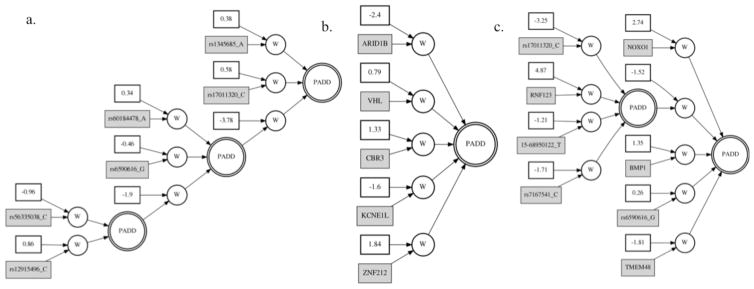
Best GENN models from the a. SNP, b. EV, and c. SNP and EV integrated analyses. The asterisks in the integrated model denote variables that were present in at least one of the top five cross validation models from the separate SNP and EV analyses. (w = constant and variable are multiplied; PADD = additive activation node)

Finally, we ran GENN with only the 6 SNPs and 5 EVs that were present in the top models shown Figure 4a. and 4b. Figure 5 shows the resulting network from this analysis (Step 3). The ANN consisted of 3/6 SNPs and 4/5 EVs from the best models and the testing r-squared value was 0.32. This is substantially greater than the three previous networks (Figure 4). Additionally, we tested the same variables using a more traditional statistical prediction method--multivariable linear regression. The adjusted r-squared value from the regression model that included all 6 SNPs and 5 expression variables was 0.23. The full regression model was highly significant, with a p-value of 2.2×10⁻¹⁶.

Fig 5.

Best model GENN analysis of variables from best SNP and EV models. Testing r-squared value = 0.32.

4. Discussion

In this study, we demonstrate a filtering-modeling pipeline for integrating different types of high-throughput data to generate meta-dimensional prediction models. We were able to build a model that includes variables from different levels of biological regulation and explained more variation than either data-type alone (Figures 4 and 5). Additionally, our best model was more predictive than the commonly used additive modeling technique. Due to its flexibility, this approach is easily extendible to other types of high-throughput data. For example, another quantitative high-throughput measurement such as proteomic data could be added to this analysis by filtering the data using the same RJ method and then adding in these filtered proteomic levels to the GENN analysis.

Notably, although the ANN from the integrated analysis had a higher r-squared value than the analyses that only included SNPs or EVs (Figure 4), it was still less predictive than the analysis that only included just the top SNPs and EVs (Figure 5). This could be a result of the combined increase in pressure on variable selection due to the larger number of predictor variables and on modeling due to the different scales of the EV and SNP values. When we reduced the variable selection pressure by only including the top variables from the EV-only and SNP-only best models, the r-squared value went up substantially. This highlights the ability of GENN to model the variables in an informative way when presented with a limited number of noise variables. Additionally, the GENN model was able to account for more outcome variation than the linear regression model indicating that the more complex modeling method of GENN identifies relationships between the variables that an additive model does not.

One caveat to our approach is that we are not able to explore conditional relationships between the different types of predictor variables. An example would be a model where a SNP in a transcription factor binding site reduces the expression of the targeted gene, which, in turn, affects the phenotype. These types of relationships could be tested by first examining significant correlations between SNPs and EVs and then using this information to guide the modeling analysis. Also, some groups are applying Bayesian networks (BNs) to data integration studies because they are able to capture this type of directionality³⁰. Future work will involve incorporating BNs into ATHENA as one of the analysis methods. Other study designs specifically address the hypothesis that SNPs are affecting the phenotype via their association with gene expression levels, such as eQTLs^31–34. These studies have provided some interesting findings but would not identify SNPs and EVs that have an effect on the phenotype independently of one another.

Interpreting the biological significance of statistical models is not a trivial task for several reasons. First, due the correlation patterns that exist in SNPs and EV data, the variables in the best models could be functional variables or variables that are highly correlated with the functional variables. There is no simple way to determine which is the case. One initial approach could be to map the top ranked SNPs and EVs back to genes to determine if the variables in the best models are representative of any given biological pathway or have similar biological function. We assessed this possibility by analyzing the RJ filtered SNPs and EVs with an online annotation tool called DAVID^35,36. The most significant biological groups after accounting for redundant pathway information in the databases were those related to immune function. This is interesting because HDL has been shown to play a role in innate and adaptive immune responses³⁷.

Notably, we did not identify any of the genes known to be highly associated with HDL-C. The gene that is arguably most strongly associated with HDL-C is CETP^38,39. To determine if our method was not able to find the effects or if the effects were simply not there, we performed a univariate linear regression analysis on each of the SNPs and then ranked the p-values. None of the SNPs in CETP were significantly associated with HDL-C in our data set (data not shown). This suggests that in this subset of individuals, other genes could be more strongly contributing to the variation in HDL-C.

Once a meta-dimensional model has been identified and shown to be predictive, the next step is to replicate the finding in an independent data set. For single SNPs, this process is relatively straightforward. For meta-dimensional models, however, it becomes less trivial due to the increased difficulty of replicating the exact effects of numerous data points simultaneously, especially if the identified variables are not completely correlated with the functional variants. One part of model validation will be to determine if the model is predictive in another data set. Additionally, the functionality of these genes could be tested in vitro or in vivo to determine if perturbation has any phenotypic effect.

The ultimate goal of identifying models that explain the genetic variability of a trait is to use this information to improve therapy or prediction and prevention in a clinical setting. Methods robust to the true nature of complex traits, like the meta-dimensional analysis pipeline presented here, are an initial step towards a more thorough understanding of the genetic architecture of complex human traits like cardiovascular disease.