Properties of cell death models calibrated and compared using Bayesian approaches

Abstract

Using models to simulate and analyze biological networks requires principled approaches to parameter estimation and model discrimination. We use Bayesian and Monte Carlo methods to recover the full probability distributions of free parameters (initial protein concentrations and rate constants) for mass-action models of receptor-mediated cell death. The width of the individual parameter distributions is largely determined by non-identifiability but covariation among parameters, even those that are poorly determined, encodes essential information. Knowledge of joint parameter distributions makes it possible to compute the uncertainty of model-based predictions whereas ignoring it (e.g., by treating parameters as a simple list of values and variances) yields nonsensical predictions. Computing the Bayes factor from joint distributions yields the odds ratio (∼20-fold) for competing ‘direct’ and ‘indirect’ apoptosis models having different numbers of parameters. Our results illustrate how Bayesian approaches to model calibration and discrimination combined with single-cell data represent a generally useful and rigorous approach to discriminate between competing hypotheses in the face of parametric and topological uncertainty.

Introduction

Mathematical models that capture the dynamics of protein modification, assembly and translocation are effective tools for studying biochemical networks involving many concurrent reactions (Kholodenko et al, 1999; Schoeberl et al, 2002; Danos et al, 2007; Gaudet et al, 2012). However, even the best-characterized networks are ambiguous with respect to patterns of protein–protein interaction and the sequence of specific reactions (the so-called ‘reaction topology’). In principle, such ambiguities can be resolved by constructing alternative models and then determining which ones exhibit the best fit to data. Such comparisons are usually performed using a set of parameters thought to fall near the global optimum for the original model (based on goodness-of-fit to data). However, given the kinds of data that can be collected from cells, parameters in realistic biochemical models are often non-identifiable, and refitting alternative models often uncovers a new set of parameters having an indistinguishably good fit. In this case, it is not clear whether the two models are equally valid. Uncertainty about parameters arises from non-identifiablility, whose ultimate origins are a dearth of quantitative data on the rates of biochemical reactions. Sethna and colleagues have pointed out that even a complete set of time-course data on the concentrations and states of all species in a biochemical model are usually insufficient to constrain the majority of rate constants, a property known as ‘sloppiness’ (Brown and Sethna, 2003; Brown et al, 2004; Frederiksen et al, 2004; Gutenkunst et al, 2007). In addition, models having different reaction topologies often differ in the numbers of free parameters. Thus, a scheme for rigorously comparing competing biochemical models must account for parametric uncertainty and potential differences in parameter numbers.

This paper describes a general-purpose framework for parameter estimation and model discrimination based on well-established Bayesian methods (Battogtokh et al, 2002; Press, 2002; Flaherty et al, 2008; Klinke, 2009; Xu et al, 2010) and applies it to a previously described ODE-based model of receptor-mediated (extrinsic) apoptosis in human cells treated with the death ligand TRAIL (the extrinsic apoptosis reaction model, EARM1.3) (Fussenegger et al, 2000; Chen et al, 2007a; Albeck et al, 2008b; Spencer et al, 2009; Ho and Harrington, 2010; Neumann et al, 2010). EARM1.3 is useful in understanding apoptosis in multiple cell types and is similar to many other models of signal transduction with respect to the numbers of parameters and amount of training data (Nelson et al, 2002; Schuster et al, 2002; Kearns and Hoffmann, 2009).

Modeling the biochemistry of apoptosis using ODEs has several justifications. The proteins involved are sufficiently abundant and their modes of interaction well enough known that ODE networks effectively describe dynamics under a range of conditions, including protein overexpression or RNAi-mediated depletion (Fussenegger et al, 2000; Hua et al, 2005; Aldridge et al, 2006, 2011; Bagci et al, 2006; Rehm et al, 2006; Chen et al, 2007a; Albeck et al, 2008b; Lavrik et al, 2009; Spencer et al, 2009; Spencer and Sorger, 2011). Mass-action models also make it straightforward to translate findings obtained with purified components to the context of multi-protein networks in living cells (Lovell et al, 2008; Chipuk et al, 2010).

Free parameters in mass-action ODE models such as EARM1.3 include initial protein concentrations, which can be determined with reasonable precision using quantitative western blotting or mass spectrometry (set in the current work to previously estimated values (Albeck et al, 2008b)) as well as forward, reverse and catalytic rate constants. Some information on kinetic parameters can be gleaned from in vitro experiments or the literature, but rate constants are usually much less certain than protein concentrations either because no in vitro data are available or because the peptidyl substrates used in vitro are poor mimics of the large protein complexes found in vivo. It is therefore necessary to estimate parameters (Mendes and Kell, 1998) by minimizing the difference between model trajectories and experimental data using methods such as genetic algorithms (Srinivas and Patnaik, 1994), Bayesian sampling (Battogtokh et al, 2002; Flaherty et al, 2008; Klinke, 2009; Xu et al, 2010) or Kalman filtering (Lillacci and Khammash, 2010).

The problem of parameter identifiability has been tackled in four conceptually distinct ways (leaving aside algorithmic specifics). The first is to consider only simple processes or small reaction networks for which identifiable models can be constructed (Bandara et al, 2009; Kleiman et al, 2011). Alternatively, for non-identifiable models, a single set of best-fit parameter values can be used. This is the approach we and others have applied in the past to model extrinsic apoptosis (White et al, 2002; Rodriguez-Fernandez et al, 2006; Singer et al, 2006; Albeck et al, 2008b). A third approach is to identify a family of ∼10²–10³ fits whose discrepancy from a best fit is less than or equal to estimated experimental error. Properties of the model that are invariant across sets of parameters are assumed to be of the greatest interest (Ingolia, 2004; Daniels et al, 2008; Chen et al, 2009). A fourth and more rigorous approach involves sampling the complete probability distribution of parameters, accounting for both experimental error and model non-identifiability, and then using the distribution in model-based prediction or model discrimination (Duran and White, 1995; Reis and Stedinger, 2005).

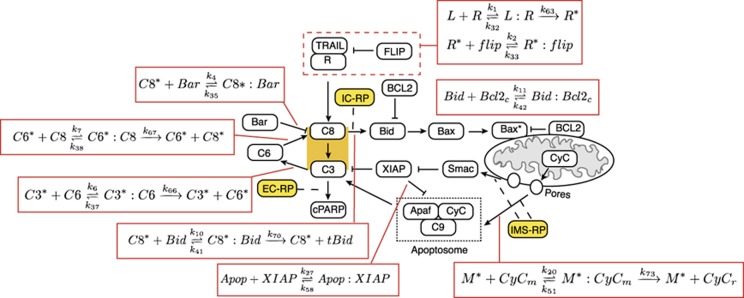
In this paper, we implement the fourth approach using EARM1.3 as an example. Cell death is triggered in EARM1.3 by binding of death ligands, such as FasL and TRAIL, to transmembrane receptors (Figure 1). This leads to activation of initiator pro-caspases-8/10 (C8) causing cleavage and activation of effector pro-caspases-3/7 (C3), which in turn leads to proteolysis of essential cellular substrates and activation of CAD nucleases, ultimately killing cells (Kaufmann and Earnshaw, 2000; Gonzalvez and Ashkenazi, 2010). Active C8 also cleaves the Bcl2-family member Bid to form tBid, which promotes pore formation and mitochondrial outer membrane permeabilization (MOMP). Sudden translocation of Smac and cytochrome c through MOMP pores into the cytosol is followed by inactivation of XIAP (the X-linked inhibitor of apoptosis protein), thereby relieving negative regulation of C3 activity and releasing active effector caspase. EARM1.3 is simplified insofar as proteins having similar activities are combined into single species as a means to reduce the number of free parameters (e.g., both caspase-3 and caspase-7 are represented in EARM1.3 by C3).

Figure 1.

Schematic representation of the extrinsic apoptosis model EARM1.3. Binding of death ligand TRAIL, formation of death-inducing signaling complex (DISC), cleavage of caspases-3, -6 and -8 (C3, C6 and C8), formation of mitochondrial pores, assembly of the apoptosome and cPARP cleavage are shown. Activating interactions such as caspase cleavage and induction of conformational changes are shown as sharp-tipped arrows; inhibitory interactions by competitive binding of proteins such as FLIP, BCL2 and XIAP are shown as flat-tipped arrows. The three fluorescent reporters IC-RP, EC-RP and IMS-RP used in experiment are denoted as yellow lozenges. Specific sets of reactions are called out in red boxes and are keyed to features discussed in subsequent figures.

With the addition of appropriate sampling procedures, EARM1.3 is also effective at modeling cell-to-cell variability in apoptosis (Rehm et al, 2009; Spencer et al, 2009). When a uniform population of cells is exposed to TRAIL, substantial differences in the time of death are observed from one cell to the next: some cells die soon after ligand exposure (<1 h), others wait 12 h or more and some cells survive indefinitely (Rehm et al, 2003). Variability arises from transiently heritable differences in protein concentrations (extrinsic noise) rather than inherently stochastic reaction kinetics (intrinsic noise), and can be modeled with ODE networks by sampling initial protein concentrations from experimentally measured log-normal distributions and running many simulations (Gaudet et al, 2012). However, understanding the origins rather than the consequences of extrinsic noise still requires stochastic simulation (Gillespie, 1977; Zheng and Ross, 1991; Hilfinger and Paulsson, 2011).

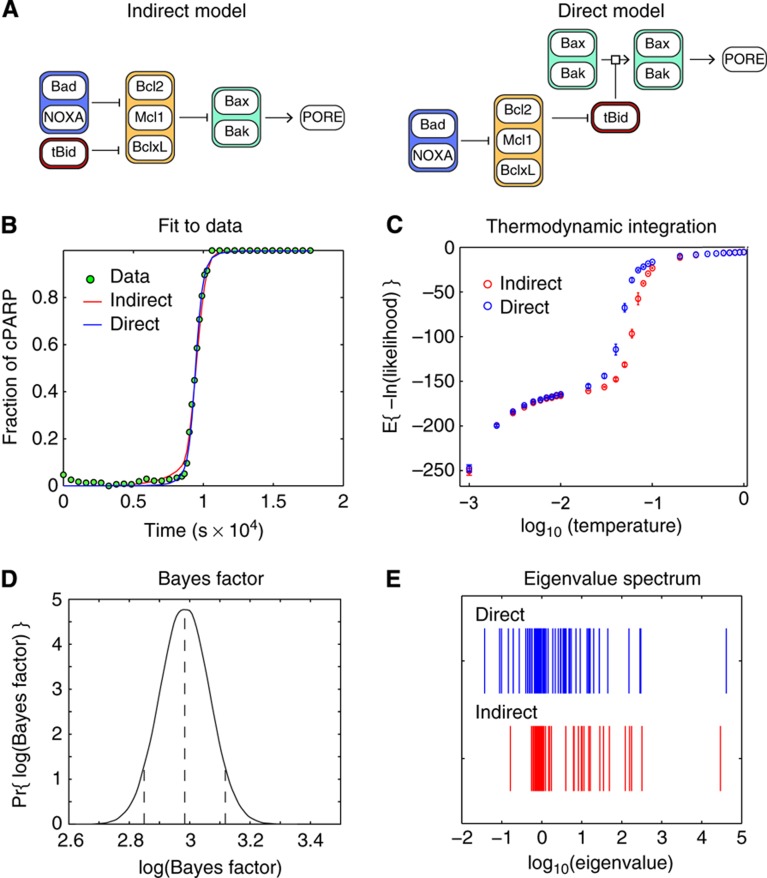
One area in which the existing EARM1.3 model is particularly simplistic is in its treatment of MOMP regulators. The Bcl2 proteins that regulate MOMP can be divided into three families: (1) pro-apoptotic BH3-only proteins, such as Noxa, tBid and Bad, which promote pore formation, (2) effectors proteins, such as Bax and Bak, which form transmembrane pores and (3) anti-apoptotic proteins, such as Bcl2, Mcl1 and BclXL, which inhibit pore formation. Conflicting hypotheses exist in the literature about whether MOMP is controlled in a ‘direct’ or ‘indirect’ manner (Lovell et al, 2008; Chipuk et al, 2010). The direct model postulates that BH3-only ‘activators,’ such as tBid and Bim, bind to Bax and Bak and induce pore-promoting conformational changes (a second class of BH3-only ‘sensitizers,’ such as Bad, are postulated to function by binding to and neutralizing anti-apoptotic proteins such as Bcl2). The indirect activation model postulates that Bax and Bak have an intrinsic ability to form pores but are prevented from doing so by association with anti-apoptotic proteins; the sole role of BH3-only proteins in this model is to antagonize anti-apoptotic proteins, thereby freeing up Bax and Bak to assemble into pores. Considerable subtlety exists with respect to the specifics of indirect and direct mechanisms, implying that it will ultimately be necessary to compare multiple versions of each model.

Bayesian estimation is well established in fields ranging from climate control to economics (Briggs, 2001; Christie et al, 2005), and its use with biochemical pathways has been pioneered by Klinke (2009), Schuttler (Battogtokh et al, 2002), Kolch (Xu et al, 2010), Vyshemirsky (Press, 1995) and others. We extend earlier work by applying Bayesian methods to the complex EARM1.3 model calibrated to time-course data from single cells. We recover statistically complete joint probability distributions for all 78 free kinetic parameters in the model using this method allowing us to explore the shapes and covariance of the distributions. We show how probabilistic model-based predictions can be computed from parameter distributions to account for experimental error and parameter non-identifiablility. Estimated parameters exhibit a remarkably high degree of covariation that appears to encode much of the information derived from calibration. Thus, it is not valid to report parameters as a simple table of values and variances. We also compute the Bayes factors for MOMP models that have different topologies (competing indirect and direct models EARM1.3I and EARM1.3D), thereby estimating their relative likelihood while accounting for different numbers of non-identifiable parameters. The fact that Bayesian methods developed for relatively small models in the physical sciences are effective with large biochemical models opens the door to rigorous reasoning about cellular mechanisms in the face of complexity and uncertainty.

Results

Sampling parameter values using MCMC walks

EARM1.3 has 69 dynamical variables representing the concentrations of proteins and protein complexes involved in cell death. We concentrate on 78 free parameters (rate constants) that control these variables (the total number of free parameters in EARM1.3I and EARM1.3ID is different, as described below). The 16 nonzero initial protein concentrations in the model were assumed to be identical to previously reported values, many of which have been measured experimentally (Spencer et al, 2009) (initial protein concentrations can also be estimated, but adding parameters to the procedure makes the calculation more time consuming; Figure 1). Calibration data on initiator and effector caspase activities were collected from single cells using two proteolysis-sensitive reporter proteins: initiator caspase reporter protein (IC-RP) measures the activity of initiator caspases-8/10 and is a metric for formation of tBid; effector caspase reporter protein (EC-RP) measures the activity of caspases-3/7 and is a metric for cleavage reactions accompanying cell death (Cohen, 1997; Albeck et al, 2008a). The amount of time between the addition of TRAIL and the activation of caspases varies from one cell to the next (Spencer et al, 2009), and EC-RP and IC-RP trajectories were therefore aligned by the time of MOMP to eliminate most cell-to-cell variability (Albeck et al, 2008a). Thus, training data represent the behavior of a ‘typical’ single cell. A time-dependent value for the variance of the data (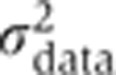) was obtained by comparing 40 single-cell trajectories for each reporter protein.

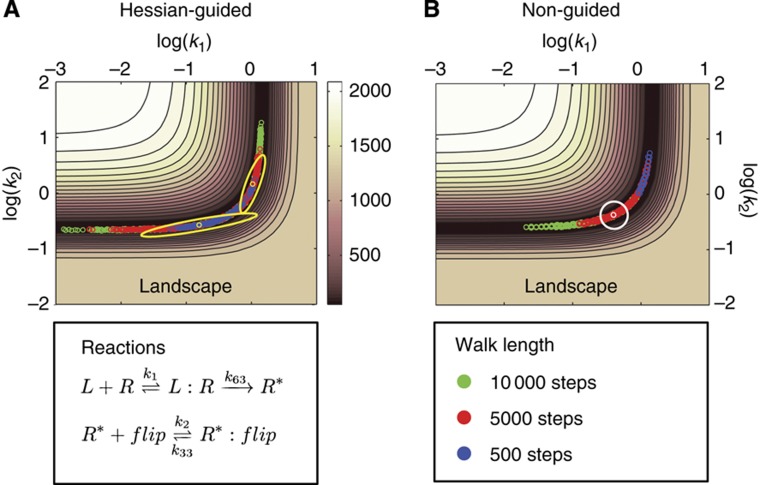
To sample the posterior distribution of the EARM1.3 parameter space, we implemented a multi-start Markov Chain Monte Carlo (MCMC) walk, using non-uniform priors and imposing a Metropolis–Hastings (M–H) criterion at each step (Box 1). Such a walk has the important property that the number of visits to a particular position in parameter space is proportional to the posterior probability, allowing parameter vectors to be sampled with the correct statistical weight (Chib and Greenberg, 1995). In Box 2 we illustrate how parameter distributions can be recovered from an MCMC walk in the auto-catalytic chemical kinetic system of Robertson (1966), a classic example from the CVODES/Sundials suite and by examining two-dimensional slices of the complex landscape of EARM1.3. In both cases, axes for the landscapes correspond to parameters and elevation corresponds to the negative log of the posterior probability (the posterior is simply the likelihood weighted by the prior; Box 1). For example, for parameters k₁ and k₂, which describe the binding of receptor R to ligand (to form active receptor R*) and binding of the anti-apoptotic FLIP protein to R*

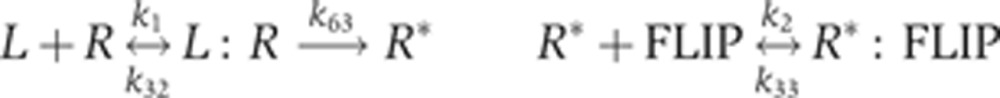we observed an L-shaped valley in the objective function with a nearly flat bottom bounded by steep walls (Figure 2). The MCMC walk samples this landscape by making a random series of movements along the valley floor and then estimating the posterior probability of each position based on a sum of squares error criterion. Estimated marginal distributions for the parameters k₁ and k₂ can be recovered from the walk by integrating out all other dimensions. We observe k₁ and k₂ to be well-constrained relative to many other parameters in the model, probably because the IC-RP reporter lies immediately downstream of reactions controlled by k₁ and k₂ (Figure 1). The two parameters balance each other out in a subtle way: k₁ is the forward rate of the ligand-binding reaction (which promotes cell death) and k₂ is the forward rate of the FLIP-binding reaction (which inhibits cell death). As a consequence, the individual parameter distributions (marginal distributions) do not capture all of the information from the walk: when the value of k₁ is high, activated receptor R* is produced more rapidly and this can be balanced by having k₂ at a high value so that formation of inactive R*:FLIP complexes is rapid. Thus, a good fit to the IC-RP trajectory can be achieved for a range of k₁ and k₂ values as long as their ratio is roughly constant. In general, we observed that ratios of parameters (or sums of the logs of parameters) were better constrained than single parameters. This was particularly obvious in the case of Robertson’s system, in which the k₁ to k₃ ratio is well estimated but individual parameters are not (Box 2). The phenomenon is also related to the fact that in simple catalytic systems, such as those studied by Michaelis–Menten, it is the ratio of k_f and k_r (i.e., K_M) that is well estimated under standard conditions, not forward and reverse rates themselves (Chen et al, 2010). Examining other 2D slices of the posterior landscape revealed a wide range of topographies and different degrees of parameter constraint. True ellipsoidal minima were relatively rare but they gave rise to the expected Gaussian marginal parameter distributions; more common were distributions in which one parameter was constrained and the other was not (in Supplementary Figure 1 we have assembled a gallery of typical 2-D landscapes and the reactions they represent, along with marginal distributions for all estimated parameters). Many marginal posterior distributions were narrower than the prior and were therefore well estimated (k₈ to k₁₂ for example) but others resembled the prior, a phenomenon we analyze in greater detail below. Relative to values previously used for EARM1.3 (Albeck et al, 2008b) Bayesian sampling yielded 33 parameters with modal values differing by ∼10-fold and 11 by ∼100-fold from previous estimates.

Parameter estimation using a Bayesian MCMC walk.

The deviation between data and model for a set of n parameters (k₁,…,k_n) is computed using the sum of squared differences:

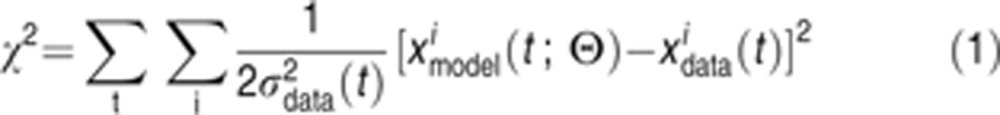where Θ≡(θ₁,…,θ_n) and θ_j≡log₁₀(k_j). The index i runs over all experiments, the index t runs over all times at which measurements are made and the index j runs over the 78 parameters. The χ² function is a conventional objective function and also the negative log of the likelihood that the data will be observed for a given set of parameters assuming that measurement errors at time t have a Gaussian distribution (with variance σ²_data(t)). According to Bayes’ rule, given a set of data the conditional distribution of a parameter vector Θ is given by:

where the symbol ‘P’ indicates probability density functions rather than probabilities as parameters are treated as continuous variables. The term P(Θ|data) is commonly known as the posterior and will be denoted as post(Θ); P(data|Θ) is the likelihood of Θ; and P(Θ) the prior of Θ. The term P(data) on the right hand side of Equation 2 (also known as the evidence for the model) is difficult to compute (in the current work we tackle this using thermodynamic integration) but for parameter estimation by MCMC sampling (see below) only the ratios of posterior values are needed, not the posterior values themselves. We therefore treated P(data) as a normalization constant yielding:

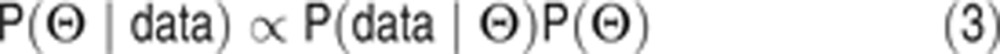We have explored several priors (see text) but the most effective was one in which the rate constants k_i were independent log-normal random variables, so that the θ_i are independent and normal, and

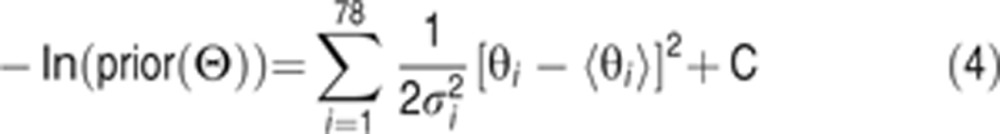where 〈θ_i〉 and 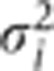are the mean and variance, respectively, of the distribution of θ_i, and C is an additive constant which does not affect the MCMC algorithm and can be ignored. The value of the log posterior for a particular parameter vector is then obtained by combining the log likelihood and the log prior (Equation 3):

This framework is commonly used to return single good-fit vectors Θ corresponding to MAP probability estimates for the parameter vector. However, we seek to generate a rich set of vectors that sample the posterior distribution of Θ. To accomplish this, we implemented a random walk in 78-dimensional parameter space using a multi-start Markov Chain Monte Carlo algorithm (MCMC). The number of steps that a particular position in parameter space is visited is proportional to the posterior probability (Chib and Greenberg, 1995). At the jth step of each MCMC walk, a Metropolis–Hastings (M–H) criterion was employed:

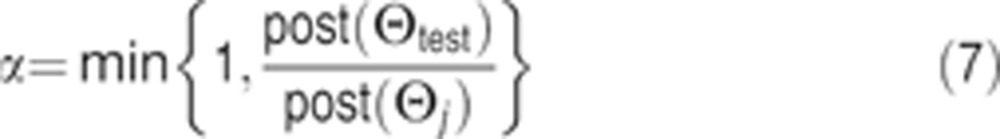where Θ_j is the current position in parameter space and Θ_test is the putative next position. A test position is accepted based on whether a randomly and uniformly chosen number between 0 and 1 is less than α (α⩽1).

A simple example of Bayesian estimation.

To illustrate how MCMC-dependent Bayesian parameter estimation works, consider an ODE model of three species (A–C) that interact via three reactions (with rates k₁ to k₃) corresponding to a classical example of an autocatalysis developed half a century ago by Robertson (Box 2 Figure A) (Robertson, 1966). First, we generate a set of synthetic data corresponding to the time-dependent concentrations of species A to C by choosing reaction rates and setting the initial concentration of reactant A to A₀=1.0 (in non-dimensional units). The resulting trajectory is sampled periodically assuming a theoretical measurement error of ±10%, which enters into the 1/2σ²_data(t) term of objective function (red bars, panel D; Box 1). We then hide knowledge of the parameter values and attempt to infer them from the synthetic measurements on all three species. In the treatment of Sethna (Gutenkunst et al, 2007) this would correspond to a situation with ‘complete’ knowledge. We perform an MCMC search giving rise to a joint posterior distribution whose marginal values and point-by-point covariation is shown in panel C. We see that the parameters of the system are non-identifiable despite complete data and that k₁ and k₃ covary: neither parameter is particularly well estimated but their ratio is well determined. This ratio has an important role in determining the trajectory of reactant C whose value can be predicted with good accuracy. Reflecting the non-identifiability of the system and the presence of experimental error, the prediction has a manifold of uncertainty, depicted in panel D as 60 and 90% confidence limits (in the case of this ‘prediction’, we trained the model on measurement of species A and B only). The inability of estimation to recover the parameter values used to generate synthetic data is not due to problems with the computational procedures. Instead, it represents a fundamental limit on our ability to understand biochemical systems based on time-course data alone.

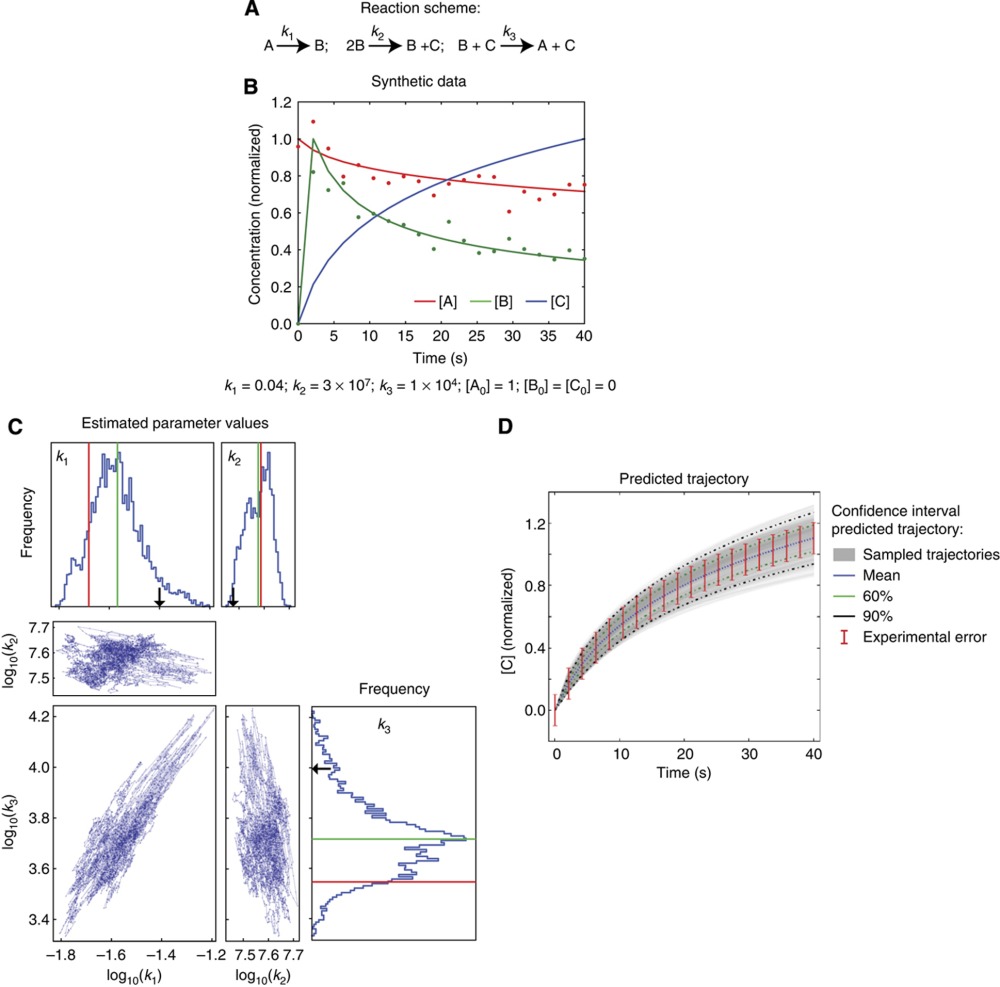Bayesian parameter for the simple, non-identifiable ‘Robertson’ system. (A) Structure of the reaction network. (B) Synthetic data generated from an ODEcorresponding to the system in A with the parameter values shown immediately below. (C) Results of Bayesian parameter estimation using data on species A and B, independent Gaussian priors and showing marginal distributions above and to the right of correlation plots for the three parameters. Red lines correspond to the best-fit parameter set and green lines to the mean of the individual marginal distribution, as in Figure 3. (D) Predicting the trajectory of species C given the posterior distribution in C. Red error bars denote one standard deviation around the mean of the data (assuming 10% error; data on C was withheld from the estimation) and green and black lines denote 60% and 90% confidence intervals of the prediction respectively.

Figure 2.

Two-dimensional slices of the parameter landscape computed by numerically evaluating the ln(posterior) over a dense set of grid points on a two-dimensional space. Superimposed in green, red and blue are MCMC walks with varying step numbers and with (left) or without Hessian-guidance (right). (A) With Hessian guidance, the longer chains of 5000 and 10 000 steps (red and green, respectively) converged by the Gelman–Rubin criterion. (B) Without Hessian guidance, none of the three chains converged. The other 76 parameter values were kept constant for this analysis.

Bootstrapping (Press, 1995) is a more conventional and widely used method for putting confidence intervals on model parameters. In bootstrapping, statistical properties of the data are computed and ‘resampling’ is used to generate additional sets of synthetic data with similar statistical properties. Deterministic fits are performed against the resampled data to give rise to a family of best fits. Bootstrapping therefore returns a family of optimum fits consistent with error in the data, whereas MCMC walks used in Bayesian estimation return the family of all possible parameter values that lie within the error manifold of the data. It is possible that the family of fits obtained through bootstrapping will identify some non-identifiable parameters but, in contrast to Bayesian estimation, there is no guarantee that parameter distributions or their point-by-point covariation are completely sampled.

Properties of MCMC walks

Performing MCMC walks across many parameters is computationally intensive and we observed that walks through the landscape of EARM1.3 proceeded slowly for either of two reasons: at the start of most walks, the landscape was flat in many directions, making it difficult to detect gradients pointing toward minima. Later in the walk, when minima were found, they were often valley like with many flat and few steep directions. In this case, the MCMC walk was inefficient, because many steps moved in directions of lower probability (this is represented by a circle of proposed moves in Figure 2).

MCMC sampling adequately captures an unknown distribution only if independent chains starting from random points converge to the same distribution. Convergence was assessed using the Gelman–Rubin test, which compares inter-chain to intra-chain variance: failing the test proves non-convergence, although passing the test does not necessarily guarantee it (see Materials and methods) (Gelman and Rubin, 1992; Brooks and Gelman, 1998). The importance of convergence is illustrated by the difference in parameter distributions recovered by convergent and non-convergent walks (Supplementary Figure 2). To improve convergence, a wide variety of ‘adaptive’ methods have been developed based on varying step size and biasing walks in certain directions (Gilks et al, 1996). A drawback of some adaptive MCMC approaches is that they alter the proposal distribution (which determines how the next step is taken) over the course of a walk and therefore have the potential to violate the stationarity requirement of M–H sampling. We sought a middle ground between stationarity and efficiency by performing MCMC walks in which ‘Hessian-guided’ adaptive moves (see Materials and methods) were performed once every 25 000 steps. Under these conditions all parameters in EARM1.3 reached convergence by Gelman–Rubin criteria. We also attempted to reach convergence without Hessian guidance by increasing the number of steps in a conventional MCMC walk to >1.5 × 10⁶; in this case 70/78 parameters converged (Table I). We discuss the technical but very important issues associated with normal and adaptive walks in the Materials and methods. Future users of our methods should note that approaches for achieving and demonstrating convergent sampling in MCMC walks remains an active area of research and improvements are likely.

Table 1. Improved chain convergence using Hessian-guided MCMC searches.

	Fraction of parameters that convergeda
MCMC stepsb	1 150 000	1 000 000	750 000	500 000	100 000	50 000
Hessian guidedc	78/78	77/78	73/78	70/78	40/78	21/78
Non-guidedd	65/78	62/78	55/78	50/78	24/78	12/78

^aAverage number of parameters for which convergence was achieved for a series of 10 MCMC walks after the indicated number of steps.

^bNumber of MCMC steps in a chain.

^cMCMC chains guided by the Hessian.

^dMCMC chains not guided by the Hessian.

Choosing priors

Pre-existing knowledge about parameters is incorporated in ‘prior distributions’ that bias sampling of posterior landscapes to values observed in earlier work or otherwise thought to be reasonable. With a biochemical system that is well studied, relatively narrow priors derived from in vitro data might make sense. However, in the current work we took a more conservative approach and used broad priors derived from physiochemical constraints likely to pertain to most biochemical reactions (use of narrower, specific priors would only serve to make calculations easier). In general, we favor soft constraints involving Gaussian priors over hard constraints. Although rate constants in a biochemical model pertain to physical process, many are actually ‘lumped’ or ‘effective’ rates in the physicochemical sense: the reactions they describe are comprised of a series of elementary association–dissociation reactions that cannot be distinguished. For an effective rate, a hard constraint is overly restrictive. We picked a prior for the on-rate of protein–protein binding centered at ∼10⁷ M⁻¹ s⁻¹, which does not violate diffusion limits and is ∼10-fold higher than theoretical values estimated by discrete simulation of linearly and rotationally diffusing bodies (Northrup and Erickson, 1992). Other plausible priors, corresponding to the mean values and variance for on-rates and off-rates, protein–protein binding constants and catalytic rate constants were obtained from a literature search (Table II). Because these include a mix of in vitro and in vivo values, they represent conservative estimates for possible parameter values (s.d.’s were ∼10²) and should be generally useful for other models in the absence of more specific prior information.

Table 2. Prior of log of parameter values derived from literature.

	Forward, first order (s−1)	Forward, second order (M−1 s−1)	Reverse, first order (s−1)	Catalytic (s−1)
Mean	−1.5	−6.0	−1.8	0.02
Variance	1.4	1.3	1.2	1.2

To evaluate the impact of priors on parameter estimation, we compared five independent Hessian-guided MCMC searches that incorporated either of two priors. The first was a uniform prior in which log(prior) was a constant (the actual value is not significant); this is equivalent to sampling in proportion to the likelihood. The second was a prior involving 78 independent Gaussian distributions, each having a mean and s.d. based on a literature value appropriate for that type of parameter. With a uniform prior, we observed that only a subset of parameters converged whereas all converged with the literature-based prior. The literature-based prior had the added benefit of minimizing the frequency with which EARM1.3 ODEs failed to integrate. MCMC walks with a uniform prior often ventured into regions of parameter space where numerical integration was not possible, presumably because the system of equations was too stiff. Conversely, we speculate that integration problems are minimized when parameter values at the extremes of the distribution are de-emphasized via the use of a log-normal prior, a potentially significant benefit.

Properties of the posterior landscape

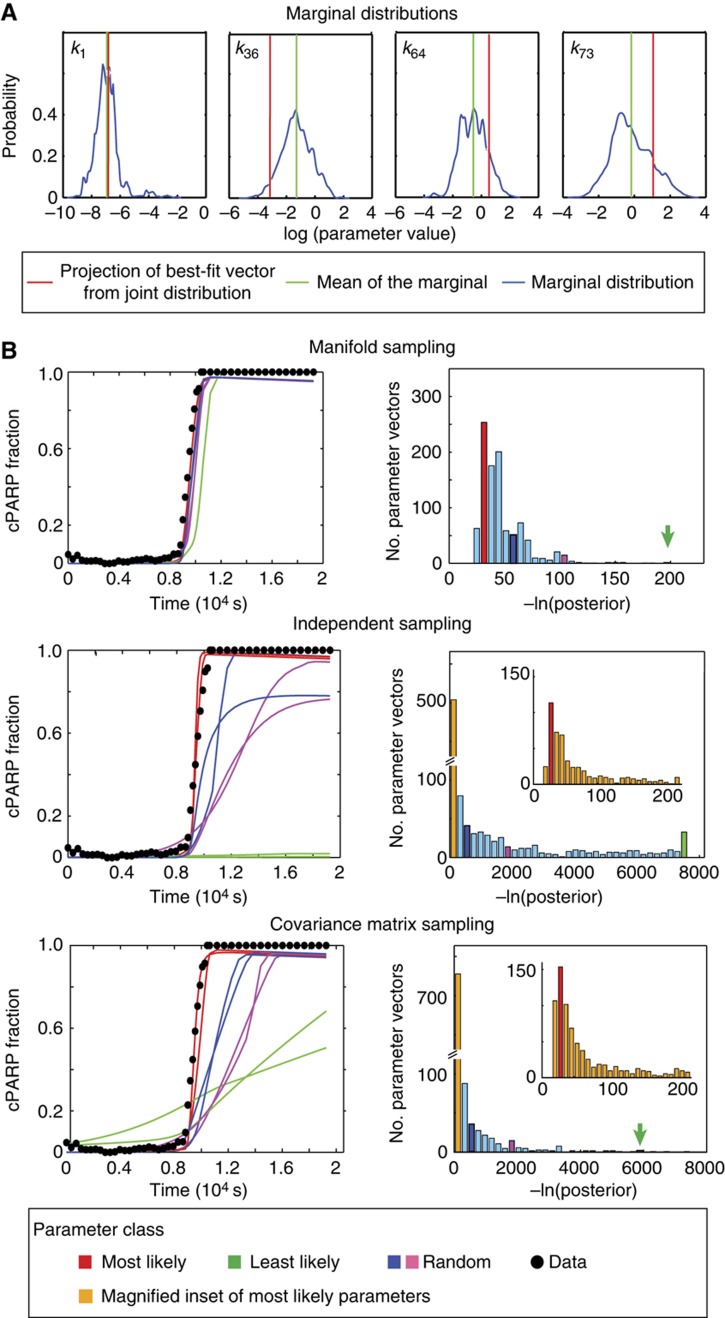
It is a basic property of Bayesian estimation that when posterior distributions are unchanged relative to prior distributions, little information is added by data. Inspection of individual (marginal) posterior distributions for EARM1.3 revealed that many were similar to the prior, implying that model calibration did not add significant new information. However, calibrated parameters exhibited significant covariation whereas distributions in the prior were independent. How much information is contained in this pattern of covariation? To begin to address this question, we selected a parameter vector (k₁….k₇₈) from the set of best fits arising from the joint posterior distribution and then projected the values of the individual component parameters to form the corresponding marginal distributions. In Figure 3A we see that the first parameter (indicated in red) from a typical best-fit vector has a value near the mean of the marginal posterior distribution for k₁ (green; this must be true because the k₁….k₇₈ vector was selected based on this property) but other well-constrained parameter values such as k₃₆, k₆₄ and k₇₃ lie well away from the means of their marginal distributions (this was true for all other vectors sampled from the posterior distribution; the same phenomenon is shown in Box 2). This makes clear that the peak of the 78-dimensional joint posterior distribution does not project onto the peaks of the marginal distributions. This is also true of the mean of the joint posterior and the means of the marginal distributions. The key point is that the best parameter estimates lie at the peak of the joint distribution and we cannot tell where this lies based on looking at marginal distributions individually.

Figure 3.

Parameter covariation is an important type of information recovered by model calibration. (A) A parameter vector drawn from the peak of the joint posterior distribution (corresponding to a best-fit parameter vector) does not always have components whose values correspond to the peaks of the corresponding marginal distributions (as illustrated for relatively identifiable parameters k₁, k₃₆, k₆₄ and k₇₃). In this case, the k₁ component of the best-fit vector matches the mean value of the marginal distribution for k₁, but this is not true of k₃₆, k₆₄ and k₇₃ or in general. (B) Predicted trajectories arising from three different types of parameter sampling. In each set of panels, pink, blue and green denote representative good, fair and poor fits. Manifold sampling: left panel shows goodness-of-fit to experimental data of a few simulated EC-RP trajectories, and right panel shows the distribution of 1000 –ln(posterior) values sampled from the joint posterior distribution (right; joint sampling). Independent sampling: similar plots but for parameters sampled from independent marginal distributions ignoring covariation. The inset panel expands the distribution for the smallest values of –ln(posterior). Covariance matrix sampling: similar plots but sampling from a multivariate log-normal distribution with mean and covariance computed from the MCMC walk.

To investigate the impact of parameter covariation on model-based prediction, EC-RP trajectories were simulated using parameter vectors derived from the posterior distribution using different sampling procedures. Vectors sampled from the manifold of the joint posterior distribution yielded a good match to experimental data as expected (‘manifold sampling’; Figure 3B). However, parameters sampled independently from marginal distributions (i.e., ignoring covariation) yielded a poor fit to experimental data (‘independent sampling’; Figure 3B). To assess whether the observed covariation could be captured in a compact manner, we computed a 78 × 78 covariance matrix for pairs of EARM1.3 parameters and generated a corresponding multivariate Gaussian distribution (Klinke, 2009) (‘covariance matrix sampling’; Figure 3B). In this case, simulated EC-RP trajectories had as poor a fit to data as trajectories generated by independent sampling.

These findings imply that a significant fraction of the information added to the posterior by calibration against data involves the discovery of non-linear covariation among parameters and this cannot be captured by a covariance matrix. To further illustrate that this information is important, we selected 10 parameters for which the difference between prior and posterior marginal distributions was the least significant (based on a t-test for the means and variances). The 10 selected parameters would conventionally be flagged as ones in which calibration had added little or no information. We then fixed the other 68 parameters at their maximum a posteriori (MAP) values and generated 10³ vectors by sampling the 10 selected parameters from independent marginal distributions. EC-RP trajectories were simulated and the −ln(posterior) of values were computed. The resulting values for the posterior were dramatically lower than the values of the posterior resulting from parameter vectors obtained by sampling from the complete 78-dimensional posterior (Supplementary Figure 3 and Figure 3B). This demonstrates that even when the prior and posterior distributions appear nearly identical, calibration adds essential information on the relationships among parameters.

From these observations we conclude that: (i) non-linear covariation in parameters, as captured in the joint posterior distribution, contains critical information, (ii) the most probable values for individual parameters do not correspond to values in best-fit vectors and (iii) treating parameters as independent values, as in a table, or approximating their relationships linearly, as in a covariance matrix, destroys information necessary for accurate model-based prediction. We can understand this conceptually by referring to the landscape of k₁ and k₂ (Figure 2); it is evident that the true relationship between the parameters is not constant but instead varies across the landscape in a complex non-linear manner. These considerations seem rather technical at first, but they have profound implications for the ways in which model parameters are recorded and used (see Discussion).

Using parameter distributions in simulation and prediction

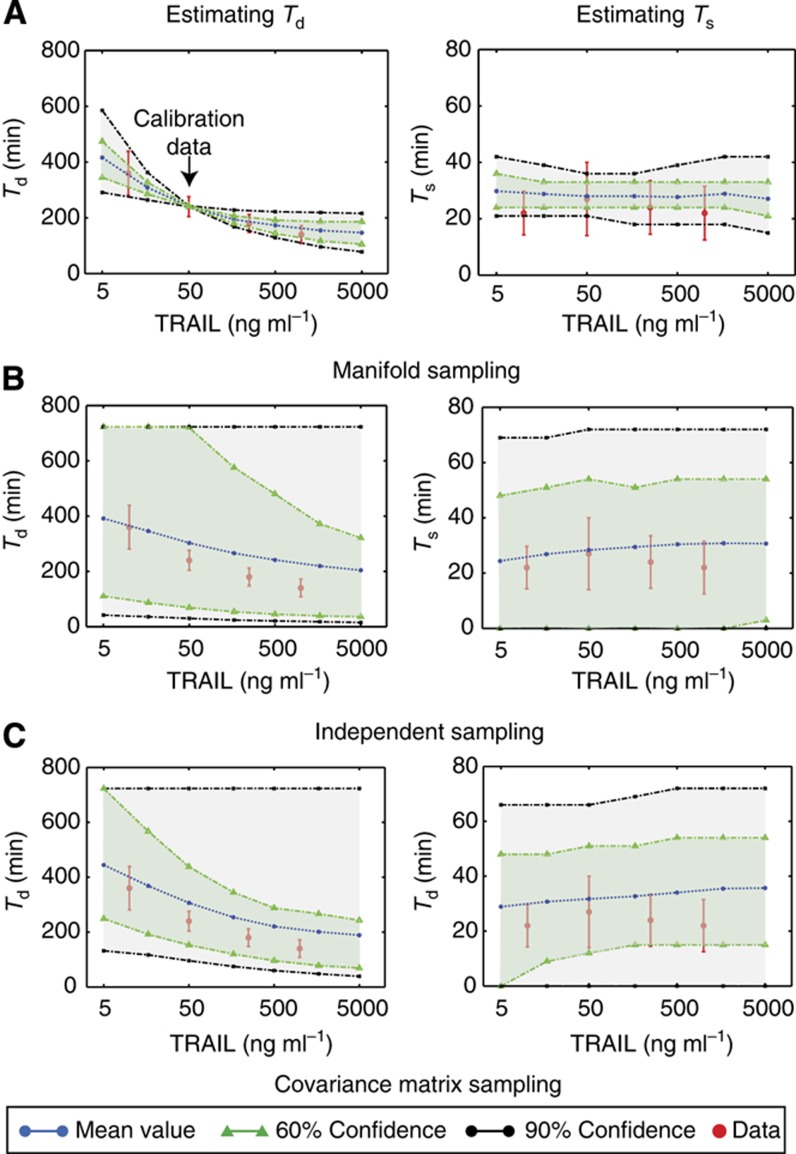
Estimation of parameter distributions makes it possible to account for both measurement error and parameter non-identifiability, when making model-based predictions. For cells exposed to a range of TRAIL concentrations, we computed two descriptors of apoptosis known to be physiologically significant for many cell types (Albeck et al, 2008b; Aldridge et al, 2011): (i) the time interval between the addition of TRAIL and half-maximal cleavage of the caspases substrates whose proteolysis accompanies cell death (i.e., the mean and variance in T_d) and (ii) the interval between initial and final cleavage of effector caspases (C3*), which captures the rapidity of death (the mean and variance in T_s (Albeck et al, 2008b)). EC-RP trajectories for cells treated with 50 ngml⁻¹ TRAIL were used for model calibration and T_s and T_d values were then predicted for 10, 250 and 1000, ngml⁻¹ TRAIL. Simulations were performed by sampling 1000 parameter vectors Θ from the posterior distributions arising from two independent MCMC chains and computing trajectories for each Θ. These predictions comprised probability density functions rather than single values and we therefore calculated 60 and 90% confidence intervals. We observed that the mean value of T_d fell with increasing TRAIL concentrations while T_s remained essentially constant, in line with experimental data (Figure 4A). Moreover, distributions had the satisfying behavior of having narrow confidence intervals at the training dose and progressively wider intervals at higher and lower doses. This illustrates two closely related points: first, quite precise predictions can be made from models despite parameter non-identifiability (Gutenkunst et al, 2007; Klinke, 2009) and second, Bayesian sampling makes it possible to compute rigorous confidence intervals for predictions that account for experimental error and our lack of knowledge about parameters. However, this requires that we correctly account for covariation in parameter estimates: independent and covariance matrix sampling of parameters dramatically impaired the ability of EARM1.3 to predict accurate values for T_s and T_d (Figure 4B and C).

Figure 4.

Using parameter vectors obtained by three different sampling methods to make model-based predictions of the time between ligand exposure and caspase activation (T_d) or between initial and complete PARP cleavage (T_s), computed using parameter vectors sampled from (A) the joint posterior distributions obtained from the MCMC walk; (B) a multivariate log-normal distribution with mean and covariance computed from the MCMC walk; (C) independent log-normal distributions with means computed from the MCMC walk. Mean values (blue dotted line) and estimated 90% (black dotted lines, gray area) and 60% confidence intervals are shown (green dotted lines, light green area along with experimental data (red). PSRF values obtained via the Gelman–Rubin convergence test for these predicted model features ranged between 1.0001 and 1.0442 for T_d and 1.0015 to 1.0343 for T_s.

Model discrimination based on computing the Bayes factor

Although the scheme described above represents a principled way to manage parametric uncertainty, it does not account for uncertainty in the structures of reaction networks. We focused on uncertainty involving pore formation by Bcl2-family proteins during MOMP (Lovell et al, 2008; Chipuk et al, 2010; Leber et al, 2010). EARM1.3D instantiates a ‘direct’ model in which MOMP activators such as tBid (Figure 5A, red lozenges) positively regulate Bak/Bax pore-forming proteins (green), and Bcl2, BclXl and Mcl1 inhibitors (yellow) block this activation (these proteins are themselves antagonized by the sensitizers Bad and NOXA). EARM1.3I instantiates an ‘indirect’ model in which Bak/Bax are always active but are held in check by Bcl2-like inhibitors, whose activity in turn is antagonized by tBid, Bad and NOXA (Figure 5A). These models represent only two of several possibilities for direct and indirect regulation of MOMP, but the important point for the current work is that they have distinct topologies and different numbers of parameters (88 for EARM1.3I and 95 for EARM1.3D).

Figure 5.

Discriminating between direct and indirect models of mitochondrial outer membrane permeablization. (A) Graphical depictions of potential indirect and direct mechanisms controlling pore formation by Bax and Bak. See text for details. (B) Both EARM1.3I indirect (red) and EARM1.3D direct (blue) models exhibited an excellent fit to experimental EC-RP trajectories. Thus, the models cannot be distinguished by simple maximum likelihood criteria. For simplicity, simulations were based on a single best-fit parameter vector. (C) Thermodynamic integration curves for the direct and indirect model. (D) Exponentiation of the differential area in the two thermodynamic curves from C provides an estimate of the Bayes factor for direct and indirect models along with the uncertainty in the estimate. On the basis of the distribution of the Bayes factor estimate (reflected in the error bars in C) the direct model is preferred to the indirect by a weight of ∼20, with the 90% confidence interval spanning a range from 16 to 24. (E) Eigenvalue analysis of the landscape around the respective maximum posterior fits shows the direct model (blue) has multiple smaller eigenvalues, suggesting that it is consistent with the data over a larger volume of parameter space and therefore exhibits greater statistical weight.

When we compared trajectories for EC-RP simulated using EARM1.3I or EARM1.3D to experimental data, we observed equally good fits, meaning that the models cannot be discriminated based on a maximum likelihood (Figure 5B). To compare the models in a Bayesian framework, we applied Bayes theorem at the level of models:

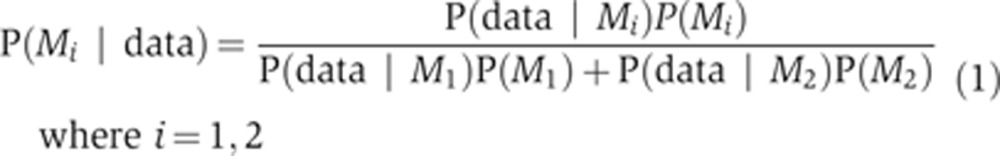where ‘data’ refers to experimental measurements against which the objective function was scored (EC-RP trajectories in the current case). M₁ refers to the direct model and M₂ to the indirect model, and as both have literature support we assumed that the models are a priori equally plausible: P(M₁)=P(M₂) (this represents the most conservative assumption). Then, Equation 1 simplifies to:

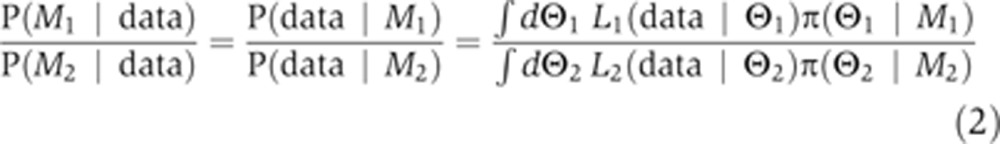where Θ₁=(θ₁ … θ₉₅) and Θ₂=(θ₁ … θ₈₈) are, respectively, the parameter vectors for models M₁ and M₂, θ_i≡log₁₀(k_i) where k_i is the i^th parameter of a particular model (all calculations are performed in log space), L_i(data|Θ_i) is the likelihood function, and π(Θ_i|M_i) is the prior for the parameters of model M_i. This ratio is known as the Bayes factor and represents the odds ratio of one model being correct over another (Kass and Raftery, 1993; Gelman and Meng, 1998), and has been used for discriminating alternate models of cross-talk in ERK and cAMP signaling (Xu et al, 2010). Both the numerator and the denominator comprise two high-dimensional integrals that represent the overlap volume between a likelihood (L(data|Θ)) and the prior for each model (π(Θ|M)). This overlap integral is also known as the evidence. The Bayes factor not only accounts for all plausible parameters based on their likelihood, it also has a built-in ‘Occam’s razor’ that explicitly accounts for the possibility that the two models have different numbers of parameters (see Discussion for details) (MacKay, 2004).

We computed the integrals in Equation 2 using a method known as thermodynamic integration. This transforms the problem of evaluating high-dimensional integrals into a problem involving a one-dimensional sum over quantities sampled from a series of MCMC walks. Sampling is weighted by a power posterior that depends on a fictitious temperature factor ranging from a value of 0 to 1 (Gelman and Meng, 1998; Lartillot and Philippe, 2006; Friel and Pettitt, 2008). For each model, three MCMC chains were run at 29 temperatures between 0 and 1. The quantity ln(likelihood) was averaged with respect to the power posterior at each temperature and over three chains, resulting in two curves, one for each model (Figure 5C; see Materials and methods for more details). The ratio of the areas under each curve converges to the logarithm of the Bayes factor. Because thermodynamic integration is a sampling method, the computed Bayes factor is subject to sampling error and must be expressed as a confidence interval. We computed the uncertainty on the areas returned by thermodynamic integration by estimating the variance at each point of the curve to generate a two-tailed confidence interval. This allowed us to conclude with 90% confidence that the direct model is 16–24 times (e^2.8 to e^3.2) more likely than the indirect model (Figure 5D).

We can better understand how the Bayes factor scores models by examining the landscape of the objective function. We approximated the landscape as an n-dimensional ellipsoid (where n refers to the number of parameters in each model) by using a Taylor series at a best-fit position in parameter space. This makes it possible to describe the landscape in terms of an ellipsoid the length of whose axes are inversely proportional to the square roots of the eigenvalues of the second-order term of the Taylor expansion (i.e., the Hessian). The direct model had more small eigenvalues than the indirect model (i.e., longer axes) and thus a greater volume of equally good parameters (Figure 5E). The notion that a model is more probable if more parameters give a good fit is frequent if informally applied, when models are ranked based on their ‘robustness’ with respect to parameter variation (Chen et al, 2007b). It is also intuitively appealing: a model that performs well only over a narrow range of parameter values which are otherwise unknown is less probable than a model that is tolerant of variation. Such reasoning is also related, conceptually, to maximum entropy and minimum information approaches (see Discussion).

Discussion

In this paper we describe a Bayesian framework for estimating free parameters in ODE-based biochemical models, making probabilistic predictions about dynamical variables and discriminating between competing models having different topologies. We illustrate the use of this approach with a previously validated and non-identifiable model of receptor-mediated apoptosis in human cells (EARM1.3). Rather than return a single set of ‘best fit’ parameters, Bayesian estimation provides a statistically complete set of parameter vectors k that samples the posterior parameter distribution given a set of experimental observations (time-lapse data from live cells in the current case) and a value for experimental error. Estimation starts with a best-guess initial distribution (the prior), which is then modulated by a sum of squares log-likelihood function that scores the difference between model and data (Box 1). Recovery of the posterior parameter distribution makes it possible to compute confidence intervals for biologically interesting properties of the model (time and rapidity of apoptosis in the current case). These confidence intervals correctly account for measurement noise and parametric uncertainty, and can be remarkably precise in the face of substantial non-identifiablility (Klinke, 2009). Simulations that include confidence intervals represent an advance on the prevailing practice of relying on error-free trajectories computed using a single set of maximum likelihood parameter values.

We also used Bayesian procedures to discriminate between competing direct and indirect models of MOMP, a key step in apoptosis. Discrimination involves estimating the evidence for the indirect model P(M_I|data) divided by the evidence for the direct model P(M_D|data), a ratio known as the Bayes factor (Kass and Raftery, 1993, 1995; Xu et al, 2010). Bayesian approaches to model discrimination account not only for uncertainty in parameter values but also for differences in the numbers of parameters. This is important because models that instantiate different hypotheses about biochemical mechanism usually have different numbers of parameters even when the number of unique model species is the same. The complexity penalty embedded in the Bayes factor represents a generalization of the Akaike or Bayesian Information Criteria (AIC and BIC) commonly used to score model likelihoods (Kass and Raftery, 1995).

In the case of MOMP, we observed that both direct and indirect models fit experimental data equally well and, thus, cannot be distinguished on a maximum likelihood basis. However, computation of the Bayes factor revealed the direct model to be ∼16–24 times more probable than the indirect model at 90% confidence, reflecting the greater range of parameter values compatible with the direct model. This formalization of a ‘robustness’ criterion for preferring the direct model is consistent with recent experiments obtained from engineered cell lines (Chipuk et al, 2010). With respect to the biological significance of this finding, however, it is important to note that published indirect and direct ‘word models’ are compatible with many different ODE networks. Thus, it will ultimately be necessary to distinguish among extended sets of competing models, not just the two presented here. With improvements in computational speed, methods for calculating the Bayes factor using ‘thermodynamic integration’ are well suited to this task.

Properties of the posterior distribution and implications for reporting parameter values

With EARM1.3, Bayesian estimation reveals substantial differences from one parameter to the next in the degree of identifiability (as reflected in the widths of the parameter distributions). This is expected given previous work showing that biochemical models are ‘sloppy’ (Gutenkunst et al, 2007) even when calibrated against ‘complete’ data on all dynamic variables (which is not the case in the current work). A basic property of Bayesian estimation is that the posterior will resemble the prior when data provide little or no additional information. Conversely, when the data are informative, the shape of the posterior will differ substantially from that of the prior. In the case of EARM1.3 modal values for posterior distributions differed from the priors for about one-third of all parameters while still falling within a biophysically plausible range (with rate constants below the diffusion limit, for example). The exact shape of the prior did not appear to be critical in achieving convergent sampling, a fortunate outcome since we used general-purpose priors applicable to all cellular functions rather than priors derived from specific analysis of apoptosis proteins. One mistake we learned to avoid was constraining the MCMC walk to a fixed interval around nominal parameter values; such hard limits result in artificially truncated marginal distributions. Gaussian priors also had the benefit of improving the fraction of parameter sets for which the EARM1.3 ODE system could be integrated.

It is incorrect to judge the impact of parameter estimation (i.e., what we learn by comparing models to data) simply by examining the shapes of individual parameter distributions: several lines of evidence show that marginal distributions contain only part of the information. Non-linear covariation among parameters accounts for the rest; it is necessary for accurate model-based simulation and cannot be approximated by a covariance matrix. The reasons for this are evident from inspection of the landscape of the objective function. The landscape is steep (the eigenvalues of the Hessian matrix are high) in directions that do not point directly along raw parameter axes (Gutenkunst et al, 2007). Thus, identifiable features of the systems correspond to ratios of rate constants (this is the basis of parameter covariation) but the value of the ratio varies through parameter space (this gives rise to curved high-probability valleys that are not well approximated by lines). By direct analogy, the identifiable parameter in a Michaelis–Menten treatment of a simple catalytic reaction is K_M, a ratio of rate constants, rather than k_f or k_r themselves ((Chen et al, 2010) see also Box 2). When parameters in a model are highly covariant, it is almost always the case that the system can be described with a simpler model involving a smaller set of more identifiable parameters. In many applications in engineering it is desirable to use such reduced models, but in the case of biochemistry, parameter non-identifiability and high covariance appear to be the cost of representing systems as sets of reversible mass-action reactions. Under the assumption that mass-action kinetics (and also stochastic kinetics obtained by solving the chemical master equation) are uniquely appropriate as a means to describe the physics of biochemical systems, we are forced to use models such as EARM1.3. However, there is no reason, from a physical perspective, to believe that proteins in a network that do not actually bind to each other alter each other’s rate constants. Thus, the presence of highly covariant parameters in best-fit vectors is not a property of the underlying biochemistry: instead, it represents a limitation on our ability to infer the properties of complex reaction networks based on the time-course data we typically acquire.

One consequence of parameter covariation in EARM1.3 is that parameter values in best-fit vectors do not correspond to the means of marginal parameter distributions, and sampling the means of marginal distributions does not result in a good fit. It is common practice in biochemical modeling to report parameters as a table of single values (with no allowance for non-identifiablility) or as a list of means and ranges. If these parameters are derived from calibration, critical information on covariation is lost. It is therefore necessary to report the actual vectors recovered by sampling the posterior parameter distribution. In principle, this is an array of size (C × M) × (N+1) where C is the number of MCMC chains, M the number of steps, and N the number of parameters (N+1 appears because we record a posterior value for each N-dimensional vector) corresponding to ∼1.5 × 10⁸ entries for EARM1.3. However, steps in MCMC chains have characteristic ‘decorrelation lengths’ over which parameter values vary relatively little (∼10²–10⁴ steps, depending on the parameter). Thinning by this amount yields an array of ∼10⁴–10⁶ entries, still a much more complex representation of parameters than the simple tabular summary assumed by current standards such as SBML. It is also important to note that the posterior landscape needs to be revisited repeatedly when adding new data or extracting new hypotheses. In this sense, parameter estimates are best viewed as computational procedures and sets of possible values rather than fixed information.

Model discrimination in the Bayesian framework

A solid theoretical foundation and large body of literature speaks to the value of Bayesian frameworks for analyzing models having different numbers of uncertain parameters (Kass and Raftery, 1995; MacKay, 2004; Xu et al, 2010). The Bayes factor described here, the odds ratio for competing models (i.e., the ratio of the evidence), is computed from an overlap integral between a likelihood and a prior (that is L(data|Θ) and π(Θ|M)). At first glance it might seem that making a model more complex would increase the number of dimensions and always increase the evidence, but a simple example shows that this is not the case. Consider a pair of one- and two-parameter models of the same hypothetical physical process and a function f that is the ratio of relevant likelihoods: f(k₁,k₂)=L(k₁,k₂)/L(k₁). The evidence for the one-parameter model is the overlap integral between its likelihood and a normalized prior ∬dk₁ L(k₁)π(k₁) and for the two-parameter model it is ∬dk₁ dk₂ L(k₁,k₂)π(k₁)π(k₂). In the case where f(k₁,k₂)<1 for all k₁, k₂ the likelihood of the two-parameter model is no better than that of the simpler one-parameter model (note that the evidence for the two-parameter model is ∬dk₁ L(k₁)π(k₁)g(k₁) where the function g(k₁)=∬dk₂ π(k₂)f(k₁,k₂) must be less than 1 everywhere, as the priors are normalized to 1). The evidence for the two-parameter model will therefore be less than the evidence for the one-parameter model, meaning that it will lose out in a Bayes factor comparison, as it should.

When the function f(k₁,k₂)>1 then it must be true that introduction of a second parameter ‘rescues’ or ‘lifts’ the likelihood function by improving the fit to data. In this case, the more complex model will have greater evidence. In the special but interesting case where f(k₁,k₂)=1 for all k₁, k₂, model 2 is completely insensitive to the new parameter. The presence of a parameter with respect to which a model is completely insensitive has no impact in model assessment (the Bayes factor is one). Finally, in the general case where f(k₁,k₂) has values both above and below 1, explicit integration is needed to determine which model is favored, precisely what we do in this paper.

The Bayes factor is not unique as a means to balance goodness-of-fit and model complexity. The most commonly used metrics are the AIC and the BIC (Akaike, 1974; Schwarz, 1978):

where n is the number of parameters, ML is the maximum likelihood value, and N is the number of data points (ML is simply the highest value achieved by the likelihood function). AIC and BIC do not explicitly account for parameter non-identifiability and the two metrics are therefore good for comparing models only in the ‘asymptotic’ limit where the number of experimental data points becomes ‘large’ and identifiability is ‘greater’ (Akaike, 1977, 1983; Kass and Raftery, 1995). It is rare in the field of biochemical modeling to explicitly check whether the conditions for computing the AIC and BIC are valid and, in our experience, they are frequently violated. In contrast, the Bayes factor is applicable even with limited data and reduces to the BIC and, under some conditions, to the AIC in the asymptotic limit (Akaike, 1977, 1983; Kass and Raftery, 1995). Moreover, whereas the AIC or BIC compare models solely on the basis of goodness-of-fit, Bayesian methods allows formal introduction of a prior degree of belief in each model. An arbitrary model (i.e., a physically impossible model) exhibiting a better fit to data might get a better AIC or BIC score than a more realistic mechanistic model, but in a Bayesian approach it would receive a low prior value. We therefore consider evaluation of the Bayes factor to be a better way than AIC or BIC to compare models when models have different numbers of non-identifiable parameters and data are limited.

Limitations of the approach

The computational approach described here has several practical and algorithmic limitations, albeit ones that can be mitigated with further work. A practical concern is that current methods for computing the Bayes factor are too slow to incorporate the full range of data we have collected from cells exposed to drugs, siRNA-mediated protein knockdown and ligand treatment. Using only a subset of available training data, computing the Bayes factor for EARM1.3 required ∼6 × 10⁴ CPU-hr (4 weeks on a 100 core general-purpose computer cluster). It should be possible to improve this by optimizing the code (e.g., porting it from MatLab to C/C++) and performing multiple analyses in parallel. It also remains to be determined how inclusion of more calibration data will alter the topology of the posterior landscape. It may become more rugged, decreasing the requirement for Hessian guidance during MCMC walks but increasing the need for simulated annealing (SA) to move out of local minima. Readers interested in these developments should check our Github repository or contact the authors directly.

An additional conceptual concern with the current work involves the way in which MCMC walks sample the posterior landscape. To establish that sampling is correct, it is necessary to show that chains starting at independent positions converge. Convergent sampling is not an abstruse point because probability distributions can differ in shape and modal value, when sampling is convergent as opposed to non-convergent. With EARM1.3 we observed that convergence was not possible in a reasonable amount of time (e.g., a week-long cluster-based calculation) using a conventional MCMC walk. We therefore used an adaptive walk involving periodic recalculation of the local landscape as a means to guide MCMC walks and improve convergence. However, this approach may violate the detailed balance requirement of M–H sampling. With large models and existing methods, we are therefore in the position of having to choose between convergent Hessian-guided chains and partially non-convergent, conventional chains ((Klinke, 2009) chose the latter alternative). Moreover, using the Gelman–Rubin test to judge convergence has the weakness that it is one-sided: failing the test demonstrates non-convergence but passing the test does not guarantee it. Analysis of posterior distributions for EARM1.3 computed in different ways suggests that we are on relatively solid ground in the current paper (we did not observe significant differences in posterior distributions using different sampling approaches), but the development of methods for analyzing MCMC walks represents an active area of research in applied mathematics and it is necessary to be aware of future developments.

For reliable, probabilistic model-based simulation, we also need to consider the fact that the sufficiency of sampling is contingent not only on the model structure and available training data, but also on the types of predictions being sought. Assuming convergence, the posterior landscape sampled by multi-start MCMC walks represents a reasonable approximation to the true but unknown posterior distribution of the parameters, but the same is not necessarily true for predictions or simulated trajectories based on these parameters: the posterior landscape may be poorly sampled in regions of parameter space that have a significant impact on some simulations. In the current work we show that MCMC chains used to predict T_s and T_d satisfy the Gelman–Rubin test, but this is a weak criterion and importance sampling using umbrella, non-Boltzmann or other methods (Allen and Tildesley, 1987) will generally be necessary to revisit regions of the landscape that have low posterior values but contribute strongly to the distribution of a prediction. This suggests a workflow in which MCMC walks based on calibration data (as described here) are only the first step in model calibration. Inclusion of any new training data mandates a new round of estimation. Additional sampling should also be performed as required by importance sampling to reliably inform predictions. Finally, the use of formal methods for modeling experimental error (Jaqaman and Danuser, 2006) should make it possible to distinguish errors arising from photon noise, infrequent sampling, incorrect normalization, etc, thereby improving the comparison between data and simulation.

Conclusions

The ubiquity of Bayesian methods in other scientific fields has motivated multiple, parallel efforts to apply the approach to biochemical models (Flaherty et al, 2008; Calderhead and Girolami, 2009; Klinke, 2009; Xu et al, 2010), but significant challenges have remained with respect to development of widely available methods for discriminating between competing models. The algorithms and open-source code described in this paper enable a rigorous approach to estimating the parameters of non-identifiable biochemical models, making model-based predictions probabilistic, and using the Bayes factor to distinguish between models with different topologies and numbers of parameters. The generic priors we report are a good starting point for estimating forward, reverse and catalytic rates in any mass-action model of cellular biochemistry, but in some cases it makes more sense to substitute narrower and more specific priors derived from previous studies in vitro and in vivo; such specific priors better capture pre-existing knowledge, improve parameter estimation and speed of computation. It is our opinion that application of rigorous probabilistic analysis of biochemical models will advance the long-term goal of understanding complex biochemical networks in diverse cell types and disease states (Klinke, 2009; Xu et al, 2010). Preliminary application of Bayesian reasoning suggests that some long-standing disputes about cell signaling can be laid to rest, (e.g., direct versus indirect control of MOMP), whereas others truly cannot be discriminated based on available data.

Materials and methods

Experimental data

All data were obtained by live-cell fluorescence microscopy of HeLa cells stably transfected with vectors expressing IC-RP and EC-RP as reported previously (Albeck et al, 2008a). Apoptosis was initiated by adding media containing 50 ngml⁻¹ TRAIL and 2.5 μgml⁻¹ cycloheximide.

Model and algorithm

The model in this paper, EARM1.3, was first described by Albeck et al (2008a,b). EARM1.3 as used in the current work differs from the original model in its inclusion of synthesis and degradation reactions for all species and its use of different nominal parameter values (Spencer et al, 2009). A summary of the algorithm is found in Supplementary Figure 4 and explained in detail below.

Initiating MCMC chains

Three to five independent MCMC chains were run simultaneously on a cluster computer. Each chain started at a random initial position in parameter space. These initial positions were obtained by multiplying the log of the nominal parameter values by a random number drawn from a uniform distribution between −1 and 1, in effect yielding a set of parameters 10-fold lower or higher than the nominal values. In log parameter space, the starting position is a point randomly chosen within a box of dimension 78 and sides of length 2. The box is centered on the nominal values, which are those reported in work on the original EARM model (Albeck et al, 2008a). The acceptance rate averaged over all chains was∼0.15–0.19. Prior work on optimal jumping rates suggests the optimal rate is 0.234 for certain asymptotic conditions and assumptions of the target distribution (Gelman et al, 1996). However, the same work noted that 0.5 is ‘reasonable’ and achieves 75% maximal efficiency. We have not determined the degree to which our system and procedures satisfy the various conditions of the theoretical optimum. Improvement in this aspect of the algorithm is therefore possible.

Simulated annealing

For the first 10% of the MCMC algorithm, SA was used to bring the chains from random initial starting points to points having high posterior values. The temperature of annealing was lowered according to the exponential function T=T₀e^{(−Decay rate*Step number)}, where T₀ is the initial temperature (set to a value of 10), step number refers to the MCMC step number and decay rate is the rate of exponential decay, chosen so that the time constant of the decay is 30% of the number of steps between Hessian calculations (25 000 steps; see below). The temperature is reduced until it reaches a value of 1. During SA, new parameter vectors are chosen by taking a step lying on the unit sphere with radius of size 0.75, centered on the current position. The radius size was heuristically determined by systematic exploration of different sizes and choosing the one that showed the most rapid and greatest success in posterior maximization. After SA is complete, the Hessian guides the determination of new parameter vectors.

Adaptive MCMC walks

Among the adaptive approaches we tried, the one that showed the greatest improvement with EARM1.3 involved taking large steps in flat directions and small steps in steep directions based on calculating the curvature of the local landscape using the Hessian (represented by yellow ellipses in Figure 2A; Table I). Hessian guidance improved convergence with EARM1.3 particularly when MCMC chains had to pass through saddle points or flat regions of the landscape. A drawback of some adaptive MCMC approaches is that they alter the proposal distribution (which determines how the next step is taken) over the course of a walk and this has the potential to violate stationarity (Muller, 1991; Atchade and Rosenthal, 2005; Andrieu and Moulines, 2006), a necessary condition for correct sampling of posterior distributions. Klinke and colleagues (Haario et al, 2001; Klinke, 2009) have proposed an alternative adaptive strategy that uses information acquired during the entire MCMC walk to construct a proposal distribution that converges to a distribution related to the Fisher information matrix. This scheme retains the properties of stationarity and provable convergence but only improves performance early in a walk. Later, if the local landscape differs substantially from the converged proposal distribution, walks become less and less efficient, and chain convergence more difficult to achieve. We therefore performed MCMC walks in which the Hessian was recalculated once every 25 000 steps. Under these conditions all parameters in EARM1.3 reached convergence by Gelman–Rubin criteria; without Hessian guidance and a conventional MCMC walk of >1.5 × 10⁶ steps, 70/78 parameters converged (Table I). Among the convergent parameters, we could detect no significant difference in the marginal posterior distributions obtained with and without Hessian guidance using a two-sample Kolmogorov–Smirnov test (Massey, 1951). We conclude that our procedures adequately estimate the posterior distribution of EARM1.3 but a tradeoff clearly exists between greater rigor in the sampling procedure (no local adaptation) and ensuring convergence for all parameters.

Hessian-directed search

To improve the performance of the MCMC search algorithm, we developed a procedure for taking large steps in directions in which the local landscape is flat and small steps in directions in which the landscape has large curvature as determined by a Hessian decomposition at selected positions in parameter space. These positions are defined by the parameter vector Θ≡(θ₁, …, θ₇₈) (we performed all calculations in log₁₀ space). The Taylor series expansion around a position Θ_hess is the following:

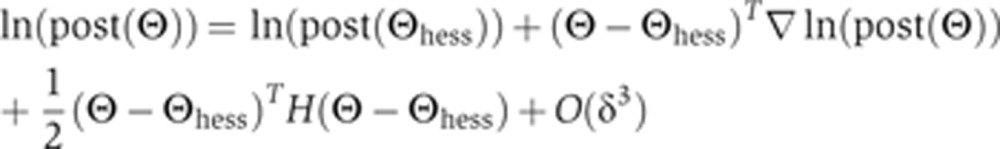Here, Θ is a position in parameter space close to Θ_hess; 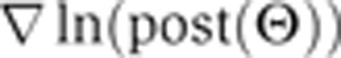and H are a central-difference gradient vector and the Hessian, respectively, evaluated at Θ_hess; and δ is the magnitude of Θ–Θ_hess. To determine whether this expansion is a good approximation to ln(post(Θ)), we calculated the correlation coefficient between Δ_true and Δ_predicted, where these quantities are defined by

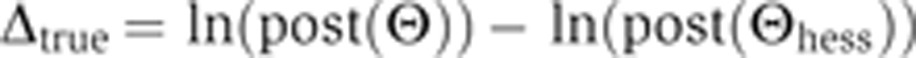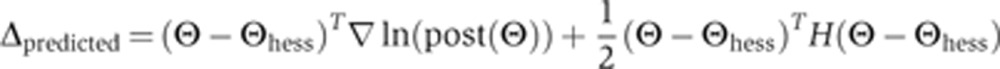The Hessian at the position Θ_hess is decomposed into the form H=UΛU^T, where Λ is a diagonal eigenvalue matrix and U is a corresponding orthonormal eigenvector matrix. By sampling points on an ellipsoid with major axes that are the eigenvectors of the Hessian and with length 10% of the corresponding inverse square root of the eigenvalues around the central point, we observed a Pearson correlation coefficient of 0.887. This suggests that the Hessian and gradient matrices represent a good estimate of the true posterior, justifying our expansion of the objective function only to second order (Supplementary Figure 5).

When SA is running, the Hessian matrix is not calculated and test positions are generated as follows:

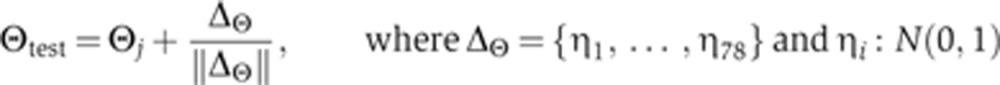Here, Δ_Θ is a 78-dimensional vector with independent and normally distributed components, η_i, normalized so that the magnitude of the step size in log space is one. Once the periodic calculation of the Hessian matrix is initiated during the MCMC walk, we use its eigenvectors to direct the walk onto a new set of orthogonal axes by repeatedly obtaining new test positions of the following form:

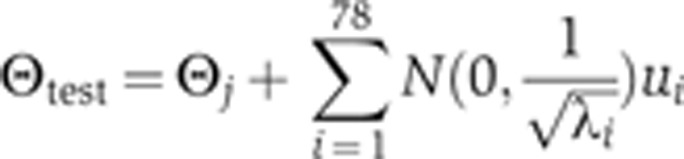where u_i and λ_i are the ith eigenvector and eigenvalue, respectively, and N(0,σ) is a random value drawn from a normal distribution with mean 0 and variance σ. As the landscape is flat in most directions, many of the eigenvalues are much less than one. To prevent the algorithm from taking steps that are too large in any particular direction, all eigenvalues <0.25 were set to 0.25, so that the variance of the Gaussian distribution from which the new step size was chosen was limited to a value of 2 in log space.

The entries of the transition matrix T_(x→y) in our MCMC algorithm are composed of a product of two terms: the probability of selecting a particular transition between two states: m_(x→y) and the probability A_(x→y) of accepting it (the M–H criterion):

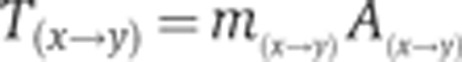The move is symmetric in that m_(x→y)=m_(y→x) as it is guided by a Hessian (kept constant for a window of 25 000 moves) centered on the current position. These qualities ensure that (as long as the Hessian is kept constant) the posterior distribution is the stationary distribution of the MCMC chain. To test for convergence of chains, we rely on the Gelman–Rubin criterion.

Gelman–Rubin convergence criterion

To obtain accurate probabilistic distributions, independent MCMC chains must reach convergence, which can be assessed by a Gelman–Rubin test (Gelman and Rubin, 1992; Brooks and Gelman, 1998). The Gelman–Rubin test is conducted by calculating the potential scale reduction factor (PSRF) for two chains. The PSRF value is given by the following expression:

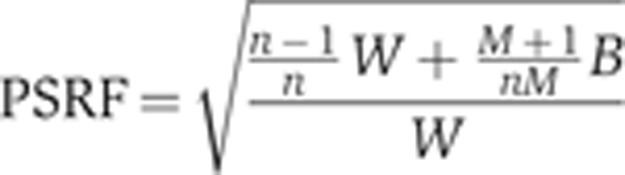Here B is the inter-chain variance, W is the intra-chain variance and M is the number of parallel MCMC chains each of which have run for n steps. In other studies, typically a PSRF value of <1.2 was used to indicate convergence. In this work we defined convergence as attaining a PSRF value of 1.1 or less. Table I shows that the parameters in three parallel Hessian-guided MCMC random walks consistently reach convergence before those in the classical MCMC random walk.

Computing the Bayes factor by thermodynamic integration

Models were compared using the Bayes factor, a ratio of integrals that can be computed in low dimensions fairly easily, for example, using the Gauss–Hermite quadrature (Kass and Raftery, 1995; Gelman, 2004). However, in high dimensions quadrature is expensive and we therefore turned to thermodynamic integration (Gelman and Meng, 1998; Lartillot and Philippe, 2006; Friel and Pettitt, 2008; Calderhead and Girolami, 2009). Thermodynamic integration relies on a constructed relation known as the power posterior, which resembles the overlap integral in the numerator or denominator in Equation 2 except for the introduction of a fictious ‘temperature’ t, a power variable to which the likelihood function is raised. Let us define z(t) by

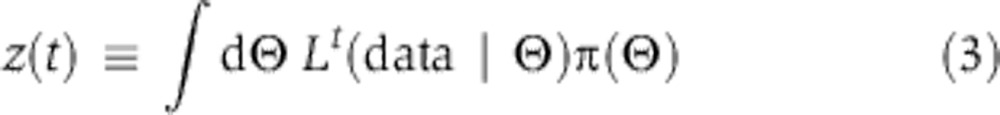At t=1, we recover the evidence (numerator or denominator in Equation 2), whereas at t=0 we obtain a value of 1 because the prior distribution integrates to 1. The temperature factor serves to flatten the likelihood function so that it resembles the likelihood and prior at t=1 and 0, respectively. Then, by the fundamental theorem of calculus, we obtain the following:

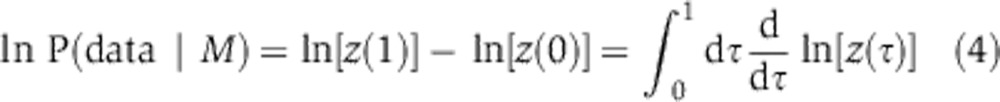The integrand is explicitly differentiable in the temperature variable.

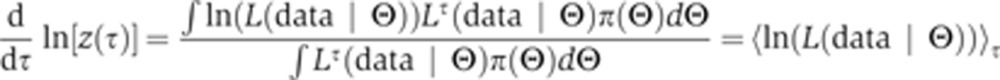The derivative is transformed into an average of the likelihood function. The bracket average is obtained by sampling from a temperature-dependent distribution (a normalized distribution that we denote as Q), which can be simulated, in the same way as the posterior, via convergent MCMC sampling. In particular, for any function f, we let:

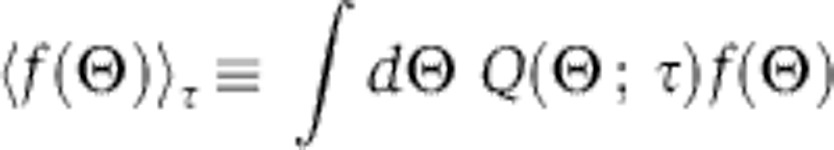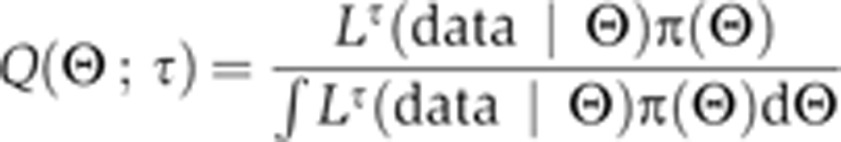In this way, calculation of a high-dimensional volume is converted into a one-dimensional integral of bracket averages over a fictitious temperature. The integrand must be estimated at each temperature via MCMC sampling. There is an appealing physical interpretation to this integral: the temperature factor ‘flattens’ the likelihood function whereas the bracket averaging calculates the likelihood function at different values of the ‘flatness’. When the temperature-based likelihood function is flattened, the sampled likelihoods will be poor (low), whereas when it is sharp and similar to the original posterior, the sampled likelihoods will be good (high). If the overlap volume is large, then the switch from poor to good will occur at low temperature (higher flatness). Conversely if the overlap volume is small, then comparatively the switch will occur at higher temperature (lower flatness). The evidence term is simply the exponential of the one-dimensional integral:

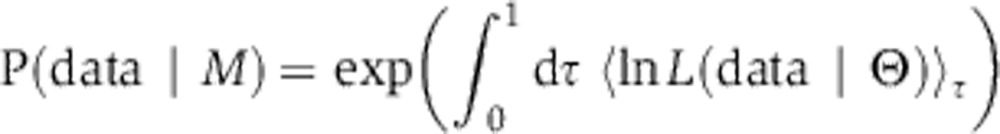The value of the bracket average 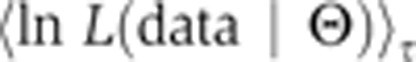was estimated by running three independent MCMC chains for 1 000 000 steps at each temperature τ. All chains achieved convergence as per the Gelman–Rubin criterion (although only the latter half of the chains were used, to allow a burn-in period for the MCMC algorithm). The integral necessary to calculate the value of ln P(data|M) in Equation 4 was then discretized over the interval τ∈[0,1]. The temperatures used to evaluate 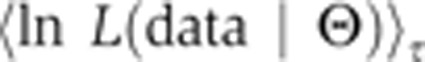were divided into three segments: τ∈[0,0.01], τ∈(0.01,0.1] and τ∈(0.1,1] comprising 11, 9 and 9, evenly spaced points, respectively. These values for the temperatures were chosen so that the smooth transition from poor likelihood values to good ones was accurately captured. The trapezoidal rule was applied to evaluate the integral:

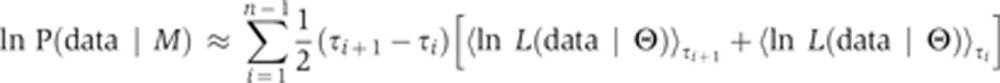Computational resources and MATLAB code

All code for simulation of the ODEs and for Bayesian sampling was written in MATLAB R2011a and is available for download at our Github repository ( https://github.com/sorgerlab/eydgahi_et_al_bayesian_estimation). A zip file of all repository contents is available ( https://github.com/sorgerlab/eydgahi_et_al_bayesian_estimation/zipball/master). An open source Python version integrated with our other modeling application PySB is also available under the name BayesSB ( http://sorgerlab.github.com/bayessb/). Parallel computation for multi-chain walks and Hessian calculations was performed on both a Windows desktop (Windows XP Service Pack 3; Intel® Core™2 CPU 6600 @ 2.40 GHz, 2.00 GB of RAM) and the RITG computing cluster at the Harvard Medical School comprising 4708 cores (451 nodes), made up of a mixture of IBM BladeCenters and Systems with 4-96 GB of memory per node, running Debian GNU/Linux 6.0.3. Each MCMC chain was run on a single node of the cluster; for every 25 000 steps, the main node created 20 parallel jobs, each of which calculated a piece of the 78 × 78 Hessian.