Skip to main content
PMC home page
EMBO Reports logoLink to EMBO Reports
. 2012 Feb 12;14(3):226–230. doi: 10.1038/embor.2013.9

How good is research really?

Measuring the citation impact of publications with percentiles increases correct assessments and fair comparisons

Lutz Bornmann 1, Werner Marx 2
PMCID: PMC3589094  PMID: 23399654

The normal method of scientific communication is to publish experimental and theoretical results and their interpretation in peer-reviewed journals. These articles and the data and analysis they contain often inspire or inform other research that either builds on the published insights or refutes or modify the original conclusions. These follow-up papers therefore cite the original articles. Thus, a scientific paper and its citations in other papers represent two quantities: “the increment of new science and the credit for its discovery” [1]. The number of citations a paper receives over time is therefore a direct measure of its usefulness to other scientists, although retracted or refuted papers can also become highly cited. However, these are exceptions.

The number of citations a paper receives over time is therefore a direct measure of its usefulness to other scientists…

Thus, publications and citations are useful measures to assess the productivity of scientists, research groups, research institutes and even whole countries. This has spawned new research fields and businesses that seek to develop algorithms or other methods to distil scientific articles and citations into a quantifier that reflects scientific productivity or quality. The highly popular journal impact factor (IF), for instance—which is the average number of citations (within one year) received by all papers in a journal published within the two subsequent years—is widely used as a proxy for the quality and scientific prestige of a journal. In research evaluation, it is also used as a proxy for the citation impact of single publications, despite the fact that the IF does not represent the citation impact of most papers in any journal [2].

Another popular indicator is the so-called ‘h index’, introduced in 2005 by physicist Jorge E. Hirsch to quantify the research output of scientists [3,4]. It was proposed as an alternative to other bibliometric indicators such as citations per paper and is defined as follows: “A scientist has index h if h of his or her Np papers have at least h citations each and the other (Np–h) papers have ≤h citations each” [3]. There are several other methods that attempt to measure the quality and quantity of science, but so far the IF and the h index are the most popular and most influential methods, given that these indicators are used routinely to make decisions about research funding, promotions and even science policy.

Experts in bibliometrics, however, avoid using both the IF and the h index because neither provide normalized values; it is not possible to compare scientists or journals from different fields or articles that have been published during different time periods. It is the same problem as, for instance, comparing the number of goals in football with handball—the average number of goals in one football game is around two and it is around 20 in a handball game. Similarly, the average number of citations in various research fields can differ easily by an order of magnitude. We cannot compare the raw numbers without some normalization; that is, by taking into account the average number of citations in a given research field during a defined time period.

Experts in bibliometrics […] avoid using both the IF and the h index because neither provide normalized values…

Since the 1980s, bibliometricians have been using reference sets to normalize the number of citations [5]. The purpose of these sets is to evaluate the citation impact of a publication against the citation impact of similar publications. The reference set contains publications in the same field (subject category), the same year and the same document type. The arithmetic mean value of the citations for all publications in the reference set is then calculated to specify an expected citation impact [6]. This enables bibliometricians to calculate a quotient—the (mean) observed citation rate divided by the mean expected citation rate. By using this quotient—the relative citation rate—instead of raw citation counts, it becomes possible to compare, for example, the citation impact of an article in a chemistry journal published five years ago with the impact of a physics article published ten years ago. Furthermore, it is possible to analyse the overall citation impact for a whole publication set, even if the papers were published in different fields or years and as different document types [7].

However, there is a significant disadvantage inherent in the calculation of means for the normalization of citations [8]. The distribution of citations over publications is usually not equal; the arithmetic mean value calculated for a reference set might be skewed by a few highly cited publications and is therefore not an appropriate measure of central tendency (8). This is why the University of Göttingen in Germany ended up second in the Leiden Ranking 2011/2012 in an analysis based on mean values. The indicator for this university “turns out to have been strongly influenced by a single extremely highly cited publication” [9]. The journal Acta Crystallographica A is another extreme example of skewed data—its IF [10] rose from 2,051 (Journal Citation Report 2008) to 49,926 (Journal Citation Report 2009) owing to a single, highly cited publication [11].Inline graphic

We need an alternative measure to generate normalized numbers and circumvent the problem of skewed data sets. In educational and psychological testing, percentiles are already used widely as a standard to evaluate an individual's test scores—intelligence tests for example—by comparing it with the percentiles of a calibrated sample [12]. Percentiles, or percentile rank classes, are also a suitable method for bibliometrics to normalize citation counts of publications in terms of the subject category and the publication year [8] and, unlike the mean-based indicators, percentiles are scarcely affected by skewed distribution. The percentile of a certain publication provides information about the impact this publication has had in comparison to other similar publications in the same subject category and publication year (and of the same document type).

The US National Science Board uses percentiles for the annual Science and Engineering Indicators to analyse the number of highly cited publications for selected countries [13]. Boyack [14] used percentiles to characterize publications in the Proceedings of the National Academy of Sciences USA from 1982 to 2001. Belter [15] analysed publications funded by the National Oceanic and Atmospheric Administration's (NOAA) Office of Ocean Exploration and Research, and commented that: “[p]ercentile ranks were selected for this analysis based on the growing consensus that they are more stable and consistent than most of the bibliometric indicators currently available” [15].

Percentiles have the additional advantage that they can be calculated relatively easily. All publications from a given subject category and publication year (and of a given document type) provide the reference set. The citations of these publications are the yardstick or expected value. The publications are sorted by citation numbers and broken down into percentile ranks with values between 0 and 100.

The publication set to be evaluated can be any ensemble, such as single papers, the publications by an individual researcher or the publication record of a research institute. The percentile of a publication is its relative position within the reference set—the higher the percentile rank, the more citations it has received compared with publications in the same subject category and publication year. For example, a value of 90 means that the publication in question is among the 10% most cited publications; the other 90% have achieved fewer citations. A value of 50 indicates the median and therefore an average impact. This way, it is possible to evaluate publications meaningfully and fairly within the same subject category and publication year as a relative scale between 0 (low impact) and 100 (high impact).

As an alternative to subject category, it is also possible to base the calculation of the expected citation impact on the journal in which a certain publication has appeared. However, individual journals are not an appropriate source from which to generate reference sets; manuscripts in high-impact journals, such as Science or Nature, would be penalized as the yard-stick would be higher. Conversely, publications in low-impact journals would seem to score highly, as it is easier to achieve a comparatively high-citation impact measured against a low-journal reference set.

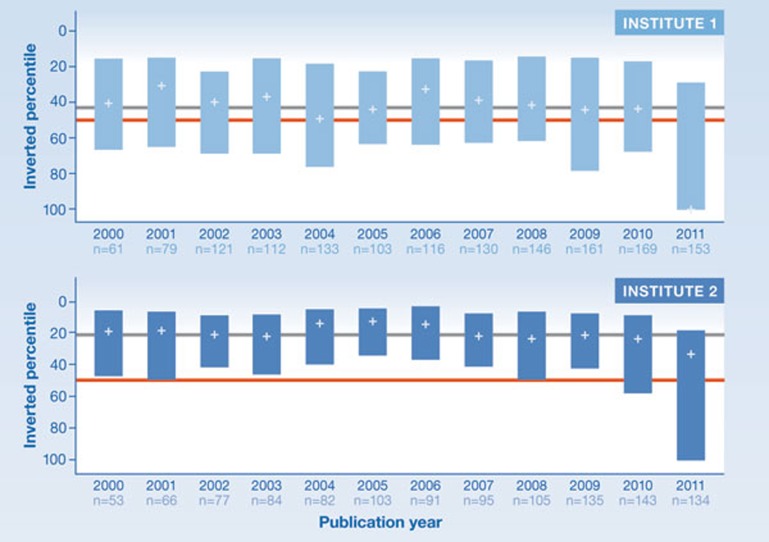
The InCites application of Thomson Reuters (http://researchanalytics.thomsonreuters.com/incites/) already provides percentiles to evaluate the impact of papers (Fig 1), but the scale is reversed—from 100 (low-citation impact) to 0 (high-citation impact). Accordingly, the lower the percentile for a publication, the more citations it has received in the same subject category and publication year. Percentiles from InCites are referred to as inverted percentiles.

Figure 1.

Figure 1

Open in a new tab

Distribution of inverted percentiles for publications between 2000 and 2011 from two research institutes (data source: InCites from Thomson Reuters).

So how does it work in practice? Table 1 shows the calculation of percentiles and inverted percentiles based on 13 publications from one year using the formula: rank divided by number of publications multiplied by 100. Such tables or reference sets are of course much larger in reality. The publication marked with an asterisk is a single publication, which is being evaluated by using percentiles. A specific reference set also allows the evaluation of multiple publications such as those of a scientist or a research institute published in the same field and year.

Table 1. Calculation of percentiles and inverted percentiles based on 13 publications from one year in a fictitious subject category.

Number of citations Ranking Total Percentile Reversed ranking Inverted percentile
35 13 13 100 1 7.69
17 12 13 92.31 2 15.38
14 11 13 84.62 3 23.08
12* 10* 13* 76.92* 4* 30.77*
10 9 13 69.23 5 38.46
9 8 13 61.54 6 46.15
7 7 13 53.85 7 53.85
5 6 13 46.15 8 61.54
4 5 13 38.46 9 69.23
3 4 13 30.77 10 76.92
2 3 13 23.08 11 84.62
1 2 13 15.38 12 92.31
0 1 13 7.69 13 100
Open in a new tab

*Publication to be evaluated.

Frequently, several publications have the same number of citations and therefore the same rank. There are various options for dealing with these cases, which are the subject of discussion in bibliometric literature [7,16,17,18,19]. Moreover, almost half of all publications are assigned by Thomson Reuters to more than one subject category. It raises the question of which of these categories should become the basis for the calculation, as in terms of citation impact, these categories are often extremely different. There are different options for handling these cases [20]. InCites only uses the subject category in which a publication does best. Another option would be to create an average percentile over all subject categories.

The distribution of percentiles in an evaluation can be illustrated with box plots. Fig 1 shows an example of publications from two research institutes over a period of ten years based on the inverted percentiles from InCites. The outer margins of the box indicate the first quartile (25% of the values) and the third quartile (75% of the values) of the publications from one institute. The cross in the middle of the box represents the median (50% of the values above and below). The lower the median, the larger the mean impact of the publication set. The position of the median within the box indicates the skewness of the citations over the publications to be evaluated.

If we randomly select a sample of publications (percentiles) from InCites, we could expect a median percentile of 50; the expected percentile of an institute is therefore 50 (red line). In the given example, the publications from Institute 1 have an average (median) percentile of about 43 during all publication years (grey line). Institute 2 performs significantly better with an average percentile of around 22. The most recent publication year normally has a high median, meaning a low impact, because many publications from this year have not been cited at all or are only rarely cited.

…mere citation figures have little meaning without normalization for subject category and publication year

As the citation data of both institutes can be treated as cluster samples from the population of all publications [21], it is possible to further test the statistical significance of the difference between the institutes. For example, the Mann–Whitney test determines the probability of a publication from Institute 1 performing worse (or better) than a publication of Institute 2 [22]; the result indicates that Institute 1 has a significantly higher probability, in statistical terms, of publishing a paper with a worse citation performance, or higher percentile, than Institute 2.

In addition to analysing the distribution of percentiles, it is possible to focus on percentile rank classes. Bornmann [23] proposes—also as an alternative to the h index [3,24]—the Ptop 10% or PPtop 10% indicators, which can be considered to belong to the group of ‘success indicators’ in bibliometrics, to evaluate an institute. These indicators count the number of successful publications by a research unit, taking into account normalization over age and field [25,26,27]. Ptop 10% is the number and PPtop 10% is the proportion of publications that belong to the top 10% most frequently cited publications. A publication belongs to this group if it is cited more often than 90% of publications published in the same field and in the same year [8,28,29]. In the example in Figure 1, these values are Ptop 10% = 208 and PPtop 10% = 14% for Institute 1 and Ptop 10% = 350 and PPtop 10% = 30% for Institute 2.

Ptop 10% and PPtop 10% have the additional benefit that they do not use an arbitrary threshold to determine the successful publications in a set, which is a disadvantage of the h index. “For instance, the h index could equally well have been defined as follows: a scientist has an h index of h if h of his publications each have at least 2h citations and his remaining publications each have fewer than 2(h+1) citations. Or the following definition could have been proposed: A scientist has an h index of h if h of his publications each have at least h/2 citations and his remaining publications each have fewer than (h +1)/2 citations” [30]. By contrast, publications that are among the 10% most cited publications in their subject category can be called ‘highly cited’ or ‘excellent’ as defined and used by many bibliometricians [9,28,31,32,33]. “A highly cited work is one that has been found useful by a relatively large number of people, or in a relatively large number of experiments” [34].

Bilbiometrics should not replace peer or expert review […] but it can generate comprehensible and reliable quantitative data for fair assessment

PPtop 10% offers a third advantage over the h index in terms of allowing direct comparisons between publication sets. Statistically, it could be expected that 10% of publications from a random sample (drawn from InCites) would belong to the top 10% of the most-cited publications in a given subject category and publication year. The expected PPtop 10% would therefore be 10%. In our example, Institute 1 with a PPtop 10% of 14% is thus only four percentage points better than the expected value of 10%, whereas Institute 2 with a PPtop 10% of around 30% is a considerable 20 percentage points better than the 10% value.

Given these advantages of both percentiles and the related Ptop 10% and PPtop 10%, various institutions are already using these measures to analyse and rank research institutions. According to the Centre for Science and Technology Studies at Leiden University in the Netherlands, “[w]e therefore regard the PPtop 10% indicator as the most important impact indicator in the Leiden Ranking” [9], which measures the scientific performance of 500 major universities worldwide. The indicator is also used in the current SCImago Institutions Ranking World Reports 2012 of research institutions (http://www.scimagoir.com/; [35]).

In summary, mere citation figures have little meaning without normalization for subject category and publication year (and also for document type). Percentile distributions and percentile rank classes allow a simple and fair citation assessment of publications against a reference data set of similar publications. Box plots of the percentile distribution provide a meaningful visualization and presentation of research performance. Such plots can be easily applied to different levels of aggregation from individual researchers to research institutes and universities, and can be used to compare different units. There is no doubt still room for improvement concerning the categorization of publication sets, but there are only a few meaningful alternative methods in bibliometrics to compare publication sets across multiple subject categories [36].

Bibliometrics has become an important field that is relevant to most scientists. Any researcher who applies for a position, tenure or grant, is well aware that his or her publication output and citation impact will be analysed, quantified and considered. Bibliometrics should not replace peer or expert review—only experts can judge research activities [37]—but it can generate comprehensible and reliable quantitative data for fair assessment. Citation-based metrics are an objective counterweight to peer review, which is inevitably prone to bias. Citation analysis is based on the votes of many experts, such as authors of scientific papers, and it is quantitative and verifiable. By using advanced bibliometric methods such as percentiles, experts can produce meaningful results on the performance of scientists, research groups and institutes.

Meanwhile, an increasing number of dedicated journals, books and conferences attest to the growing importance of bibliometrics. Applying bibliometrics to bibliometrics itself reveals a rapid expansion of the relevant literature with about 1,500 papers published per year in the field. In June 2010, Nature published a series of articles on citation analysis [38,39,40]. But bibliometrics is not without shortcomings. Its weakness is not necessarily the method itself, but a lack of background information and understanding of what the data really mean and what they do not mean. A survey among Nature readers revealed growing use, but only limited satisfaction—less than a quarter of respondents said they were quite satisfied, whilst most were not very satisfied or not satisfied at all. The use of poor and inadequate indicators, such as the h index or the IF, to make decisions about research funding or career progression might be a main reason why many scientists continue to have serious reservations about the use of bibliometrics.

Citation analysis is based on the votes of many experts, such as authors of scientific papers, and it is quantitative and verifiable

The goal of bibliometric research itself is the development and testing of new performance indicators for research evaluation. For example, to address specific disadvantages of the original h index, nearly 40 variants of the h index have been proposed, most of which are redundant in terms of their application [41]. We need new citation impact indicators that normalize for any factors other than quality that influence citation rates and that take into account the skewed distributions of citations across papers. The percentile indicators described in this paper might provide a solution.

graphic file with name embor20139i2.jpg

Open in a new tab

Lutz Bornmann

graphic file with name embor20139i3.jpg

Open in a new tab

Werner Marx

Footnotes

The authors declare that they have no conflict of interest.

References

  1. Greene M (2007) The demise of the lone author. Nature 450: 1165. [DOI] [PubMed] [Google Scholar]
  2. Bornmann L, Marx W, Gasparyan AY, Kitas GD (2012) Diversity, value and limitations of the journal impact factor and alternative metrics. Rheumatol Int 32: 1861–1867 [DOI] [PubMed] [Google Scholar]
  3. Hirsch JE (2005) An index to quantify an individual's scientific research output. Proc Natl Acad Sci USA 102: 16569–16572 [DOI] [PMC free article] [PubMed] [Google Scholar]
  4. Bornmann L, Daniel H-D (2007) What do we know about the h index? J Am Soc Inf Sci Technol 58: 1381–1385 [Google Scholar]
  5. Vinkler P (2010) The Evaluation of Research by Scientometric Indicators. Oxford, UK: Chandos [Google Scholar]
  6. Schubert A, Braun T (1986) Relative indicators and relational charts for comparative assessment of publication output and citation impact. Scientometrics 9: 281–291 [Google Scholar]
  7. Bornmann L, Leydesdorff L, Mutz R (2013) The use of percentiles and percentile rank classes in the analysis of bibliometric data: opportunities and limits. J Informetr 7: 158–165 [Google Scholar]
  8. Bornmann L, Mutz R, Marx W, Schier H, Daniel H-D (2011) A multilevel modelling approach to investigating the predictive validity of editorial decisions: do the editors of a high-profile journal select manuscripts that are highly cited after publication? J R Stat Soc Ser A Stat Soc 174: 857–879 [Google Scholar]
  9. Waltman L et al. (2012) The Leiden Ranking 2011/2012: data collection, indicators, and interpretation. J Am Soc Inf Sci Tec 63: 2419–2432 [Google Scholar]
  10. Garfield E (2006) The history and meaning of the journal impact factor. JAMA 295: 90–93 [DOI] [PubMed] [Google Scholar]
  11. Dimitrov JD, Kaveri SV, Bayry J (2010) Metrics: journal's impact factor skewed by a single paper. Nature 466: 179. [DOI] [PubMed] [Google Scholar]
  12. Jackson C (1996) Understanding Psychological Testing. Leicester, UK: British Psychological Society [Google Scholar]
  13. National Science Board (2012) Science and Engineering Indicators. Arlington, Virginia, USA: National Science Foundation [Google Scholar]
  14. Boyack KW (2004) Mapping knowledge domains: characterizing PNAS. Proc Natl Acad Sci USA 101: 5192–5199 [DOI] [PMC free article] [PubMed] [Google Scholar]
  15. Belter C (2013) A bibliometric analysis of NOAA's Office of Ocean Exploration and Research. Scientometrics [Epub ahead of print] doi:; DOI: 10.1007/s11192-012-0836-0 [DOI] [PMC free article] [PubMed] [Google Scholar]
  16. Bornmann L (2013) The problem of percentile rank scores used with small reference sets. J Am Soc Inf Sci Tec (in the press) [Google Scholar]
  17. Leydesdorff L (2012) Accounting for the uncertainty in the evaluation of percentile ranks. J Am Soc Inf Sci Tec 63: 2349–2350 [Google Scholar]
  18. Rousseau R (2012) Basic properties of both percentile rank scores and the I3 indicator. J Am Soc Inf Sci Tec 63: 416–420 [Google Scholar]
  19. Schreiber M (2012) Inconsistencies of recently proposed citation impact indicators and how to avoid them. J Am Soc Inf Sci Tec 63: 2062–2073 [Google Scholar]
  20. Bornmann L (2013) Assigning publications to multiple subject categories for bibliometric analysis: an empirical case study based on percentiles. J Doc (in the press) [Google Scholar]
  21. Bornmann L, Mutz R (2013) The advantage of the use of samples in evaluative bibliometric studies. J Informetr 7: 89–90 [Google Scholar]
  22. Conroy RM (2012) What hypotheses do ‘nonparametric’ two-group tests actually test? Stata Journal 12: 1–9 [Google Scholar]
  23. Bornmann L (2013) How to analyse percentile citation impact data meaningfully in bibliometrics: The statistical analysis of distributions, percentile rank classes and top-cited papers. J Am Soc Inf Sci Tec (in the press) [Google Scholar]
  24. Bornmann L, Daniel H-D (2009) The state of h index research. Is the h index the ideal way to measure research performance? EMBO Rep 10: 2–6 [DOI] [PMC free article] [PubMed] [Google Scholar]
  25. Kosmulski M (2012) Modesty-index. J Informetr 6: 368–369 [Google Scholar]
  26. Franceschini F, Galetto M, Maisano D, Mastrogiacomo L (2012) The success-index: an alternative approach to the h-index for evaluating an individual's research output. Scientometrics 92: 621–641 [Google Scholar]
  27. Kosmulski M (2011) Successful papers: a new idea in evaluation of scientific output. J Informetr 5: 481–485 [Google Scholar]
  28. Bornmann L, de Moya Anegón F, Leydesdorff L (2012) The new Excellence Indicator in the World Report of the SCImago Institutions Rankings 2011. J Informetr 6: 333–335 [Google Scholar]
  29. Leydesdorff L, Bornmann L, Mutz R, Opthof T (2011) Turning the tables in citation analysis one more time: principles for comparing sets of documents J Am Soc Inf Sci Tec 62: 1370–1381 [Google Scholar]
  30. Waltman L, van Eck NJ (2012) The inconsistency of the h-index. J Am Soc Inf Sci Tec 63: 406–415 [Google Scholar]
  31. Tijssen R, van Leeuwen T (2006) Centres of research excellence and science indicators. Can ‘excellence’ be captured in numbers? In Ninth International Conference on Science and Technology Indicators (ed Glänzel W), pp 146–147. Leuven, Belgium: Katholieke Universiteit Leuven [Google Scholar]
  32. Tijssen R, Visser M, van Leeuwen T (2002) Benchmarking international scientific excellence: are highly cited research papers an appropriate frame of reference? Scientometrics 54: 381–397 [Google Scholar]
  33. Sahel JA (2011) Quality versus quantity: assessing individual research performance. Sci Transl Med 3: 84cm13. [DOI] [PMC free article] [PubMed] [Google Scholar]
  34. Garfield E (1979) Citation Indexing—its Theory and Application in Science, Technology, and Humanities. New York, USA: Wiley [Google Scholar]
  35. SCImago Reseach Group (2012) SIR World Report 2012. Granada, Spain: University of Granada [Google Scholar]
  36. Bornmann L, Mutz R, Neuhaus C, Daniel H-D (2008) Use of citation counts for research evaluation: standards of good practice for analyzing bibliometric data and presenting and interpreting results. ESEP 8: 93–102 [Google Scholar]
  37. Bornmann L (2011) Scientific peer review. Annu Rev Inform Sci 45: 199–245 [Google Scholar]
  38. van Noorden R (2010) Metrics: a profusion of measures. Nature 465: 864–866 [DOI] [PubMed] [Google Scholar]
  39. Anon (2006) Cash-per-publication...is an idea best avoided. Nature 441: 785–786 [DOI] [PubMed] [Google Scholar]
  40. Anon (2010) How to improve the use of metrics. Nature 465: 870–872 [DOI] [PubMed] [Google Scholar]
  41. Bornmann L, Mutz R, Hug SE, Daniel H-D (2011) A meta-analysis of studies reporting correlations between the h index and 37 different h index variants. J Informetr 5: 346–359 [Google Scholar]

Articles from EMBO Reports are provided here courtesy of Nature Publishing Group

RESOURCES