Shape-Based Classification of 3D Head Data

Abstract

Craniofacial disorders are one of the most common category of birth defects worldwide, and are an important topic of biomedical research. In order to better understand these disorders and correlate them with genetic patterns and life outcomes, researchers need to quantify the craniofacial anatomy. In this paper we introduce several different craniofacial descriptors that are being used in research studies for two craniofacial disorders: the 22q11.2 deletion syndrome (a genetic disorder) and plagiocephaly/brachycephaly, disorders caused by pressure on the head. Experimental results show that our descriptors show promise for quantifying craniofacial shape.

1 Introduction

Researchers at the Seattle Children’s Hospital Craniofacial Center (SCHCC) study craniofacial disorders in children. They wish to develop new computational techniques to represent, quantify, and analyze variants of biological morphology from imaging sources such as stereo cameras, CT scans and MRI scans. The focus of their research is the introduction of principled algorithms to reveal genotype-phenotype disease associations. We are collaborating in two research studies at SCHCC for the study of craniofacial anatomy. The first study is of children with the 22q11.2 deletion syndrome, a genetic disease, which causes abnormalities of the face, including such features as asymmetric face shape, hooded eyes, bulbous nasal tip, and retrusive chin, among others (Figure 1a). The second study is of infants with plagiocephaly or brachycephaly, two conditions in which a portion of the child’s head, usually at the back, becomes abnormally flat (Figure 1b). Our objective is to provide feature-extraction tools for the study of craniofacial anatomy from 3D mesh data obtained from the 3dMD active stereo photogrammetry system at SCHCC. These tools will produce quantitative representations (descriptors) of the 3D data that can be used to summarize the 3D shape as pertains to the condition being studied and the question being asked.

Fig. 1.

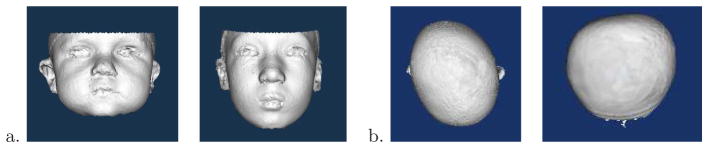
3D mesh data. a) Faces of 2 children with 22q11.2 deletion syndrome; b) Tops of heads of children with plagiocephaly (left) and brachycephaly (right).

This paper describes our work on extracting shape descriptors from 3D craniofacial data in the form of 3D meshes and using them for classification. Section 2 discusses related work from both medical image analysis and computer vision. Section 3 describes our procedures for data acquisition and preprocessing. Section 4 explains the descriptors we have developed for studies of the 22q11.2 deletion syndrome and related classification results. Section 5 discusses the descriptors we have developed for studies of plagiocephaly and brachycephaly and experimental results. Section 6 concludes the paper.

2 Related Work

There are two main classes of research related to this work: medical studies of craniofacial features and 3D shape analysis from computer vision. Traditionally, the clinical approach to identify and study an individual with facial dysmorphism has been through physical examination combined with craniofacial anthropometric measurements [7]. Newer methods of craniofacial assessment use digital image data, but hand measurement or at least hand labeling of landmarks is common.

With respect to 22q11.2DS, craniofacial anthropometric measurements prevail as the standard manual assessment method; automated methods for its analysis are limited to just two. Boehringer et al. [2] applied a Gabor wavelet transformation to 2D photographs of individuals with ten different facial dysmorphic syndromes. The generated data sets were then transformed using principal component analysis (PCA) and classified using linear discriminant analysis, support vector machines, and k-nearest neighbors. The dense surface model approach [4] aligns training samples according to point correspondences. It then produces an “average” face for each population being studied and represents each face by a vector of PCA coefficients. Neither method is fully automatic; both require manual landmark placement.

There has also been some semiautomated work on analysis of plagiocephaly and brachycephaly. Hutchison et al. [5] developed a technique called HeadsUp that takes a top view digital photograph of infant heads fitted with an elastic head circumference band equipped with adjustable color markers to identify landmarks. The resulting photograph is then automatically analyzed to obtain quantitative measurements for the head shape. Zonenshayn et al. [10] used a headband with two adjustable points and photographs of the headband shape to calculate a cranial index of symmetry. Both these methods analyze 2D shapes for use in studying 3D craniofacial anatomy

Computer vision researchers have not, for the most part, tackled shape-based analysis of 3D craniofacial data. The most relevant work is the seminal paper on face recognition using eigenfaces [8]. Work on classification and retrieval for 3D meshes has concentrated on large data sets containing meshes of a wide variety of objects. In the SHREC shape retrieval contest, algorithms must distinguish between such objects as a human being (in any pose!), a cow, and an airplane. A large number of descriptors have been proposed for this competition; the descriptor that performs best is based on the shapes of multiple 2D views of the 3D mesh, represented in terms of Fourier descriptors and Zernike moments [3].

3 Data Acquisition and Preprocessing

The 3D data used in this research was collected at the Craniofacial Center of Seattle Children’s Hospital for their studies on 22q11.2 deletion syndrome, plagiocephaly, and brachycephaly. The 3dMD imaging system uses four camera stands, each containing three cameras. Stereo analysis yields twelve range maps that are combined using 3dMD proprietary software to yield a 3D mesh of the patient’s head and a texture map of the face. Our project uses only the 3D meshes, which capture the shape of the head.

An automated system to align the pose of each mesh was developed, using symmetry to align the yaw and roll angles and a height differential to align the pitch angle. Although faces are not truly symmetrical, the pose alignment procedure can be cast as finding the angular rotations of yaw and roll that minimized the difference between the left and right side of the face. The pitch of the head was aligned by minimizing the difference between the height of the chin and the height of the forehead. If the final alignment is not satisfactory, it is adjusted by hand, which occurred in 1% of the symmetry alignments and 15% of the pitch alignments.

4 Shape-Based Description of 3D Face Data for 22q11.2 Deletion Syndrome

22q11.2 deletion syndrome has been shown to be one of the most common multiple anomaly syndromes in humans [6]. Early detection is important as many affected individuals are born with a conotruncal cardiac anomaly, mild-to-moderate immune deficiency and learning disabilities, all of which can benefit from early intervention.

4.1 Descriptors

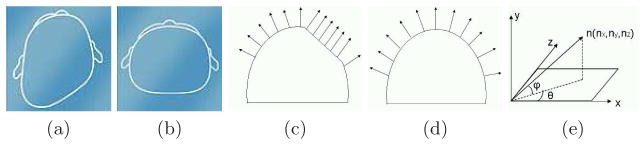
Since 3D mesh processing is expensive and the details of the face are most important for our analysis, we constructed three different global descriptors from the 3D meshes: 2D frontal and side snapshots of the 3D mesh (Figure 2a), 2.5D depth images (Figure 2b), and 1D curved line segments (Figure 2c). The 2D snapshots are merely screen shots of the 3D mesh from the front and side views. The 2.5D depth images represent the face on an x-y grid so that the value of a pixel at point (x,y) is the height of the point above a plane used to cut the face from the rest of the mesh. The curved line segment is a 1D representation of the fluctuations of a line travelling across the face. Curved line segments were extracted in multiple positions in both the vertical and horizontal directions. We experimented with 1, 3, 5, and 7 line segments in each direction; Figure 2d shows a grid of 3 × 3 lines. The curved line shown in Figure 2c came from the middle vertical line of the grid. Each of the three descriptors was transformed using PCA, which converted its original representation into a feature vector comprised of the coefficients of the eigenvectors. Since there were 189 individuals in our full data set, this allowed for a maximum 189 attribute representation. Our analyses determined that the 22q11.2 syndrome, because of its subtle facial appearance, required the entire set of 189 coefficients.

Fig. 2.

a) 2D snapshot of the 3D mesh from front and side views; b) 2.5D depth representation in which the value of each pixel is the height above a cutting plane; c) 1D curved line segment; d) grid of curved line segments.

We are also working on automatic detection and description of local features known to be common manifestations of 22q11.2DS. The bulbous nasal tip is a nasal anomaly, which is associated with a ball-like nasal appearance. The depth ND of the nose is detected as the difference in height between the tip of the nose and its base. A sequence of nasal tip regions NT_i are produced by varying a depth threshold i from ND down to 1, stopping just before the nasal tip region runs into another region (usually the forehead). For each NT_i, its bounding box BNT_i and an ellipse E_i inscribed in that box are constructed and used to calculate two nasal features, rectangularity R_i and circularity C_i, and a severity score S^f for each feature f.

$$\begin{array}{l}{R}_i=\mathit{area}({NT}_i)/\mathit{area}({\mathit{BNT}}_i)\\ C_i=\left(\mathit{area}({NT}_i)-\mathit{area}(E_i)\right)/\mathit{area}({\mathit{BNT}}_i)\\ S^f=\mid \{i\mid f_i>f_t\}\mid /ND\end{array}$$

where f_t is a threshold for feature f, empirically chosen to be stable over multiple data sets. The bulbous nose coefficient B is then defined as a combination of rectangularity and circularity: B = S^rect(1 − S^circ).

4.2 Classification Experiments

We have run a number of classification experiments using the PCA representations of the three descriptors. Our experiments use the the WEKA suite of classifiers [9] with 10-fold cross validation to distinguish between affected and control individuals. We calculated the following performance measures: accuracy (percent of all decisions that were correct), recall (percentage of all affected individuals that are correctly labeled affected), and precision (percentage of individuals labeled affected that actually are affected).

Although testing on a balanced set is common practice in data mining, our data set only included a small number of affected individuals. The full data set included 189 individuals (53 affected, 136 control). Set A106 matched each of the 53 affected individuals to a control individual of closest age. Set AS106 matched each of the 53 affected individuals to a control individual of same sex and closest age. Set W86 matched a subset of 43 affected self-identified white individuals to a control individual of same ethnicity, sex and closest age. Set WR86 matched the same 43 affected white individuals to a control individual of same ethnicity, sex and age, allowing repeats of controls where same-aged subjects were lacking. The full data set obtained the highest accuracy (75%), but due to a large number of false positives, its precision and recall were very low (.56 and .52, respectively). The W86 data set achieved the highest results in precision and recall, and its accuracy was approximately the same as the full data set (74%); it was thus selected as most appropriate for this work.

For the human viewer, the 3D Snapshot is considered to hold much more information than the 2.5D representation. As shown in Table 1, we found no statistically significant difference in classifier performance for the two different representations. However, since the 2.5D representation retains the 3D shape of the face, it is better suited to developing algorithms for finding 3D landmarks used in local descriptor development. For the curved lines, the 3 and 5 vertical line descriptors performed the best, even outperforming the more detailed 2.5D depth image as shown in Table 1, while horizontal lines performed poorly. For the local nasal tip features, the combination of all three features gave the best performance. The local nasal tip results are promising considering that the nose is only one of several different facial areas to be investigated.

Table 1.

Comparison of 2D snapshots, 2.5D depth representations, vertical curved lines, and local nasal features using the Naive Bayes classifier on the W86 data set.

	2D snap	2.5D depth	1 line	3 lines	5 lines	7 lines	Rect. Sev.	Circle Sev.	Bulb. Coef.	Nasal Feat.
Precision	0.88	0.80	0.81	0.88	0.88	0.79	0.67	0.71	0.77	0.80
Recall	0.63	0.69	0.68	0.70	0.73	0.62	0.59	0.63	0.58	0.67
Accuracy	0.76	0.76	0.75	0.80	0.82	0.72	0.64	0.68	0.70	0.75

5 3D Shape Severity Quantification and Localization for Deformational Plagiocephaly and Brachycephaly

Deformational plagiocephaly (Figure 3a) refers to the deformation of the head characterized by a persistent flattening on the side, resulting in an asymmetric head shape and misalignment of the ears. Brachycephaly (Figure 3b) is a similar condition in which the flattening is usually located at the back of the head, resulting in a symmetrical but wide head shape. Current shape severity assessment techniques for deformational plagiocephaly and brachycephaly rely on expert scores and are very subjective, resulting in a lack of standard severity quantification. To alleviate this problem, our goal was to define shape descriptors and related severity scores that can be automatically produced by a computer program operating on 3D mesh data.

Fig. 3.

(a) Example of plagiocephaly. (b) Example of brachycephaly ((a) and (b) are from www.cranialtech.com). (c) Surface normal vectors of points that lie on a flat surface and will create a peak in the 2D angle histogram. (d) Surface normal vectors of points that lie on a more rounded surface and will be spread out in the histogram bins. (e) Azimuth and elevation angles of a 3D surface normal vector.

Our original dataset consisted of 254 3D head meshes, each assessed by two human experts who assigned discrete severity scores based on the degree of the deformation severity at the back of the head: category 0 (normal), category 1 (mild), category 2 (moderate), and category 3 (severe). To avoid inter-expert score variations, heads that were assigned different scores by the two human experts were removed from the dataset. The final dataset for our experiments consisted of 140 3D meshes, with 50 in category 0, 46 in category 1, 35 in category 2, and 9 in category 3.

Our method for detecting plagiocephaly and brachycephaly on the 3D meshes uses 2D histograms of the azimuth and elevation angles of surface normals. The basic idea behind the methodology is that on flat surfaces of the skull, which are approximately planar, all the surface normals point in the same direction. An individual with plagiocephaly or brachycephaly will have one or more such flat spots, and the larger they are the more surface normals will point in that direction (Figure 3c). Unaffected individuals are expected to have a more even distribution of surface normal directions, since their heads are more rounded (Figure 3d).

We calculate the surface normal at each point on the posterior side of the head and represent each by the azimuth and elevation angles, as shown in Figure 3e. Since our descriptors are histograms, the computed angles must be converted into a small number of ranges or bins. In our work we use 12 bins each for azimuth and elevation angles and construct a 144-bin 2D histogram. Each bin represents an azimuth/elevation combination that corresponds to a particular area of the head and contains the count of normals with that combination. We defined a severity score for the left and right sides of the back of the head using the appropriate bins. The left posterior flatness score is the sum of the histogram bins that correspond to azimuth angles ranging from −90° to −30° and elevation angles ranging from −15° to 45°, while the right posterior flatness score is the sum of the bins for azimuth angles ranging from −150° to −90° and elevation angles ranging from −15° to 45°. Figure 4 shows 16 relevant bins of the 2D histograms for 7 different individuals with expert scores ranging from −3 to 3; scores < 0 indicate left posterior flatness, while expert scores > 0 indicate right posterior flatness. The histogram for the unaffected individual (Expert score 0) has no bins with high counts. The histogram for individuals with right posterior flatness have high bin counts in columns 1–2 of the 2D histogram, while individuals with left posterior flatness have high bin counts in columns 3–4.

Fig. 4.

Most relevant bins of 2D histograms of azimuth and elevation angles of surface normal vectors on 3D head mesh models. As the severity of flatness increases on the side of the head, the peak in the 2D histogram becomes more prominent

5.1 Classification Experiments

We have run a number of experiments to measure the performance of our shape severity scores in distinguishing individuals with head shape deformation. As in the 22q11.2 deletion syndrome experiments, we used accuracy, precision and recall to measure the performance of our method. The objective of our first two experiments was to measure the performance of our left and right posterior flatness scores. We calculated these scores for all the heads in our dataset and used an empirically obtained threshold of t = 0.15 to distinguish individuals with either left or right posterior flatness. As shown in Table 2, our left and right posterior flatness scores agree well with the experts, particularly on the left side. Note that the experts chose only the side with the most flatness to score, whereas the computer program detected flatness on both sides; this accounts for some of the discrepancy. For the third experiment, we calculated an asymmetry score as the difference between left posterior and right posterior flatness of the affected individuals and compared it to asymmetry scores provided by the experts. The results in Table 2 show that our method performs quite well. Furthermore, the bins with high counts can be projected back onto the heads to show doctors where the flatness occurs and for additional use in classification.

Table 2.

Performance of left, right and asymmetry posterior flatness scores.

	Left score	Right score	Asymmetry score
Precision	0.88	0.77	0.96
Recall	0.92	0.88	0.88
Accuracy	0.96	0.82	0.96

6 Generality of Approach and Conclusion

The descriptors we have developed were motivated by particular craniofacial disorders: 22q11.2 deletion syndrome and plagiocephaly/brachycephaly. The global descriptors are basic representations that we claim can be useful to quantify most, if not all, craniofacial disorders. In order to illustrate this point, we have begun a study of midface hypoplasia, a flattening of the midface of individuals, often present in 22q11.2DS, but of particular interest in those with cleft lip/palate. We used vertical curved lines in the midcheek area to produce one set of descriptors and the angle histograms projected onto the faces (instead of the backs of the heads) to produce a second set. Figure 5 illustrates the difference between two individuals without midface hypoplasia and two who are affected. The curved lines, which seem only slightly different to computer vision researchers, were considered to be highly differentiable by the craniofacial experts. The projection of the angle histograms to the faces shows an interesting pattern, whose 2D snapshot can be used in classification. We conclude that our descriptors are general representations that are useful in quantifying craniofacial anatomy for use by doctors and biomedical researchers.

Fig. 5.

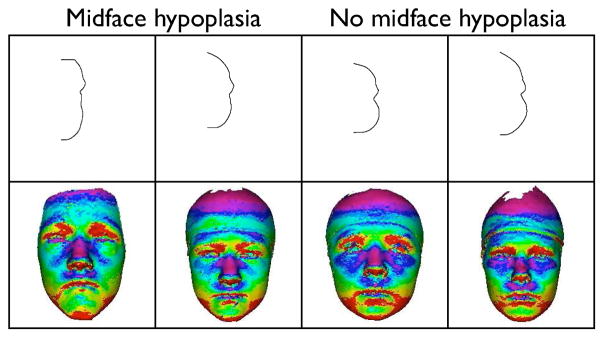
Comparison of cheek lines and projected angle histograms for individuals with flat midface vs. unaffected individuals.