Power Comparison of Admixture Mapping and Direct Association Analysis in Genome-Wide Association Studies

Abstract

When dense markers are available, one can interrogate almost every common variant across the genome via imputation and single nucleotide polymorphism (SNP) test, which has become a routine in current genome-wide association studies (GWASs). As a complement, admixture mapping exploits the long-range linkage disequilibrium (LD) generated by admixture between genetically distinct ancestral populations. It is then questionable whether admixture mapping analysis is still necessary in detecting the disease associated variants in admixed populations. We argue that admixture mapping is able to reduce the burden of massive comparisons in GWASs; it therefore can be a powerful tool to locate the disease variants with substantial allele frequency differences between ancestral populations. In this report we studied a two-stage approach, where candidate regions are defined by conducting admixture mapping at stage 1, and single SNP association tests are followed at stage 2 within the candidate regions defined at stage 1. We first established the genome-wide significance levels corresponding to the criteria to define the candidate regions at stage 1 by simulations. We next compared the power of the two-stage approach with direct association analysis. Our simulations suggest that the two-stage approach can be more powerful than the standard genome-wide association analysis when the allele frequency difference of a causal variant in ancestral populations, is larger than 0.4. Our conclusion is consistent with a theoretical prediction by Risch and Tang ([2006] Am J Hum Genet 79:S254). Surprisingly, our study also suggests that power can be improved when we use less strict criteria to define the candidate regions at stage 1.

INTRODUCTION

Admixture mapping has been proposed as an efficient approach for localizing genes in a recent admixed population in which the risk alleles have different frequencies among the ancestral populations. The idea of using the linkage disequilibrium (LD) due to the population admixture process was proposed half a century ago [Rife, 1954], but it took nearly four decades to gain serious attention [Briscoe et al., 1994; Chakroborty and Weiss, 1988; Mc-Keigue, 1998; Risch, 1992; Stephens et al., 1994], and only recently the panels of ancestral informative markers (AIMs) and relevant statistical methods have become available [Zhu et al., 2008a]. Since the publications of the first genome-wide admixture study for hypertension [Zhu et al., 2005] in African Americans, a range of traits and diseases have been studied using admixture mapping, e.g., multiple sclerosis [Reich et al., 2005], prostate cancer [Freedman et al., 2006, Bock et al., 2009], hypertension [Zhu and Cooper, 2007, Zhu et al., 2011], type 2 diabetes [Elbein et al., 2009; Kao et al., 2008], breast cancer [Fejerman et al., 2009], obesity [Basu et al., 2009a, Cheng et al., 2009], lipid levels [Basu et al., 2009b], and retinal vascular caliber [Cheng et al., 2010]. Systematic reviews of historical perspective, AIM panels, and software packages, as well as recent successes in mapping human diseases of recently admixed populations can be found in the literature [Winkler et al., 2010; Zhu et al., 2008a].

When different populations have different disease prevalence, it is reasonable to assume that the genetic causal variants may have different risk allele frequencies in different populations [Halder and Shriver, 2003]. For a chromosome segment where a causal variant resides, affected individuals descended from the recent admixture of two ethnic populations may have an increased probability of inheriting the alleles from the ethnic population with higher disease-susceptibility allele frequency. In modern admixed populations, such as African Americans and Hispanic Americans, the admixture process has been occurring in the past 20 generations. Linkage disequilibrium due to the admixture process should thus extend over a long genetic distance. In African Americans, for example, ancestry blocks were observed to extend for 17–20 centimorgans (cM) on average [Montana and Pritchard, 2004; Parra et al., 1998; Patterson et al., 2004; Smith et al., 2004; Tang et al., 2006; Zhu et al., 2006]. Because of the long-range LD, admixture mapping is able to map regions of interest by using a small number (i.e., hundreds to thousands) of genome-wide AIMs.

Genome-wide association studies (GWASs) have led to the discovery of thousands of alleles associated with human diseases and traits [Hindorff et al., 2009]. Because of the large number of SNPs analyzed, however, GWASs incur a stiff statistical penalty [Risch and Merikangas, 1996]. In the presence of dense marker sets, it should be instructive to integrate the advantages of SNP association testing and admixture mapping analysis. For independent familial triads, Tang et al. [2010] quantified the contribution of allele-based and ancestry-based Transmission Disequilibrium Test (TDT) tests and proposed a chi-square statistic of two degrees of freedom to integrate the two TDT tests. They found that the contribution of association evidence from ancestry is limited when testing a causal variant or a variant in strong LD with the causal variant. Ancestry can be more informative than a direct association test when a causal variant has a large allele frequency difference among ancestral populations. For unrelated individuals, Lettre et al. [2011] proposed summing up the chi-square statistic of genotype effect and the chi-square of local ancestry effect, assuming that the sum followed a chi-square distribution with two degrees of freedom (SUM), without consideration of the correlation between a local ancestry and genotypes, which can exist [Qin et al., 2010; Wang et al., 2011]. More recently, Pasaniuc et al. [2011] proposed a one degree of freedom method, MIX, to combine the signals from admixture mapping and SNP association analysis for case control studies. For a systematic review of latest approaches for disease association analysis in admixed populations, see Seldin et al. [2011]. To our knowledge, the two-degree TDT, SUM, and the one degree of freedom MIX methods share the same null hypothesis that there is no SNP association and no ancestry association with a trait. Thus, a rejection of the null hypothesis can be interpreted as there is association evidence contributed by either SNP association or ancestry association or both. As we know, the ancestry association can occur in a much wider genome region than the SNP association. Therefore, we may expect that the significant evidence identified by the joint analysis will fall in a genome region. In general, we usually perform a SNP-based association analysis in a GWAS at the first hand. A variant with a sufficiently large effect size can be captured by a direct association analysis, regardless of the allele frequency difference among ancestral populations. It is also possible that the variants with less effective sizes and substantial allele frequency differences in ancestral populations can be identified by the joint analysis, although the interpretation should be careful because possibly a region is detected rather than a locus. However, the joint test suffers the penalty of the same number of tests as in GWAs as well as the increased degrees of freedom. In this paper, we aim to search for the variants within admixture mapping peaks. By doing so, we are potentially able to identify variants missed by the conventional genome-wide association analysis. We studied a two-stage approach for association analysis in an admixed population similar to the method of Zhu et al. [2011]. The original method calculates P-value by estimating the effective number of tests. Here we propose to estimate P-values by permutation, which should be much more accurate than estimating the effective number of tests. At the first stage, we identify ancestry genomic regions by applying admixture mapping analysis. At the second stage, we only test the SNPs with substantial allele frequency differences among ancestral populations in the regions identified at the first stage. These markers can be correlated due to the allele frequency differences in ancestral populations. Because of the significant reduction of the number of tests, we argue that the two-stage approach can improve power to detect the associated variants whose allele frequency differences in ancestral populations are large. To control the family wise error rate (FWER) at a preset nominal level, we established significance thresholds for the SNP association test via permutations. We also demonstrated the advantage of admixture mapping following by SNP association test to identify causal SNPs in GWASs of recently admixed populations. The significance thresholds established in this report would serve as a guideline for the GWASs in African Americans, but the idea of our method is broadly applicable to other admixed populations.

METHODS

For N unrelated individuals from an admixed population, let y_i, A_i, a_ij and g_ij be a continuous trait value, global ancestry, SNP-specific ancestry, and genotype score at SNP j ( = 1, …, M) of individual i ( = 1, …, N), respectively. In context, global ancestry A_i is calculated as the genome-wide proportion of the ith individual’s alleles inherited from a given ancestral population, SNP-specific ancestry a_ij is referred to as the proportion of the ith individual’s alleles inherited from the given ancestral population at the jth SNP, and the genotype g_ij is coded as the number of a reference allele at SNP j of the ith individual. Let α be the nominal FWER of a genome-wide study for SNP association.

DIRECT GENOME-WIDE ASSOCIATION ANALYSIS

The direct genome-wide association analysis tests each available SNP across the genome and declaims SNP j to be significant if η_j ≜ −log₁₀( P_gj) > η_FB, where η_FB = −log₁₀(α/M), P_gj is the observed P-value to test for single SNP association, namely, tests for β₂ = 0 under the linear regression y_i = β₀ + β₁ A_i + β₂ g_ij + ε_i, and M is the number of independent tests on the genome. Any covariates can be adjusted straightforwardly. The threshold η_FB is very stringent when M is large. Due to the LD among the markers, a popular threshold in current GWAS is ${\eta }_{FB}^{\ast }=-{log}_{10}(5\times {10}^{-8})=7.30$, which corresponds to 1 million independent tests across the genome.

TWO-STAGE APPROACH

At the first stage, we perform admixture mapping analysis to define chromosome regions associated with a phenotype. We compute ξ_j = −log₁₀( P_aj) at the jth SNP, where P_aj is a P-value to test for a locus specific ancestry: γ₁ = 0 in the linear regression $y_i^{\ast }={\gamma }_0+{\gamma }_1{a}_{ij}+e_i$ , where $y_i^{\ast }$ is the residual of y_i after adjusting for the global ancestry by performing the linear regression y_i = α₀ + α₁ A_i + e_i. Any covariates can be included in the model without difficulty. Using ξ_j across the genome, we construct genomic regions, which potentially harbor quantitative trait loci. In general, we first search the peaks of ξ_j that is greater than a predefined threshold ξ (i.e., = 1, 2, 3, 4). For each ξ_j^*, we define a genomic region as an interval where ξ_j = ξ_j^* − 1 for all the consecutive SNPs around the SNP j^*. We assume a peak observed in testing local ancestry association is attributed to variants with substantial allele frequency differences between ancestral populations. From each interval defined in testing local ancestry association, we exclude the SNPs with ancestral allele difference smaller than a given δ (i.e., δ = 0.1, 0.2, …, 0.8). For a given (ξ, δ) pair, let m genome-wide SNPs be retained at stage 1 and reindexed as 1, …, m. At the second stage, we compute η_j = −log₁₀( P_gj) for the m-retained SNPs and claim SNPs j to be significant if η_j > η_*, where η_* = η_*(ξ, δ, α) is a permutation-based significance threshold, which is dependent on values of (ξ, δ, α). In this report, we set a genome-wide significance level α = 0.05.

SIGNIFICANCE THRESHOLDS

Let ( $y_{i1}^{\ast },\dots ,y_{iN}^{\ast }$) be the ith ( = 1, …, 1,000) permutation of ( $y_1^{\ast },\dots ,y_N^{\ast }$), the trait residuals as aforementioned. For each permutation, we first perform admixture mapping analysis to define candidate regions using threshold ξ and identified the m SNPs with allele frequency difference between ancestral populations greater than δ. We then compute the T value of each permutation, where T = max{η₁, …, η_m} for testing the SNPs at stage 2. We sort all the 1,000 T values as T₍₁₎ > · · · > T_(1,000), and set η_* = T_(1,000×α). Using this procedure, we empirically established the thresholds (Table I) for α = 0.05 and various (ξ, δ) pairs by simulating N = 2,000 African Americans using the HapMapII YRI (Yoruban in Ibadan, Nigeria) and CEU (Centre d’Etude du Polymorphisme Humain collected in Utah) data, which contain almost 2 million SNPs.

TABLE I.

Genome-wide significance thresholds for the two-stage schemes of diverse admixture screenings

ξ	δ
	0.1	0.2	0.3	0.4	0.5	0.6	0.7	0.8
1	6.74	6.65	6.50	6.18	5.80	5.37	4.85	4.12
2	6.32	6.20	6.05	5.86	5.59	5.20	4.78	3.97
3	5.73	5.71	5.59	5.36	5.14	4.85	4.54	3.74
4	4.85	4.85	4.76	4.72	4.57	4.17	3.71	2.21

SIMULATION DESIGNS

We mimicked 2,000 African-American genomes by applying the software GenoAnceBase0 of Qin et al. [2010] to the CEU and YRI haplotypes in the HapMap II database. For this task, we first applied the software ADMIXPROGRAM [Zhu et al., 2006] to the Maywood dataset to infer the individual’s SNP-specific ancestries for the 701 Maywood subjects using 2,606 selected ancestry informative SNPs [Kang et al., 2010]. We observed that the distribution of individual genome-wide CEU allele portions can be well fitted by Beta (4.8, 19.2), the beta distribution with mean 0.2 and standard deviation 0.08. Based on this distribution, we simulated an admixed population with average 20% European and 80% African ancestries. Specifically, we simulated N_i individuals with average ancestries w_i. For each individual, we simulated the genotypes at the SNPs on 22 autosomes using HapMap dataset, which included ~2M SNPs with complete haplotype information for CEU, YRI, and CHB/JPT samples. For each chromosome, we simulated the number of crossover points s from the Poisson distribution of mean μ = l × g × 10⁻⁷, where l was a chromosome length, g was the number of generations since the initial admixture occurring for an individual’s ancestors and was randomly sampled from 1 to 10. Then, we uniformly distributed s crossovers across the chromosome. Next, we randomly sampled haplotype segments from CEU or YRI HapMap data between two crossovers independently according to the average ancestry w_i.

To establish the thresholds η_*, we simulated individual trait values from model I: y_i = A_i φ + e_i, where A_i is the proportion of the individual i’s alleles inherited from CEU over the 2 million SNPs, e_i ~ N(0, var(e )) and φ is the coefficient such that var(y) = 1 and φ²var(A) = 1 − var(e). This model does not include any specific SNP contribution to the phenotype and can be used to establish the genome-wide significance thresholds for the two-stage approach. We set var(e) = 0.9 in our empirical exploration. For power comparison, we simulated individual trait values from model II: y_i = A_i φ + g_ij ψ + e_i, where j is a randomly selected SNP of given δ, representing the allele frequency difference in ancestral populations (Tables II and III), e_i ~ N(0, var(e )) φ and ψ are the coefficients such that var(y) = 1, and ${\phi }^{2}var(A)={\psi }^{2}var(g)=\frac{1}{2}(1-var(e))$. We considered two scenarios for power comparisons: the causal SNP accounts for 0.5% and 1% total trait variation, correspondingly, var(e) = 0.99 and 0.98. For each given value of var(e), we computed the coefficients as $\phi =\sqrt{\frac{1}{2}(1-var(e))/var(A)}$ and $\psi =\sqrt{\frac{1}{2}(1-var(e))/var(g)}$ by assuming the independence between global ancestry and the causal SNP genotype.

TABLE II.

Eight SNPs of higher CEU allele frequencies

SNP	Base pair	fADX	fCEU	fYRI	Δ = fCEU − fYRI
rs135109	34410452	0.54	0.62	0.52	0.1
rs2240175	29651847	0.50	0.66	0.46	0.2
rs12162984	45406571	0.50	0.74	0.44	0.3
rs138531	45382843	0.55	0.88	0.48	0.4
rs6000310	35258500	0.45	0.84	0.34	0.5
rs6519270	40408612	0.35	0.83	0.23	0.6
rs1001223	32093247	0.42	0.97	0.27	0.7
rs9626496	43409827	0.28	0.91	0.11	0.8

TABLE III.

Eight SNPs of higher YRI ancestry

SNP	Base pair	fADX	fCEU	fYRI	Δ = fYRI − fCEU
rs7291350	46245854	0.47	0.4	0.5	0.1
rs1013339	37304626	0.50	0.33	0.53	0.2
rs1984387	33446241	0.45	0.21	0.51	0.3
rs4821987	39767215	0.52	0.21	0.61	0.4
rs6000303	35254273	0.57	0.18	0.68	0.5
rs6001217	20868194	0.74	0.27	0.87	0.6
rs137129	41350266	0.67	0.12	0.82	0.7
rs5998832	31991960	0.74	0.11	0.91	0.8

RESULTS

SIGNIFICANCE THRESHOLDS

We first tabled the thresholds to declare genome-wide significance for the two-stage approach by simulations. The thresholds are dependent on the threshold ξ at stage 1 to define candidate regions in admixture mapping and the selected SNPs tested at stage 2, which are dependent on δ, the difference between ancestral allele frequencies. We simulated trait values under the null hypothesis that there is no SNP contributing to the trait variation. Our thresholds η_* for declaring significance were calculated at the nominal FWER level α = 0.05. Table I presents these thresholds for different (ξ, δ) pairs. As anticipated, the threshold η_* decreased when admixture association threshold ξ and marker specific informative content δ increased. For all (ξ, δ) pairs in the table, the corresponding η_* values were uniformly smaller than the traditional GWAS significance level ${\eta }_{\mathit{GWAS}}^{\ast }=7.30$. As ξ increased from 1 to 4 and δ increased from 0.1 to 0.8, the significant threshold η_* decreased from 6.74 to 2.21. Increasing ξ will result in less genome regions to be detected by admixture mapping, whereas increasing ξ will result in less SNPs in a region to be tested in association analysis. Both will reduce the number of tests.

POWER COMPARISON

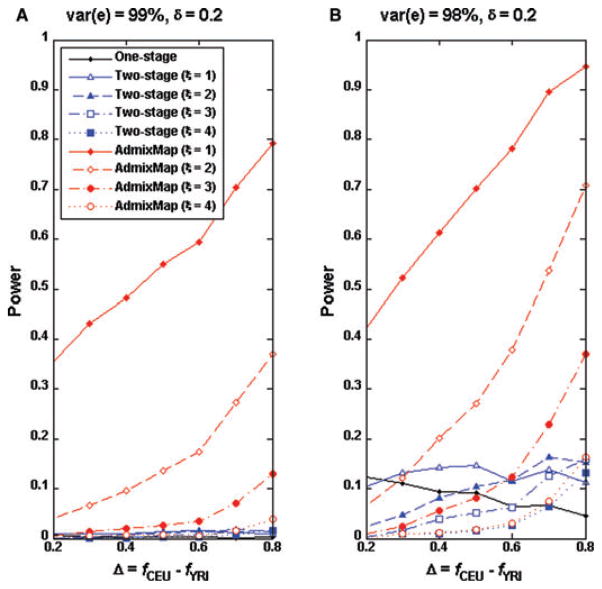
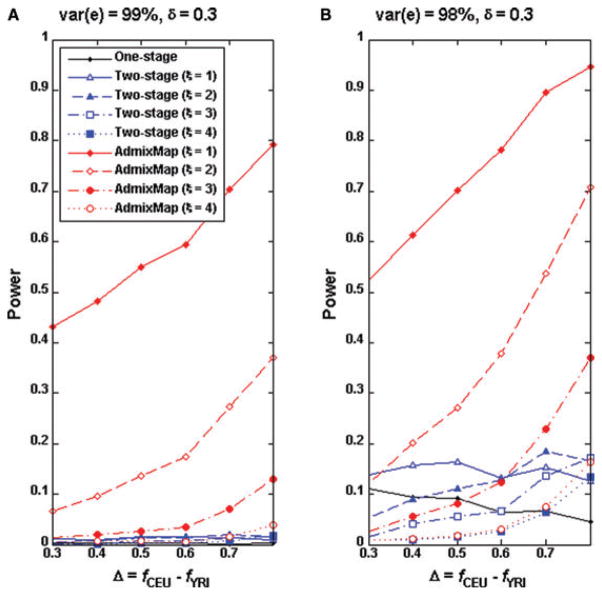
We evaluated the power of the standard one-stage method and that of the two-stage approach under various scenarios. We chose chromosome 22 as the region that a causal SNP located. We randomly selected eight SNPs with high CEU and lower YRI allele frequencies (Table II) and each of these SNPs served as a causal SNP under the genetic model II. For a selected SNP, we simulated 2,000 unrelated individuals. We evaluated the power of both methods based on 1,000 replicates. Figures 1A and B present the power curves for the two-stage approach and single SNP-based genome-wide association analysis. We set δ = 0.2 so that only the SNPs with allele frequencies ≥ 0.2 were tested in second stage of the association test. In general, neither the two-stage approach nor the single SNP analysis has power when a causal SNP accounts for 0.5% of the trait variation (Fig. 1A). When a causal SNP explains 1% of the trait variation, we observed that the power of two-stage approach increases as the causal allele frequency difference Δ increases, while the single SNP association analysis decreases slightly. The two-stage approach appears less powerful than the single SNP association test when Δ < 0.25 but becomes more powerful when Δ increases (Fig. 1B). When the two-stage approach is more powerful than the single SNP test depends on the threshold ξ for the admixture mapping at the first stage. Interestingly, the power of the two-stage approach is quite dependent on the first stage threshold. For example, the smaller the threshold ξ is at stage 1, the more power the two-stage approach has. However, this pattern changes when Δ > 0.7. To further examine this pattern, we plotted the power curves of admixture mapping for different thresholds ξ. It can be observed that the power of the two-stage approach is bounded by the power of admixture mapping at stage 1. We next increased δ to 0.3 (Figs. 2A and B), which means we only tested the SNPs with allele frequency differences ≥ 0.3, therefore reducing the number of testing SNPs at stage 2. We observed similar power patterns as at δ = 0.2 although power was improved compared to δ = 0.2. However, it should be noted that the two-stage approach has less power for δ = 0.3 than for δ = 0.2 when Δ < 0.3 because we have a greater chance to miss a causal SNP by choosing δ = 0.3. From Figures 1B and 3B (Δ < 0.3), we observed that the two-stage method is not as powerful as a standard genome-wide association analysis for the quantitative trait loci (QTLs) with small allele frequency differences between ancestral populations.

Fig 1.

Power comparisons for single SNP association test and the two-stage approach of δ = 0.2 when the causal SNPs have higher allele frequency in CEU than in YRI data. The genotype and ancestry data of the entire genomes of 2,000 individuals were simulated by the program GenoAnceBase0 (Qin et al., 2010). For each given Δ value (the causal allele frequency difference between the ancestral populations), one SNP was randomly selected from all of those of the same Δ value on autosome 22, as listed in Table II. Both panels shared identical causal SNPs. Using each of the eight SNPs as the causal SNP, 1,000 replicates of 2,000 trait values were simulated as described in the text.

Fig 2.

Power comparisons for single SNP association test and the two-stage approach of δ = 0.3 when the causal SNPs have higher allele frequency in CEU than in YRI data. The genotype and ancestry data of the entire genomes of 2,000 individuals were simulated by the program GenoAnceBase0 (Qin et al., 2010). For each given Δ value (the causal allele frequency difference between the ancestral populations), one SNP was randomly selected from all of those of the same Δ value on autosome 22, as listed in Table II. Both panels shared identical causal SNPs. Using each of the eight SNPs as the causal SNP, 1,000 replicates of 2,000 trait values were simulated as described in text.

Fig 3.

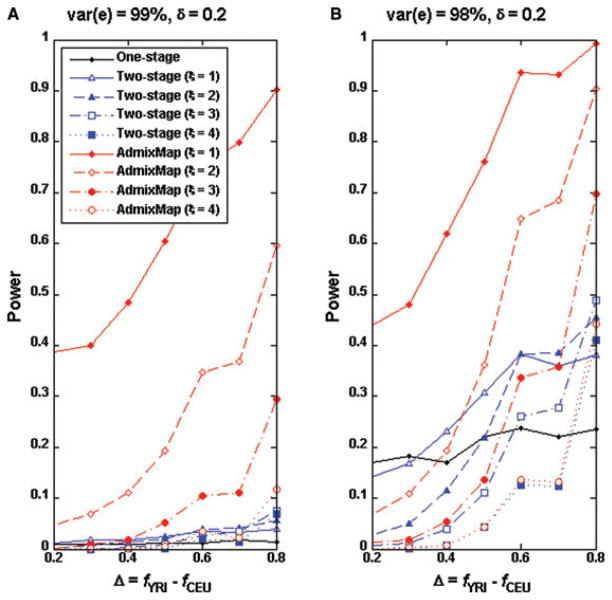
Power comparisons for single SNP association test and the two-stage approach of δ = 0.2 when the causal SNPs have higher allele frequency in YRI than in CEU data. The genotype and ancestry data of the entire genomes of 2,000 individuals were simulated by the program GenoAnceBase0 (Qin et al., 2010). For each given Δ value (the causal allele frequency difference between the ancestral populations), one SNP was randomly selected from all of those of the same Δ value on autosome 22, as listed in Table III. Both panels shared identical causal SNPs. Using each of the eight SNPs as the causal SNP, 1,000 replicates of 2,000 trait values were simulated as described in text.

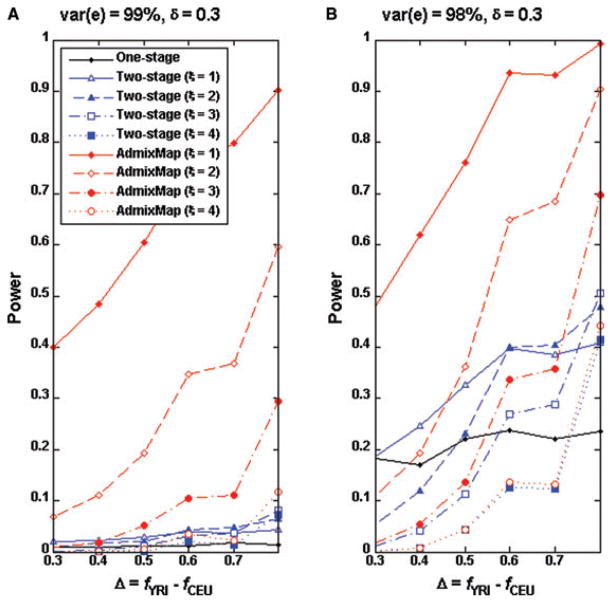
Because the power of admixture mapping also depends on which ancestral population has higher causal allele frequency, we randomly selected eight SNPs with higher YRI and lower CEU allele frequencies (Table III) and each of these SNPs served as a causal SNP under the genetic model II. We observed similar power patterns when CEU has higher causal allele frequency (Figs. 3 and 4). In general, we observed that the power for the two-stage approach and single SNP association is larger for a causal SNP with higher allele frequency in the YRI sample than in the CEU sample when the analysis is conducted in an African-American sample.

Fig 4.

Power comparisons for single SNP association test and the two-stage approach of δ = 0.3 when the causal SNPs have higher allele frequency in YRI than in CEU data. The genotype and ancestry data of the entire genomes of 2,000 individuals were simulated by the program GenoAnceBase0 (Qin et al., 2010). For each given Δ value (the causal allele frequency difference between the ancestral populations), one SNP was randomly selected from all of those of the same Δ value on autosome 22, as listed in Table III. Both panels shared identical causal SNPs. Using each of the eight SNPs as the causal SNP, 1,000 replicates of 2,000 trait values were simulated as described in text.

DISCUSSION

Tang et al. [2010] studied the contribution of allele-based and ancestry-based association tests under a family design and suggested that the two tests can provide nonredundant information. Thus, a joint test of the allele and ancestry potentially improves statistical power over the allele-based test when the causal variant has a large allele frequency difference in ancestral populations. A similar idea has been applied to population-based samples [Lettre et al., 2011]. More recently, Pasaniuc et al. [2011] proposed MIX as a one degree of freedom method to combine the signals from admixture mapping and SNP association analysis for case control studies. However, the null hypothesis of the joint test is that neither a SNP nor its ancestry at the testing SNP is associated with the trait of interest. A rejection of such null hypothesis would suggest either a SNP or its ancestry is associated with the trait. Given a rejection, further analysis is necessary to tell whether the SNP is associated with the trait. In this report, we focused on detecting the genetic variants whose allele frequencies in ancestral populations are substantially different. Such variants will contribute the association evidence, which can be observed in admixture mapping analysis. It is possible that the allele-based test in GWAS will detect these variants, although the power can be limited by the large penalty due to multiple tests. We thus argue that testing the SNPs only with substantial allele frequency differences in ancestral populations in the genomic regions defined by admixture mapping analysis can improve the power to detect causal variants. Such power improvement is mainly attributed to the great reduction of the number of tests. Our simulations suggest that the two-stage approach is more powerful than the standard single SNP test when the allele frequency difference in ancestry populations is large. Our observation is generally consistent with a theoretical prediction by Risch and Tang [2006], who suggested direct association tests can be more powerful than admixture mapping when Δ is small. Zhu et al. [2011] performed the two-stage analysis of blood pressure in CARe African-American samples and were able to detect NPR3 gene associated with blood pressure traits. However, this association was missed by the genome-wide association analysis in the same samples [Fox et al., 2011]. We also observed that the power of the two-stage approach is larger when a lower threshold is applied to define the genomic regions in admixture mapping at stage 1 than a higher threshold until the causal allele frequency difference is at least greater than 0.7. This is not entirely surprising because the power of the two-stage approach depends on the power of admixture mapping, which is determined by the allele frequency difference between ancestral populations. The power of the two-stage approach is also affected by the threshold δ value that determines which SNPs are to be tested at stage 2. Although a large δ value will reduce the number of SNPs to be tested and therefore improves the power, the danger is that true causal variants or the SNPs in strong LD with the causal variants would be possibly filtered out. Thus, we suggest that both lower thresholds for stage 1 and 2 may be used, i.e., ξ = 2 and δ = 0.2 in practice. It should be noted that associations can still occur in the absence of admixture signal, as demonstrated by the association of PHYIN1 locus with asthma in African-American and African-Caribbean populations [Torgerson et al., 2011]. The two-stage method is not as powerful as a standard one-stage method to detect such variants. Thus, we do not suggest that the two-stage analysis replace the conventional GWAS analysis. Rather, the two-stage analysis should be considered as a complementary method to the conventional GWAS analysis.

We acknowledged that the possible confounding from local ancestry should be addressed as in Qin et al. [2010], Wang et al. [2011], Pasaniuc et al. [2011], and Seldin et al. [2011]. For fine mapping, it is necessary to adjust for local ancestry to eliminate the effect due to local ancestry [Qin et al., 2010] even though it may reduce power in association analysis when adjusting for local ancestry. Although we did not study the impact of local ancestry in this manuscript, i.e., the confounding of the local ancestry, the general conclusion in this paper still holds.

In this report, we did not directly compare the power of the two-stage approach and the joint test of ancestry and allele association because these two methods in fact test different null hypotheses. However, both methods do share the similarity that the power will be improved when the causal SNP allele frequency difference increases. We tabulated the significance levels to determine genome-wide significance for the two-stage approach when different thresholds are applied at stage 1 and a different set of SNPs are tested at stage 2 (Table I), which should be useful in practice. The method may also apply for binary traits even though we focused our simulations on quantitative traits only. The test statistic used in the method is a scaled Armitage trend test statistic and has identical asymptotic null distribution with the Armitage trend statistic as used by Price et al. [2006], Pasaniuc et al. [2011], Seldin et al. [2011], and Zhu et al. [2008b] for binary traits. In Table I, we assume local ancestries can be accurately inferred. In practice, local ancestries must be inferred in general. Several statistical methods can be applied when AIMs are genotyped [Zhu et al., 2008a]. When dense markers are available, software such as SABER [Tang et al., 2006] and HAPMIX of Price et al. [2009] can be applied to infer local ancestries. Serious local ancestry inference errors may either inflate the type I error rate or reduce statistical power in admixture mapping analysis. However, dense SNPs genotyped across the genome allow inferring local ancestries to be highly accurate, as suggested by Price et al. [2009]. Thus, we expect the local ancestry inference errors to have very limited impact in our method.