Organizing syllables into groups — Evidence from F₀ and duration patterns in Mandarin

Abstract

In this study we investigated grouping-related F₀ patterns in Mandarin by examining the effect of syllable position in a group while controlling for tone, speaking mode, number of syllables in a group, and group position in a sentence. We analyzed syllable duration, F₀ displacement, ratio of peak velocity to F₀ displacement (v_p/d ratio) and shape of F₀ velocity profile (parameter C) in sequences of Rising, Falling and High tones. Results showed that syllable duration had the most consistent grouping-related patterns. In a short phrase of 1–4 syllables, duration is longest in the final position, second longest in the initial position, and shortest in the medial positions. In Rising and Falling tone sequences, syllable duration was positively related to F₀ displacement, but negatively related to v_p/d ratio. Sequences consisting of only the High tone, however, showed no duration-matching F₀ variations. Modeling simulations with a second-order linear system showed that duration variations alone could generate F₀ displacement and v_p/d ratio variations comparable to those in actual data. We interpret the results as evidence that grouping is encoded directly by syllable duration, while the corresponding variations in F₀ displacement, v_p/d ratio and velocity profile are the consequences of duration control.

1. Introduction

It is generally believed that in a multi-syllabic utterance individual syllables are not evenly arranged, but organized into separate groups even when there are no pauses involved. But the nature of such grouping and how it is phonetically realized are not well understood. The present study is an attempt to improve our understanding of syllable organization by examining how syllable duration and fine-detailed F₀ trajectories in Mandarin are related to syllable grouping.

There have been many descriptive accounts of syllable organization in Mandarin, and there is a general agreement that syllables are organized into prosodic or rhythmic units, referred to as feet (Duanmu, 2000; Feng, 1998; Shih, 1986). It has been argued that such organization is based on a prosodic hierarchy relatively independent of syntax (Shih, 1986; Speer, Shih & Slowiaczek, 1989). A foot in Mandarin has been proposed to vary in size, from 1 to 3 syllables (Feng, 1998; Duanmu, 2000). It has also been suggested that sometimes two adjacent feet are further organized into a super foot (Shih, 1986). There has been little agreement, however, on how feet are phonologically formed in Mandarin (Chen, 2000). In fact, completely opposite opinions are held as to whether foot formation is based on stress (Duanmu, 2000) or has little to do with stress (Feng, 1998), and if stress is involved, whether the pattern inside a foot is strong-weak (Duanmu, 2000; Feng, 1998) or weak-strong (Chao, 1968).

The proposed foot-related stress for Mandarin is different from lexical stress in a stress language like English. For English, word stress is lexical, because it serves to contrast certain words from others. There is good agreement as to which syllable in an English word is stressed and which is not, although the exact acoustic correlates of stress are still a topic of research (de Jong 2004; Fry, 1958; Kochanski et al., 2005). For Mandarin, the closest parallel to English lexical stress is the neutral tone, which is also lexically contrastive (Chao, 1968; Yip, 2002), and is phonetically similar to the unstressed syllable in English at least in terms of duration (Lin, 1985) and F₀ (Chen & Xu, 2006; Xu & Xu, 2005). But the neutral tone is generally regarded as a tonal rather than a stress phenomenon, and it occurs only in a small number of Mandarin words, about 6.7% (Li, 1981) or 4.6% (Mi, 1986). Other than the neutral tone, there are no equivalents to word stress in English, as most words in Mandarin are not distinguished by stress (Chen, 2000; Duanmu, 2000).

Acoustic evidence for grouping-related stress in Mandarin has recently been reported, however. Kochanski, Shih and Jing (2003) have examined patterns of prosodic strength in Mandarin through quantitative modeling of F₀ contours. They define prosodic strength in terms of how fully a tone is realized against contextual influences: the more fully a tone is realized, the greater its prosodic strength. They report that Mandarin words tend to exhibit alternating patterns in terms of prosodic strength, and that there is a clear strong-weak tendency in disyllabic words, thus supporting the views of Duanmu (2000) and Feng (1998). They further report that the strong-weak pattern is repeated at a higher level in four-syllable words, with the first disyllabic unit having greater prosodic strength than the second, thus exhibiting a hierarchical structure as suggested in Shih (1986).

In the Stem-ML model of tone and intonation proposed by Kochanski and Shih (2003), tones are realized as deviations from lexically determined tonal templates, i.e., tone-specific ideal F₀ shapes, under the influence of the surrounding tones. F₀ at each time point is calculated as a function of the current and nearby tonal templates and their levels of prosodic strength. As a result, the preceding and following tones exert the same amount of influence on the target tone, other things being equal. In such a system, the contextual influences on a tone is also weakly related with the duration of the syllable carrying the tone, because the influences of the surrounding tones would decrease as their temporal distances from the current tone center increased. Indeed, they find that measured prosodic strength is positively correlated with syllable duration. But this also means that the fullness of target realization, and hence the measured prosodic strength, is partially attributable to syllable duration. This raises the question as to whether the same patterns of prosodic strength also correspond to the duration patterns found in previous studies.

There have been some experimental data on durational patterns in Mandarin. Xu (1999) reports that a disyllabic word has a short-long duration pattern regardless of whether it is focused, or whether it is utterance-initial or utterance-final. Chen (2006) finds that syllables in quadrasyllabic words exhibit a 3 1 2 4 duration pattern (larger number indicating longer duration) in the utterance final position, but a 3 1 2 3 pattern in an utterance medial position. These patterns pose tough problems for previous theories about Mandarin prosodic patterning. That is, assuming that a four-syllable group consists of two disyllabic feet (Shih, 1986), the first and second feet would have opposite stress/strength patterns given that duration is positively related to lexical stress, as found in English (Fry, 1958; de Jong, 2004), and negatively related to the neutral (weak) tone in Mandarin (Lin, 1985). A relevant question then is whether position-related lengthening is for the sake of stress or to mark the position. For English, at least, the domain-final lengthening similar to that found by Chen (2006) is relatively independent of stress (Cooper, Lapointe & Paccia, 1977; Nakatani, O’Connor & Aston, 1981). To complicate things further, however, Kochanski et al. (2003) also find that when final lengthening happens in Mandarin, the model-simulated prosodic strength is actually lower than in a non-final position, where syllable duration is relatively short.

To better understand the effect of the stress-duration relation on F₀, it is important to note that dynamic patterns of F₀, just like those of formants, are a product of an articulatory process. There has been evidence that kinematic measurements of F₀ movements closely resemble those of articulatory movements. Xu and Sun (2002) have reported highly linear relations between peak velocity and amplitude of F₀ movements when measured in semitones,ⁱ which resemble those reported for movements of articulators such as the lips, jaw and tongue (Hertrich & Ackermann, 1997; Kelso et al., 1985; Ostry & Munhall, 1985; Vatikiotis-Bateson & Kelso, 1993). Thus we may treat continuous F₀ as a quasi-articulatory measurement, and interpret its kinematic patterns in articulatory terms.ⁱⁱ The linear relation between peak velocity and displacement has been modeled as the behavior of a second-order dynamical system such as a linear mass-spring system (Kelso et al., 1985; Nelson, 1983; Ostry, Keller & Parush, 1983). In such a system, displacement as a function of time exhibits an asymptotic trajectory toward the equilibrium point of the system. The equilibrium point thus serves as an attractor toward which the system converges over time regardless of its initial state (Kelso, Saltzman & Tuller, 1986; Saltzman & Munhall, 1989). Such convergence over time is also seen in F₀ contours of a tone when preceded by different tones (Xu, 1997, 1999). The tonal convergence behavior has been modeled as a damped 3rd-order system driven by tone-associated pitch targets that serve as forcing functions (Prom-on, Xu & Thipakorn, 2009), based on the Target Approximation model (Xu & Wang, 2001).

For a second-order linear system, the ratio of peak velocity to placement (henceforth v_p/d ratio) has been considered to reflect the “stiffness” of the system (Kelso et al., 1985; Ostry et al., 1983; Ostry & Munhall, 1985; Perkell et al., 2002). Stiffness may be viewed as an index of the activities of the muscles involved in producing the movement (Perkell et al., 2002) approaching a target. In such a dynamical system, the fullness of target attainment can be independently affected by stiffness and movement duration. That is, given a stiffness level, the longer the movement duration, the closer the targeted state is approached by the end of the movement; likewise, given a movement duration, the higher the stiffness level, the better the target is attained by the end of the movement.

Another kinematic parameter related to stiffness is the ratio of peak velocity to average velocity of a unidirectional movement, known as parameter C (Munhall, Ostry & Parush, 1985; Ostry & Munhall, 1985; Perkell et al., 2002). It is computed with equation [1] (Munhall et al., 1985:458).

$$P/A=C/T$$ [1]

where P is peak velocity, A is movement amplitude and T is movement time. Parameter C provides an index of the shape of the velocity profile, and has been used as another measurement of articulatory strength (Munhall et al., 1985; Ostry & Munhall, 1985; Perkell et al., 2002).

It is thus possible to study the separate contributions of syllable duration and articulatory strength to patterns of F₀ variation related to syllable grouping. The present study tries to answer three general questions in this regard: (1) What are the basic patterns of F₀ variation related to syllable grouping in Mandarin? (2) How are they related to syllable duration? and (3) How are they related to articulatory strength?

Our approach is to examine duration and F₀ trajectories in words and phrases of varying lengths to look for patterns related to syllable grouping, and at the same time check for evidence of articulatory strength. These words and phrases should carry tone sequences whose F₀ patterns are highly sensitive to variations in duration and articulatory strength. Tone sequences consisting of all Rising (R) tones or all Falling (F) tones may serve this purpose, because for these dynamic tones F₀ has to successively move in two opposite directions within a syllable. This would exert great articulatory pressure on the F₀ production system. It has been shown that the maximum voluntary speed of pitch change is approached during these tones (Xu & Sun, 2002), and that, despite the increased speed, much more extensive F₀ undershoot occurs during dynamic tones than during static tones such as High and Low (Kuo, Xu & Yip, 2007). These tone sequences are thus ideal for testing the sensitivity of target undershoot to changes both in duration and in articulatory strength. The grouping patterns of these words and phrases need to be guaranteed by their meanings as well as syntactic structure, which can help avoid the problem of trying to examine cause and effect at the same time. For this reason, we need to use real words and meaningful phrases instead of nonsense sequences. This also means that some syllables in these words and phrases may differ slightly in their segmental structures, but the differences should not be large enough to confound the main effects.

The possible contribution of articulatory strength to syllable grouping can be examined by taking kinematic F₀ measurements similar to those taken in articulatory studies, including displacement, peak velocity, v_p/d ratio, movement duration and parameter C. To identify separate contributions of movement duration and articulatory strength based on these measurements, however, modeling simulations need to be performed.

It is also possible that syllable grouping can be signaled by directly manipulating F₀ height. This possibility can be examined by looking at sequences of H tones, where the tonal targets would stay high and level throughout, allowing any F₀ variations related to syllable grouping to stand out readily.

2. Method

2.1. Stimuli

The stimuli, as shown in Table 1, consist of words and phrases that naturally form 1, 2, 3 and 4 syllable groups when put into the carrier frames shown in Table 2. The stimulus words and phrases were divided into two groups based on their tonal composition. In one group the target sequences were composed of syllables with dynamic tones, including R tone only (all-R), F tone only (all-F) and alternating R and F tones (RF) or F and R tones (FR). The all-R and all-F sequences are predicted to exhibit reduced F₀ movements due to high articulatory pressure, as discussed earlier, and the RF and FR sequences would contrast them with much larger F₀ movements due to low articulatory pressure. In sequences marked as R#RRR and F#FFF the first syllable is a monosyllabic word, whereas the RRRR and FFFF sequences consist of two disyllabic words. In the other group the target sequences were composed solely of syllables with the H tone (all-H). To ensure continuous F₀ contours, and to reduce F₀ perturbation caused by consonants (Shih, 2001; Xu & Xu, 2003), only syllables with initial sonorant consonants were used. To reduce variability due to vowel intrinsic F₀ (Lehiste & Peterson 1961; Shi & Zhang, 1987; Whalen & Levitt, 1995), only phrases with/i/and/u/as the nuclear vowels were used as the all-H stimuli.

Table 1.

List of stimuli and their compositions.

Group	Tone	Pinyin	Glossary
all-R	R	nán	south
	RR	yún nán	Yunnan (province name)
	RRR	yún nán rén	Yunnanese
	RRRR	yún nán rén mín	the people of Yunnan
	R#RRR	nán yún nán rén	male Yunnanese
all-F	F	yòng	use
	FF	wài yòng	external use
	FFF	wài yòng yào	external medicine
	FFFF	wài yòng yào liàng	external medicine dosage
	F#FFF	màn wài yòng yào	slow external medicine
RF	RF	rán liào	fuel
	RFR	rán liào méi	fuel coal
	RFRF	rán liào méi mò	fuel coal dust
FR	FR	yàn yú	mackerel
	FRF	yàn yú ròu	mackerel meat
	FRFR	yàn yú ròu wán	mackerel meat ball
all-H	H	wū	black
	HH	wū yī	witch doctor
	HHH	wū yī wū	the witch doctor is black
	HHHH	wū yī wū yī ng	witch doctor and black eagle

Table 2.

List of carriers.

Carrier	Tone group	Pinyin	Glossary
Pre-target	all-R, FR	tā huái yí	He suspects that…
	all-F, RF	tā xiāng xìn	He believes that…
	all-H	tā dān xīn	He is worried that…
Post-target	All groups	niàn bù hăo	… cannot read well

The carrier frames are divided into pre-target carriers and post-target carriers, as shown in Table 2. The pre-target carriers are designed to control the preceding tonal context for all target sequences, and they each end with a verb (to suspect, believe or worry). The post-target carrier, used on half of trials, is to make the target sequence non-final in a sentence. It starts with a verb (to read). These pre- and post-target carriers thus make sure that the target sequence always forms a group well separated from the rest of the sentence even when no pauses are involved.

The pre-target carrier for the all-R sequences ended with R tone to create the same high articulatory pressure for the first tone in the target sequence as for the rest of the tones in the sequence. But the same pre-target carrier was also used for the FR sequences to create the same low articulatory pressure as for the rest of the tones in the sequence. For the same reason, the pre-target carrier for the all-F and RF sequences ended with the F tone to create similar high or low articulatory pressure. The pre-target carrier for the all-H sequences ended with H tone to minimize F₀ movements due to the carrier.

To control for focus effects, each sentence was preceded by a leading question, which was to prevent subjects from saying the sentence with a non-final focus. A non-final focus would have the effect of extensively expanding the on-focus pitch range and suppressing the post-focus pitch range (Xu, 1999). For the all-R and FR sequences, the leading question was tā huái yí shén me? ‘What does he suspect?’ For the all-F and RF sequences, the leading question was tā xiāng xìn shén me? ‘What does he believe?’ These questions would lead speakers to always put focus on the sentence-final word or phrase. As found in previous research, final focus does not introduce drastic pitch range expansion in Mandarin (Liu & Xu, 2005; Xu, 1999).

Two speaking modes were used as a way of cross-validating the effects of articulatory effort. (a) Quiet conversation: The subject was comfortably seated in front of the microphone, and read aloud the sentences as if speaking to a person standing one meter away. (b) Public lecture: The subject stood in front of the microphone and read aloud the sentences as if speaking to a large audience in a lecture hall.

The target sentences (target sequences + the carriers) and their precursor questions were repeated five times, and printed in Chinese in random order. The total number of sentence pairs was:

$$20(\text{sequences})\times 2(\text{final}\text{or}\text{non}-\text{final})\times 2(\text{speaking}\text{modes})\times 5(\text{repetitions})=400.$$

2.2. Subjects

To guarantee minimal dialectical variability, only native Mandarin speakers born and raised in Beijing participated as subjects. They were eight university students, aged 19–22, four females and four males. They were recruited from universities in the city of Guangzhou and were paid for their participation. None of them reported having any speech disorders.

2.3. Recording Procedure

The recording was conducted in the Language Laboratory in the Department of Applied Linguistics at Jinan University, Guangzhou, China. Four of the subjects, two males and two females, recorded in the conversation mode first and then in the lecture mode. The other four used the lecture mode first and then the conversation mode. This was to control for potential order effect related to fatigue, familiarity with the material, etc. During the recording, care was taken to make sure that subjects used the same normal speaking rate for both modes. The sentences were presented in random order, and a different order was used for each subject. The leading questions were recorded beforehand by the second author in both conversation mode and lecture mode. For each trial, an appropriate leading question was played either through headphones or a loudspeaker to the subject in a particular mode and then the subjects read aloud the target sentence in the same mode. The subjects were instructed not to pause in the middle of a sentence. If a mistake was made as judged by the experimenter, the subject was asked to repeat the sentence. Each subject went through a number of practice trials before the start of the real trials.

2.4. F₀ extraction and labeling

The acoustic analysis was done by a procedure using a custom-written Praat (Boersma, 2001) script. The script (based on an more general purpose version, cf. Xu, 2005–2009 for an updated version which includes all the previous functions) allowed us to generate accurate F₀ tracks by manually rectifying the markings of individual vocal pulses. When the script was run, two windows, one with pulse markings and the other with TextGrid together with the waveform, were displayed. The vocal pulse markings generated by Praat were then manually corrected in the pulse window for errors such as missed or double marked cycles.

Labeling was done in the TextGrid window. The onset and offset of each target sequence was manually labeled. For the dynamic sequences, the F₀ peaks and valleys were first manually labeled but then algorithmically readjusted by the script. The segmentation of syllables in the all-H sequences was done by referring to the change of F2 in the spectrogram. There is a fast F2 transition around the boundary of each syllable, as the nuclear vowels in the high tone sequences alternate between/i/and/u/. For/wu/, the point of F2 minimum was marked as syllable onset. For yi, the point of F2 maximum was marked as the onset.ⁱⁱⁱ The Praat script then converted the vocal periods into F₀ values, and smoothed the resulting F₀ curves with a trimming algorithm to eliminate abrupt bumps and sharp edges (cf. Xu, 1999).

2.5. Measurements

From the F₀ curves of the dynamic tone sequences produced by each subject, the following measurements were taken.

MaxF₀ (st) — Highest F₀ in semitones in each unidirectional pitch movement. The conversion from Hz to semitones was done with the equation:

$$st=12{log}_2{f}_0$$ [2]

in which the reference F₀ is assumed to be 1 Hz.

MinF₀ (st) — Lowest F₀ in semitones in each unidirectional pitch movement.

F₀ displacement (rise or fall) — F₀ difference (in st) between adjacent MaxF₀ and MinF₀. For the all-R and all-F sequences, there are two unidirectional pitch movements in each syllable. The earlier movement is referred to as the transition and the later movement the tone proper. Thus for each syllable in those cases, two displacements were computed accordingly.

Mean F₀ displacement — Average of the transition and the tone proper displacements, for the all-R and all-F sequences only.

Movement duration (rise or fall) — Time interval between adjacent F₀ maximum and minimum.

Peak velocity — Positive and negative extrema in the velocity curve corresponding to the rising and falling ramps of each unidirectional pitch movement. A velocity curve was computed by taking the first derivative of an F₀ curve after it has been smoothed by low-pass filtering it at 20 Hz with the Smooth command in Praat. Following Hertrich and Ackermann (1997), the velocity curve itself was not smoothed so as not to reduce the magnitude of peak velocity.

v_p/d ratio — Ratio of peak velocity to F₀ displacement. There are two measurements for each syllable in the all-R and all-F sequences, one for the transition, and one for the tone proper.

Mean v_p/d ratio — Average of v_p/d ratio in the transition and tone proper of a syllable. For all-R and all-F sequences only.

Parameter C = Peak velocity/Average velocity (= F₀ displacement/F₀ duration). This is an index of the shape of the velocity profile as discussed in the introduction. There are two C values for each syllable in the all-R and all-F sequences, one for the transition, and one for the tone proper.

Mean C — Average C of the transition and tone proper of a syllable. For all-R and all-F sequences only.

Mean up-down cycle duration — Sum of transition and tone proper durations in each syllable, for the all-R and all-F sequences only.^iv

For the all-H sequences, the following measurements were taken.

Maxf₀ (st) — Highest F₀ in a syllable.

Meanf₀ (st) — Average of all F₀ values in a syllable.

Duration — Time interval between the onset and offset labels, whose placement was explained in 2.4.

To make sure that measuring v_p/d ratio and parameter C is justified for F₀, we made scatter plots of peak velocity as a function of F₀ displacement with all the data points from all subjects. The relation between the two was found to be highly linear, with r² of simple linear regressions ranging from 0.73 to 0.94. The strength of the linearity as related to the experimental factors will be discussed in the next section.

3. Analyses and Results

3.1. General strategy

The overall goal of the analysis is to identify F₀ and duration patterns related to syllable grouping, and to assess the role of articulatory strength, if any, in signalling grouping information. Our strategy is to first exhaustively examine all the factors included in the design of the study, including speaking mode, tone sequence, location in sentence, phrase length and tone, before turning specifically to the factor most directly related to grouping, namely, within-group position. The possible involvement of articulatory strength is assessed by examining how kinematic measurements such as v_p/d ratio and parameter C vary with within-group position.

Prior to any numerical analysis, mean F₀ curves are first examined to identify general patterns of various effects. Figures 1 and 2 display mean F₀ curves showing the effects of speaking mode, position in sentence, phrase length and within-group position. These curves are obtained by first averaging over (syllable-sized) time-normalized F₀ curves of all repetitions by all subjects, and then plotting them over the average time computed from mean F₀ up-down cycle duration at each position in a tone sequence. Detailed observations will be discussed next together with the results of statistics analyses.

Fig. 1.

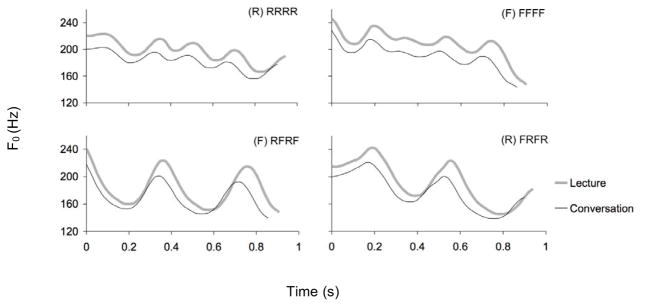
MeanF₀ curves under the effects of speaking mode and articulatory pressure. Thick line — Mean F₀ curves of all-R, all-F, RF and FR sentences in lecture mode. Thin line — Mean F₀ curves in conversation mode.

Fig. 2.

Effects of location in sentence and phrase length on Mean F₀ curves of all-R and all-F sequences. Thin line — sentence final; thick line — non-final.

3.2. Effect of speaking mode and tone sequence

From Figure 1, two effects of speaking mode can be seen. First, F₀ is higher in lecture mode than in conversation mode. Second, F₀ displacement is larger in lecture mode than in conversation mode. Quantitative analyses of the effect of speaking mode are shown in Table 3, which displays the means of various measurements broken down by Speaking mode, Location in sentence and Tone. Also displayed in Table 3 are the F and p values of 4-way ANOVAs with Speaking mode (lecture/conversation), Location in sentence (sentence-final/non-final), Tone (all-R/all-F) and Phrase length (1–4 syllables) as independent variables^v.

Table 3.

Mean values of Maxf₀, Minf₀, mean F₀ displacement, mean v_p/d ratio, Mean C and up-down cycle duration of all the tone sequences under the effects of Speaking mode, Location in sentence, Tone and Phrase length. Also displayed are the F and p values of the main effects of a 4-factor ANOVA.

	Speaking mode		Location in sentence		Tone sequence		Phrase length
	lecture	conversation	non-final	final	all-R	all-F	1	2	3	4
Maxf0 (st)	93.44	91.79	93.26	91.97	91.59	93.63	93.54	92.54	92.33	92.04
	F(1,7) = 14.09		F(1,7) = 33.43		F(1,7) = 69.86		F(3,21) = 28.49
	p = 0.007		p = 0.001		p < 0.001		p < 0.001
Minf0 (st)	88.7	87.7	89	87.4	87.8	88.59	86.79	88.07	88.67	89.26
	F(1,7) = 7.48		F(1,7) = 42.6		F(1,7) = 8.06		F(3,21) = 50.77
	p = 0.029		P < 0.001		p = 0.025		p < 0.001
Mean F0 displacement (st)	3.69	3.09	3.38	3.4	3.45	3.34	5.64	3.45	2.45	2.03
	F(1,7) = 26.51		F(1,7) = 0.014		F(1,7) = 0.33		F(3,21) = 87.69
	p = 0.001		p = 0.909		p = 0.585		p < 0.001
Mean vp/d ratio	16.88	17.3	16.85	17.33	16.23	17.94	13.84	16.07	18.75	19.68
	F(1,7) = 0.345		F(1,7) = 0.34		F(1,7) = 6.789		F(3,21) = 10.81
	p = 0.575		p = 0.578		p = 0.035		p < 0.001
Mean C	1.90	1.88	1.8	1.98	1.92	1.86	2.07	1.90	1.82	1.76
	F(1,7) = 0.225		F(1,7) = 11.18		F(1,7) = 0.892		F(3,21) = 6.75
	p = 0.649		p = 0.012		p = 0.376		p = 0.002
Up-down cycle duration	251.1	239.2	239.5	250.9	265.4	225	314.8	247.4	213.8	204.6
	F(1,7) = 5.43		F(1,7) = 2.14		F(1,7) = 30.08		F(3,21) = 92.59
	p = 0.053		p = 0.187		p = 0.001		p < 0.001

Speaking mode has significant effects on MaxF₀, MinF₀ and Mean F₀ displacement, but not on mean v_p/d ratio, mean C or up-down cycle duration. That both MinF₀ and MaxF₀ significantly increased from conversation mode to lecture mode indicates that there may be an increase of subgottal pressure (Ohala, 1978) in the lecture mode. There is no significant difference in up-down cycle duration between sentence-final (i.e., without post-carrier) and non-final curves (with post-carrier). This indicates that average syllable duration is not significantly different for the two sentence locations.

There is a significant interaction between speaking mode and tone on MaxF₀ (F[1,7] = 16.98, p = 0.004). The MaxF₀ difference between two sentence locations (final and non-final) is slightly larger in lecture mode than in conversation mode.

Figure 1 also shows that, as predicted, F₀ displacement is much larger in the RF and FR sequences than in the all-R and all-F sequences. This may have to do with the difference in articulatory pressure between the two kinds of sequences. In the all-R and all-F sequences, F₀ has to make a sharp turn both at the onset and near the center of the syllable. In the RF and FR sequences, no F₀ turn is necessary at the syllable onset or offset. The reduction in the number of F₀ turns seems to have allowed F₀ to make much larger displacements than in the all-R and all-F sequences. Furthermore, the RF and FR sequences seem to lack positional variations in F₀ displacement which the current study wants to explore. For this reason, and also because the F₀ continuity at the syllable boundaries does not allow analysis of syllable-sized F₀ contours, the RF and FR sequences will not be further analyzed in the following sections.

3.3. Effect of location in sentence and phrase length

Figure 2 displays mean F₀ curves of the all-R and all-F sequences broken down by Tone, Phrase length and Location in sentence. In each plot, the thin curve is sentence-final while the thick curve is non-final. Location in sentence affects mostly the overall F₀ of the later part of the sequence. The sentence-final curves have greater F₀ decline than the non-final curves, and the differences are the largest in the last syllable. The duration of the sentence final curves is also slightly longer than those of the non-final ones. The results of 4-factor ANOVAs in Table 3 show that both MaxF₀ and MinF₀ are significantly lower in sentence final position than in non-final position, and mean C is greater in sentence final than non-final position. But the differences in v_p/d ratio, displacement and up-down cycle duration are not significant.

There is a marginally significant interaction between Location in sentence and Speaking mode on MaxF₀ (F[1,7] = 6.17, p = 0.042). This is due to slightly larger difference between lecture and conversation modes in the non-final position than in the sentence-final position. There is also a significant 3-way interaction: location-in-sentence tone length. This is due to the excessively low F₀ (84.4 st) that occurred in the F tone only when it is carried by a monosyllabic word in the sentence final position. This is a phenomenon similar to what has been reported by Xu (1997) that the very low F₀ at the end of the F tone is seen only in isolation. Here we see that it occurs also in a sentence final position. None of the 4-way interactions are significant.

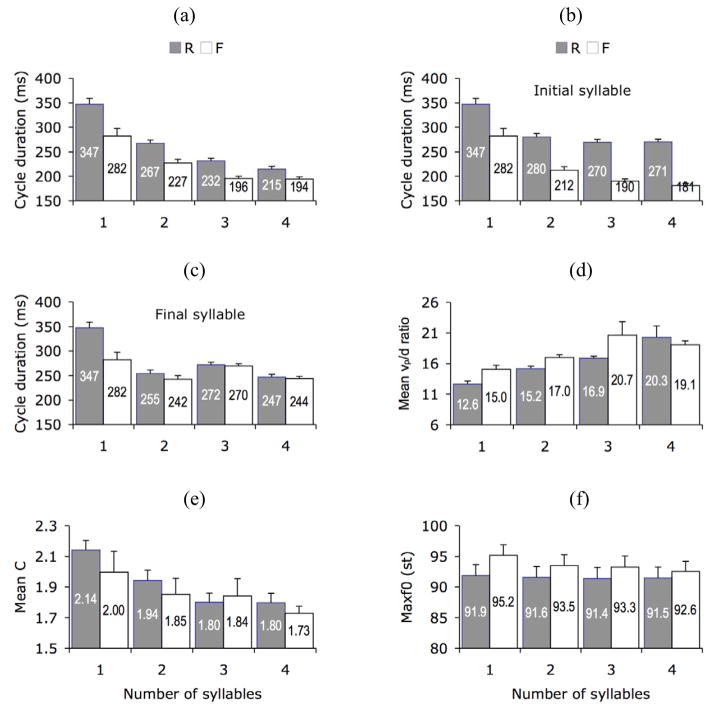
In addition to the effect of Location in sentence, Figure 2 also shows the effect of Phrase length and Syllable position. As the number of syllables in a phrase increases, the overall duration of the phrase also increases. But the two increments are not proportional to each other, because, as shown in Figure 3a, as phrase length increases, the duration of individual syllables decreases.

Fig. 3.

Various measures of all-R and all-F sequences as a function of phrase length and tone. (a) Mean up-down cycle duration. (b) Mean up-down cycle duration of the initial syllable. (c) Mean up-down cycle duration of the final syllable. (d) Mean v_p/d ratio. (e) Mean C. (f) Mean maxF₀

However, as shown in Figures 3b and 3c, for the first and last syllables, the largest shortening occurs from mono-syllable to disyllable sequences. Further shortening is much smaller in the initial syllable, and even inconsistent in the final syllable. This is because the medial syllables in the 3- and 4-syllable sequences are very short, as will be seen in the analysis of positional effects. Thus the progressive shortening in Figure 3a comes from two different sources. There are also significant effects of Phrase length on mean v_p/d ratio and mean C. As can be seen in Figure 3d, the differences in mean v_p/d ratio are in the opposite direction of the differences in up-down cycle duration. As duration decreases, mean v_p/d ratio increases. The direction of change in mean C, on the other hand, is similar to that of duration. Finally, Figure 3f shows that mean maxf₀ largely remains the same. { Fig. 3 about here }

3.4. Effect of tone

From Figure 2 it can be seen that the overall duration of the all-R sequences is longer than that of all-F sequence, which is reflected in the individual up-down cycle duration seen in Table 3. The difference is highly significant, but there is also a significant interaction between Tone and Phrase length on duration (F[1,7] = 5.08, p = 0.008). As seen in Figure 3a, the durational difference between the two tones becomes smaller as phrase length increases. But Figures 3b and 3c show that the reduction in durational differences between the two tones mainly occurs in the initial syllable. Table 3 also shows significant effects of Tone on MaxF₀ and v_p/d ratio. But there is also a significant interaction between Tone and Phrase length on MaxF₀ (F[1,7] = 9.56, p < 0.001). As can be seen in Figure 3f, the interaction on MaxF₀ is due to its reduction in the F tone as phrase length increases, with a corresponding lack of change in the R tone.

3.5. Effect of syllable grouping: Variation due to within-group position

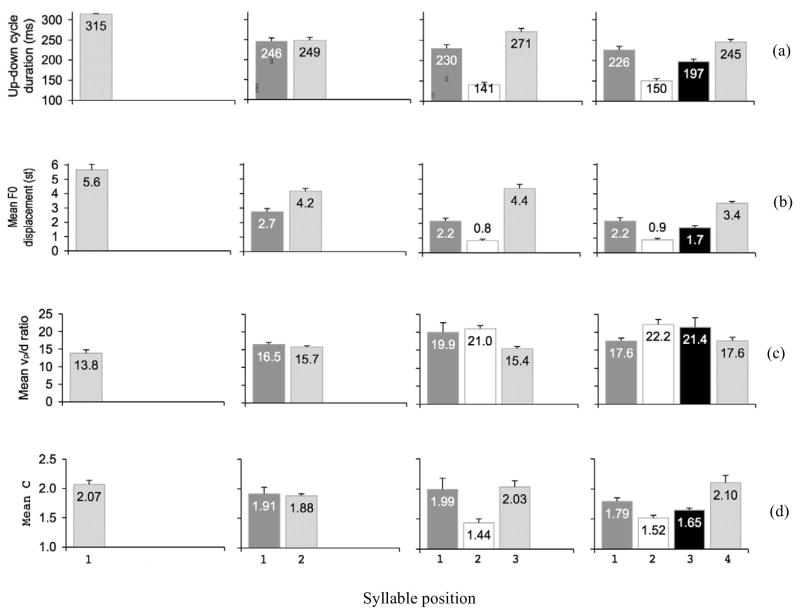
The F₀ curves in Figure 2 suggest that grouping is most prominently manifested in patterns of F₀ displacement and movement duration, which vary not only with phrase length, but also with position within the sequence. Figures 4a and 4b display bar graphs of up-down cycle duration and mean F₀ displacement at different positions in sequences of different lengths. Figures 4c and 4d show corresponding values of mean v_p/d ratio and mean C. In all multisyllabic sequences the final syllable is the longest, while the initial syllable is the second longest (although the difference is not significant in the 2-syllable sequences as seen in Table 4); the first medial syllable is always the shortest, while the second medial syllable is the second shortest. Nearly identical patterns can be seen in mean F₀ displacement.

Fig. 4.

(a) Mean up-down cycle duration at different syllable positions with different phrase lengths. (b) Corresponding mean F₀ displacement. (c) Corresponding mean v_p/d ratio.

Table 4.

Effect of syllable position on mean up-down cycle duration, MaxF₀, MinF₀, mean F₀ displacement, mean peak-velocity/displacement and mean C in 2-syllable, 3-syllable and 4-syllable sequences. The mean values of the 1-syllable sequences are also listed again as reference.

	1-syllable	2-syllable		3-syllable			4-syllable
		initial	final	initial	medial	final	Initial	medial1	medial2	final
Mean up-down cycle duration	314.85	246.28	248.52	230	140.82	270.77	225.7	150.14	197.2	245.36
		F(1,7) = 0.05		F(2,14) = 81.55			F(3,21) = 40.88
		p = 0.83		p < 0.001			p < 0.001
MaxF0 (st)	93.54	92.98	92.11	92.8	92.34	91.86	92.89	92.12	91.75	91.41
		F(1,7) = 8.15		F(2,14) = 10.56			F(3,21) = 14.71
		P = 0.025		p <= 0.002			p < 0.001
MinF0 (st)	86.79	89.1	87	90.67	89.08	86.25	90.84	90.35	88.98	86.86
		F(1,7) = 95.32		F(2,14) = 78.92			F(3,21) = 105.47
		p < 0.001		p < 0.001			p < 0.001
Mean F0 displacement	5.64	2.74	4.16	2.16	0.83	4.38	2.15	0.88	1.71	3.37
		F(1,7) = 37.45		F(2,14) = 71.14			F(3,21) = 48.4
		p < 0.001		p < 0.001			p < 0.001
Mean vp/d ratio	13.84	16.45	15.708	19.89	20.97	15.41	17.56	22.17	21.39	17.63
		F(1,7) = 0.875		F(2,14) = 4.07			F(3,21) = 3.358
		p = 0.381		p = 0.04			p = 0.038
Mean C	2.07	1.914	1.881	1.993	1.437	2.032	1.79	1.515	1.645	2.099
		F(1,7) = 0.087		F(2,14) = 7.002			F(3,21) = 14.03
		p = 0.777		p = 0.008			p < 0.001

The mean v_p/d ratio values in Figure 4c, however, show an opposite pattern: wherever duration is longer and displacement is larger, v_p/d ratio is lower. The pattern of mean C in Figure 4d, interestingly, seems to be much more similar to those of duration and F₀ displacement.

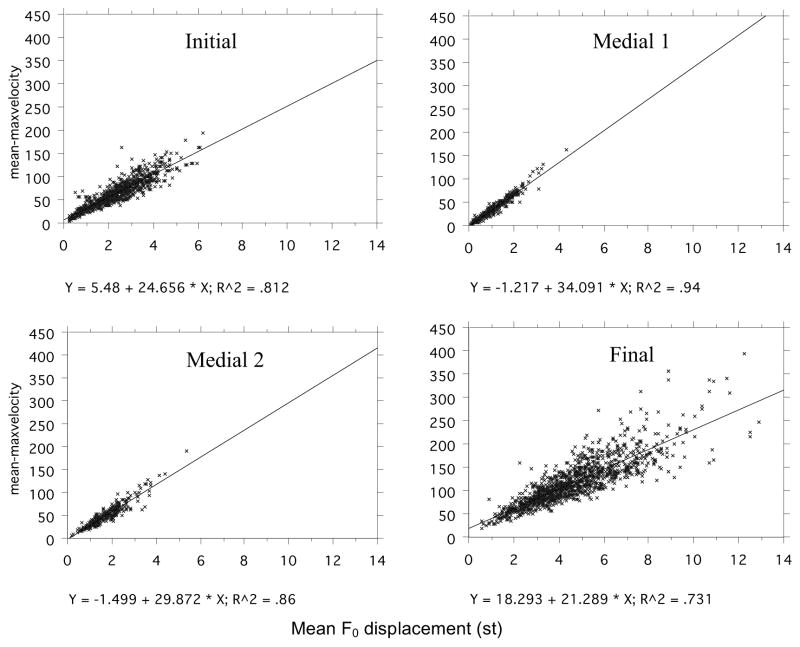
To further understand the relationship among these measurements, it is important to examine whether kinematic F₀ measurements show similar relations as articulatory movements found in previous studies. Figure 5 shows regressions of peak velocity over mean F₀ displacement (average of rise and fall within each cycle). The regressions are divided into 4 positions based on displacement size: initial, medial 1, medial 2 and final. Phrase final position includes the final position in multisyllabic phrases as well as the monosyllabic words, which have the largest displacement. Likewise, the second position in both 3-syllable and 4-syllable phrases are grouped together as medial 1 because both positions have the smallest displacement.

Fig. 5.

Simple linear regressions of F₀ peak velocity over F₀ displacement for different syllable positions: initial, medial 1 (2nd syllable of 3- and 4-syllable sequences), medial 2 and final (final syllable of all sequences, including monosyllables) positions.

Highly linear relations are seen in all the plots in Figure 5, which resemble those of articulatory movements (e.g., Ostry & Munhall, 1985; Hertrich & Ackermann, 1997; Kelso et al., 1985; Vatikiotis-Bateson & Kelso, 1993). However, the degree of linearity differs depending on the position of the syllable in a phrase. It is higher in the medial positions than in the initial and final positions. Also, the slope of the regression line is steeper in the medial than in the initial and final positions. These differences are related to the size of F₀ displacement: the smaller the size, the higher the correlation, and the steeper the regression line.

Figure 6 shows scatter plots of mean v_p/d ratio, mean C and mean F₀ displacement. In Figure 6a, mean F₀ displacement is positively related to up-down cycle duration, but the correlation seems to be moderate, which is again similar to what has been reported for articulatory movements (Kelso et al., 1985). Nevertheless, the overall trend is consistent with Figure 4c, where patterns of F₀ displacement closely parallel those of movement duration. In Figure 6b, v_p/d ratio appears to be negatively, though nonlinearly, related to up-down cycle duration. This pattern is also similar to what has been reported for articulatory movements (Munhall et al., 1985; Ostry & Munhall, 1985). In Figure 6c, mean C appears to be positively but also non-linearly related to up-down cycle duration. This pattern, once more, has been seen in articulatory data (Adams, Weismer & Kent, 1993). In general, therefore, the patterns seen here parallel many that have been reported for articulatory movements, which suggest that they can be interpreted in articulatory terms. Detailed interpretations will be discussed later in 4.2 based on simulations with a second-order linear system.

Fig. 6.

Scatter plots of F₀ displacement (a), mean v_p/d ratio (b) and mean C (c) as functions of up-down cycle duration.

3.6. Effect of regrouping

Figure 7 displays mean F₀ contours of four-syllable sequences with different internal structures. In each plot, the upper curve consists of two consecutive disyllabic words, while the bottom curve consists of a mono-syllabic word followed by a tri-syllabic word. The overall height difference in each plot is due to the different y-axes used (50–250 Hz for the AB+CD sequences and 100–300 Hz for the A+BCD sequences) for the sake of separating the curves in the plot.

Fig. 7.

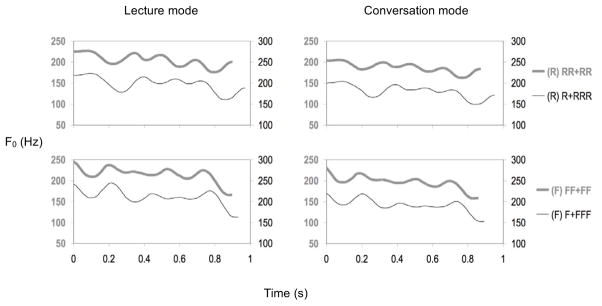
Effects of regrouping on Mean F₀ curves of all-R and all-F sequences. Thick line — AB+CD sequences, with y-axis on the left; thin line — A+BCD sequences, with y-axis on the right.

The differences in grouping has led to visible differences in both up-down cycle duration and F₀ displacement, in the same manner of correspondence as seen in Figure 2: the longer the syllable, the greater the displacement. Compared to that of RR+RR and FF+FF, the first syllable of R+RRR and F+FFF is lengthened and its F₀ displacement expanded. The F₀ contours of the last three syllables have become more like those of the tri-syllabic sequences in Figure 2, with the medial (i.e., 3rd overall) syllable having the shortest duration and smallest F₀ displacement. This is more clearly seen in the F-tone sequences (lower panel) than in the R-tone sequences. The shifted duration and displacement patterns due to regrouping are summarized in the upper panel of Table 5, which more straightforwardly shows the consistency between duration and F₀ displacement as related to regrouping.

Table 5.

Upper panel: Mean up-down cycle duration and F₀ displacement in the AB+CD and A+BCD phrases at each syllable position. Lower panel: Results of paired t-tests comparing up-down cycle duration and F₀ displacement between the AB+CD and A+BCD phrases at each syllable position.

		Cycle duration (ms)		F0 displacement (st)
Grouping	Position	Mean	Std. Error	Mean	Std. Error
AB + CD	1	225.65	11.06	2.153	0.270
	2	150.10	7.31	0.882	0.121
	3	197.15	7.58	1.711	0.173
	4	245.30	7.26	3.371	0.215
A + BCD	1	261.05	9.81	3.072	0.398
	2	174.70	6.05	1.032	0.234
	3	147.60	8.15	0.538	0.135
	4	249.85	10.15	3.377	0.332
t-tests		t (df = 31)	Sig. (2-tailed)	t (df = 31)	Sig. (2-tailed)
AB + CD vs. A + BCD	1	7.827	.000	6.764	.000
	2	5.121	.000	2.579	.015
	3	−9.021	.000	−9.084	.000
	4	2.513	.000	6.764	.000

The lower panel of Table 5 shows the results of paired t-tests comparing mean up-down cycle duration and mean F₀ displacement between the AB+CD and A+BCD sequences at each syllable position. With the exception of duration in final syllable position and displacement in the second syllable position, the differences between the AB+CD and A+BCD sequences are highly significant, indicating rather dramatic durational readjustments. Specifically, compared to the AB+CD sequences, the first and second syllables in the A+BCD sequence are both significantly lengthened, and the third syllable significantly shortened. There is also a slight lengthening of the last syllable. Comparable changes in F₀ displacement are also significant.

The effect of regrouping has also largely settled our initial concerns about vowel intrinsic duration as a potential confound. It is known that low vowels are intrinsically longer than high vowels. In the RR+RR sequence, the vowel in syllable 2 ([a]) is lower than the other three vowels ([y], [], [i]). However, its duration is the shortest (151.0 ms). In the R+RRR sequence, the vowel of syllable 2 becomes [y], but its duration is much longer (175.3 ms). Thus in this case at least, grouping-related duration patterning seems to have overridden the effect of vowel intrinsic duration.

3.7. All-H sequences

Table 6 shows syllable duration, MaxF₀ and MeanF₀ of the all-H sequences broken down by Phrase length and Syllable position, and the results of 3-factor (Speaking mode, Location in sentence and phrase length) ANOVAs. The F₀ values show very small, though statistically significant, movements across syllables. The largest difference in MaxF₀ between adjacent syllables is 0.19 st (between syllable 1 and syllable 2 in the three-syllable group), which is very small compared to the F₀ values of the all-R and all-F groups shown in Table 4. In contrast, the syllable duration values in Table 6 show basically the same patterns as those of the all-R and all-F sequences in Table 4. Because of the very small differences among the F₀ curves of the H-sequences of different lengths, F₀ contours virtually coincide with each other, and so no contour plots are shown here.

Table 6.

Mean values of syllable duration, MaxF₀ and MeanF₀ in the all-H sequences broken down by Phrase length and Syllable position. Also displayed are the corresponding F and p values of 3-factor (Speaking mode, Location in sentence, Syllable position) repeated measures ANOVAs.

	1-syllable	2-syllable		3-syllable			4-syllable
		initial	final	initial	medial	final	initial	medial1	medial2	final
Syllable duration	248.98	197.4	232.4	185.5	194.4	249.7	191.4	182.6	188.7	242.3
		F(3,21) = 21.33		F(3,21) = 25.24			F(3,21) = 24.3
		p = 0.002		p < 0.001			p < 0.001
MaxF0 (st)	94.15	94.09	93.97	94.14	93.95	93.93	94.10	93.97	93.88	93.84
		F(3,21) = 2.69		F(3,21) = 16.0			F(3,21) = 15.09
		p = 0.145		p < 0.001			p < 0.001
MeanF0 (st)	93.73	93.73	93.52	93.77	93.52	93.55	93.74	93.53	93.51	93.46
		F(3,21) = 9.83		F(3,21) = 11.06			F(3,21) = 7.07
		p = 0.016		p = 0.001			p = 0.002

4. Discussion and Further Analysis

Three general questions were raised at the beginning of the present study: (1) What are the basic patterns of F₀ variation related to syllable grouping in Mandarin? (2) How are they related to syllable duration? (3) How are they related to articulatory strength? In regard to the first question, the current data show that F₀ variations are highly sensitive to within-group position in sequences of dynamic tones such as R and F. The magnitude of F₀ movement in a dynamic tone is much larger at the edges of a group than in the middle. If we use a notational system in which a larger number represents a larger movement, the magnitude patterns of 2-, 3- and 4-syllable groups are 1 2, 2 1 3, and 3 1 2 4, respectively. For the 4-syllable groups, however, the duration values of the two middle syllables are swapped when the group internal word structure is A+BCD instead of AB+CD. This kind of patterning is found to be independent of tone, speaking mode and position of the group in sentence. In the all-H sequences, in contrast, no position-specific F₀ patterns are found other than the slight monotonic decline over time. This indicates a lack of direct grouping-related F₀ height manipulation in general, because any F₀ variation related to syllable grouping would have become obvious in the all-H sequences in Table 6. This is further highlighted by the fact that, while the duration of the all-H sequences shows basically the same patterns as those of the all-R and all-F sequences, F₀ only shows small monotonic decline over time. In regard to the second question, the present data suggest that the positional F₀ variation patterns in the dynamic tone sequences are clearly related to syllable duration. To answer the third question, however, we need to carefully consider the underlying dynamic articulatory mechanisms, as will be discussed next.

4.1. Maximum speed of pitch change

Recall that our use of the all R-tone and all F-tone sequences was to force speakers to generate laryngeal movements that are as fast as articulatorily possible, because for both tones there need to be two F₀ movements in opposite directions within a syllable (Xu & Wang, 2001). According to Xu and Sun (2002), at the maximum speed of voluntary pitch change (obtained by having subjects imitate, to the best of their ability, resynthesized alternating high-low steady-state pitch sequences at a rate well beyond human ability — 12 pitch shifts per second), the minimum amount of time it takes to raise or lower pitch is quasi-linearly related to the size of F₀ displacement in semitones:

$$t=89.6+8.7d(\text{pitch}\text{raising})$$ [3]

$$t=100.4+5.8d(\text{pitch}\text{lowering})$$ [4]

where t is minimum movement time in millisecond and d is F₀ displacement in semitones.

To assess how F₀ movements in the present data compare to the finding of Xu and Sun (2002), we used equations [3] and [4] to calculate the minimum time needed for the amount of F₀ displacement found at each syllable position shown in Figure 4b, and plotted them in Figure 8. Also plotted are the up-down cycle duration in Figure 4a and the difference between the two values (measured – predicted). As can be seen, at phrase-final positions the measured duration is consistently longer than the predicted duration, whereas in the medial positions the measured duration is consistently shorter than the predicted duration. This suggests that laryngeal movements are likely to be near or at the physiological limit of maximum speed in the medial positions, but some distance away from that limit in the initial and final positions.

Fig. 8.

Up-down cycle duration shown in Figure 4a (white bars), minimum time needed for making the amount of F₀ displacement at each syllable position shown in Figure 4b, computed with equations [3] and [4] (grey bars), and the difference between the two (measured – predicted) (dark bars). The separate bar clusters show values for the 1–4 syllable sequences, respectively.

4.2. Contribution of articulatory effort: Is there any?

In Figure 4, position-specific patterns of v_p/d ratio show largely opposite patterns from those of F₀ displacement and duration: The smaller the value of F₀ displacement and duration, the greater the v_p/d ratio. This might mean that greater articulatory effort is exerted for shorter and smaller movements than for longer and larger movements if v_p/d ratio is taken as an indicator of articulatory stiffness as discussed in the introduction. To see if this could be the case, we simulated the relation between v_p/d ratio and movement duration with a critically damped second-order linear system (which has been widely used to characterize articulatory and F₀ movements, e.g., Fujisaki, 2003; Kelso et al., 1985; Nelson, 1983; Ostry, Keller & Parush, 1983) expressed with the equation:

$$x_p(t)=x_0{e}^{-{\omega }_{n}t}+({\omega }_n{x}_0+v_0)t{e}^{-{\omega }_{n}t}$$ [5]

where ω_n is the natural frequency of the system related to stiffness ( ${\omega }_n=\sqrt{\frac{k}{m}}$, where k is stiffness and m is mass), x₀ and v₀ are initial displacement and initial velocity, respectively, and t is time.

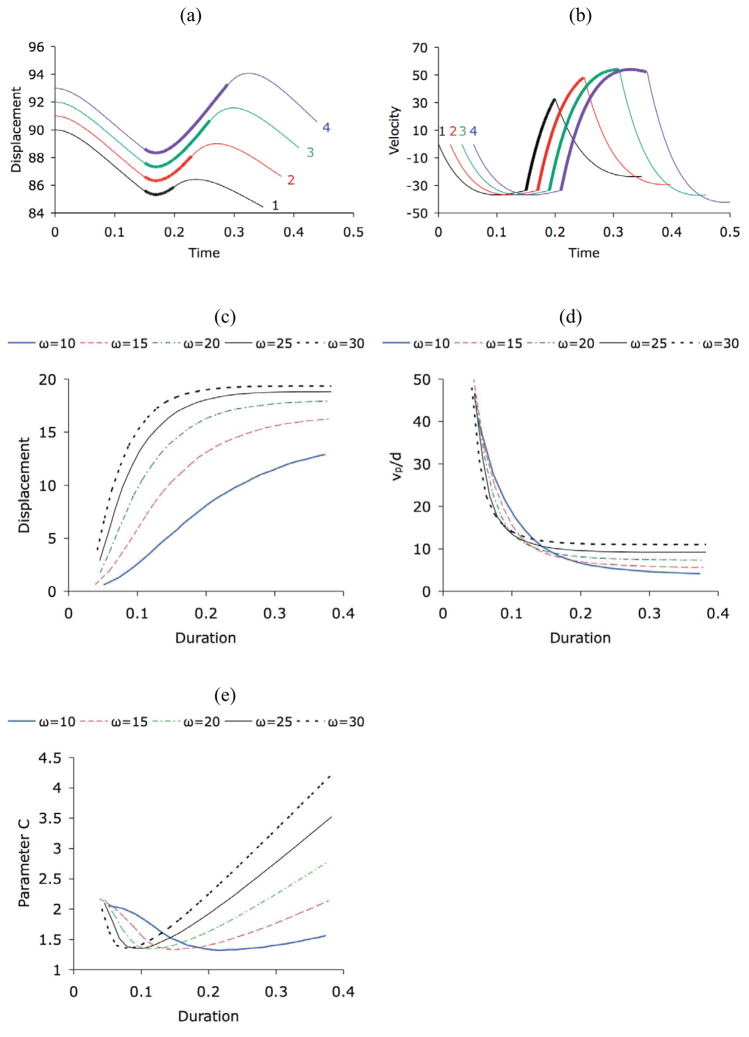
The results of the simulations are displayed in Figure 9. Figure 9a shows trajectories each consisting of three contiguous movements, with movement divisions indicated by changes of line thickness. The y-axes for trajectories 2, 3 and 4 are offset by 1, 2 and 3, respectively, so as to separate their initial portions which are otherwise completely overlapped up to the end of the second movement. The duration of movements 1 and 3 is fixed at 0.15, while that of movement 2 varies across 0.05, 0.08, 0.11 and 0.14. Each movement is a curve that asymptotically approaches an equilibrium point from an initial state. The initial state of movement 1 is defined by x₀ = 90 and v₀ = 0. For movements 2 and 3, x₀ and v₀ are directly transferred from the final displacement and velocity of the previous movements. As can be seen, such a state transfer leads to a delay of the turning point across adjacent movements whenever v₀ is nonzero. The equilibrium points of the three movements are set at 80, 100 and 80, respectively. None of them is achieved by the end of the corresponding movement, however. This is because for all the movements, the natural frequency ω_n, which is related to stiffness as explained above, is set to 10, a level at which displacement of the second movement exhibits clear duration dependency similar to that seen in Figures 4 and 6. Figure 9a therefore demonstrates that it is possible to simulate duration dependency with a second-order system even when stiffness is fixed.

Fig. 9.

(a) Simulated movement trajectories based on a critically damped second-order linear system defined by equation [5]. See text for details about the parameters used. (b) Velocity profiles of the trajectories in (a). (c) Simulated displacements as a function of duration at different stiffness levels indicated by ω_n. (d) Simulated v_p/d ratios as a function of duration at different stiffness levels. (e) Simulated parameter C (peak-velocity/average-velocity) as a function of duration at different stiffness levels.

Figure 9b displays velocity profiles, i.e., the first derivative, of the trajectories in Figure 9a. Here again, the division of adjacent movements are indicated by changes in line thickness. The time axes of profiles 2, 3 and 4 are right-shifted by 0.02, 0.04 and 0.06, respectively, to avoid complete overlap up to the end of the second movement. As can be seen, the peak velocity of the second movement, i.e., the height of each profile, increases with movement duration. However, the amount of increase gradually reduces, and there is no further increase from profile 3 to profile 4. This means that in a second-order system, peak velocity does not always show the same duration dependency as displacement.

Figures 10c, 10d and 10e display displacement, v_p/d ratio and parameter C measured from simulated trajectories like those in Figures 10a and 10b, as functions of duration. Each function is from a set of 25 curves generated with a given ω_n as indicated by the legends. These functions are therefore analogous to the scatter plots in Figure 6, and should help us interpret those distribution patterns, assuming that F₀ production can be likened to a critically damped second-order linear system. In Figure 9c displacement shows clear duration dependency when ω_n, hence stiffness, is relatively small. As ω_n increases, the function becomes increasingly non-linear, and displacement levels off when it approaches the equilibrium point as duration continues to increase. This suggests that the kind of duration dependency seen in Figures 4 and 6 is more like a second-order system with low rather than high stiffness.

In Figure 9d v_p/d ratio is a highly non-linear function of duration, with a quick drop from a very high level at very short duration to a relatively low plateau at long duration. This means that in a second-order system, peak velocity is very high relative to displacement when duration is short, but its increase is slower than that of displacement as the movement becomes longer, as can be seen in the comparison between Figure 9a and 9b. Furthermore, when movement duration becomes sufficiently long, both displacement and peak velocity stop increasing because the equilibrium point is almost attained. The scatter plot in Figure 6b most resembles the elbow of the functions in Figure 9d, and the gentle curvature there is more like a function with lower ω_n rather than one with higher ω_n. In general, the simulations here suggest that the variability of v_p/d ratio in Figure 6b is more unambiguously related to duration than to stiffness, because the latter could have remained constant while v_p/d ratio still exhibits a negative relation to duration as in Figure 9d. This implies that the shorter movements with greater v_p/d ratios in Figure 6a do not necessarily have greater stiffness, assuming that F₀ contour production is similar to a second-order linear system.

That v_p/d ratio is greater in shorter movements than in longer movements has been a general finding in previous research on articulatory movements (e.g., Adams et al., 1993; Edwards et al., 1991; Munhall et al., 1985; Ostry et al., 1985; Perkell et al., 2002). What has not been clear is the nature of such a negative relation. It has been suggested, with the assumption that v_p/d ratio directly reflects stiffness, that stiffness is used to control speech rate, and lowering stiffness is to slow down articulation in order to lengthen a movement (Browman & Goldstein, 1989; Munhall et al., 1985; Ostry et al., 1985; Saltzman & Munhall, 1989). Other studies, however, have suggested that speech rate is not solely or directly controlled by stiffness (Adams et al., 1993; Edwards et al., 1991; Byrd & Saltzman, 2003). What the above simulations show is that without first clarifying the relation between v_p/d ratio and stiffness as a function of duration, it is hard to accurately assess the real contribution of stiffness.

The curves in Figure 9e show a peculiar relationship between parameter C and duration. Each curve starts at a value near 2, which means peak velocity is twice as high as mean velocity of the movement, and then quickly drops below 1.5 before starting to rise. This final rise is easily comprehensible, because as the movement asymptotes near the equilibrium point, mean velocity will become smaller and smaller, whereas peak velocity should remain the same as can be seen in Figure 9b. Looking at Figure 6c again, it seems that the pattern there somewhat resembles the parameter C function with ω_n = 15 in Figure 9e rather than a function that adopts increasingly greater ω_n as duration becomes longer. In fact, judging from the slow rise in parameter C in Figure 6c, if stiffness does change with increasing duration, the change is more likely be a reduction given that the final rises at most of the stiffness levels in Figure 9e are faster than the slope in Figure 6c.

To sum up the simulation results, the greatest similarity between the simulated data and those shown in Figures 4 and 6 is the duration dependency of displacement, which suggests a low level of stiffness that would generate frequent undershoot within normal duration ranges. The second greatest similarity is the negative relation between movement duration and v_p/d ratio, which, unfortunately, does not provide direct evidence of increased stiffness with shortened duration as has been suggested previously (e.g., Kelso et al., 1985; Ostry et al., 1983; Ostry & Munhall, 1985). However, this ambiguity does not constitute clear negative evidence either. More research is therefore needed to clarify this critical issue. The least similarity between the simulated data and those shown in Figure 6 is seen in parameter C, because the simulated functions display complex shapes with little resemblance to the actual data. Again, further research on the discrepancy is needed.

4.3. Overall implications

4.3.1. Unlikely involvement of stress

The findings of the present study raise serious questions about existing proposals on foot-internal structures in Mandarin. First, none of the existing proposals about the foot-internal stress patterns seems to be supportable, whether syllable duration or magnitude of F₀ movement is treated as the correlate of stress. Given that in 3-syllable or 4-syllable groups the middle syllable(s) has/have both smaller F₀ displacement and shorter syllable duration, it is hard to argue that a foot is either iambic or trochaic. Second, the results from the all-H sequences suggest that phrase-level syllable grouping in Mandarin does not involve direct F₀ height manipulations. Third, the idea that syllable grouping is encoded directly by articulatory strength did not find support in the present data. Although it was found that v_p/d ratio, which has been taken as an indicator of articulatory stiffness in previous research, is somewhat negatively related to F₀ displacement and syllable duration, simulations with a critically damped second-order system show that v_p/d ratio is negatively and non-linearly related to duration even when the input stiffness of the model remains constant. Thus there is a lack of evidence for the involvement of stiffness in generating larger F₀ movements. The present data therefore suggest that duration is the parameter most directly related to syllable grouping.

4.3.2. Nature of grouping-related duration patterns: Temporal distance as code for relational distance

Interestingly, the durational patterns found here for Mandarin are reminiscent of the position-specific duration patterns reported for languages like English that do have distinctive lexical stress. The first is constituent-initial and constituent-final lengthening (Cooper et al., 1977), as seen in the fact that in 3-syllable and 4-syllable phrases the last syllable is always the longest and the first syllable the second longest, as shown in Figure 4a and Table 5. The second is polysyllabic shortening (Klatt, 1976; Lehiste, 1972; Turk & Shattuck-Hufnagel, 2000), as seen in the fact that, as the number of syllables in a syllable group increases, the duration of all individual syllables shortens, as shown in Figure 3a for the all-R and all-F sequences and in Table 5 for the all-H sequences. It has been argued, however, that the phenomenon of polysyllabic shortening can be largely accounted for by a word- or phrase-level lengthening effect (Nakatani et al., 1981). While this may be an unresolved issue for English, the present data suggest that the shortening effect in Mandarin is actually stronger than in English. First, from monosyllabic to disyllabic words, the final syllable shortens substantially in Mandarin (Figures 3c, 4a), but not in English (Fig. 4 and 5 in Nakatani et al., 1981). Second, from disyllabic to tri- and quadra-syllabic words the newly added medial syllables are much shorter than the initial syllables in Mandarin (Figure 4a), whereas medial syllables are only slightly shorter than initial syllables in English (also Fig. 4 and 5 in Nakatani et al., 1981). Such language-specific duration patterns seem worthy of further investigations.

Note that there is an inevitable dilemma in treating the duration patterns found here as solely due to either a lengthening or shortening effect. A lengthening-only account would regard the medial syllables as the ultimate duration reference, with the implication that the ideal duration is one that would result in severe undershoots, as is obvious in Figure 2. A shortening-only account, on the other hand, would mean treating the longest possible syllable as the reference, which is just as absurd. Thus there is a need to go beyond simply calling the duration variation as lengthening or shortening and consider, instead, the true nature of duration patterning as related to syllable grouping. Some interesting clues can be seen in the effect of regrouping. As shown in Figure 7, in a A+BCD phrase both the first and second syllables are lengthened as compared to a AB+CD phrase. Such lengthening increases the distance between the onsets of the two syllables, making the two syllables temporally farther apart from each other. Likewise, the shortening of the second syllable in a A+BCD phrase makes the two syllables closer to each other. Furthermore, the much lengthened final syllable of a phrase greatly increases its distance from the onset of the following phrase. Also, it is known that a very strong boundary is often associated with a pause (Lea, 1980; O’Malley et al., 1973; Swerts, 1997). Thus both pre-boundary duration and pause duration affect the temporal distance between the onset of the pre-boundary constituent and the onset of the post-boundary constituent. This suggests that temporal distance is used to indicate relational distance. In other words, durational variation related to syllable grouping appears to serve as an affinity index, as proposed in Xu (2009), which iconically encodes the closeness of adjacent constituents.

Affinity index is similar to the notion of boundary strength (Beckman & Edwards, 1990; Byrd & Saltzman, 2003; Lehiste, Olive & Streeter, 1976; Shattuck-Hufnagel & Turk, 1996; Wightman et al., 1992). Syllable duration as a correlate of boundary strength has been reported previously. Edwards et al. (1991:381) have suggested that the “phrase-final position is specified in terms of a durational target”. Wagner (2005) reports evidence that there are gradient durational variations closely corresponding to hierarchical syntactic structures. He argues that the syntax-prosody relation is much more direct than has been assumed in major theories of prosodic phonology. The notion of affinity index is more general than that of boundary strength, however, because it assumes that the relation between every pair of syllables is encoded by their temporal distance from each other. As such the affinity index is likely to be highly gradient rather than categorical, as has been demonstrated by Wagner (2005). Note that the gradiency of affinity index does not mean that it cannot be used to signal boundaries of units like word, phrase or foot. Rather, given its sensitivity to inter-constituent relations in general, any units that are functionally operative could be signaled by affinity index.

One thing in the present data that cannot be fully explained in terms of inter onset interval as proposed in Xu (2009) is the longer duration of initial syllable when compared to the medial ones. One possibility is that it is the distance from the onset of the earlier syllable and the offset, rather than the onset, of the later syllable that serves as the affinity index. Thus the initial syllable in a group is longer than the medial syllables because it is not shortened by being pressed into the final syllable of the preceding group. Further research is needed to explore this possibility.

4.3.3. Implications for understanding stress in general

Finally, although one of the goals of the present study is to examine the likely involvement of stress in manifesting syllable grouping, because our focus has been on F₀ and duration, we have not examined all the phonetic properties previously reported for stress. For example, it has been shown that a stressed syllable has not only higher F₀ (Fry, 1958; Xu & Xu, 2005; Prom-on et al., 2009), but also higher intensity (Fry, 1958), shallower spectral tilt (Sluijter & van Heuven, 1996), more extreme formant patterns (de Jong, 1995) or higher F1 (Beckman, Edwards & Fletcher, 1992). But what the present results have suggested is that it is not sufficient to just take sparsely sampled measurements of these parameters. Finer sampling than has been used is needed to reveal their dynamic trajectories. We have also learned that it is possible to subject acoustic measurements to the kind of dynamic analysis typically applied only to articulatory data. Thus whether any or all of the above-mentioned stress-related parameters are used independent of duration to signal syllable grouping can be known only after their dynamic patterns have been carefully examined.

5. Conclusion

The goal of the present study is to find out if there exist consistent F₀ and duration patterns related to syllable grouping at the phrase level in Mandarin, and to explore their possible underlying articulatory mechanisms. We examined both conventional measurements for tone, such as maximum and minimum F₀, F₀ displacement, and movement duration, and measurements that had been used mainly for articulatory data, including peak velocity, v_p/d ratio and parameter C. We found that syllable duration had the most consistent patterns related to syllable grouping. In a short phrase of 1–4 syllables, duration was longest in the final position, second longest in the initial position, and shortest in the medial positions. F₀ displacement showed patterns commensurate with syllable duration. However, v_p/d ratio exhibited the opposite patterns. Modeling simulations demonstrated that v_p/d ratio increased with shortened duration even when stiffness of a second-order linear system remained constant. This suggests an ambiguity of v_p/d ratio as an indicator of stiffness. This finding should have interesting implications for research on dynamic movements in speech in general. In syllable sequences consisting of only the H tone, there were no F₀ variations that matched the duration patterns. Thus syllable grouping seems to be primarily encoded with duration adjustments. We propose that the essence of such adjustment is to iconically encode inter-constituent affinity: the shorter the temporal distance between adjacent units, the closer they are related to each other.