Shape detection of Gaborized outline versions of everyday objects

Abstract

We previously tested the identifiability of six versions of Gaborized outlines of everyday objects, differing in the orientations assigned to elements inside and outside the outline. We found significant differences in identifiability between the versions, and related a number of stimulus metrics to identifiability [Sassi, M., Vancleef, K., Machilsen, B., Panis, S., & Wagemans, J. (2010). Identification of everyday objects on the basis of Gaborized outline versions. i-Perception, 1(3), 121–142]. In this study, after retesting the identifiability of new variants of three of the stimulus versions, we tested their robustness to local orientation jitter in a detection experiment. In general, our results replicated the key findings from the previous study, and allowed us to substantiate our earlier interpretations of the effects of our stimulus metrics and of the performance differences between the different stimulus versions. The results of the detection task revealed a different ranking order of stimulus versions than the identification task. By examining the parallels and differences between the effects of our stimulus metrics in the two tasks, we found evidence for a trade-off between shape detectability and identifiability. The generally simple and smooth shapes that yield the strongest contour integration and most robust detectability tend to lack the distinguishing features necessary for clear-cut identification. Conversely, contours that do contain such identifying features tend to be inherently more complex and, therefore, yield weaker integration and less robust detectability.

1. Introduction

Gabor elements are in widespread use as experimental visual stimuli, owing to the fact that these elements match the receptive field properties of orientation-selective simple cells in primary visual cortex and are thus well suited to the targeted stimulation of specific and relatively small subpopulations of neurons (Loffler, 2008; Marčelja, 1980). The use of “snakes” rendered by combining Gabors at different positions and with different orientations has long become commonplace to study the process of contour integration (Field, Hayes, & Hess, 1993; see Loffler, 2008 for a comprehensive review). In addition, displays consisting of Gabor elements have served to investigate texture grouping and segmentation (e.g. Casco et al., 2009; Giora & Casco, 2007; Harrison & Keeble, 2008) and to study the grouping of both contours and textured surfaces in conjunction (Machilsen & Wagemans, 2010).

In the contour integration literature, the underlying linking mechanism is traditionally hypothesized to rely on local interactions between neighbouring cells in primary visual cortex (V1). There is, however, evidence that more global shape properties influence contour integration. One often-researched example is the allegedly enhanced detectability of closed versus open contours (Kovács & Julesz, 1993; Mathes & Fahle, 2007; but see also Tversky, Geisler, & Perry, 2004). Other studies found evidence for the importance of constant direction and magnitude of curvature, rather than closure per se (Pettet, 1999; Pettet, McKee, & Grzywacz, 1998). In any case, this body of research indicates that contour linking can depend in part on shape properties that only emerge when integrating over a larger spatial extent than that of connections between neighbouring V1 cells. Although such spatial integration could be mediated by long-range connections within early visual areas, electrophysiological recordings suggest the involvement of extra-striate areas (Loffler, 2008), particularly V4, where curvature is strongly represented (Pasupathy & Connor, 1999).

All aforementioned studies used artificial and fairly simple shapes as stimuli, from open contour fragments and simple textured areas to circular, elliptic, or other basic geometric shapes for contours and textures. We reasoned that if one is interested in the role higher-level brain areas might play in contour integration, then it makes sense to use stimuli that are likely to elicit responses at the highest levels of the visual hierarchy. One possibility is to use contours corresponding to real-world objects' shapes. In a previous study (Sassi, Vancleef, Machilsen, Panis, & Wagemans, 2010), we gathered identification norms for Gaborized outline versions of the Snodgrass and Vanderwart (1980) set, designed precisely with this purpose in mind. The aim was to start from a stimulus set that has a long tradition of being used in visual perception research (e.g. De Winter, & Wagemans, 2008; Dickerson & Humphreys, 1999; Gaffan & Heywood, 1993; Lloyd-Jones & Luckhurst, 2002; Magnié, Besson, Poncet, & Dolisi, 2003; Panis, De Winter, Vandekerckhove, & Wagemans, 2008; Panis & Wagemans, 2009; Rossion & Pourtois, 2004; Soldan, Hilton, Cooper, & Stern, 2009; Torfs, Panis, & Wagemans, 2010; Wagemans et al., 2008), and to create new versions of these stimuli geared towards studies of contour and texture grouping.

Sassi et al. (2010) tested the identifiability of six different versions of these Gaborized outlines using a computerized free naming task. Stimulus versions differed with regard to the orientations of background elements inside and outside the contour, whereas element positions remained constant across versions. Contour elements also retained their curvilinear (C) orientations in all versions. Interior elements were given either random orientations (R) or orientations parallel (P) to the main axis of the outline shape (for details, see Sassi et al., 2010). Exterior elements were given either random orientations (R), or orientations parallel (P) or orthogonal (O) to the main axis, resulting in a total of six permutations of interior and exterior element arrangements.

Besides providing norms for the identifiability of the Gaborized outlines, the results of Sassi et al. (2010) established a ranking order of the stimulus versions in terms of identifiability. Average identification performance clearly benefited from placing iso-oriented Gabor textures within and outside the contour. Of the six versions tested, two contained homogeneously oriented textures both inside and outside the contour: the version with orthogonal exterior, curvilinear contour, and parallel interior element orientations (OCP); and the version with parallel exterior, curvilinear contour, and parallel interior orientations (PCP). Both the OCP and PCP versions were significantly better identified than the version with randomized exterior, curvilinear contour, and randomized interior orientations (RCR), which most closely resembles the typical arrangement used in studies focusing on contour integration in isolation. OCP outlines were, on average, also somewhat easier to identify than PCP, although the performance difference between the two was not statistically significant. An example of each of the stimulus versions described here is shown in the left column of Figure 1.

Figure 1.

Three Gaborized outline versions (OCP, PCP, and RCR) of Snodgrass object no. 98 “fox” (target-present, left) and their target-absent counterparts (right). The 0° jitter level shown here contains perfectly curvilinear contour elements and, in the OCP and PCP versions, perfectly aligned interior and exterior elements. Each target-absent stimulus contains the exact same orientations as its target-present counterpart, but the elements are randomly positioned.

In addition, the Sassi et al. (2010) study found three stimulus metrics to be generally predictive of the identifiability of the embedded outline: the number of Gabor elements that form the contour, the number of elements contained in the area inside each contour, and the mean inter-element angle along the contour path. Briefly summarized, contour length was positively linearly related to identifiability, whereas the mean inter-element angle and the number of interior elements showed a quadratic, inverted U-shaped, relationship to identifiability. In other words, there was an identifiability advantage for longer contours, whereas extreme values—both low and high—of the remaining two metrics generally corresponded to lower identifiability. The effects of the stimulus metrics were framed within a theory of object identification that distinguishes two stages: a bottom-up grouping stage followed by a top-down matching stage (Panis et al., 2008; Panis & Wagemans, 2009; Torfs et al., 2010; see also Biederman, 1987). Accordingly, certain subsets of the stimuli with low identifiability were characterized as suffering primarily from problematic contour integration whereas the low identifiability of other subsets was interpreted as reflecting difficulties in matching the integrated shape to memory representations (see Sassi et al., 2010 for detailed analyses and discussion).

In this study, we ran a yes/no detection task using three variants of the stimulus versions mentioned above (OCP, PCP, and RCR). We systematically jittered the orientations of each element in the display to weaken both the grouping by contour integration, and the grouping by orientation similarity of the interior and exterior elements in the OCP and PCP versions. The data presented here describe the robustness, in terms of how much orientation jitter can be tolerated, of shape detectability on the basis of Gabor contours and textures for a diverse set of complex everyday object shapes. We investigated whether the effect of orientation jitter on detectability differed between stimulus versions and/or depending on the stimulus metrics as it did for identifiability in Sassi et al. (2010). Comparing the results of the detection and identification tasks also allowed us to further substantiate the interpretation in terms of grouping versus matching difficulties of the findings from the previous study.

We note here that the level of identification specificity required by Sassi et al.'s (2010) scoring rules, save for a few exceptions, generally corresponded to basic-level categorization (Rosch, Mervis, Gray, Johnson, & Boyes-Braem, 1976). There has been some debate surrounding the distinction between detection and basic-level categorization within the object recognition literature. Typical models of object recognition assume that visual objects need to be matched to stored knowledge for categorization but not for detection (e.g. Riesenhuber & Poggio, 1999). Grill-Spector and Kanwisher (2005), however, showed that participants did not need more processing time for basic-level categorization than for detection of objects in natural images, and controversially claimed the two to be mutually necessary or equivalent processes. Bowers and Jones (2008) subsequently showed that detection did require less processing time than categorization if Grill-Spector and Kanwisher's (2005) paradigm was modified by removing the mask presented after each stimulus and by selecting the available responses for the categorization task from the same superordinate category (e.g. presenting “dog” and “cat,” rather than “dog” and “car” as response alternatives). Finally, Mack, Gauthier, Sadr, and Palmeri (2008) showed that detection also required less time than categorization when the natural images used as stimuli were inverted or degraded by adding visual noise.

Although this literature suggests that detection and basic-level categorization may indeed be based on the same information or process in specific cases (as initially reported in Grill-Spector & Kanwisher, 2005), we had a number of reasons to expect differences between our identification and detection tasks. First, we did not use masking in either experiment (see Bowers & Jones, 2008). Second, our identification task (Sassi et al., 2010) required a basic-level response to a free naming task rather than a choice from a fixed number of alternatives. This further increased categorization difficulty compared with Bowers and Jones' (2008) study and also further lessened the likelihood that participants would be able to purposely focus on particular features indicative of specific categories. Finally, our stimuli were strongly degraded (see Mack et al., 2008) compared with natural images: the Gaborized outlines required contour integration, and/or texture grouping and texture segmentation, to extract a shape that itself was a rendering of an outline derived from a line drawing. Considering the relatively degraded nature of the stimuli—compared with the natural images typically used in this line of research—and the demands of the free naming task in the identification experiment, we predicted a number of differences and similarities in performance between identification and detection.

Regarding the stimulus versions, we expected to find a qualitatively similar pattern to Sassi et al. (2010). Machilsen and Wagemans (2010) have previously shown that an interior texture consisting of a cluster of similarly oriented elements embedded in a background of randomly oriented elements allows shape detection even in the absence of curvilinear contour elements, whereas earlier work by Nygård (2009) showed that such textures without contours do not allow shape identification (see also Nygård, 2009; Nygård, Sassi, & Wagemans, 2011). For this reason, we expected the OCP version, of which the interior and exterior could be segmented on the basis of the difference in average orientation, to show a clear advantage over the other versions in the detection task, where contour integration need not be the limiting factor. Although the similarly oriented interior and exterior textures of PCP stimuli would not allow orientation-based segmentation, the mostly uniformly oriented display might cause contour element positions to pop out due to their different curvilinear orientations. Hence, we also expected PCP versions to yield better performance than RCR versions, in which shape detection relies entirely on the grouping of contour elements, as in the typical contour detection experiment.

As for the effects of the different shape metrics, in order for the interpretation of Sassi et al. (2010) to be corroborated, any decreases in identification performance hypothesized to be due to mainly matching problems should be mitigated in the detection task, for which we assume matching the shape to memory is not a necessary condition. Specifically, we do not expect the lower performance for extreme—both large and small—numbers of interior elements and for small values of the average inter-element angle, as found in the identification task, to show up in the detection results. In addition, certain grouping difficulties might be alleviated in a detection task, but this would concern very specific cases, namely those in which an incomplete grouping failed to incorporate one or more features essential for identification (see Sassi et al., 2010) but might still allow detection.

2. Experiment

2.1. Participants

Two hundred and sixty-eight first-year psychology students—232 women and 36 men—aged 17–37 (M = 18.38, SD = 1.60) took part as a mandatory component of their curriculum. Participants were explicitly instructed to wear any corrective glasses or contact lenses usually worn during everyday activities, and had not previously taken part in experiments with similar or related stimuli.

2.2. Stimuli

The stimulus set was based on a previously selected set of 184 outlines of everyday objects (De Winter & Wagemans, 2008; Sassi et al., 2010) derived from the Snodgrass and Vanderwart (1980) collection of line drawings. The 184 outlines were embedded in arrays of non-overlapping, even-symmetric Gabor elements on a uniform grey background, yielding Gaborized outlines similar to those employed in Sassi et al. (2010). Although the previous study yielded a considerable set of well-identifiable contours, it also highlighted a number of limitations of the stimuli, some of which could be overcome by relatively simple manipulations to enhance the resolution of the Gabor rendering. Using smaller Gabor elements placed in a denser arrangement results in finer sampling of the contour shape. This renders the outline smoother and thus easier to integrate (see e.g. Field et al., 1993), and at the same time preserves more detailed shape features that should facilitate the matching of the integrated shape to stored knowledge.

In this study, we used Gabor elements defined by the product of a sinusoidal luminance grating with a frequency of 5 cycles per degree and a circular Gaussian with a standard deviation of 0.06°. The stimulus construction procedure was very similar to that of Sassi et al. (2010), but is, nevertheless, explained in considerable detail later, owing to a number of non-negligible differences.

We positioned the centroid of each object outline in the centre of a 496 × 496 pixels array, and scaled each outline to the maximum possible size for which no side of its bounding rectangle was within 30 pixels of the sides of the whole array. Starting from a random location on the outline, Gabor elements were placed along the outline at regular intervals of 2.7 times the Gabor wavelength, with small adjustments to the inter-element distance permitted when necessary to avoid spatial overlap between neighbouring elements. All such contour elements were oriented curvilinearly, that is, parallel to the local tangent of the object outline. We then added randomly positioned elements inside and outside the Gaborized outline until each array contained a total of 1,100 elements.

Subsequently, we checked for each of the 184 arrays separately whether the local density was similar between interior, contour, and exterior elements. For each Gabor element located sufficiently far from the array's edge to be surrounded on all sides by other elements, we determined the mean Euclidean distance of the element to its nine nearest neighbours in the Gabor array. Differences between the grand means of these Euclidean distances for the groups of interior, contour, and exterior elements were tested by comparing each pairwise difference with its approximate null distribution obtained from 10,000 random permutations of the individual per-element mean Euclidean distances. When necessary, the placement of interior and exterior elements for a particular array was repeated until no significant differences in local density were observed.

Table 1 summarizes the distributions of the number of contour, interior, and exterior elements across the resulting set of 184 Gabor arrays. In addition, Table 1 contains summary statistics for the distribution across the set of two shape properties: compactness (area divided by squared perimeter; see Zusne, 1970) and mean contour path angle (mean absolute value of the difference in orientation between pairs of consecutive contour elements, expressed in degrees of arc). A full listing with metrics for the individual stimuli is available as Supplementary Material on our website at http://www.gestaltrevision.be/en/resources/supplementary-material/76-resources/supplementary-material/228.

Table 1. Summary statistics on the distribution of the number of contour, interior and exterior Gabor elements, compactness, and mean path angle across the set of 184 Gaborized outlines (statistics Q₁ and Q₃ denote the first and third quartiles, respectively). The compactness value is defined as the ratio (A/P²) of the continuous area (A) to the squared perimeter (P) of the embedded outlines. As rescaling has no effect on this ratio, the compactness values for each of our stimuli are exactly the same as those in Sassi et al. (2010).

	Number of Gabor elements			Compactness	Mean path angle
	Contour	Interior	Exterior
M	89.12	205.95	804.93	0.0297	18.83
SD	22.77	125.46	130.22	0.0175	8.94
Min	49	10	441	0.0029	5.59
Q1	72	111	722.5	0.0156	12.08
Mdn	84	182	819	0.0263	16.72
Q3	105.5	277.5	896.5	0.0400	23.93
Max	153	535	1032	0.0728	58.51

Comparing the properties of the present stimulus set with those in Sassi et al. (2010, Table 1), it is obvious that using denser arrays and rescaling the embedded outlines indeed resulted in Gaborized outlines that were longer and smoother, containing more elements with on average smaller inter-element angles. Evidently, this finer sampling of the contour also provided more detailed information with regard to the outline shape. Thus, we predicted a general increase in identifiability compared with the results of Sassi et al. (2010), as both the initial grouping of the contours and the later matching of the grouped shape to memory representations (see Panis et al., 2008; Panis & Wagemans, 2009; Torfs et al., 2010) should be facilitated with the present stimuli.

We created three versions of each of the 184 Gaborized outlines, 552 stimuli in total, only differing in the orientations of interior and exterior elements. Element positions as well as orientations of contour elements were kept constant across stimulus versions. We created three combinations of interior and exterior orientations: orthogonal exterior, curvilinear contour, parallel interior (OCP); parallel exterior, curvilinear contour, parallel interior (PCP); and randomized exterior, curvilinear contour, randomized interior (RCR). An example of each stimulus version is shown in the left column of Figure 1.

We re-ran the identification task of Sassi et al. (2010) using these new, denser stimuli, to check whether their relative ranking order of the versions and their effects of stimulus metrics were replicated, and whether identification rates would indeed increase. Briefly summarizing the findings of the identification task, the ranking order for these three versions was replicated and performance for OCP stimuli was now significantly higher than for PCP stimuli. Overall identifiability showed an increase as expected, and the linear effect of contour length and quadratic, inverted U-shaped effect of the number of interior elements were replicated. The quadratic effect of the mean path angle found in the previous study was, however, not replicated. Instead, we found a simpler linear effect that predicted lower performance for larger mean path angles, and this trend was specifically significant for the OCP and RCR versions but not for the PCP version. The lower performance for small mean path angles, interpreted by Sassi et al. (2010) as mostly due to matching difficulties, appeared to have been mitigated by the higher density stimuli. A detailed report of the findings of the identification task, including all stimuli and identification rates for each of them, is available for download as Supplementary Material to this article. We will return to these findings below in the discussion of the results of the detection experiment.

We created further variants of the stimuli to serve as target-present stimuli in our detection task, by adding jitter to the local orientations of all elements in the arrays. For each of the 552 (184 objects × 3 versions) stimuli, we first generated the highest possible jitter level by assigning each element a random orientation. Subsequently, we created eight intermediate jitter levels by interpolating linearly spaced steps between the original and fully randomized orientations for each element in every array. Thus, we obtained 10 instances of each of the 552 arrays, with maximum levels of element orientation jitter ranging from 0° to 90°, in steps of 10°. For each stimulus version, the left columns of Figures 1–3 contain examples of target-present stimuli with orientation jitter levels of maximum 0°, 90°, and 40°, respectively.

Figure 3.

The three Gaborized outline versions of Snodgrass object no. 98 “fox” (target-present, left) and their target-absent counterparts (right) at the 40° jitter level. Element positions remain identical, but by linear interpolation between the original (Figure 1) and random (Figure 2) orientations each element has an orientation deviation (again matched between target-present and target-absent stimuli) of up to 40° from original.

Figure 2.

The three Gaborized outline versions of Snodgrass object no. 98 “fox” (target-present, left) and their target-absent counterparts (right) at the 90° jitter level. Compared with Figure 1, element positions are identical but each element in the target-present display has been assigned a random orientation, which was then assigned to the corresponding target-absent element as well.

We then created sets of target-absent stimuli, each matched pairwise to a set of target-present stimuli belonging to a particular object. Each set of target-absent stimuli was created by first filling a new array with 1,100 randomly positioned elements while ensuring that average inter-element spacing did not differ from that of the corresponding target-present set. In order to also match the local element orientations between specific target-absent and target-present arrays, we generated a random mapping so that each element in the target-absent array corresponded to one element in the target-present array. Three sets of 10 target-absent stimuli were then created by mapping the element orientations from each jitter level and stimulus version in the target-present set to the corresponding jitter level and stimulus version in the target-absent set. Thus, after repeating this process for all sets of target-present arrays, the end result was a target-absent counterpart for each of the 5520 target-present arrays, containing the exact same element orientations, in a random but comparably dense spatial arrangement. The right columns of Figures 1–3 display the target-absent counterparts to each of the target-present stimuli shown in the left column.

The complete set of stimuli is available for download as Supplementary Material to this article. In addition, the software used to generate the stimuli has since been expanded, documented, and made publicly available as the Grouping Elements Rendering Toolbox for Matlab (Demeyer & Machilsen, 2012).

2.3. Procedure

Participants sat in a classroom equipped with 32 identical computer systems, taking part in groups of up to 30 at a time. Each of them viewed the 496 × 496 pixel Gabor arrays on a 17-inch CRT monitor, set to 1024 × 768 pixel display resolution and 75-Hz refresh rate. From an approximate but not strictly controlled viewing distance of 0.6 m, angular size of the stimuli was approximately 14° both horizontally and vertically.

We designed the yes/no detection task using the E-Prime software suite (Schneider, Eschman, & Zuccolotto, 2002). Written instructions before the start of the experiment informed participants that they would be shown arrays either containing a shape or not, and that their task was to indicate whether or not this was the case by pressing the left or right mouse button, respectively. To acquaint participants with the task, they were shown a number of example target-present arrays containing simple geometric shapes and a number of target-absent arrays, each with varying degrees of orientation jitter. The correct response was stated before each set of example arrays, and participants were required to press the correct response button to advance through the examples.

During the actual experiment, each trial consisted of a single array displayed in the centre of the screen until a response was recorded. We did not impose any fixed limits on presentation duration as we had only had the opportunity to pilot test the task on expert observers, and we sought to avoid making the task unnecessarily difficult for naïve participants by presenting stimuli too briefly or making it unnecessarily tedious by forcing them to view the stimuli for a fixed or minimum duration before accepting responses. Instead, we measured reaction times but relied on the participants to find a suitable pace themselves. To this end, the written instructions informed participants that they would be shown no less than 736 arrays, but that 30 minutes would be ample time for anyone to perform the task at a relatively quick, but not rushed, pace. Participants received no feedback on their responses, and as soon as a response button was pressed, the next array was displayed.

Stimulus version (OCP, PCP, or RCR) was manipulated between participants. Within each version, we generated 50 pseudorandomizations, ensuring that (a) every participant was shown two out of the ten target-present arrays for each object, and two out of the ten corresponding target-absent arrays; and (b) every group of five consecutive participants for a particular stimulus version provided exactly one response to each of the target-present and target-absent arrays of that version. The order of trials was randomized for each participant. All 268 participants completed one session of 736 trials, which across participants yielded 17–18 responses to each of the 11,040 unique Gabor arrays.

3. Results

3.1. Reaction times and data trimming

As the first step in processing the data, we examined the reaction times to look for any that might point towards unreliable responses. Participants responded well within 1 s on average (M = 866 ms) although the distribution was strongly positively skewed (Mdn = 608 ms, SD = 959 ms). Some excessively long or implausibly short reaction times were immediately evident.

We thought it preferable to remove the records with the very longest reaction times, as participants were not individually supervised and it was therefore unclear what was causing these extremely delayed responses, with reaction times occasionally in the tens of seconds. Some participants may have been distracted, for instance, or some may have taken miniature breaks at their leisure. Removing these records from the data set would place the focus on the data collected while participants were performing the task as we had intended, at a steady pace and with relatively short presentation durations. We reasoned that the very shortest reaction times, occasionally even below 50 ms, must have been due to accidental button presses. Hence, we decided to remove the records with the shortest reaction times from the dataset as well.

Although the choice of precise bounds for trimming the data was necessarily arbitrary, we opted to remove the 2% of records with the most extreme reaction times (the highest and lowest percentile). This resulted in an upper bound of 4655 ms, making allowance for considerable decision time, while keeping presentation time below the 5 s maximum used in our identification experiments (see Sassi et al., 2010; Supplementary Material), and disregarding the most markedly delayed responses. The resulting lower bound was 215 ms, which was sufficiently strict to eliminate the most obvious errors without rejecting potentially real, stimulus-dependent responses. This method of trimming the data naturally left the median reaction time unaltered at 608 ms, and resulted in a somewhat less skewed distribution (M = 810 ms, SD = 617 ms). The trimmed dataset contained 14–18 responses to each of the stimuli, with only 9 out of the 11,040 different bitmaps retaining fewer than 15 responses.

Although the amount of trimming performed was relatively conservative, it did not appear to introduce any systematic bias—by stimulus version, jitter level, target-present versus target-absent, or even object identity—in the retained responses, whereas attempts at stricter trimming started showing evidence for such biases. In this respect and with regard to the upper bound specifically, it should be noted that participants were never explicitly asked to perform the task as fast as possible on every trial, but to pace themselves across the experimental session as a whole. Thus, it is not at all unlikely that they genuinely and consciously took several seconds to reach a decision on a small amount of difficult or ambiguous trials, without this necessarily being an indication of distraction. We did not perform further detailed analyses of reaction time, but cursory exploration of target-present versus target-absent trials showed that median reaction times were indeed the longest for target-present stimuli at intermediate jitter levels, where participants are likely to be somewhat ambivalent towards how to respond. The lowest and highest jitter levels in target-present trials generally elicited fast yes or no responses, respectively. Median reaction times to target-absent stimuli were comparably short, and were stable across all jitter levels.

3.2. Performance by stimulus version and jitter level

As expected, performance in target-absent trials was consistently high. Averaged across object shapes and participants, the proportions of false alarms were small and stable across jitter levels, but differed among the between-subjects conditions of stimulus version: approximately 2% for the OCP version, 5% for PCP, and 4% for RCR. Average performance in target-present trials, too, followed the expected pattern, decreasing monotonically with increasing jitter. Maximum performance was markedly higher for the OCP version (ranging from 97% to 3% for 0° and 90° of jitter, respectively) compared with PCP (from 81% to 5%) and RCR (from 85% to 5%).

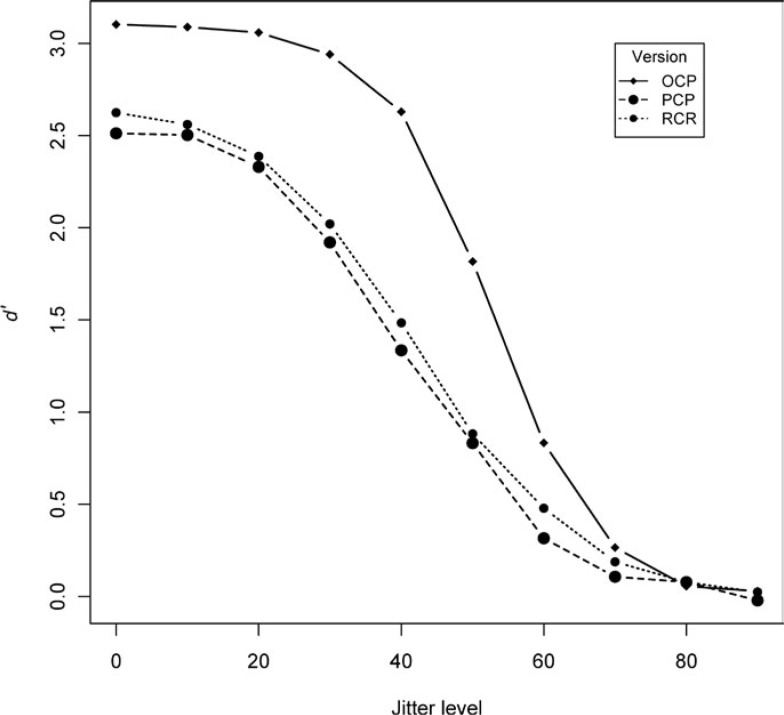
Figure 4 shows sensitivity measures d′ calculated by stimulus version and jitter level, across participants and objects. The d′ values, which aggregate across target-present and target-absent trials taking response bias into account, paint the same picture as the percentages correct. Sensitivity was highest and most robust to orientation jitter in the OCP condition, where performance was near perfect at the lowest jitter levels. Between the PCP and RCR conditions, sensitivity was similar, with d′ for both versions asymptoting at lower levels than for OCP, and starting to decrease already from lower levels of orientation jitter.

Figure 4.

d′ by stimulus version and by jitter level, across all participants and object shapes.

At the zero jitter level, participants in the OCP condition were on average nearly unbiased (criterion c = 0.06), whereas those in the PCP and RCR conditions showed a moderately conservative bias (c = 0.38 and 0.32, respectively). As the number of hits decreased with orientation jitter whereas the number of false alarms remained relatively constant, c increased monotonically with orientation jitter in all conditions up to the level of 90°, at which there was essentially no difference between target-present and target-absent stimuli. The increase was most pronounced in the OCP version (c = 1.92 at 90° jitter), reaching a lower maximum in the PCP (c = 1.63) and RCR (c = 1.65) versions. Taken together, the d′ and c values show that participants in the OCP condition were more accurate in terms of both hits and rejections than those in the PCP and RCR conditions, for whom misses occurred much more frequently even without orientation jitter and false alarm rates were higher as well.

3.3. Relationships between stimulus metrics and detectability in the different conditions

The focus of our statistical analyses was on finding general relationships between the stimulus metrics shown in Table 1 and the detectability, or robustness to jitter, of the respective object shapes in our stimuli. To obtain a metric for this robustness to jitter, we first recalculated d′ for each subset of responses to target-present and target-absent trials corresponding to the same object, version, and jitter level. As participants were never shown the same stimulus twice, this necessarily meant that data were combined across different observers in the same stimulus version condition. However, systematic differences in observers' bias between the different conditions were controlled for by using this sensitivity measure. Extreme values of the number of hits or false alarms that would have resulted in an undefined d′ were adjusted using the 1/N correction suggested for yes/no experiments by Hautus and Lee (2006), that is, by simply subtracting or adding one hit or false alarm. A complete listing of d′ values for each combination of object, version, and jitter level is available as Supplementary Material.

For each object and stimulus version, we then determined the highest jitter level with a d′ value greater than or equal to 1.5, and used these threshold jitter levels as the dependent variable for subsequent model fitting. The threshold level of 1.5 for d′ corresponded roughly to a traditional threshold of 75% correct across target-present and target-absent trials corresponding to the same object, version, and jitter level. As it turned out, the 1.5 criterion for d′ differentiated well between the different objects and versions. The resulting threshold jitter levels ranged from 0° to 70°. There were 21 cases—out of 552 object × stimulus version combinations—of a particular object and version not reaching the criterion even without any orientation jitter. These cases were nevertheless assigned the lowest possible threshold jitter level of 0° and included in the analyses that we report below, as we reasoned that their low detectability might be informative with regard to the role of our stimulus metrics in contour detection. (However, we later performed analyses from which we excluded these 21 cases. Those additional analyses are not reported in detail here, but showed that the inclusion or exclusion of these stimuli had no bearing on the results.)

Using the threshold jitter levels as the outcome variable, and fixed effects of stimulus version and our stimulus metrics (see Table 1) as the explanatory variables, we fitted multilevel regression models. Because we were not focusing on the idiosyncratic effects of specific object shapes, we included object identity as a random factor in all candidate models. We added a random object identity × stimulus version interaction, to account for some of the variability in the effect of stimulus version on particular object shapes. The inclusion of these random effects served to keep the focus on those effects of stimulus version and of the stimulus metrics that generalize across the entire set.

On the basis of preliminary analyses by stimulus version, we fitted several models to the combined data from all versions, testing for a main effect of stimulus version, main linear and quadratic effects of the number of contour elements, number of interior elements, and mean path angle, and interactions of each of these numerical predictors with the stimulus version factor. Note that the value used for the mean path angle metric for each object was that which corresponded to the contour without orientation jitter, and did not derive from the actual inter-element angles at the threshold jitter level. We used a manual stepwise procedure in which χ² likelihood ratio tests between pairs of nested models served to decide on the inclusion of the main effects, and of interactions of stimulus version with the remaining predictors in the model. The final model retained the random object × stimulus version interaction.

Table 2 summarizes the effects in the fixed part of the model. The fixed main effect of stimulus version contributed significantly to model fit. However, not all pairwise differences between versions were significant. The estimates and p values in Table 2 use RCR as the reference level and show that the threshold jitter level for the PCP version was slightly lower than but did not differ significantly from the RCR version. Threshold jitter for the OCP version, however, was significantly higher than for RCR and PCP (both Bonferroni-corrected p < .001), which did not differ significantly from each other, as confirmed by additional model fits using either OCP or PCP as the reference level (not included in Table 2). The stimulus version factor additionally interacted with all three remaining numerical predictors present in the model: the number of contour elements, number of interior elements, and mean path angle.

Table 2. Parameter estimates, standard errors, test statistic values, and p values for the fixed effects in the final model.

Parameter	Estimate	SE	t	p
RCR vs. OCP	15.4	0.73	21.13	<.001∗∗
RCR vs. PCP	−1.14	1.06	−1.08	.281
# Contour	9.24 × 10−2	4.00 × 10−2	2.31	.022∗
# Contour × OCP	−1.29 × 10−1	3.93 × 10−2	−3.27	.001∗∗
# Contour × PCP	−0.90 × 10−1	5.69 × 10−2	1.58	.114
# Interior	85.60	18.96	4.51	<.001∗∗
(# Interior)2	13.26	18.10	0.73	.464
# Interior × OCP	−81.82	18.66	−4.38	<.001∗∗
(# Interior)2 × OCP	17.43	17.81	0.98	.328
# Interior × PCP	127.20	27.00	4.71	<.001∗∗
(# Interior)2 × PCP	−99.18	25.77	−3.85	<.001∗∗
Mean path angle	−254.30	21.73	−11.70	<.001∗∗
Mean path angle2	54.69	18.32	2.98	.003∗∗
Mean path angle × OCP	161.94	21.38	7.57	<.001∗∗
Mean path angle2 × OCP	−29.06	18.03	−1.61	.108
Mean path angle × PCP	−05.61	30.93	6.65	<.001∗∗
Mean path angle2 × PCP	−27.57	26.09	−1.06	.291

Note: ^∗p < .05

^∗∗p < .01.

There was a significant positive effect of the number of contour elements within the RCR and PCP versions, whereby detection of longer contours was generally more robust to orientation jitter. A slightly but not significantly more pronounced positive effect was apparent in the PCP version, where the threshold jitter level increased or decreased more steeply as a function of the number of contour elements. Within the OCP version, on the contrary, the estimate corresponded to a negative, but non-significant trend (p = .14 for the refitted model with OCP as the reference level, not included in Table 2, which instead contains the significant interaction term for the OCP version).

We found a significant quadratic effect of the number of interior elements, but the precise relationship to the threshold jitter level again varied between versions. Within the RCR version, only the first-degree term was significant (see Table 2), and the effect corresponded to a relatively constant threshold jitter level for small to average numbers of interior elements followed by an increase in the threshold jitter level for larger numbers of interior elements. Both the first- and second-degree interaction terms for the PCP version (versus RCR as the reference) were significant. There, large numbers of interior elements also corresponded to the highest threshold jitter levels, but a much stronger decrease in the threshold jitter level was apparent with smaller numbers of interior elements. For the OCP (versus RCR) interaction, only the first-degree interaction term was significant. Within the OCP version, the fitted values described a U-shaped relationship, with higher threshold jitter levels for both the largest and smallest numbers of interior elements.

Finally, the model contained a quadratic effect of the mean path angle, which again interacted with the different stimulus versions. Within the RCR version, both the first- and second-degree terms were significant, and threshold jitter decreased monotonically with increasing mean path angle. The first-degree interaction term for the PCP version (versus RCR) was significant, and the fitted values for the PCP version show a U-shaped relationship, with a trend towards higher threshold jitter levels for the smallest and largest mean path angle values. The first-degree interaction term for the OCP versus RCR comparison was significant as well. Within the OCP version, threshold jitter decreased monotonically from small to average mean path angles, after which the threshold remained stable for average to large mean path angles.

4. Discussion

4.1. Detectability differences between stimulus versions

The graphical comparison of d′ by jitter level between the stimulus versions shown in Figure 4, as well as our subsequent analyses, showed a striking difference in the robustness to orientation jitter of the OCP version, on the one hand, and the PCP and RCR versions, on the other hand (both the OCP versus PCP and OCP versus RCR comparisons resulted in a p < .001).

The detectability advantage for the OCP version was expected, as it is the only version for which the target-present stimuli contain two distinct textured regions that can be segmented based on their different orientations, and as Machilsen and Wagemans (2010) have shown, observers readily combine the available contour and texture information when deciding on the presence of a shape within Gabor arrays. Unlike in an identification task, the grouping by orientation similarity of a central textured region that stands out from its surround can be sufficient to detect a shape, without necessarily having a very detailed shape representation or being able to identify the shape in question. Consequently, contour integration was not strictly necessary to detect an object in the OCP version, and this is also reflected in our findings with regard to the stimulus metrics (see later).

Second, contour integration itself can benefit from the OCP arrangement as well, as contour elements within an OCP stimulus have a higher probability of being surrounded by near-perpendicular orientations on one side of the contour, due to the orthogonality of the orientations within and outside the contour. As Dakin and Baruch (2009) have shown by measuring the exposure duration necessary for contour shape discrimination, a near-perpendicular surround facilitates contour grouping whereas a near-parallel surround interferes with it. Robol, Casco, and Dakin (2012) found that this effect generalizes to a simpler contour localization task more akin to our detection task. They report the same effect on the required exposure duration as well as a similar effect on the tolerance for orientation jitter, and provide evidence that the detrimental influence of the near-parallel surround is largely explained by crowding.

These effects of the near-perpendicular and near-parallel surrounds actually contribute to the significant difference between the OCP and PCP versions in two ways. Although in OCP stimuli a near-perpendicular surround was more likely than in PCP, PCP stimuli potentially contained a near-parallel surround on both the interior and exterior of certain contour segments—which, by definition, was never the case for OCP stimuli. This difference was further accentuated by the choice of the main axis orientation for the interior and exterior elements in PCP stimuli. As shapes tend to be elongated along this axis, significant portions of the PCP contours were surrounded by near-parallel orientations on both sides.

Whereas the higher resistance to jitter for the OCP version than for both other versions was expected, the similarity in average performance between the PCP and RCR versions was not. We predicted the same ranking order as found in our identification experiments, but the d′s shown in Figure 4 initially suggested a reversal thereof. Despite the fact that detectability of the RCR version appeared to be slightly more robust to orientation jitter than the PCP version though, the difference between the two was not significant (p = .28) according to our further analysis of the threshold jitter level.

There were, however, significant differences in the effects of our numerical predictors between conditions (see later for a detailed discussion of the individual numerical predictors). These interaction effects reflect that certain subsets of stimuli do yield different threshold jitter levels in the two conditions. Average threshold jitter was higher for PCP than for RCR versions of longer, more angular contours (with large numbers of contour elements and large mean path angles, see later), which implies that contour integration difficulties with the RCR versions of these stimuli were mitigated by the additional texture grouping cue in the PCP versions. Conversely, PCP showed less robustness to jitter than RCR for another subset of narrow, elongated object shapes (short contours with small mean path angles and small numbers of interior elements, see later). In these cases, the PCP version contained a near-parallel surround along the majority of the contour. This introduced a different grouping problem: unwanted grouping of contour elements with the near-parallel surrounding elements, which rendered these contours very difficult to detect. This offset the advantage of the PCP version for the longer and more angular contours and nullified the difference between PCP and RCR when averaging across all objects. We return to these findings and substantiate our interpretation in more detail in the discussion of the individual stimulus metrics later.

The above still leaves the question of why we found an advantage of PCP over RCR in the identification task run with the same stimuli (see the Supplementary Material for a detailed report). We propose the following explanation. On the one hand, the grouping problems specific to PCP affected mostly stimuli for which identification performance was inherently restricted by matching problems in all versions (short contours with small mean path angles and small numbers of interior elements, see also Sassi et al., 2010 and the Supplementary Material to this article). The grouping difficulties specific to the PCP version of this subset did not manifest themselves in the identification task due to a floor effect whereby performance was poor across all versions: although the RCR and OCP versions could be more readily grouped and detected—as the results of the detection task show—many of the integrated contour shapes were simply too indistinct for clear-cut matching to memory, and thus the grouping advantage of the RCR and OCP versions ultimately provided no significant benefit to identification compared with PCP. Switching to a detection task where matching was no longer necessary boosted performance for the RCR and OCP versions, revealing the specific grouping disadvantage of PCP for this subset of shapes.

On the other hand, the grouping problems specific to RCR affected longer, more angular contours for which mainly grouping—rather than matching—problems affected all versions in the identification task, but were most pronounced for RCR. As the identification performance differences here were predominantly due to the grouping stage, switching to a detection task that eliminates the matching simply preserved the grouping disadvantage of the RCR version. Taken together, this means that the grouping problems specific to RCR affected the outcome of both tasks, while those specific to PCP only manifested themselves in the detection task. Therefore, in the identification task RCR yielded lower average performance, whereas in the detection task, the PCP disadvantage happened to offset that of RCR on average, resulting in approximately equal mean threshold jitter for the two conditions.

In what follows, we examine how the stimulus metrics in the model relate to the detectability of each of the three stimulus versions. The number of contour elements, the number of interior elements, and the mean path angle all showed different effects depending on stimulus version, and their effects also differed from those found in our identification tasks. As in Sassi et al. (2010), we use targeted visual inspection of stimuli with extreme values—below the first quartile or above the third quartile of the distribution of each metric across all 184 shapes—of each of the metrics, and characterize these subsets of stimuli as succinctly as possible, to better interpret the effects of our metrics.

4.2. Contour length

Within the PCP and RCR versions, the fitted model suggested a benefit for longer contours, and this effect was more pronounced, but not significantly so, for PCP compared with RCR. Within the OCP version, contour length did not have a significant effect. The subset of short contours with the lowest threshold jitter levels in the PCP version consisted almost entirely of straight and narrow shapes such as object no. 237 “toothbrush” shown in Figure 5. The detection of this subset of stimuli was without a doubt strongly affected by the presence of a near-parallel surround along most of the contour in the PCP version, which explains why the low performance for shorter contours tends to be exacerbated in this version. This group notably contained nine cases, out of a total of 21 across all versions, of shapes that did not reach the 1.5 threshold for d′ even with zero orientation jitter, no. 237 “toothbrush” being one of them.

Figure 5.

Continuous outline and Gaborized versions (0° jitter) of object no. 237 “toothbrush.” The orthogonal surround of OCP rendered the shape highly salient (threshold jitter level: 60°) whereas the parallel surround of PCP suppressed the shape to the extent that even the perfectly aligned version shown here did not reach the d9 criterion of 1.5. The threshold jitter level for the RCR version was 40°.

The group of short contours with low threshold jitter levels in the RCR condition was much more heterogeneous than the set of almost strictly stick- or bar-shaped objects described above, and proved difficult to characterize succinctly. Consequently, it was difficult to isolate a single specific reason why such shorter contours were more difficult to integrate. The more clearly interpretable finding for the RCR version was that, despite the increase in threshold jitter with increasing contour length, longer contours did not quite reach the same average threshold jitter levels as their OCP and PCP versions. This was due to the fact that many of the longest contours also had large mean path angle values and were angular, jagged contours for which integration was most impeded in the RCR version. Compare, for instance, the different versions of no. 93 “fly” shown in Figure 6. Despite the trend towards higher threshold jitter for longer contours, the longest RCR contours also comprised six shapes, out of a total of 21 across all versions, which did not reach the 1.5 threshold for d′ even without orientation jitter.

Figure 6.

Continuous outline and Gaborized versions (0° jitter) of object no. 93 “fly.” Detectability of this long and irregular contour suffered most in the RCR version (threshold jitter level: 20°). The OCP and PCP versions yielded identical threshold jitter levels of 40°.

The reasons for the absence of a significant contour length effect within the OCP version are twofold. First, the group of short and almost strictly stick- or bar-shaped objects described above was not at a disadvantage here, but rather, the near-perpendicular surround of the OCP version rendered them highly salient, as can be seen by comparing the OCP and PCP versions of no. 237 “toothbrush” in Figure 5. Second, for the longest contours (e.g. no. 93 “fly” in Figure 6), observers could also rely on the grouping of a sizeable textured interior area, rendering detection less sensitive to any contour integration difficulties for such stimuli.

4.3. Number of interior elements

Across all three versions, contours with large numbers of interior elements yielded high threshold jitter levels on average. In our identification experiments (Sassi et al., 2010; Supplementary Material), we found consistently low performance across all versions for these stimuli. As a group, these shapes are compact, with a large surface surrounded by a smooth and relatively featureless contour without many marked protrusions (e.g. no. 214 “spool of thread” in Figure 7). We had therefore reasoned that these contours are in theory easy to integrate (according to, for instance, association field models such as that of Field et al., 1993) and that the low identification performance was mostly due to matching problems. The findings of our detection experiment confirm that when matching is superfluous, these contours are among the most robust to orientation jitter. The large and solid interior surface of these stimuli evidently creates a strong texture segmentation cue in the OCP version, but the fact that stimuli with large numbers of interior elements are generally also smooth contours with long straight parts along different orientations—that is, long and smooth contour segments are not confined to the main axis orientation that would be suppressed in the PCP stimuli—means that they show strong contour integration as well. For instance, the three versions of no. 214 “spool of thread” in Figure 7 reached the same threshold jitter level of 60° in all versions.

Figure 7.

Continuous outline and Gaborized versions (0° jitter) of object no. 214 “spool of thread.” Detection of this smooth and compact shape was very robust to orientation jitter in all versions: OCP, PCP, and RCR all yielded the same threshold jitter level of 60°.

Threshold jitter levels for the stimuli with the smallest numbers of interior elements differed between the versions. Most contours in this subset were also among the short contours that yielded low threshold jitter levels in the PCP version (see a discussion of contour length effect in Section 4.2) such as no. 237 “toothbrush” shown in Figure 5. In our earlier identification study (Sassi et al., 2010), we found low performance for these stimuli in all versions. Due to the simple shapes of these contours, which consist for the most part of long straight segments that should be readily integrated, we had again interpreted this low performance as resulting from matching difficulties (but see the Supplementary Material for a discussion of grouping difficulties with the PCP version of the new stimuli). Our present findings again substantiated this interpretation. For the RCR version, the threshold jitter level for these stimuli with small numbers of interior elements was not lower than for average numbers of interior elements, indicating that both types of contours integrated equally well. In the OCP version, contour integration of these narrow, elongated shapes was further enhanced by the near-perpendicular surround, yielding higher threshold jitter levels than for contours with average numbers of interior elements. Finally, in the PCP version, the final model shows low threshold jitter levels due to the grouping problems specific to the near-parallel surround in this version. The three versions of object no. 237 “toothbrush” in Figure 5 exemplify the general performance pattern for this subset of stimuli with few interior elements, reaching a high threshold jitter level of 60° in the OCP condition, a somewhat lower 40° in the RCR condition, and failing to reach the d′ threshold at all in the PCP condition.

4.4. Mean path angle

The previous (Sassi et al., 2010) identification study had found an inverted U-shaped pattern whereby both very small and very large mean path angles corresponded to lower identification performance, and interpreted this finding as evidence for matching problems with small mean path angles but contour integration problems with larger mean path angles. However, when we re-ran the identification task with the present stimuli (see the Supplementary Material for details) we no longer found a disadvantage for small mean path angles. Although we stand by our previous interpretation, the increased density of our displays may have mitigated both matching and contour integration problems by rendering the outlines simultaneously smoother in terms of path angle and more detailed in terms of the features that can be sampled sufficiently well by Gabor elements to be recognized. Hence, the data presented here do not corroborate or otherwise qualify our earlier interpretation with regard to the detrimental effect of small mean path angles in Sassi et al. (2010).

The effects of the mean path angle in the final model of the detection data were quadratic, but in OCP and RCR the resulting curvilinear relationship nevertheless boiled down to a monotonic decrease in average threshold jitter level with increasing mean path angle. The general effect is thus qualitatively similar to the detrimental effect of large mean path angles found in the identification data and, likewise, was more pronounced in RCR than in OCP (see also Supplementary Material). This similarity between the identification and detection effects substantiates our interpretation that grouping problems underlie the diminished performance for contours with larger mean path angles. Object no. 93 “fly” is one example of such a contour: the “contour-only” RCR version yielded a threshold jitter level of only 20°, whereas the OCP version—containing a textured interior that allows orientation-based segmentation, as well as a locally near-perpendicular surround in several locations along the contour—still reached a threshold jitter level of 40°.

Although the fitted values for the PCP version corresponded to a shallow U-shaped relationship, upon inspection the difference between it and the remaining versions again turned out to be qualitatively the same as what we found when testing the identifiability of the denser stimuli (see also Supplementary Material). On the one hand, the advantage for small mean path angles was still present but far less pronounced in PCP due to near-parallel orientations suppressing some of the simpler stick- or bar-shaped contours (such as no. 237 “toothbrush” in Figure 5) that contributed to this effect in the other two versions. On the other hand, there was a slight upturn in performance for the very highest mean path angles in the PCP version. These angular and jagged contours have appendages in different directions, sometimes orthogonal to the shape's main axis, and in these cases the PCP arrangement actually provided near-perpendicular surround for sizeable parts of the contour, aiding its integration. For instance, a subset of these contours consisted of four-legged animals whose main axis was close to horizontal, causing the animal's vertically oriented legs to be surrounded by near-perpendicular orientations on both the interior and exterior. The PCP version of object no. 93 “fly” in Figure 6 shows a similar phenomenon.

5. Conclusion

This study revisited the idea of using Gaborized contours of everyday objects as perceptual grouping stimuli, which was previously explored in the identification experiments of Sassi et al. (2010). Building on the results of the previous study, we created higher density variants of three of the stimulus versions (OCP, PCP, and RCR) and re-ran the identification task (see Supplementary Material) before using additional variants of the stimuli with jittered local element orientations in a detection experiment that we reported here in detail.

Except for the identification difficulties for a subset of stimuli with small mean path angles, which were mitigated by the increase in density, the majority of the key findings from Sassi et al. (2010) were replicated when we re-ran the identification task, and the results of the detection task corroborated our earlier interpretations of these findings in terms of whether they reflected problematic matching of shapes to stored knowledge versus problematic perceptual grouping per se.

The decrease in both identifiability and robustness of detection to orientation jitter with increasing mean path angle, and the way this relationship varied between the stimulus versions, was consistent between the two tasks. This constitutes convincing evidence for the interpretation that this effect is the result of contour integration difficulties—which are to be expected with large path angles according to all current models of contour integration—that are modulated by the different orientations surrounding the contour in the different stimulus versions (see Dakin & Baruch, 2012; Robol et al., 2012).

Likewise, the low identifiability but high robustness to jitter we found for contours with large numbers of interior elements underline that these shapes are in fact among the easiest to integrate, but are simply too indistinct to be reliably matched to memory representations. The same argument applies to the contours with small numbers of interior elements in the OCP and RCR versions. These results show a trade-off between the detection and identification of our stimuli. Although mostly straight or smoothly curved contours and large solid surfaces make for strong grouping and thus robust detection of contours and textures, they often lack the clearly recognizable features necessary for identification. Conversely, contours with conspicuous features that are diagnostic of object identity are inherently more complex and thus yield somewhat weaker grouping.

The identification task conducted with our new, denser stimuli (see Supplementary Material) showed the expected ranking order (OCP > PCP > RCR). In the detection task, however, we found no significant difference between PCP and RCR. Our further analyses showed that PCP versions of longer, more angular contours were more robust to orientation jitter than their RCR versions. RCR versions of narrow, elongated object shapes proved more robust than their PCP versions containing a near-parallel surround. These differences between the versions simply offset each other when averaging across all object shapes.

The reason why we did find significantly better performance for PCP in identification tasks is that the grouping problems specific to PCP affect mainly shapes that are insufficiently distinct for clear-cut matching to stored knowledge. In an identification task, performance with these shapes is inherently poor across all versions due to matching problems, and whether the contour was well integrated in the first place or not does not alter the outcome. Hence, the specific grouping disadvantage of PCP does not manifest itself in identification performance, which results in higher average performance than RCR.

In sum, this study continued to develop the approach, introduced in Sassi et al. (2010), of using Gaborized contours of everyday objects as perceptual grouping stimuli, by comparing detection to identification. Our results replicated, and allowed us to substantiate, key findings from the previous study, shedding more light on the effects of our stimulus metrics and on the performance differences between the different stimulus versions. In addition, this study resulted in a new and considerably expanded stimulus set. During the course of our experiments, we collected solid data on the identifiability and detectability of these stimuli. We make detailed records for each stimulus available, as well as the individual stimulus images, as part of the Supplementary Material to this article.

Biography

Michaël Sassi (1983) received his master's degree in experimental psychology from the University of Leuven, where he is currently working on a PhD project supervised by Johan Wagemans. His research aims to investigate the potential influences of global or large-scale stimulus properties as well as high-level processing on perceptual grouping in general and contour integration in particular.

Bart Machilsen (1980) studied psychology at the University of Leuven, where he did his PhD research under supervision of Johan Wagemans. He is currently a postdoctoral fellow in the Laboratory of Experimental Psychology. In collaboration with Dr. Maarten Demeyer, he refined and integrated the stimulus construction algorithms described in the current research paper into an open-access Matlab toolbox (www.gestaltrevision.be/gert). His present research interests include processes of perceptual organization, temporal aspects of visual perception, natural scene statistics, and predictive coding.

Johan Wagemans (1963) has a BA in psychology and philosophy, an MSc and a PhD in experimental psychology, all from the University of Leuven, where he is currently a full professor. Current research interests are mainly in so-called mid-level vision (perceptual grouping, figure-ground organization, depth and shape perception) but stretching out to low-level vision (contrast detection and discrimination) and high-level vision (object recognition and categorization), including applications in autism, arts, and sports (see www.gestaltrevision.be).