Construction of boundary-surface-based Chinese female astronaut computational phantom and proton dose estimation

Abstract

With the rapid development of China's space industry, the importance of radiation protection is increasingly prominent. To provide relevant dose data, we first developed the Visible Chinese Human adult Female (VCH-F) phantom, and performed further modifications to generate the VCH-F Astronaut (VCH-FA) phantom, incorporating statistical body characteristics data from the first batch of Chinese female astronauts as well as reference organ mass data from the International Commission on Radiological Protection (ICRP; both within 1% relative error). Based on cryosection images, the original phantom was constructed via Non-Uniform Rational B-Spline (NURBS) boundary surfaces to strengthen the deformability for fitting the body parameters of Chinese female astronauts. The VCH-FA phantom was voxelized at a resolution of 2 × 2 × 4 mm³for radioactive particle transport simulations from isotropic protons with energies of 5000–10 000 MeV in Monte Carlo N-Particle eXtended (MCNPX) code. To investigate discrepancies caused by anatomical variations and other factors, the obtained doses were compared with corresponding values from other phantoms and sex-averaged doses. Dose differences were observed among phantom calculation results, especially for effective dose with low-energy protons. Local skin thickness shifts the breast dose curve toward high energy, but has little impact on inner organs. Under a shielding layer, organ dose reduction is greater for skin than for other organs. The calculated skin dose per day closely approximates measurement data obtained in low-Earth orbit (LEO).

INTRODUCTION

In explorations of outer space, aircraft crew members are under constant threat of cosmic radiation from Galactic Cosmic Rays (GCRs) and Solar Particle Events (SPEs), which are associated with different radioactive particles. When particles pass through the human body, interactions occur with target tissues, resulting in energy losses. Radiation levels in space are considered to be much higher than those due to routine terrestrial radiation [1]. Excessive exposure increases the risks of radiation, including both acute and long-term effects, and in particular the probability of cancer [2, 3]. Of the typical particles of space radiation, protons are of particular concern because they are charged and have a wide energy range [4]; they also combine both high and low linear energy transfer (LET) characteristics, in the form of a non-uniform dose distribution. Radiation exposure from protons is an important health-related concern for astronauts, especially for long space flights [5]. It is possible to investigate the radiation effect of protons through dosimetric studies performed with accelerators; however, some aspects of these studies should be taken into consideration. First, the energy of proton-initiated space radiation is beyond 10⁴MeV, in contrast to the general level of external exposure of 10²MeV in proton therapy. Second, space radiation particles have a wide continuous spectrum, while accelerators generally produce almost monoenergetic particles. Third, the direction of the irradiation is an important consideration in the space scenario, whereas beams are usually unidirectional in hadron therapy.

Since the official start of China Manned Space Engineering (CMSE) in 1992, the technological progression from the Shenzhou-I spacecraft to the first manned spacecraft Shenzhou-V has been highly successful, enabling China to become the third country to achieve manned space exploration. In the past decade, astronauts from Shenzhou-VII performed space activities successfully in 2008, and Shenzhou-VIII accomplished a rendezvous and docking mission in 2011. In addition, China's first batch of female astronauts has recently undertaken a flight mission. These achievements are all milestones in the history of China's space industry, and point toward future successes.

To predict radiation hazards and to plan protection strategies for personnel in orbit, it is important to determine the three-dimensional dose distribution within a human body under exposure [6]. Two main approaches are adopted for this purpose: measurement by thermoluminescent detectors and simulation using computational anthropomorphic phantoms [7, 8]. There are many limitations in direct measurement: the results cannot be obtained before the actual flight or in real time; it is difficult to distinguish among the various influencing factors under various conditions; and the measurement device increases the payload of the spacecraft, thus raising expenditure. In contrast, the method based on simulation and computational phantoms has superior flexibility and usability, and has been applied broadly [9–13].

In the 1970s, the National Aeronautics and Space Administration (NASA) of the USA developed a computational anatomical male (CAM) phantom and a computational anatomical female (CAF) phantom for risk assessment of space radiation [9, 10]. The utility of the anatomical models for estimating exposure to specific body organs has been demonstrated by the creation of mathematical phantoms, a type of computational phantom with a history of more than 40 years, in which equations are utilized to define the body shape and internal organs. Besides the mathematical phantom, a voxel-based phantom is also employed, with a number of person-specific phantoms [11–13]. Also used in space radiation dosimetry is the Golem phantom from the Gesellschaft für Strahlenforschung (GSF) voxel-based phantom family, which was derived from whole-body computed tomography (CT) examination of a male leukaemia patient [14]. The CAM and CAF phantoms are modelled using constructive solid geometry (CSG) techniques, which facilitate rapid dose calculation, but these phantoms are limited in their ability to represent anatomical details. The Golem phantom is a typical voxel-based phantom, being based on voxel matrices segmented from tomographic images. The advantage of this type of phantom is its improved anatomical fidelity, while having the disadvantage of discontinuities around organ contour and contact regions. In addition, scaling of the phantom can only be performed by adjusting the voxel dimensions. With the development of computer graphics, Non-Uniform Rational B-Spline (NURBS) has been increasingly employed for boundary representation in phantoms because of its benefits in terms of anatomic realism and spatial deformation, and the fact that it takes advantage of the most desirable features of both the mathematical phantom and the voxel-based phantom [15–18].

In the present study, we developed a computational anatomical phantom by NURBS modelling of the cryosectional colour photographic images of a 19-year-old adult female cadaver. The phantom was further tailored according to the physical characteristics of Chinese female astronauts and the International Commission on Radiological Protection (ICRP) reference adult female. Using the Monte Carlo code MCNPX, proton radiation transport was simulated with a wide energy range, and organ-absorbed doses and effective doses were calculated. Results were then compared with the MIRD female phantom, the ICRP female phantom, the VCH male phantom and the sex-averaged doses. Fast approximate calculation of daily skin dose was achieved based on the skin organ dose and the on-orbit proton spectrum from the Shenzhou spacecraft. The objectives of this work are to (1) develop a standard female astronaut computational phantom for Monte Carlo simulations; (2) study proton radiation dosimetry; and (3) provide reference dose estimates to enable rapid dose assessment in Chinese human space flight activities.

MATERIALS AND METHODS

Phantom construction and modification

Original phantom

As an original phantom, the Visible Chinese Human adult female (VCH-F) phantom established in this article was derived from VCH high-precision datasets. Following successive cryosectioning of a 19-year-old female cadaver (height 156 cm; weight 46 kg; organs fully developed), 8556 trans-axial colour photographs were obtained. Image resolution was 3024 × 2016 pixels with slice intervals of 0.20 mm and spatial resolution of 0.10 × 0.10 × 0.20 mm³. These high-resolution images enable the identification of anatomical structures. The original images were prepared for organ segmentation after image registration. The segmented organs were then labelled with a specific identification number [19, 20]. Segmentation was performed with the assistance of anatomy experts and with a colour atlas [21]. The resultant female phantom included all of the major tissue and organ systems of the human body: the skeletal, alimentary, respiratory, urogenital, endocrine and circulatory systems. Organ masses in the VCH-F phantom were calculated as the product of organ volume and the reference density, using elemental mass fractions and tissue densities recommended by ICRU Report 44 [22] and ICRP Publication 89 [23].

Process of NURBS phantom construction

To achieve more realistic anatomy and to implement personalized deformation, a female NURBS phantom was established with Chinese female anatomical characteristics, based on fine 3D reconstruction. NURBS employs the features of both existing model representations (mathematical and voxel) to enable deformation to be performed using only a few control points, either for scaling or for rotation [24]. The specific process is described as follows, and demonstrated in Fig. 1.

1. Using the left kidney as an example, the results of organ segmentation (Fig. 1a, b and c) are used to construct a triangular mesh model and a reconstructed surface model (Fig. 1d and e).

2. The mesh model containing organ structural information is imported into the Rhinoceros3D modelling software (McNeel North America, Seattle, WA, USA), and a NURBS organ is generated after extracting the organ section using the 2D section line contour tool (Fig. 1f).

3. Using the lofting command to set the parameters, the 2D section lines are selected and a simply connected 3D curve surface is established based on NURBS (Fig. 1g); further optimization is performed. The smoothing rate is higher for this model compared with the earlier mesh model based on triangles (e.g. Fig. 1d).

4. From the point of view of radiation simulation calculation, the NURBS model cannot be directly used because currently available Monte Carlo codes cannot accept the NURBS geometry before voxelization. For this reason, the NURBS model must be transformed into a voxel model of specific resolution, as follows. First, the NURBS model is remeshed (Fig. 1h) to produce a more uniform distribution of triangles compared with the mesh models shown in Fig. 1d and e, which reflect the surface continuity of the organ. The remeshed model is then transformed into a voxel model according to the resolution needed for practical use (Fig. 1i), and has a resultant high degree of anatomical fidelity while having a much smoother surface.

Fig. 1.

Comparison of the models of the left kidney in different steps from an anterior–posterior perspective: (a)–(c) the segmentation results; (d) the original triangular mesh model; (e) reconstructed surface model; (f) extracted contours used for generation of NURBS object; (g) NURBS model; (h) remeshed model; and (i) voxelized model.

Intention and target of phantom modification

The two targets of original phantom modification are also the objective criteria that regulate the process of constructing the VCH-FA phantom, and are as follows. (1) The organ masses agree with the ICRP reference data within 1% relative error. Effective dose is calculated for a standard/reference human and not for a specific individual. Adjustment for mass may reduce the significance of difference in comparison with other phantoms, but promotes rationality, representativeness and usability. (2) The anatomical descriptions of body characteristics are in accordance with the statistical data of the first batch of Chinese female astronauts, with relative error less than 1%.

Adjustments were performed in Rhinocerosby scaling and fitting each organ in turn. The locations of internal organs, including the skeletal, alimentary, respiratory, urogenital, endocrine and circulatory systems, were adjusted according to the original centroid, while avoiding overlapping of adjacent organs layer by layer. Major improvements include remodelling of the intestines and modification of body characteristics and organ masses.

The intestine and skeleton present challenges for phantom modelling. Because there is little interspace among the small intestine, ascending colon, transverse colon, descending colon, sigmoid colon and rectum, and because the intestinal wall is extremely thin, their boundaries and topologies are difficult to distinguish. A voxel phantom is based on segmented intestine images, and thus lacks anatomical fidelity and accuracy. However, it is a feature of the NURBS representation method that the intestine and colon models for the original VCH-F phantom have good consistency in region and are also highly deformable in shape. The partial central shafts of the intestines were obtained first. Reference values for physiological intestinal length (100 cm for the large intestine and 260 cm for the small intestine) [23] and mass requirements were then used to set the NURBS models of the large and small intestine within these regions with an acceptable level of accuracy. The irregular twists and turns of both the large and small intestines were carefully redefined on the basis of the anatomical characteristics and local details.

In the developed phantom, the skeleton was divided into mineral bone and bone marrow, including red bone marrow (RBM) and yellow bone marrow (YBM). Bone marrow was segmented from the original images using an improved threshold-based method [25]. This method avoids artificial arbitrary choice to some extent and is more accurate than the simple threshold method that is based on the image colour value alone. In the VCH-FA NURBS phantom, the RBM and YBM mesh models were retained for authenticity and accuracy. Because bone marrow is contained within trabecular tissue having very small channels (on the order of tens of microns), tests indicate that a large degree of error would be introduced if bone marrow were represented in whole-body geometry. After parameter adjustment, the original bone marrow voxels were matched to the VCH-FA bones.

Finally, the organ masses must be checked after the voxelization process to reduce errors resulting from conversion of the smooth NURBS surface to the discontinuous voxel surface. When the absolute value of the error exceeded 1%, organ volume was readjusted with great care and voxelized again. Furthermore, special attention was paid to regions prone to overlapping or out of bounds. Two methods were adopted to check overlaps, in both three dimensions and two dimensions. In the former method, we inspected the 3D VCH-FA NURBS phantom directly using the collision detection tool to find overlaps. In the latter method, the 3D boundary detection problem was translated into a voxel array traversal problem. The position of each voxel was recorded to identify whether any two voxels had the same position. The great majority of overlaps can be checked and corrected by the former method; however, a few overlaps occurring in the voxelized phantom, as a result of the voxelization process, also require correction.

Transport calculation for proton radiation

Optimization of voxel size

For Monte Carlo dose calculation, the human phantom must be voxelized and imported to transport code. During transformations across NURBS-based and voxel-based phantoms, voxel size affects the description of the phantom mainly on the edge of the organs. Oversize voxels lead to distortion of the organ edge with sawtoothing, which influences the track of particle transport and subsequently affects the dose value. From the point of view of simulation calculations, as a precise expression of the object involved in the transportation process, smaller voxels lead to better results. Increasing the number of voxels, however, lengthens the simulation time beyond the allowable limit, so in practice the most precise phantom possible is used. Ideally, the organs are also defined more accurately if voxel size is adjusted to the target anatomical structure (smaller voxels for smaller organs), which would increase the precision of the dosimetry results for small organs. However, the code restricts the resolution to a uniform value across the whole phantom, including all organs and anatomical components.

The influence of voxel size on mass difference before and after voxelization was tested for voxel sizes of 2 × 2 × 4 mm³, 4 × 4 × 8 mm³and 8 × 8 × 16 mm³. As shown in Table 1, the latter two voxel sizes resulted in errors greater than 5%, which is several times the value for the former (less than 1%). The significant errors found for voxel sizes of 4 × 4 × 8 mm³and 8 × 8 × 16 mm³indicate that the influence of voxel size on the radiation system cannot be ignored, especially for small organs and organs with irregular shape.

Table 1.

Mass differences before and after voxelization of different voxel size

Organs	Voxel size (mm3)	Differences (mv– mn) / mn(%)
Liver	2 × 2 × 4	–0.98
	4 × 4 × 8	3.00
	8 × 8 × 16	3.06
Pancreas	2 × 2 × 4	–0.96
	4 × 4 × 8	–6.56
	8 × 8 × 16	–7.63
Urinary bladder	2 × 2 × 4	–0.33
	4 × 4 × 8	11.68
	8 × 8 × 16	14.54
Gallbladder	2 × 2 × 4	–0.80
	4 × 4 × 8	4.30
	8 × 8 × 16	11.03
Oesophagus	2 × 2 × 4	0.36
	4 × 4 × 8	–13.09
	8 × 8 × 16	–21.50
Oviduct	2 × 2 × 4	0.00
	4 × 4 × 8	22.84
	8 × 8 × 16	–50.86
Thyroid	2 × 2 × 4	0.01
	4 × 4 × 8	3.35
	8 × 8 × 16	22.49
Urethra	2 × 2 × 4	0.10
	4 × 4 × 8	34.13
	8 × 8 × 16	91.62
Intestine	2 × 2 × 4	–0.94
	4 × 4 × 8	15.05
	8 × 8 × 16	20.95
Skin	2 × 2 × 4	0.91
	4 × 4 × 8	72.18
	8 × 8 × 16	70.91

The voxel size of the VCH-FA phantom is set as 2 × 2 × 4 mm³, which is converted to a matrix size of 280 × 180 × 460. The number of voxels is 23 184 000, which is close to the MCNPX limit (maximum of 25 million voxels) and is among the highest-resolution phantoms that are used for actual simulation calculations.

Setting of MCNPX for Monte Carlo calculations

The Monte Carlo technique is well established in radiation dosimetry research and is widely used to model energy transfer and deposition through random numbers and probability distributions, integrating an anthropomorphic computational phantom with radiation particle transport. To refine the radiation dose calculations, various options can be specified regarding particle information, including type, energy, spatial position and direction, as well as the 3D geometry and elemental composition of the phantom.

In the present study, we adopted a well-benchmarked and well-validated Monte Carlo code package, MCNPX [26], from the Los Alamos National Laboratory (LANL).

MCNPX is a general-purpose radiation transport code, an extended version of Monte Carlo N-Particle (MCNP), and can transport all particle types up to the teravolt energy range via theoretical models from the Los Alamos High-Energy Transport (LAHET) code system. In the process of particle transportation, both cross-sectional data and physics models were employed. In the calculations, particle interactions at low energies were treated by cross-sectional data from the Evaluated Nuclear Data Files (ENDF/B-VII). In the energy spectrum above 150 MeV, mixing and matching of physics models and data tables were enabled via the ‘Mix-and-Match’ algorithm in MCNPX. The data tables were used when energy was below the maximum value, while the models were adopted above this energy. The VCH-FA phantom was set as in space, receiving irradiation from all directions. Sixteen discrete energies, ranging from 5 MeV to 10 GeV for isotropic beam sources, were simulated with 35 million particle histories. The secondary particles were defined in the data card. F6+ heat detectors were adopted in MCNPX for energy deposition by all transported particles, including protons, electrons, neutrons, photons, deuterons, tritons, ³He ions and alpha particles. Total doses were counted by F6+ tally cards and shown in the output files.

Setting of shielding

For the purpose of higher anatomy accuracy and standardized (or personalized) radiation protection from space radiation conditions, the VCH-FA phantom was established based on NURBS and implemented in MCNPX simulation code with isotropic proton irradiation, which is an idealized model for exposures against GCR and SPEs during space exploratory missions by astronauts. To reproduce the conditions of actual measurement, the shielding effects of the orbital spacecraft must be accounted for. A 5-mm-thick cylindrical shell (1.35 g/cm²thickness) of aluminium was adopted as a shielding layer to reproduce the same characteristics in the simulation model as in the experimental configuration. The shielding could be set in various ways depending on the experimental scenario for measurements.

Calculation of radiation quantities

Absorbed dose and effective dose

The energy deposited by protons and all secondary particles was obtained from the MCNPX for the region of interest. Energy impartation from the secondary particles was also included in the mean value of the stochastic quantity. The mean dose D_Twas derived from the quotient of the mean energy imparted to matter, by the organ or tissue mass. The effective dose Ecan be calculated according to the equation:

(1)

where w_Tis the tissue weighting factor, w_Ris the radiation weighting factor and H_Tis the equivalent dose.

From the VCH-FA data, it is possible to obtain the sex-averaged dose as recommended in ICRP103. The recommendations for tissue weighting factors (from ICRP publication 103) for both females and males are shown in Table 2. The sex-averaged tissue weighting factors are based on current scientific data of the biology and physics of irradiation. Compared with older recommendations, the factor for gonads (ovaries for females and testes for males) decreased from 0.20 to 0.08, and the factor for the bladder, oesophagus, liver and thyroid decreased from 0.05 to 0.04, while the factor for breast tissue and the remainder increased from 0.05 to 0.12. The remaining categories were also altered, by the addition of extrathoracic airways, gallbladder, lymphatic nodes, oral mucosa and prostate, while discarding the brain and upper large intestine [27, 28].

Table 2.

Tissue weighting factors in ICRP Publication 103 [28]

Tissue	Tissue weighting factor
	Female	Male
Testes	0	0.08
Ovaries	0.08	0
Bone surface	0.01	0.01
Bladder	0.04	0.04
Bone marrow, red	0.12	0.12
Brain	0.01	0.01
Breast	0.12	0.12
Colon	0.12	0.12
Liver	0.04	0.04
Lungs	0.12	0.12
Oesophagus	0.04	0.04
Salivary glands	0.01	0.01
Skin	0.01	0.01
Stomach	0.12	0.12
Thyroid	0.04	0.04
Remaindera	0.12	0.12

^aComponent organs for remainder in ICRP 103: adrenals, extrathoracic airways, gallbladder, heart, kidneys, lymphatic nodes, muscle, oral mucosa, pancreas, prostate, small intestine, spleen, thymus and uterus/cervix.

Sex-averaged dose estimation is necessary and valuable for radiological protection purposes. The arithmetically weighted mean dose of the organs, including 13 remainder tissues for each sex, can be calculated as follows and adopted to calculate conversion coefficients and dose coefficients:

(2)

where H_T^Mis the equivalent dose assessed for organ or tissue Tof the reference male and H_T^Fis the equivalent dose assessed for organ or tissue Tof the reference female.

Rapid approximate calculation of daily dose

Doses in space are much higher than on Earth, being typically about 1 mSv per day for astronauts in low-Earth orbit (LEO). Before manned space missions took place, radiation exposure assessment of astronauts in the space environment was an effective method for ensuring that the irradiation remained within the limit of acceptable health risks, and was performed prospectively by calculating skin-absorbed dose for comparison with radiation exposure risk limits related to stochastic tissue reactions. For instance, before the launch of spacecraft, we could pre-estimate the skin-absorbed dose of astronauts. Combining the energy deposition calculated at single-point energies above with the on-orbit proton spectrum obtained from the trapped proton model, we could estimate the potential dose before execution of the mission, or assess on-orbit organ doses based on actual measurement values in real-time.

The proton dose can be calculated from the integral of the differential proton spectrum f(e) and the dose energy spectrum D_T(e) as follows:

(3)

where Φ denotes the fluence rate of the spherical surface, tdenotes the total flight time and edenotes energy.

To perform a rapid assessment, the differential proton spectrum can be represented approximately via a few discrete points. The dose can be determined as follows:

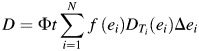(4)

where Ndenotes the number of discrete points.

RESULTS AND DISCUSSION

Three-dimensional structure of the VCH-FA NURBS phantom

A 3D view of the VCH-FA NURBS phantom is shown in Fig. 2. The skin and muscle are set to translucent to enable visualization of the internal organs and skeleton. More than 30 organs and tissues are defined.

Fig. 2.

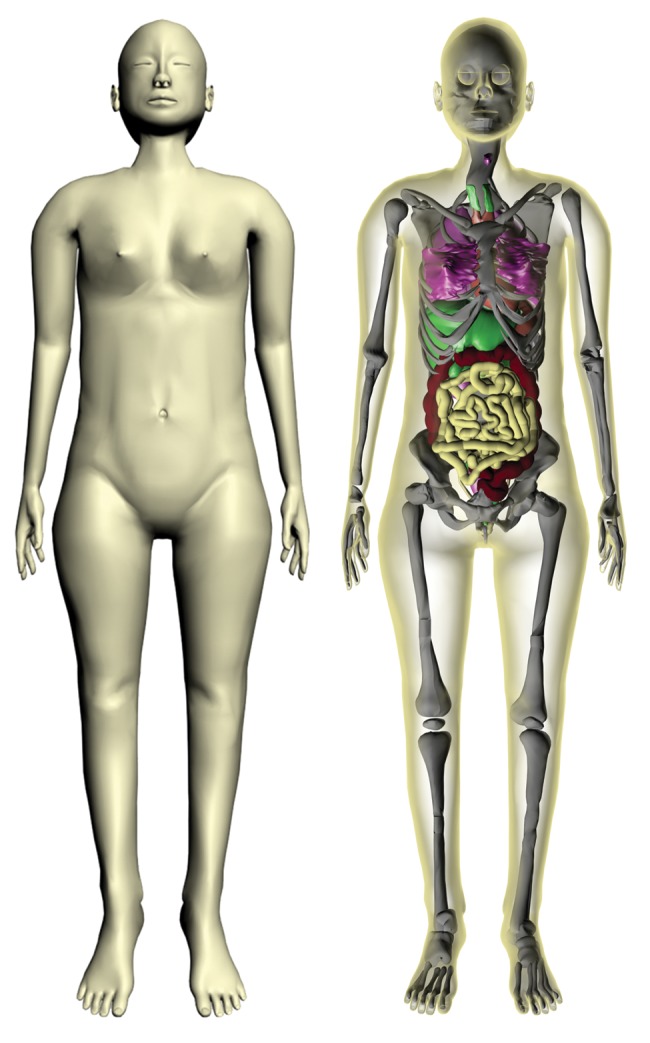
Three dimensional view of the VCH-FA phantom (skin on the left and internal organs on the right).

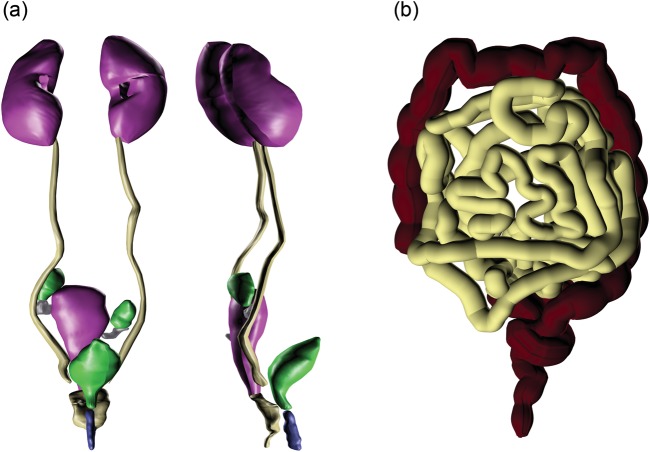
As a representative system containing small structures, the urogenital system was carefully identified and modified. A 3D view of the urogenital organs is shown in Fig. 3a. The models of the large and small intestine in Fig. 3b show a high degree of local detail. Every effort has been made to ensure that the anatomical characteristics of the final VCH-FA phantom provide a scientific and valid basis for the intended application.

Fig. 3.

Three-dimensional view of the urogenital organs and the intestines.

Comparison of computational phantoms

Comparison of VCH-FA phantom and VCH male phantom

Because of the differences in biological structures between females and males, it is necessary to compare absorbed dose between females and males to investigate gender differences and obtain sex-averaged values in space radiation conditions. The most significant difference between male and female phantoms is the reproductive system (ovaries, oviduct, uterus, vagina, breast etc. in females), which is of critical importance in terms of human physiological and physical characteristics. In the VCH-FA phantom, the reproductive system was identified in great detail, especially the oviducts, ureters, urethra and vagina. These small organs are not included in most other phantoms or reference data. Comparison of the mass of the main tissues and organs between the VCH-FA phantom and the VCH male phantom revealed similar masses for most organs, with ratios of 0.78–1.38 for the adrenals, brain, oesophagus, eyeballs, gallbladder, heart, intestines, kidneys, liver, red bone marrow (RBM), salivary glands, skin, thymus, thyroid and urinary bladder (average relative deviation, 1.38%). Greater discrepancies in mass were found in four organs, with relative deviation of 135% for the pancreas, 46% for the skeleton, 40% for the stomach and 39% for the spleen. Difference in organ mass between the genders is attributable to body sizes and physiological features. In addition, lung mass of the VCH-FA phantom is 52% of that of the VCH male phantom, because in the latter, blood is included in the total lung mass. The total mass of the reproductive organs is 602.08 g (breasts, ovaries, oviducts, uterus and vagina) in the VCH-FA phantom, and 40.60 g (epididymes, prostate and testes) in the VCH male phantom. The reproductive organs play an important role in space radiation studies and their tissue weighting factors are of great importance in determining effective dose. Hence, the efforts in the present study to produce accurate and reliable representation of urogenital organs represent an important contribution for the evaluation of radiation risks to female astronauts.

Comparison of VCH-FA phantom with other female phantoms

Several adult female phantoms are described for radiation dose assessment [29–34]. Table 3lists published organ and tissue masses for several female phantoms (including the adrenals, brain, breasts, colon, oesophagus, eyeballs, gallbladder, heart, intestines, kidneys, liver, lungs, ovaries, pancreas, salivary glands, spleen, thymus, thyroid, ureters, urinary bladder, and uterus) as well as a comparison of differences in organ mass between the VCH-FA phantom and other adult female phantoms.

Table 3.

Organ mass comparison for the VCH-FA phantom with ICRP reference female [23], IAEA reference Asian female [34] and MIRD female [35]

Organ	Mass (g)				Mass difference (%)
	VCH-FA	ICRP ref.	Asian ref.	MIRD	VCH-FA/ICRP ref.	VCH-FA/Asian ref.	VCH-FA/MIRD
Adrenal	12.94	13.00	13.00	10.30	–0.46	–0.46	25.63
Brain	1296.11	1300.00	1320.00	1404.00	–0.30	–1.81	–7.68
Breast	496.00	500.00	300.00	360.88	–0.80	65.33	37.44
Colon	674.74	680.00	540.00	580.63	–0.77	24.95	16.21
Oesophagus	35.13	35.00	30.00	35.46	0.37	17.10	–0.93
Eyeballs	15.13	15.00	12.00	—	0.87	26.08	—
Gallbladder	55.55	56.00	44.00	57.68	–0.80	26.25	–3.69
Heart	614.69	620.00	620.00	581.95	–0.86	–0.86	5.63
Intestine	871.77	880.00	720.00	838.24	–0.94	21.08	4.00
Kidneys	273.55	275.00	280.00	249.90	–0.53	–2.30	9.46
Liver	1386.24	1400.00	1400.00	1417.50	–0.98	–0.98	–2.21
Lungs	415.85	420.00	338.00	572.00	–0.99	23.03	–27.30
Muscle and fat	35 723.26	35 500.00	33 000.00	—	0.63	8.25	—
Ovaries	10.94	11.00	11.00	10.71	–0.55	–0.55	2.15
Oviduct	2.10	2.10	5.00	—	0.00	–58.00	—
Pancreas	118.84	120.00	110.00	65.52	–0.97	8.04	81.38
RBM	833.40	900.00	780.00	1050.00	–7.40	6.85	–20.63
Salivary gland	69.76	70.00	62.00	—	–0.34	12.52	—
Skeleton	7876.38	7800.00	6400.00	7650.00	0.98	23.07	2.96
Skin	2321.02	2300.00	1800.00	2321.70	0.91	28.95	–0.03
Spleen	129.63	130.00	120.00	126.14	–0.28	8.02	2.77
Stomach	369.61	370.00	290.00	312.00	–0.11	27.45	18.46
Thymus	19.84	20.00	22.00	28.12	–0.80	–9.82	–29.45
Thyroid	17.00	17.00	17.00	12.50	0.00	0.00	36.00
Ureter	15.08	15.00	15.00	—	0.53	0.53	—
Urethra	3.00	3.00	6.00	—	0.00	–50.00	—
Urinary bladder	39.87	40.00	30.00	35.88	–0.33	32.90	11.12
Uterus	79.50	80.00	70.00	79.04	–0.62	13.57	0.58
Vagina	13.54	—	14.00	—	—	–3.29	—

Because mass adjustment was performed (as described above), VCH-FA organ masses show excellent agreement with the values from the ICRP reference female, within 1% relative deviation, with an average relative deviation of –0.26%. The reason for the discrepancy is that blood is not included in the VCH-FA phantom. The total body weight of the VCH-FA phantom is in line with the value stated by the Chinese National Standard of Occupational Health regarding reference individuals for use in radiation protection (54 kg).

The relative deviations in organ mass between VCH-FA and the IAEA reference Asian female are greater, with 14 organs within 10%, 11 organs between 10% and 30%, and 4 organs greater than 30%, although the average organ mass deviation is 8.48%. The total body weight of the IAEA reference Asian female is 51 kg, which is 5.56% less than VCH-FA.

Comparing VCH-FA with the MIRD phantom, the mean mass deviation is 7.36%, with only three exceptions beyond 30%. The values for thyroid, breast and pancreas are 36.00%, 37.44% and 81.38%, respectively. The difference in the mass of the pancreas represents a significant difference, which is mainly derived from the definition method (particularly shape restrictions) of the MIRD phantom.

Organ-absorbed dose and comparison

Influence of organ mass and anatomic structures

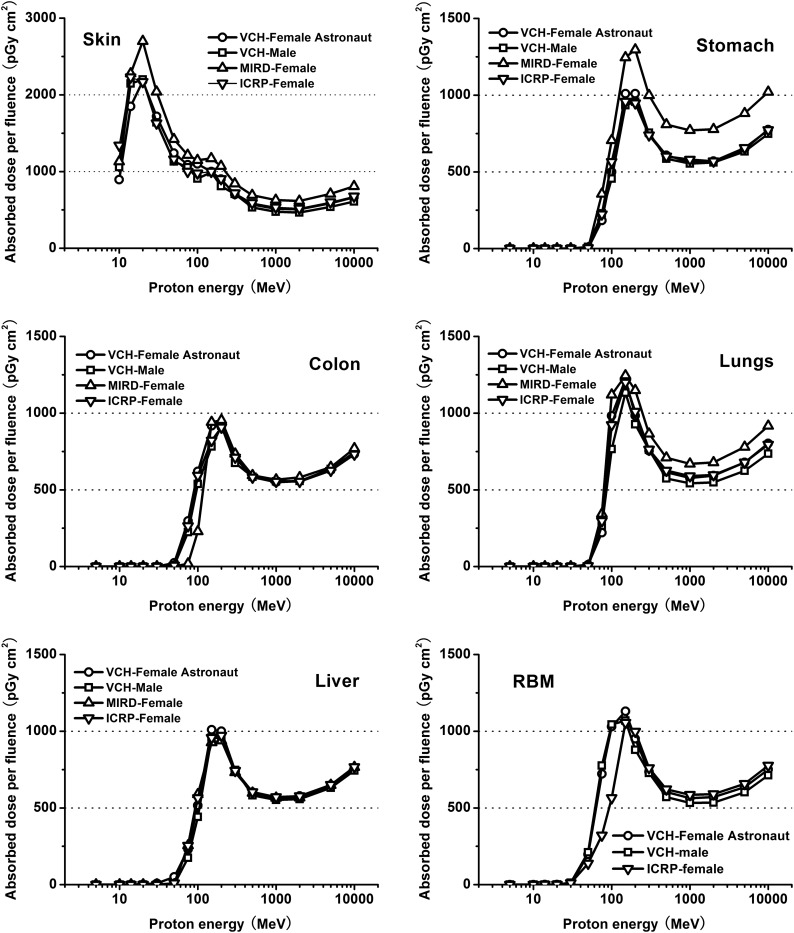
In the present study, proton transport was simulated in the VCH-FA phantom, the MIRD female phantom [35], the ICRP reference female phantom [36] and the VCH male phantom [37] under strictly the same conditions. The organ doses were calculated under proton energies ranging from 5 MeV to 10 GeV. Figure 4compares the evaluated organ doses for the skin, lungs, colon, stomach, liver and the RBM of the phantoms. The sharp, narrow peaks on the absorbed dose curves reflect proton absorption in tissue from energy loss as the particles travel through biological tissues. The peak energy varies according to the distance to the target organs from the outline surface.

Fig. 4.

Comparison of absorbed dose per proton fluence for skin, stomach, colon, lungs, liver and RBM of phantoms.

As the energy increases for proton energy lower than 1000 MeV, the organ dose curve first rises before falling, presenting a local maximum related to the Bragg peak of protons characterized by the fact that their tracks are almost completely absorbed within the organs. When proton energy is relatively low, most protons are stopped within a short depth of penetration and deposit most of their energy in the skin, which can be seen in the distinctive absorbed dose curves for the skin. When proton energy is above 50 MeV, the protons and secondary particles are able to travel farther to the internal organs. Protons slow down relatively quickly when they pass through biological tissues, with most of their energy deposited at the end of their path as Bragg peaks. Hence, the internal organs yield higher doses during irradiation to reach maximum values of around 100–200 MeV. Discrepancies in absorbed dose for the same organs among the four phantoms at 100, 200 and 1000 MeV ranged from –0.33% to –16.05% for skin, –0.17% to 28.33% for lungs, 0.45% to 170.87% for colon, 1.99% to –29.15% for stomach, 0.49% to 16.97% for liver and –1.34% to 82.37% for RBM. Among these, RBM was not included in the MIRD female phantom because of the difficulty in defining the numerous discrete parts via mathematical equations.

The comparison of radiation quantities among the VCH-FA phantom, the VCH male phantom, the MIRD female phantom and the ICRP female phantom suggests that absorbed proton doses for organs are related to many factors, including definition type, organ mass and anatomical structure (e.g. position, distribution and geometry). In VCH-FA and MIRD, dose deviation was greater than 10%, even above 100 MeV, for skin, lungs and stomach. The mean dose deviations of these three organs were –16.92%, –11.76% and –24.37%, respectively. As mentioned above, the mass deviations were –0.03%, –27.30% and 18.46%, correspondingly. The stomach has the smallest organ mass in the MIRD female but receives the highest absorbed dose per fluence because it is close to the body surface. Furthermore, although organ mass differences are greater between VCH-FA and the VCH male than between VCH-FA and MIRD, dose discrepancies are more obvious in the MIRD phantom, which indicates that definition type is of great importance for dose calculation. The results also imply that absorbed dose is sensitive to the distance from the outline surface to the concerned organ or system. In radiation dosimetry practice, it is difficult to represent the correct depth of all internal organs in the simplified trunk of the MIRD phantom, and this may result in overestimation of absorbed dose for some internal organs, especially for relatively low energies at critical values of particle penetration. Regarding RBM, the masses of three phantoms were similar, with discrepancies of around 7.00%, but dose deviation comparing the VCH-FA phantom with the ICRP phantom exceeded 40.00% at energy from 50 MeV to 100 MeV, and was within 5.00% from 200 MeV to 10 000 MeV. The dose discrepancies arise mainly from the differences in RBM distribution, which are related to the segmentation method. When the proton energy is higher than 1000 MeV, the dose curves rise continuously. Dose deviation is less prominent at higher energy than at lower energy because statistical uncertainties are reduced when particles penetrate through body tissue.

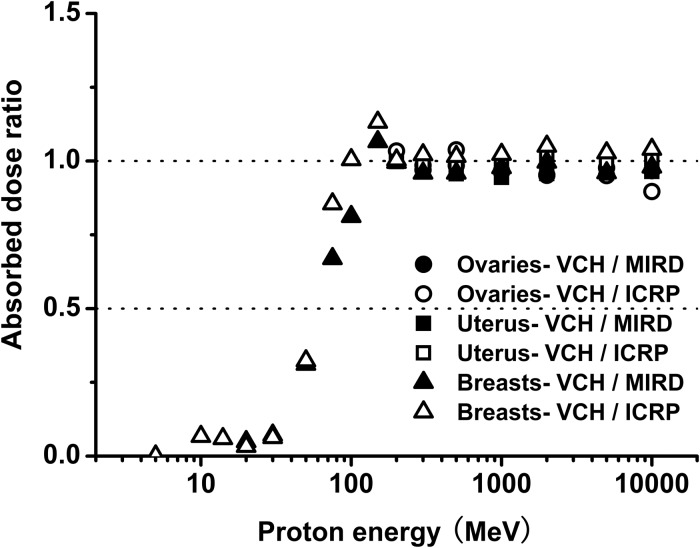
The radio-sensitivity of the reproductive system makes it particularly important to obtain accurate and reliable dose for sex-specific organs. Comparing absorbed dose in the reproductive system among the three female phantoms, results show remarkable agreement within the limits of statistical uncertainty. As illustrated in Fig. 5, mean organ dose ratios for the VCH-FA phantom compared with the MIRD and ICRP phantoms at energy levels above 150 MeV were 99.02% and 99.70% for the ovaries, 98.00% and 102.57% for the uterus, and 98.65% and 103.90% for the breast, respectively. The mass ratios were 99.45% and 102.15% for the ovaries, 99.38% and 100.58% for the uterus, and 99.20% and 137.44% for the breast, respectively. From 50 MeV to 100 MeV, mean dose ratios were 59.75% and 72.75% for the breast. This result indicates that the dose discrepancy is closely related to the particle energy. In the high-energy range, dose ratios tend towards constant values. These results also verify that as well as mass, other important factors influencing organ dose are anatomic position, organ shape and distance to the outline surface.

Fig. 5.

Organ dose ratio of ovaries, uterus and breasts.

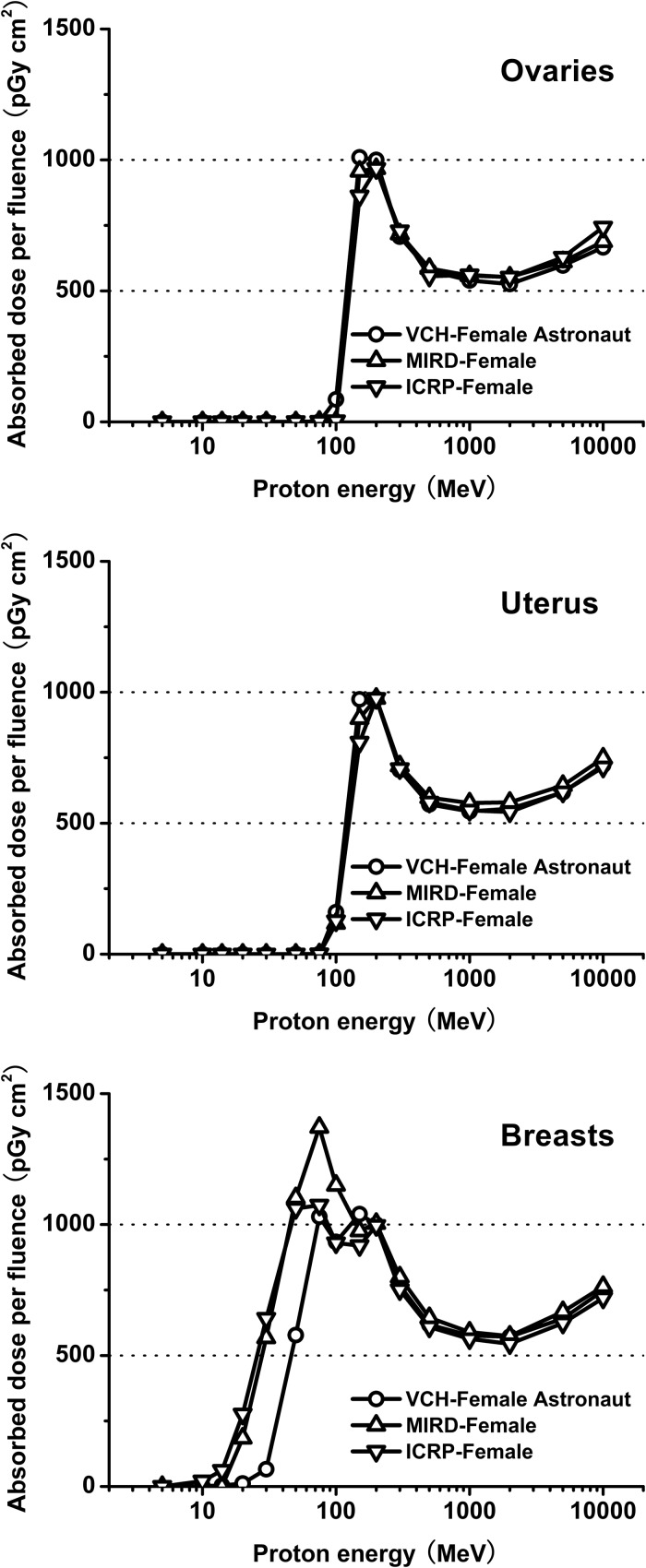
In addition, Fig. 6shows that at energies from 20 to 50 MeV, absorbed dose for breast is much lower in the VCH-FA compared with the other phantoms, while doses for the ovaries and uterus are well correlated; at higher energies, the difference in absorbed dose for breast between the VCH-FA and other phantoms decreases. The results may be attributed to the thicker skin in that region of the VCH-FA phantom. At low energies, the penetration depth of protons is limited [28]. Most of the low-energy protons are absorbed in the skin, with few deposited in the breast. Although our findings demonstrate that the skin will have little influence on absorbed dose in the inner organs, for breast tissue, the Bragg peak shifts towards higher energies at about 20 MeV. Furthermore, in the research field of radiation protection, shielding strategies are important factors to be considered, especially for human space exploration. The skin could be considered a natural spacesuit in the form of the innermost layer. The spacesuit itself, having the role of a ‘second skin’, contributes significantly to protecting the astronaut from radiation hazards. At lower energies, the doses to shielding layers increase with rising energy when the Bragg peak is developed in them. The effect of particle penetration will decrease if the stopping power of the shielding layers improves with an increase in layer number or an increase in areal density. Particles able to penetrate the shielding layers must then be of even higher energies, and thus the Bragg peak may shift towards a higher energy range within the body of the astronaut.

Fig. 6.

Absorbed dose per proton fluence for ovaries, uterus and breasts.

In the simulations, statistical uncertainty in most organs was less than 2.00%, which is more precise than in the results commonly obtained by dosimeters in physical experiments. However, small organs such as the oviducts, urethra, adrenals, thyroid and thymus present relatively high statistical uncertainties of between 1.00% and 10.00%. Statistical uncertainty is estimated as less than 11.00% in deeply located internal organs.

Influence of voxel size

The influence of voxel size on dose results can be illustrated in the analysis of two different cases. In the first case, in different phantoms, the voxels change in size but not in number. The phantom is elongated or shrunk through scaling of voxel size in the coronal, sagittal or horizontal plane. This method is convenient but impractical, first because proportion varies for each component among the phantoms; second, anatomical structures will be severely distorted when great disparity exists among phantoms. The results of this situation were calculated in our previously published study [37]. Voxel size was shown to have an impact on organ dose. In the low-energy range, there were obvious dose discrepancies for both large and small organs. For energy levels above 1000 MeV, the discrepancies decrease before gradually stabilizing.

In the second case, for a phantom or an organ, the voxel number decreases when voxel size increases. This method was established in the present study and the dose values were compared. The total mass differences of 4 × 4 × 8 mm³and 8 × 8 × 16 mm³compared with 2 × 2 × 4 mm³are 2.42% and 2.41%, respectively. The majority of dose discrepancies were within 10%. More significant dose differences were observed in small organs. In the low-energy region, the discrepancies reached 85% for organs such as the oviducts; while in the high-energy range, this value decreased to 49% for organs such as the adrenals. This finding indicates that voxel size is responsible for systematic effects in the final dose results.

Effective dose and comparison

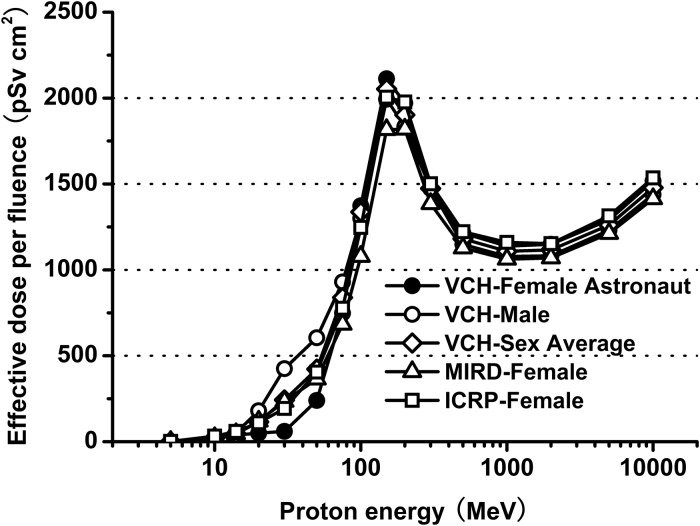
Table 4summarizes the results of effective dose per unit fluence under ISO irradiation of proton-initiated incident radiation with all transported particles for the VCH-FA phantom, VCH male phantom, MIRD female phantom, and ICRP female phantom. The sex-averaged dose was calculated by the arithmetically weighted value of VCH-FA and VCH male data, and complied with that recommended by ICRP103 [28].

Table 4.

Effective dose per unit fluence (pSv cm²) under ISO irradiation of proton energy on phantoms

Energy(MeV)	Effective dose per unit fluence (pSv cm2)
	VCH-FA	VCH-male	MIRD-female	ICRP-female
5	0.45	0.65	0.97	1.26
10	19	24	23	32
14	39	52	46	59
20	50	180	119	110
30	60	425	235	193
50	240	605	364	405
75	748	930	683	777
100	1373	1300	1078	1247
150	2112	1993	1816	2005
200	1971	1834	1819	1977
300	1475	1474	1385	1501
500	1214	1148	1127	1222
1000	1138	1078	1062	1160
2000	1149	1082	1069	1153
5000	1291	1231	1212	1314
10000	1517	1439	1414	1535

The effective dose curves for VCH-FA, VCH male, sex-averaged, MIRD female and ICRP female phantoms all present the same trend, as shown in Fig. 7. For energies below 150 MeV, the effective dose curves rise rapidly with increasing energy levels, and reach peaks at proton energies of approximately 150 MeV. The peak is caused by the Bragg peak of protons at that energy. There is a large variation in values in this range, and the slopes of the curves are steep. The minimum and maximum effective doses per fluence are 0.45 and 2112 pSv cm², respectively. After the local maximum of effective dose, the value first decreases in the range of 150–1000 MeV, before rising once more. The increase in effective dose at the end of the curves is caused mainly by the effect of intensive nuclear interactions. The effective doses are well correlated at high energies, where the penetrating power of the protons is much stronger and anatomical structure has less influence.

Fig. 7.

Comparison of effective dose per proton fluence from VCH-FA phantom, VCH male phantom, sex-averaged, MIRD female phantom and ICRP female phantom.

There were no large dose discrepancies among the sex-averaged, VCH-FA and VCH male phantoms, but objective differences do exist. The minimum and maximum absolute differences of effective dose per fluence are 0.10 and 183 pSv cm², respectively. The results of the present study indicate that a degree of uncertainty would exist if radiation protection quantities from only one gender were considered as standards. Consequently, dosimetry of the VCH-FA female phantom and calculation of the sex-averaged dose are necessary for estimation of space radiation dose.

We multiplied the organ doses by the tissue weighting factors and radiation weighting factors provided in ICRP Publication 103. Tissue weighting factors for breast and skin are 0.12 and 0.01, respectively. As mentioned above, locally thick skin results in the right-shift phenomenon, and thus the absorbed doses for breast brought about a 64–172-pSv cm²reduction in the effective dose at 20–50 MeV for VCH-FA, compared with that for the ICRP female phantom. The calculated effective doses are significantly lower for VCH-FA than for the ICRP female at these low energies. The dose ratios between VCH-FA and the ICRP female are only 45.45% at 20 MeV, 31.09% at 30 MeV and 59.26% at 50 MeV. The corresponding values are 96.27–110.10% for energy levels higher than 75 MeV. These comparisons suggest that for low-energy proton transportation, the local skin thickness influences female effective dose, especially in the thoracic cavity region. The results also indicate the distinctive features of the VCH-FA phantom compared with other phantoms, and prove the value of the VCH-FA phantom for dosimetry of Chinese female astronauts.

Dose assessment for space radiation

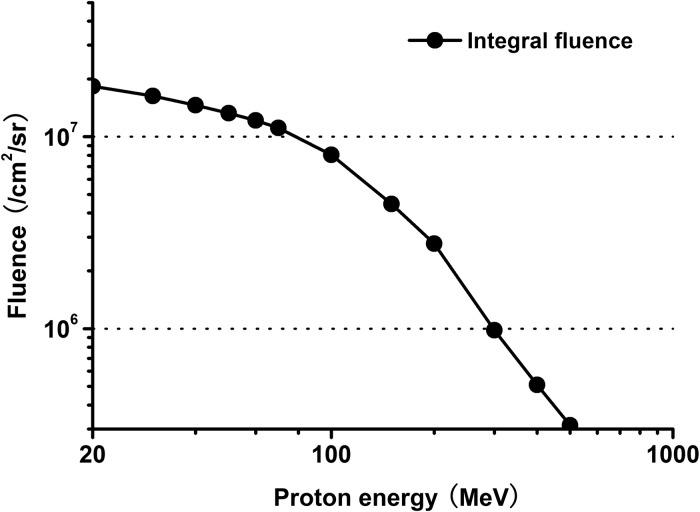
Figure 8shows the proton spectrum used in our calculations, which was obtained from trapped proton model PSB97 during missions of the Shenzhou spacecraft series in LEO, with eccentricity of 0.0002767, inclination of 42.4211°, perigee height of 332 km and apogee height of 336 km.

Fig. 8.

Proton fluence spectrum during the mission in LEO.

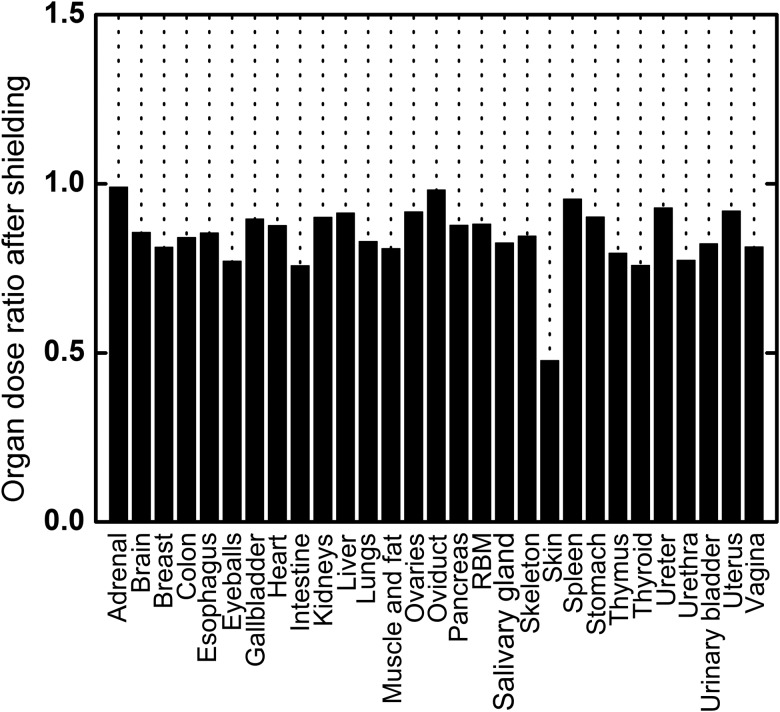
As a common tool, thermoluminescent detectors (TLDs) [38–40] made with LiF were adopted to measure skin dose at five single points on an astronaut. The actual measurement values ranged from 0.20–0.50 mGy/day for Shenzhou spacecraft series operations, with an average value of 0.29 mGy and error within 5%. These values are in line with mission measurement data from the American space shuttle [41] and do not exceed the Chinese National Standard of Radiation Protection requirements for spacecraft crew modules (ID: GJB 4018-2000). The calculated result of skin-absorbed dose under shielding for this mission is 0.27 mGy per day, which differs from the measurement value by 6.90%. The calculated whole-body daily dose is 0.18 mGy, which reflects a certain loss of energy in the process of penetrating the material, with fewer radiation particles able to pass through and reach the human body, thus decreasing the organ doses after shielding. As shown in Fig. 9, organ dose ratios range from 0.758–0.991, with an average value of 0.861. These values indicate that the shielding effect reduces organ doses by about 14%. A special case is the skin, the outermost layer of the phantom, which has a dose ratio of 0.478. From the curve of absorbed dose per proton fluence for skin without shielding, the Bragg peak characteristic at about 20 MeV has been observed, as discussed above. For a shielding thickness of 1.35 g/cm², particles below 30 MeV are restrained, while fluences are high in that range; this explains the 52.20% decrease in skin dose. In contrast, doses of inner organs in the low-energy region are already limited without shielding, and thus the dose losses are not great.

Fig. 9.

Organ dose ratio after shielding of 1.35 g/cm²thickness.

Further calculations for more complex exposure with multiple particle events are a subject for future study. It is vital to perform further investigations to enable evaluation of dose in phantoms of various body types and postures because accuracy is extremely important in space radiation dose estimation for pre-task and real-time radiation protection.

FUNDING

This work was supported by the Program for New Century Excellent Talents in University (grant number NCET-10-0386), the National Key Technology R&D Program (grant number 2011BAI12B05), the National High Technology Research and Development Program 863 (grant numbers 2009AA7035020H, 2010AA7035020H), the State Key Laboratory of Space Medicine Fundamentals and Application (grant number SMFA09A10) and the National Science Fund for Distinguished Young Scholars of China (grant number 11105131).