Sensitivity Analyses of Exposure Estimates from a Quantitative Job-exposure Matrix (SYN-JEM) for Use in Community-based Studies

Abstract

Objectives: We describe the elaboration and sensitivity analyses of a quantitative job-exposure matrix (SYN-JEM) for respirable crystalline silica (RCS). The aim was to gain insight into the robustness of the SYN-JEM RCS estimates based on critical decisions taken in the elaboration process.

Methods: SYN-JEM for RCS exposure consists of three axes (job, region, and year) based on estimates derived from a previously developed statistical model. To elaborate SYN-JEM, several decisions were taken: i.e. the application of (i) a single time trend; (ii) region-specific adjustments in RCS exposure; and (iii) a prior job-specific exposure level (by the semi-quantitative DOM-JEM), with an override of 0 mg/m³ for jobs a priori defined as non-exposed. Furthermore, we assumed that exposure levels reached a ceiling in 1960 and remained constant prior to this date. We applied SYN-JEM to the occupational histories of subjects from a large international pooled community-based case–control study. Cumulative exposure levels derived with SYN-JEM were compared with those from alternative models, described by Pearson correlation (_Rp) and differences in unit of exposure (mg/m³-year). Alternative models concerned changes in application of job- and region-specific estimates and exposure ceiling, and omitting the a priori exposure ranking.

Results: Cumulative exposure levels for the study subjects ranged from 0.01 to 60 mg/m³-years, with a median of 1.76 mg/m³-years. Exposure levels derived from SYN-JEM and alternative models were overall highly correlated (R_p > 0.90), although somewhat lower when omitting the region estimate (_Rp = 0.80) or not taking into account the assigned semi-quantitative exposure level (R_p = 0.65). Modification of the time trend (i.e. exposure ceiling at 1950 or 1970, or assuming a decline before 1960) caused the largest changes in absolute exposure levels (26–33% difference), but without changing the relative ranking (_Rp = 0.99).

Conclusions: Exposure estimates derived from SYN-JEM appeared to be plausible compared with (historical) levels described in the literature. Decisions taken in the development of SYN-JEM did not critically change the cumulative exposure levels. The influence of region-specific estimates needs to be explored in future risk analyses.

INTRODUCTION

The SYNERGY project is a large pooled analysis of case–control studies on the joint effects of occupational carcinogens and smoking in the development of lung cancer (Olsson et al., 2011). As of August 2011, SYNERGY comprises 39 518 subjects (17 705 cases and 21 813 controls) from 13 European countries and Canada. The full occupational history for each subject was registered, including job title and start and stop year. All individual jobs were coded according to the ‘International Standard Classification of Occupations (ISCO), 1968’ [International Labour Office (ILO, 1968)]. Together, the subjects’ work histories cover a period from the early 1920s until 2010.

To perform retrospective quantitative exposure assessment in these community-based studies, exposure modelling of measurement data was conducted for respirable crystalline silica (RCS) (Peters et al., 2011b). The predictions resulting from this statistical model formed the basis for a quantitative job-exposure matrix (JEM). This JEM (SYN-JEM) should enable assignment of RCS exposure estimates to each job performed by each subject within the SYNERGY population.

Sensitivity analyses are essential to judge the influence of critical decisions taken in the derivation of exposure estimates. Exposure modelling provides the opportunity to describe these decisions and to test their influence. Quantitative models and JEMs have been applied successfully in several (mainly industry-based) studies (Kromhout et al., 1997; Steenland et al., 2001; Boffetta et al., 2003; Verma et al., 2011; Friesenet al., 2012). Unfortunately, sensitivity analyses of the applied method are seldom published. Some exceptions to this are studies in the US mining, among utility workers and in a Chinese population cohort (Kromhout et al., 1997; Heederik and Attfield, 2000; Stewart et al., 2010; Vermeulen et al., 2010; Friesen et al., 2012).

To our knowledge, this is the first time a quantitative exposure assessment method has been created for pooled analyses of multinational community-based studies. We here describe the elaboration of SYN-JEM and show, using sensitivity analyses, the effects of various model parameters on the exposure estimates. Modelling uncertainties (e.g. handling of measurements below limit of detection) are not a subject of this article. We aim to provide insight into the influence of key decisions in the exposure assessment process and the robustness of exposure estimates resulting from this JEM to be used for epidemiological analyses in the SYNERGY project.

METHODS

A general population JEM (i.e. DOM-JEM) was created for, among others, RCS, assigning ordinal exposure levels of ‘no’, ‘low’, or ‘high’ exposure to all ISCO 1968 job codes (Peters et al., 2011a). These ordinal levels take into account both intensity and probability of exposure. These assigned classifications were used as a prior in the statistical model. A mixed-effect model for RCS exposure based on 23 640 personal measurements was elaborated, as described previously (Peters et al., 2011b). This model resulted in estimates for region (Random_region; Canada, France, Germany, the UK, and Northern, Southern and Western Europe), job title (Random_job; for 428 ISCO codes with exposure measurements available), year (_βyear; –6% per year), a prior exposure ranking based on the general population DOM-JEM [_{βJEM score}; no, low, or high exposure (Peters et al., 2011a)], and sampling duration (_{βsampling duration} × 480 min). The latter was applied to predict the exposure level for an 8-h work shift (480 min). Measurement strategy, highly correlated to reason for measurements, was also included in the original statistical model in order to standardize all estimates to a representative work situation. Subsequently, the expression used for the predictions in the quantitative SYN-JEM is given below (all RCS levels were in mg/m³): Ln(Y) = Intercept + βJEM score + Randomjob +Randomregion+ βyear + (βsampling duration × 480 min)

SYN-JEM consists of three axes: job, region, and year. The exponent of the natural log-transformed exposure level [ln(Y)] provides an annual geometric mean exposure level to RCS for a given job, region, and year. These model predictions were used to develop SYN-JEM. The main steps involved in this process, as well as possible alternatives, are described below. An overview of the alternatives is presented in Table 1.

Table 1.

. Description of the base model for SYN-JEM and alternative models (A–I).

SYN-JEM predictions based on
• Job-specific estimate (when at least five measurements were available for that particular job, else the estimate of the most similar job was assigned • Region-specific estimate • Time trend estimate from 1960 onwards (before 1960 an exposure ceiling was assumed) • Estimate for the a priori exposure ranking of low or high exposed (an override of 0 mg/m3 was applied to all non-exposed jobs)
Changes made to SYN-JEM for the alternative models
A	The region-specific estimate was omitted in the predictions
B	All job-specific estimates were used in the predictions, irrespective of the number of measurements available (i.e. not restricted by a minimum of five)
C	For jobs with lack of measurement data—which consequently had no job-specific estimate—only the calibrated DOM-JEM rating was assigned, instead of the manually assigning of the job-specific estimate from the most similar job
D	The job-specific estimate was omitted in the predictions for all jobs
E	The region- and job-specific estimates were omitted in the predictions for all jobs
F	The assumed exposure ceiling in the time trend was shifted: the linear time trend went back 10 more years (to 1950 instead of 1960). Consequently, the early years were assigned the exposure level of 1950
G	The assumed exposure ceiling in the time trend was shifted: the linear time trend went back 10 years less (to 1970 instead of 1960). Consequently, the early years were assigned the exposure level of 1970
H	The linear time trend from 1960 onwards remained, but instead of an exposure ceiling before, a decline back to the early years was assumed. We applied the same slope, but in the opposite direction. The peak of exposure level was consequently assumed to be at 1960
I	The DOM-JEM prior was omitted in the statistical model. When there were no sufficient measurement data (n < 5) available—and consequently no job-specific estimate could be assigned—the exposure level was assigned to be 0 mg/m3

Region

Measurements were categorized by region/country as a result of limited numbers of measurements in some countries. Estimates for all regions in the SYNERGY population could be derived from the statistical model, except for Central and Eastern European (CEE) countries due to the absence of measurement data. For this region, which was assumed to be relatively high exposed, the highest region/country estimate was assigned (i.e. UK). The difference between the highest and the lowest region/country estimate (Northern Europe) was a factor of 4.5. As indicated in our previous paper (Peters et al., 2011b), the region/country effect may reflect different working techniques and conditions, or regional differences in silica content in minerals and materials. However, it cannot be excluded that the region/country effect is partially driven by confounding factors for which adjustment was insufficient (especially coding of measurement strategies might have been problematic). The effect of not assigning a region/country effect (i.e. no difference in job estimates by region/country) was explored as an alternative model (alternative model A).

Job estimates

We assigned a job-specific estimate to jobs classified as exposed by the DOM-JEM and with exposure measurements available. An arbitrary minimum of five measurements per job title was set to reduce the influence of sampling error (Kim et al., 2011). If there were fewer or no data points for a job (37% of the a priori assumed exposed job titles), the estimate from a similar job was applied. In these cases, the most comparable job was manually assigned by one of the authors (S.P.), based on the ISCO job description and DOM-JEM score. For jobs coded with less detail, i.e. at the unit group (three-digit ISCO code) or major group level (two digits), the job-specific estimate was calculated by the weighted mean of the jobs at the five-digit ISCO code within that unit or major group.

We tested the influence of the several choices made in the assignment of job-specific estimates. The first alternative (alternative B) was not to use the arbitrary requirement of at least five measurements, but assigning all estimates derived from the model irrespective of the number of measurements available. All jobs were rated by the DOM-JEM into non-, low, and high exposed. These categories were subsequently calibrated by the measurement data. The second alternative was therefore to assign only the calibrated DOM-JEM rating to the job titles without enough data points (n < 5) available (alternative C), instead of assigning the estimate of the most similar job manually. The third alternative was not to assign any job-specific estimate, but to assign only estimates to job titles based on the calibrated DOM-JEM rating for low and high exposed jobs (alternative D). Additionally, to test the combination of the decisions taken in steps I and II, we also omitted both the region- and job-specific estimates (alternative E).

Time trend

In our model, we estimated an overall linear time trend of –6% per year (Peters et al., 2011b). This time trend was applied for the period from 1960 onwards. Personal data used for the statistical model only covered the time period starting in the late 1970s, but stationary data were available since 1960. The stationary data showed a similar linear trend for the full period (see online material). Since we have no exposure measurement information before 1960, an exposure ceiling was assumed for those early years, assigning the 1960-estimate to all previous years. This assumption was intended to avoid assigning unrealistic exposures to jobs held in the beginning of the 20th century, as would happen when fully back extrapolating the observed time trend. The line is presented in Fig. 1 with the label ‘SYN-JEM’.

Fig. 1.

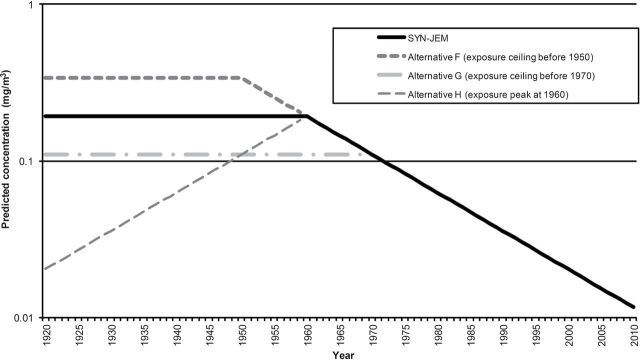
Time trend as applied for SYN-JEM and alternative models F, G, and H.

We explored several alternatives for the time trend used in SYN-JEM. We first shifted the year (±10 years) before which we applied the exposure ceiling [i.e. 1950 (alternative F) and 1970 (alternative G)]. In addition, we explored the effect of not assuming a ceiling, but having the exposure levels decrease towards the beginning of the work histories in the SYNERGY study (1920; alternative H). The slope of the time trend was assumed similar before and after 1960 (i.e. 6% per year), but in opposite direction. Figure 1 illustrates all considered alternative time trends compared with SYN-JEM. As described above, extrapolation of the linear time trend back to 1920—without exposure ceiling—was not considered as a reasonable alternative as it would lead to unrealistic exposure levels in 1920 (>1.8 mg/m³ on average). Also region- and industry-specific time trends were considered. However, due to data limitations, these trends were estimated rather imprecise, resulting in unrealistic estimates. Therefore, region- and industry-specific time trends were not considered to be reasonable alternatives.

DOM-JEM prior

The statistical model provided job-specific estimates for each job with measurement data, irrespective of the a priori job rating. Hence, also job-specific estimates were provided for jobs considered to be non-exposed if there were measurements. However, those measurements are likely to represent only exceptional situations as exposure does not generally occur in these jobs. For example, although motor vehicle mechanics are generally not exposed to RCS, there were RCS measurements in our data set for this occupational group. As an override, we assigned an exposure level of 0 mg/m³ to jobs classified as non-exposed by the DOM-JEM. The use of the DOM-JEM as a prior in the statistical model allowed also for calibration of exposure levels. Jobs classified as low exposed were a factor 0.6 lower than high exposed jobs.

As an alternative, we tested the model without application of the DOM-JEM prior (alternative I). This is the only alternative where we actually changed the underlying statistical model that we used for the predictions in SYN-JEM. All job-specific estimates based on at least five measurement data points were assigned, regardless of the DOM-JEM exposure rating. Jobs without sufficient measurement data(n < 5) were assumed non-exposed in this alternative.

Comparison of alternatives with SYN-JEM

Job histories of 37 959 subjects from the SYNERGY population with a complete job history and information on tobacco consumption were used to generate exposure profiles using SYN-JEM and alternatives. Cumulative RCS exposure levels (expressed as mg/m³-years) and average exposure levels (mg/m³) for the exposed years were calculated. The alternative approaches (alternatives A–I, as described above) were compared with SYN-JEM in order to evaluate the influence of critical decisions in the exposure assessment process. We compared the exposure levels for all subjects in the SYNERGY population derived from the alternative approaches with those based on SYN-JEM. Pearson correlations (R _p) plus the absolute difference in cumulative exposure estimates were calculated. Results based on Spearman correlations were essentially similar, and we therefore only show the Pearson correlations.

RESULTS

RCS exposure data were available for 130 (71%) of the 183 exposed job titles based on the DOM-JEM, of which 181 were present in the SYNERGY population. For 107 job titles (59%), at least five measurements were available.

Table 2 shows the cumulative and average exposure levels for the RCS exposed subjects (n 5 9423) in the SYNERGY population. The overall median was 1.76 mg/m³-years with a range of 0.30–6.43 mg/m³-years for the 10th–90th percentile. The highest median cumulative exposure levels were observed for CEE countries and Canada with 3.87 and 3.77 mg/m³-years, respectively. The lowest median levels were found for France (0.94 mg/m³-years) and Germany (1.17 mg/m³-years). With regard to year of birth, the highest cumulative exposure levels were observed for subjects born between 1930 and 1939 (2.16 mg/m³-years), apart from the one exposed person born before 1909 (7.94 mg/m³-years). Average exposure levels (for exposed years) showed a similar pattern. Cumulative and average exposure levels were moderately correlated among the exposed(R _p 5 0.46). Please note that Table 2 only gives an illustration of the estimated exposure levels. This does not allow for comparison between countries and time periods as the subjects originate from different study populations for which the distribution of study characteristics might be different (e.g. age, sex, jobs, rural or urban populations).

Table 2.

Exposure to RCS among exposed subjects in the SYNERGY population.

		Totalpopulation, n	Exposed, n	%	Cumulative exposure(mg/m3-years)		Average exposure(mg/m3)
					Median	10th–90th percentile	Median	10th–90th percentile
Total		37 959	9423	(25%)	1.76	0.30–6.43	0.12	0.05–0.38
Region	Canada	3890	470	(12%)	3.77	0.96–13.2	0.42	0.15–0.60
	CEE countries	5293	1164	(22%)	3.87	0.89–13.3	0.34	0.11–0.68
	France	7146	1632	(23%)	0.94	0.15–3.52	0.08	0.02–0.16
	Germany	8435	3350	(40%)	1.17	0.22–4.14	0.11	0.06–0.20
	Northern Europe	3321	418	(13%)	2.29	0.39–6.61	0.11	0.05–0.22
	Southern Europe	8266	2156	(26%)	2.37	0.53–6.57	0.14	0.07–0.25
	UK	1357	204	(15%)	2.75	0.79–13.2	0.44	0.12–0.69
	Western Europe	251	29	(12%)	3.46	0.89–8.59	0.19	0.08–0.52
Year of birth	1900–1909	23	1	(4%)	7.94	–	0.19	–
	1910–1919	2410	602	(25%)	1.97	0.27–6.19	0.12	0.08–0.22
	1920–1929	10 213	3156	(31%)	2.00	0.33–6.80	0.14	0.08–0.42
	1930–1939	12 479	3319	(27%)	2.16	0.44–7.29	0.14	0.06–0.44
	1940–1949	8152	1551	(19%)	1.38	0.28–5.08	0.11	0.04–0.38
	1950–1959	3489	597	(17%)	0.77	0.13–2.99	0.07	0.02–0.22
	1960–1969	1044	185	(18%)	0.49	0.60	0.03	0.01–0.09
	1970–1979	139	12	(9%)	0.15	0.22	0.02	0.01–0.04
	1980–1989	10	0	(0%)	–	–	–	–

Table 3 shows the comparison of cumulative exposure levels derived with SYN-JEM and the alternative approaches. Overall, the alternative RCS exposure estimates were highly correlated to the primary set of estimates from SYN-JEM. Changes in application of the time trend or job-specific estimates showed Pearson correlations of 0.98 and higher. Somewhat lower correlations were observed when no region-specific estimates (alternative A) or job estimates (alternative D) were assigned (R _p 5 0.80 and 0.91 in the full population, respectively). The correlation decreased further when both region- and job-specific estimates were not assigned (alternative E: R _p 5 0.74). Omitting the DOM-JEM prior from the statistical model led to a lower correlation to estimated exposure levels from the original model (alternative I: R _p 5 0.65).

Table 3.

Comparison of cumulative exposure levels to RCS (mg/m³-years) within the SYNERGY population based on SYN-JEM and alternative models.

			Pearson correlation		Cumulative exposure level(mg/m3-years RCS)
			All subjects(n 5 37 959)	Exposed(n 5 9423)	Mean	Median (differenceto SYN-JEM)	10th–90th percentile
SYN-JEM			1.00	1.00	2.86	1.76	0.30–6.43
Alternative models
A	No region-specific estimate		0.80	0.67	3.35	2.17 (+23%)	0.41–7.93
B	No requirement ≥5 measurements		0.99	0.99	2.81	1.69 (–4%)	0.29–6.34
C	Common mean for job code without data		0.98	0.97	2.84	1.76 (+0%)	0.29–6.38
D	No job-specific estimate		0.91	0.86	2.20	1.46 (–17%)	0.26–4.58
E	No region- or job-specific estimate		0.74	0.58	2.52	1.83 (+4%)	0.41–5.80
F	Time trend: exposure ceiling before 1950		0.99	0.98	3.60	2.27 (+29%)	0.39–8.11
G	Time trend: exposure ceiling before 1970		0.99	0.99	2.02	1.18 (–33%)	0.19–4.54
H	Time trend: peak at 1960		0.99	0.98	2.32	1.31 (–26%)	0.18–5.34
I	No DOM-JEM prior in statistical modela		0.65	0.63	2.59	1.41 (–20%)	0.28–6.18

a10 938 subjects were considered exposed with alternative I.

Differences in median cumulative exposure levels were small for changes in job-specific estimates (alternative B: –4%; alternative C: 0%), but larger when no job-specific estimate was applied (alternative D: –17%). Alternative time trend extrapolations gave highly correlated exposure levels (R _p ≥ 0.98), but showed larger differences in absolute cumulative exposure. When assuming an exposure ceiling before 1950 (alternative F), the median exposure level was 29% higher than when based on SYN-JEM (with an exposure ceiling before 1960). For alternative G, with an exposure ceiling before 1970, the difference was –33%. When an exposure peak at 1960 and declining exposure levels before 1960 were assumed (alternative H), the median exposure level was 26% lower. Predictions without the DOM-JEM prior (alternative I) resulted in a 20% lower median cumulative exposure level. Results for average exposure levels were essentially similar.

DISCUSSION

RCS exposure levels derived with SYN-JEM and alternative models were overall highly correlated(R _p > 0.90), although somewhat lower when omitting the region-specific estimate (R _p 5 0.80) or DOM-JEM prior in the model (R _p 5 0.65). The high correlations indicate that the relative ranking of the jobs/subjects did not depend heavily on the decisions made in the exposure assessment process. The assigned RCS exposure estimates therefore seem robust. However, the absolute levels did differ by the different strategies and, as a result, risk estimates expressed as risk per unit of exposure could change.

Exposure intensity levels derived from the underlying statistical model were consistent with the scientific literature (Peters et al., 2011b). Also the cumulative exposure levels calculated with SYN-JEM for exposed subjects (median 1.76 mg/m³-years; range 0.01–60) were in line with levels reported in literature. For example, in the German porcelain industry (1938–2006), cumulative RCS exposure levels ranged from 0.006 to 40.6 mg/m³-years with a median of 0.56 mg/m³-years (Birk et al., 2010). For US granite workers, a median cumulative exposure level of 0.72 mg/m³-years was reported based on data collected from 1924 to 1977 (Attfield and Costello, 2004). Median cumulative exposure levels to RCS in studies pooled by Steenland et al. (2001) ranged from 0.13 mg/m³-years (US industrial sand) to 11.4 mg/m³-years(Australian gold mine) (Steenland et al., 2001). Thus, the order of magnitude of cumulative exposure levels derived with SYN-JEM appears to be realistic.

Exposure assessment is an important component of epidemiological studies. Low-quality exposure assessment may cause misclassification of exposure and consequently mask risks. Sensitivity analyses can provide insight into the derivation of the exposure estimates to be used for epidemiological analyses and the need for publication of the applied strategies and evaluations has been emphasized (Stewart, 1999; Heederik and Attfield, 2000). Nevertheless, there are only few studies that have performed such detailed analyses. In the recently published Diesel Exhaust in Miners Study, the exposure assessment process was extensively evaluated (Stewart et al., 2010; Vermeulen et al., 2010). This was done for assumptions made in the development of exposure groups, modelling of historical trends, identification of agents used for estimations, and selection of the arithmetic mean as the exposure metric. Correlations of R _p ≥ 0.87were reported for alternative historical trends (Stewart et al., 2010). This is comparable to the high correlations we observed when applying alternative time trend models. Similar correlations (between 0.64 and 0.97) were also found in a study comparing six JEMs with different grouping strategies for magnetic field exposure (Kromhout et al., 1997). The biggest difference in cumulative exposure levels we observed was a change of 33%. The changes in cumulative exposure levels in the magnetic field exposure study were somewhat larger, ranging from –53 to +43% compared with the JEM used in original analysis (Kromhout et al., 1997).

The largest changes in assigned exposure levels were related to the application of the time trend. Although we covered a wide time frame of 50 years with RCS measurements (Peters et al., 2012), we had no information on exposure levels before 1960. In such case–control studies as ours, where retrospective exposure assessment back to 1920 is needed, assumptions on exposure levels for this time period are inevitable. It is therefore important that such assumptions and their influence on exposure levels are made explicit to enable appropriate interpretation of the obtained quantitative risk estimates.

The most influential factors in the design of SYN-JEM on relative ranking of exposure appeared to be the effect of region/country and the DOM-JEM prior. Only few studies paid attention to regional differences in exposure levels (de Vocht et al., 2006; Liu et al., 2011). Although it is likely that occupational exposures might differ between countries, it is unknown to what level. As we have shown with current sensitivity analyses, the assignment of the region-specific estimates from the model did affect the resulting exposure levels. Therefore, investigation of regional differences in occupational exposure levels needs more attention.

Risk estimates in epidemiological analyses, however, will be mostly influenced by subjects shifting from the exposed group to the non-exposed and vice versa. Due to the use of the DOM-JEM as a prior, this classification was fixed. Changes to the region-specific estimates may result in lower or higher exposure levels, but subjects will not be classified differently as exposed or non-exposed. The region-specific estimate will therefore only be of minor influence on the overall risk estimate for silica exposure, but may affect the shape of the exposure–response relation. Only in alternative I—the model without the DOM-JEM prior—could subjects be classified differently. Here, 11% of the subjects shifted from the non-exposed to the exposed group. This shift was caused by jobs assumed to be non-exposed, but for which there were five or more measurements available. Seven percentage of the total population shifted from exposed to non-exposed with alternative I due to jobs without measurement data. Thanks to the relatively good data coverage for RCS exposure, the model without prior was still highly correlated to SYN-JEM. However, when fewer measurement data would be available—a likely scenario for other agents—omitting the prior might be problematic since too many exposed subjects will be misclassified as non-exposed because of missing data. Application of the DOM-JEM as a prior might prevent this type of misclassification, as it allows assigning an estimate for low or high exposure, even in the absence of measurement data.

Cumulative exposure levels are the product of exposure intensity and duration of jobs. Since the number of years worked does not change in the different models, correlations depend potentially to a large extent on the range in exposure duration. In a comparison of the performance of different exposure assessment approaches in a study among asphalt workers, cumulative exposure levels to bitumen fume appeared to be highly correlated to exposure duration (R _sp 5 0.83). Average exposure levels were much less of influence, as the correlation with cumulative exposure levels was only 0.07 (Burstyn et al., 2003). The correlations with cumulative exposure in our study were 0.46 and 0.56 for average exposure level and duration, respectively. In our exposure assessment method, it appears that cumulative exposure levels were almost equally driven by intensity of exposure and duration of exposure.

In conclusion, exposure estimates derived with SYN-JEM appeared to be plausible compared with levels reported in the scientific literature. Results show that the choices made during the development of SYN-JEM regarding the application of estimates from the statistical model did not critically change cumulative exposure levels. Therefore, SYN-JEM appeared to be a robust exposure assessment method for occupational RCS exposure. SYN-JEM will enable estimation of lifetime exposure to RCS for individual subjects in the SYNERGY population and further investigation of the association between RCS exposure and lung cancer risk. The influence of the different model specifications on future risk analyses needs further exploration, particularly for region-specific estimates.

FUNDING

German Social Accident Insurance (DGUV); International Agency for Research on Cancer (IARC); Institute for Prevention and Occupational Medicine of the DGUV; Institute of the Ruhr- University Bochum (IPA); Institute for Risk Assessment Sciences at Utrecht University (IRAS); Canadian Inst Health Research and Guzzo-SRC Chair in Environment and Cancer; Canadian Cancer Society and the Occupational Cancer Research Ctr of Ontario; French agency of health security (ANSES); French National Research Agency (ANR); Organization for the Research on Cancer (ARC); National Institute of Cancer (INCA); Fondation for Medical Research (FRM); French Institute for Public Health Surveillance (InVS); French Ministry of work, solidarity and public function (DGT); Fondation de France; German Federal Ministry of Education, Science, Research, and Technology; the Ministry of Labour and Social Affairs; EC’s INCO-COPERNICUS programme; Polish State Committee for Scient. Research; Roy Castle Foundation; Intramural Research Program of the National Institutes of Health (NIH), National Cancer Institute (NCI), Division of Cancer Epidemiology and Genetics (DCEG); Intramural Research Program, Lombardy Region; Istituto Nazionale per l'Assicurazione contro gli Infortuni sul Lavoro (INAIL); European Union Nuclear Fission Safety Program; Italian Ass. Cancer Research; Region Piedmont; Compagnia di San Paolo; Dutch Ministry of Health, Welfare & Sports; National Institute of Public Health & the Environment; Europe Against Cancer Progr; Instituto Universitario de Oncologia; Universidad de Oviedo Asturias; the Fondo de Investigaciones Sanitaria; FIS; Ciber de Epidemiologia y Salud Publica (CIBERESP); the Swedish Council for Work Life Research;Swedish EPA.