A novel approach to cancer staging: application to esophageal cancer

Abstract

A novel 3-step random forests methodology involving survival data (survival forests), ordinal data (multiclass forests), and continuous data (regression forests) is introduced for cancer staging. The methodology is illustrated for esophageal cancer using worldwide esophageal cancer collaboration data involving 4627 patients.

1. INTRODUCTION

Cancer staging describes anatomic extent or severity of individual cancers related to their life history (survival) (National Cancer Institute, 2004, American Joint Committee on Cancer, 2002). Cancer cases are broadly classified into stage groupings reflecting survival. These groupings are intended to facilitate communication among physicians and between physician and patient, direct treatment recommendation, permit prognostician, and facilitate research based on a standard nomenclature.

The goal of cancer staging is to group cancer characteristics for which patient survival differs between groups (distinctiveness), consistently decreases with increasing stage group (monotonicity), and is similar within a group (homogeneity) (American Joint Committee on Cancer, 2002). Cancer is staged into 5 groups. By convention, Stage 0 is generally reserved for noninvasive cancer and Stage IV for cancer that has spread to distant sites. This leaves only Stages I, II, and III as targets for data-driven stage groupings. Ideally, these stage groupings should be equally spaced in survival.

Staging of cancer poses challenges to statistical methodology. Satisfying the simultaneous requirements that stage groupings be distinctive, monotonic, and homogeneous in survival is difficult, especially when the data analysis involves additional cancer characteristics beyond the classic ones describing anatomic extent of the cancer. Matters are often further complicated because the relationship between regression variables and survival can be complex, involving nonlinear effects as well as multiway interactions of variables. Discovering such relationships, while conforming to the requirements of staging, is challenging and requires sophisticated methodology.

In this paper, we focus on staging for esophageal cancer. Currently, staging of esophageal cancer is based solely on anatomic extent of disease using an orderly, progressive grouping of TNM cancer classifications (Table 1). TNM stands for 3 anatomic features of esophageal cancer: measured depth of tumor (cancer) invasion into the esophageal wall and adjacent tissues (T), presence of cancer metastases to regional lymph nodes (cancer-positive nodes) along the esophagus (N), and presence of cancer metastases to distant sites (M). There are 5 subclassifications of T, 2 of N (absence N0 or presence N1 of cancer-positive nodes), and 2 of M (absence M0 or presence M1 of distant metastases). See Figure 1(a) and Table 1.

Table 1.

Current American Joint Committee on Cancer TNM classifications and stage groupings of esophageal cancer (American Joint Committee on Cancer, 2002), slightly modified for clarity

TNM classifications
Primary tumor (T)
TX	Primary tumor cannot be assessed
Tis	Carcinoma in situ (noninvasive cancer)
T1	Tumor invades mucosa (T1a) or submucosa (T1b)
T2	Tumor invades muscularis propria
T3	Tumor invades adventitia
T4	Tumor invades adjacent structures
Regional lymph nodes (N)
NX	Regional lymph nodes cannot be assessed
N0	No regional lymph node metastasis
N1	Regional lymph node metastasis (cancer-positive lymph nodes)
Distant metastasis (M)
MX	Distant metastasis cannot be assessed
M0	No distant metastasis
M1	Distant metastasis (M1a†, M1b‡)
NonTNM cancer characteristics
Histopathologic type	Squamous cell carcinoma, adenocarcinoma
Histologic grade (G)
GX	Grade cannot be assessed
G1	Well differentiated
G2	Moderately differentiated
G3	Poorly differentiated
G4	Undifferentiated
Stage groupings
0	Tis	N0	M0
I	T1	N0	M0
IIA	T2–3	N0	M0
IIB	T1–2	N1	M0
III	T3	N1	M0
	T4	Any N	M0
IV	Any T	Any N	M1
IVA	Any T	Any N	M1a
IVB	Any T	Any N	M1b

^†M1a = metastases to select nonregional lymph nodes.

^‡M1b = other distant metastases.

Fig. 1.

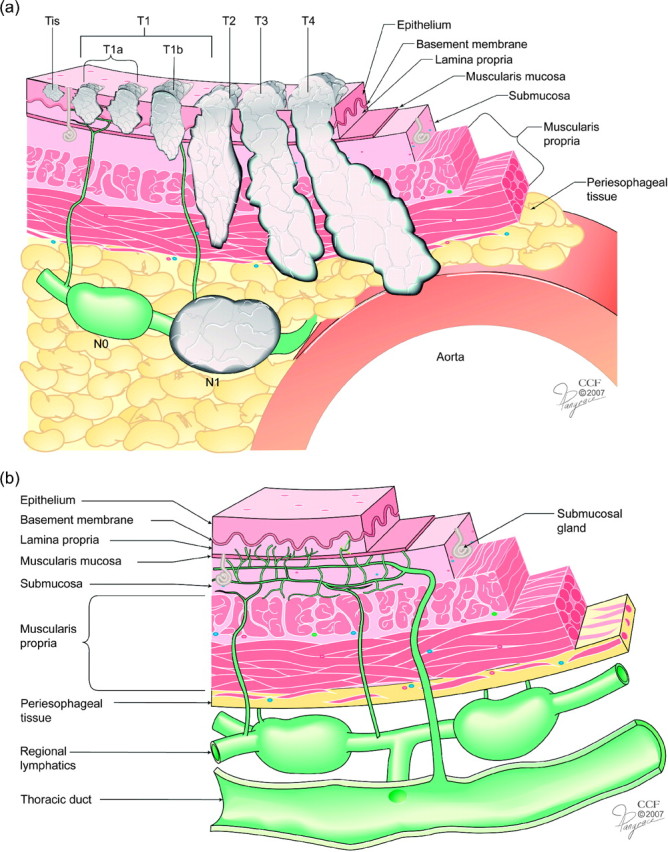
(a) Current anatomic cancer classification for esophageal cancer. Anatomic cancer classification is by depth of cancer invasion (T) and regional lymph node classification (N), defined by absence (N0) or presence (N1) of cancer-positive lymph nodes. Distant metastasis (M) not illustrated. (b) Unique lymphatic drainage of esophagus is both intramural and longitudinal, which couples T and N. There are direct connections from superficial lymphatics to regional lymphatics without a barrier effect of the muscularis propria and treacherous bypass channels directly connecting the submucosal lymphatic plexus and thoracic duct.

TNM classifications are overly simplistic, in part because they reflect the anatomic extent of cancer. Other cancer characteristics are known to affect prognosis for esophageal cancer. For T, these include location of the cancer along the length of the esophagus (Goan and others, 2007), histopathologic cell type (squamous cell carcinoma vs. adenocarcinoma [Siewert and others, 2001, Rice and others, 2007]), which differs between east and west, and histologic grade (G), a crude reflector of biologic activity (Rice and others, 2007). For N, an increasing number of cancer-positive regional lymph nodes is associated with progressively decreasing survival in a nonlinear fashion (Rice and others, 2003; Rizk and others, 2006). The unique lymphatic anatomy of the esophagus (Figure 1b) allows spread of cancer to regional lymph nodes with minimal cancer invasion, resulting in an interaction of T with N (Rice and others, 1998). These complex interactions among TNM classifications characteristics defy an orderly, progressive stage grouping from T to N to M as in current staging (Table 1). Additionally, nonlinear and complex interactions are also anticipated with inclusion of non-TNM cancer characteristics such as histopathologic cell type, location, and histologic grade.

Integrating these interrelated characteristics into 5 general cancer stage groupings (Stages 0, I–IV) posed a challenging statistical problem and was the motivation for our methodology. This resulted in an innovative statistical strategy involving a 3-step data-driven approach that includes application of random forests (RF) (Breiman, 2001) to survival data (random survival forests [RSF]), ordinal data (multiclass forests), and continuous data (regression forests). Our rationale for using RF is that it is known to be extremely adaptive to data, is able automatically to recover nonlinear effects and complex interactions among variables, and yields accurate nonparametric prediction over test data. For example, in a large experiment involving both simulated as well as real data (that included the esophagus data considered here), prediction error performance of RSF was found consistently better than competing methods (Ishwaran and others, 2008). Excellent prediction performance for multiclass and regression forests have also been shown in extensive experiments (Breiman, 2001).

By being excellent predictors, forests become powerful tools for understanding associations of prognostic factors with patient outcome and describing prognostic groups. This might seem surprising because single trees, and not forests, are often thought of as better tools for understanding data. However, even with very large sample sizes (as here), single trees yield limited insight into associations, unless these associations are relatively simple. By being poor predictors, trees are by extension also poor prognosticators.

2. WORLDWIDE ESOPHAGEAL CANCER COLLABORATION DATA

Esophageal cancer is uncommon, and prevalence of characteristics varies around the world. We base our analysis on de-identified data obtained from 13 esophageal cancer treatment centers in Asia (Fourth Hospital of Hebei Medical University Shijiazhuang, Hebei, China; University of Hong Kong, Hong Kong, China), Europe (Helsinki University Central Hospital, Helsinki, Finland; Universitair Ziekenhuizen Leuven, Leuven, Belgium), and North America (Cleveland Clinic, Cleveland, OH; Fox Chase Cancer Center, Philadelphia, PA; Indiana University Medical Center, Indianapolis, IN; M.D. Anderson Cancer Center, Houston, TX; Mayo Clinic, Rochester, MN; Medical University of South Carolina, Charleston, SC; Memorial Sloan-Kettering Cancer Center, New York, NY; Oregon Health & Science University, Portland, OR; University of Rochester, Rochester, NY).

These worldwide esophageal cancer colloboration data comprised 7885 patients who had surgery for esophageal cancer. Of these, 4627 had surgery alone with no added chemotherapy or radiotherapy, making cancer characteristics and survival data interpretable. This subset of patients (Table 2) was used for our analysis. The primary outcome used in the analysis was time to death, measured from date of surgery. Follow-up averaged 3.3 ± 3.3 years, median 2.1 years. Of the 4627 patients, 2561 died by end of follow-up (less than 5% of these survived beyond 6.7 years); the remainder were right censored.

Table 2.

Current TNM classifications and non-TNM cancer and patient characteristics

Characteristics	n†	Mean ± standard deviation or frequency (%)
Age (years)	4625	62 ± 11
Male	4626	3562 (77)
Race	3587
White		2339 (65)
Asian		1168 (33)
Other		80 (2)
East (part of world)	4627	1168 (25)
Location (location of cancer)	4344
Upper third (1)		177 (4)
Middle third (2)		1172 (27)
Lower third (3)		2995 (69)
Length (cancer length cm)	2229	3.3 ± 2.5
T	4609
is (0)		335 (7)
1‡		1040 (23)
2		755 (16)
3		2329 (51)
4		150 (3)
N	4616
0		2584 (56)
1		2032 (44)
M	4564
0		4208 (92)
1§		356 (8)
G (histologic grade)	3816
G1 (1)		1228 (32)
G2 (2)		1257 (33)
G3 (3)		1324 (35)
G4 (4)		7 (0)
Cell (histopathologic cell type)	4595
Squamous cell carcinoma (0)		1841 (40)
Adenocarcinoma (1)		2754 (60)
Nodes sampled (number of nodes sampled)	3921	16.8 ± 16.1
Nodes (number of cancer-positive lymph nodes)	4507
0		2584 (57)
1		547 (12)
> 1		1376 (31)
R (resection margins)	4123
R0¶ (0)		3572 (87)
R1‖ (1)		434 (11)
R2# (2)		117 (3)

^†Nonmissing cases.

^‡T1a and T1b.

^§M1a and M1b.

^¶R0 = cancer free.

^‖R1 = microscopic.

^#R2 = macroscopic

3. RF APPROACH TO STAGE GROUPING

3.1. Predicted survival outcome (RSF)

RSF methodology (Ishwaran and others, 2008) was employed to calculate an ensemble survival curve and predicted outcome for each patient. A total of 45 variables was used in the analysis. These included TNM classifications, number of lymph nodes removed at surgery, number of cancer-positive lymph nodes, other non-TNM cancer characteristics, patient demographics, and additional variables to adjust for country, institution, year of surgery, and residual cancer at resection margin. These latter variables, as well as patient demographics, although not used in the eventual stage groupings, were necessary to ensure that the predicted outcome properly accounted for risk factors and other variables that may affect survival.

A forest of 1000 random survival trees was used in the analysis. Tree nodes were split using log-rank splitting by finding the variable maximizing the log-rank test over all its possible splits (Ishwaran and others, 2008). Computations were implemented using the randomSurvivalForest R-package under its default settings (Ishwaran and Kogalur, 2008b). Missing data for variables were imputed using forest imputation (Ishwaran and others, 2008). However, because of anatomic dependence among TNM classifications, TNM missing data were not imputed, although few of these data were missing (0.3%, 0.2%, and 1% for T, N, and M, respectively). Indicator functions identifying whether a variable had missing data were assessed for predictiveness; subsequent analyses found no such effect. Therefore, we concluded that TNM missing data played no crucial role in our cancer stage groupings.

In growing the forest, trees were grown to full size under the constraint that the minimum number of deaths in a node was equal to 3 (the default setting for the software used). This yielded trees that on average had 278 terminal nodes. Growing deep trees is a general principle of random forest methodology (Breiman, 2001). Doing so yields “strong trees,” that is ones with low bias. To ensure low variance, trees must also be distinct, that is they must be made as decorrelated as possible. This was accomplished by introducing 2 forms of randomization into the tree growing process (Breiman, 2001). First, trees were grown using independent bootstrap sampled data. Second, when growing a tree, each node in the tree used a randomly selected subset of variables to split on (the number of variables equaled the square root of the total number of variables available for the node).

On average, each bootstrap survival tree was constructed from 63.2% of the data (bagged data). The remaining 36.7% of the data, referred to as out-of-bag (OOB) data, and the bagged tree, were used to construct an OOB survival curve for each patient. This was done by dropping OOB data down a bootstrapped survival tree and extracting the Kaplan–Meier survival function for a patient (the survival function determined by the patient's terminal node membership [Ishwaran and others, 2008]). On average, this yielded approximately 367 OOB survival curves for each patient; these were averaged to yield an OOB ensemble survival curve for each patient. Likewise, an OOB ensemble cumulative hazard function (CHF) was calculated for each patient. Summing this ensemble CHF over the observed survival times yielded the predicted outcome 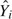, referred to as (OOB) ensemble mortality. Ensemble mortality is a key quantity estimated in an RSF analysis and provides a summary value indicating mortality for a patient. For each patient i, it represents expected number of deaths if all patients were similar to i. Ensemble mortality has been shown to be a highly accurate predictor of survival (Ishwaran and others, 2008).

Patients were ordered by increasing OOB ensemble mortality and stratified into 25 subgroups in equal percentile increments of 4%. The averaged OOB ensemble survival curve was calculated for each group (thin gray lines, Figure 2). Note that there is inherent monotonicity among curves, although this is not necessarily a property of ensemble mortality. Patient survival decreases as OOB ensemble mortality increases (top to bottom), and although curves have different shapes, they are nonoverlapping.

Fig. 2.

Thin gray lines are RSF OOB ensemble survival curves stratified by OOB ensemble mortality (stratification in equal percentile increments of 4%). Superimposed thick black curves represent one possible template grouping for developing a stage grouping.

Distinctiveness and monotonicity of survival present an opportunity for stage grouping. The thick black curves superimposed on Figure 2, labeled a through j, represent one possible template. These were selected because they were reasonably well spaced (distinctive) at 5 years (5-year survival is an important end point for clinical management of esophageal cancer). Other proposed templates are equally possible. Indeed, in the following section, we explore the use of random template groupings.

The 45 variables used in the analysis were ordered by variable importance (VIMP), which measures change in prediction error on test data when a given variable is removed (Breiman, 2001). VIMP was calculated by permuting a variable (noising it up) over OOB data. Using the modified OOB data, a new OOB ensemble CHF was calculated for each patient and this was used to calculate OOB ensemble mortality 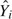^*. VIMP equaled the difference in prediction error using 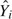^* (the noised up predictor) compared to 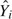(Ishwaran and others, 2008). A positive value for VIMP indicated that prediction error increased under noising up and that the variable was predictive. See Breiman (2001), Ishwaran and others (2008), Ishwaran (2007), Nason and others (2004), Lunetta and others (2004), Bureau and others (2005) and Diaz-Uriarte and Alvarez de Andres (2006) for background and further illustrations of VIMP.

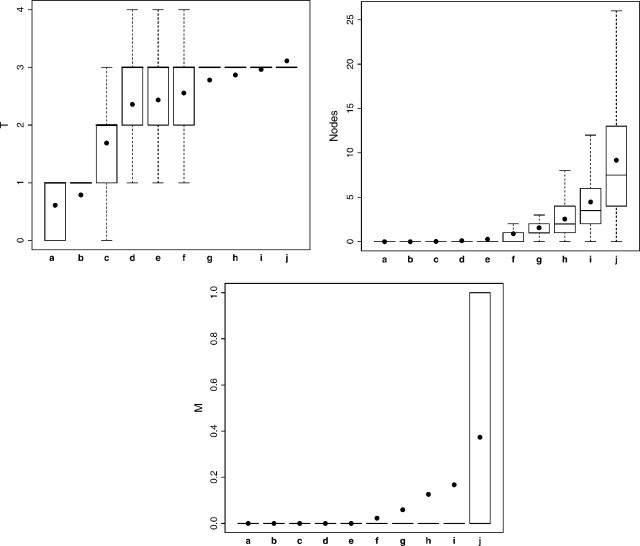
The most predictive variable by VIMP was T classification. Figure 3 shows how T, from Tis (0) through T4, varies as a function of the proposed template (see Table 2 for the coding used for T). Template group increases (survival decreases) as depth of cancer invasion (T) increases; however, there is a mixture of T classifications in early template groupings.

Fig. 3.

Box plots for variables T, Nodes, and M used in an RSF analysis stratified by template grouping of Figure 2. Box includes 25th and 75th percentiles; horizontal line within box is median; dots within box are means.

The next most predictive variable was number of cancer-positive lymph nodes (Nodes). Figure 3 shows there is an increase in the number as the template group increases. Groupings a through e have no cancer-positive lymph nodes. M classification, eighth in order of VIMP, is also included in Figure 3. Its value is zero for a through e. Thus, a pattern emerges for grouping cancers: early cancers primarily consist of N0M0 cancers, whereas for more advanced cancers, there is M involvement coupled with a substantial number of cancer-positive lymph nodes (N1M1).

The top 10 variables and their VIMPs were T (1.85%), Nodes (0.92%), Age (0.39%), Nodes Sampled (0.23%), Location (0.17%), year of surgery (0.12%), G (0.10%), M (0.09%), N (0.08%), and R (0.08%) (see Table 2 for a description of these variables).

3.2. Monotonicity and distinctiveness of survival (multiclass random forests: RF-C)

The proposed template in Figure 2 demonstrated monotonicity and distinctiveness of survival based upon a predetermined stratification. To demonstrate that these properties held in general, we used multiclass RF methodology (RF-C). In this approach, we randomly selected a template grouping. To do so, we ordered patients by increasing OOB ensemble mortality and then randomly selecting 9 OOB ensemble mortality values for defining group boundaries. Each template grouping yielded 10 groups which were labeled a through j, in order of group boundary values (i.e. group labels increased alphabetically as mortality increased). These group labels were used as the outcome in a multiclass RF analysis.

A total of 1000 random template groupings was used. A RF-C regression was used for each random template grouping using the same 45 regression variables as in the RSF analysis. Each RF-C regression was comprised of a forest of 1000 random bootstrap classification trees, with majority voting used for group label prediction. Trees were grown to full size using Gini index splitting, and when growing a tree, each node used a randomly selected subset of variables to split on (size equal to the square root of the total number of variables available at the node). Computations were implemented using the randomForest R-package (Liaw and Wiener, 2007).

Recall that monotonicity of patients’ survival curves is not necessarily a property of OOB ensemble mortality. If survival curves were not monotonic and distinctive when ordered by OOB ensemble mortality, then random template groupings a through j would not be ordinal, and group labels would be predicted poorly.

To test this was not the case, the averaged confusion matrix from the 1000 forest analyses was calculated (Table 3). Misclassification error appeared substantial for almost all groups. However, looking across rows of the matrix (the group labels from a random template), we found this primarily due to misclassification across immediate adjacent predicted groups but not distant predicted groups. Importantly, this pattern demonstrated that OOB ensemble mortality grouped patients into distinctive groups, thus demonstrating distinctiveness of survival. Further, because this pattern held consistently across all rows, this demonstrated monotonicity of survival.

Table 3.

Averaged confusion matrix using RF-C. Rows correspond to random template grouping and columns to OOB RF-predicted groupings. Entries in the confusion matrix are the averaged frequencies (rounded to the nearest integer) from 1000 RF-C regressions. The last column in the matrix is the averaged misclassification error

Random template group	RF-predicted group label										Misclass error
	a	b	c	d	e	f	g	h	i	j
a	444	34	9	2	0	0	0	0	0	0	0.226
b	43	381	39	10	3	1	0	0	0	0	0.460
c	13	45	355	41	13	4	1	0	0	0	0.508
d	3	17	51	323	41	15	6	2	0	0	0.554
e	1	6	19	48	295	44	16	5	1	0	0.596
f	0	2	6	18	47	314	46	16	6	1	0.596
g	0	1	3	7	17	46	331	45	16	4	0.578
h	0	0	1	2	6	17	48	311	46	15	0.574
i	0	0	0	1	2	5	15	45	356	45	0.513
j	0	0	0	0	0	1	3	11	40	399	0.301

3.3. Cancer stage groupings based on homogeneity (regression forests: RF-R)

To obtain a more detailed understanding into how patient and cancer characteristics varied by survival, we used RF regression (RF-R). For each random template grouping, we applied a separate RF-R regression to patients within each of its 10 groups. OOB ensemble mortality, 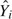, was used for the outcome and for regression variables we used the same 45 variables as before. Each of the 10 regression analyses yielded VIMP for a given variable for a given random template group. To standardize VIMP, we divided it by the variance of OOB ensemble mortality within each template group and then averaged these values over the 1000 random template groupings (Table 4). Standardized VIMP in each column represents predictiveness of a variable within a group. A standardized VIMP of zero signifies a variable nonpredictive of survival within a group and thus identifies a variable that can define a homogeneous stage group. On the other hand, a nonzero standardized VIMP signifies a variable that should be used to subdivide a stage group into more homogeneous subgroups. Each RF-R analysis used 1000 random bootstrap regression trees, grown using mean squared error splitting. Trees were grown to full size under the constraint that the minimum size of a terminal node was 5, and when growing a tree, each node of a tree used a randomly selected subset of variables to split on (size equal to one-third of the number of variables available for splitting). Computations were implemented using the randomForest R-package (Liaw and Wiener, 2007).

Table 4.

Standardized VIMP from RF-R analysis of OOB ensemble mortality stratified by random template grouping. Values averaged over 1000 random template groupings. Only variables used for cancer stage grouping (American Joint Committee on Cancer, 2002) are shown

Cancer characteristics	Random template group
	a	b	c	d	e	f	g	h	i	j
T	0.138	0.171	0.188	0.144	0.112	0.079	0.050	0.032	0.026	0.018
Nodes	0.000	0.010	0.023	0.050	0.087	0.123	0.159	0.182	0.221	0.215
N	0.001	0.014	0.025	0.049	0.074	0.100	0.089	0.043	0.028	0.006
G	0.133	0.083	0.073	0.059	0.053	0.043	0.032	0.026	0.025	0.040
Cell	0.032	0.067	0.055	0.030	0.020	0.015	0.013	0.013	0.017	0.024
Location	0.017	0.052	0.067	0.065	0.048	0.030	0.018	0.016	0.012	0.009
M	0.000	0.000	0.001	0.001	0.003	0.006	0.010	0.013	0.027	0.136

Early and intermediate stage groupings.

For template groups a through d, standardized VIMP was small to near zero for number of cancer-positive nodes (Nodes), N, and M. This indicated homogeneity and that early stage groupings require that N0 and M0 be part of their definition. The large standardized VIMP for T classification (T) in groups a through f showed T to be informative for early stage groupings (in general, a standardized VIMP for a variable greater than 5% was found to be predictive; in some instances identifying survival differences of up to 10%). The large standardized VIMP for histopathologic cell type (Cell) in groups b and c identified distinctive survival between patients with squamous cell carcinoma and adenocarcinoma. Also interesting was the large standardized VIMP for histologic grade (G) in groups a through e and the large standardized VIMP for location of the cancer along the esophagus (Location) in groups b through d. Finally, large standardized VIMP was seen for number of cancer-positive lymph nodes for groups e through j, showing that this variable plays a key role in advanced stage groupings.

To investigate these findings more closely, we used a conditional plot (coplot) with survival plotted against age (which spreads data points), conditioned on G and Cell, and with T indicated by color (Figure 4). Plotted on the vertical axis was predicted 5-year survival obtained by extracting the value of survival at 5 years from a patients’ OOB ensemble survival curve. Data were restricted to N0M0 cancers in order to focus on early and intermediate stage groupings. The figure revealed an interesting Location–G–Cell–T interrelationship. Most pronounced was the effect of histopathologic cell type. This made it apparent that squamous cell carcinomas and adenocarcinomas should be stage grouped separately. However, to avoid excessive detail that unnecessarily complicates description of our methodology, we hereafter focus only on the stage grouping for the adenocarcinomas. Stage groupings for both types of esophageal cancers using our methodology are reported elsewhere (American Joint Committee on Cancer, 2009; Rice and others, 2009).

Fig. 4.

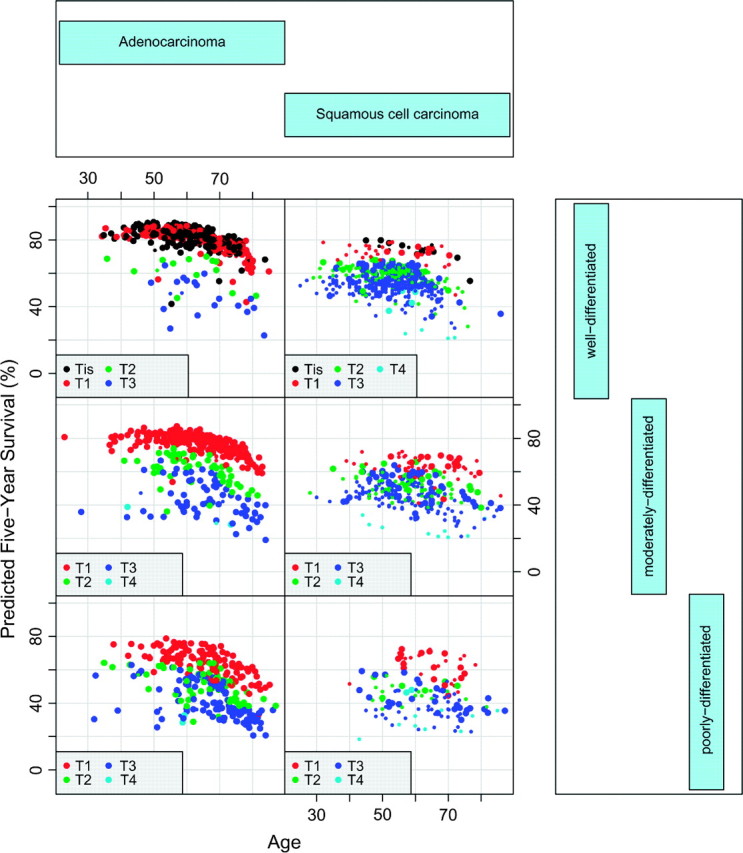
Coplot of 5-year predicted survival against age, conditioned by histopathologic cell type and G (upper, middle, and lower rows are G1, G2, and G3–4, respectively). Data restricted to N0M0 cancers. Large colored points indicate tumors whose primary cancer location is the lower thoracic esophagus.

Considering the adenocarcinoma data (left-hand side of Figure 4), we observed a strong G-effect. Patients with T1N0M0G1–2 cancers had better survival than those with T1N0M0G3 cancers. Additionally, patients with T2N0M0G1–2 cancers had better survival than those with T2N0M0G3 cancers and had comparable survival to those with T1N0M0G3 cancers. Interestingly, G did not affect survival for T3–4N0M0 cancers.

Table 5 presents another way to interpret the data. Reported on the left-hand side is frequency of adenocarcinoma N0M0 cancers stratified by predicted 5-year survival in increments of 5%. For example, the first 3 rows report cancer frequencies for survival between 80% and 90% and show that these cancers are almost exclusively Tis or T1N0M0G1–2. As survival decreases, cancers become exclusively T2–4N0M0, and finally exclusively T3–4N0M0, with survival for T4N0M0 being worse.

Table 5.

Left-hand side records frequencies for adenocarcinoma esophageal N0M0 data stratified by 5-year predicted survival (first column of table). Right-hand side are frequencies using adenocarcinoma N1M0 data. Variables NT1, NT2, NT3, and NT4, also included, are averaged number of cancer-positive lymph nodes, stratified by T1, T2, T3, and T4, respectively

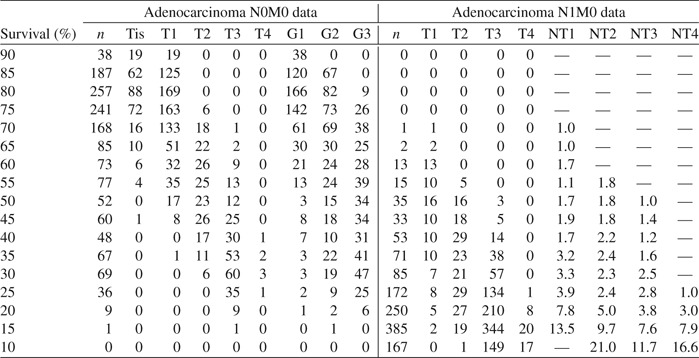Combining these results leads to the stage groupings summarized in Table 6.

Table 6.

Adenocarcinoma esophageal early and intermediate stage groupings

Stage	T	Nodes	M	G
0	is	0	0	Any
IA	1	0	0	1–2
IB	1	0	0	3
	2	0	0	1–2
IIA	2	0	0	3
IIB	3	0	0	Any
IIIA	4	0	0	Any

Intermediate and late stage groupings.

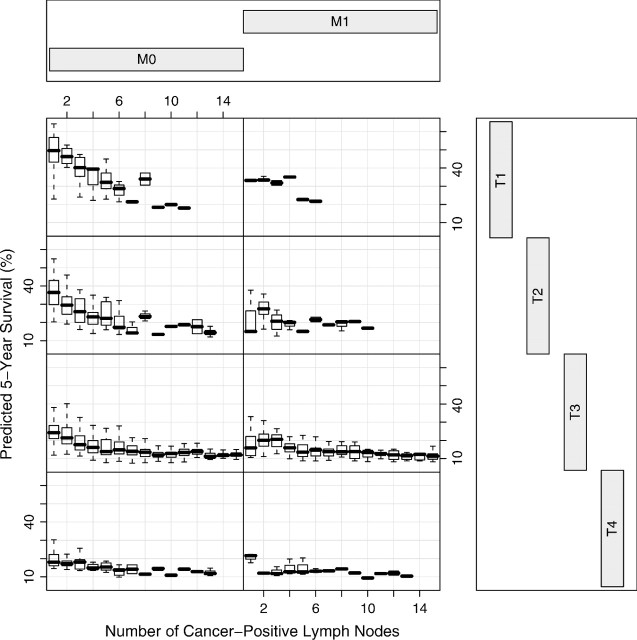
Next we investigated N1M0–1 cancers. Figure 5 presents box plots of 5-year predicted survival against number of cancer-positive lymph nodes, conditioned by T and M. It was constructed using only the adenocarcinoma data. Figure 5 reveals that cancer-positive lymph nodes are noninformative of survival for M1 cancer (right-hand side). In contrast, number of cancer-positive nodes has an important nonlinear relationship to survival for M0 cancers (left-hand side). This relationship also depends strongly on T classification.

Fig. 5.

Box plots of 5-year predicted survival against number of cancer-positive lymph nodes, conditioned by T and M for adenocarcinoma esophageal data. Number of positive lymph nodes is truncated at 15 to improve visualization.

Using Figure 5, and the right-hand side of Table 5, we filled out the remainder of Table 6. We followed convention and placed all M1 patients (any T any N) in Stage IV. The remaining N1M0 patients were placed in Stages II and III, with Stage III subdivided into IIIA, IIIB, IIIC, and IIID. Table 7 and Figure 6 present our data-driven stage grouping.

Table 7.

Data-driven adenocarcinoma esophageal stage groupings

Stage	T	Nodes	M	G
0	is	0	0	Any
IA	1	0	0	1–2
IB	1	0	0	3
	2	0	0	1–2
IIA	2	0	0	3
	1	1–2	0	Any
IIB	3	0	0	Any
IIIA	1	3–5	0	Any
	2	1–2	0	Any
	4	0	0	Any
IIIB	1	6 +	0	Any
	2	3–5	0	Any
	3	1–2	0	Any
IIIC	2	6 +	0	Any
	3	3–5	0	Any
	4	1–5	0	Any
IIID	3–4	6 +	0	Any
IV	Any	Any	1	Any

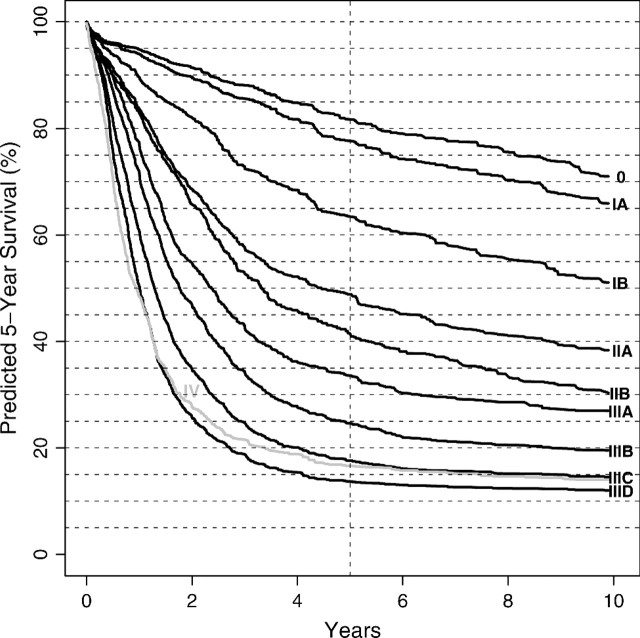
Fig. 6.

RSF ensemble survival curves for adenocarcinoma esophageal data-driven stage groupings.

Verifying homogeneity of survival within stage groupings.

To assess homogeneity of survival for our stage groupings (Table 7), we used an RF-R analysis. As before, we used OOB ensemble mortality 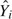for the outcome variable, but for regressors, we used T, Nodes, N, G, and M. These are the subset of variables that uniquely define our stage groups. One RF-R analysis was used for each stage group (1000 trees were used). For each analysis, the OOB error rate (mean square error [MSE]) was standardized by the variance of OOB mortality within that group. This is a measure of survival homogeneity. If regressors are noninformative, as they should be if stage groupings are homogeneous, then the OOB error rate will be high, and consequently homogeneity will be large. A value of 100% represents perfect homogeneity. On the other hand, a value of 0% indicates a stage grouping where survival can be predicted perfectly using regressor variables (because MSE is zero). A value of 0% indicates complete departure from homogeneity.

Homogeneity values for Stages 0, IA, IB, IIA, IIB, IIIA, IIIB, IIIC, IIID, and IV were 100.0%, 99.9%, 96.1%, 100.0%, 100.0%, 88.5%, 96.8%, 90.7%, 78.8%, and 71.1%, respectively. Excepting Stage IV (where we found a T effect; we discuss issues regarding Stage IV in 4), homogeneity was observed to be excellent, with some groups achieving near or perfect homogeneity (note that Stage 0 has 100% homogeneity by definition).

4. DISCUSSION

4.1. Importance of stage grouping

For many cancers, multiple treatment options exist that range from simple, to highly toxic, to palliative care. In the middle range (generally Stage IB, II, and IIIA for esophageal cancer), removing cancer surgically is presently the most efficacious therapy. For early stage cancers (Stage 0 and IA), tissue ablation at esophagoscopy is a treatment option. For locally advanced cancers (IIIB, IIIC, IIID), surgery alone is inadequate and generally requires toxic chemotherapy and radiation and possibly surgery. For Stage IV, palliative therapy is all that can be offered. The benefit of this data-driven staging system is that it facilitates these decisions. This standard nomenclature allows assessment of new treatment modalities in comparison with standard ones. Importantly, it provides a means for accurate prognostician and communication.

4.2. Complex interplay between variables

Orderly progression of TNM characteristics in the current esophageal cancer stage groupings (Table 1) assumed that each variable was additive (non-interrelated) and all cancers within the group behaved similarly. It is now widely documented that TNM characteristics of esophageal cancer are strongly interrelated. It has been difficult with conventional multivariable techniques to capture the interplay among these characteristics (high-order interactions) (Rice and others, 2003), and this is addressed by our novel methodology. Our approach confirms this complex interplay and provides a simple and biologically plausible stage grouping involving TNM as well as non-TNM cancer characteristics. Our analysis identified a strong histopathologic cell type effect, so much so that the 2 cell types can be separately staged (American Joint Committee on Cancer, 2009; Rice and others, 2009). Focusing on the adenocarcinomas, we found histologic grade in combination with T to be highly predictive of survival in early stage groupings (N0M0 data). In contrast, advanced stage groupings are determined exclusively by T, N, and M classification. For N1M0 cancers, T classification interplays with number of cancer-positive lymph nodes. Generally, the more cancer-positive lymph nodes, the poorer the survival.

4.3. The three principles of cancer staging

Importantly, our results comply with the 3 established principles of cancer staging. The criteria of survival being distinct and monotonically decreasing with increasing stage grouping are clearly evident from Figure 6 which presents the RSF ensemble survival curves for our stage grouping (Table 7). Only Stage IV, comprising M1 cancers (any T any N), deviates from these criteria. The explanation for this apparent contradiction is surgical bias: patients with M1 cancers are not referred for surgery; M1 cancer generally is an unanticipated surgical finding in an otherwise early stage cancer. Thus, we believe that this is an artifact of the data and not a limitation of our methodology. Monotonicity and distinctiveness of the proposed stage grouping are not unexpected. Recall that these properties were confirmed in the RF-C analysis that explored random template groupings (Table 3).

The third property of staging, homogeneity of survival within stage group, is also implicit in our approach. A RF-R analysis of OOB ensemble mortality within stage group was specifically used to promote homogeneity. Variables found to be predictive within a group (Table 4) were considered for subdividing stage groupings into further homogeneous subgroups. In Section 3.3, we formally assessed homogeneity and found that most achieved values over 90%. In some cases homogeneity was 100%.

4.4. Generalizability and forests as a tool for prognostication

The use of out-of-bagging and emphasis on prediction as a measure of performance, as opposed to goodness of fit and other measures based on fitted data, ensures generalizability of our method. It is superior to stage groupings based on intuition (American Joint Committee on Cancer, 2002; Skinner and others, 1986, Dickson and others, 2001), univariable analysis (Ellis and others, 1997), and parametric and semiparametric multivariable analyses (Rice and others, 2003; Korst and others, 1998; Balch and others, 2001). Further, the approach of combining trees resolves the well-known instability of single trees grown using recursive partitioning (Ruczinski and others, 2004; Breiman, 1996). Instability is a consequence of high prediction error and involves a trade-off between bias and variance. Growing a shallow tree reduces variance, improves interpretation, but introduces bias and inflates prediction error. Growing a richer tree reduces bias but can inflate variance. Determining the optimal size of the tree involves balancing these quantities. However, even with very large sample sizes, a tree grown to optimal depth will have relatively poor prediction performance if the underlying model is complex. To improve prediction error, and ultimately prognostician, a forest of trees is needed. Forests have a uniform approximating property that allows them to recover highly complex functions. For example, Ishwaran and Kogalur (2008a) showed that an RSF could uniformly approximate the underlying true survival function. This is a property not possessed by single survival trees.

We emphasize that standard methods, especially those based on parametric modeling, should be used with caution when the goal is prognostication. Unless one knows which interactions and nonlinear effects are to be included in the model, interpretation of the data will be limited—and inference possibly misleading. Even if one has reasonable insight into which variables to include in the model, inference can still suffer due to strong assumptions made by conventional methods. Consider Table 8. Listed in the table are the estimated hazard ratios for each variable and their lower and upper 95% confidence values from fitting a Cox regression to the combined adenocarcinoma and squamous cell data. The model included key main effects and interactions identified in our data-driven analysis (for clarity of presentation, and to ensure convergence of the algorithm, we only included the most influential terms). Almost all main effects are highly significant (a notable exception being histopathologic cell type), whereas, surprisingly, many of the interactions are only moderately significant (e.g. the interaction between histopathologic cell type and T). Cox regression relies on the assumption of proportional hazards, and if this assumption is not met, inference suffers. There was evidence here of departure from the assumption of proportional hazards (p-value [Grambsch and Therneau, 1994], 0.013).

Table 8.

Cox regression analysis of adenocarcinoma and squamous cell esophageal data using key variables and interactions identified by the RF data-driven analysis. Columns show hazard ratio and their lower and upper 95% confidence values for each variable

	Hazard	Lower CI	Upper CI
Cell	12.694	0.407	396.089
T1	17.461	1.036	294.329
T2	33.060	2.186	500.049
T3	48.566	3.260	723.452
T4	157.224	9.774	2529.111
G	6.841	2.709	17.275
N	2.127	1.926	2.350
Age	1.015	1.011	1.020
Location	0.814	0.738	0.898
Cell:T1	0.046	0.001	1.626
Cell:T2	0.039	0.001	1.354
Cell:T3	0.085	0.003	2.731
Cell:T4	0.042	0.001	2.865
Cell:G	0.162	0.018	1.473
T1:G	0.177	0.065	0.479
T2:G	0.175	0.068	0.449
T3:G	0.159	0.063	0.403
T4:G	0.120	0.045	0.316
Cell:T1:G	7.430	0.783	70.469
Cell:T2:G	7.484	0.799	70.094
Cell:T3:G	6.434	0.702	58.981
Cell:T4:G	8.929	0.823	96.853

CI, confidence interval.

4.5. Other applications

Finally, although we focused on esophageal cancer in illustrating our methodology, this approach can be used to stage other cancers. Furthermore, for any application demanding patients be grouped into a small number of distinct, monotonic, homogeneous subsets, as in cancer staging, this 3-part RF methodology, or some variant of it, is applicable.

FUNDING

Daniel and Karen Lee Endowed Chair in Thoracic Surgery and the Kenneth Gee and Paula Shaw, PhD, Chair in Heart Research at Cleveland Clinic.